NIEPEWNOŚĆ POMIARU

Zgodnie z zaleceniami międzynarodowymi

„niepewność

pomiaru”

w nowym i rozszerzonym znaczeniu jest

podstawowym pojęciem, które należy wiązać z wynikiem
pomiaru.
 
Pojęcie to w dużym zakresie zastępuje stosowane
dotychczas pojęcie

„błędu pomiaru”.

 
Najogólniej niepewność pomiaru wiąże się z określoną
wartością

rozrzutu wartości

, które można przypisać

wielkości mierzonej, o błędzie zaś mówi się w przypadku
wyraźnego odstępstwa (różnicy) wyniku pomiaru od
wartości rzeczywistej lub poprawnej.
 

Błąd pomiaru

można i należy wyeliminować. To, co

pozostaje po wyeliminowaniu błędu pomiaru, jest

niepewnością pomiaru

.

1. Podstawowe pojęcia

1.1. Wynik pomiaru

– wartość przypisana wielkości

mierzonej uzyskana drogą pomiaru, wraz z niepewnością tej
wartości. Wynik pomiaru bez oszacowanej niepewności
pomiaru nazywany jest wynikiem pomiaru surowym i nie ma
większego znaczenia w dalszych jego zastosowaniach.
 

1.2. Niepewność pomiaru

– parametr związany z wynikiem

pomiaru, charakteryzujący rozrzut wartości, które można w
uzasadniony sposób przypisać mierzonej wielkości.
Niepewność pomiaru może być wyrażona za pomocą
odchylenia standardowego, połową szerokości przedziału
odpowiadającego określonemu poziomowi ufności lub
wyznaczona na podstawie zakładanego rozkładu
prawdopodobieństwa opartego na posiadanych informacjach
lub doświadczeniu.

1. Podstawowe pojęcia

1.3.

Niepewność standardowa

–

niepewność wyniku pomiaru
wyrażona przez odchylenie
standardowe.

1.4. Szacowanie typu A
niepewności

– metoda

szacowania niepewności za
pomocą analizy statystycznej
serii pojedynczych wyników.

15. Szacowanie typu B
niepewności

– metoda

szacowania niepewności za
pomocą metod innych niż analiza
statystyczna serii pojedynczych
wyników.

1. Podstawowe pojęcia

1.6.

Złożona

niepewność

standardowa

–

niepewność standardowa wyniku pomiaru
otrzymanego na podstawie pomiaru kilku
wielkości.

1.7.

Niepewność

rozszerzona

–

wielkość

określająca przedzwartości wokół wyniku
pomiaru, taki, że można oczekiwać, iż
obejmuje on dużą część rozkładu wartości,
które można w określony sposób przypisać
wielkości mierzonej. Niepewność rozszerzona
bywa traktowana jako poziom ufności lub
niepewność całkowita.

1.8. Współczynnik pokrycia k

– współczynnik

liczbowy zastosowany jako mnożnik złożonej
niepewności standardowej w celu otrzymania
niepewności rozszerzonej. Przyjmuje się
zwykle dla rozkładu normalnego i rozkładu
Studenta wartości z przedziału od 2 do 3. Dla
rozkładów innych współczynnik pokrycia
obliczany jest na podstawie zależności
wynikających z tych rozkładów.

1. Podstawowe pojęcia

1.9. Błąd pomiaru

– różnica między wynikiem

pomiaru a wartością rzeczywistą mierzonej
wielkości. Ponieważ wartość rzeczywista nie
może być określona, w praktyce stosuje się
wartość poprawną.
 

1.10.Błąd

przypadkowy

–

różnica

między

wynikiem pomiaru a średnią z nieskończonej
liczby pomiarów tej samej wielkości mierzonej,
wykonanych

w

warunkach

powtarzalności.

Ponieważ można wykonać tylko skończoną liczbę
pomiarów,

można

więc

dokonać

jedynie

oszacowania błędu przypadkowego.
 

1.11.Błąd systematyczny

– różnica między

średnią z nieskończonej liczby pomiarów
wykonanych w warunkach powtarzalności, a
wartością rzeczywistą wielkości mierzonej. Błąd
systematyczny i jego przyczyny nie mogą być
znane dokładnie, jednak w wielu przypadkach
możliwe jest znaczne jego wyeliminowanie.

1. Podstawowe pojęcia

1.12.

Poziom

ufności,

„poziom

ufności”

–

prawdopodobieństwo z jakim wartość rzeczywista
wielkości mierzonej mieści się w przedziale wokół
wyniku pomiaru określonym niepewnością pomiaru.

Terminy „confidence level” i „level of confidence”.
Polskim odpowiednikiem pierwszego z nich jest
termin poziom ufności. Ponieważ nie ma przyjętego
powszechnie odpowiednika dla drugiego z nich, a
ma on podobne choć nieco inne znaczenie, stąd
stosujemy dla niego termin powstały z
odpowiednika pierwszego przez dodanie
cudzysłowu, czyli „poziom ufności”. Można mówić o
poziomie ufności wtedy gdy u(x

i

) jest otrzymane

tylko z szacowań typu A.
Analogiczne uwagi można podać odnośnie
przedziału ufności.

2. Zasady określania niepewności

pomiaru.

2.1. Szacowanie typu A niepewności standardowej.

Jeśli wykonano n pojedynczych pomiarów X

i,k

wielkości

wejściowej

X

i

,

o

oszacowaniu

x

i

równającemu się X

i

, to niepewność standardowa

tego oszacowania wynosi:
 
 
gdzie jest odchyleniem średnim kwadratowym
średniej obliczonym wg wzoru:
 

gdzie:
X

i,k

– jest to wynik k-tego pojedynczego pomiaru

wielkości X

i

;

- jest wartością średnią n pomiarów.

 

 

i

i

X

s

x

u



 

i

X

s

 









1

1

2

,













n

n

X

X

X

s

n

k

i

k

i

i

i

X

2.2. Szacowanie typu B niepewności

standardowej

 

2.2.1.

Jeśli

oszacowanie

x

i

jest

wzięte

z

dokumentacji producenta, świadectwa kalibracji,
literatury czy innych źródeł i jego niepewność jest
pewną wielokrotnością odchylenia standardowego,
to niepewność standardowa u(x

i

) może być

przyjęta jako równa tej podanej niepewności
podzielonej przez tą wielokrotność.

W przypadkach, kiedy można założyć, że przy
obliczaniu

przedziałów

niepewności

przyjęto

rozkład

normalny,

odchylenie

standardowe

otrzymuje się dzieląc podaną niepewność przez
odpowiedni współczynnik związany z rozkładem
normalnym.

Dla „poziomów ufności” 90%, 95%, 99% wartości
odpowiednich współczynników wynoszą 1,64; 1,96;
2,58.

2.2. Szacowanie typu B niepewności

standardowej

2.2.2. Jeśli wiadomo, że wartość wielkości
wejściowej X

i

leży w przedziale od a

-

do a

+

z

prawdopodobieństwem

100%

i

rozkład

możliwych

wartości

tej

wielkości

jest

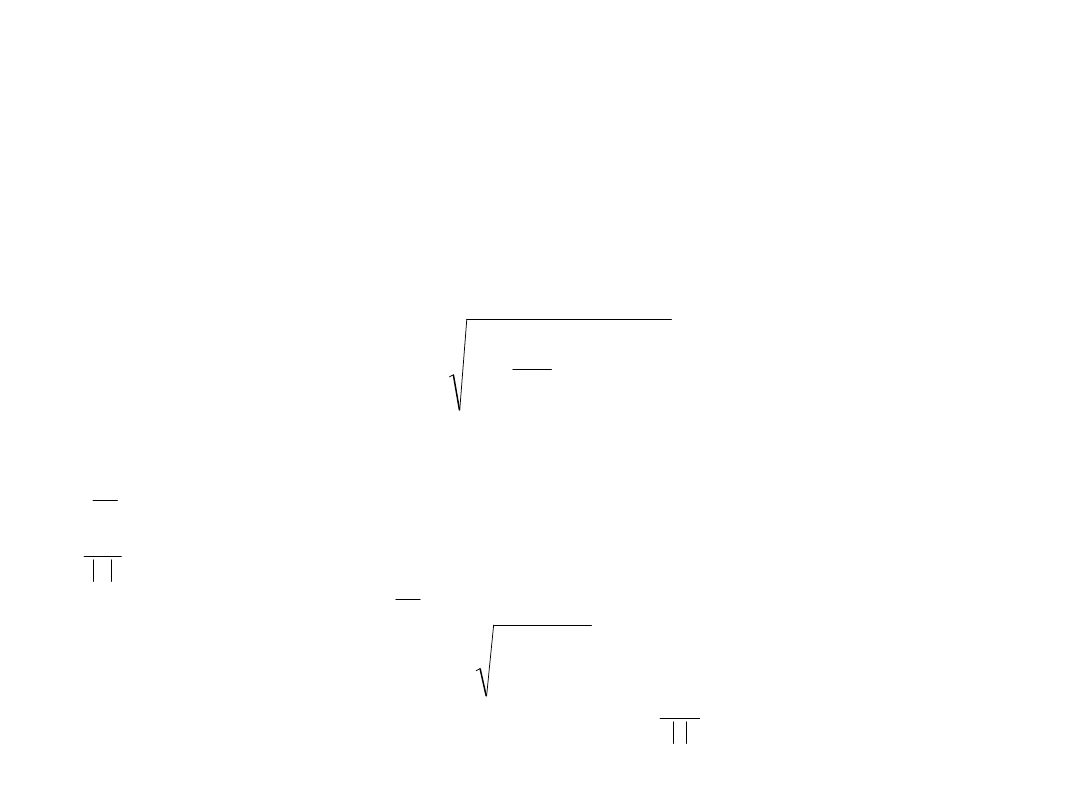
prostokątny (równomierny), to można przyjąć:

gdzie:

 

3

a

x

u

i



2









a

a

a

2.3. Określanie złożonej niepewności

standardowej.

Zakłada się, że wielkość mierzona Y jako wielkość
wyjściowa jest wyrażona przez wielkości wejściowe X

1

,

X

2

, ..., X

N

za pomocą wzoru:

 
Y = f(X

1

, X

2

, ..., X

N

)

 Niepewność standardową złożoną wielkości y będącej
oszacowaniem wartości fizycznej Y, oznaczoną u

c

(y),

oblicza się ze wzoru:
 

gdzie wielkość u(x

i

) jest niepewnością standardową

obliczoną w wyniku szacowania typu A lub szacowania typu
B,
jest pochodną cząstkową funkcji f względem x

i

.

jest względną niepewnością standardową dla x

i

.

Przyjmując oznaczenia oraz u

i

(y)=c

i

u(x

i

) można

napisać:

Względna niepewność złożona wielkości y wynosi .

 

 

























N

i

i

i

c

x

u

x

f

y

u

1

2

2

i

x

f





 

i

i

x

x

u

i

i

x

f

c







 

 







N

i

i

c

y

u

y

u

1

2

 

y

y

u

c

2.4. Określanie niepewności rozszerzonej

 

2.4.1. Określenie

złożonej niepewności

standardowej u

c

(y),

którą zaleca się podawać, gdy

ma ona być przedmiotem dalszych obliczeń, nie
zawsze jest wystarczające.
Oblicza się wtedy tzw. niepewność rozszerzoną,
którą zaleca się podawać gdy jest to wynik
końcowy i nie będzie on podlegał dalszej
„obróbce” oraz dla pewnych zastosowań w handlu,
w przemyśle, w przepisach prawnych, w ochronie
zdrowia i zapewnieniu bezpieczeństwa, gdzie jest
potrzebne podanie przedziału wartości, wewnątrz
którego z dużym prawdopodobieństwem mieści się
wartość rzeczywista wielkości.

2.4. Określanie niepewności

rozszerzonej.

2.4.2.

Niepewność rozszerzoną U

oblicza się

wg wzoru:

 
U = ku

c

(y)

 gdzie u

c

(y) jest niepewnością złożoną y,

k jest współczynnikiem pokrycia.
- dla

normalnego

rozkładu

prawdopodobieństwa i rozkładu t-Studenta
współczynnik k przyjmuje wartości z przedziału
od 2 do 3.

Wartości

odpowiadające

odpowiednim

poziomom i liczbie efektywnych stopni swobody
zebrane są w ogólnodostępnych tablicach.

-

dla

prostokątnego

rozkładu

prawdopodobieństwa współczynnik k oblicza się
z zależności:

        
 
(gdzie p jest założonym poziomem ufności).

 

3

p

p

k



3.   Zasady podawania niepewności

pomiaru.

 
3.1. Gdy jako miarę podaje się złożoną niepewność
standardową, powinno się:
-   - podać pełną definicję mierzonej wielkości;
-  -

jasno

i

jednoznacznie

podać

wartość

oszacowania y dla wielkości fizycznej Y i jego
niepewność używając tych samych jednostek;
-  jeśli zachodzi potrzeba, podać względną
niepewność standardową.

-       Zalecane są cztery sposoby zapisu u

c

(y).

3.   Zasady podawania niepewności

pomiaru

Przykłady (w których podana jest wartość masy
wzorca m):

1)   m = 100,02147g ze złożoną niepewnością
standardową u

c

= 0,00035g

2)   m = 100,02147(35)g, gdzie liczba w nawiasie
jest wartością złożonej niepewności standardowej u

c

wyrażoną w jednostkach ostatniego rzędu wartości
liczbowej wielkości mierzonej.

3)   m = 100,02147(0,00035)g, gdzie liczba w
nawiasie

jest

wartość

złożonej

niepewności

standardowej wyrażona w jednostkach podawanego
wyniku.

4)   m = (100,021470,00035)g, gdzie  niepewność

jest złożoną niepewnością standardową u

c

.

Zaleca się stosować raczej sposoby 1) - 3), a jeśli 4),
to koniecznie z objaśnieniem co oznacza liczba
stojąca za znakiem „ ”.

3.   Zasady podawania niepewności

pomiaru

3.1. Gdy jako

miarę niepewności dla y stosuje się

niepewność rozszerzoną U

, to powinno się:

-         podać definicję wielkości mierzonej;
-         podać wynik pomiaru jako Y = y  U, stosując

te same jednostki
dla y i U;
-       podać wartość u

c

oraz wartość k, zastosowaną

do obliczenia U;
jeśli potrzeba, to również względną
niepewność rozszerzoną;
- podać przybliżony „poziom ufności”.