Niepewność 

pomiaru 

uncert@gum.gov.pl

 

WWWWWWWWWWWWWWW

WYRAŻANIE

NIEPEWNOŚCI

POMIARU

PRZEWODNIK

BIPM 

Międzynarodowe Biuro Miar

IEC   

Międzynarodowa Komisja Elektrotechniczna

IFCC 

Międzynarodowa Federacja Chemii Klinicznej

ISO   

Międzynarodowa Organizacja Normalizacyjna

IUPAC 

Międzynarodowa Unia Chemii Czystej

i Stosowanej

IUPAP 

Międzynarodowa Unia Fizyki Teoretycznej

i Stosowanej

OIML 

Międzynarodowa Organizacja Metrologii

Prawnej

Główny Urząd Miar

Guide to the expression of 
uncertainty in measurement

Międzynarodowy 

dokument

wydany przez BIPM, IEC, IFCC,
ISO, IUPAC, IUPAP, OIML
w 1993 i 1995 roku

 

 

niepewność pomiaru

parametr 

związany 

z 

wynikiem 

pomiaru, 

charakteryzujący  rozrzut  wartości,  które  można  w 
uzasadniony sposób przypisać wielkości mierzonej

 

 

niepewność standardowa

niepewność  wyniku  pomiaru  wyrażona  w  formie 
odchylenia standardowego

 

i

x

u

 

złożona niepewność standardowa

niepewność standardowa wyniku pomiaru określana, gdy 
wynik  ten  jest  otrzymywany  z  wartości  pewnej  liczby 
innych  wielkości,  równa  pierwiastkowi  kwadratowemu  z 
sumy wyrazów, będących wariancjami lub kowariancjami 
tych  innych  wielkości  z  wagami  zależnymi  od  tego  jak 
wynik  pomiaru  zmienia  się  wraz  ze  zmianami  tych 
wielkości
 

 

y

u

c

 

Prawo propagacji niepewności

 

 























N

i

i

i

x

u

x

f

y

u

1

2

2

2

c





j

i

N

i

N

i

j

j

i

x

x

u

x

f

x

f

,

2

1

1

1

 



















 

 

 niepewność rozszerzona

wielkość określająca przedział wokół wyniku pomiaru, od 
którego to przedziału oczekuje się, że obejmie dużą część 
rozkładu  wartości,  które  w  uzasadniony  sposób  można 
przypisać wielkości mierzonej

U

 

 

y

u

k

U

c





k – współczynnik 
rozszerzenia

u

c

(y) – złożona niepewność standardowa

 

m = 100,02147

(35)

 g

Zapis niepewności pomiaru

m = 100,02147 g ± 

0,69 mg 

dla poziomu ufności 95 %

 

Probabilistyczny model niepewności 

pomiaru

- rachunek zmiennych 
losowych

- statystyka matematyczna

 

zmienna losowa (ciągła)

zmienna,  która  może  przyjmować  dowolną  wartość  ze 
skończonego lub nieskończonego przedziału określonego 
zbioru 

i 

z 

którą 

związany 

jest 

rozkład 

prawdopodobieństwa

 

Parametry zmiennej losowej

 









d





g



  -  wartość oczekiwana

  -  odchylenie standardowe



  











d

2

2







g

 

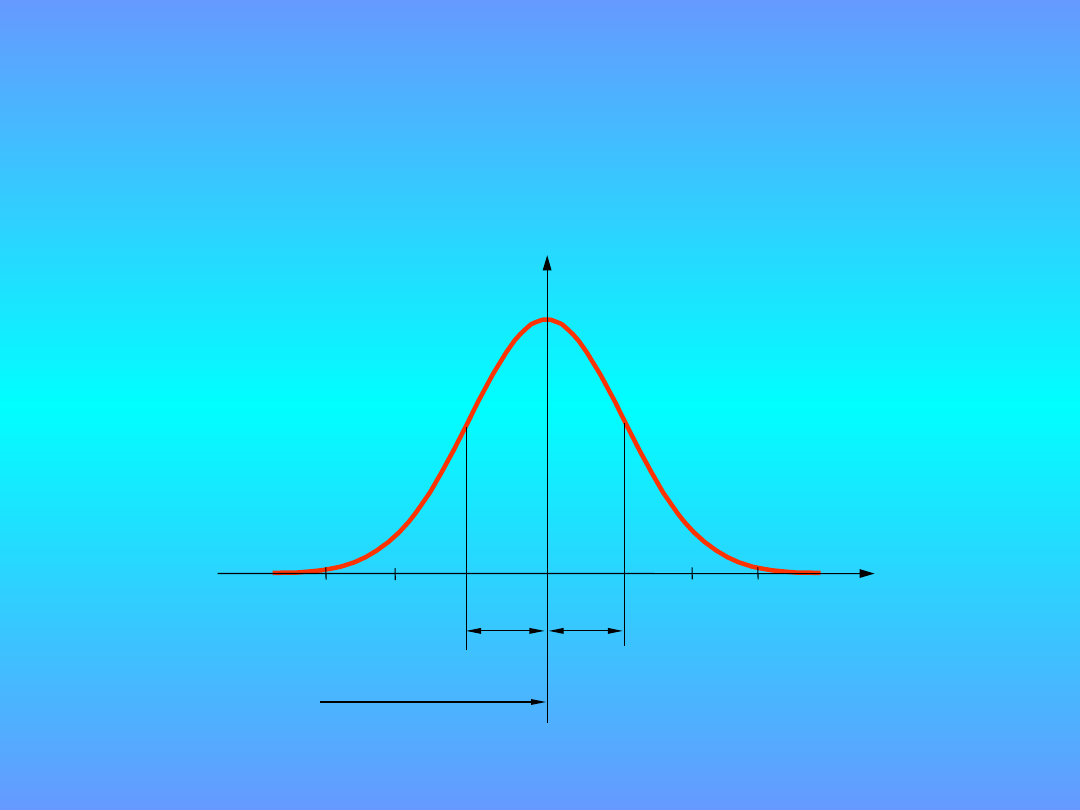
Rozkład normalny

3

2

1

-1

-2

-3







g(



)



 

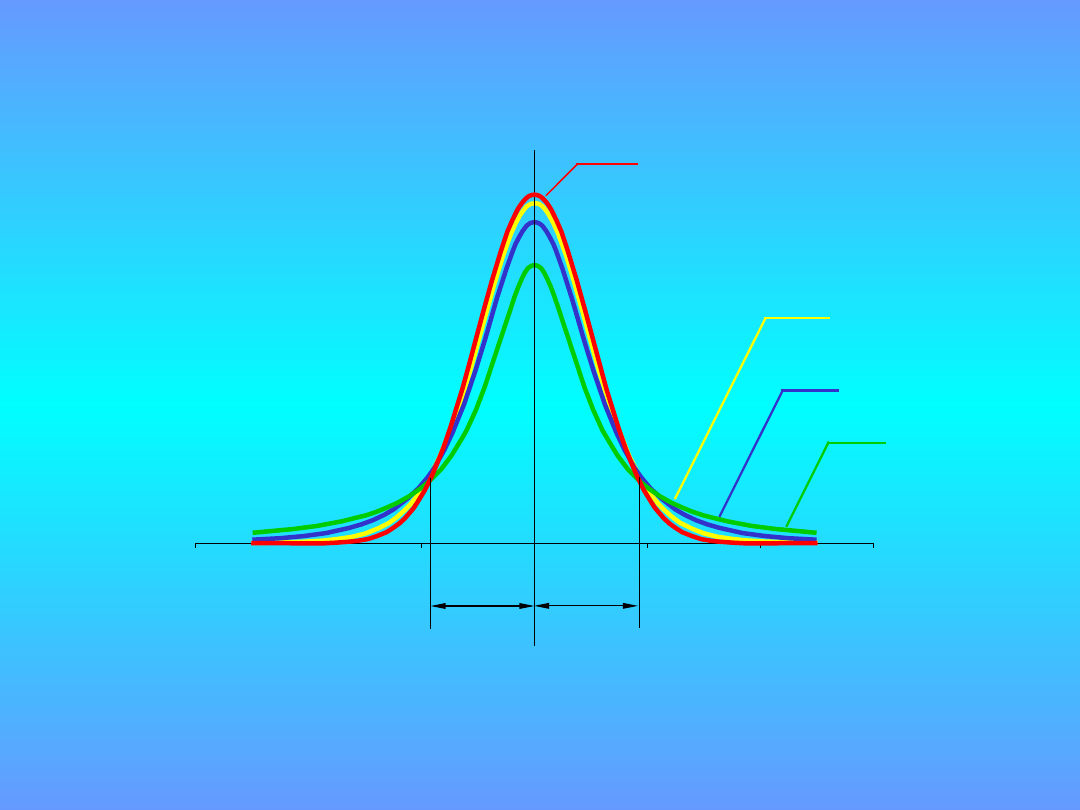
Rozkład 

Studenta

-4

-2

2

4

v = 


v = 
10

v = 
3

v= 
1

 

p

v

f

t

,



t

t

 

v 

t(v) 

v 

t(v) 

v 

t(v) 

1 

12,7062 

19 

2,0930 

44 

2,0154 

2 

4,3027 

20 

2,0860 

46 

2,0129 

3 

3,1824 

21 

2,0796 

48 

2,0106 

4 

2,7764 

22 

2,0739 

50 

2,0086 

5 

2,5706 

23 

2,0687 

55 

2,0040 

6 

2,4469 

24 

2,0639 

60 

2,0003 

7 

2,3646 

25 

2,0595 

65 

1,9971 

8 

2,3060 

26 

2,0555 

70 

1,9944 

9 

2,2622 

27 

2,0518 

80 

1,9901 

10 

2,2281 

28 

2,0484 

90 

1,9867 

11 

2,2010 

29 

2,0452 

100 

1,9840 

12 

2,1788 

30 

2,0423 

120 

1,9799 

13 

2,1604 

32 

2,0369 

150 

1,9759 

14 

2,1448 

34 

2,0322 

200 

1,9719 

15 

2,1314 

36 

2,0281 

250 

1,9695 

16 

2,1199 

38 

2,0244 

300 

1,9679 

17 

2,1098 

40 

2,0211 

400 

1,9659 

18 

2,1009 

42 

2,0181 

500 

1,9647 

 

Wartości kwantyli rozkładu Studenta dla poziomu 

ufności 95 %

 

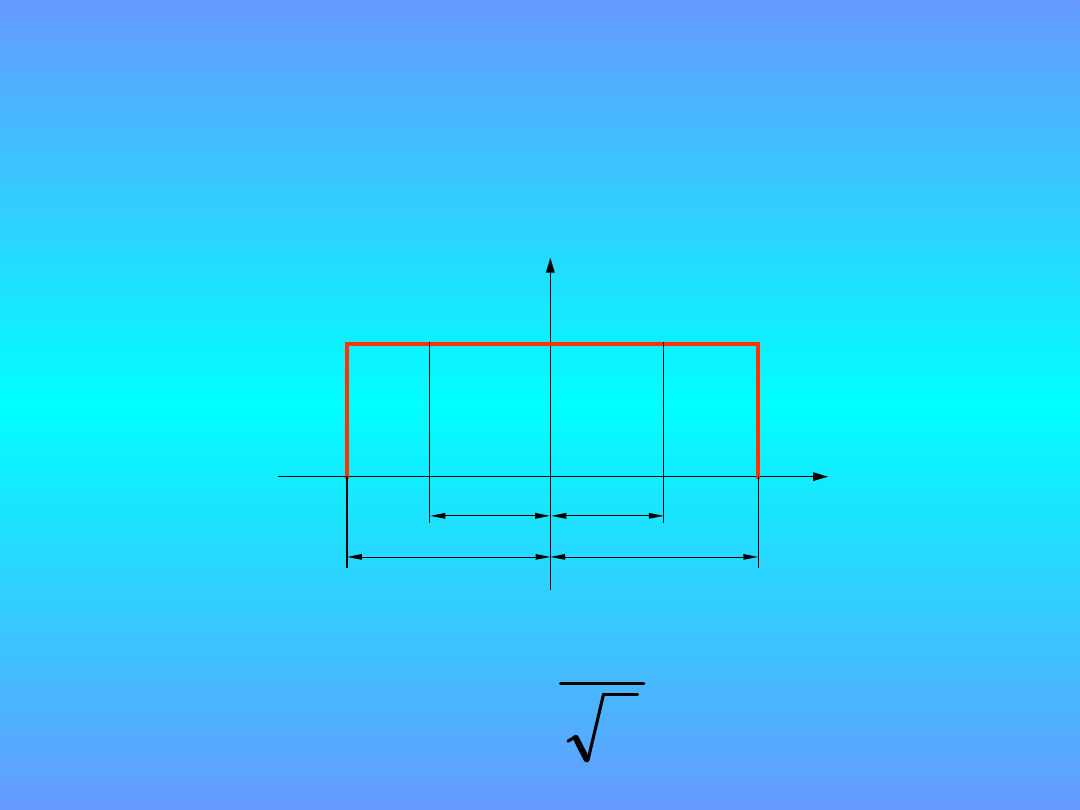
Rozkład 
prostokątny

a



a



3

a





 

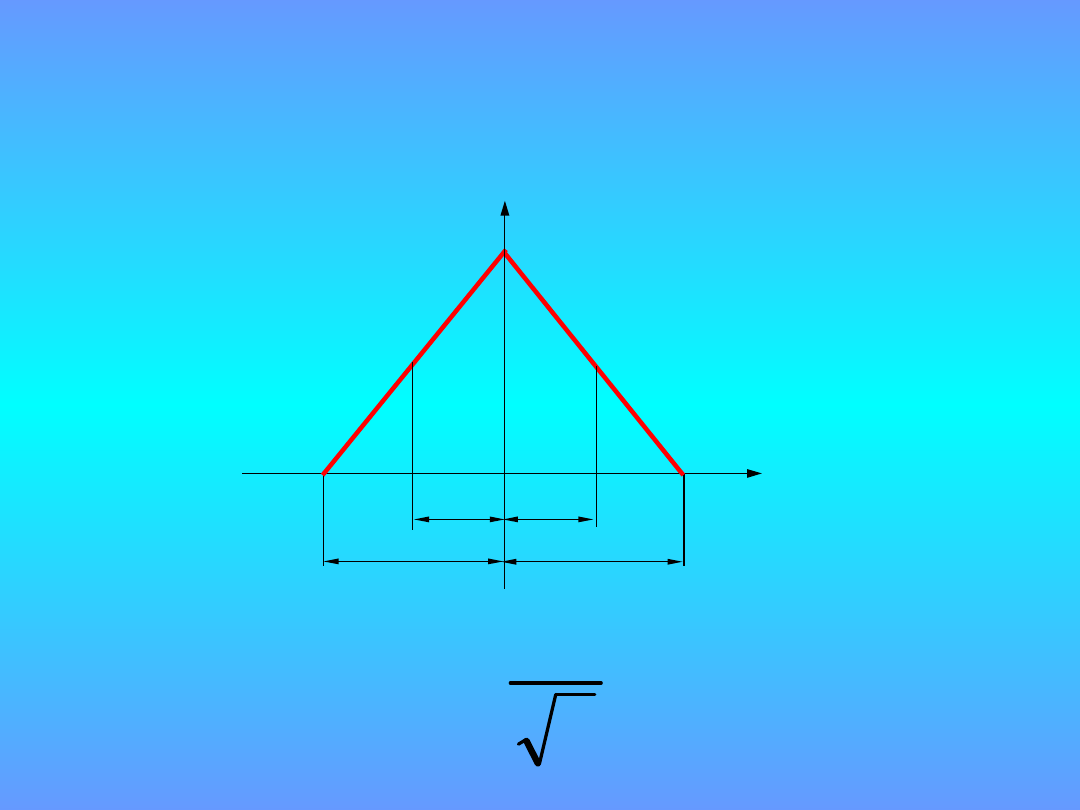
Rozkład 
trójkątny

a

a





6

a





 

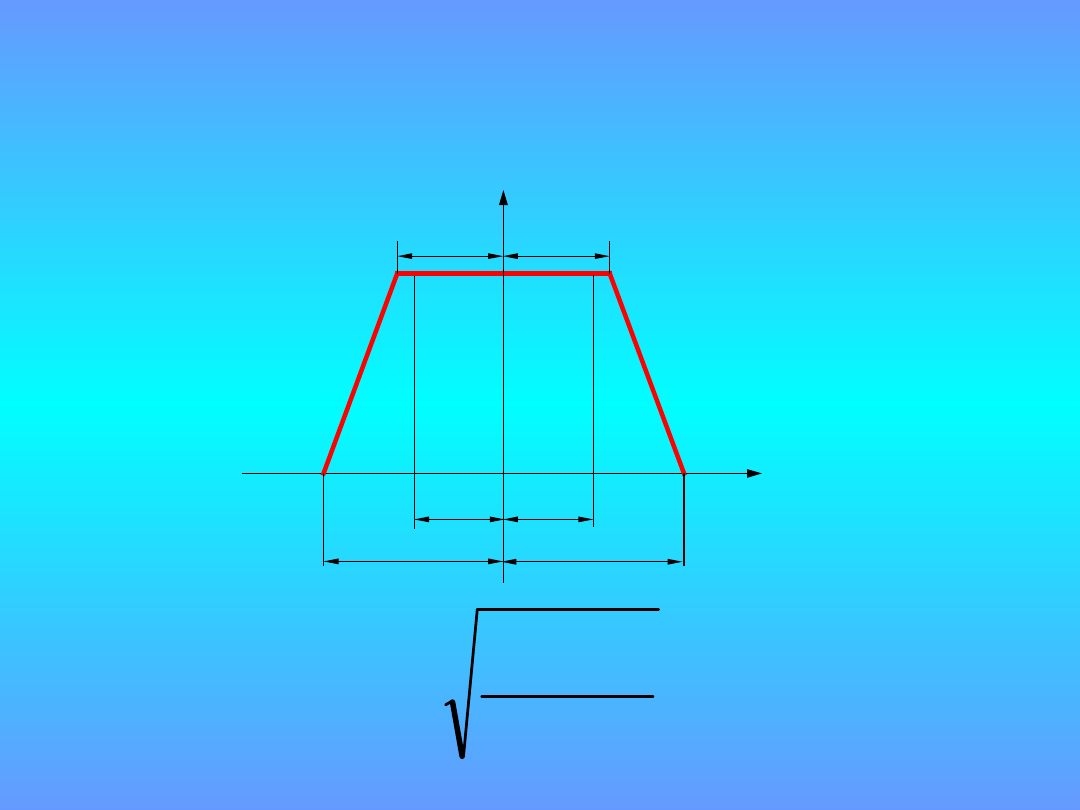
Rozkład 
trapezowy

a

a





b

b

6

2

2

b

a 





 

przedział ufności

najmniejszy przedział pomiędzy dwoma 
kwantylami rozkładu dla wartości wielkości 
mierzonej, które wyznaczają poziom ufności 95 
%

 

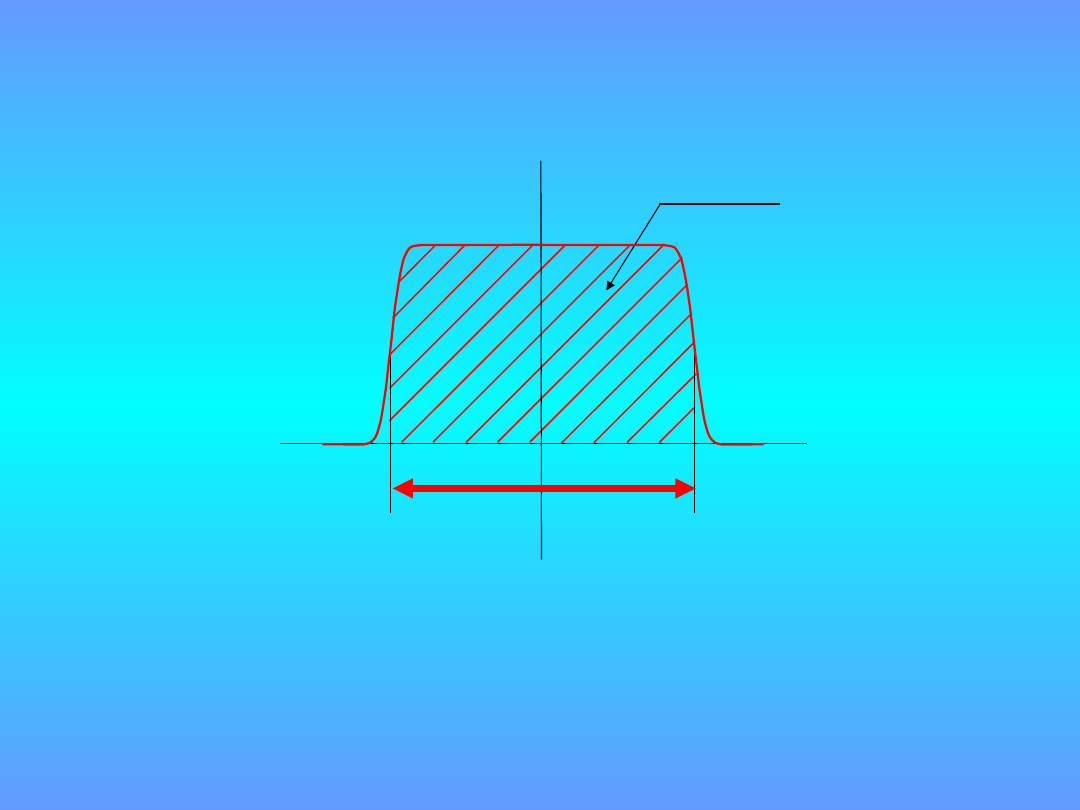
p=95 %

Przedział ufności

I

 

(y) = [ y

low 

,  y

high 

] 

y

low

y

high

 

 



1

low



G

y





p

G

y









1

high

Granice przedziału ufności

kwantyl rzędu 



kwantyl rzędu 



 + p

p =  95 
%

 

Kryteria matematyczne dla przedziału 

ufności





 

min

1

1















G

p

G

 













p

G

g

G

g













1

1

 

Wielkość wyjściowa:





N

x

x

f

y

,

,

1





Matematyczny model wielkości 

mierzonej

x

i 

 - wielkości wejściowe

 





N

Δ

N

Δ

x

x

x

x

f

y







ˆ

,

,

ˆ

1

1



i

Δ

i

i

x

x

x



 ˆ

 

 

n

N

i

i

Δ

i

i

Δ

N

i

i

x

x

y

n

x

x

y

y

y





































1

1

1

ˆ



 

2

dla

0





















n

x

x

y

n

i

Δ

i

i

Δ

N

i

i

x

x

y

y

y













1

ˆ

 

Równanie wielkości mierzonej

i

i

x

y

c







N

Δ

N

Δ

x

c

x

c

y

y











1

1

ˆ





N

x

x

f

y

ˆ

,

,

ˆ

ˆ

1





N

Δ

N

Δ

Δ

x

c

x

c

y

y

y













1

1

ˆ

 

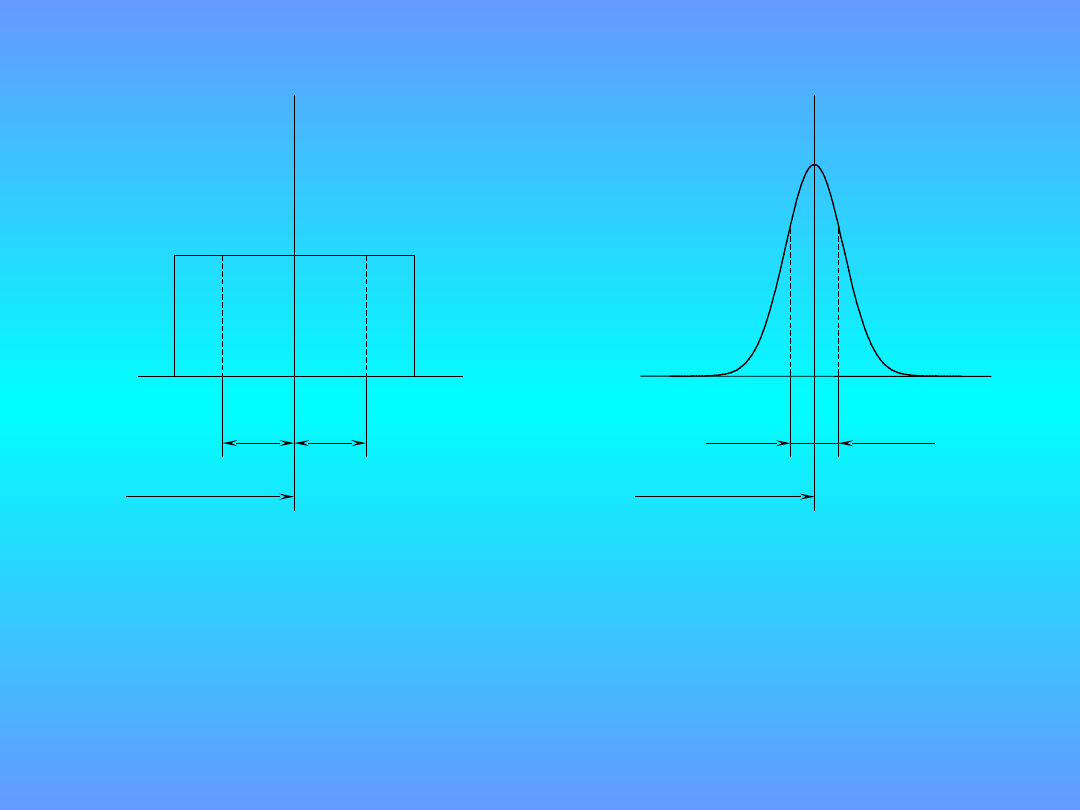
Wielkość wejściowa



i

 – wartość oczekiwana



i

 – odchylenie standardowe

g

i

(



i

) – funkcja gęstości prawdopodobieństwa

  



i

  



i



i

g

i

(



i

)

    



j

  



j



j

g

j

(



j

)

 

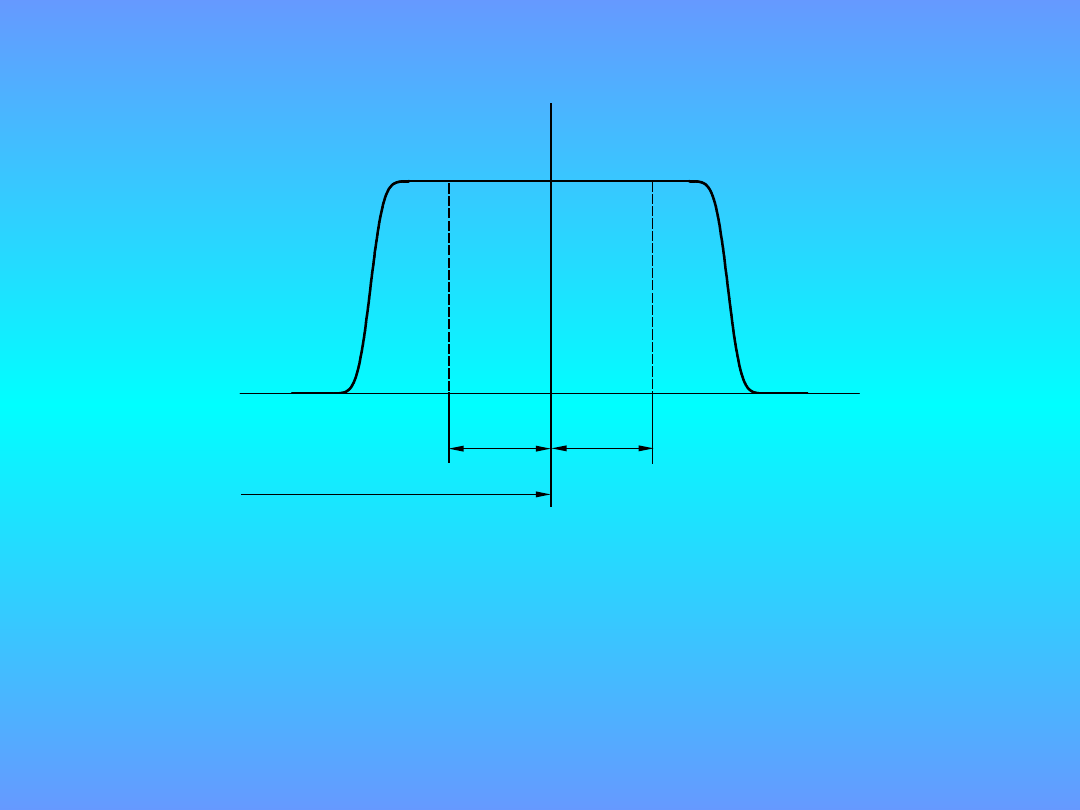
Wielkość wyjściowa





N

f







,

,

1





2

2

2

1

2

1

2

N

N

c

c















 

 

 

N

N

g

g

g















1

1

g(



)







 

Założenia modelu 

matematycznego

1. Wielkość wyjściowa funkcją liniową 

wielkości wejściowych

2. Wielkości wejściowe zmiennymi losowymi 

niezależnymi

3. Symetryczne rozkłady wielkości 

wejściowych:

     Studenta, normalny, prostokątny, 

trójkątny, trapezowy

 

y

Symetryczny przedział ufności

I(y) 

 





U

y

U

y

y

I







,

p=95 %

U

U

 

y

Niepewność rozszerzona dla poziomu 

ufności 95 %

 

%

95

d











p

g

U

y

U

y





p=95 %

U

U

g(



)



 

 

 

 

N

N

g

g

g













...

1

1

 

 

  



i

i

i

i

i

i

i

i

i

g

g

g

g













d

 

1

1

1





















Splot funkcji gęstości 

prawdopodobieństwa

 

 

 





PN

g

g



Funkcja gęstości wielkości 

wyjściowej

 

 













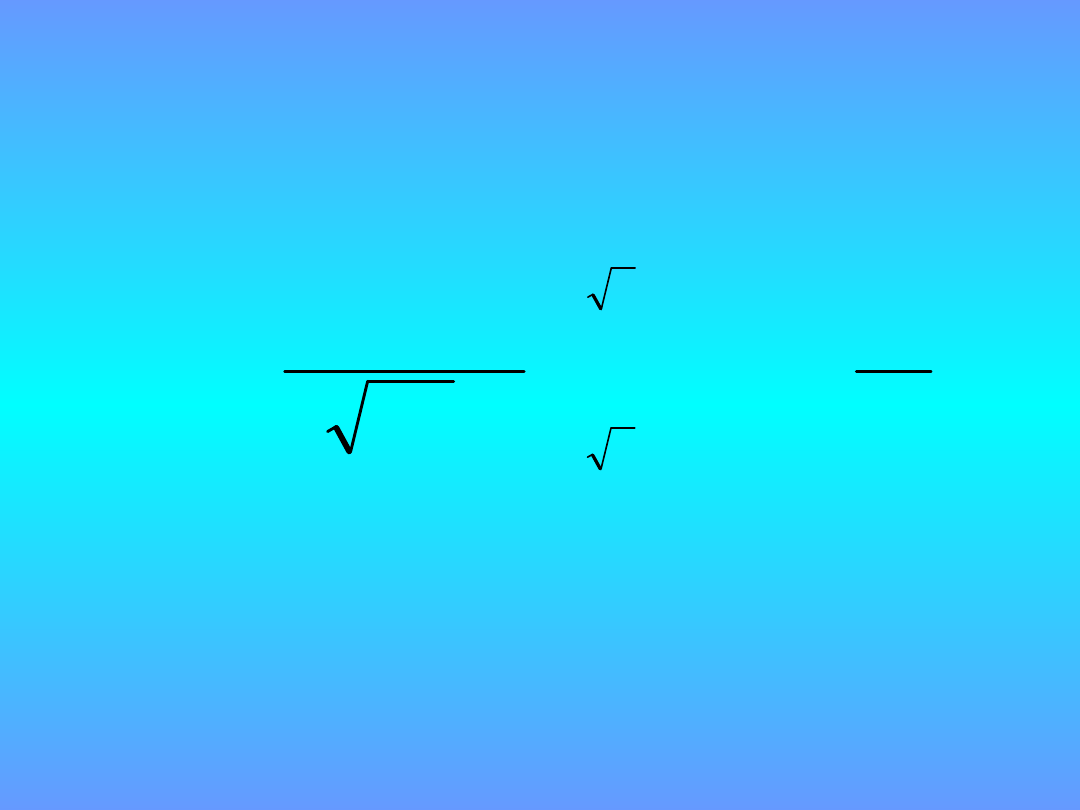
d

 

2

exp

6

2

1

3

3

2

PN





























r

r

r

g

Funkcja gęstości rozkładu typu PN

 

N

P







r

Parametr rozkładu typu PN

 

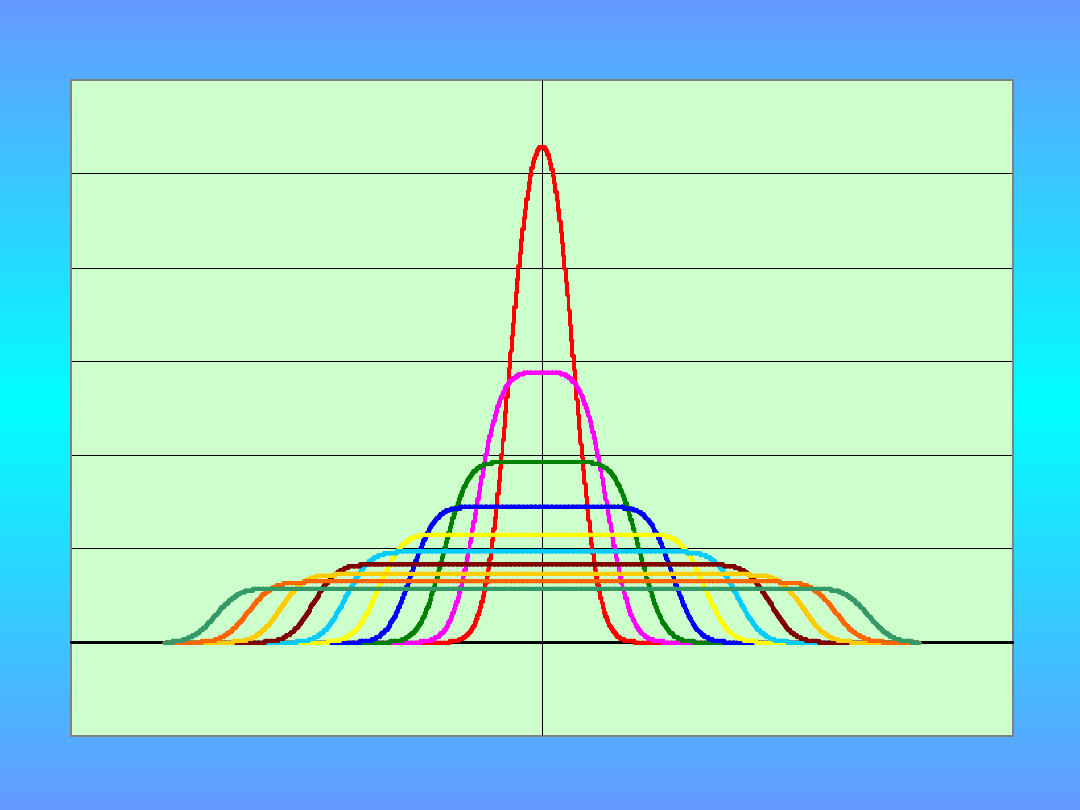
r =1

r =2

r =3

r =4

r =5

r 

=6

r 

=8

r 

=10

Rozkład typu PN

 

 

p

r

f

k

,

PN



Kwantyl rozkładu typu PN

 

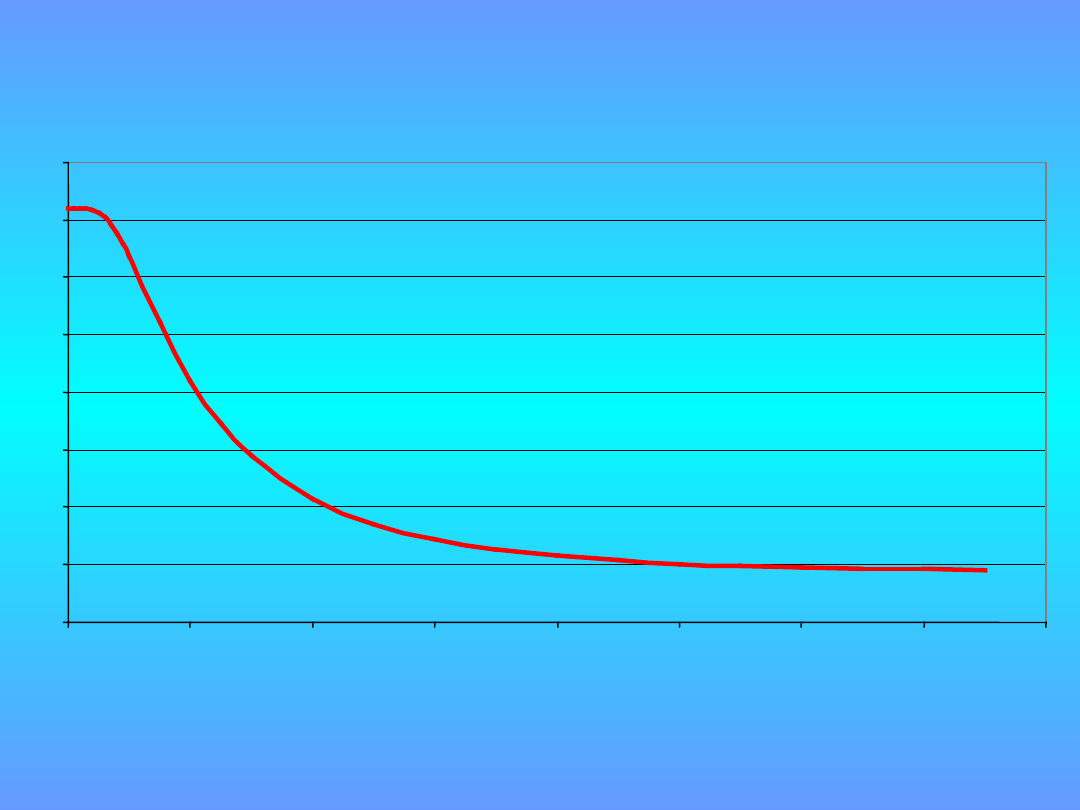
1,6

1,65

1,7

1,75

1,8

1,85

1,9

1,95

2

0

2

4

6

8

10

12

14

16

k

r

p = 95 %

 

p

r

f

k

,

PN



 

r 

k

PN 

r 

k

PN

 

r 

k

PN

 

r 

k

PN

 

r 

k

PN

 

r 

k

PN

 

0 

1,9600 

2 

1,8102 

4 

1,7070 

6 

1,6720  8 

1,6575  10  1,6508 

0,1  1,9600  2,1  1,8016  4,1  1,7043  6,1  1,6710  8,1  1,6571  11  1,6488 
0,2  1,9598  2,2  1,7936  4,2  1,7017  6,2  1,6700  8,2  1,6566  12  1,6474 
0,3  1,9593  2,3  1,7860  4,3  1,6993  6,3  1,6690  8,3  1,6562  13  1,6464 
0,4  1,9580  2,4  1,7788  4,4  1,6970  6,4  1,6681  8,4  1,6558  14  1,6457 
0,5  1,9553  2,5  1,7721  4,5  1,6948  6,5  1,6672  8,5  1,6554  15  1,6452 
0,6  1,9510  2,6  1,7657  4,6  1,6928  6,6  1,6664  8,6  1,6550  16  1,6448 
0,7  1,9449  2,7  1,7598  4,7  1,6908  6,7  1,6656  8,7  1,6546  17  1,6446 
0,8  1,9371  2,8  1,7541  4,8  1,6889  6,8  1,6648  8,8  1,6543  18  1,6444 
0,9  1,9278  2,9  1,7488  4,9  1,6871  6,9  1,6641  8,9  1,6539  19  1,6443 

1 

1,9174 

3 

1,7438 

5 

1,6854 

7 

1,6634  9 

1,6536  20  1,6443 

1,1  1,9063  3,1  1,7391  5,1  1,6838  7,1  1,6627  9,1  1,6532  30  1,6446 
1,2  1,8948  3,2  1,7347  5,2  1,6822  7,2  1,6620  9,2  1,6529  40  1,6449 
1,3  1,8831  3,3  1,7305  5,3  1,6807  7,3  1,6614  9,3  1,6526  50  1,6451 
1,4  1,8716  3,4  1,7266  5,4  1,6793  7,4  1,6608  9,4  1,6523  60  1,6452 
1,5  1,8603  3,5  1,7228  5,5  1,6780  7,5  1,6602  9,5  1,6521  70  1,6453 
1,6  1,8493  3,6  1,7193  5,6  1,6767  7,6  1,6596  9,6  1,6518  80  1,6453 
1,7  1,8388  3,7  1,7160  5,7  1,6754  7,7  1,6591  9,7  1,6515  90  1,6453 
1,8  1,8288  3,8  1,7128  5,8  1,6742  7,8  1,6585  9,8  1,6513  100  1,6454 
1,9  1,8192  3,9  1,7098  5,9  1,6731  7,9  1,6580  9,9  1,6510 

  1,6454 

 

Kwantyl rozkładu typu PN dla poziomu ufności 95 %

 

Niepewność rozszerzona

   



















N

i

i

y

u

k

v

t

k

U

1

2

N

PN

 

k

PN

r

u

            

 

do 

wartości

k

PN

r

u

             

do wartości

k

PN

r

u

            

 

do 

wartości

1,96

0,5090

1,85

1,6410

1,74

3,1930

1,95

0,6985

1,84

1,7380

1,73

3,4410

1,94

0,8240

1,83

1,8390

1,72

3,7300

1,93

0,9280

1,82

1,9460

1,71

4,0740

1,92

1,0220

1,81

2,0600

1,70

4,4925

1,91

1,1110

1,80

2,1820

1,69

5,0235

1,90

1,1980

1,79

2,3135

1,68

5,7350

1,89

1,2840

1,78

2,4560

1,67

6,7760

1,88

1,3700

1,77

2,6120

1,66

8,5975

1,87

1,4580

1,76

2,7845

1,65



1,86

1,5480

1,75

2,9765

Wartości współczynnika rozszerzenia dla poziomu 

ufności 95 %

 

Iloraz udziału

 

 

 

y

u

y

u

y

u

r

i

i

u

2

2

c





 

y

u

i

największy udział wielkości wejściowej
o rozkładzie prostokątnym

 

Iloraz            

udziału

Współczynnik 

rozszerzenia

0  r

u

 < 1

k

PN

 = k

N

1  r

u

  10

k

PN

 = k

T

r

u

  10

k

PN

 = k

P

Przybliżenie wartości współczynnika 

rozszerzenia k

PN

 

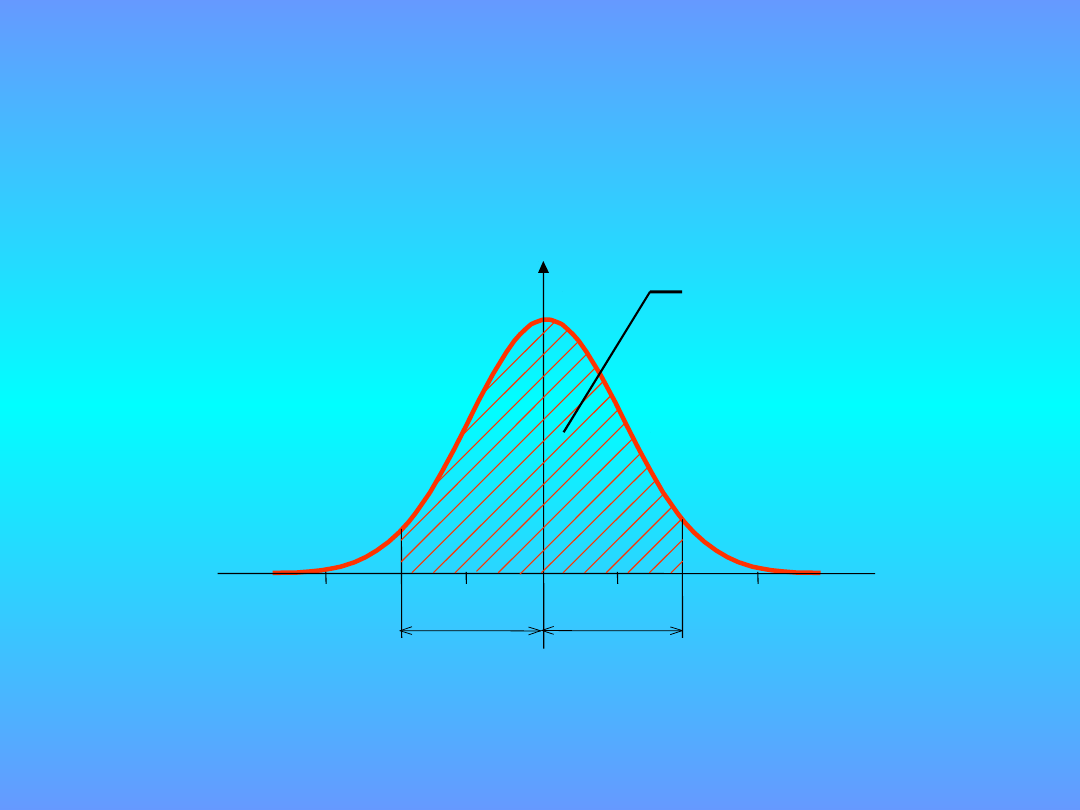
k

N

 = 1,96  dla  p = 95 %

k·u

3

2

k·u

1

-1

-2

-3

 

p

 

 

p

a

a

k·
u

k·
u

b

b









p

r

r

r

k











1

2

1

1

3

2

T

b

a

b

a

r







 

1,6

1,65

1,7

1,75

1,8

1,85

1,9

1,95

0

2

4

6

8

10

12

k

T

r

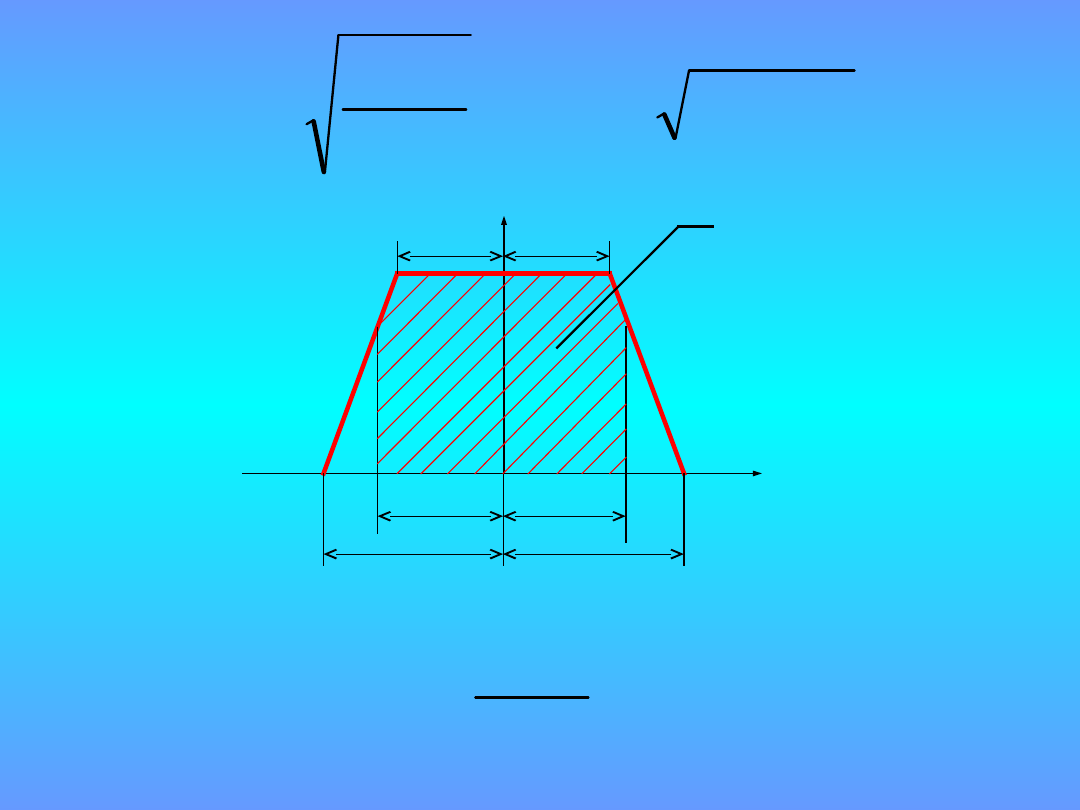
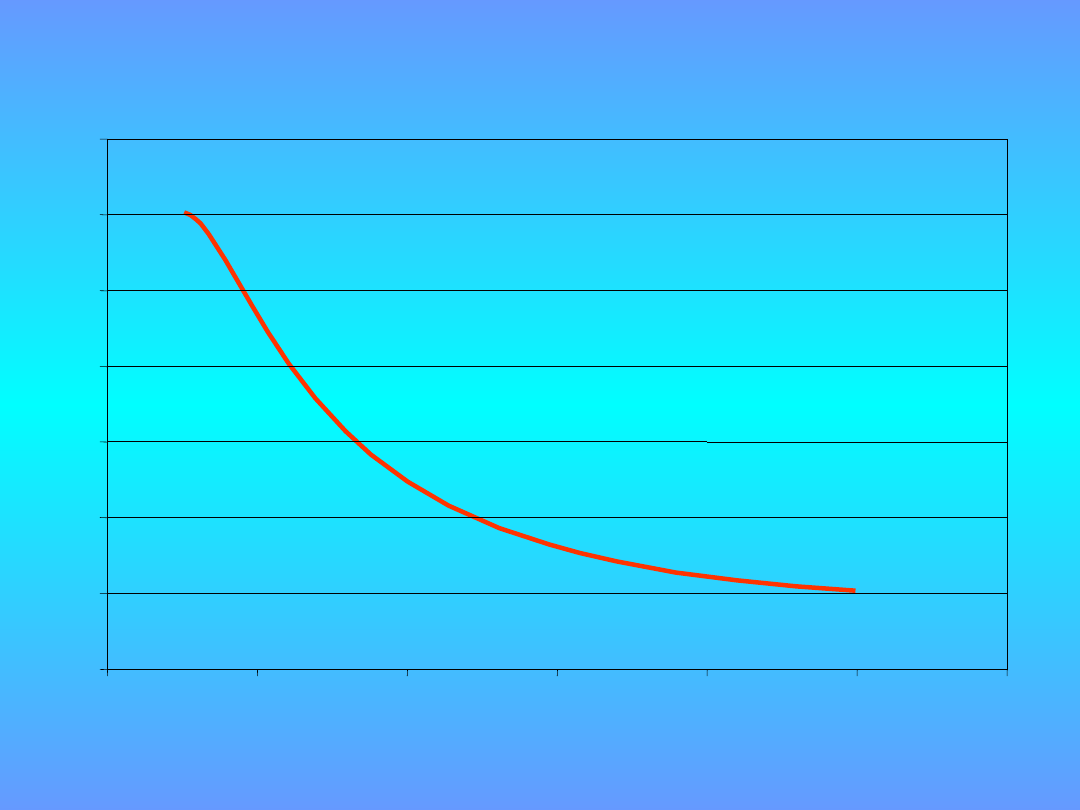
Współczynnik rozszerzenia dla rozkładu 

trapezowego

p = 95 %

k

T

 = 1,9  1,65 

 

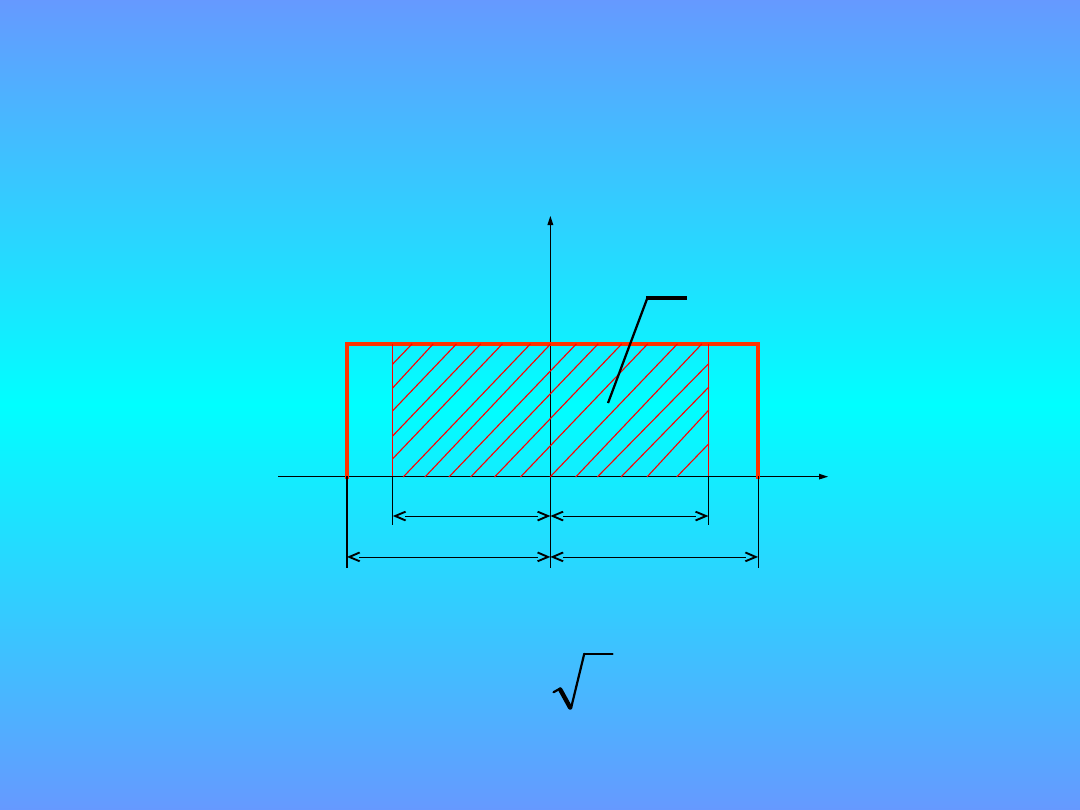
a

k·
u

a

k·u

 

p

p

k

3

P



k

P

 = 1,65  dla  p = 95 %

 

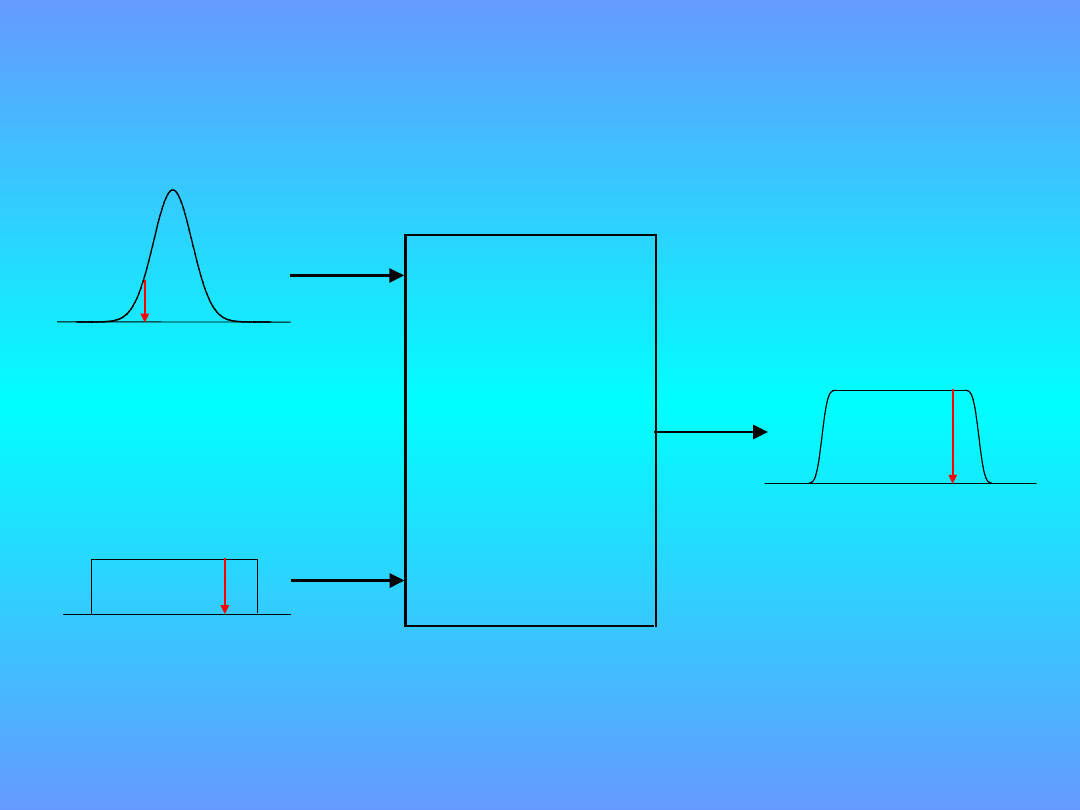
Symulacja Monte Carlo

 

X

f

Y 



1

x

N

x

y

 

Symulacja Monte Carlo





N

x

x

f

y

,

,

1





1. Przyjęcie modelu matematycznego określającego 
      relacje pomiędzy wielkościami wejściowymi 
      a wielkością wyjściową

 

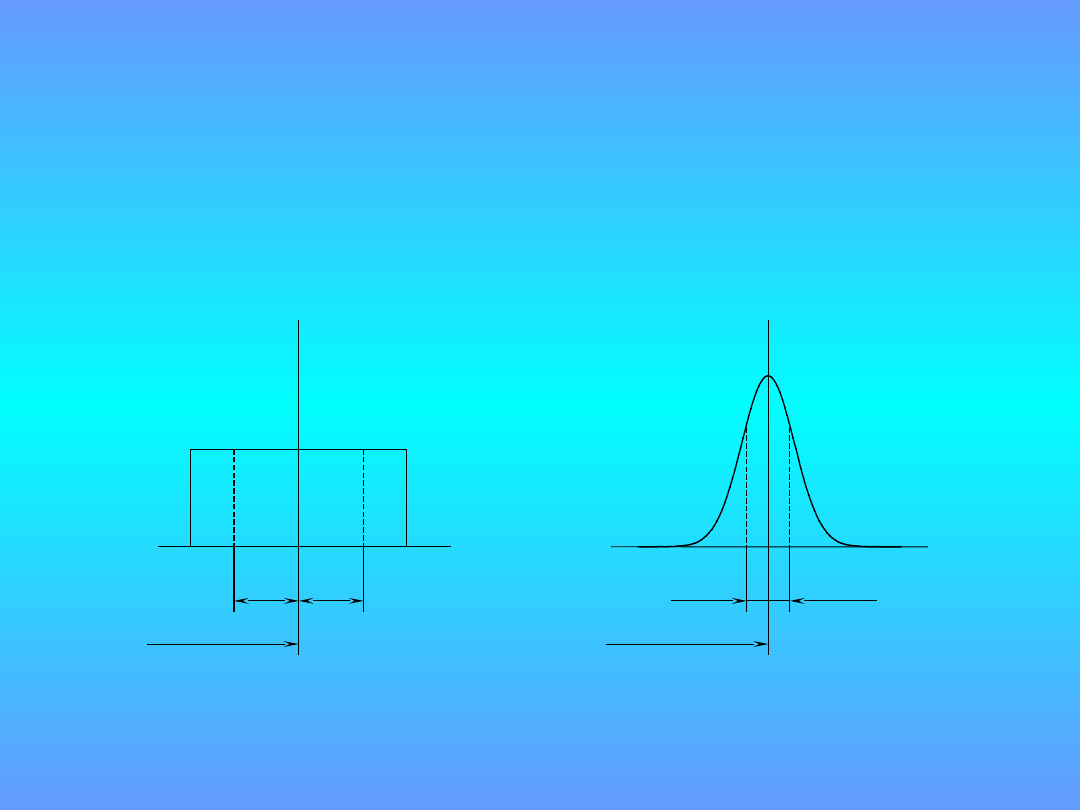
Symulacja Monte Carlo

2. Przyjęcie rozkładów dla wielkości wejściowych

  



i

  



i



i

g

i

(



i

)

    



j

  



j



j

g

j

(



j

)

wielkość 
wejściowa  x

i

wielkość 
wejściowa  x

j

 

Symulacja Monte Carlo

3. Wybór liczby próbkowania – M 

6

10



M

 

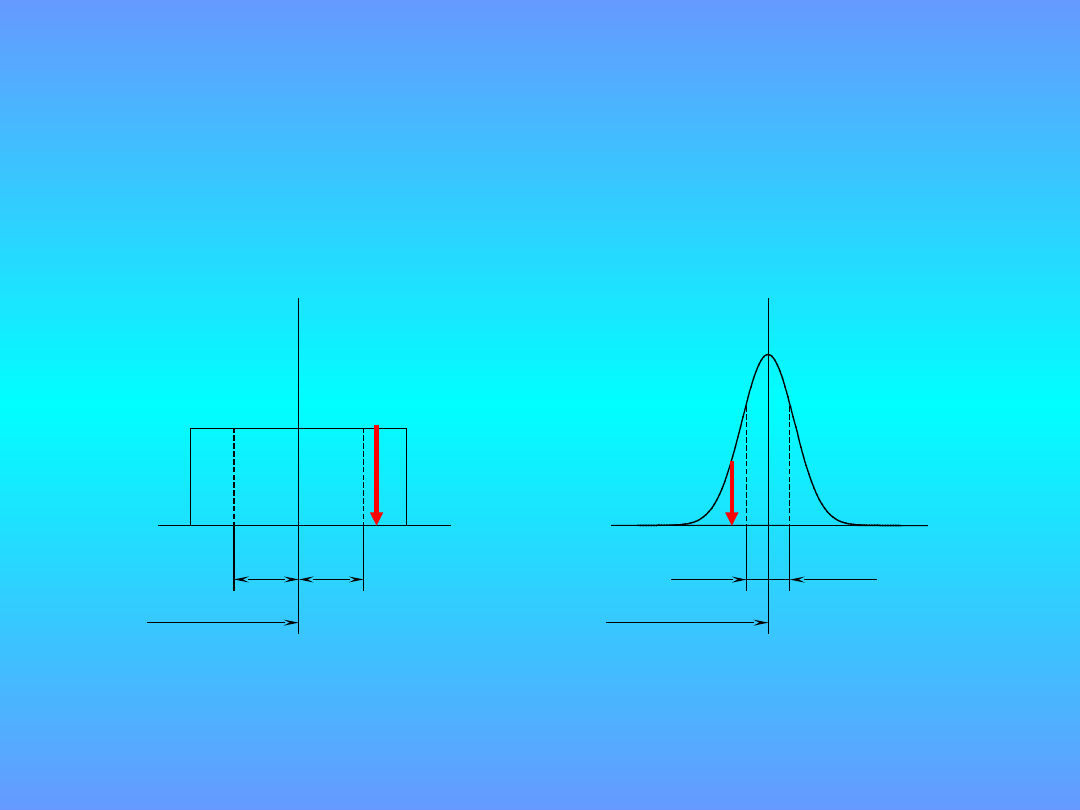
Symulacja Monte Carlo

4. Próbkowanie losowe wartości wielkości 
     wejściowych

   



i

   



i



i

g

i

(



i

)

   



j

   



j



j

g

j

(



j

)

wielkość 
wejściowa  x

i

wielkość 
wejściowa  x

j

x

i,

r

x

j,r

 

Symulacja Monte Carlo

5. Obliczenie wartości wielkości wyjściowej 





r

N

r

r

x

x

f

y

,

,

1

,

,



 

Symulacja Monte Carlo

6. Sortowanie wartości wielkości wyjściowej 
    zgodnie z niemalejącym porządkiem





 





1

1









r

r

r

y

y

y

 

Symulacja Monte Carlo

7. Wyznaczenie skumulowanego prawdopodobieństwa

M

r

p

r

5

,

0





 

Symulacja Monte Carlo

8. Wyznaczenie dystrybuanty wielkości wyjściowej

)

(

2

/

1

)

(

ˆ

)

(

)

1

(

)

(

r

r

r

y

y

M

y

M

r

G

















 





1







r

r

y

y



 

Symulacja Monte Carlo

9. Wyznaczenie przedziału ufności

 













p

G

g

G

g













1

1

ˆ

ˆ





 





1

1

ˆ

ˆ









G

p

G

=  min

 









p

G

G

y

I













1

1

ˆ

,

ˆ

)

(

 

Symulacja Monte Carlo

10. Wyznaczenie estymaty wielkości wyjściowej







M

r

r

y

M

y

1

1

ˆ

 

Symulacja Monte Carlo

11. Wyznaczenie niepewności standardowej















M

r

r

y

y

M

y

u

1

2

2

ˆ

1

1

)

ˆ

(

 

Zapis wyniku pomiaru

I(V) = [0.98, 
1.09] V

V = 1.02 
V

u(V ) = 0.03 
V

 

Zapis wyniku pomiaru

I(V) = [0.983, 1.088] 
V

V = 1.024 
V

u(V ) = 
0.028 V