
Wskaźniki
ekonomiczno - techniczne
wiercenia otworów
Opracowała:
mgr inż. Angelika Druzgała

Wstęp
Rozwój techniki umożliwia wytwarzanie coraz
to lepszych narzędzi wiertniczych (świdrów
i koronek wiertniczych).
Bardziej trwałe narzędzia dają możliwość
poprawy
wartości
wskaźników
techniczno-ekonomicznych wiercenia.

Wskaźniki techniczno – ekonomiczne wiercenia
• Wskaźnik średniej mechanicznej prędkości
wiercenia,
• Wskaźnik marszowej prędkości wiercenia,
• Wskaźnik wydajności świdra,
• Wskaźnik kosztu jednostkowego.

Średnia mechaniczna prędkość wiercenia
Średnia mechaniczna prędkość wiercenia v
m
:
T
dt
v
v
T
0
t
m
gdzie:
T – czas pracy świdra; [h],
v
t
– chwilowa prędkość wiercenia; [m/h].
𝑣
𝑚
=
𝑣
𝑡
∙ 𝑇
𝑇

Średnia mechaniczna prędkość wiercenia
𝑣
𝑡
=
∆𝐻
𝑇
gdzie:
∆H -
przyrost głębokości otworu; [m],
T - czas pracy świdra; [h].
dt
dH
v
t
Chwilowa prędkość wiercenia:

Średnia mechaniczna prędkość wiercenia
Wiercąc otwór dąży się do maksymalizacji
tego wskaźnika.
Kryterium to stosuje się podczas wiercenia
płytkich otworów
lub takich gdzie zachodzi
konieczność szybkiego przewiercenia niewielkiego
odcinka otworu.
max
v
m

Marszowa prędkość wiercenia
Marszowa prędkość wiercenia v
M
:
gdzie:
T – czas pracy świdra; [h],
T
ZW
– czas zapuszczania, wyciągania, wymiany świdra i płukania
otworu; [h],
v
t
– chwilowa prędkość wiercenia; [m/h] .
ZW
T
0
t
M
T
T
dt
v
v
𝑣
𝑀
=
𝑣
𝑡
∙ 𝑇
𝑇 + 𝑇𝑧𝑤

Wiercąc otwór dąży się do maksymalizacji tego
wskaźnika.
Wskaźnik ten:
•
odnosi się do uzyskania maksymalnej prędkości
wiercenia otworu (etapu wiercenia otworu).
•
reprezentuje w przybliżeniu technikę osiągnięcia
minimalnego czasu wykonania otworu w tym
przewiercania skał na dużych głębokościach
Marszowa prędkość wiercenia
max
v
M

Wydajność świdra
Wydajności świdra H :
gdzie:
T – czas pracy świdra; [h],
v
t
– chwilowa prędkość wiercenia; [m/h] .
T
0
t
dt
v
H

Wiercąc otwór dąży się do maksymalizacji tego wskaźnika.
Wskaźnik powyższy stosuje się jako wyznacznik pracy
świdra w przypadku jeśli celem jest osiągnięcie jak
największego przewiertu narzędziem.
Wydajność świdra
max
H

Koszt jednostkowy
Kosztu jednostkowego K :
gdzie:
T – czas pracy świdra; [h],
T
ZW
– czas zapuszczania, wyciągania, wymiany świdra, płukania
otworu; [h],
v
t
– chwilowa prędkość wiercenia; [m/h],
Q – koszt jednej godziny pracy urządzenia; [zł/h],
q – koszt zakupu świdra [zł].
T
t
ZW
dt
v
q
Q
T
T
K
0
)
(
𝐾 =
𝑇
𝑧𝑤
+ 𝑇 ⋅ 𝑄 + 𝑞
𝑣
𝑡
∙ 𝑇

Wiercąc otwór dąży się do minimalizacji
kosztu jednostkowego.
Wskaźnik
minimalnego
kosztu
jednostkowego pozwala ocenić i wybrać
narzędzia dające możliwość wywiercenia otworu
jak najmniejszym nakładem finansowym.
Koszt jednostkowy
min
K

Podsumowanie
Wskaźnik
Oznaczenie
Cel
Średniej mechanicznej prędkości
wiercenia
v
m
maksimum
Marszowej prędkości wiercenia
v
M
maksimum
Wydajności świdra
H
maksimum
Kosztu jednostkowego
K
minimum

Zadanie 1
W oparciu o wskaźnik mechanicznej średniej prędkości wiercenia
2,5 m/h oraz czas pracy świdra 30 h wyznacz miąższość
przewierconych przez niego skał.

Zadanie 1
Dane:
Szukane:
v
m
= 2,5 [m/h]
H = ?
T = 30 [h]
Rozwiązanie:
T
dt
v
v
T
0
t
m
dT
dH
v
t
dH
dt
v
H
0
t
0
t

Zadanie 1
Założenie: T = t
T
dH
v
H
0
m
T
v
H
m
30
5
,
2
H
Odpowiedź: H=75 [m]

Zadanie 2
Odwiercono
odcinek
otworu
od
głębokości
700
m
do głębokości 820 m. Podczas wiercenia określono, że prędkość
chwilowa wiercenia wyniosła 6 m/h. Oblicz ile czasu trwało
przewiercenie podanej miąższości skał?

Zadanie 2
Dane:
Szukane:
H
1
= 700 [m]
T = ?
H
2
= 820 [m]
v
t
= 6 [m/h]
Rozwiązanie:
T
dt
v
v
T
0
t
m
T
T
v
v
t
m
t
m
v
v
dT
dH
v
t
T
0
t
H
H
dt
v
dH
2
1
t
1
2
v
H
H
T
Odpowiedź: T = 20 [h]

Zadanie 3
Oblicz wartość wskaźnika marszowej prędkości wiercenia jeśli czas
wiercenia wynosi 20 godzin, czas zapuszczania - wyciągania 25
godzin. Przewiert świdrem w pierwszych 10 godzinach wynosił
5 m/h, natomiast w kolejnych 10 godzinach 4m/h.

Zadanie 3
Dane:
Szukane:
T = 20 [h]
v
M
= ?
Tzw= 25 [h]
v
t1
= 5 [m/h] T
1
= 10 [h]
v
t2
= 4 [m/h] T
2
= 10 [h]
Rozwiązanie:
Tzw
T
T
v
v
t
M
Odpowiedź: v
M
= 2 [m/h]
ZW
T
t
M
T
T
dt
v
v
0

Zadanie 4
Odwiercono odcinek otworu o średnicy 311 [mm] od głębokości
100 [m] do 1060 [m]. Wiedząc, że odcinek H
1
= 420 [m] do
H
2
= 900 [m] odwiercono trzema świdrami pracującymi po 40
godzin każdy, a czas wyciągania/zapuszczania świdra dla danej
głębokości dany jest funkcją T
ZW
= T
p
+T
ZS
+0,01·x [h]. Oblicz
marszową prędkość wiercenia otworu na tym odcinku. Za czas
płukania otworu przed wyciągnięciem przewodu wiertniczego
przyjąć T
p
= 2 [h] oraz czas zmiany świdra T
ZS
= 1 [h].

Zadanie 4
Dane:
Szukane:
H
1
= 420 [m]
v
M
= ?
H
2
= 900 [m]
T
g1
= T
g2
= T
g3
= 40 [h]
T
ZW
= T
p
+T
ZS
+0,01·x [h]
T
ZS
= 1 [h]
T
p
= 2 [h]
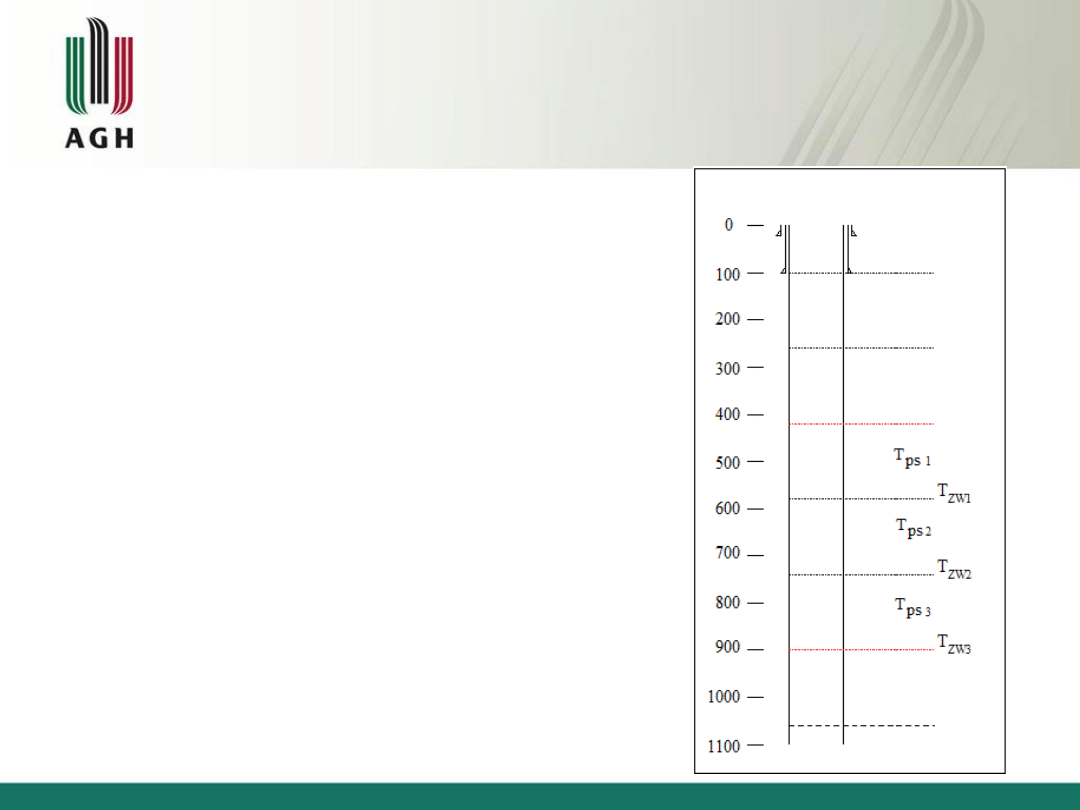
Zadanie 4
Rozwiązanie:
T
ZW
= T
ZW1
+T
ZW2
+T
ZW3
T
ZW1
= T
p
+T
ZS
+0,01·580
T
ZW1
= 2+1+5,8
T
ZW1
= 8,8 [h]
T
ZW2
= T
p
+T
ZS
+0,01·740
T
ZW2
= 10,4 [h]
T
ZW3
= T
p
+T
ZS
+0,01·900
T
ZW3
= 12 [h]

Zadanie 4
T
ZW
= T
ZW1
+T
ZW2
+T
ZW3
T
ZW
= 8,8 + 10,4 + 12
T
ZW
= 31,1 [h]
T
ps
= T
ps1
+ T
ps2
+ T
ps3
T
ps
= 120 [h]
Odpowiedź:
v
M
= 3,18 [m/h]
120
420
900
v
t
dt
dH
v
t
(2)
p s
T
t
H
H
dt
v
dH
0
2
1
ps
t
T
H
H
v
1
2
[m/h]
4
v
t
ZW
ps
T
t
M
T
T
dt
v
v
g
0
(4)
ZW
ps
ps
t
M
T
T
T
v
v
1
,
31
120
120
4
v
M
v
M
= 3,18 [m/h]

Zadanie 5
Mając do dyspozycji trzy typy świdrów o następujących cenach:
a) 30 tys. zł, b) 39 tys. zł, c) 100 tys. zł
i zakładając dla wszystkich taką samą chwilową prędkość wiercenia v
t
= 4
[m/h] wskaż świder dla którego jednostkowy koszt otworu jest najniższy.
Koszt godziny pracy urządzenia Q = 3 tys. zł/h, a czas pracy świdra a) 40
[h], b) 60 [h], c) 120 [h]. Pierwszy świder wykonał pracę na 3 odcinkach,
drugi na 2 natomiast trzeci na 1 odcinku podanych głębokości
przewiercania. Obliczenia dokonać dla wariantu:
1) Przewiercanie interwału 100 – 580 [m],
2) Przewiercanie interwału 300 – 780 [m].
Czas płukania otworu przed wyciągnięciem przewodu wiertniczego i czas
zmiany świdra przyjąć jak w zadaniu poprzednim.

Zadanie 5
Dane:
Szukane:
Q = 3 [tys. zł/h]
Przy którym świdrze
T
psa
= 40 [h]
jednostkowy koszt otworu
T
psb
= 60 [h]
jest najniższy? K=?
T
psc
= 120 [h]
q
a
= 30 [tys. zł]
q
b
= 39 [tys. zł]
q
c
= 100 [tys. zł]
v
t
= 4 [m/h]
Rozwiązanie:
T
t
ZW
dt
v
q
Q
T
T
K
0
)
(
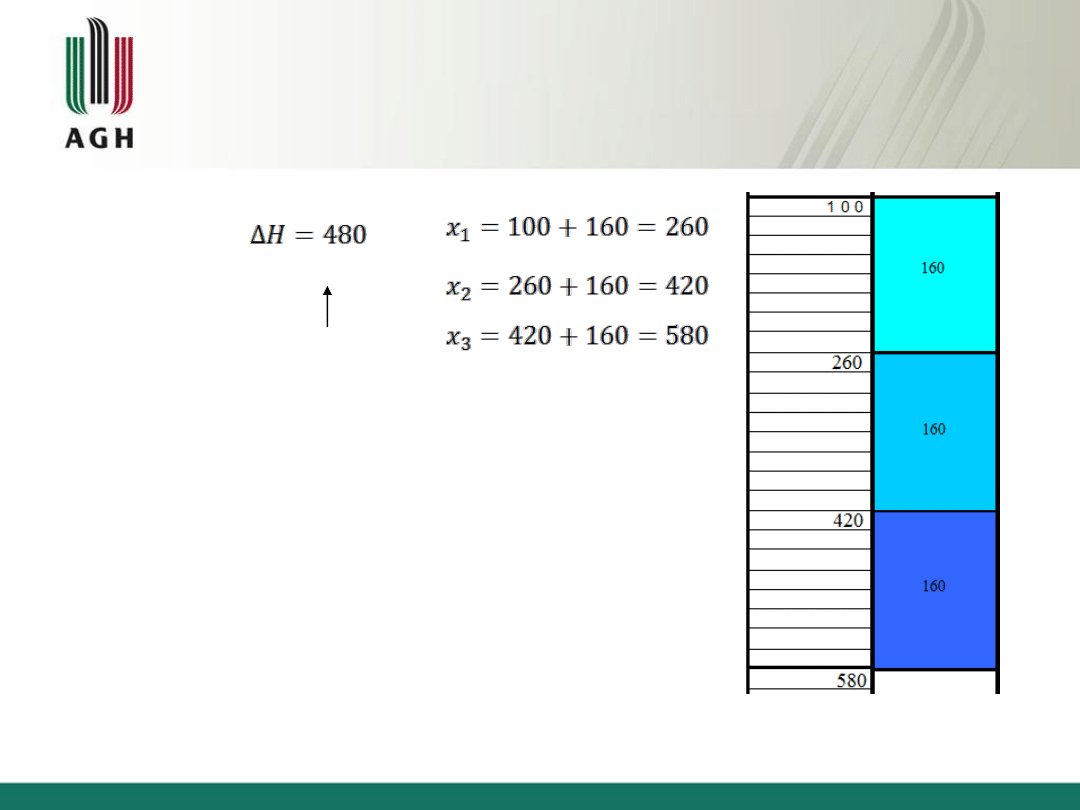
Zadanie 5
T
ZW
= T
ZW1
+T
ZW2
+T
ZW3
T
ZW
= 5,6 + 7,2 + 8,8=21,6 h
1)
H
1
= 100 [m]
H
2
= 580 [m]
480:3=160
(3 odcinki)
40h
40h
40h
T
ZW
= T
p
+T
ZS
+0,01·x
T
ZW1
= T
p
+T
ZS
+0,01·260
T
ZW1
= 2+1+2,6=5,6 h
T
ZW2
= T
p
+T
ZS
+0,01·420
T
ZW2
= 2+1+4,2=7,2 h
T
ZW3
= T
p
+T
ZS
+0,01·580
T
ZW3
= 2+1+5,8=8,8 h
a)
T
1
= T
2
= T
3
=40h
T= T
1
+ T
2
+ T
3
T = 120 h

T
t
a
ZW
a
dt
v
q
Q
T
T
K
0
1
)
(
T
v
q
Q
T
T
K
t
a
ZW
a
)
(
1
120
4
30
3
3
)
120
6
,
21
(
1
a
K
K
1a
= 1073 [zł/m]
(Na każdym z 3 odcinków wykorzystujemy po
jednym świdrze za kwotę 30 tys. zł)
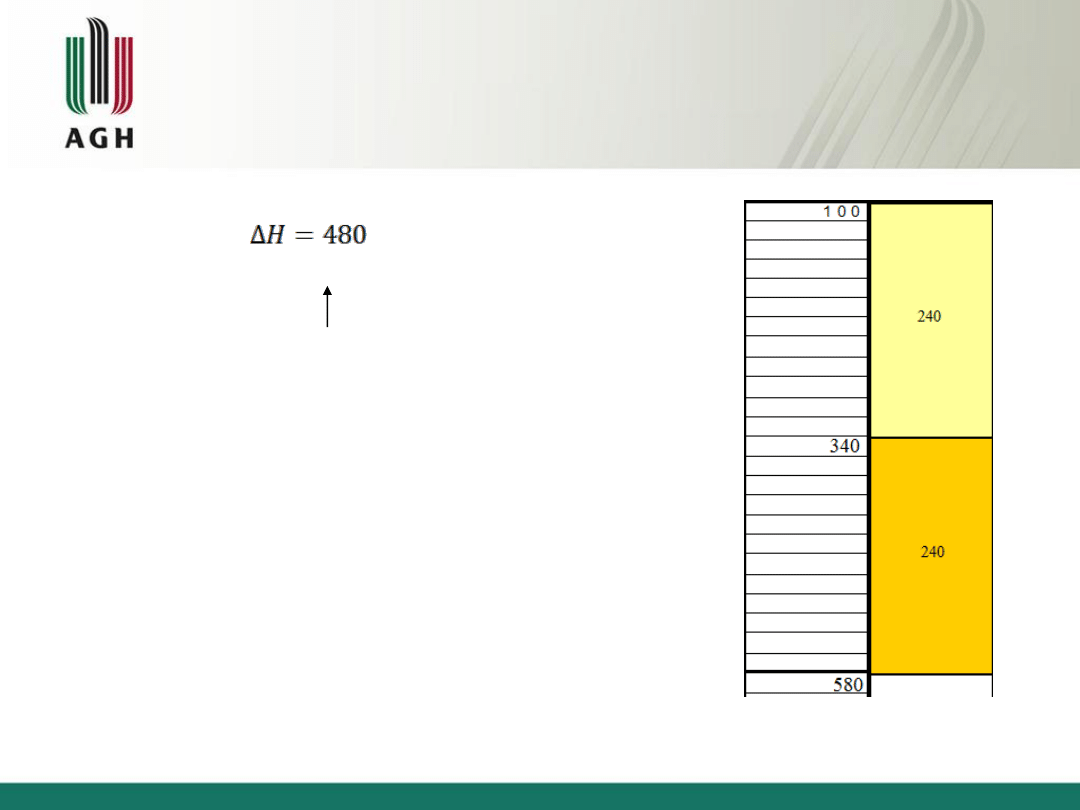
Zadanie 5
T
ZW
= T
ZW1
+T
ZW2
T
ZW
= 6,4 + 8,8=15,2 h
1)
H
1
= 100 [m]
H
2
= 580 [m]
480:2=240
(2 odcinki)
60h
60h
T
ZW
= T
p
+T
ZS
+0,01·x
T
ZW1
= T
p
+T
ZS
+0,01·340
T
ZW1
= 2+1+3,4=6,4 h
T
ZW2
= T
p
+T
ZS
+0,01·580
T
ZW2
= 2+1+5,8=8,8 h
b)
T
1
= T
2
= 60h
T= T
1
+ T
2
T = 120 h
𝑥
1
= 100 + 240 = 340
𝑥
2
= 340 + 240 = 580

g
T
t
b
ZW
b
dt
v
q
Q
T
T
K
0
1
)
(
T
v
q
Q
T
T
K
t
b
ZW
b
)
(
1
120
4
39
2
3
)
120
2
,
15
(
1
b
K
K
1b
= 1008 [zł/m]
(Na każdym z 2 odcinków wykorzystujemy po
jednym świdrze za kwotę 39 tys. zł)

Zadanie 5
T
ZW
=T
ZW1
= 8,8 h
1)
H
1
= 100 [m]
H
2
= 580 [m]
120h
T
ZW
= T
p
+T
ZS
+0,01·x
T
ZW1
= T
p
+T
ZS
+0,01·580
T
ZW1
= 2+1+5,8=8,8 h
c)
T
1
= 120h
𝑥
1
= 100 + 480 = 580

T
t
c
ZW
c
dt
v
q
Q
T
T
K
0
1
)
(
T
v
q
Q
T
T
K
t
c
ZW
c
)
(
1
120
4
100
1
3
)
120
8
,
8
(
1
c
K
K
1c
= 1013 [zł/m]
(Na 1 odcinku wykorzystujemy jeden świder za
kwotę 100 tys. zł)

Zadanie 5
Odpowiedź:
W pierwszym przypadku najniższy koszt jednostkowy uzyskuje się dla świdra b
K
1b
= 1008 [zł]
Wyszukiwarka
Podobne podstrony:
Analiza techniczno ekonomiczna Nieznany (2)
00 Program nauki Technik ekonom Nieznany
Wskazniki techniczo ekonomiczn wiercenia otworu
Wskazniki techniczo ekonomiczn wiercenia otworu zadania
Wybrane wskaźniki techniczno ekonomiczne pozyskania drewna na przykładzie Nadleśnictwa Radzyń Podlas
Wybrane wskaźniki techniczno, analiza ekonomiczna w transporcie i spedycjii
materialy bezpieczenstwo ekonom Nieznany
Lampki wskaznikowe zestawu wska Nieznany
janus, procesy i techniki wytwa Nieznany
Podstawy techniki mikroprocesor Nieznany
Egzamin pisemny TECHNIK USLUG K Nieznany
04 Scinanie techniczneid 5186 Nieznany
statystytka analiza struktury, A Egzamin zawodowy TECHNIK EKONOMISTA!
00 Program nauki Technik masazy Nieznany
ANALIZA TECHNICZNA KONTRAKTOW T Nieznany (2)
14 Stosowanie technik laczenia Nieznany (2)
egzamin z geologi i ekonomiki u Nieznany
więcej podobnych podstron