MODEL POJAZDU DO TRANSPORTU

PALIW PŁYNNYCH NA PRZYKŁADZIE WYBRANEGO

OPERATORA TRANSPORTOWEGO

Uwagi wstępne

Celem opracowania jest wskazanie na jedną z możliwości analizy gotowości pojazdów
metodami modelowania i symulacji komputerowej na przykładzie pojazdów
eksploatowanych przez wybranego operatora transportu paliw płynnych. Realizację
tego celu przeprowadzono w następujących krokach:
•

prezentacja systemu pojazdów wybranego operatora transportu paliw płynnych;

•

stworzenie modelu matematycznego stanów eksploatacyjnych pojazdu do
transportu paliw płynnych;

•

opis symulacyjnego modelu komputerowego oraz wskazanie możliwości jego
zastosowania do analiz gotowości pojazdów do transportu paliw płynnych.

O systemie pojazdów wybranego operatora transportu paliw płynnych

Ważnym elementem systemów logistycznych jednego z koncernów paliwowych
działających w Polsce są spółki transportowe. W ramach spółek transportowych
funkcjonują dyspozytornie. Zadaniem dyspozytorów pracujących we wszystkich
spółkach transportowych jest organizacja dostaw paliw do stacji paliw koncernu oraz do
jego klientów indywidualnych. Dostawy paliw do stacji własnych koncernu odbywają
się według ściśle określonego planu. W planie tym uwzględnia się m.in.:
−

obszar działania spółki transportowej,

−

punkty zaopatrzenia (bazy magazynowe koncernu),

−

liczbę stacji paliw koncernu leżących w obszarze działania spółki transportowej.
W ramach jednej ze spółek transportowych koncernu paliwowego działa m.in.

dyspozytornia Y. Dyspozytornia Y dostarcza paliwa płynne do kilkudziesięciu stacji
paliw koncernu. Stacje te są rozmieszczone głównie w jednym z południowych
województw a punktami ich zaopatrzenia są trzy bazy magazynowe.

W dyspozytorni Y zadania transportu paliw płynnych realizowane są za pomocą

ośmiu zestawów transportowych (pojazdów). Są to zestawy transportowe dwojakiego
rodzaju. Pierwszy rodzaj zestawu tworzą ciągnik siodłowy i naczepa cysternowa.
Drugim rodzajem zestawu jest autocysterna składająca się z samochodu i
zamontowanego na jego podwoziu wielokomorowego zbiornika cysternowego.

Wszystkie zestawy transportowe eksploatowane w dyspozytorni Y zostały

wprowadzone do użytkowania jako nowe a ich obsługiwanie w spółce transportowej
jest prowadzone przez specjalnie do tego celu zorganizowany serwis obsługowy.

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

2

Stany eksploatacyjne pojazdu do transportu paliw płynnych

Podstawą analizy procesu eksploatacji pojazdów do transportu paliw płynnych
eksploatowanych w dyspozytorni Y są zdarzenia eksploatacyjne zidentyfikowane w
życiu tych pojazdów. Głównymi zdarzeniami eksploatacyjnymi są rozpoczęcia i
zakończenia planowych lub nieplanowych obsług pojazdów. Chwile czasowe tych
zdarzeń mogą być ustalane m.in. na podstawie dokumentacji procesów obsługiwania
pojazdów.

Na podstawie analizy informacji zawartych w dokumentacji procesów

obsługiwania pojazdów stwierdzono, że proces eksploatacji

{

}

0

:

)

(

5

≥

t

t

X

pojazdów do

transportu paliw płynnych jest on procesem pięciostanowym. Proces ten przyjmuje:

•

X

5

(t) = 1,

gdy pojazd w chwili t znajduje się w użytkowaniu (jest zdatny);

•

X

5

(t) = 2,

gdy w chwili t w pojeździe wykonywana jest obsługa okresowa pierwsza

i naprawa bieżąca w związku z zauważonymi uszkodzeniami;

•

X

5

(t) = 3,

gdy w chwili t w pojeździe wykonywana jest obsługa okresowa druga

i naprawa bieżąca w związku z zauważonymi uszkodzeniami;

•

X

5

(t) = 4,

gdy w chwili t w pojeździe wykonywana jest obsługa okresowa trzecia

i naprawa bieżąca w związku z zauważonymi uszkodzeniami;

•

X

5

(t) = 5,

gdy w chwili t w pojeździe wykonywana jest naprawa bieżąca.

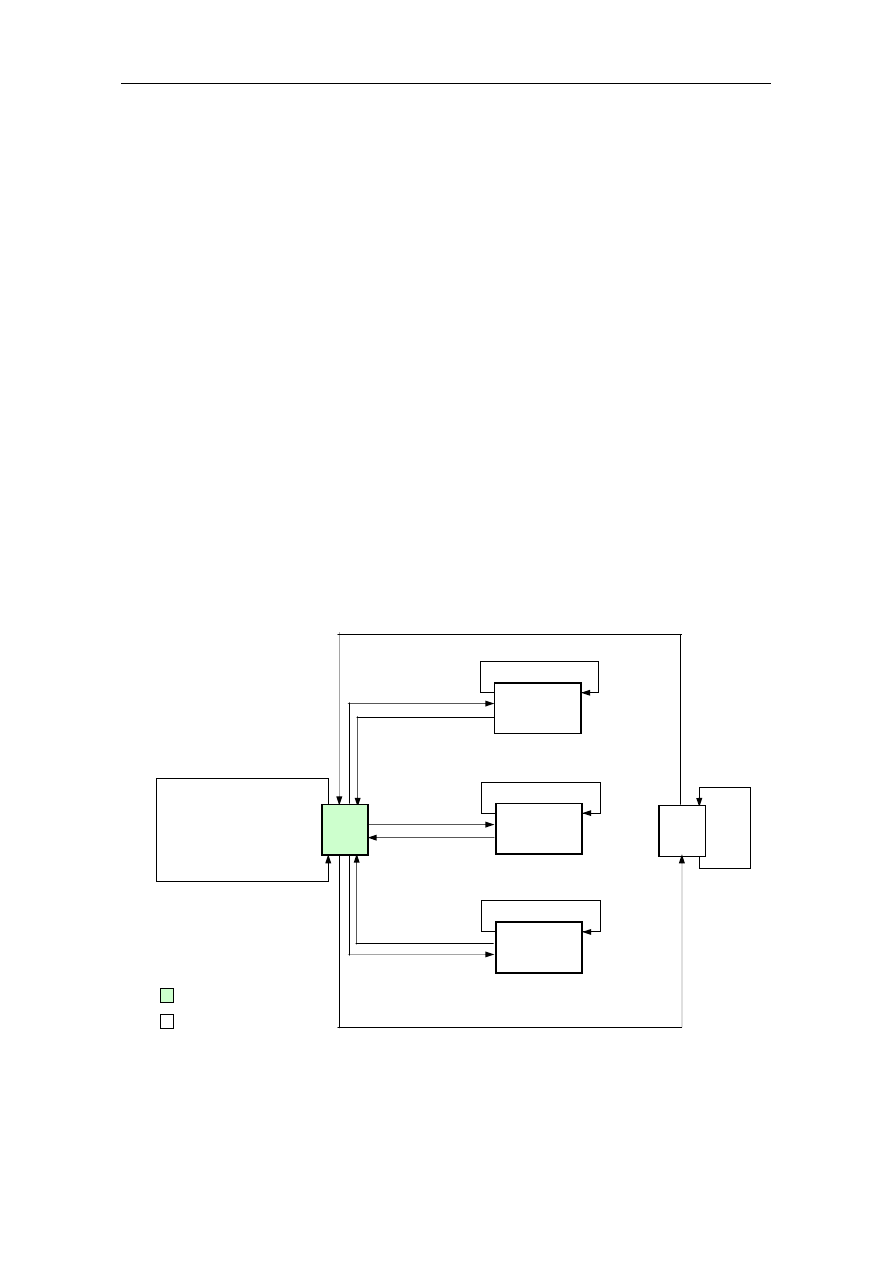
Na podstawie zidentyfikowanych stanów eksploatacyjnych pojazdów zbudowano

graf stanów modelu pojazdu do transportu paliw płynnych (rys. 1).

Rys. 1. Graf stanów modelu pojazdu do transportu paliw płynnych, gdzie: 1 (Z) – stan zdatności
(użytkowania) pojazdu, 2 (NB_OT-1) – stan obsługi okresowej pierwszej z naprawą bieżącą,
3 (NB_OT-2) – stan obsługi okresowej drugiej z naprawą bieżącą, 4 (NB_OT-3) – stan obsługi
okresowej trzeciej z naprawą bieżącą, 5 (NB) – stan naprawy bieżącej (wyjaśnienie pozostałych oznaczeń
znajduje się w tekście)

− stany zdatności

− stany niezdatności

5

NB

2

NB_OT-1

3

NB_OT-2

4

NB_OT-3

1
Z

t

,

∆

⋅

1

5

λ

t

,

∆

⋅

5

1

λ

t

,

∆

⋅

4

1

λ

t

,

∆

⋅

1

3

λ

t

,

∆

⋅

3

1

λ

t

,

∆

⋅

1

2

λ

t

,

∆

⋅

2

1

λ

t

,

∆

⋅

1

4

λ

t

,

∆

⋅

−

1

4

1 λ

t

,

∆

⋅

−

1

3

1 λ

t

,

∆

⋅

−

1

2

1 λ

t

,

∆

⋅

−

1

5

1 λ

(

)

t

,

,

,

,

∆

⋅

+

+

+

−

5

1

4

1

3

1

2

1

1

λ

λ

λ

λ

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

3

Model matematyczny pojazdu do transportu paliw płynnych

Przyjmuje się, że proces

{

}

0

:

)

(

≥

t

t

X

eksploatacji pojazdów do transportu paliw

płynnych jest procesem Markowa. Proces stochastyczny

{

}

0

:

)

(

≥

t

t

X

nazywamy

procesem Markowa, jeżeli dla dowolnego ciągu parametrów

n

n

t

t

...

t

t

<

<

<

<

−1

1

0

,

dowolnych

R

∈

<

<

<

<

−

n

n

x

x

...

x

x

1

1

0

oraz

,...

,

n

2

1

=

zachodzi równość

.

( )

( )

( )

( )

{

}

( )

( )

{

}

1

1

0

0

1

1

1

1

−

−

−

−

=

=

=

=

=

=

=

n

n

n

n

n

n

n

n

x

t

X

x

t

X

P

x

t

X

,

x

t

X

,...,

x

t

X

x

t

X

P

.

(1)

Równość ta oznacza, że bezpośredni wpływ na stan procesu w chwili t

n

ma jego

stan w chwili t

n-1

.

Dalej będą rozważane procesy Markowa o co najwyżej przeliczalnym zbiorze

stanów

{

}

5

4

3

2

1

,

,

,

,

=

S

i zbiorze parametrów czasowych

)

0

+∞

=< ,

T

.

Konsekwencją przyjętych założeń jest fakt, że sumaryczne czasy przebywania

pojazdu w i-tych stanach przed przejściem do j-tych stanów, opisują zmienne losowe o
rozkładach wykładniczych i funkcji gęstości prawdopodobieństwa postaci:

( )

t

j

,

i

j

,

i

j

,

i

t

f

⋅

−

⋅

=

λ

λ

e

,

{

}

5

4

3

2

1

,

,

,

,

j

,

i

∈

,

(2)

gdzie λ

i,j

są intensywnościami przejść ze stanów i-tych do stanów j-tych.

Wyznaczenie charakterystyk eksploatacyjnych pojazdu (wyznaczanych głównie

na podstawie prawdopodobieństw stanów modelu pojazdu) odwzorowywanego
zbudowanym tu modelem jest konsekwencją rozwiązania następującego równania:

(

) ( )

P

P

P

∆

⋅

=

∆

+

t

t

t

(3)

gdzie:

( )

t

P

− wektor prawdopodobieństw przebywania pojazdu w stanach w chwili t,

(

)

t

t

∆

+

P

− wektor prawdopodobieństw przebywania pojazdu w stanach w chwili (t+∆t),

P

∆

− macierz prawdopodobieństw przejść między stanami

S

P

∈

=

j

,

i

,

t

p

ij

)]

(

[

∆

Z przyjętych założeń i z rys. 1 wynika następująca postać macierzy

prawdopodobieństw przejść między stanami modelu pojazdu:

(

)

































∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

+

+

+

−

=

t

t

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

1

5

1

5

1

4

1

4

1

3

1

3

1

2

1

2

5

1

4

1

3

1

2

1

5

1

4

1

3

1

2

1

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

1

∆

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

P

(4)

Zatem równanie (4.3) można zapisać w postaci:

[

] [

]

×

=

∆

+

∆

+

∆

+

∆

+

∆

+

)

(

P

),

(

P

),

(

P

),

(

P

),

(

P

)

(

P

),

(

P

),

(

P

),

(

P

),

(

P

5

4

3

2

1

5

4

3

2

1

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

(

)

































∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

+

+

+

−

×

t

t

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

1

5

1

5

1

4

1

4

1

3

1

3

1

2

1

2

5

1

4

1

3

1

2

1

5

1

4

1

3

1

2

1

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

1

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

(5)

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

4

lub równoważnie:

(

) ( )

(

)

( )

( )

+

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

+

+

+

−

⋅

=

∆

+

t

t

t

t

t

t

t

t

,

,

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

1

P

P

]

[1

P

P

λ

λ

λ

λ

λ

λ

( )

( )

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

+

1

5

5

1

4

4

P

P

λ

λ

(

) ( )

( )

]

-

[1

P

P

P

1

2

2

2

1

1

2

t

t

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

λ

λ

(

) ( )

( )

]

-

[1

P

P

P

1

3

3

3

1

1

3

t

t

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

λ

λ

(6)

(

) ( )

( )

]

-

[1

P

P

P

1

4

4

4

1

1

4

t

t

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

λ

λ

(

) ( )

( )

]

-

[1

P

P

P

1

5

5

5

1

1

5

t

t

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

ζ

ζ

Po przekształceniu układu (6) otrzymujemy:

(

) ( )

( )

(

)

( )

( )

+

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

+

+

+

⋅

−

=

−

∆

+

t

t

t

t

t

t

t

t

t

,

,

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

1

1

P

P

P

P

P

λ

λ

λ

λ

λ

λ

( )

( )

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

+

1

5

5

1

4

4

P

P

λ

λ

(

) ( ) ( )

( )

t

t

t

t

t

t

t

,

,

∆

⋅

⋅

−

∆

⋅

⋅

=

−

∆

+

1

2

2

2

1

1

2

2

P

P

P

P

λ

λ

(

) ( ) ( )

( )

t

t

t

t

t

t

t

,

,

∆

⋅

⋅

−

∆

⋅

⋅

=

−

∆

+

1

3

3

3

1

1

3

3

P

P

P

P

λ

λ

(7)

(

) ( ) ( )

( )

t

t

t

t

t

t

t

,

,

∆

⋅

⋅

−

∆

⋅

⋅

=

−

∆

+

1

4

4

4

1

1

4

4

P

P

P

P

λ

λ

(

) ( ) ( )

( )

t

t

t

t

t

t

t

,

,

∆

⋅

⋅

−

∆

⋅

⋅

=

−

∆

+

1

5

5

5

1

1

5

5

P

P

P

P

λ

λ

Następnie

(

) ( )

( )

(

)

( )

( )

+

⋅

+

⋅

+

+

+

+

⋅

−

=

∆

−

∆

+

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

1

1

P

P

P

P

P

,

,

t

t

t

t

t

t

t

λ

λ

λ

λ

λ

λ

( )

( )

1

5

5

1

4

4

P

P

,

,

t

t

λ

λ

⋅

+

⋅

(

) ( )

( )

( )

1

2

2

2

1

1

2

2

P

P

P

P

,

,

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

(

) ( )

( )

( )

1

3

3

3

1

1

3

3

P

P

P

P

,

,

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

(8)

(

) ( )

( )

( )

1

4

4

4

1

1

4

4

P

P

P

P

,

,

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

(

) ( )

( )

( )

1

5

5

5

1

1

5

5

P

P

P

P

,

,

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

Obliczając granicę po obu stronach równań układu można zapisać, że:

(

) ( )

( )

(

)

( )

( )

+

⋅

+

⋅

+

+

+

+

⋅

−

=

∆

−

∆

+

→

∆

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

1

1

0

P

P

P

P

P

lim

,

,

t

t

t

t

t

t

t

t

λ

λ

λ

λ

λ

λ

( )

( )

1

5

5

1

4

4

P

P

,

,

t

t

λ

λ

⋅

+

⋅

+

(

) ( ) ( )

( )

1

2

2

2

1

1

2

2

0

P

P

P

P

lim

,

,

t

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

→

∆

(

) ( ) ( )

( )

1

3

3

3

1

1

3

3

0

P

P

P

P

lim

,

,

t

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

→

∆

(

9)

(

) ( ) ( )

( )

1

4

4

4

1

1

4

4

0

P

P

P

P

lim

,

,

t

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

→

∆

(

) ( ) ( )

( )

1

5

5

5

1

1

5

5

0

P

P

P

P

lim

,

,

t

t

t

t

t

t

t

λ

λ

⋅

−

⋅

=

∆

−

∆

+

→

∆

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

5

a gdy zauważy się, że:

(

) ( )

( )

t

t

t

t

t

t

i

i

i

t

d

dP

P

P

lim

0

=

∆

−

∆

+

→

∆

,

S

∈

i

dla

,

(10)

to

( )

( )

(

)

( )

( )

( )

( )

1

5

5

1

4

4

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

1

P

P

P

P

P

d

dP

,

,

,

,

t

t

t

t

t

t

t

λ

λ

λ

λ

λ

λ

λ

λ

⋅

+

⋅

+

⋅

+

⋅

+

+

+

+

⋅

−

=

( )

( )

( )

1

2

2

2

1

1

2

P

P

d

dP

,

,

t

t

t

t

λ

λ

⋅

−

⋅

=

( )

( )

( )

1

3

3

3

1

1

3

P

P

d

dP

,

,

t

t

t

t

λ

λ

⋅

−

⋅

=

(11)

( )

( )

( )

1

4

4

4

1

1

4

P

P

d

dP

,

,

t

t

t

t

λ

λ

⋅

−

⋅

=

( ) ( )

( )

1

5

5

5

1

1

5

P

P

d

dP

,

,

t

t

t

t

λ

λ

⋅

−

⋅

=

Układ (11) jest układem równań różniczkowych liniowych o stałych współczynnikach. W
warunkach ustalonych, tzn.

( )

0

d

dP

,

t

t

i

=

( )

S

∈

=

i

,

t

i

i

dla

P

P

,

(12)

układ ten przyjmuje postać następującą:

(

)

1

5

5

1

4

4

1

3

3

1

2

2

1,5

1,4

1,3

1,2

1

P

P

P

P

P

0

,

,

,

,

λ

λ

λ

λ

λ

λ

λ

λ

⋅

+

⋅

+

⋅

+

⋅

+

+

+

+

⋅

−

=

1

2

2

2

1

1

P

P

0

,

,

λ

λ

⋅

−

⋅

=

1

3

3

3

1

1

P

P

0

,

,

λ

λ

⋅

−

⋅

=

(13)

1

4

4

4

1

1

P

P

0

,

,

λ

λ

⋅

−

⋅

=

1

5

5

5

1

1

P

P

0

,

,

λ

λ

⋅

−

⋅

=

.

Z układu równań (13) wynikają następujące zależności:

1

1

2

2

1

2

P

P

⋅

=

,

,

λ

λ

1

1

3

3

1

3

P

P

⋅

=

,

,

λ

λ

(14)

1

1

4

4

1

4

P

P

⋅

=

,

,

λ

λ

1

1

5

5

1

5

P

P

⋅

=

,

,

λ

λ

.

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

6

Ponieważ

5

4

3

2

1

P

P

P

P

P

1

+

+

+

+

=

,

(15)

więc po podstawieniu (15) otrzymujemy:

1

1

5

5

1

1

1

4

4

1

1

1

3

3

1

1

1

2

2

1

1

P

P

P

P

P

1

⋅

+

⋅

+

⋅

+

⋅

+

=

,

,

,

,

,

,

,

,

λ

λ

λ

λ

λ

λ

λ

λ

,

(16)

a prawdopodobieństwo przebywania pojazdu w poszczególnych stanach modelu można opisać
następującymi wzorami:

,

,

,

,

,

,

,

,

,

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

1

1

P

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

=

(17)

,

,

,

,

,

,

,

,

,

,

,

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

2

2

1

2

1

1

P

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

⋅

=

(18)

,

,

,

,

,

,

,

,

,

,

,

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

3

3

1

3

1

1

P

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

⋅

=

(19)

,

,

,

,

,

,

,

,

,

,

,

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

4

4

1

4

1

1

P

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

⋅

=

(20)

.

,

,

,

,

,

,

,

,

,

,

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

5

5

1

5

1

1

P

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

⋅

=

(21)

Uwzględniając to, że suma prawdopodobieństw przebywania pojazdu w stanach zdatności

(rys. 1) jest współczynnikiem gotowości pojazdu K

g

oraz suma prawdopodobieństw przebywania

pojazdu w stanach niezdatności (rys. 1) jest jego współczynnikiem niegotowości K

ng

,

otrzymujemy odpowiednio

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

1

1

P

,

,

,

,

,

,

,

,

g

K

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

=

=

,

(22)

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

1

5

5

1

1

4

4

1

1

3

3

1

1

2

2

1

5

4

3

2

1

1

P

P

P

P

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

ng

K

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

⋅

















+

+

+

=

+

+

+

=

.

(23)

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

7

Komputerowy model symulacyjny pojazdu do transportu paliw płynnych

Formuły matematyczne modelu pojazdu do transportu paliw oprogramowano w
symulatorze komputerowym WMM_5_0.xls. Symulator WMM_5_0.xls jest aplikacją
opracowaną w programie Microsoft Excel. Użytkownik symulatora ma do dyspozycji dwa
arkusze robocze: Mat_WMM_5_0 i Sym_WMM_5_0.

Arkusz roboczy Mat_WMM_5_0 spełnia funkcję pomocniczą. Umieszczono w nim graf

stanów modelu pojazdu oraz podstawowe formuły matematyczne modelu (rys. 2).

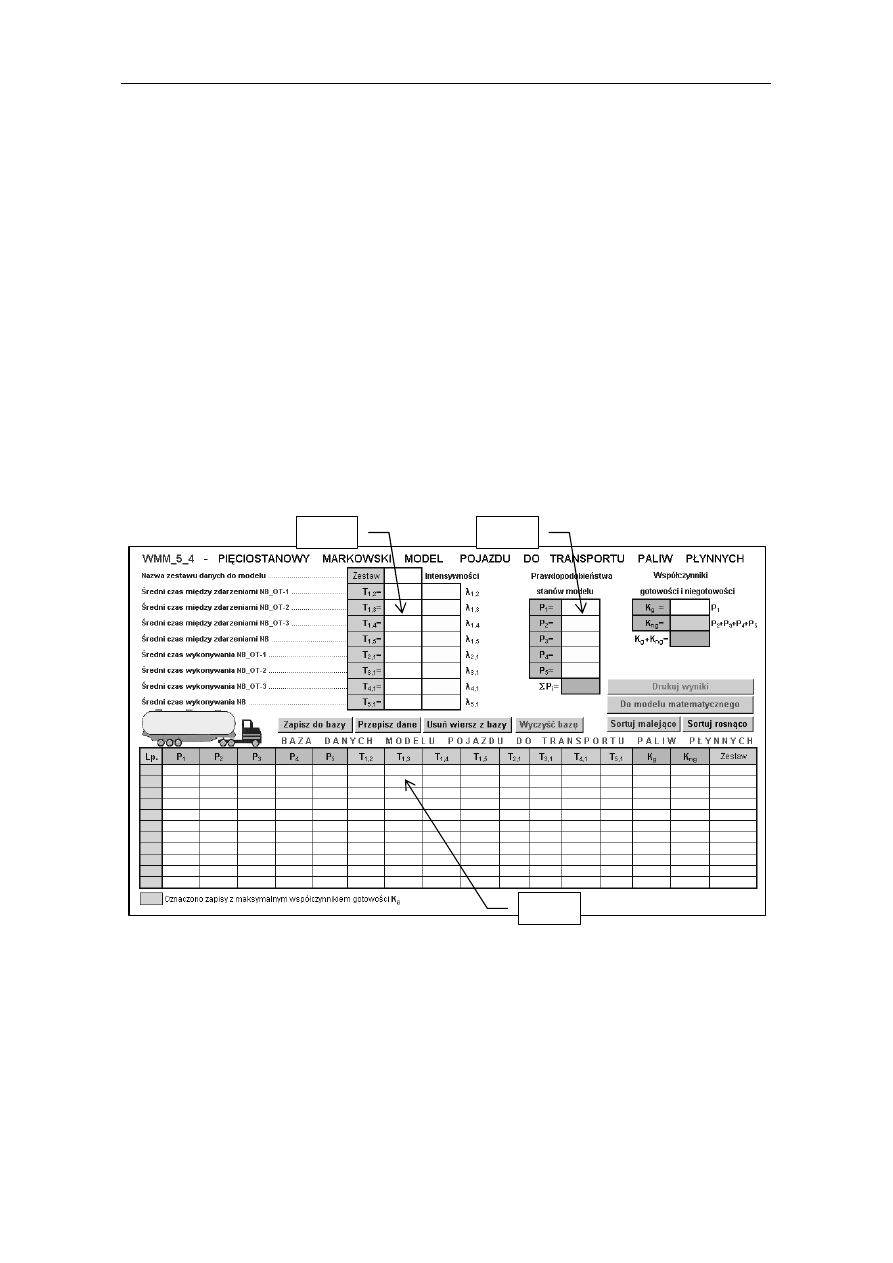
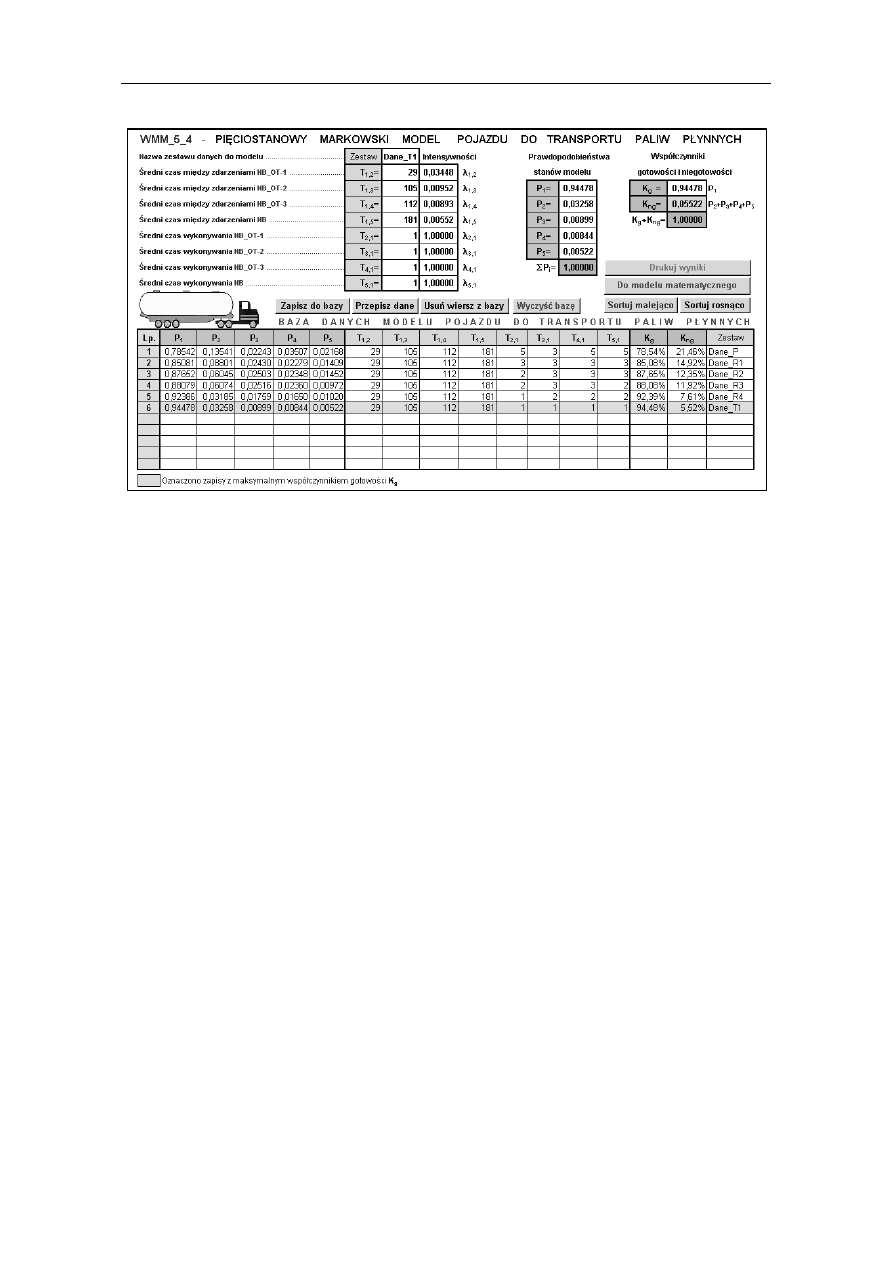
Arkusz roboczy Sym_WMM_5_0 jest arkuszem symulacyjnym (rys. 3). Można w nim

wskazać trzy następujące części:
−

formularz do wprowadzania danych wejściowych modelu (część 1),

−

zakres przedstawiający wyniki obliczeń dokonanych według formuł modelu
matematycznego (część 2),

−

tabela będąca bazą danych wejściowych i odpowiadających im wyników obliczeń
(część 3).

Rys. 3. Widok arkusza roboczego Sym_WMM_5_0 symulatora WMM_5_0.xls w fazie wyjściowej do

badań

Część 3

Część 1

Część 2

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

8

W formularzu do wprowadzania danych wejściowych (początkowych) modelu

deklaruje się:
−

wartość średnią T

1,2

sumarycznych czasów t

1,2

pracy pojazdu między sąsiednimi

zdarzeniami rozpoczęcia obsługi okresowej pierwszej połączonej z naprawą
bieżącą (rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu
pojazdu w stanie pierwszym modelu między sąsiednimi zdarzeniami przejścia z
tego stanu do stanu drugiego modelu); na rys. 3 tę daną wejściową opisano

−

Średni czas między zdarzeniami NB_OT-1;

−

wartość średnią T

1,3

sumarycznych czasów t

1,3

pracy pojazdu między sąsiednimi

zdarzeniami rozpoczęcia obsługi okresowej drugiej połączonej z naprawą bieżącą
(rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu pojazdu w
stanie pierwszym modelu między sąsiednimi zdarzeniami przejścia z tego stanu
do stanu trzeciego modelu); na rys. 3 tę daną wejściową opisano

− Średni czas

między zdarzeniami NB_OT-2;

−

wartość średnią T

1,4

sumarycznych czasów t

1,4

pracy pojazdu między sąsiednimi

zdarzeniami rozpoczęcia obsługi okresowej trzeciej połączonej z naprawą bieżącą
(rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu pojazdu w
stanie pierwszym modelu między sąsiednimi zdarzeniami przejścia z tego stanu
do stanu czwartego modelu); na rys. 3 tę daną wejściową opisano

− Średni czas

między zdarzeniami NB_OT-3;

−

wartość średnią T

1,5

sumarycznych czasów t

1,5

pracy pojazdu między sąsiednimi

zdarzeniami rozpoczęcia naprawy bieżącej (rozumianą inaczej jako wartość
średnia sumarycznego czasu pobytu pojazdu w stanie pierwszym modelu między
sąsiednimi zdarzeniami przejścia z tego stanu do stanu piątego modelu); na rys. 3
tę daną wejściową opisano

− Średni czas między zdarzeniami NB;

−

wartość średnią T

2,1

czasów t

2,1

wykonywania obsługi okresowej pierwszej

połączonej z naprawą bieżącą (rozumianą inaczej jako wartość średnia czasu
pobytu pojazdu w stanie drugim modelu przed przejściem z tego stanu do stanu
pierwszego modelu); na rys. 3

− Średni czas wykonywania NB_OT-1;

−

wartość średnią T

3,1

czasów t

3,1

wykonywania obsługi okresowej drugiej

połączonej z naprawą bieżącą (rozumianą inaczej jako wartość średnia czasu
pobytu pojazdu w stanie trzecim modelu przed przejściem z tego stanu do stanu
pierwszego modelu); na rys. 3

− Średni czas wykonywania NB_OT-2;

−

wartość średnią T

4,1

czasów t

4,1

wykonywania obsługi okresowej trzeciej

połączonej z naprawą bieżącą (rozumianą inaczej jako wartość średnia czasu
pobytu pojazdu w stanie czwartym modelu przed przejściem z tego stanu do stanu
pierwszego modelu); na rys. 3

− Średni czas wykonywania NB_OT-3;

−

wartość średnią T

5,1

czasów t

5,1

wykonywania naprawy bieżącej (rozumianą

inaczej jako wartość średnia czasu pobytu pojazdu w stanie piątym modelu przed
przejściem z tego stanu do stanu pierwszego modelu); na rys. 3

− Średni czas

wykonywania NB.
W symulatorze WMM_5_0.xls umieszczono specjalne procedury operacyjne.

Oprogramowanie wszystkich procedur operacyjnych zostało umieszczone w arkuszu
makr. W wersji użytkowej symulatora arkusz makr jest ukryty. Procedury operacyjne są
przypisane do specjalnych przycisków i nadane są im odpowiednie nazwy (rys. 3).

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

9

Przykład zastosowania modeli do analizy gotowości pojazdów

Na podstawie analizy rzeczywistego systemu eksploatacji pojazdów do transportu paliw
płynnych oraz na podstawie przeprowadzenia procedury modelowania, zbudowano
markowski model matematyczny tych pojazdów i jego odwzorowanie komputerowe
WMM_5_0.xls. W specjalnie zbudowanej bazie danych BD_Y.xls zarejestrowano
przebieg procesu eksploatacji (od 1 stycznia 2000 do 31 grudnia 2001) zestawów
transportowych użytkowanych w dyspozytorni Y. Na podstawie informacji
zgromadzonych w tej bazie można wyznaczać wartości wielkości wejściowych do
modelu komputerowego.

•

Sformułowanie problemu badawczego

W dyspozytorni Y użytkowanych jest pięć zestawów transportowych

składających się z ciągnika siodłowego i naczepy cysternowej (Zestaw_CN_1,
Zestaw_CN_2, Zestaw_CN_3, Zestaw_CN_4 i Zestaw_CN_5). Niech eksploatację
zestawu transportowego opisują charakterystyki czasu zestawione w tabeli 1.

Na podstawie charakterystyk eksploatacyjnych zamieszczonych w tabeli 1

przygotowano zestaw danych wejściowych (początkowych) Dane_P do symulatora
komputerowego WMM_5_0.xls. Po wykonaniu obliczeń stwierdzono m.in., że
wynikający z danych Dane_P współczynnik gotowości zestawów transportowych
kształtuje się na poziomie K

g

=0,78 (tabela 2 i rys. 4) .

Tabela 1. Zestawienie charakterystyk eksploatacyjnych zestawu transportowego ciągnik siodłowy

z naczepą cysternową

Lp.

Opis charakterystyk eksploatacyjnych zestawów transportowych

umieszczonych jako dane wejściowe

w symulatorze komputerowym WMM_5_0 (rys. 3 − część 1)

Oznaczenie

danych

wejściowych

Wartości

danych

Dane_P

1. Średni czas między zdarzeniami NB_OT-1

T

1,2

[dni]

29

2. Średni czas między zdarzeniami NB_OT-2

T

1,3

[dni]

105

3. Średni czas między zdarzeniami NB_OT-3

T

1,4

[dni]

112

4. Średni czas między zdarzeniami NB

T

1,5

[dni]

181

5. Średni czas wykonywania NB_OT-1

T

2,1

[dni]

5

6. Średni czas wykonywania NB_OT-2

T

3,1

[dni]

3

7. Średni czas wykonywania NB_OT-3

T

4,1

[dni]

5

8. Średni czas wykonywania NB

T

5,1

[dni]

5

Źródło: badania własne

Należy rozważyć wdrożenie do eksploatacji zestawów transportowych

użytkowanych w dyspozytorni Y takich przedsięwzięć techniczno-organizacyjnych aby
współczynnik gotowości tych zestawów był nie mniejszy niż

K

g

=0,85.

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

10

Rozwiązanie problemu badawczego
W celu rozwiązania postawionego problemu badawczego wykonano szereg

symulacji z uwzględnieniem różnych przedsięwzięć techniczno-organizacyjnych.
Niektóre z symulowanych przedsięwzięć pozwoliły osiągnąć współczynnik gotowości
zestawów transportowych na poziomie co najmniej K

g

=0,85. Zestawy danych opisujące

najbardziej realne z tych przedsięwzięć oznaczono odpowiednio: Dane_R1, Dane_R2,
Dane_R3, Dane_R4 (tabela 2 i rys. 4).

Sposób interpretacji tych przedsięwzięć

− przy założeniu, że realizacja zadań

transportowych odbywa się za pomocą tych samych zestawów transportowych (o tych
samych charakterystykach niezawodnościowych) i które są kierowane do obsługiwania
według dotychczasowych zasad

− jest następujący:

−

Dane_R1

− ograniczenie do 3 dni czasu pobytu zestawów transportowych w

stanach (wg rys. 1): NB_OT-1, NB_OT-2, NB_OT-3 i NB; pozwala to osiągnąć
współczynnik gotowości K

g

=0,85 (tabela 2 i rys. 4);

−

Dane_R2

− ograniczenie do 2 dni czasu pobytu zestawów transportowych w

stanie NB_OT-1 przy zachowaniu pozostałych warunków obsługi jak w
Dane_R1; pozwala to osiągnąć współczynnik gotowości K

g

=0,87 (tabela 2 i

rys. 4);

−

Dane_R3

− ograniczenie do 2 dni czasu pobytu zestawów transportowych w

stanie NB przy zachowaniu pozostałych warunków obsługi jak w Dane_R2;
pozwala to osiągnąć współczynnik gotowości K

g

=0,88 (tabela 2 i rys. 4);

−

Dane_R4

− ograniczenie do 1 dnia czasu pobytu zestawów transportowych w

stanie NB_OT-1 przy zachowaniu pozostałych warunków obsługi jak w
Dane_R3; pozwala to osiągnąć współczynnik gotowości K

g

=0,92 (tabela 2 i

rys. 4).

Tabela 2. Zestawienie danych i wybranych rozwiązań problemu badawczego

Wartości danych wejściowych i wyniki obliczeń współczynnika

gotowości dla rozpatrywanych zestawów rozwiązań

techniczno−organizacyjnych

Lp.

Oznaczenie

danych

wejściowych

i współczynnika

gotowości

Dane_P

Dane_R1

Dane_R2

Dane_R3

Dane_R4

Dane_T1

1.

T

1,2

[dni]

29

29

29

29

29

29

2.

T

1,3

[dni]

105

105

105

105

105

105

3.

T

1,4

[dni]

112

112

112

112

112

112

4.

T

1,5

[dni]

181

181

181

181

181

181

5.

T

2,1

[dni]

5

3

2

2

1

1

6.

T

3,1

[dni]

3

3

3

3

2

1

7.

T

4,1

[dni]

5

3

3

3

2

1

8.

T

5,1

[dni]

5

3

3

2

2

1

9.

K

g

[−]

0,78

0,85

0,87

0,88

0,92

0,94

Źródło: badania własne

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

11

Rys. 4. Widok arkusza roboczego Sym_WMM_5_0 symulatora WMM_5_0.xls w z wynikami badań

Przy identycznych założeniach można teoretycznie przyjąć, że minimalny czas

pobytu zestawów transportowych w stanach NB_OT-1, NB_OT-2, NB_OT-3 i NB
może być jednodniowy. Po przygotowaniu stosownego zestawu danych (Dane_T1) i
dokonaniu obliczeń stwierdzono, że takie przedsięwzięcie zapewniłoby współczynnik
gotowości K

g

=0,94 (tabela 2 i rys. 4). Wynik ten ma przede wszystkim walor

poznawczy. Warto tu jednak zaznaczyć, że takie parametry pracy służb serwisowych

−

ze względów technicznych i organizacyjnych

− nie są możliwe. Z tego względu dalsze

realne możliwości zwiększenia współczynnika gotowości zestawów transportowych
wiązać się mogą jedynie z podjęciem przedsięwzięć technicznych zwiększających
niezawodność pojazdów np. prowadzących do ograniczenia lub całkowitego
wyeliminowania z ich eksploatacji stanów NB.

Warunki eksploatacji zestawów transportowych odwzorowane w Dane_R1,

Dane_R2, Dane_R3, Dane_R4 pozwalają spełnił warunek K

g

≥0,85. Według autora

niniejszej pracy można je uznać za możliwe do spełnienia. Konieczne jest jednak
usprawnienie organizacji pracy serwisu Południe polegające na ograniczenia czasu
wykonywania obsług technicznych i napraw bieżących zestawów transportowych.

Plik: Pojazd_Operator_Transportu_Paliw.doc opr. Adam Kadziński, Sławomir El

12

Podsumowanie

W opracowaniu przeprowadzono analizę procesu eksploatacji pojazdów do transportu
paliw płynnych użytkowanych w jednej z dyspozytorni paliwowej spółki transportowej.
Dokonano prezentacji wybranego do analizy systemu operatora transportowego przez:
wskazanie na obszar jego działania, przedstawienie pojazdów do transportu paliw
płynnych eksploatowane w systemie i opis realizowanych przez nie zadań.

Punktem wyjścia prowadzonych analiz stał się zarejestrowany w bazie danych

przebieg procesu eksploatacji pojazdów do transportu paliw płynnych. Na tej podstawie
zidentyfikowano stany eksploatacyjne pojazdów i możliwości zmian tych stanów.
Pozwoliło to na stworzenie i rozwiązanie wielostanowego matematycznego modelu
pojazdu do transportu paliw płynnych. Model matematyczny odwzorowano w
komputerowym modelu symulacyjnym o nazwie WMM_5_0.Xls.

W części aplikacyjnej opracowania sformułowano i rozwiązano przykładowy

problem badawczy. W ramach tego przykładu dokonano badań symulacyjnych kilku
zestawów

rozwiązań

techniczno-organizacyjnych

pozwalających

zwiększyć

współczynnik gotowości pojazdów użytkowanych w przykładowej dyspozytorni spółki
transportowej świadczącej w Polsce usługi m.in. na rzecz koncernów paliwowych.