Plik: Autobus_Analiza_Gotowości.doc

ANALIZA GOTOWOŚCI AUTOBUSÓW NA PRZYKŁADZIE

WYBRANEGO OPERATORA ZBIOROWEGO TRANSPORTU

PASAŻERSKIEGO

1. Wprowadzenie

Badania obiektów w warunkach ich rzeczywistej eksploatacji, w szczególności

zaś badania pojazdów, są z reguły pracochłonne. Ich przeprowadzenie związane jest z
wieloma trudnościami organizacyjnymi. Podejmując ryzyko takich badań, będących
kosztownym przedsięwzięciem, należy gruntownie przeanalizować ich niezbędność,
celowość i zakres. Często więc eksperymentowanie na rzeczywistym systemie zastępuje
się badaniami metodami modelowania i symulacji.

Praktyka w zupełności potwierdziła słuszność twierdzenia, że prawidłowe

przygotowanie i zaprogramowanie badań jest niezbędnym warunkiem ich powodzenia.
Stąd nie lekceważąc innych etapów, najwięcej uwagi, wysiłku, środków rzeczowych i
finansowych, należy poświęcić na przygotowanie badań. W fazie prowadzenia analiz
należy uwzględnić takie elementy jak: cel badań, specyfika obiektu badań, ograniczenia
czasowe, możliwości organizacyjno-finansowe, możliwości zastosowania techniki
rejestrowania informacji na etapie ich zbierania, możliwości przetwarzania i
opracowywania wyników badań.

Uwzględniając wskazane tu elementy, przygotowanie do analizy i analizę procesu

eksploatacji autobusów w wybranym systemie operatora transportowego, prowadzono
w następujących etapach:
••••

opis wybranego do analizy systemu operatora transportu autobusowego;

••••

stworzenie bazy danych procesu eksploatacji autobusów;

••••

opracowanie modelu matematycznego i symulacyjnego stanów eksploatacyjnych
autobusów,

••••

wskazanie możliwości zastosowań opracowanych modeli.

2. Wybór autobusów do analiz procesu eksploatacji

W ramach zbiorowego transportu samochodowego występują różne formy i typy

przedsiębiorstw. W zbiorowym samochodowym transporcie pasażerskim wyróżnić
można transport: miejski, wewnętrzny (obsługujący proces produkcyjny jednego
przedsiębiorstwa), regionalny, międzyregionalny, międzymiastowy, dalekobieżny,
międzynarodowy. Od wielu lat w Polsce niepodzielnie w publicznej komunikacji
zbiorowej

największym

operatorem

(przewoźnikiem)

jest

Przedsiębiorstwo

Komunikacji Samochodowej (PKS). W Polsce jest 174 PKS. Operatorzy ci zaspokajają
najniezbędniejsze potrzeby transportowe miast i terenów wiejskich.

Podstawowym elementem systemów logistycznych operatorów zbiorowego

transportu pasażerskiego jest tabor autobusowy. Analizowany w niniejszej pracy
operator transportowy działa w ramach oddziału głównego i dwóch oddziałów
terenowych. Każda z jednostek dysponuje własnym taborem autobusowym. Czasowo
niektóre z autobusów mogą być przesuwane do dyspozycji innych jednostek tego
samego operatora transportowego. W jednostkach tych eksploatowanych jest łącznie
155 autobusów.

Adam Kadziński

2

Podstawową marką jaką dysponuje analizowany operator transportowy są

autobusy Autosan (łącznie 75 pojazdów). Tego rodzaju autobusy są najliczniej
wykorzystywane przez polskich operatorów transportu pasażerskiego. Jest to związane
m.in. ze stosunkowo niską ceną ich zakupu, z kosztami eksploatacji tych pojazdów oraz
różnorodnym i funkcjonalnym ich wyposażeniem..

Do dalszych analiz z autobusów Autosan, którymi dysponuje operator

transportowy losowo wybrano 10 pojazdów.

3. Baza danych procesu eksploatacji autobusów

Podstawą analizy procesu eksploatacji autobusów eksploatowanych w systemie

wybranego operatora transportowego będą zdarzenia eksploatacyjne zidentyfikowane w
życiu tych pojazdów. Głównymi zdarzeniami eksploatacyjnymi są rozpoczęcia i
zakończenia planowych lub nieplanowych obsług autobusów. Chwile czasowe tych
zdarzeń mogą być ustalane m.in. na podstawie dokumentacji procesów użytkowania i
obsługiwania autobusów.

Do analizy procesu eksploatacji autobusów zbudowano bazę danych zdarzeń

eksploatacyjnych. Bazę tę przygotowano w formacie programu Microsoft Excel i
zapamiętano w pliku BD_Autobus.Xls. Rekord bazy danych składa się z pól:

♦

Nr rekordu − typ: liczba,

♦

Data kalendarzowa − typ: data,

♦

Oznaczenie stanu eksploatacyjnego autobusu − typ: tekst.
Dla każdego z wylosowanych autobusów eksploatowanych przez operatora

transportowego utworzono oddzielną bazę danych w postaci arkusza roboczego pliku
BD_Autobus.Xls. W bazach danych umieszczono rekordy odpowiadające eksploatacji
autobusów w okresie 2 lat.

4. Model stanów eksploatacyjnych autobusu

4.1. Stany eksploatacyjne autobusu

Podstawą analizy procesu eksploatacji autobusów eksploatowanych przez

wybranego do analizy operatora zdarzenia eksploatacyjne zidentyfikowane w życiu
tych pojazdów. Głównymi zdarzeniami eksploatacyjnymi są rozpoczęcia i zakończenia
planowych lub nieplanowych obsług autobusów. Chwile czasowe tych zdarzeń mogą
być ustalane m.in. na podstawie dokumentacji procesów użytkowania i obsługiwania
autobusów.

Na podstawie analizy informacji zawartych w dokumentacji procesów

użytkowania i obsługiwania autobusów stwierdzono, że proces eksploatacji

{

}

0

:

)

(

4

≥

t

t

X

pojedynczego autobusu jest procesem czterostanowym. Proces ten przyjmuje:

•

X

4

(t) = 1,

gdy autobus w chwili t jest zdatny i znajduje się w stanie pracy (P);

•

X

4

(t) = 2,

gdy w chwili t w autobusie wykonywane są obsługi okresowe:

pierwsza (OT-1), druga (OT-2) lub trzecia (OT-3);

•

X

4

(t) = 3,

gdy w chwili t w autobusie wykonywana jest naprawa bieżąca (NB)

w związku z zauważonymi uszkodzeniami;

•

X

4

(t) = 4,

gdy w chwili t zdatny do wykonywania zadań autobus przebywa w

rezerwie (R).
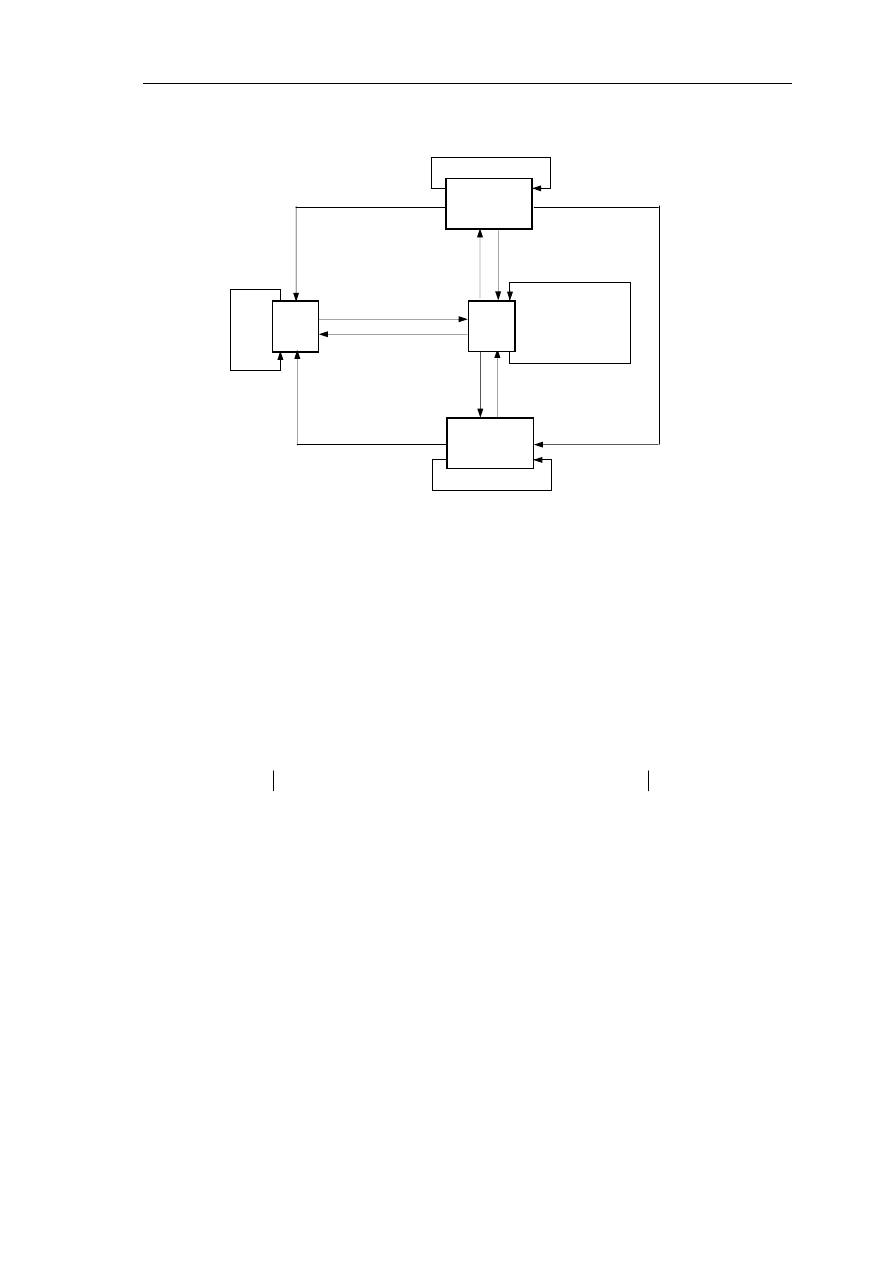
Na podstawie zidentyfikowanych stanów eksploatacyjnych autobusu zbudowano

graf jego stanów eksploatacyjnych pokazany na rysunku 1.

Adam Kadziński

3

Rys. 1. Graf stanów eksploatacyjnych autobusu, gdzie: 1 (P) – stan zdatności (użytkowania) autobusu,
2 (OT-1,2,3) – stan obsług okresowych pierwszej, drugiej i trzeciej, 3 (NB) – stan naprawy bieżącej,
4 (R) – stan przebywania w rezerwie

4.2. Model matematyczny autobusu

Przyjmuje się, że proces eksploatacji autobusów jest procesem Markowa. Proces

stochastyczny

{

}

0

:

)

(

≥

t

t

X

nazywamy procesem Markowa, jeżeli dla dowolnego ciągu

parametrów

n

n

t

t

...

t

t

<

<

<

<

−1

1

0

, dowolnych

R

∈

<

<

<

<

−

n

n

x

x

...

x

x

1

1

0

oraz

,...

,

n

2

1

=

zachodzi równość

.

( )

( )

( )

( )

{

}

( )

( )

{

}

1

1

0

0

1

1

1

1

−

−

−

−

=

=

=

=

=

=

=

n

n

n

n

n

n

n

n

x

t

X

x

t

X

P

x

t

X

,

x

t

X

,...,

x

t

X

x

t

X

P

.

(1)

Równość ta oznacza, że bezpośredni wpływ na stan procesu w chwili t

n

ma jego

stan w chwili t

n-1

.

Dalej będą rozważane procesy Markowa o co najwyżej przeliczalnym zbiorze

stanów

{

}

4

3

2

1

,

,

,

=

S

i zbiorze parametrów czasowych

)

0

+∞

=< ,

T

.

Konsekwencją przyjętych założeń jest fakt, że sumaryczne czasy przebywania

pojazdu w i-tych stanach przed przejściem do j-tych stanów, opisują zmienne losowe o
rozkładach wykładniczych i funkcji gęstości prawdopodobieństwa postaci:

( )

t

j

,

i

j

,

i

j

,

i

t

f

⋅

−

⋅

=

α

α

e

,

{

}

4

3

2

1

,

,

,

j

,

i

∈

,

(2)

gdzie α

i,j

są intensywnościami przejść ze stanów i-tych do stanów j-tych.

4

R

2

OT-1,2,3

3

NB

1

P

Adam Kadziński

4

Zmienną α

i,j

w równaniu (2) należy rozumieć jako intensywność przejścia

autobusu ze stanu i-tego do stanu j-tego, którą można wyznaczyć z zależności:

j

,

i

j

,

i

T

1

=

α

,

{

}

4

3

2

1

,

,

,

j

,

i

∈

,

(3)

gdzie T

i,j

jest wartością średnią wyznaczoną z realizacji t

i,j

zmiennej losowej będącej

sumarycznym czasem przebywania autobusu w i-tym stanie przed przejściem do
stanu j-tego.
W dalszej części opisu modelu matematycznego przyjęto taką konwencję zapisu,

że:

{

}

4

3

2

1

,

,

,

,

)

(

,

,

,

l

...

j

i

...

l,

i

j

,

i

l

,...,

j

,

i

∈

+

+

=

α

α

α

.

(4)

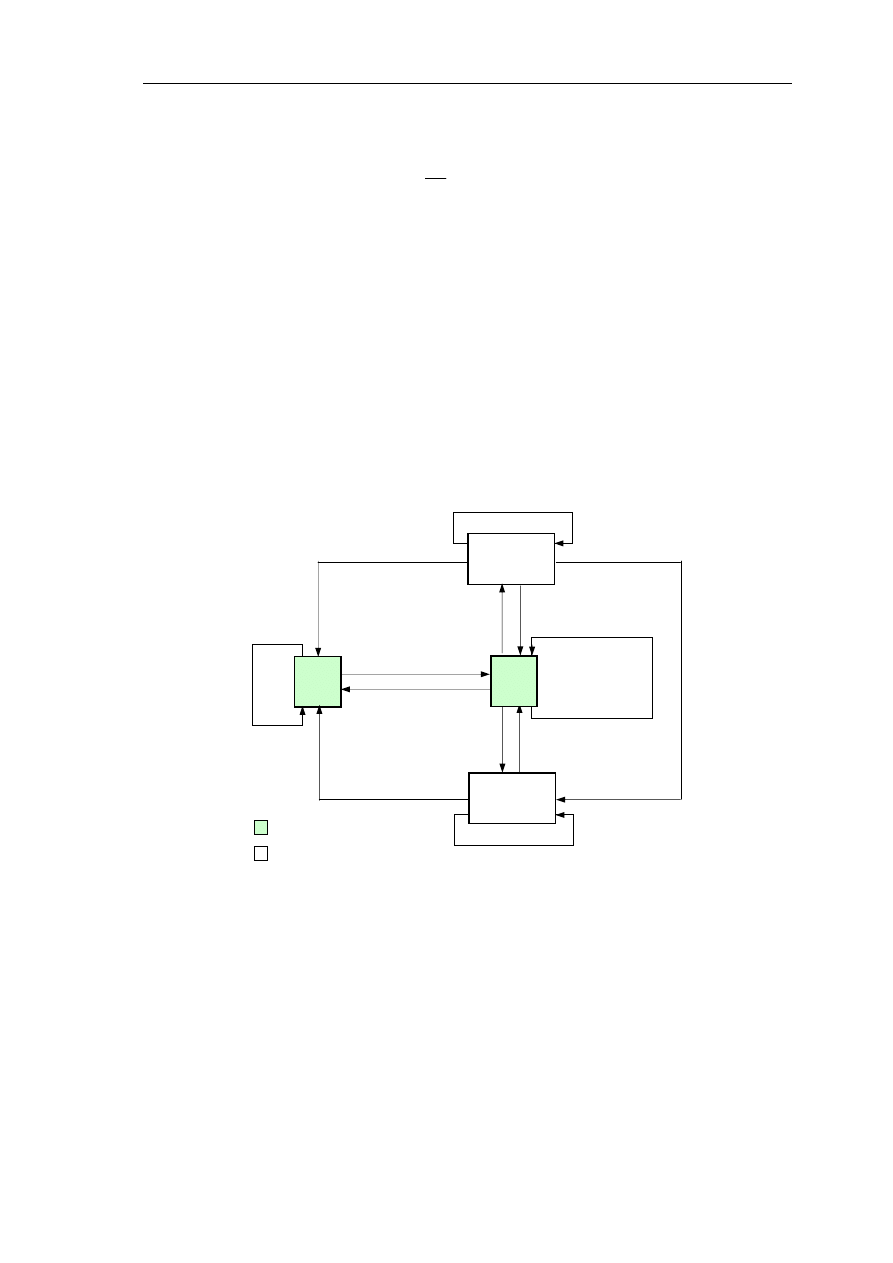
Graf stanów czterostanowego modelu autobusu z formułami matematycznymi na

prawdopodobieństwa przejść między jego stanami pokazano na rysunku 2.

Rys. 2. Graf stanów czterostanowego modelu autobusu (znaczenie oznaczeń stanów autobusu jak

na rys. 1, zaś wyjaśnienie pozostałych oznaczeń zamieszczono w tekście)

Wyznaczenie charakterystyk eksploatacyjnych autobusu odwzorowywanego

zbudowanym tu modelem jest konsekwencją rozwiązania następującego równania:

(

) ( )

P

P

P

∆

⋅

=

∆

+

t

t

t

(5)

gdzie:

( )

t

P

− wektor prawdopodobieństw przebywania autobusu w stanach w chwili t,

(

)

t

t

∆

+

P

− wektor prawdopodobieństw przebywania autobusu w stanach w chwili

(t+

∆t),

P

∆

− macierz prawdopodobieństw przejść między stanami

{

}

4

3

2

1

)]

(

[

∆

,

,

,

j

,

i

,

t

p

ij

∈

=

P

− stany zdatności

− stany niezdatności

4

R

2

OT-1,2,3

3

NB

t

,

∆

⋅

2

1

α

t

,

∆

⋅

−

(2,3,4)

1

1 α

t

,

∆

⋅

1

2

α

t

∆

⋅

1

,

3

α

t

,

∆

⋅

3

1

α

t

,

∆

⋅

3

2

α

t

,

∆

⋅

−

(1,4)

3

1 α

t

,

∆

⋅

−

(1,3,4)

2

1 α

t

,

∆

⋅

4

1

α

t

,

∆

⋅

1

4

α

t

,

∆

⋅

4

3

α

t

,

∆

⋅

4

2

α

t

,

∆

⋅

−

1

4

1 α

1

P

Adam Kadziński

5

Z przyjętych założeń i z rysunku 2 wynika następująca postać macierzy

prawdopodobieństw przejść między stanami modelu autobusu:





























∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

−

=

t

t

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

,

,

,

,

1

4

3

4

3

2

4

3

2

1

1

0

0

1

0

1

1

∆

α

α

α

α

α

α

α

α

α

α

α

α

α

4,1

3,4

(1,4)

3,1

2,4

2,3

)

(1

2,1

1,4

1,3

1,2

)

(

P

(6)

Zatem równanie (5) można zapisać w postaci:

[

] [

]

×

=

∆

+

∆

+

∆

+

∆

+

)

(

P

),

(

P

),

(

P

),

(

P

)

(

P

),

(

P

),

(

P

),

(

P

4

3

2

1

4

3

2

1

t

t

t

t

t

t

t

t

t

t

t

t





























∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

−

∆

⋅

∆

⋅

∆

⋅

∆

⋅

∆

⋅

−

×

t

t

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

,

,

,

,

1

4

3

4

3

2

4

3

2

1

1

0

0

1

0

1

1

α

α

α

α

α

α

α

α

α

α

α

α

α

4,1

3,4

(1,4)

3,1

2,4

2,3

)

(1

2,1

1,4

1,3

1,2

)

(

(7)

lub równoważnie:

(

) ( )

(

)

( )

( )

( )

t

t

t

t

t

t

t

t

t

t

,

,

,

,

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

−

⋅

=

∆

+

1

4

4

1

3

3

1

2

2

1

1

1

P

P

P

1

P

P

α

α

α

α

(2,3,4)

(

) ( )

( )

(

)

t

t

t

t

t

t

,

,

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

(1,3,4)

2

2

2

1

1

2

-

1

P

P

P

α

α

(

) ( )

( )

( )

(

)

t

t

t

t

t

t

t

t

∆

⋅

−

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

(1,4)

,

3

3

3

,

2

2

3

,

1

1

3

1

P

P

P

P

α

α

α

(8)

(

) ( )

( )

( )

( )

(

)

t

t

t

t

t

t

t

t

t

t

,

,

,

,

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

+

1

4

4

4

3

3

4

2

2

4

1

1

4

-

1

P

P

P

P

P

α

α

α

α

Po przekształceniu układu (6) otrzymujemy:

(

) ( )

( )

( )

( )

( )

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

−

=

−

∆

+

1

4

4

1

3

3

1

2

2

1

1

1

1

P

P

P

P

P

P

α

α

α

α

(2,3,4)

(

) ( ) ( )

( )

t

t

t

t

t

t

t

,

,

∆

⋅

⋅

−

∆

⋅

⋅

=

−

∆

+

(1,3,4)

2

2

2

1

1

2

2

P

P

P

P

α

α

(

) ( ) ( )

( )

( )

t

t

t

t

t

t

t

t

t

,

,

,

∆

⋅

⋅

−

∆

⋅

⋅

+

∆

⋅

⋅

=

−

∆

+

(1,4)

3

3

3

2

2

3

1

1

3

3

P

P

P

P

P

α

α

α

(9)

(

) ( ) ( )

( )

( )

( )

t

t

t

t

t

t

t

t

t

t

t

,

,

,

,

∆

⋅

⋅

−

∆

⋅

⋅

+

∆

⋅

⋅

+

∆

⋅

⋅

=

−

∆

+

1

4

4

4

3

3

4

2

2

4

1

1

4

4

P

P

P

P

P

P

α

α

α

α

Następnie

(

) ( )

( )

( )

( )

( )

1

4

4

1

3

3

1

2

2

1

1

1

1

P

P

P

P

P

P

,

,

,

,

t

t

t

t

t

t

t

t

α

α

α

α

⋅

+

⋅

+

⋅

+

⋅

−

=

∆

−

∆

+

(2,3,4)

(

) ( ) ( )

( )

(1,3,4)

,

,

t

t

t

t

t

t

2

2

2

1

1

2

2

P

P

P

P

α

α

⋅

−

⋅

=

∆

−

∆

+

(

) ( ) ( )

( )

( )

(1,4)

,

,

,

t

t

t

t

t

t

t

3

3

3

2

2

3

1

1

3

3

P

P

P

P

P

α

α

α

⋅

−

⋅

+

⋅

=

∆

−

∆

+

(10)

(

) ( ) ( )

( )

( )

( )

1

4

4

4

3

3

4

2

2

4

1

1

4

4

P

P

P

P

P

P

,

,

,

,

t

t

t

t

t

t

t

t

α

α

α

α

⋅

−

⋅

+

⋅

+

⋅

=

∆

−

∆

+

Adam Kadziński

6

Obliczając granicę po obu stronach równań układu można zapisać, że:

(

) ( )

( )

( )

( )

( )

1

4

4

1

3

3

1

2

2

1

1

1

1

0

P

P

P

P

P

P

lim

,

,

,

,

t

t

t

t

t

t

t

t

t

α

α

α

α

⋅

+

⋅

+

⋅

+

⋅

−

=

∆

−

∆

+

→

∆

(2,3,4)

(

) ( ) ( )

( )

(1,3,4)

,

,

t

t

t

t

t

t

t

2

2

2

1

1

2

2

0

P

P

P

P

lim

α

α

⋅

−

⋅

=

∆

−

∆

+

→

∆

(

) ( ) ( )

( )

( )

(1,4)

,

,

,

t

t

t

t

t

t

t

t

3

3

3

2

2

3

1

1

3

3

0

P

P

P

P

P

lim

α

α

α

⋅

−

⋅

+

⋅

=

∆

−

∆

+

→

∆

(11)

(

) ( ) ( )

( )

( )

( )

1

4

4

4

3

3

4

2

2

4

1

1

4

4

0

P

P

P

P

P

P

lim

,

,

,

,

t

t

t

t

t

t

t

t

t

α

α

α

α

⋅

−

⋅

+

⋅

+

⋅

=

∆

−

∆

+

→

∆

a gdy zauważy się, że:

(

) ( )

( )

t

t

t

t

t

t

i

i

i

t

d

dP

P

P

lim

0

=

∆

−

∆

+

→

∆

,

S

∈

i

dla

,

(12)

to

( )

( )

( )

( )

( )

1

4

4

1

3

3

1

2

2

1

1

1

P

P

P

P

d

dP

,

,

,

,

t

t

t

t

t

t

α

α

α

α

⋅

+

⋅

+

⋅

+

⋅

−

=

(2,3,4)

( ) ( )

( )

(1,3,4)

,

,

t

t

t

t

2

2

2

1

1

2

P

P

d

dP

α

α

⋅

−

⋅

=

( ) ( )

( )

( )

(1,4)

,

,

,

t

t

t

t

t

3

3

3

2

2

3

1

1

3

P

P

P

d

dP

α

α

α

⋅

−

⋅

+

⋅

=

(13)

( ) ( )

( )

( )

( )

1

4

4

4

3

3

4

2

2

4

1

1

4

P

P

P

P

d

dP

,

,

,

,

t

t

t

t

t

t

α

α

α

α

⋅

−

⋅

+

⋅

+

⋅

=

Układ (11) jest układem równań różniczkowych liniowych o stałych współczynnikach. W
warunkach ustalonych, tzn.

( )

0

d

dP

,

t

t

i

=

( )

S

∈

=

i

,

t

i

i

dla

P

P

,

(14)

układ ten przyjmuje postać następującą:

1

4

4

1

3

3

1

2

2

1

1

P

P

P

P

0

,

,

,

,

α

α

α

α

⋅

+

⋅

+

⋅

+

⋅

−

=

(2,3,4)

(1,3,4)

,

,

2

2

2

1

1

P

P

0

α

α

⋅

−

⋅

=

(1,4)

,

,

,

3

3

3

2

2

3

1

1

P

P

P

0

α

α

α

⋅

−

⋅

+

⋅

=

(15)

1

4

4

4

3

3

4

2

2

4

1

1

P

P

P

P

0

,

,

,

,

α

α

α

α

⋅

−

⋅

+

⋅

+

⋅

=

Z układu równań (13) wynikają następujące zależności:

1

2

2

1

2

P

P

⋅

=

(1,3,4)

,

,

α

α

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

3

P

P

⋅















⋅

+

=

(1,3,4)

(1,4)

(1,4)

α

α

α

α

α

α

(16)

1

,

2

2

,

1

,

3

3

,

2

1

,

4

4

,

3

,

3

3

,

1

1

,

4

4

,

3

,

2

2

,

1

1

,

4

4

,

2

1

,

4

4

,

1

4

P

P

⋅















⋅

⋅

+

⋅

+

⋅

+

=

(1,3,4)

(1,4)

(1,4)

(1,3,4)

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

Adam Kadziński

7

Ponieważ

4

3

2

1

P

P

P

P

1

+

+

+

=

,

(17)

+

⋅















⋅

+

+

⋅

+

=

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

2

2

,

1

1

P

P

P

1

(1,3,4)

(1,4)

(1,4)

(1,3,4)

α

α

α

α

α

α

α

α

1

,

2

2

,

1

,

3

3

,

2

1

,

4

4

,

3

,

3

3

,

1

1

,

4

4

,

3

,

2

2

,

1

1

,

4

4

,

2

1

,

4

4

,

1

P

⋅















⋅

⋅

+

⋅

+

⋅

+

+

(1,3,4)

(1,4)

(1,4)

(1,3,4)

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

,

(18)

a prawdopodobieństwo przebywania autobusu w poszczególnych stanach modelu można opisać
następującymi wzorami:

,

1

1

1

P

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

4

4

,

3

1

,

4

4

,

2

,

3

3

,

2

,

2

2

,

1

1

,

4

4

,

1

,

3

3

,

1

1















⋅

+

⋅

+















+

+

⋅

+

+

+

=

(1,3,4)

(1,4)

(1,4)

(1,4)

(1,3,4)

(1,4)

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

(19)

1

2

2

1

2

P

P

⋅

=

(1,3,4)

,

,

α

α

(20)

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

3

P

P

⋅















⋅

+

=

(1,3,4)

(1,4)

(1,4)

α

α

α

α

α

α

(21)

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

4

4

,

3

,

2

2

,

1

1

,

4

4

,

2

1

,

4

4

,

1

4

P

P

⋅





























⋅

+

⋅

+

⋅

+

=

(1,3,4)

(1,4)

(1,4)

(1,3,4)

α

α

α

α

α

α

α

α

α

α

α

α

α

α

(22)

Uwzględniając to, że suma prawdopodobieństw przebywania autobusu w stanach

zdatności (rys. 2) jest współczynnikiem gotowości autobusu K

g

oraz suma prawdopodobieństw

przebywania autobusu w stanach niezdatności (rys. 2) jest jego współczynnikiem niegotowości
K

ng

, otrzymujemy odpowiednio















⋅

+

⋅

+















+

+

⋅

+

+

+





























⋅

+

⋅

+

⋅

+

+

=

+

=

(1,3,4)

(1,4)

(1,4)

(1,4)

(1,3,4)

(1,4)

(1,3,4)

(1,4)

(1,4)

(1,3,4)

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

4

4

,

3

1

,

4

4

,

2

,

3

3

,

2

,

2

2

,

1

1

,

4

4

,

1

,

3

3

,

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

4

4

,

3

,

2

2

,

1

1

,

4

4

,

2

1

,

4

4

,

1

4

1

1

1

1

P

P

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

g

K

,

(23)















⋅

+

⋅

+















+

+

⋅

+

+

+

⋅

+

+

=

+

=

(1,3,4)

(1,4)

(1,4)

(1,4)

(1,3,4)

(1,4)

(1,3,4)

(1,4)

(1,4)

(1,3,4)

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

1

,

4

4

,

3

1

,

4

4

,

2

,

3

3

,

2

,

2

2

,

1

1

,

4

4

,

1

,

3

3

,

1

,

2

2

,

1

,

3

3

,

2

,

3

3

,

1

,

2

2

,

1

3

2

1

1

P

P

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

ng

K

.

(24)

Adam Kadziński

8

4.3. Komputerowy model symulacyjny autobusu

Formuły matematyczne modelu autobusu

oprogramowano

w

symulatorze

komputerowym Symulator_Autobusu.xls. Program Symulator_Autobusu.xls jest aplikacją
opracowaną w programie Microsoft Excel.

Podstawową częścią symulatora jest arkusz roboczy Model_symulacyjny_autobusu.

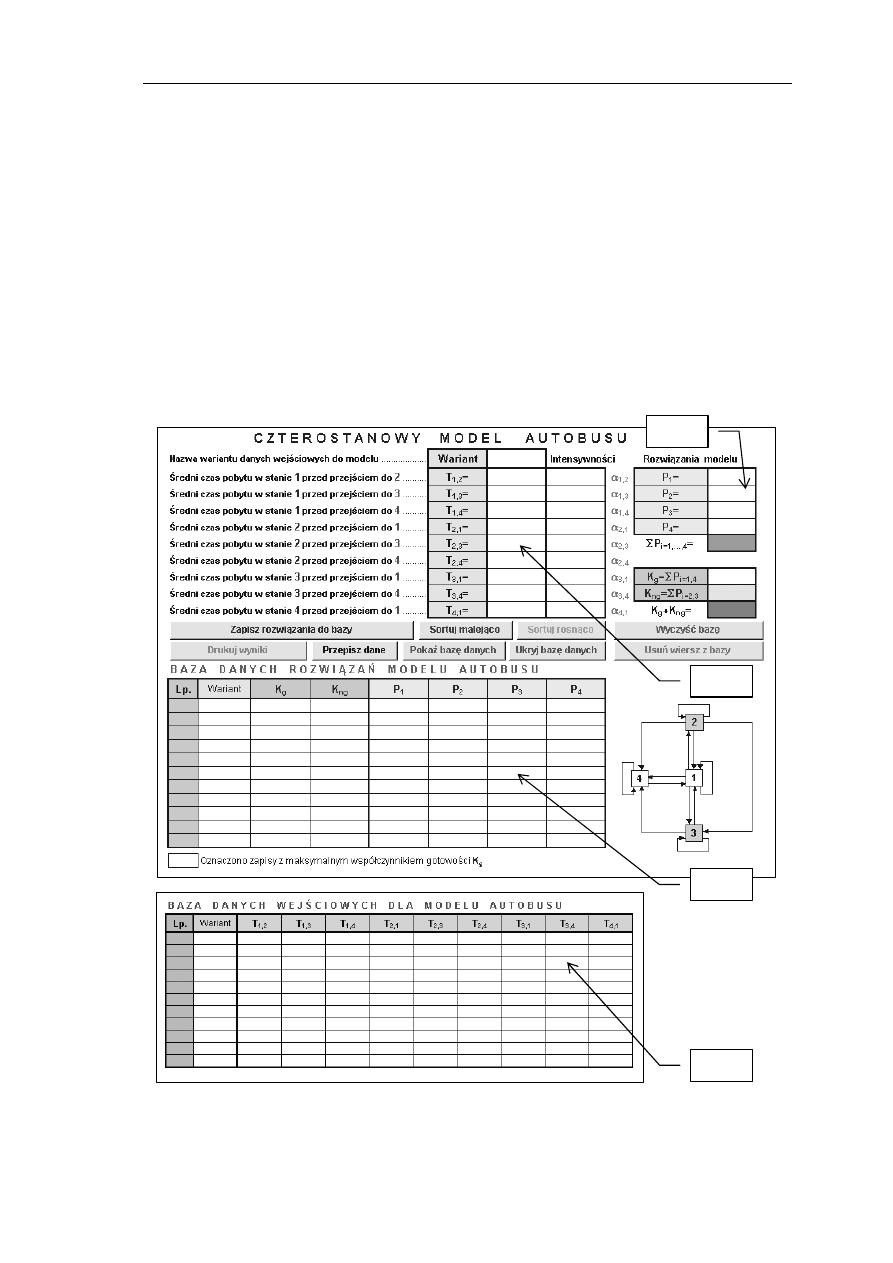
Można w nim wskazać cztery następujące części (rys. 3):

−

formularz do wprowadzania danych modelu (

część 1

),

−

zakres przedstawiający wyniki obliczeń dokonanych według formuł modelu
matematycznego (

część 2

),

−

tabela stanowiąca bazę danych kolejnych zestawów (wariantów) danych wejściowych
modelu (część 3),

−

tabela stanowiąca bazę danych wyników obliczeń dla odpowiednich zestawów danych
wejściowych modelu (część 4).

Rys. 3. Widok arkusza roboczego Model_symulacyjny_autobusu symulatora Symulator_autobusu.xls w fazie

wyjściowej do badań

Część 1

Część 2

Część 4

Część 3

Adam Kadziński

9

W formularzu do wprowadzania danych modelu (rys. 3 −

część 1

) deklaruje się:

−

wartość średnią T

1,2

sumarycznych czasów t

1,2

pracy autobusu między sąsiednimi

zdarzeniami rozpoczęcia jednej z obsług okresowych (rozumianą inaczej jako
wartość średnia sumarycznego czasu pobytu autobusu w stanie pierwszym
modelu między sąsiednimi zdarzeniami przejścia z tego stanu do stanu drugiego
modelu); na rys. 3 tę daną wejściową opisano − Średni czas pobytu w stanie 1
przed przejściem do 2;

−

wartość średnią T

1,3

sumarycznych czasów t

1,3

pracy autobusu między sąsiednimi

zdarzeniami rozpoczęcia naprawy bieżącej (rozumianą inaczej jako wartość
średnia sumarycznego czasu pobytu autobusu w stanie pierwszym modelu między
sąsiednimi zdarzeniami przejścia z tego stanu do stanu trzeciego modelu); na
rys. 3 tę daną wejściową opisano − Średni czas pobytu w stanie 1 przed
przejściem do 3;

−

wartość średnią T

1,4

sumarycznych czasów t

1,4

pracy autobusu między sąsiednimi

zdarzeniami przejścia do stanu rezerwy (rozumianą inaczej jako wartość średnia
sumarycznego czasu pobytu autobusu w stanie pierwszym modelu między
sąsiednimi zdarzeniami przejścia z tego stanu do stanu czwartego modelu); na
rys. 3 tę daną wejściową opisano − Średni czas pobytu w stanie 1 przed
przejściem do 4;

−

wartość średnią T

2,1

sumarycznych czasów t

2,1

wykonywania jednej z obsług

technicznych autobusu między sąsiednimi zdarzeniami skierowania po obsłudze
do pracy (rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu
pojazdu w stanie drugim modelu między sąsiednimi zdarzeniami przejścia z tego
stanu do stanu pierwszego modelu); na rys. 3 tę daną wejściową opisano − Średni
czas pobytu w stanie 2 przed przejściem do 1;

−

wartość średnią T

2,3

sumarycznych czasów t

2,3

wykonywania jednej z obsług

technicznych autobusu między sąsiednimi zdarzeniami skierowania po obsłudze
do naprawy bieżącej (rozumianą inaczej jako wartość średnia sumarycznego
czasu pobytu pojazdu w stanie drugim modelu między sąsiednimi zdarzeniami
przejścia z tego stanu do stanu trzeciego modelu); na rys. 3 − Średni czas pobytu
w stanie 2 przed przejściem do 3;

−

wartość średnią T

2,4

sumarycznych czasów t

2,4

wykonywania jednej z obsług

technicznych autobusu między sąsiednimi zdarzeniami skierowania po obsłudze
do rezerwy (rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu
pojazdu w stanie drugim modelu między sąsiednimi zdarzeniami przejścia z tego
stanu do stanu czwartego modelu); na rys. 3 − Średni czas pobytu w stanie 2 przed
przejściem do 4;

−

wartość średnią T

3,1

sumarycznych czasów t

3,1

przeprowadzania naprawy bieżącej

autobusu między sąsiednimi zdarzeniami skierowania po naprawie do pracy
(rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu pojazdu w
stanie trzecim modelu między sąsiednimi zdarzeniami przejścia z tego stanu do
stanu pierwszego modelu); na rys. 3 − Średni czas pobytu w stanie 3 przed
przejściem do 1;

−

wartość średnią T

3,4

sumarycznych czasów t

3,4

przeprowadzania naprawy bieżącej

autobusu między sąsiednimi zdarzeniami skierowania po naprawie do rezerwy
(rozumianą inaczej jako wartość średnia sumarycznego czasu pobytu pojazdu w
stanie trzecim modelu między sąsiednimi zdarzeniami przejścia z tego stanu do
stanu czwartego modelu); na rys. 3 − Średni czas pobytu w stanie 3 przed
przejściem do 4;

Adam Kadziński

10

−

wartość średnią T

4,1

czasów t

4,1

przebywania autobusu w rezerwie (rozumianą

inaczej jako wartość średnia czasu pobytu pojazdu w stanie czwartym modelu
przed przejściem z tego stanu do stanu pierwszego modelu); na rys. 3 − Średni
czas pobytu w stanie 4 przed przejściem do 1.
W aplikacji Symulator_Autobusu.xls umieszczono specjalne procedury operacyjne.

Oprogramowanie wszystkich procedur operacyjnych zostało umieszczone w arkuszu
makr. W wersji użytkowej symulatora arkusz makr jest ukryty. Procedury operacyjne są
przypisane do specjalnych przycisków i nadane są im odpowiednie nazwy (rys. 3).
Pełna lista i znaczenie procedur operacyjnych przedstawiają się następująco:

•

zapis wariantu (zestawu) danych wejściowych i odpowiadających im wyników
obliczeń

do

baz

danych

modelu

autobusu

(przycisk

»Zapisz rozwiązania do bazy«),

•

sortowanie baz danych modelu autobusu w każdym z pól rekordu baz (przyciski
»Sortuj malejąco« i »Sortuj rosnąco«); przed naciśnięciem przycisku należy
wskazać pole rekordu − przez umieszczenie w nim kursora − według którego ma
nastąpić sortowanie,

•

usuwanie wybranych rekordów z baz danych (przycisk »Usuń wiersz z bazy«);
przed naciśnięciem przycisku należy wskazać rekord − przez umieszczenie w nim
kursora − który ma zostać usunięty,

•

całkowite czyszczenie baz danych (przycisk »Wyczyść bazę«),

•

przepisanie danych ze wskazanego rekordu bazy danych wejściowych do
formularza danych wejściowych modelu (przycisk »Przepisz dane«); przed
naciśnięciem przycisku należy wskazać rekord − przez umieszczenie w nim
kursora − z którego dane mają ulec przepisaniu,

•

ukrywanie i ponowne pokazywanie bazy danych wejściowych modelu autobusu
(przyciski »Ukryj bazę danych« i »Pokaż bazę danych«),

•

drukowanie aktualnej postaci arkusza roboczego Model_symulacyjny_autobusu a
m.in. wszystkich rekordów baz danych (przycisk »Drukuj wyniki«).

Adam Kadziński

11

4.4. Przykłady zastosowania modeli autobusu

♦ Problem badawczy 1

Na podstawie informacji zgromadzonych w bazach danych odpowiadających

eksploatacji autobusów w okresie 2 lat należy wyznaczyć średnie sumaryczne czasy
pobytu poszczególnych autobusów (wg oznaczeń pojazdów przyjętych w
podrozdziale 2) w stanach i-tych przed przejściem do stanów j-tych (wg oznaczeń
stanów jak na rys. 1). Zestawienia średnich sumarycznych czasów pobytu w stanach
i-tych przed przejściem do stanów j-tych - dla dwu wybranych autobusów -
zamieszczono w tabelach 1 i 2.

Tabela 1

Zestawienie średnich sumarycznych czasów pobytu autobusu A1

w stanach i-tych przed przejściem do stanów j-tych

Lp.

Opis średnich sumarycznych czasów pobytu

jak w symulatorze komputerowym

Symulator_Autobusu.xls – rys. 3

Oznaczenie

średnich

czasów

Wartości średnich

czasów

[dni]

1. Średni czas pobytu w stanie 1 przed przejściem do stanu 2

T

1,2

39,3

2. Średni czas pobytu w stanie 1 przed przejściem do stanu 3

T

1,3

69,8

3. Średni czas pobytu w stanie 1 przed przejściem do stanu 4

T

1,4

28,5

4. Średni czas pobytu w stanie 2 przed przejściem do stanu 1

T

2,1

2,0

5. Średni czas pobytu w stanie 2 przed przejściem do stanu 3

T

2,3

24,0

6. Średni czas pobytu w stanie 2 przed przejściem do stanu 4

T

2,4

8.0

7. Średni czas pobytu w stanie 3 przed przejściem do stanu 1

T

3,1

5,8

8. Średni czas pobytu w stanie 3 przed przejściem do stanu 4

T

3,4

52,0

9. Średni czas pobytu w stanie 4 przed przejściem do stanu 1

T

4,1

1,0

Źródło: badania własne

Tabela 2

Zestawienie średnich sumarycznych czasów pobytu autobusu A3

w stanach i-tych przed przejściem do stanów j-tych

Lp.

Opis średnich sumarycznych czasów pobytu

jak w symulatorze komputerowym

Symulator_Autobusu.xls – rys. 3

Oznaczenie

średnich

czasów

Wartości średnich

czasów

[dni]

1. Średni czas pobytu w stanie 1 przed przejściem do stanu 2

T

1,2

74,4

2. Średni czas pobytu w stanie 1 przed przejściem do stanu 3

T

1,3

95,7

3. Średni czas pobytu w stanie 1 przed przejściem do stanu 4

T

1,4

27,9

4. Średni czas pobytu w stanie 2 przed przejściem do stanu 1

T

2,1

2,4

5. Średni czas pobytu w stanie 2 przed przejściem do stanu 3

T

2,3

19,0

6. Średni czas pobytu w stanie 2 przed przejściem do stanu 4

T

2,4

brak zdarzenia

7. Średni czas pobytu w stanie 3 przed przejściem do stanu 1

T

3,1

2,1

8. Średni czas pobytu w stanie 3 przed przejściem do stanu 4

T

3,4

15,0

9. Średni czas pobytu w stanie 4 przed przejściem do stanu 1

T

4,1

1,0

Źródło: badania własne

Adam Kadziński

12

Tak przygotowane zestawy danych jak w tabelach 1 i 2, mogą być pomocne do

wyznaczenia charakterystyk eksploatacyjnych kolejnych autobusów. Lista tych
charakterystyk może przedstawiać się następująco:
-

prawdopodobieństwo stanu zdatności i realizacji przez autobus zadań − P

1

,

-

prawdopodobieństwo przeprowadzania obsług okresowych autobusu − P

2

,

-

prawdopodobieństwo przeprowadzania napraw bieżących autobusu − P

3

,

-

prawdopodobieństwo przebywania autobusu w rezerwie − P

4

,

-

współczynnik gotowości autobusu − K

g

,

-

współczynnik niegotowości autobusu − K

ng

.

Do wyznaczenia charakterystyk eksploatacyjnych autobusów wykorzystano

Symulator_Autobusu.xls opracowany na podstawie czterostanowego markowskiego
modelu autobusu. W tabeli 3 zestawiono obliczone wartości charakterystyk
eksploatacyjnych wszystkich badanych autobusów. Dodatkowo wyniki tych obliczeń
(posortowane wg rosnącego współczynnika gotowości autobusu) wraz z listą
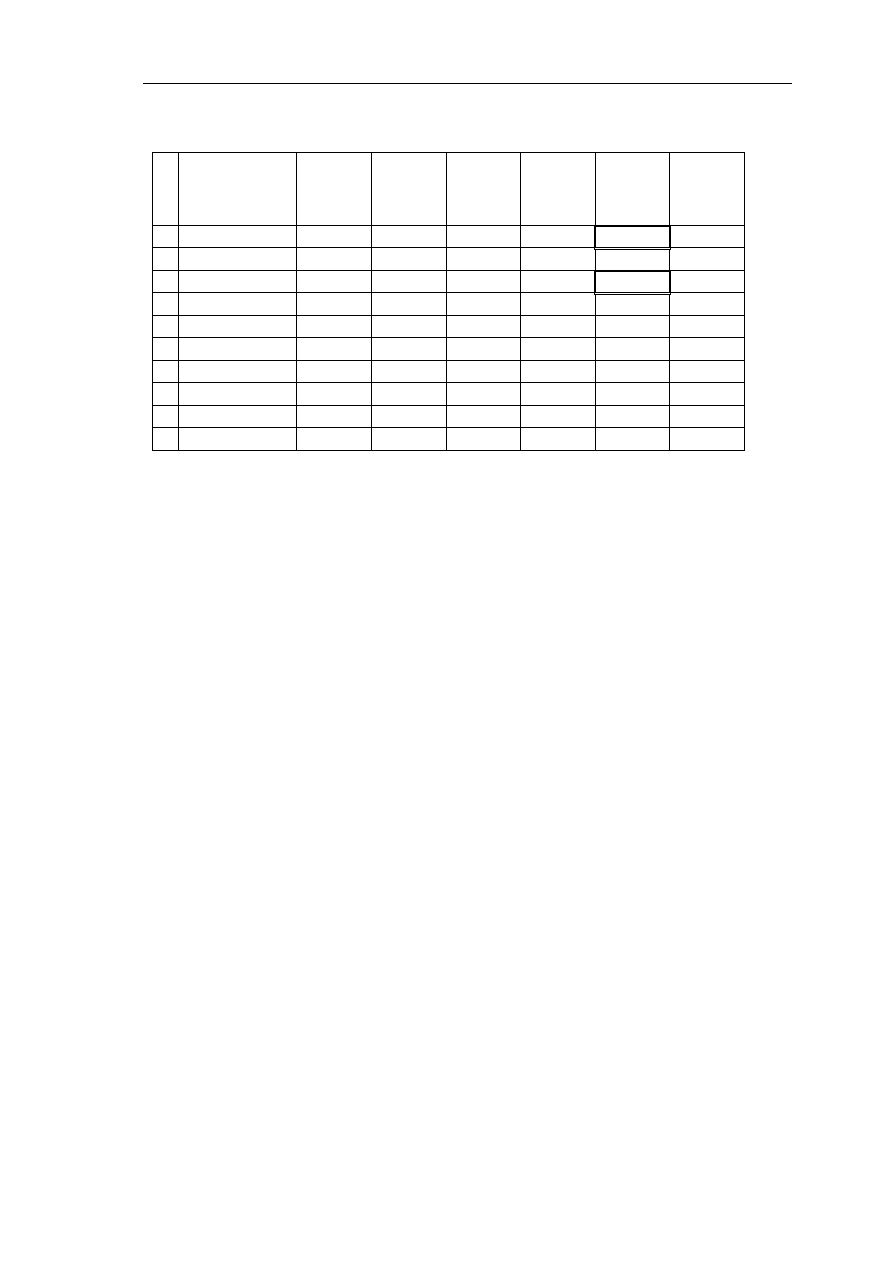
wszystkich danych wejściowych, przedstawiono na rysunku 4.

Adam Kadziński

13

Rys. 4. Widok symulatora komputerowego Symulator_Autobusu.xls z wartościami charakterystyk

eksploatacyjnych wszystkich badanych autobusów i listą danych wejściowych odpowiadającymi

problemowi badawczemu 1

Adam Kadziński

14

Tabela 3

Zestawienie charakterystyk eksploatacyjnych dziesięciu badanych autobusów

Lp.

Oznaczenie

autobusu

P

1

P

2

P

3

P

4

K

g

K

ng

1.

A1

0,86006

0,03283

0,07145

0,03566

0,8957

0,1043

Min

2.

A2

0,88513

0,04082

0,03154

0,04251

0,9276

0,0724

3.

A3

0,91914

0,02632

0,02025

0,03429

0,9534

0,0466

Max

4.

A4

0,91980

0,0592

0,02686

0,02742

0,9472

0,0528

5.

A5

0,89198

0,03964

0,02591

0,04246

0,9344

0,0656

6.

A6

0,90428

0,01920

0,03284

0,04368

0,9480

0,0520

7.

A7

0,89353

0,04922

0,01846

0,03880

0,9323

0,0677

8.

A8

0,89970

0,02460

0,03704

0,03867

0,9384

0,0616

9.

A9

0,88600

0,02314

0,05665

0,03421

0,9202

0,0798

10.

A10

0,89202

0,02597

0,04500

0,03701

0,9290

0,0710

Źródło: badania własne

Ze zrealizowanych obliczeń wynika, że najmniejszym współczynnikiem

gotowości charakteryzuje się autobus A1, zaś największym współczynnikiem
gotowości legitymuje się autobus A3 (tabela 3).

Relatywnie najniższy współczynnik gotowości autobusu A1 wynika głównie ze

stosunkowo częstego kierowania autobusu do przeglądów okresowych i konieczności
przeprowadzania częstych napraw bieżących (tabela 1). Dodatkowo niewątpliwie na
niski współczynnik gotowości autobusu A1 ma wpływ znaczna wartość średniego
czasu wykonywania napraw bieżących tego autobusu (5,8 dnia – tabela 1).

Adam Kadziński

15

♦ Problem badawczy 2

Przyjmijmy, że proces eksploatacji pojedynczego autobusu odwzorowuje

markowski czterostanowy model. Niech eksploatację przeciętnego autobusu
wykorzystywanego przez wybranego operatora transportowego opisują charakterystyki
czasowe stanów eksploatacyjnych zestawione w tabeli 4.

Tabela 4

Zestawienie średnich sumarycznych czasów pobytu przeciętnego autobusu (ustalonego na podstawie

autobusów A1

÷ A10) w stanach i-tych przed przejściem do stanów j-tych

Lp.

Opis danych wejściowych (początkowych)

jak w symulatorze komputerowym

Symulator_Autobusu.xls – rys. 4.3

Oznaczenie

danych

wejściowych

Wartości danych

zestawu

Aśr_1-10 [dni]

1. Średni czas pobytu w stanie 1 przed przejściem do stanu 2

T

1,2

61,1

2. Średni czas pobytu w stanie 1 przed przejściem do stanu 3

T

1,3

71,0

3. Średni czas pobytu w stanie 1 przed przejściem do stanu 4

T

1,4

28,2

4. Średni czas pobytu w stanie 2 przed przejściem do stanu 1

T

2,1

2,8

5. Średni czas pobytu w stanie 2 przed przejściem do stanu 3

T

2,3

21,8

6. Średni czas pobytu w stanie 2 przed przejściem do stanu 4

T

2,4

9,0

7. Średni czas pobytu w stanie 3 przed przejściem do stanu 1

T

3,1

3,3

8. Średni czas pobytu w stanie 3 przed przejściem do stanu 4

T

3,4

16,3

9. Średni czas pobytu w stanie 4 przed przejściem do stanu 1

T

4,1

1,0

Źródło: badania własne

Takie jak w tabeli 4 charakterystyki średnich sumarycznych czasów pobytu

autobusu w określonych stanach przed przejściem do innych możliwych stanów
(zgodnie z modelem jak na rys. 2) generują współczynnik gotowości pojazdu
K

g

= 0,9333 (zestaw danych i rozwiązań Aśr_1-10 w tabeli 5).

Interesującym wydaje się uzyskanie odpowiedzi na pytanie: „O ile zwiększy się

współczynnik

gotowości

autobusu

o

charakterystykach

czasowych

stanów

eksploatacyjnych autobusu przeciętnego, gdy skróceniu ulegną czasy pobytu w stanie
obsług okresowych (stan 2 – rys. 3) i w stanie napraw bieżących (stan 3 – rys. 3)?”.

W celu odpowiedzi na postawione pytanie przygotowano kilka zestawów danych

wejściowych modelu odpowiadających różnym wariantom średnich czasów trwania
obsług okresowych (T

2,1

) i napraw bieżących (T

3,1

). Zestawy danych wejściowych i

współczynnik gotowości uzyskany przy tych warunkach eksploatacji autobusów
zestawiono w tabeli 5, natomiast na rysunku 5 pokazano wydruk wyników obliczeń
wszystkich charakterystyk eksploatacyjnych autobusów uzyskanych za pomocą
symulatora komputerowego Symulator_Autobusu.xls

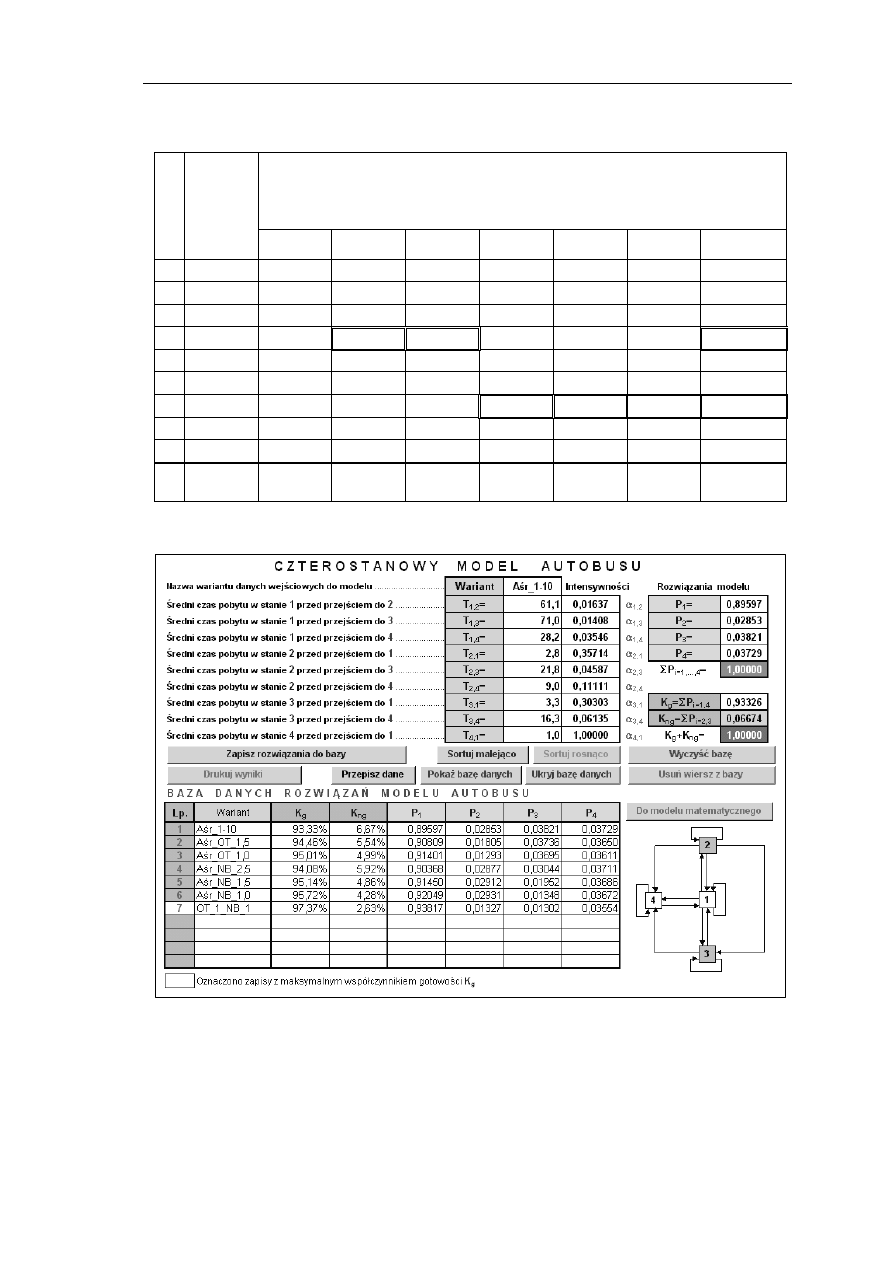
Adam Kadziński

16

Tabela 5

Zestawy danych i niektóre rozwiązania w problemie badawczym 2

Lp.

Oznacz.

danych i

współcz.

gotowości

Wartości danych wejściowych i wyniki obliczeń współczynnika gotowości

dla zestawów (wariantów) danych

Aśr_1-10 Aśr_OT_1,5 Aśr_OT_1,0 Aśr_NB_2,5 Aśr_NB_1,5 Aśr_NB_1,0 OT_1_NB_1

1.

T

1,2

[dni]

61,1

61,1

61,1

61,1

61,1

61,1

61,1

2.

T

1,3

[dni]

71,0

71,0

71,0

71,0

71,0

71,0

71,0

3.

T

1,4

[dni]

28,2

28,2

28,2

28,2

28,2

28,2

28,2

4.

T

2,1

[dni]

2,8

1,5

1,0

2,8

2,8

2,8

1,0

5.

T

2,3

[dni]

21,8

21,8

21,8

21,8

21,8

21,8

21,8

6.

T

2,4

[dni]

9,0

9,0

9,0

9,0

9,0

9,0

9,0

7.

T

3,1

[dni]

3,3

3,3

3,3

2,5

1,5

1,0

1,0

8.

T

3,4

[dni]

16,3

16,3

16,3

16,3

16,3

16,3

16,3

9.

T

4,1

[dni]

1,0

1,0

1,0

1,0

1,0

1,0

1,0

10.

K

g

[

−]

0,9333

0,9446

0,9501

0,9408

0,9514

0,9572

0,9737

Źródło: badania własne

Rys. 5. Wydruk wyników obliczeń charakterystyk eksploatacyjnych autobusów uzyskanych za pomocą

symulatora komputerowego Symulator_Autobusu.xls a związanych z problemem badawczym 2

Zestawy danych traktowane jako warianty zmian technicznych i/lub

organizacyjnych (tabela 5 i rys. 5) w eksploatacji autobusów należy rozumieć m.in.
następująco:

Adam Kadziński

17

•

Aśr_OT_1,5 − skrócić czasy t

2,1

(czasy wykonywania przeglądów okresowych) do

takich aby ich wartość średnia T

2,1

była nie większa niż 1,5 dnia;

•

OT_1_NB_1 − skrócić czasy t

2,1

(czasy wykonywania przeglądów okresowych)

do takich aby ich wartość średnia T

2,1

była nie większa niż 1 dzień i jednocześnie

skrócić czasy t

3,1

(czasy wykonywania napraw bieżących) do takich aby ich wartość

średnia T

3,1

była nie większa niż 1 dzień.

Z przedstawionych rezultatów badań symulacyjnych wynika, że poprzez

skrócenie czasów pobytu autobusu w stanie obsług okresowych i/lub w stanie napraw
bieżących, można uzyskać zwiększenie współczynnika gotowości od wartości
K

g

=0,9333 (zestaw danych Aśr_1-10) do wartości K

g

=0,9737 (zestaw danych

OT_1_NB_1).

5. Podsumowanie

W pracy przeprowadzono analizę procesu eksploatacji autobusów wybranego

operatora transportowego. Dokonano prezentacji wybranego do analizy systemu
operatora transportowego przez: wskazanie na obszar jego działania, przedstawienie
pojazdów eksploatowanych w systemie i opis realizowanych przez nie zadań.

Punktem wyjścia prowadzonych analiz stał się zarejestrowany w bazie danych

przebieg procesu eksploatacji autobusów. Na tej podstawie zidentyfikowano stany
eksploatacyjne autobusów i możliwości zmian tych stanów. Pozwoliło to na stworzenie
i

rozwiązanie

wielostanowego

matematycznego

modelu

autobusu.

Model

matematyczny odwzorowano w komputerowym modelu symulacyjnym o nazwie
Symulator_autobusu.xls.

W części aplikacyjnej pracy sformułowano i rozwiązano przykładowe problemy

badawcze. W ramach tych przykładów dokonano badań symulacyjnych kilku zestawów
rozwiązań techniczno-organizacyjnych pozwalających m.in. zwiększyć współczynnik
gotowości autobusów użytkowanych przez wybranego do analizy operatora zbiorowego
transportu pasażerskiego.