
Uogólnienie mocy biernej
Grzegorz Kosobudzki

Plan wystąpienia
• Moce w obwodach z sinusoidalnymi
przebiegami napięcia i prądu
• Teoria mocy S.Fryzego
• Teoria mocy C. Budeanu
• Teorie mocy – rozkład prądu na składowe
• Moce wg IEEE 1459-2010
• Uogólniona moc bierna
• Podsumowanie
2

3
Moc prądu sinusoidalnego
)
sin(
2
)
sin(
2
t
I
i
t
U
u
)
2
sin(
sin
))
2
cos(
1
(
cos
t
UI
p
t
UI
p
p
p
p
ui
p
q
a
q
a
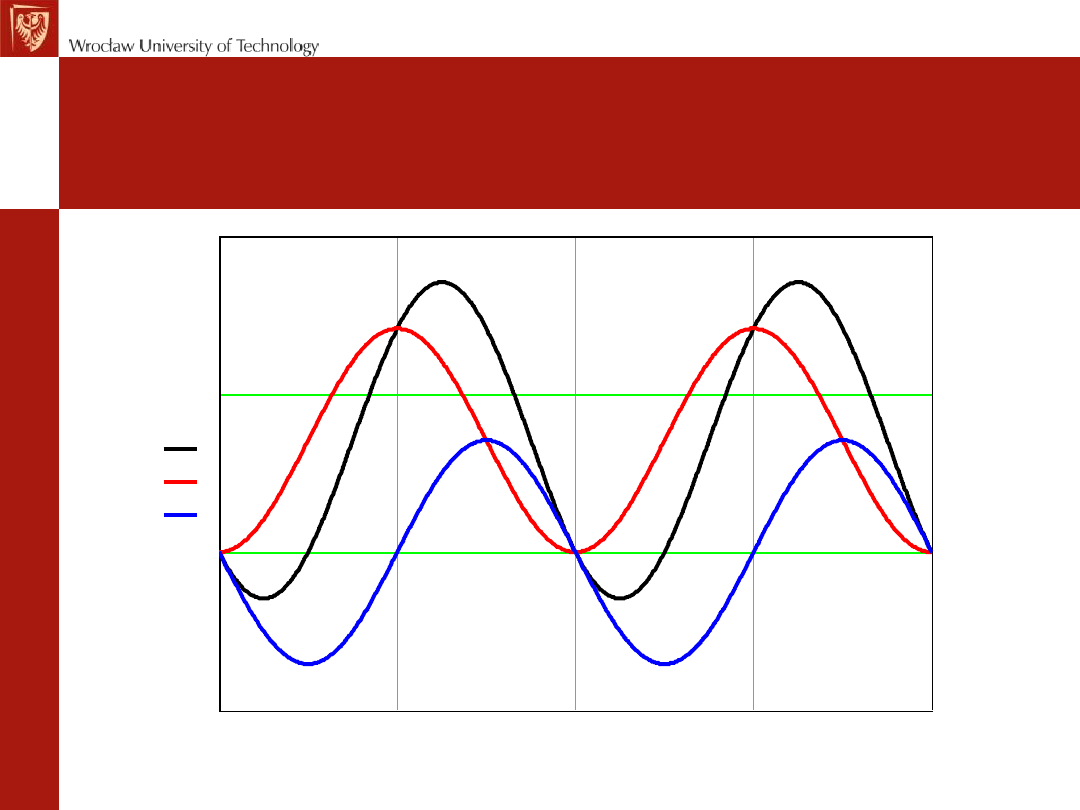
4
Moc prądu sinusoidalnego
0
0.01
0.02
0.03
0.04
2
1
0
1
2
u t
( )
i t
( )
t
0
5 10
3
0.01
0.015
0.02
1
0
1
2
p t
( )
pa t
( )
pq t
( )
t
5
Moc prądu sinusoidalnego
C
R
i
L
u
Q
P
S
k
k
k
k
t
T
t
t
T
t
dt
ui
T
dt
p
T
P
1
1
2
2
2
S
Q
P
cos
UI
P
sin
UI
Q
L
C
U
Q
1
2
R
U
P
2
UI
S

6
Moc prądu niesinusoidalnego
Teoria A. Ilioviciego - 1925r
T
T
i
idt
T
qudt
T
Q
0
0
T
T
d
dt
dt
du
i
T
dt
dt
di
u
T
Q
0
0
1
1
qd
T
dq
T
Q
i
idu
udi
Q
d
2
1
2
1
1
1
sin
n
n
n
n
n
n
d
nQ
I
nU
Q
d
i
eq
Q
Q
Q
1
1
1
sin
1
n
n
n
n
n
n
i
Q
n
I
U
n
Q

7
Moc prądu niesinusoidalnego
Teoria C.Budeanu -1927
1
0
0
cos
n
n
n
n
I
U
I
U
P
1
sin
n
n
n
n
B
I
U
Q
2
2
2
B
Q
P
S
2
2
2
2
D
Q
P
S
B

8
Moc prądu niesinusoidalnego
Teoria S.Fryzego -1931
)
(
)
(
)
(
t
i
t
i
t
i
F
a
)
(
)
(
)
(
2
t
u
G
t
u
U
P
t
i
e
a
2
2
2
F
a
I
I
I
2
2
2
F
Q
P
S
D
Q
B
Q
F
S
2
2
2
B
F
Q
D
Q

9
Moc prądu niesinusoidalnego
- rozkład prądu na składowe
• -
i
a
(t)
prąd czynny wg S.Fryzego
• - i
r
(t)
prąd bierny wg koncepcji Shepherda i Zakikhaniego.
• - i
s
(t) – nowy składnik został nazwany prądem rozrzutu pojawia się
w odbiorniku, w którym konduktancja G
n
dla składowych
harmonicznych zmienia się wraz z numerem harmonicznej
i(t)=i
a
(t)+i
s
(t)+i
r
+...
N
n
t
jn
n
e
n
e
s
e
U
G
G
U
G
G
t
i
1
Re
2
)
(
0
0
2
2
2
2
2
2
u
g
r
S
a
I
I
I
I
I
I

Moce prądu niesinusoidalnego
wg IEEE 1459-2010
10
2
1
2
1
2
2
0
2
2
1
2
1
2
2
0
2
2
2
1
2
2
2
2
1
2
2
1
1
I
I
I
I
I
U
U
U
U
U
I
I
dt
i
kT
I
U
U
dt
u
kT
U
h
h
H
h
h
H
H
kT
H
kT

Moce prądu niesinusoidalnego wg IEEE
1459 – moce chwilowe
11
h
h
h
h
h
a
q
a
t
h
I
U
I
U
p
p
p
p
))
2
2
cos(
1
(
cos
0
0
h
h
h
h
h
h
n
n
m
m
n
m
n
m
h
h
h
h
h
q
t
h
U
I
t
h
I
U
t
n
t
m
I
U
t
h
I
U
p
)
sin(
2
)
sin(
2
))
sin(
)
sin(
))
2
2
sin(
sin
0
0

Moce prądu niesinusoidalnego wg IEEE
1459 – moc czynna
12
H
kT
a
kT
kT
P
P
P
dt
p
kT
dt
p
kT
dt
ui
kT
P
1
1
1
1

Moce prądu niesinusoidalnego wg IEEE
1459 – moc pozorna
13
2
2
2
1
1
1
1
1
2
2
2
2
2
2
1
2
)
)(
(
)
(
)
(
H
H
H
I
V
H
H
H
V
H
V
I
H
I
H
V
I
N
N
D
P
S
THD
THD
S
I
U
S
THD
S
I
U
D
THD
S
I
U
D
S
D
D
S
S
S
S

Moce wg IEEE 1459 – moc bierna
prądu sinusoidalnego
14
kT
kT
kT
kT
dt
idt
u
kT
dt
udt
i
kT
idu
udi
dt
dt
du
i
kT
dt
dt
di
u
kT
Q
UI
Q
]
[
]
[
2
1
2
1
1
1
sin

Moce wg IEEE 1459 – moc bierna
prądu niesinusoidalnego
15
kT
dt
dt
u
i
kT
Q
I
U
Q
]
[
sin
1
1
1
1
1
1
2
2
P
S
N

Właściwości przypisywane mocy biernej
• Moc bierna związana jest z oscylacjami
energii pomiędzy źródłem a odbiornikiem.
• Moc bierna występuje w obwodach
zawierających indukcyjność lub pojemność
(elementach gromadzących energię w polu
elektrycznym lub magnetycznym),
16

Właściwości stawiane nowej definicji mocy
biernej
• Wielkość niezależna od mocy czynnej.
• Addytywna – bilansowana w systemie
• W obiekcie zawierającym tylko
rezystancje o jednoznacznej
charakterystyce jest równa zeru
• Kompensacja mocy biernej zmniejsza prąd
• Posiada interpretację fizyczną ???
• Jest mniejsza od mocy pozornej ???
17

Stosowane sposoby definicji i obliczania
mocy biernej
18
• Przesunięcie prądu lub napięcia o 90
o
• Ortogonalizacja wektora (Budeanu).
• Utworzenie z „trójkąta mocy” składnika
ortogonalnego do mocy czynnej.
• Obrócenie funkcji (napięcia lub prąd) we
wzorze na moc czynną (iloczynie
skalarnym prądu i napięcia)

Moc bierna - obrócenie funkcji
19
T
T
i
idt
T
qudt
T
Q
0
0
T
T
d
dt
dt
du
i
T
dt
dt
di
u
T
Q
0
0
1
1
qd
T
dq
T
Q
i
idu
udi
Q
d
2
1
2
1
k
k
t
T
t
d
k
d
k
idt
uD
D
T
X
1
)
(
i
D
d
u
D
T
X
d
k
d
k
1
)
(
1
2
2
2
dt
d
D
1
D
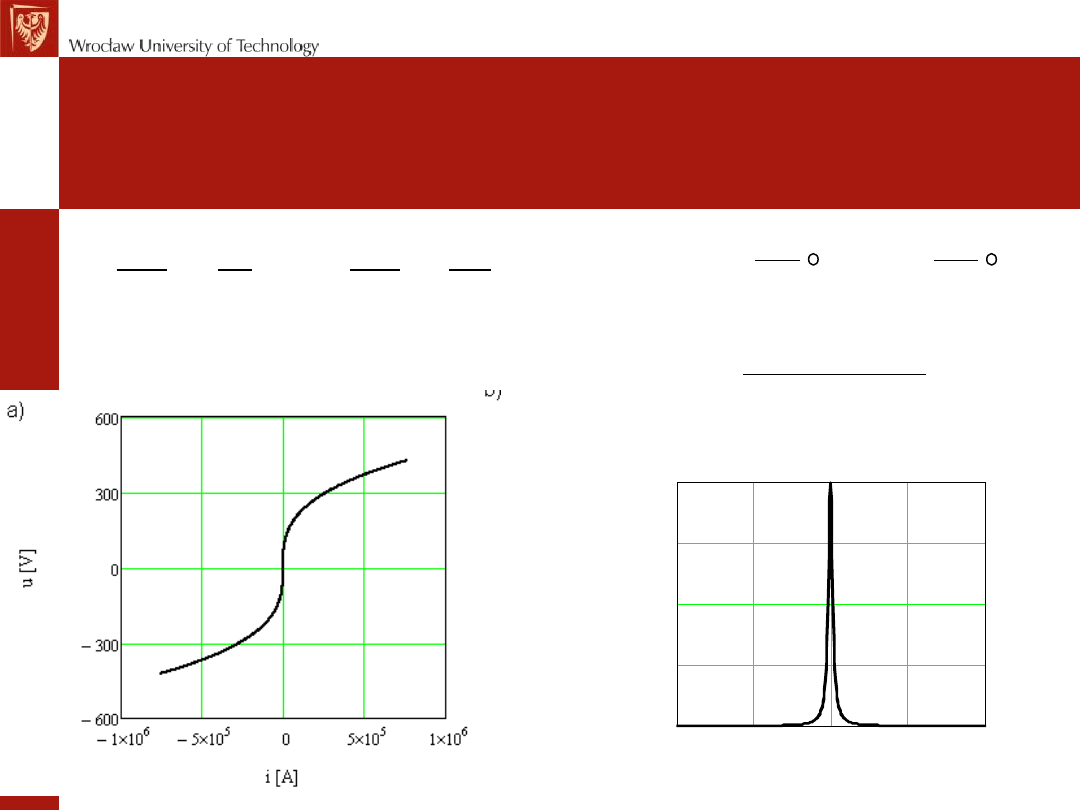
Q=0 dla obiektu o jednoznacznej
charakterystyce u-i
20
]
[
10
01
.
0
100
)
(
2
u
u
R
T
T
d
dt
dt
du
i
T
dt
dt
di
u
T
Q
0
0
1
1
idu
udi
Q
d
2
1
2
1
200
100
0
100
200
0
2.5
5
7.5
10
u[V]
R
a)
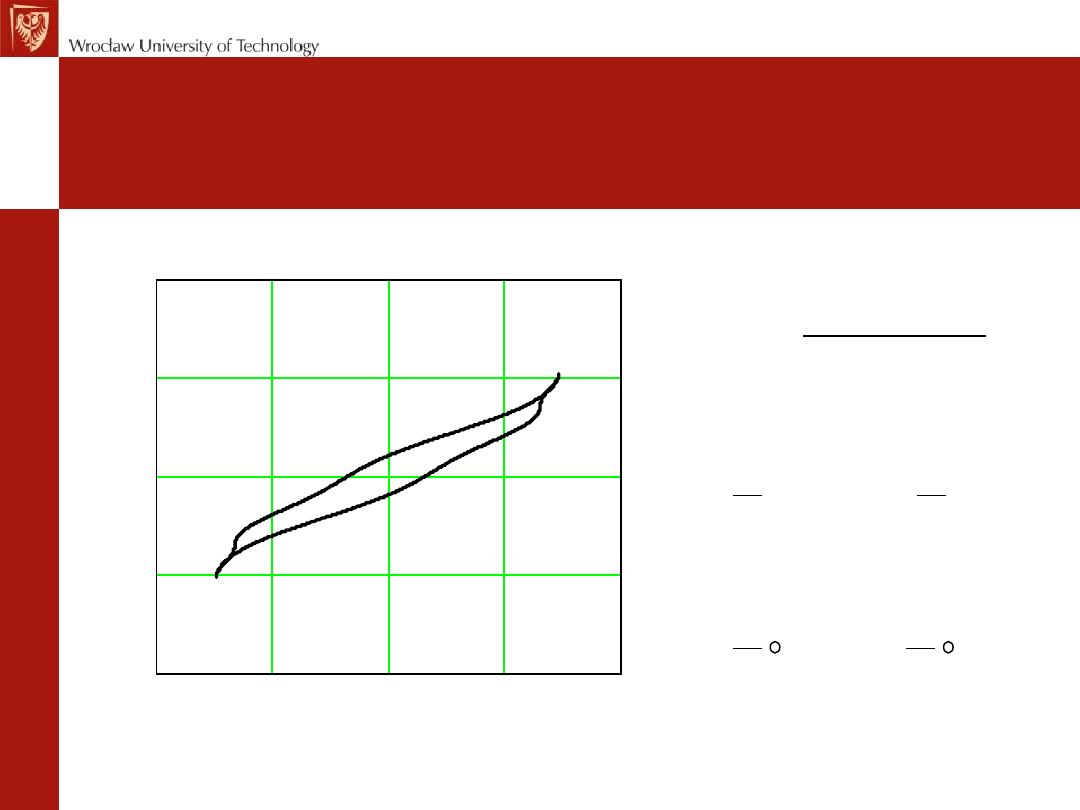
Q≠0 dla obiektu o jednoznacznej
charakterystyce u-i
21
]
[
10
01
.
0
100
)
(
2
u
u
R
6
10
5
3
10
5
0
3 10
5
6 10
5
400
200
0
200
400
i [A]
u
[V
]
1
10
3
500
0
500
1 10
3
2
1
0
1
2
q [C]
b)
T
T
i
idt
T
qudt
T
Q
0
0
qd
T
dq
T
Q
i

Pętla bierna (u-i) - przykład
22
u
0
0
i
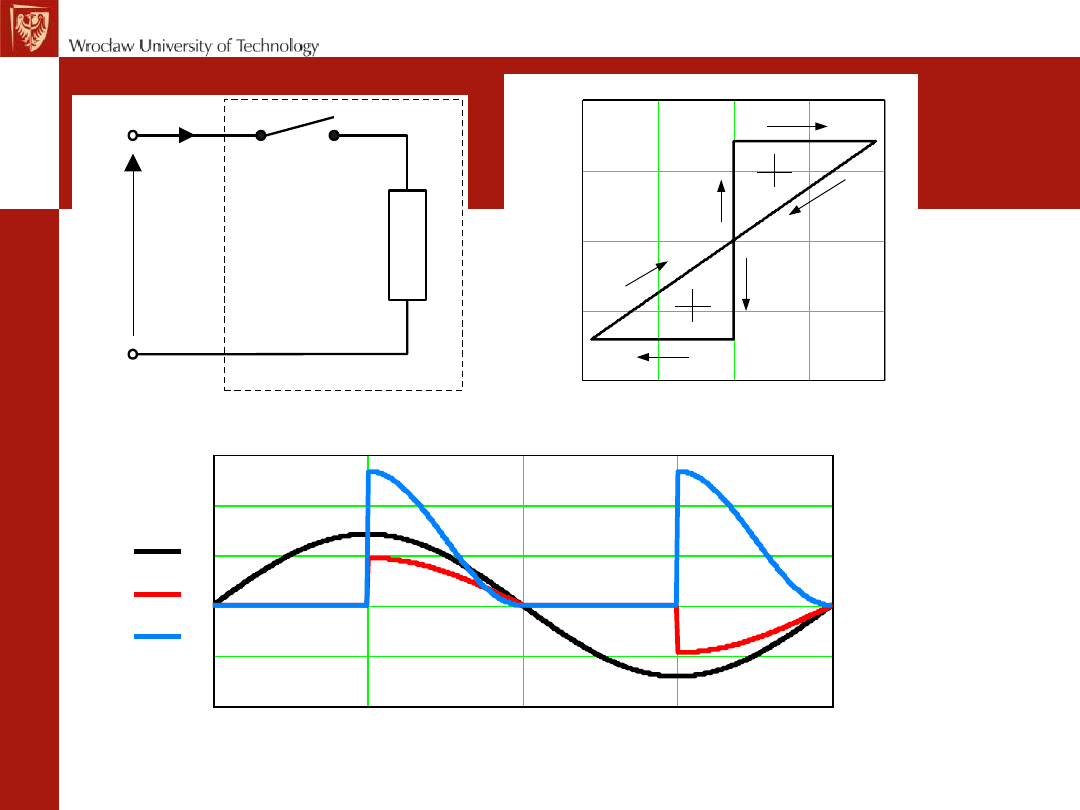
Q>0
23
0
5 10
3
0.01
0.015
0.02
4
2
0
2
4
6
u
i
p
czas
R
i
u
K
2
1
0
1
2
4
2
0
2
4
i [A]
u
[V
]
a)
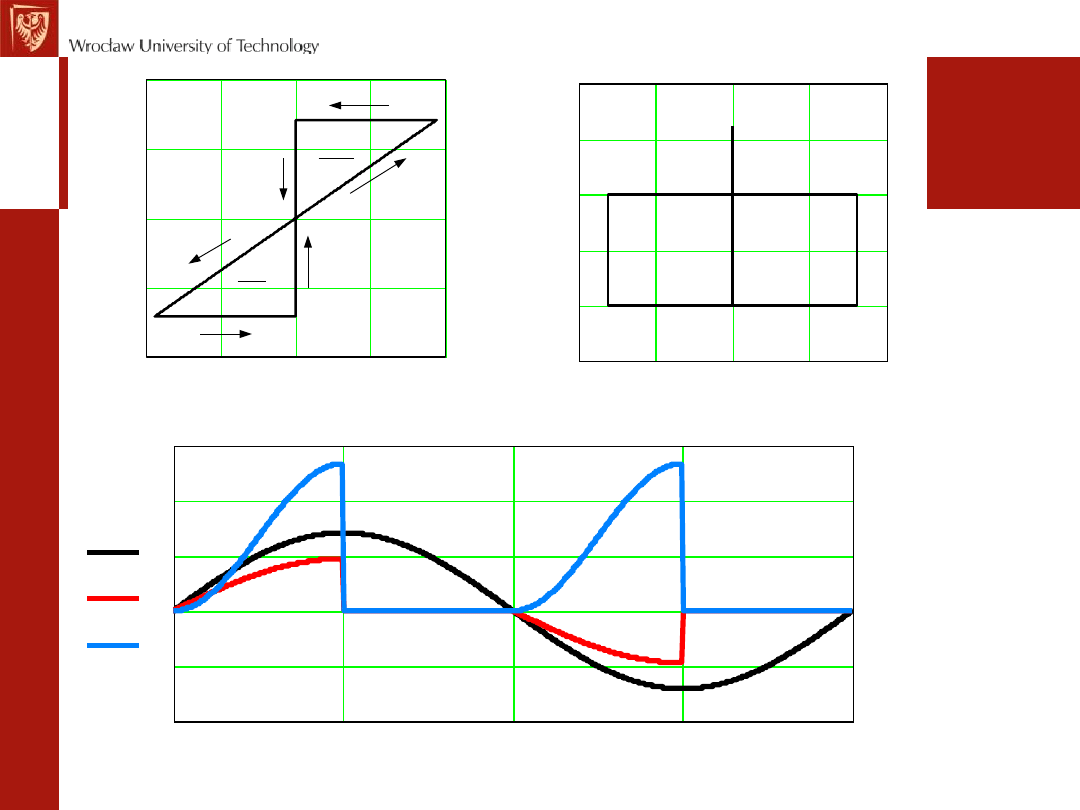
Q<0
24
0
5 10
3
0.01
0.015
0.02
4
2
0
2
4
6
u
i
p
czas
2
1
0
1
2
4
2
0
2
4
i [A]
u
[V
]
a)
400
200
0
200
400
0.5
0
0.5
1
1.5
2
u[V]
G
[S
]
a)
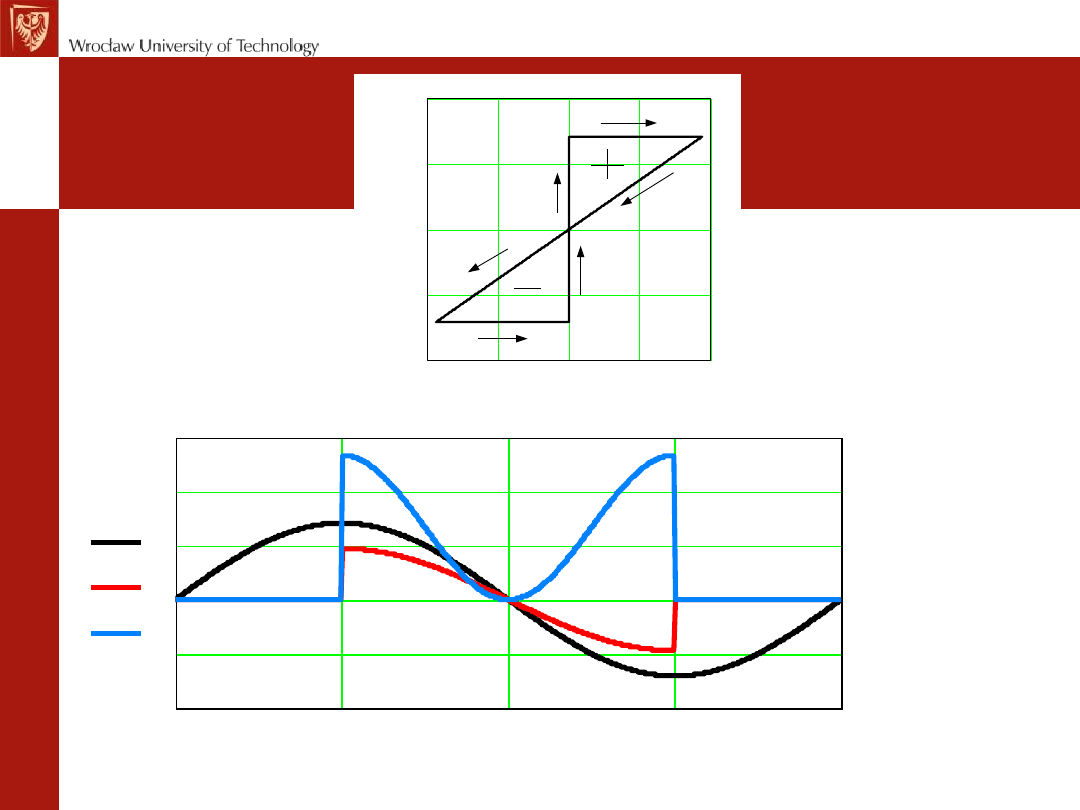
Q=0
25
0
5 10
3
0.01
0.015
0.02
4
2
0
2
4
6
u
i
p
czas
2
1
0
1
2
4
2
0
2
4
i [A]
u
[V
]
a)

Q – powierzchnia pętli u-i
26
u
dt
dG
t
G
dt
du
t
G
t
u
dt
d
dt
di
)
(
)
(
)
(
T
t
t
d
k
k
dt
dt
dG
u
Q
2
4
1
k
k
k
d
G
u
Q
2
4
1
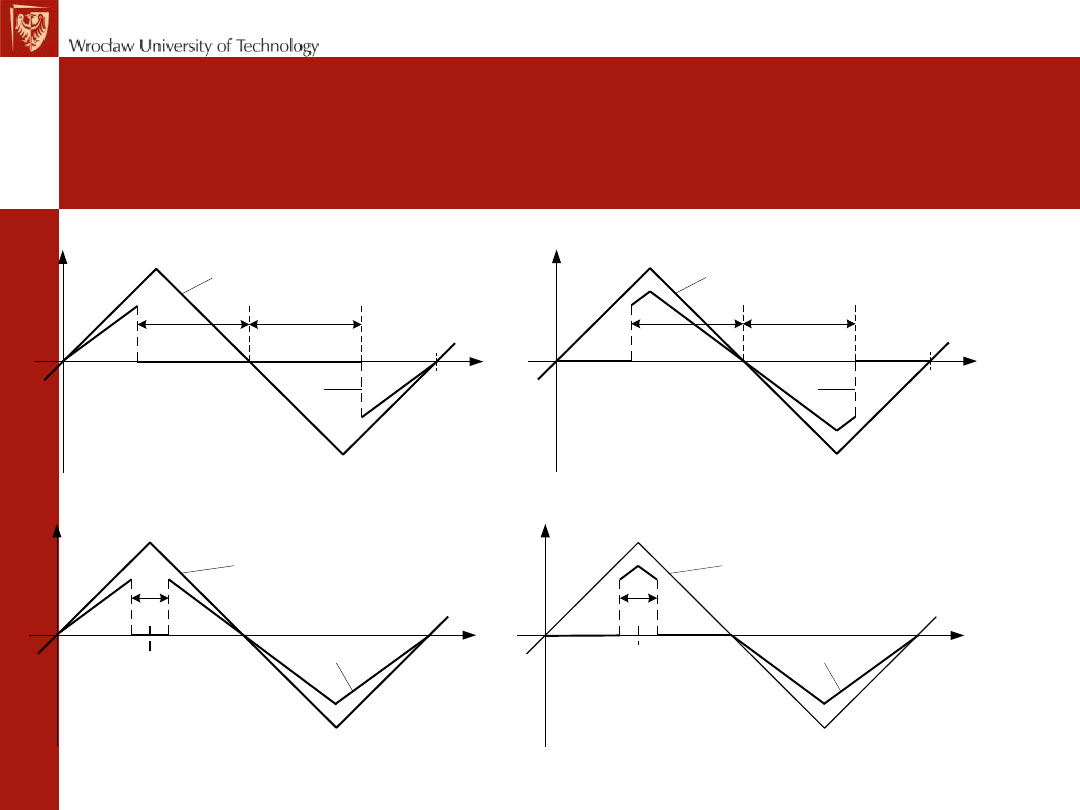
Q=0 powierzchnia pętli u-i
27
u
i
u;i
T/2
T
t
a)
u
i
u;i
T/2
T
t
b)
T
u
i
u;i
T/2
t
T/4
c)
T
u
i
u;i
T/2
t
T/4
d)

Dziękuję za uwagę
Wyszukiwarka
Podobne podstrony:
Moc bierna 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
moc bierna
Moc bierna
Moc bierna
Urzadzenia moc bierna
11 moc czynna bierna i pozorna
82 Dzis moj zenit moc moja dzisiaj sie przesili przeslanie monologu Konrada
8 Właściwa Praca, moc, energia całość
Opad Biernackiego OB
Praca, moc, energia teoria0001
Cudowna moc drzemki cuddrz
Jak określić moc wina, Balum Balum, Wina, Nalewki, Wódki - Domowy Wyrób
Biernacka - Fascynacje czytelnicze, Materiały do egzaminu z dydaktyki (licencjat)
Moc borowin, Studium kosmetyczne, Chemia kosmetyczna
Moc Ducha świętego w liturgii
Zadania Praca, moc, energia
Oczyszczająca moc
więcej podobnych podstron