
25 marca 2008
Cyfrowe układy kombinacyjne
1
25 marca 2008
Cyfrowe układy kombinacyjne
2
Cyfrowe
układy
kombinacyjne
Cyfrowe
Cyfrowe
uk
uk
ł
ł
ady
ady
kombinacyjne
kombinacyjne
25 marca 2008
Cyfrowe układy kombinacyjne
3
Cyfrowe
układy
kombinacyjne
Cyfrowe
Cyfrowe
uk
uk
ł
ł
ady
ady
kombinacyjne
kombinacyjne
Uk
Uk
ł
ł
ady kombinacyjne charakteryzuje funkcja, kt
ady kombinacyjne charakteryzuje funkcja, kt
ó
ó
ra ka
ra ka
ż
ż
demu stanowi
demu stanowi
wej
wej
ś
ś
ciowemu X
ciowemu X
i
i
∈
∈
X jednoznacznie przyporz
X jednoznacznie przyporz
ą
ą
dkowuje stan 0 lub 1 sygna
dkowuje stan 0 lub 1 sygna
ł
ł
u
u
wyj
wyj
ś
ś
ciowego
ciowego
y
y
i
i
X1
X1
X2
X2
X3
X3
Xn
Xn
Y1
Y1
Y2
Y2
Y3
Y3
Yn
Yn
25 marca 2008
Cyfrowe układy kombinacyjne
4
CMOS Inverter
and
Logic
Gates
CMOS
CMOS
Inverter
Inverter
and
and
Logic
Logic
Gates
Gates
25 marca 2008
Cyfrowe układy kombinacyjne
5
CMOS Inverter
CMOS
CMOS
Inverter
Inverter
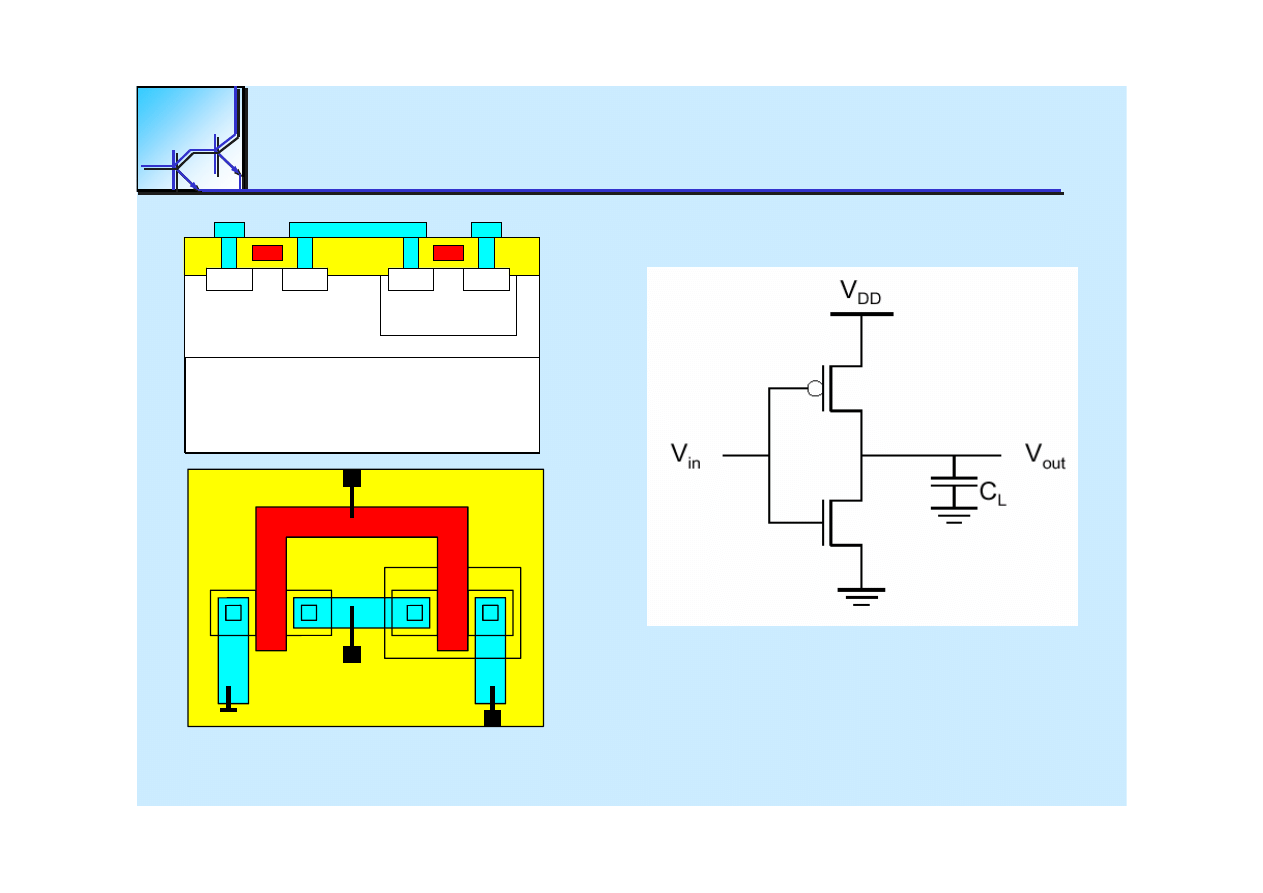
25 marca 2008
Cyfrowe układy kombinacyjne
6
CMOS Inverter
CMOS
CMOS
Inverter
Inverter
n
n+
p
p+
p+
n+
n+
V
IN
V
OUT
V
SS
V
DD
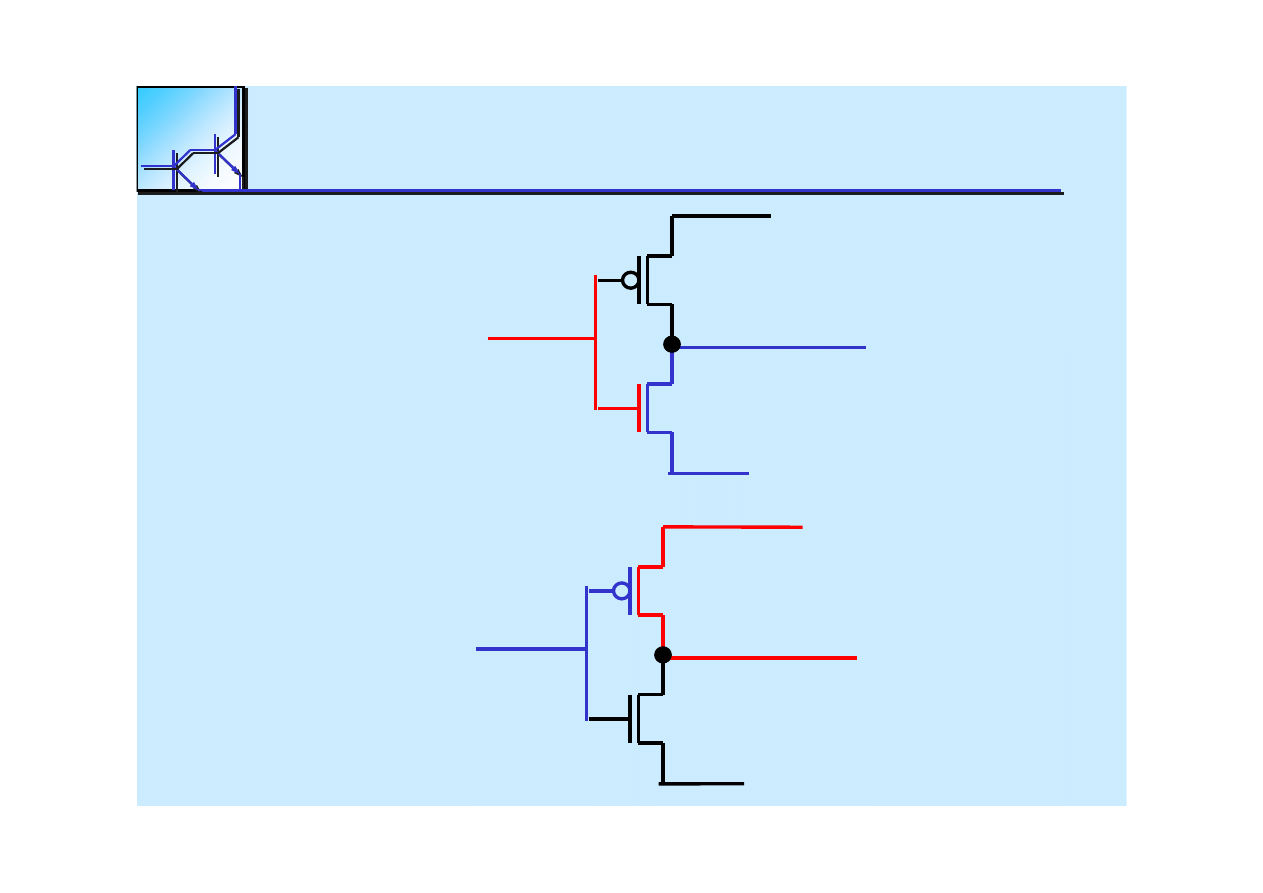
25 marca 2008
Cyfrowe układy kombinacyjne
7
Inverter
Inverter
Inverter
V
V
SS
SS
V
V
DD
DD
F=V
F=V
SS
SS
PMOS
PMOS
NMOS
NMOS
In = V
In = V
DD
DD
V
V
SS
SS
V
V
DD
DD
F=V
F=V
DD
DD
PMOS
PMOS
NMOS
NMOS
In = V
In = V
SS
SS
1
1
1
0
0
0
25 marca 2008
Cyfrowe układy kombinacyjne
10
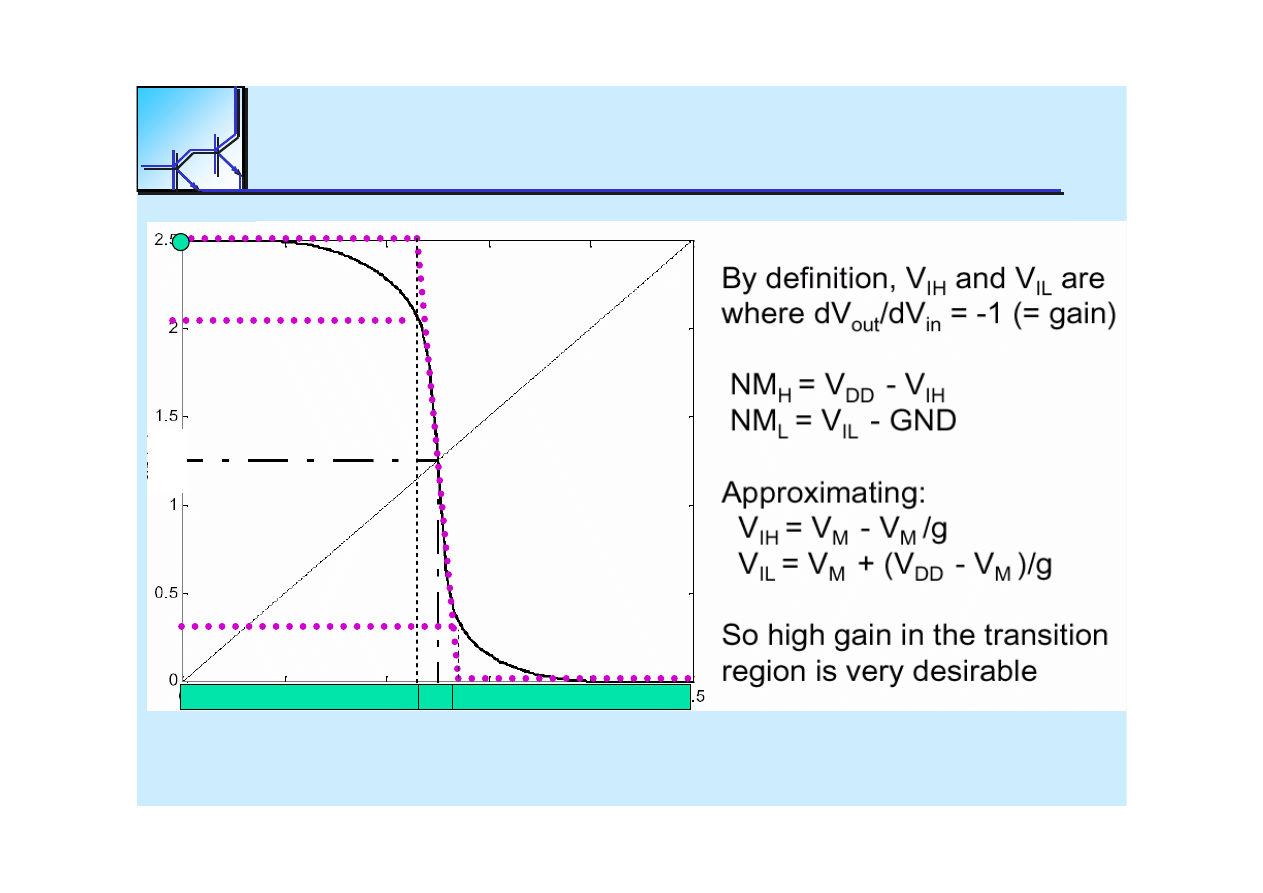
Switching
Switching
Threshold
Threshold
25 marca 2008
Cyfrowe układy kombinacyjne
11
Noise
Margins
Noise
Noise
Margins
Margins
V
V
IN
IN
V
V
M
M
V
V
Out
Out
V
V
IL
IL
V
V
IH
IH
V
V
OL
OL
V
V
OH
OH
25 marca 2008
Cyfrowe układy kombinacyjne
12
Dynamic
Dynamic
Behaviour
Behaviour
25 marca 2008
Cyfrowe układy kombinacyjne
13
Dynamic
Behaviour
Dynamic
Dynamic
Behaviour
Behaviour
V
V
DD
V
V
OUT
OUT
V
V
IN
IN
= 0
= 0
V
V
IN
IN
= V
= V
DD
DD
V
V
DD
V
V
OUT
OUT
25 marca 2008
Cyfrowe układy kombinacyjne
14
Dynamic
Behaviour
Dynamic
Dynamic
Behaviour
Behaviour
V
V
DD
V
V
OUT
OUT
V
V
IN
IN
= 0
= 0
V
V
IN
IN
= V
= V
DD
DD
V
V
DD
V
V
OUT
OUT
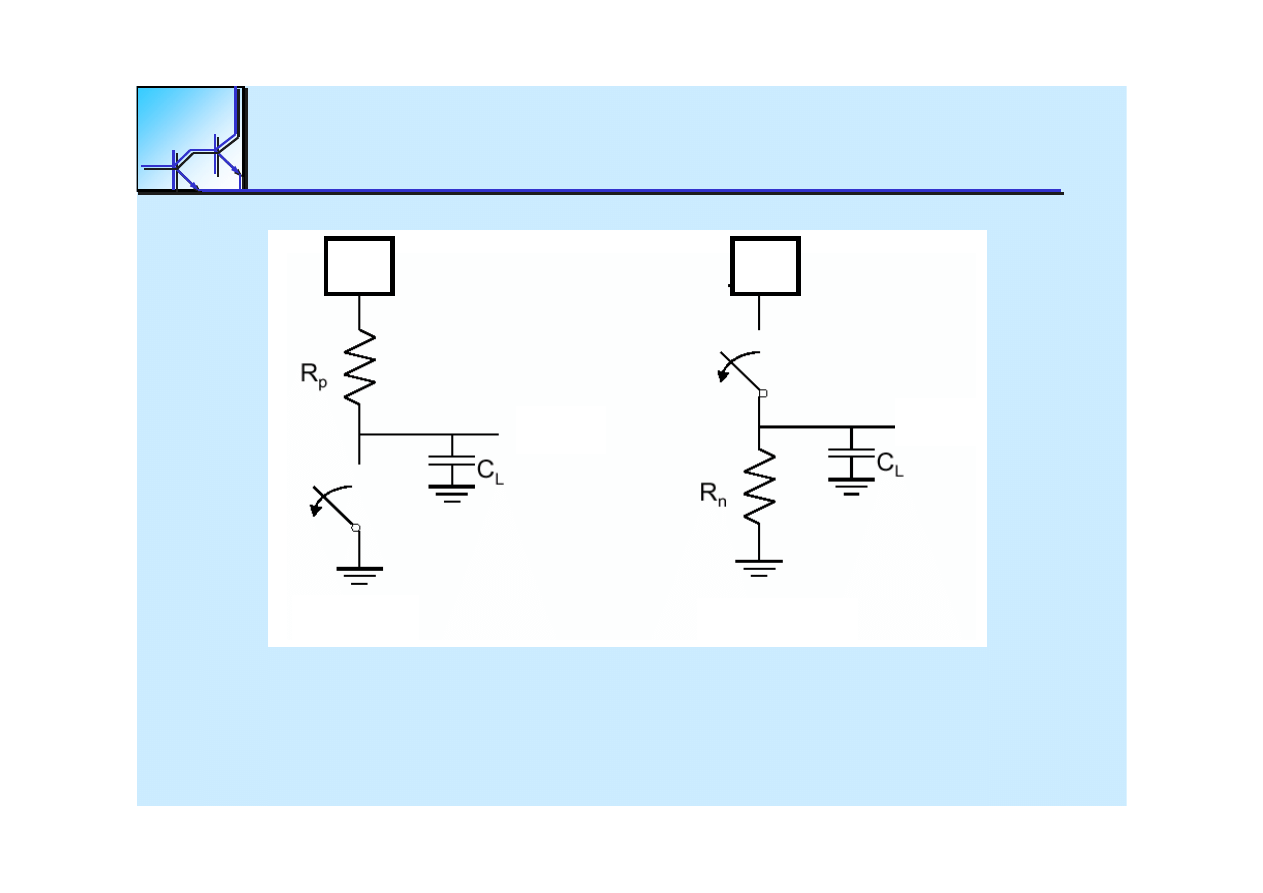
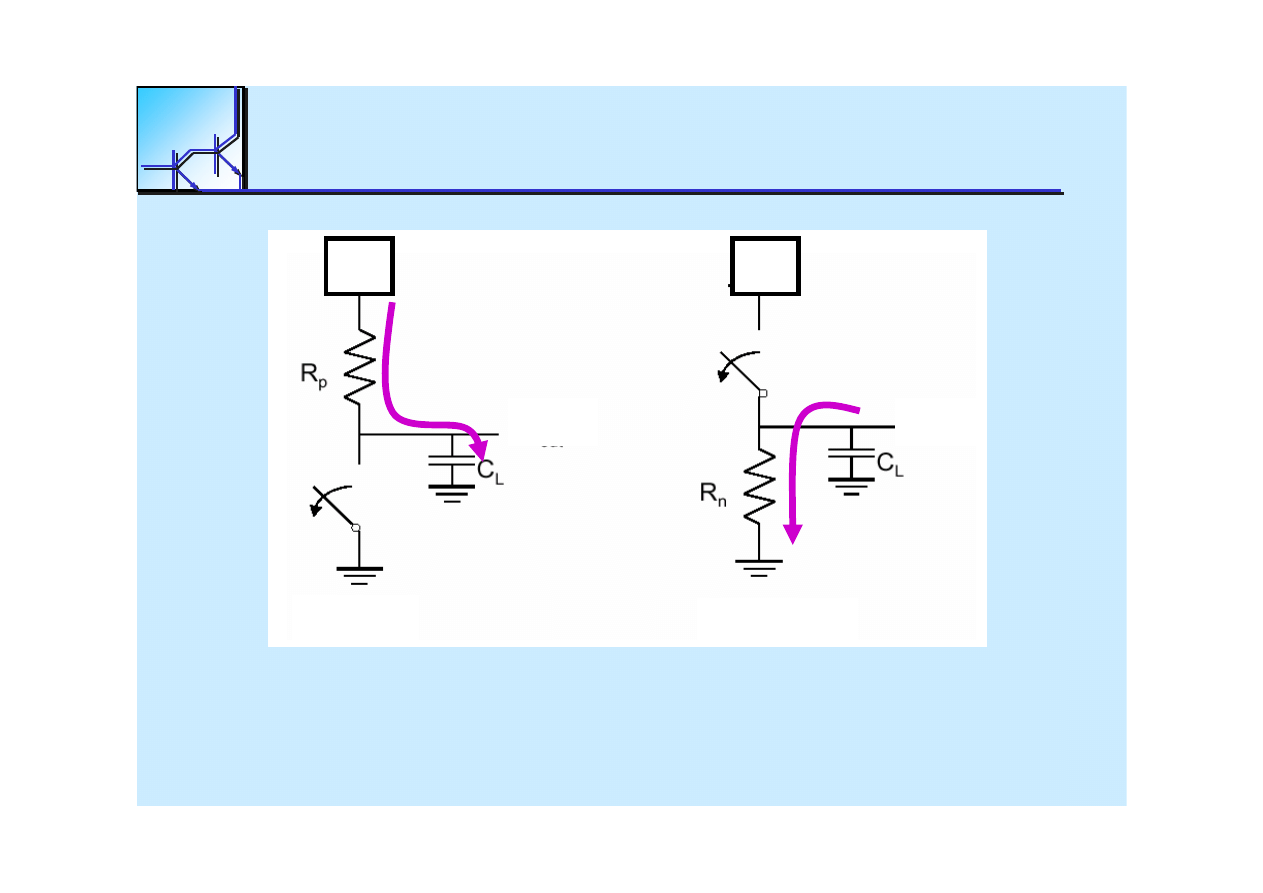
Gate response time is determined by the time to
Gate response time is determined by the time to
charge C
charge C
L
L
through
through
R
R
p
p
(discharge C
(discharge C
L
L
through
through
R
R
n
n
)
)
25 marca 2008
Cyfrowe układy kombinacyjne
15
Capacitance
Capacitance
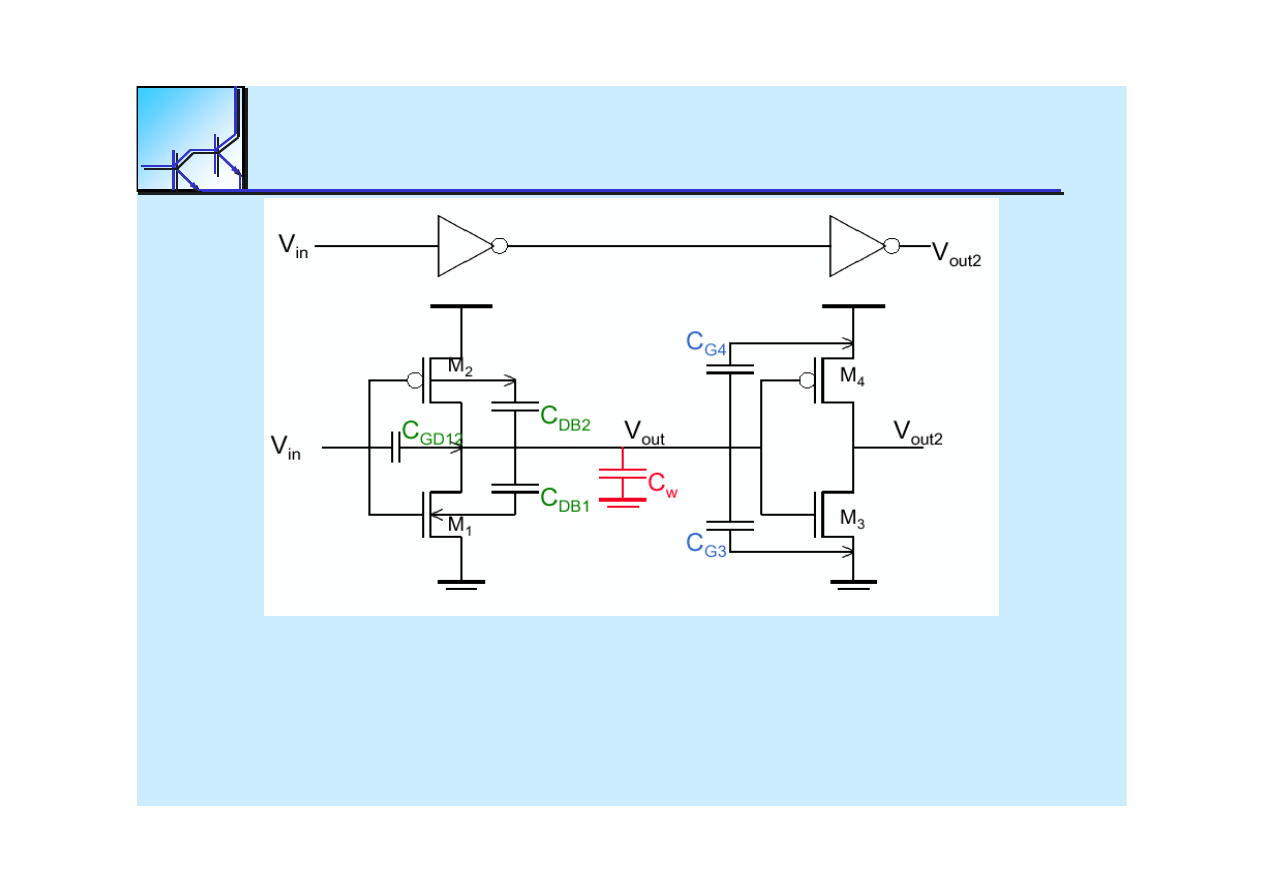
25 marca 2008
Cyfrowe układy kombinacyjne
16
Capacitance
Sources
Capacitance
Capacitance
Sources
Sources
wiring capacitance
wiring capacitance
intrinsic MOS transistor capacitances
intrinsic MOS transistor capacitances
extrinsic MOS transistor capacitances
extrinsic MOS transistor capacitances
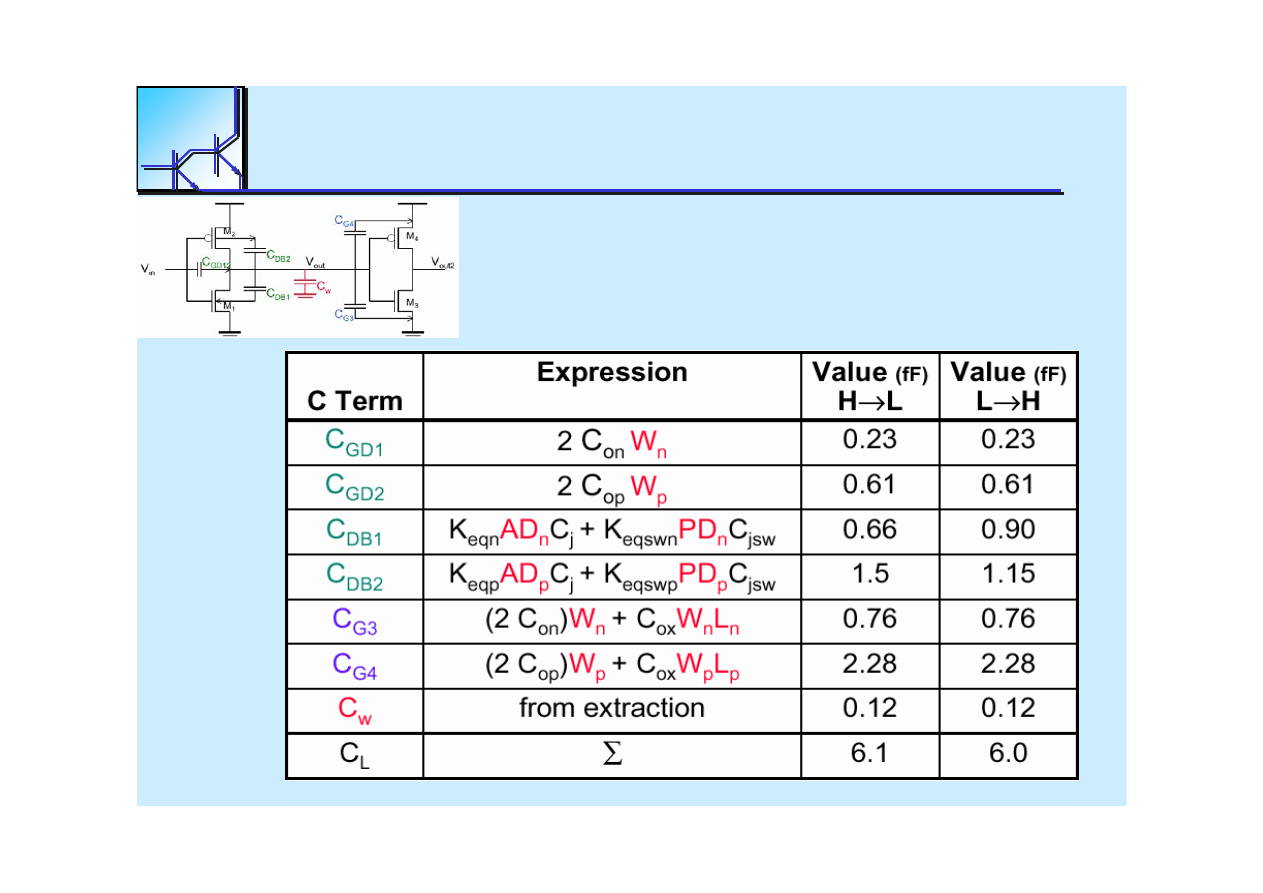
25 marca 2008
Cyfrowe układy kombinacyjne
17
Capacitance
Calculations
Capacitance
Capacitance
Calculations
Calculations
25 marca 2008
Cyfrowe układy kombinacyjne
18
Czas propagacji
Czas propagacji
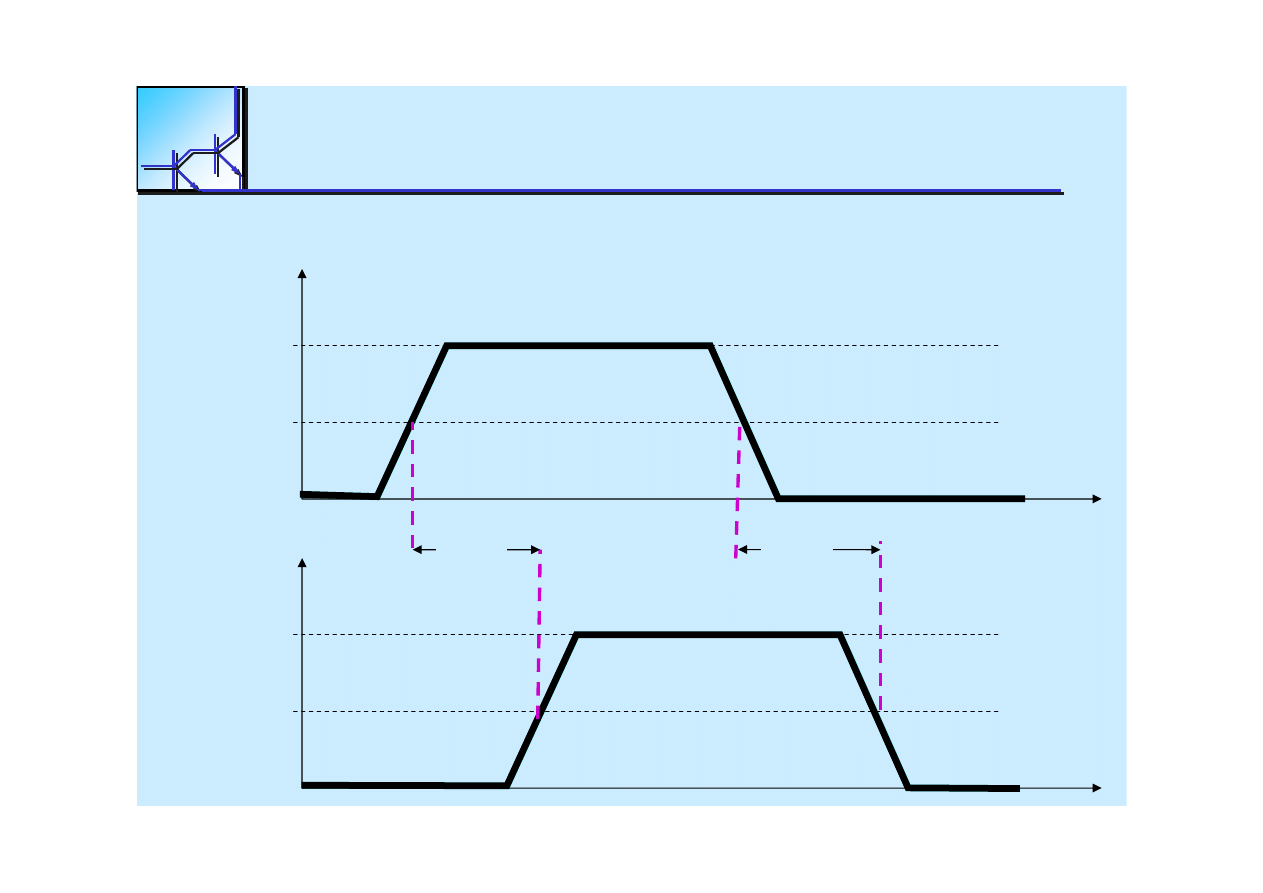
25 marca 2008
Cyfrowe układy kombinacyjne
19
Czas propagacji
Czas propagacji
Czas propagacji
t
t
V
V
in
in
V
V
max
max
V
V
max
max
/2
/2
0
0
t
t
V
V
out
out
V
V
max
max
V
V
max
max
/2
/2
0
0
t
t
PLH
PLH
t
t
PHL
PHL
Czas propagacji
Czas propagacji
:
:
tplh
tplh
,
,
tphl
tphl
,
,
op
op
ó
ó
ź
ź
nienie mierzone od
nienie mierzone od
momentu, gdy sygna
momentu, gdy sygna
ł
ł
wej
wej
ś
ś
ciowy osi
ciowy osi
ą
ą
gnie 50% warto
gnie 50% warto
ś
ś
ci
ci
maksymalnej, do czasu kiedy sygna
maksymalnej, do czasu kiedy sygna
ł
ł
wyj
wyj
ś
ś
ciowy
ciowy
osi
osi
ą
ą
gni
gni
ę
ę
50
50
% warto
% warto
ś
ś
ci maksymalnej. Generalnie
ci maksymalnej. Generalnie tplh
tplh
≠
≠
tphl
tphl
.
.
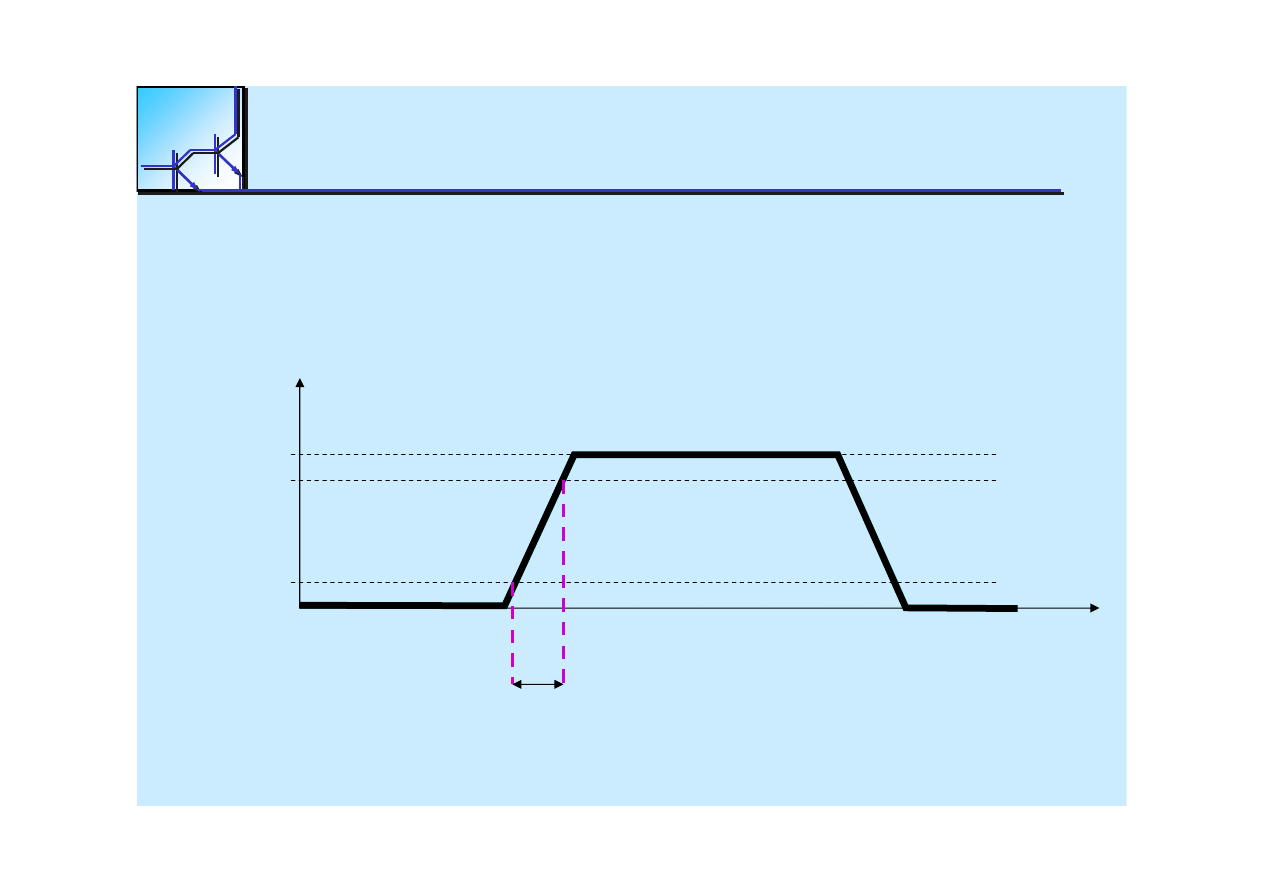
25 marca 2008
Cyfrowe układy kombinacyjne
20
Czas propagacji
Czas propagacji
Czas propagacji
t
t
V
V
in
in
V
V
max
max
0,9
0,9
V
V
max
max
0,1
0,1
Vmax
Vmax
0
0
t
t
r
r
Czas narastania (
Czas narastania (
Rise Time
Rise Time
)
)
:
:
tr
tr
,
,
czas potrzebny do wzrostu
czas potrzebny do wzrostu
sygna
sygna
ł
ł
u od 10% do 90% jego warto
u od 10% do 90% jego warto
ś
ś
ci maksymalnej.
ci maksymalnej.
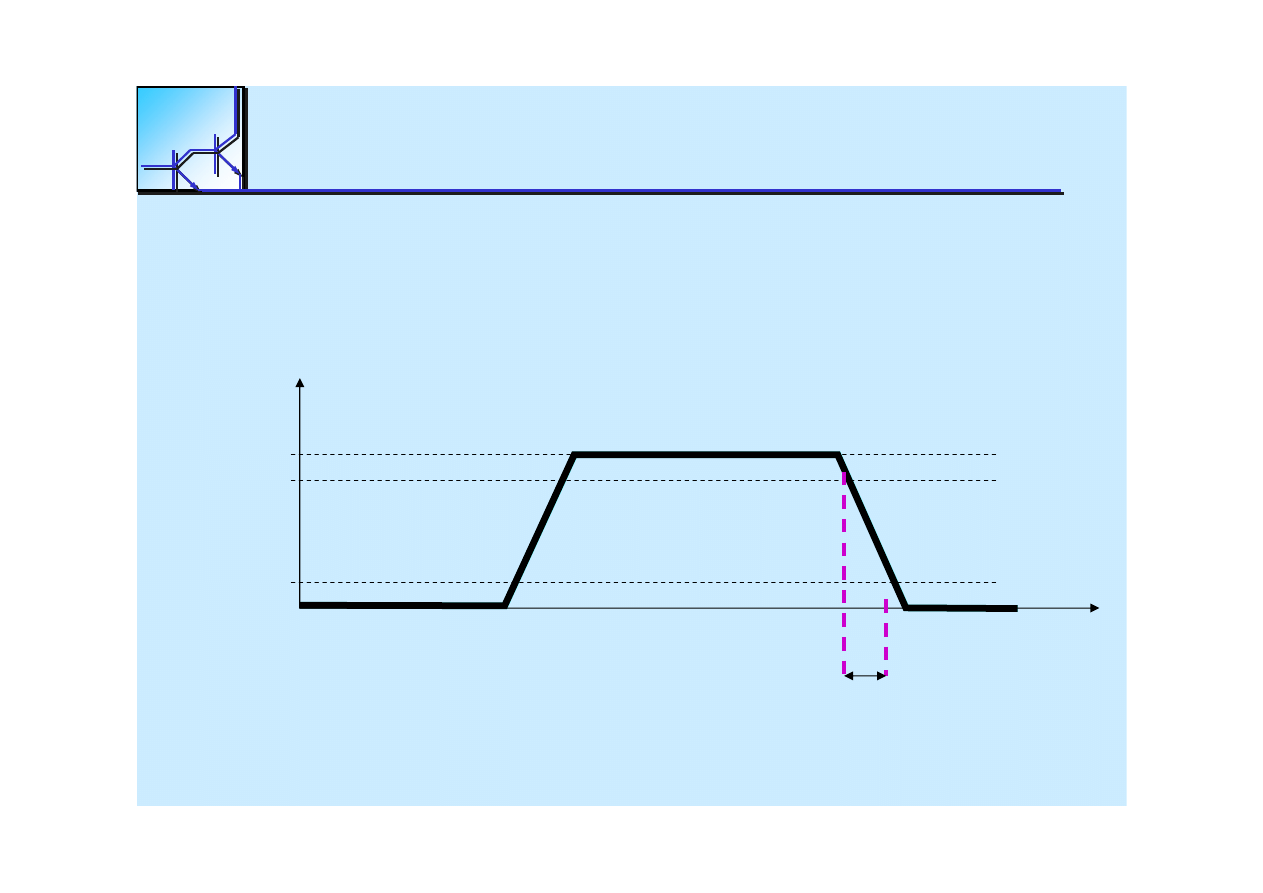
25 marca 2008
Cyfrowe układy kombinacyjne
21
Czas propagacji
Czas propagacji
Czas propagacji
t
t
V
V
in
in
V
V
max
max
0,9
0,9
V
V
max
max
0,1
0,1
Vmax
Vmax
0
0
t
t
f
f
Czas opadania (
Czas opadania (
Fall Time
Fall Time
)
)
:
:
tf
tf
,
,
czas potrzebny do spadku sygna
czas potrzebny do spadku sygna
ł
ł
u od
u od
90% do 10% jego warto
90% do 10% jego warto
ś
ś
ci maksymalnej.
ci maksymalnej.
25 marca 2008
Cyfrowe układy kombinacyjne
22
Czas propagacji w układach kombinacyjnych
Czas propagacji w uk
Czas propagacji w uk
ł
ł
adach kombinacyjnych
adach kombinacyjnych
Czas propagacji sygna
Czas propagacji sygna
ł
ł
u w uk
u w uk
ł
ł
adzie wyznaczany jest to
adzie wyznaczany jest to
najwi
najwi
ę
ę
ksze op
ksze op
ó
ó
ź
ź
nienie jakie mo
nienie jakie mo
ż
ż
e wyst
e wyst
ą
ą
pi
pi
ć
ć
w uk
w uk
ł
ł
adzie
adzie
5
5
ns
ns
12
12
ns
ns
5
5
ns
ns
12
12
ns
ns
8
8
ns
ns
T
T
p
p
= 5
= 5
ns
ns
+ 12
+ 12
ns
ns
= 17
= 17
ns
ns
T
T
p
p
= 8
= 8
ns
ns
+ 12
+ 12
ns
ns
= 20
= 20
ns
ns
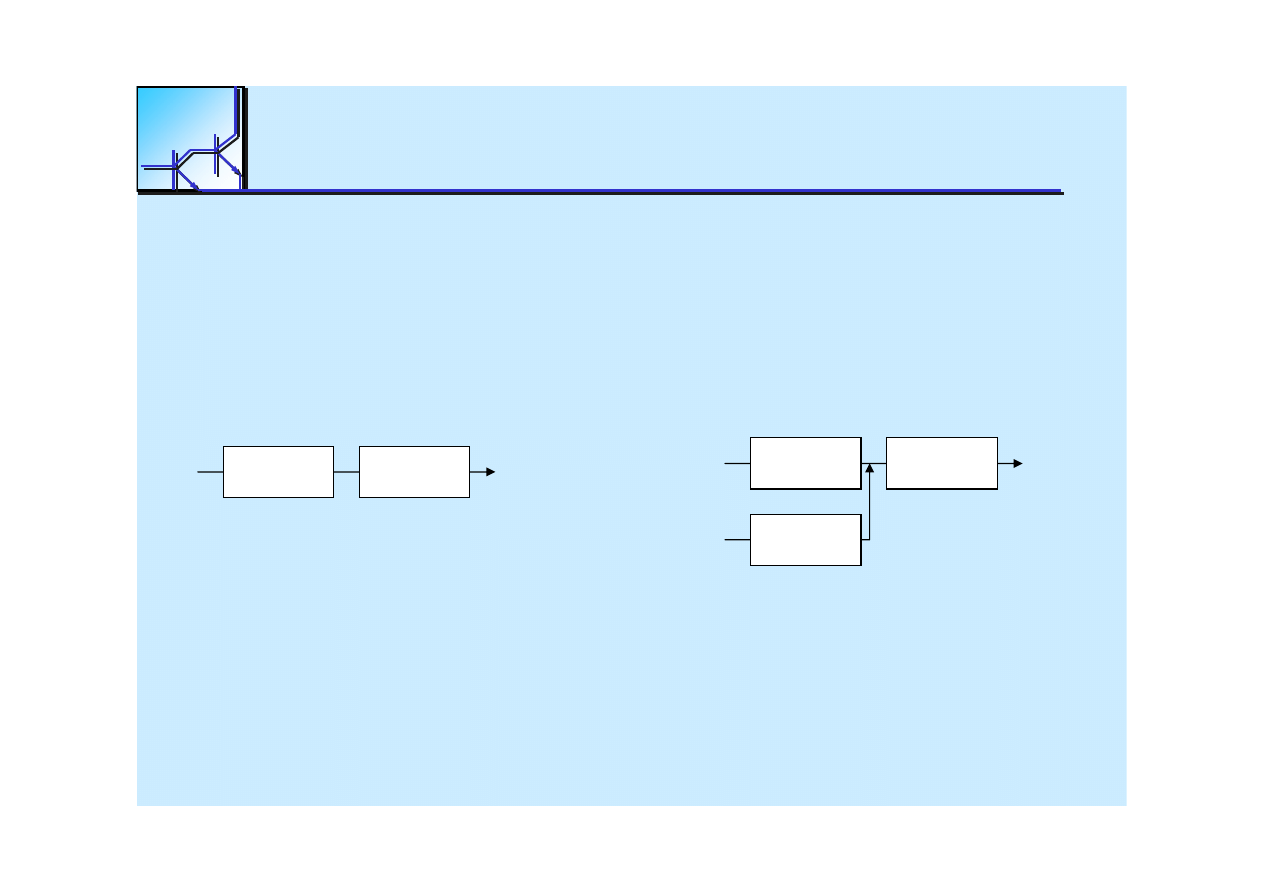
25 marca 2008
Cyfrowe układy kombinacyjne
23
Czas propagacji w układach
kombinacyjnych
Czas propagacji w uk
Czas propagacji w uk
ł
ł
adach
adach
kombinacyjnych
kombinacyjnych
Using gates with
Using gates with
fi
fi
nite
nite
propagation delays,
propagation delays,
t
t
plh
plh
and
and
t
t
phl
phl
instead of zero gate
instead of zero gate
delays used in functional analysis.
delays used in functional analysis.
x
x
z
z
y
y
x z
x z
x z
x z
x z
x z
1
1
V
V
in
in
I1 I2 I3
I1 I2 I3
Gate
Gate
t
t
PLH
PLH
t
t
PHL
PHL
Invert
Invert
12
12
8
8
XOR
XOR
18
18
13
13
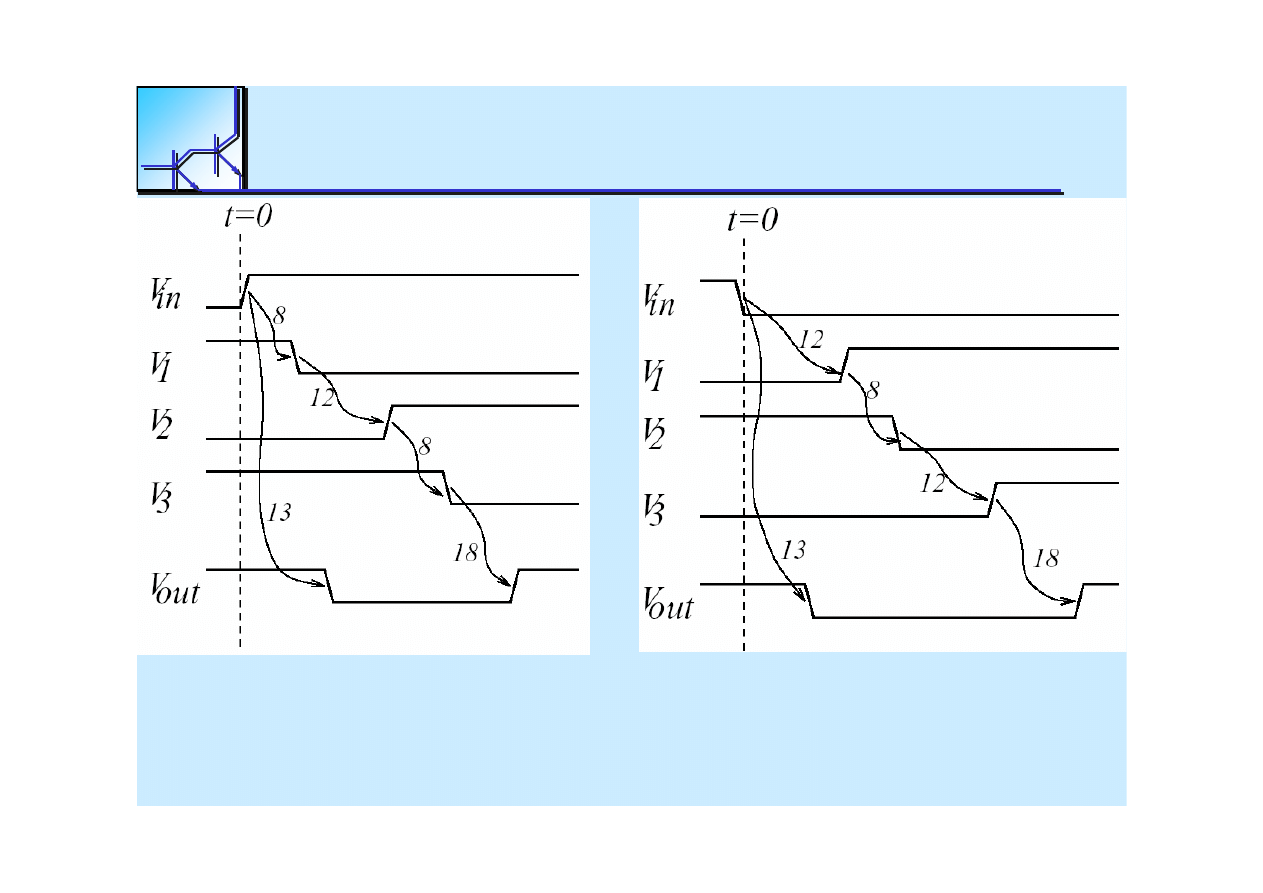
25 marca 2008
Cyfrowe układy kombinacyjne
24
Propagation Delay of Combinational
Circuits
Propagation Delay of Combinational
Propagation Delay of Combinational
Circuits
Circuits
input low
input low
-
-
to
to
-
-
high transition
high transition
input high
input high
-
-
to
to
-
-
low transition
low transition
25 marca 2008
Cyfrowe układy kombinacyjne
25
Inverter
Propagation
Delay
Inverter
Inverter
Propagation
Propagation
Delay
Delay
Determine the worst case propagation delay through
Determine the worst case propagation delay through
the circuit
the circuit
5
5
ns
ns
12
12
ns
ns
5
5
ns
ns
12
12
ns
ns
8
8
ns
ns
T
T
p
p
= 5
= 5
ns
ns
+ 12
+ 12
ns
ns
= 17
= 17
ns
ns
T
T
p
p
= 8
= 8
ns
ns
+ 12
+ 12
ns
ns
= 20
= 20
ns
ns
25 marca 2008
Cyfrowe układy kombinacyjne
26
Propagation Delay of Combinational
Circuits
Propagation Delay of Combinational
Propagation Delay of Combinational
Circuits
Circuits
Using gates with
Using gates with
fi
fi
nite
nite
propagation delays,
propagation delays,
t
t
plh
plh
and
and
t
t
phl
phl
instead of zero gate
instead of zero gate
delays used in functional analysis.
delays used in functional analysis.
x
x
z
z
y
y
x z
x z
x z
x z
x z
x z
1
1
V
V
in
in
I1 I2 I3
I1 I2 I3
Gate
Gate
t
t
PLH
PLH
t
t
PHL
PHL
Invert
Invert
12
12
8
8
XOR
XOR
18
18
13
13
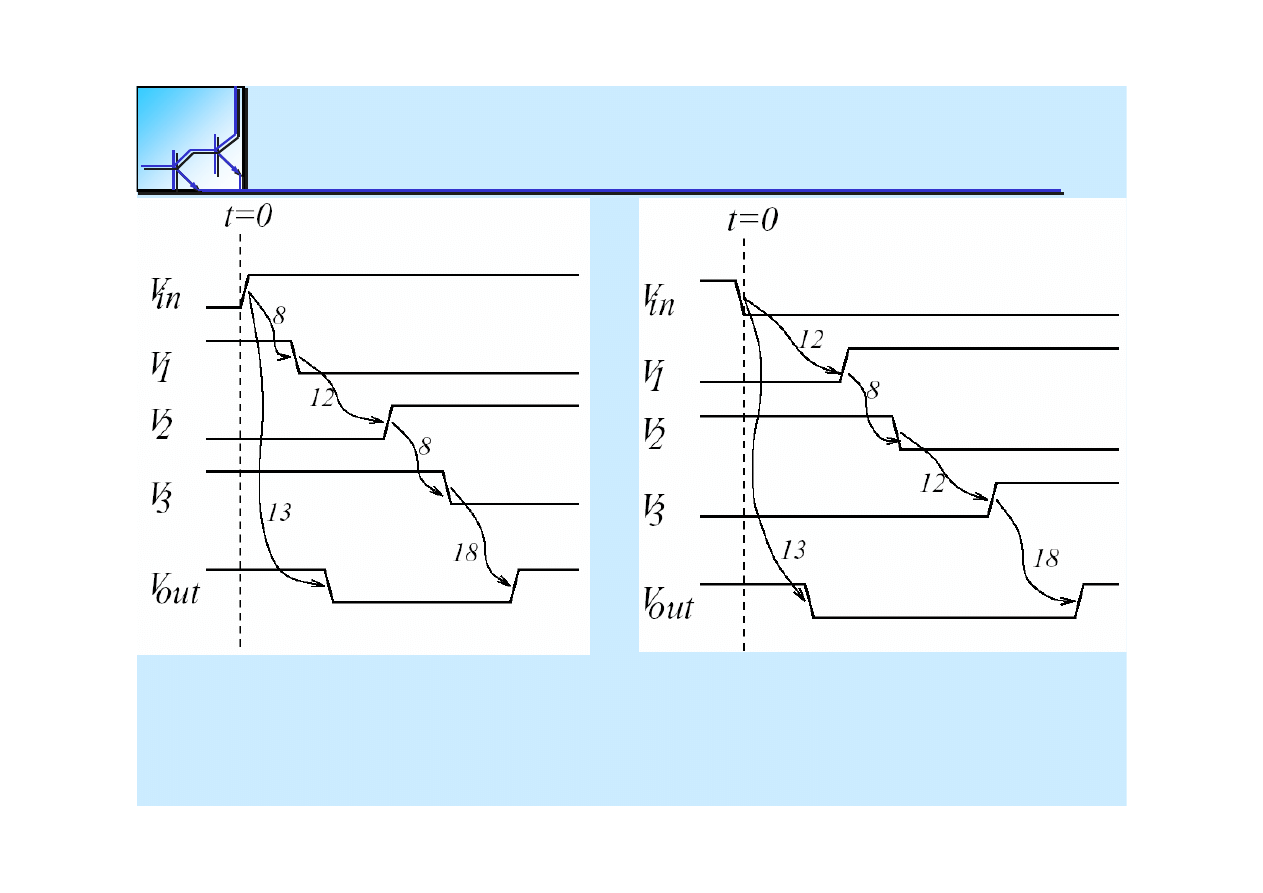
25 marca 2008
Cyfrowe układy kombinacyjne
27
Propagation Delay of Combinational
Circuits
Propagation Delay of Combinational
Propagation Delay of Combinational
Circuits
Circuits
input low
input low
-
-
to
to
-
-
high transition
high transition
input high
input high
-
-
to
to
-
-
low transition
low transition
25 marca 2008
Cyfrowe układy kombinacyjne
28
Power
Power
Consumption
Consumption
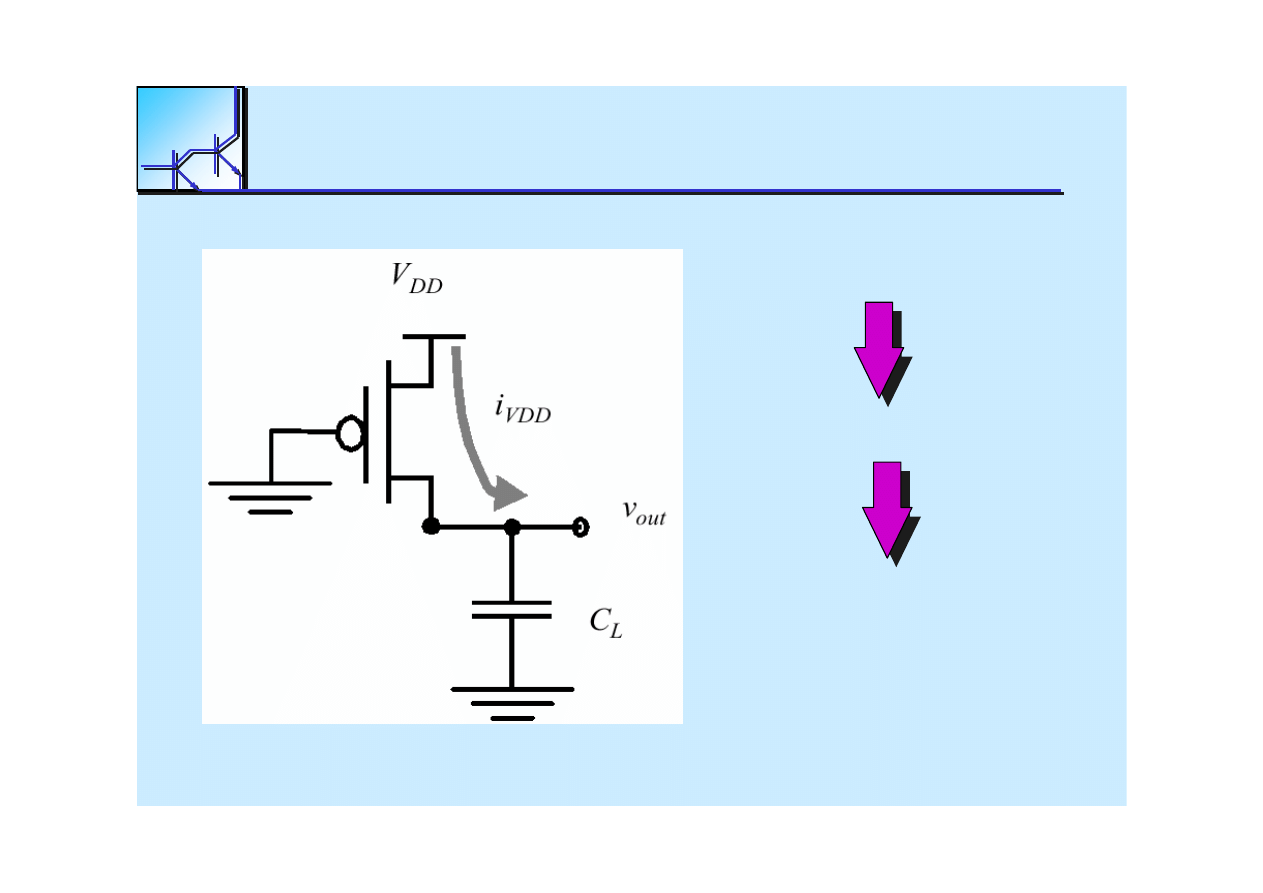
25 marca 2008
Cyfrowe układy kombinacyjne
29
Dynamic
Power Consumpsion
Dynamic
Dynamic
Power
Power
Consumpsion
Consumpsion
P
dyn
= C
L
• V
DD
2
• f
P
P
dyn
dyn
= C
= C
L
L
•
•
V
V
DD
DD
2
2
•
•
f
f
P
P
dyn
dyn
= 6fF
= 6fF
•
•
2.5V
2.5V
2
2
•
•
500MHz = 20
500MHz = 20
μ
μ
W
W
1M
1M
gates
gates
P
tot
= 20W
P
P
tot
tot
= 20W
= 20W
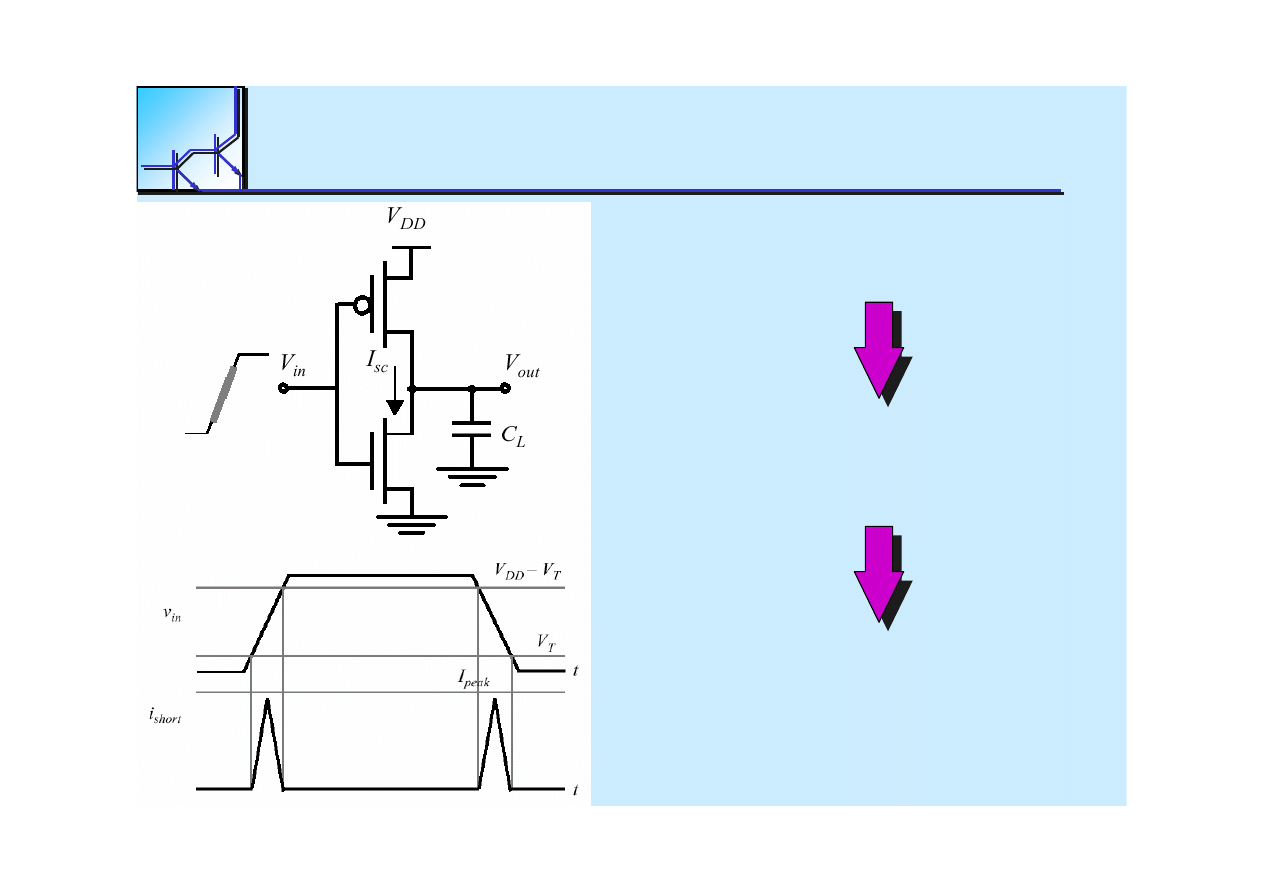
25 marca 2008
Cyfrowe układy kombinacyjne
30
Direct-Path
Currents
Power Consumpsion
Direct
Direct
-
-
Path
Path
Currents
Currents
Power
Power
Consumpsion
Consumpsion
P
d
= t
s
• I
Peak
• V
DD
• f
P
P
d
d
=
=
t
t
s
s
•
•
I
I
Peak
Peak
•
•
V
V
DD
DD
•
•
f
f
P
P
dyn
dyn
= 100ps
= 100ps
•
•
50
50
μ
μ
A
A
•
•
2.5V
2.5V
•
•
500MHz
500MHz
= 6.25
= 6.25
μ
μ
W
W
1M
1M
gates
gates
P
P
tot
tot
= 6.25 W
= 6.25 W
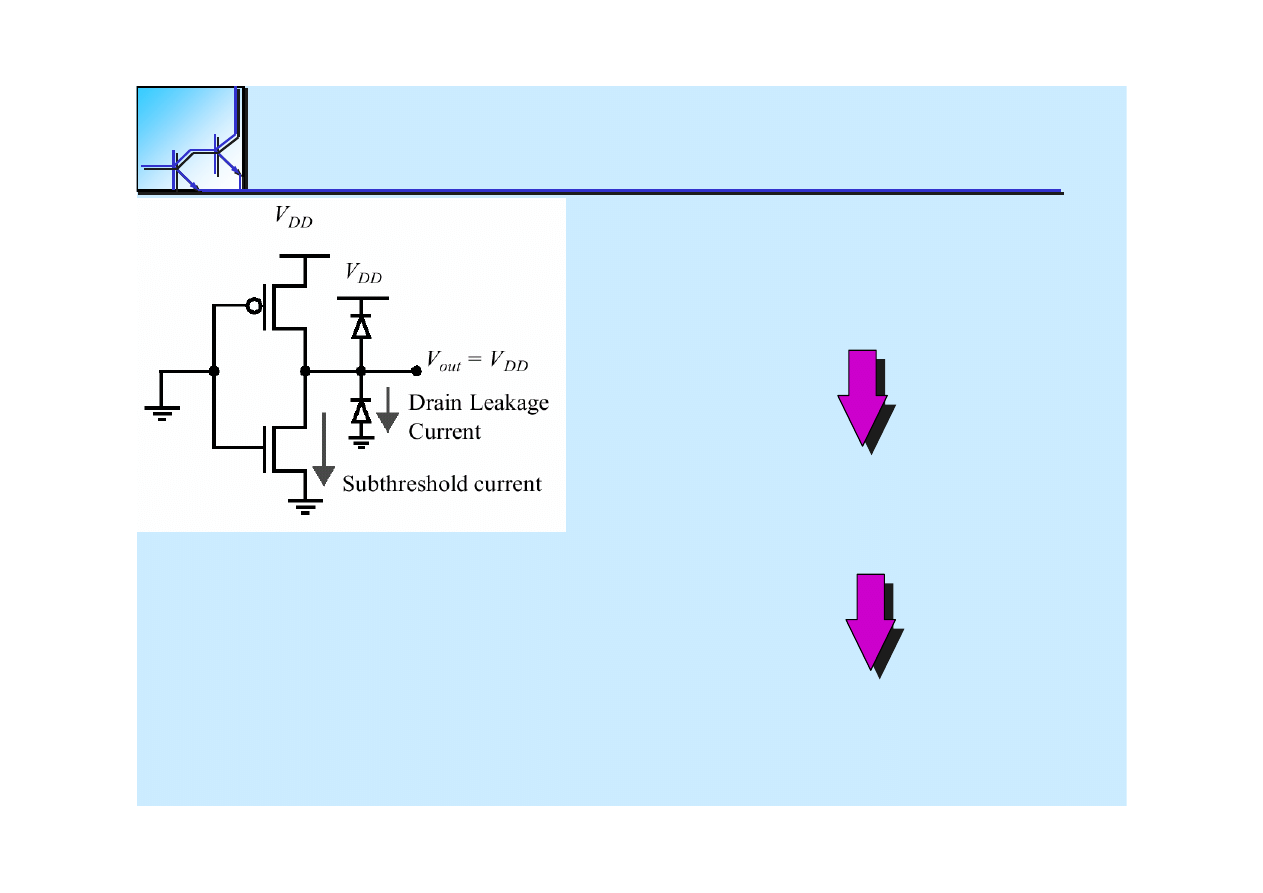
25 marca 2008
Cyfrowe układy kombinacyjne
31
Static
Power Consumpsion
Static
Static
Power
Power
Consumpsion
Consumpsion
P
stat
= I
stat
•
V
DD
P
P
stat
stat
=
=
I
I
stat
stat
•
•
V
V
DD
DD
P
P
stat
stat
= 10pA/
= 10pA/
μ
μ
m
m
2
2
•
•
0.5
0.5
μ
μ
m
m
2
2
•
•
2.5V
2.5V
= 125
= 125
pW
pW
1M
1M
gates
gates
P
P
tot
tot
= 125
= 125
μ
μ
W
W
25 marca 2008
Cyfrowe układy kombinacyjne
32
Bramki
Logiczne
Bramki
Bramki
Logiczne
Logiczne
25 marca 2008
Cyfrowe układy kombinacyjne
33
Contents
Contents
Contents
•
NAND & NOR
•
AND
•
3 –state Inverter
•
Transmission Gate
•
XOR
•
Complex Gates
•
•
NAND & NOR
•
AND
•
3 –state Inverter
•
Transmission Gate
•
XOR
•
Complex Gates
•
25 marca 2008
Cyfrowe układy kombinacyjne
34
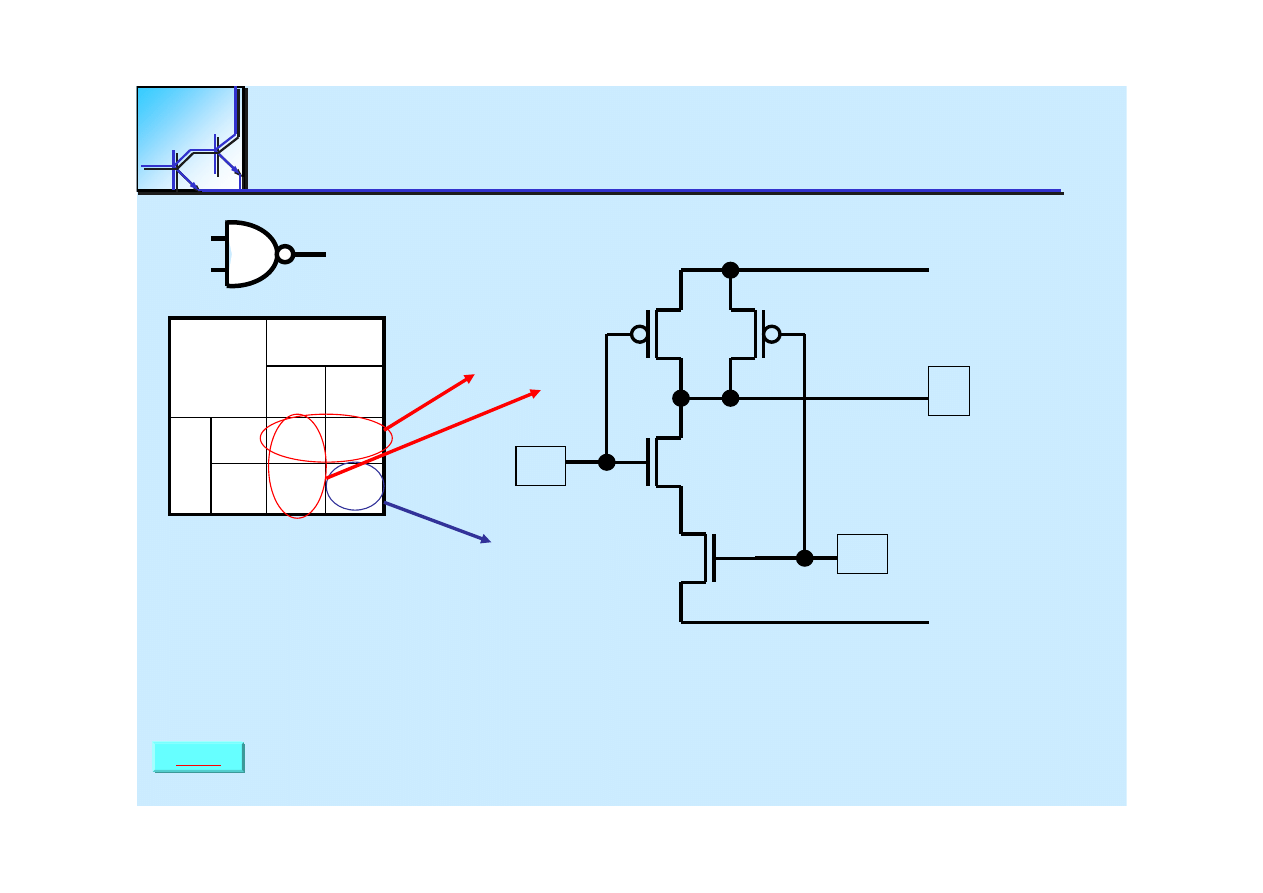
NAND & NOR
NAND & NOR
25 marca 2008
Cyfrowe układy kombinacyjne
35
The
NAND
Gate
The
The
NAND
NAND
Gate
Gate
A
B
F
F
F
B
B
0
0
1
1
A
A
0
0
1
1
1
1
1
1
1
1
0
0
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
NMOS
NMOS
F = A
F = A
’
’
+ B
+ B
’
’
F
F
’
’
= A
= A
•
•
B
B
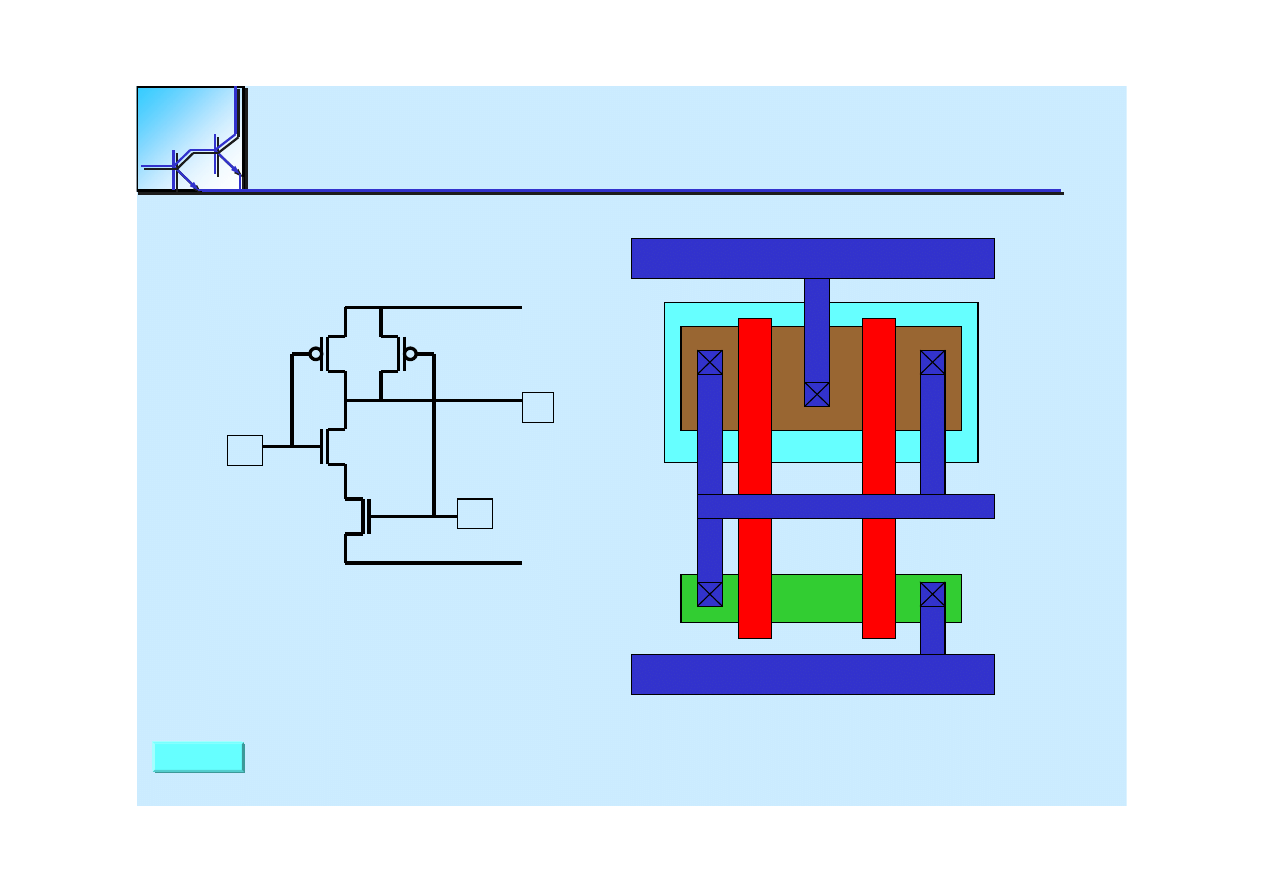
25 marca 2008
Cyfrowe układy kombinacyjne
36
The
NAND Gate
The
The
NAND
NAND
Gate
Gate
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
NMOS
NMOS
V
V
DD
DD
V
V
SS
SS
F
F
A
A
B
B
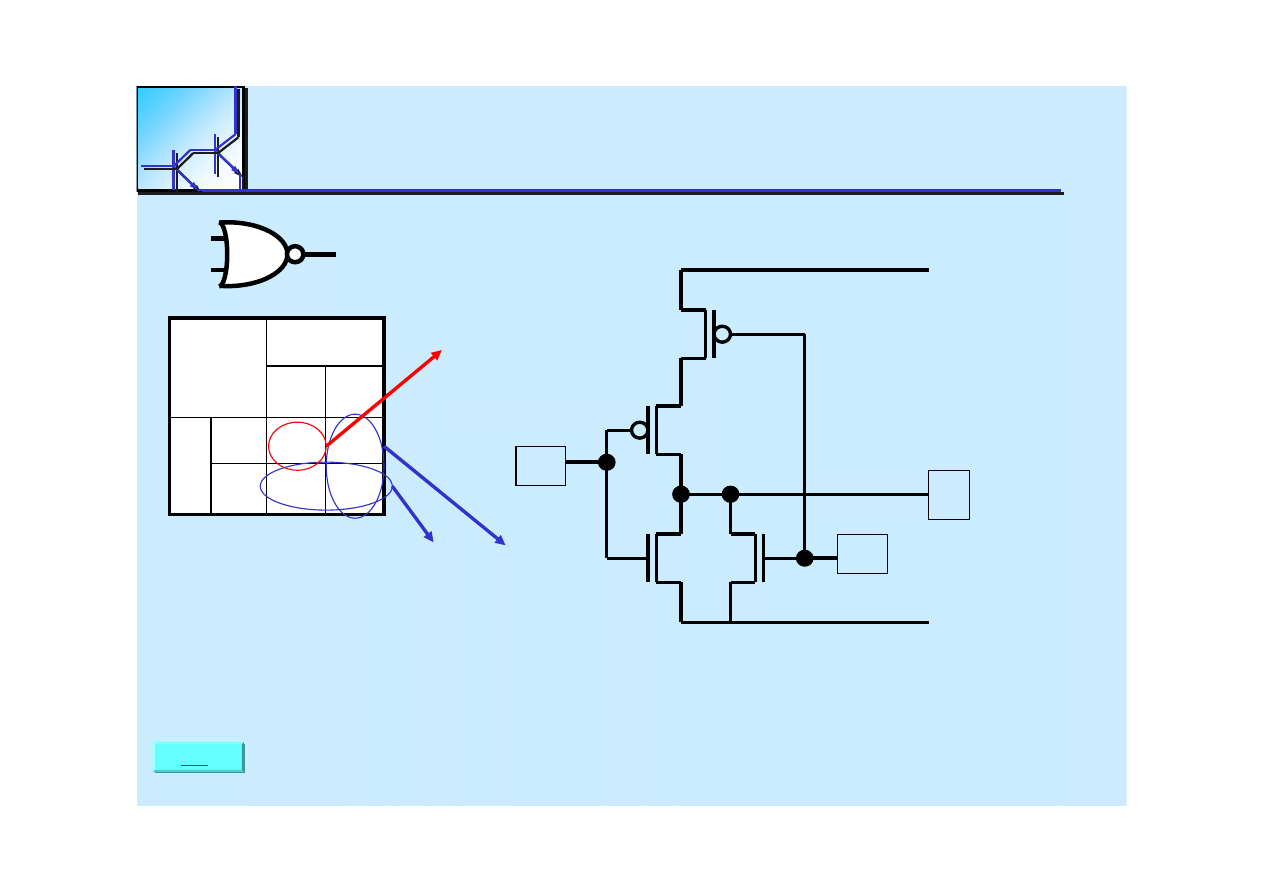
25 marca 2008
Cyfrowe układy kombinacyjne
37
The
NOR Gate
The
The
NOR
NOR
Gate
Gate
F
F
B
B
0
0
1
1
A
A
0
0
1
1
0
0
1
1
0
0
0
0
F
F
’
’
= A + B
= A + B
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
F = A
F = A
’
’
•
•
B
B
’
’
A
B
F
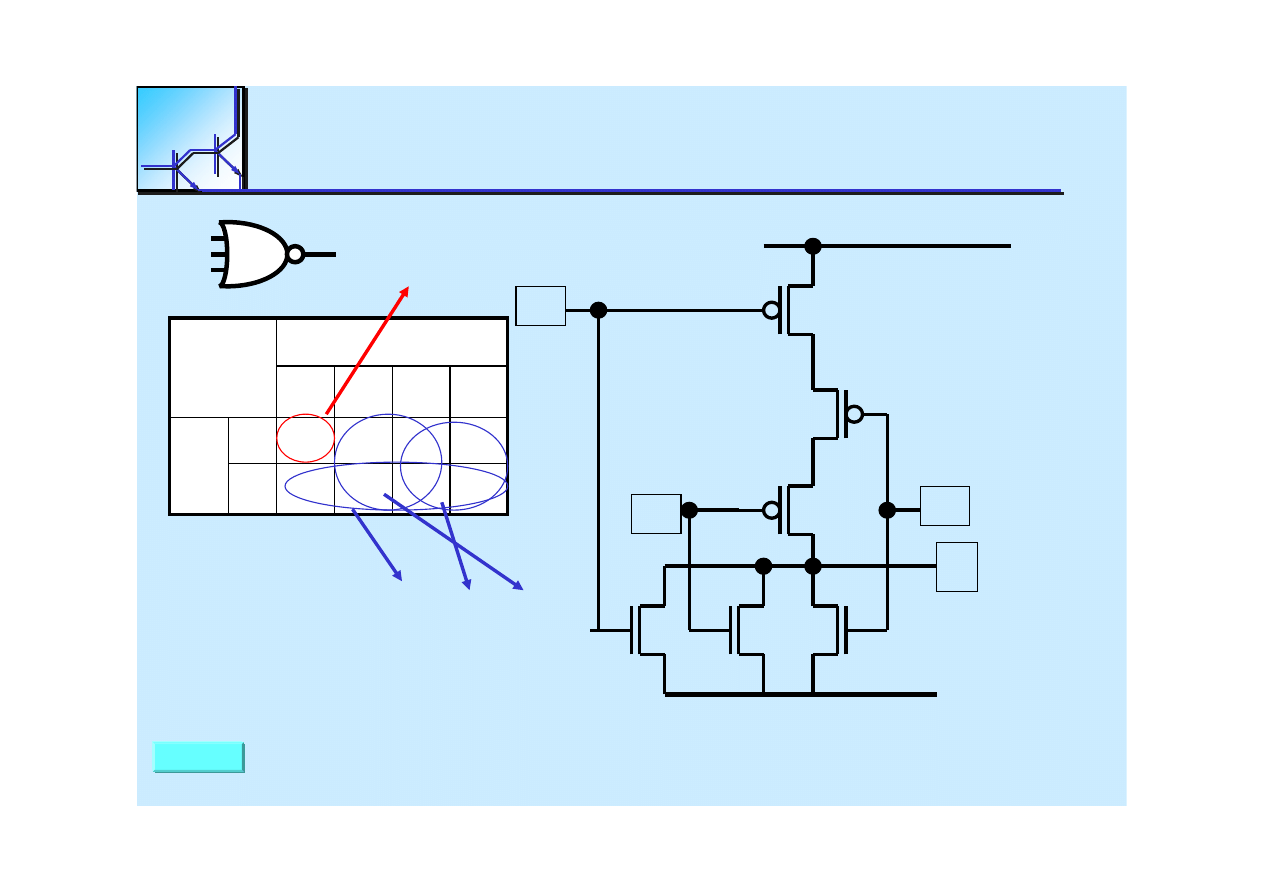
25 marca 2008
Cyfrowe układy kombinacyjne
38
The
3 Input
NOR Gate
The
The
3
3
Input
Input
NOR
NOR
Gate
Gate
F
F
BC
BC
00
00
01
01
11
11
10
10
A
A
0
0
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
F
F
’
’
=A + B + C
=A + B + C
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
NMOS
NMOS
F=A
F=A
’•
’•
B
B
’•
’•
C
C
’
’
A
B
F
C
C
C
25 marca 2008
Cyfrowe układy kombinacyjne
39
AND
AND
AND
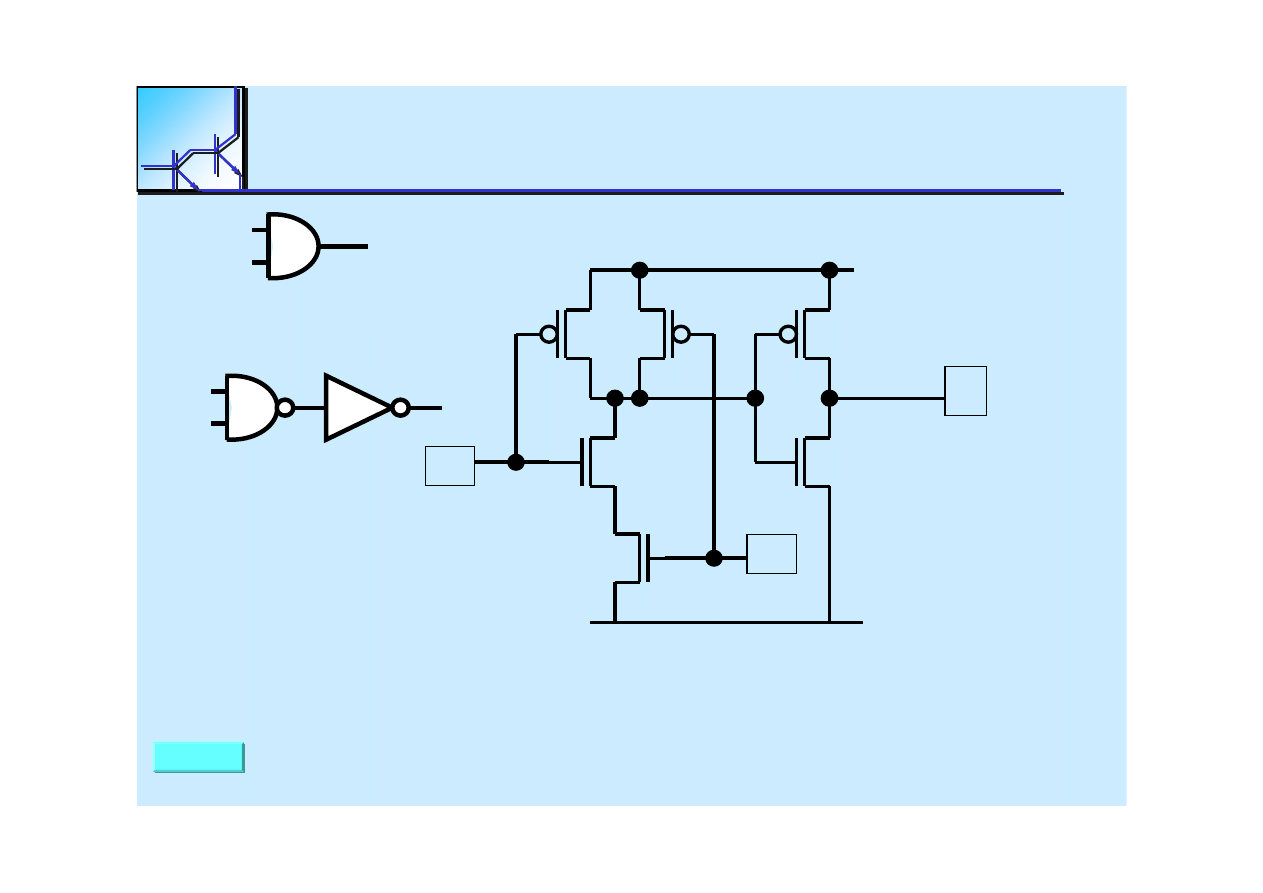
25 marca 2008
Cyfrowe układy kombinacyjne
40
The
AND Gate
The
The
AND
AND
Gate
Gate
A
B
F
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
NMOS
NMOS
A
B
F
=
=
25 marca 2008
Cyfrowe układy kombinacyjne
41
3 –state
Inverter
3
3
–
–
state
state
Inverter
Inverter
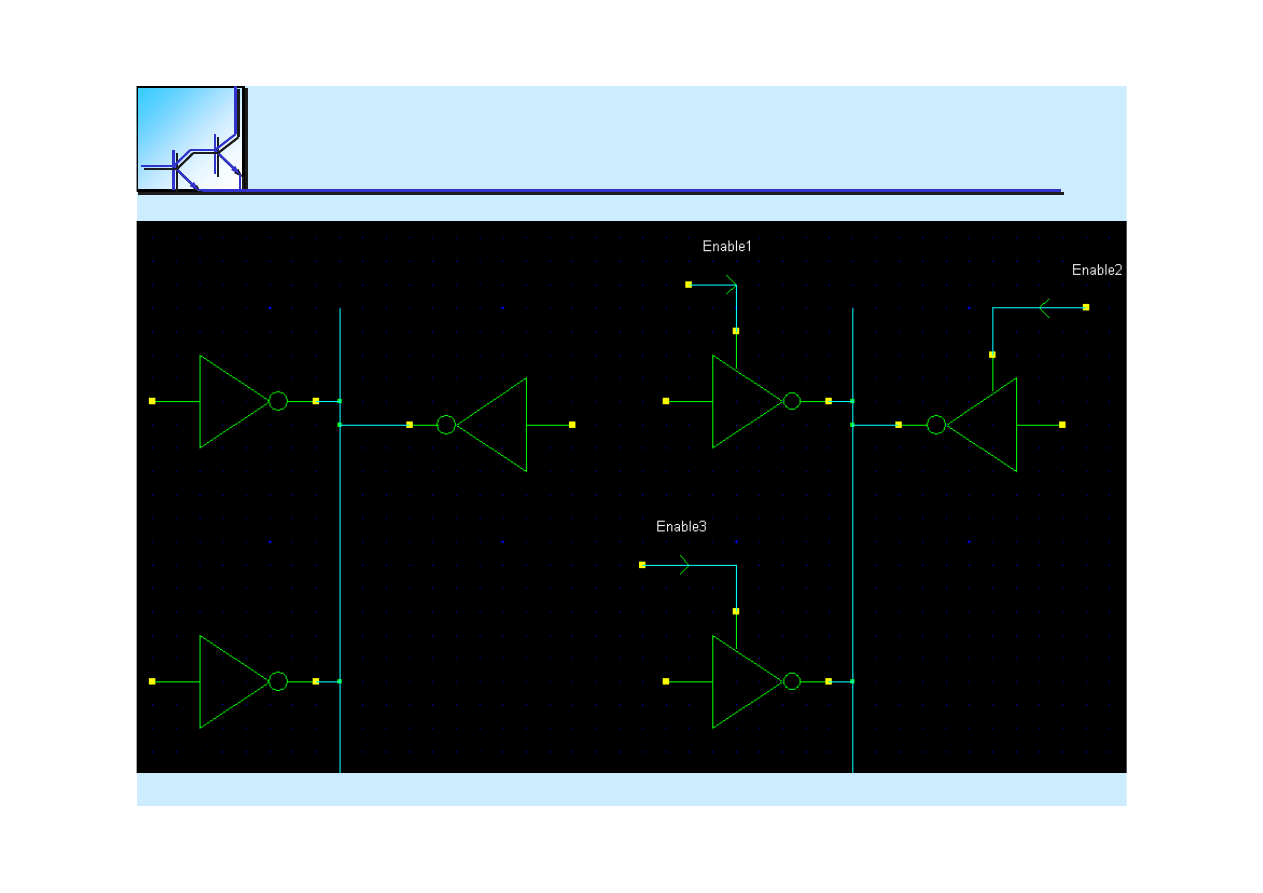
25 marca 2008
Cyfrowe układy kombinacyjne
42
Enable
input
case
Enable
Enable
input
input
case
case
Logic
conflict
Logic
Logic
conflict
conflict
One active
at
each
time
One
One
active
active
at
at
each
each
time
time
25 marca 2008
Cyfrowe układy kombinacyjne
43
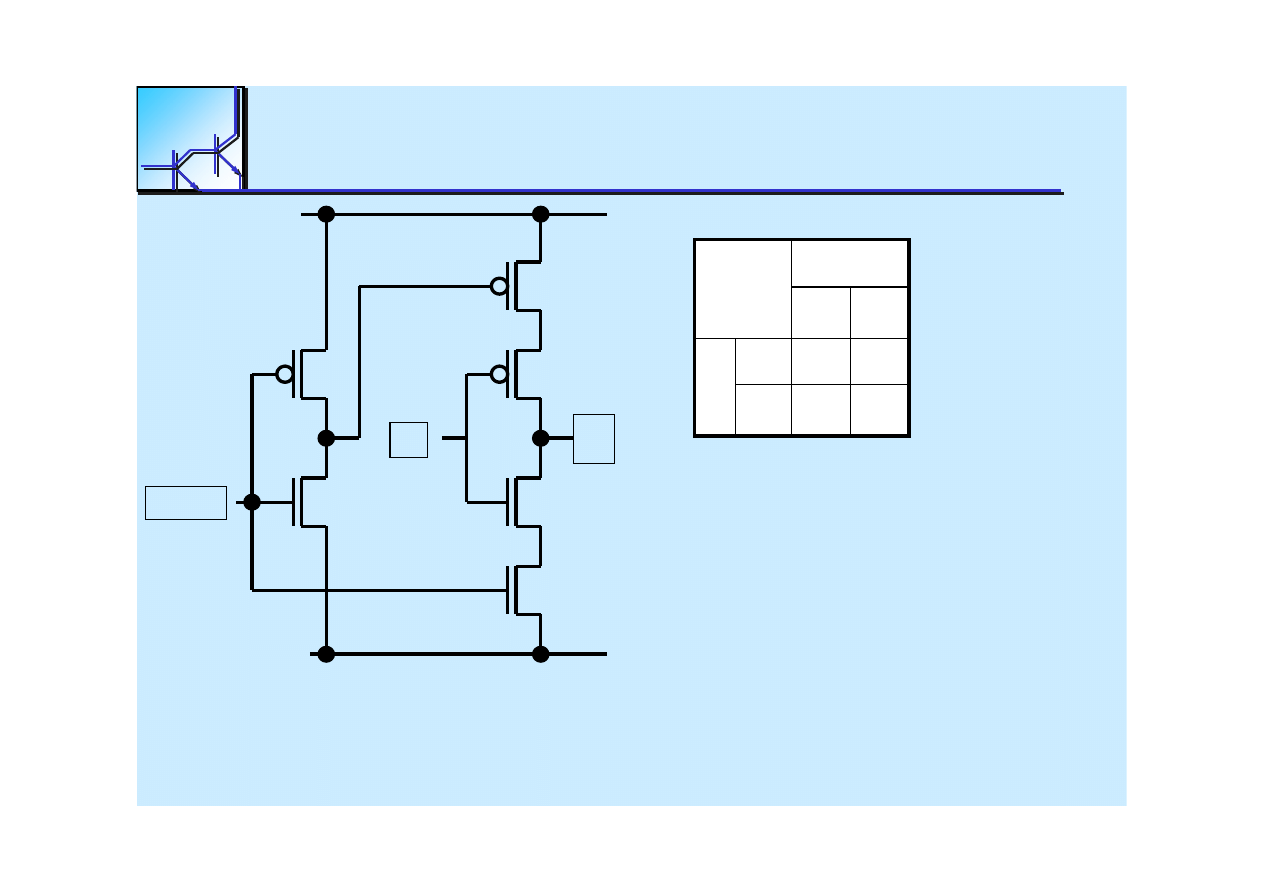
The
3 State
Inverter
The
The
3
3
State
State
Inverter
Inverter
F
F
Enable
Enable
0
0
1
1
In
In
0
0
x
x
1
1
1
1
x
x
0
0
V
V
DD
DD
F
F
PMOS
PMOS
NMOS
NMOS
In
In
Enable
Enable
V
V
SS
SS
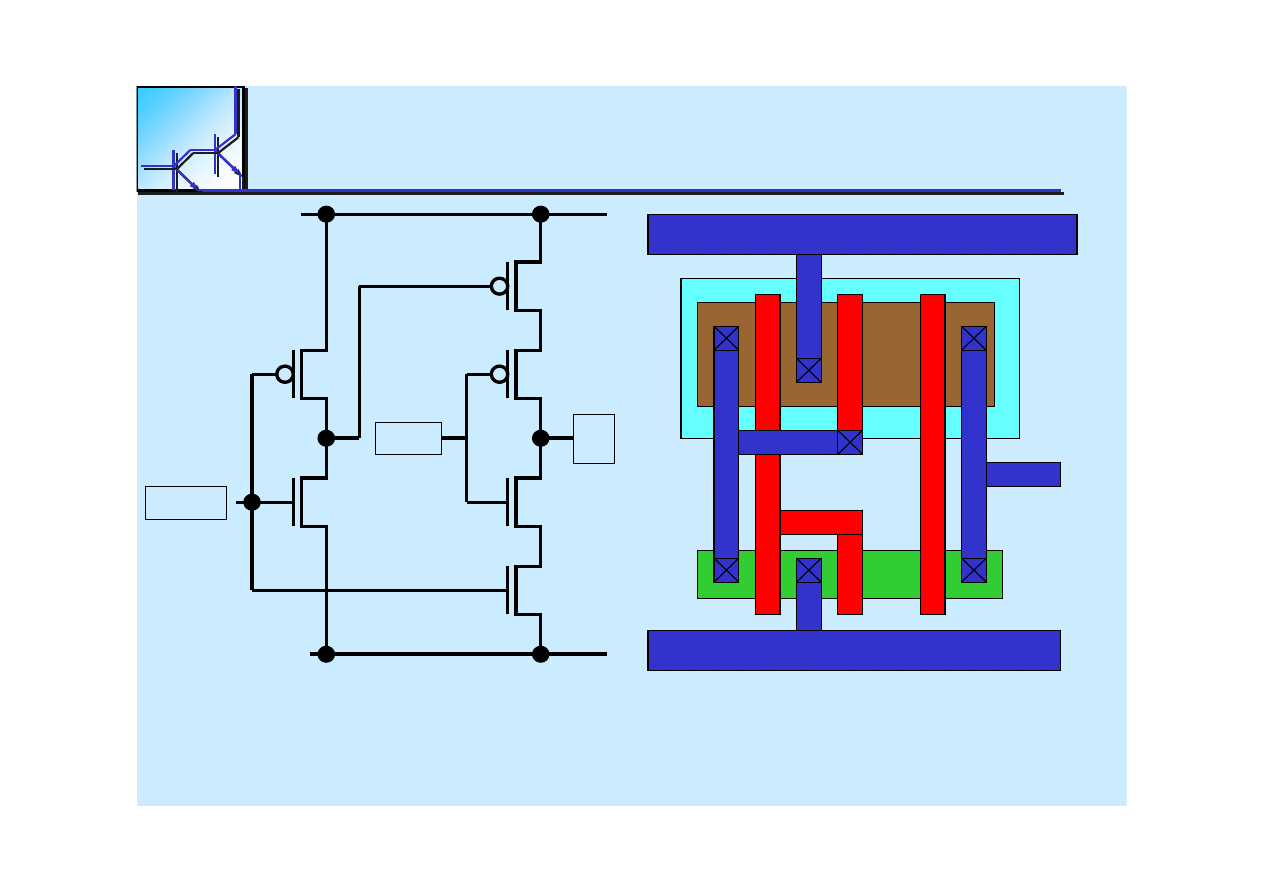
25 marca 2008
Cyfrowe układy kombinacyjne
44
The
3 State
Inverter
The
The
3
3
State
State
Inverter
Inverter
V
V
DD
DD
V
V
SS
SS
Enable
Enable
F
F
V
V
DD
DD
F
F
PMOS
PMOS
NMOS
NMOS
Data
Data
Enable
Enable
V
V
SS
SS
Data
Data
25 marca 2008
Cyfrowe układy kombinacyjne
45
Transmission Gate
Transmission Gate
Transmission Gate
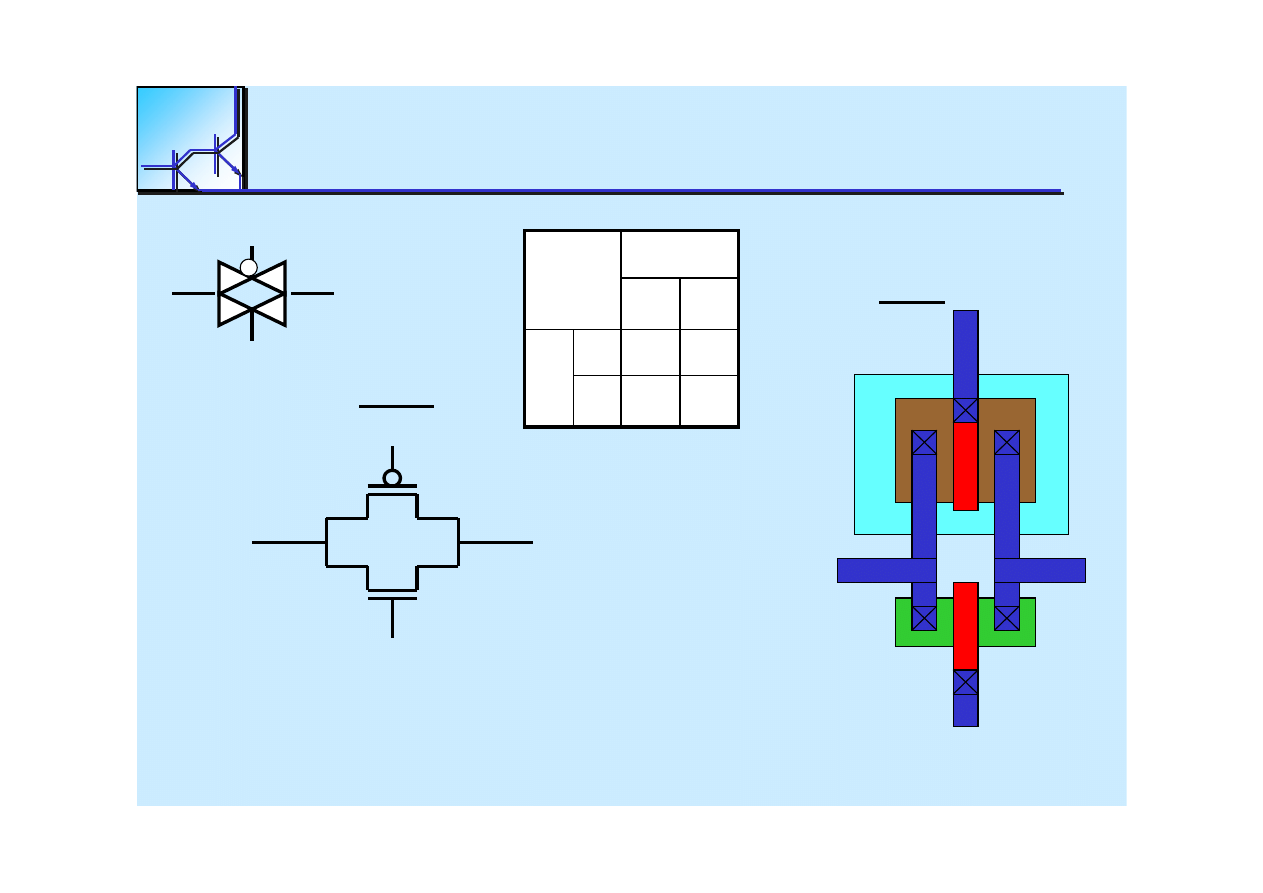
25 marca 2008
Cyfrowe układy kombinacyjne
46
The
Transmission
Gate
The
The
Transmission
Transmission
Gate
Gate
Enable
Enable
Enable
Enable
Input
Input
Ouput
Ouput
Out
Out
Enable
Enable
0
0
1
1
In
In
0
0
x
x
0
0
1
1
x
x
1
1
Out
Out
In
In
Enable
Enable
Enable
Enable
In
In
Out
Out
En
En
’
’
En
En
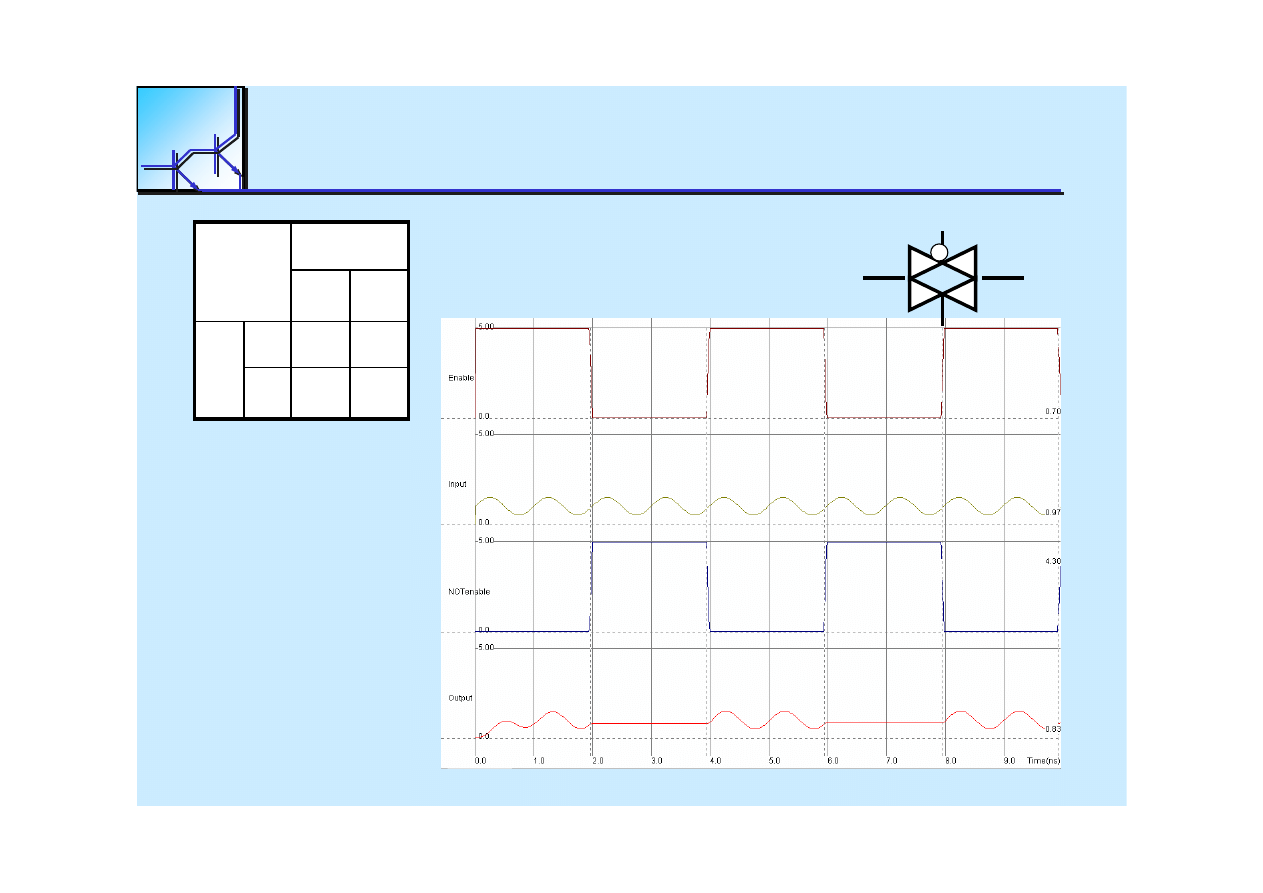
25 marca 2008
Cyfrowe układy kombinacyjne
48
The
Transmission
Gate
The
The
Transmission
Transmission
Gate
Gate
Out
Out
Enable
Enable
0
0
1
1
In
In
0
0
x
x
0
0
1
1
x
x
1
1
In
In
Out
Out
En
En
’
’
En
En
25 marca 2008
Cyfrowe układy kombinacyjne
49
Shift Register
Shift Register
Shift Register
25 marca 2008
Cyfrowe układy kombinacyjne
50
Complex Gates
Complex Gates
Complex Gates
25 marca 2008
Cyfrowe układy kombinacyjne
51
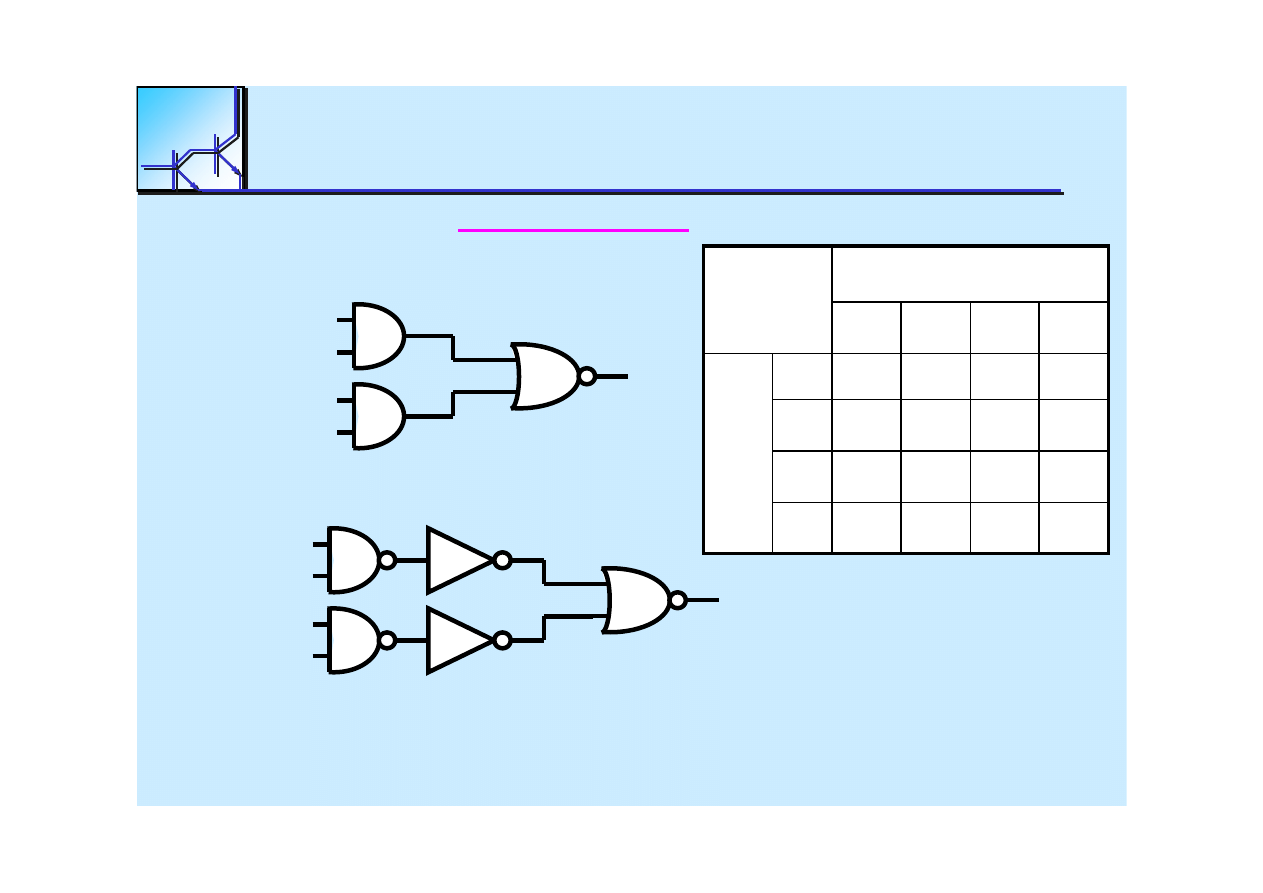
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
F = (A
F = (A
•
•
B) + (C
B) + (C
•
•
D)
D)
There are two way to design logic circuit:
There are two way to design logic circuit:
•
•
Gate level design
Gate level design
-
-
basic design elements are gates
basic design elements are gates
•
•
Transistor level design
Transistor level design
–
–
basic design elements are transistors
basic design elements are transistors
How to design logic function?
How to design logic function?
25 marca 2008
Cyfrowe układy kombinacyjne
52
The
Complex
Gate
–
gate level design
The
The
Complex
Complex
Gate
Gate
–
–
gate level design
gate level design
F = (A
F = (A
•
•
B) + (C
B) + (C
•
•
D)
D)
F
A
B
C
D
A
B
C
D
F
=
=
F
F
CD
CD
00
00
01
01
11
11
10
10
AB
AB
00
00
1
1
1
1
0
0
1
1
01
01
1
1
1
1
0
0
1
1
11
11
0
0
0
0
0
0
0
0
10
10
1
1
1
1
0
0
1
1
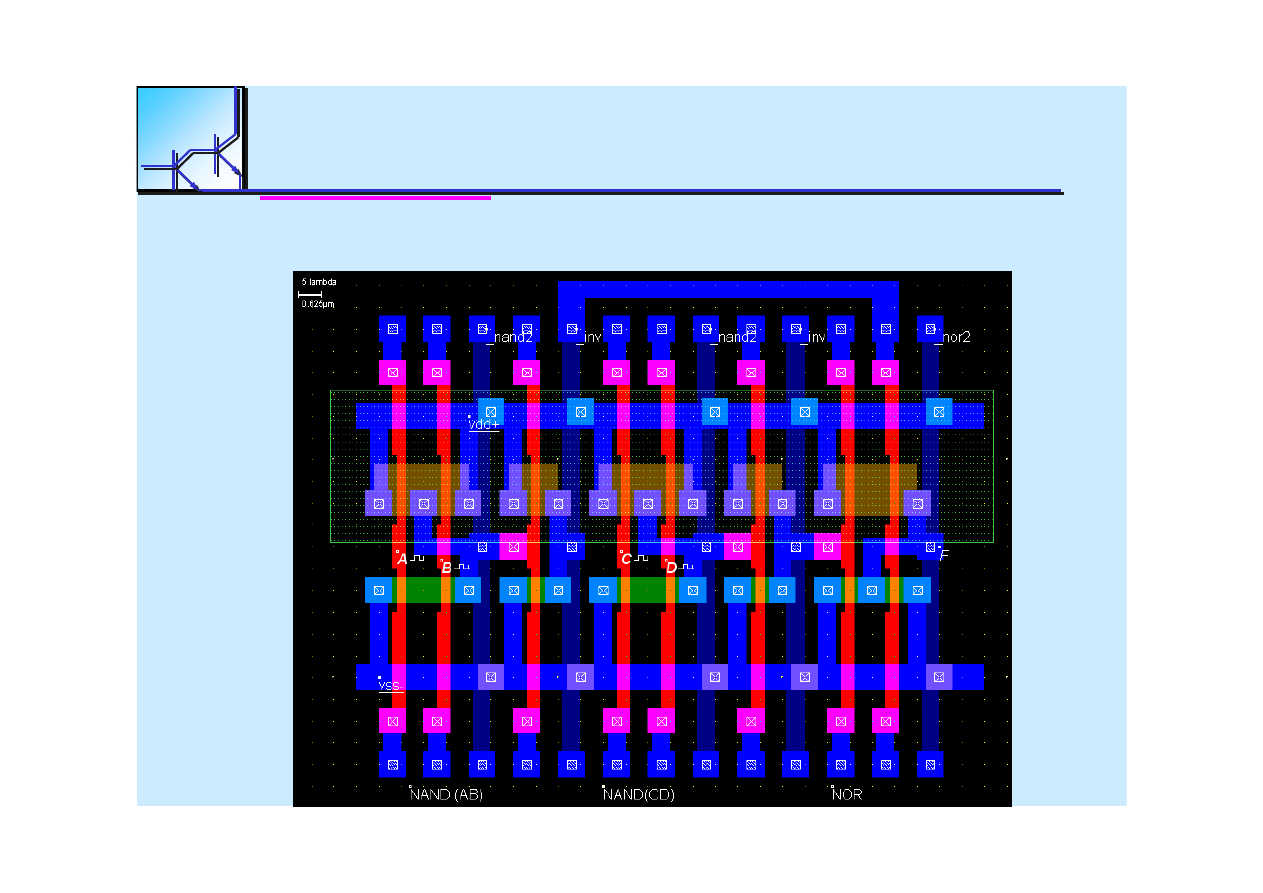
25 marca 2008
Cyfrowe układy kombinacyjne
53
The
Complex
Gate
–
gate level design
The
The
Complex
Complex
Gate
Gate
–
–
gate level design
gate level design
Circuit consists
Circuit consists
16
16
transistors
transistors
F = (A
F = (A
•
•
B) + (C
B) + (C
•
•
D)
D)
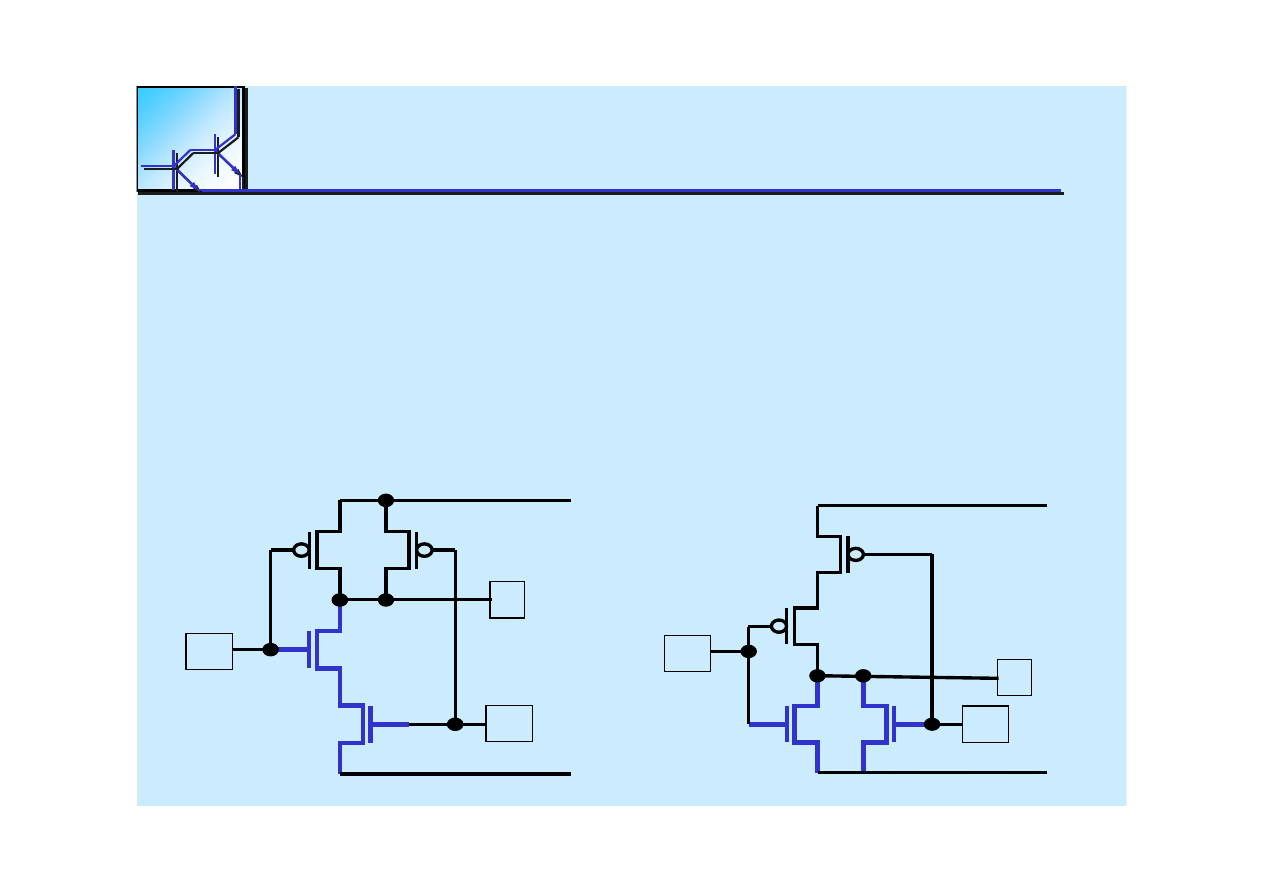
25 marca 2008
Cyfrowe układy kombinacyjne
54
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
NMOS network:
NMOS network:
AND
AND
operator translates into NMOS transistor in series
operator translates into NMOS transistor in series
OR
OR
operator translates into NMOS transistor in parallel
operator translates into NMOS transistor in parallel
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
NMOS
NMOS
NAND gate
NAND gate
NOR gate
NOR gate
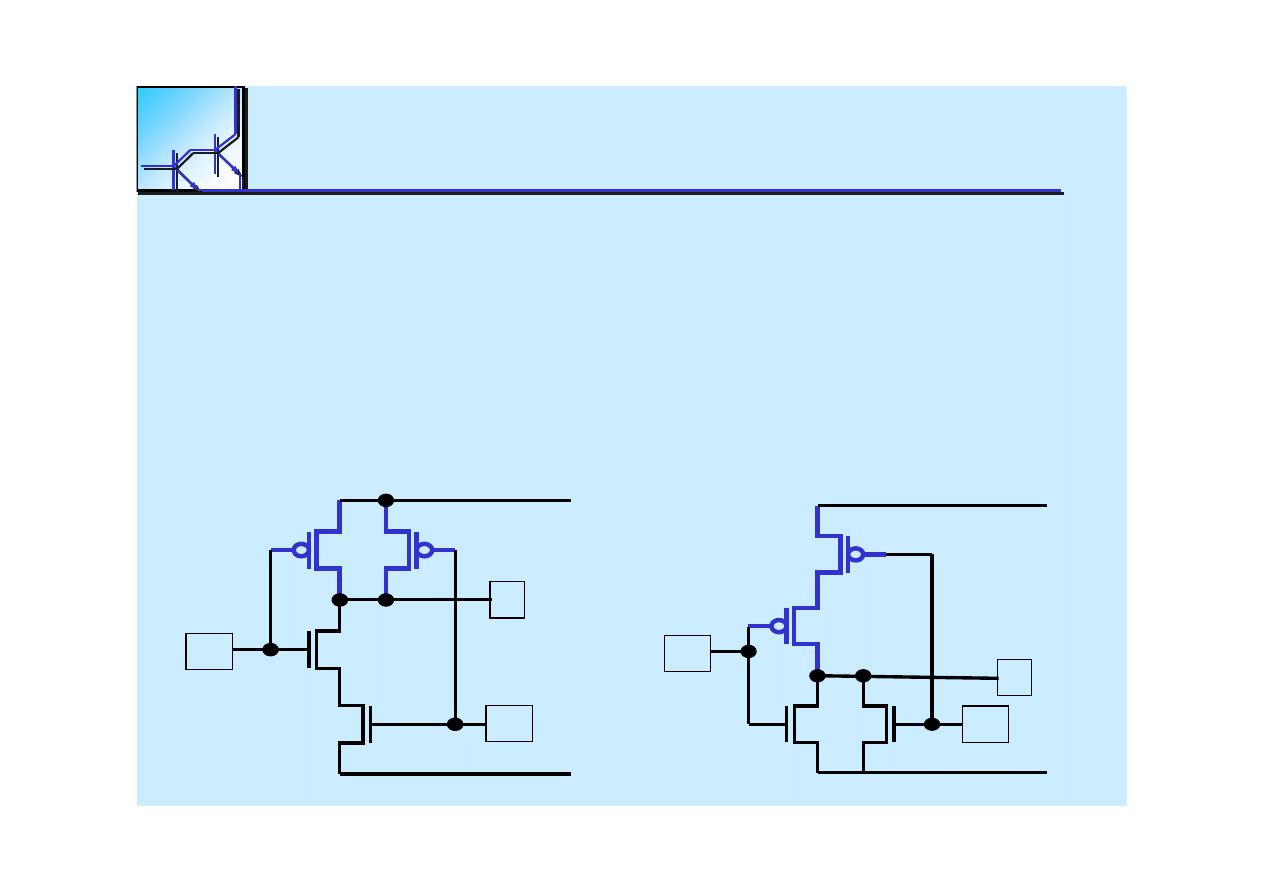
25 marca 2008
Cyfrowe układy kombinacyjne
55
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
PMOS network
PMOS network
AND
AND
operator translates into PMOS transistor in parallel
operator translates into PMOS transistor in parallel
OR
OR
operator translates into PMOS transistor in series
operator translates into PMOS transistor in series
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
NMOS
NMOS
NMOS
NMOS
NAND gate
NAND gate
V
V
SS
SS
V
V
DD
DD
F
F
B
B
A
A
PMOS
PMOS
PMOS
PMOS
NMOS
NMOS
NOR gate
NOR gate
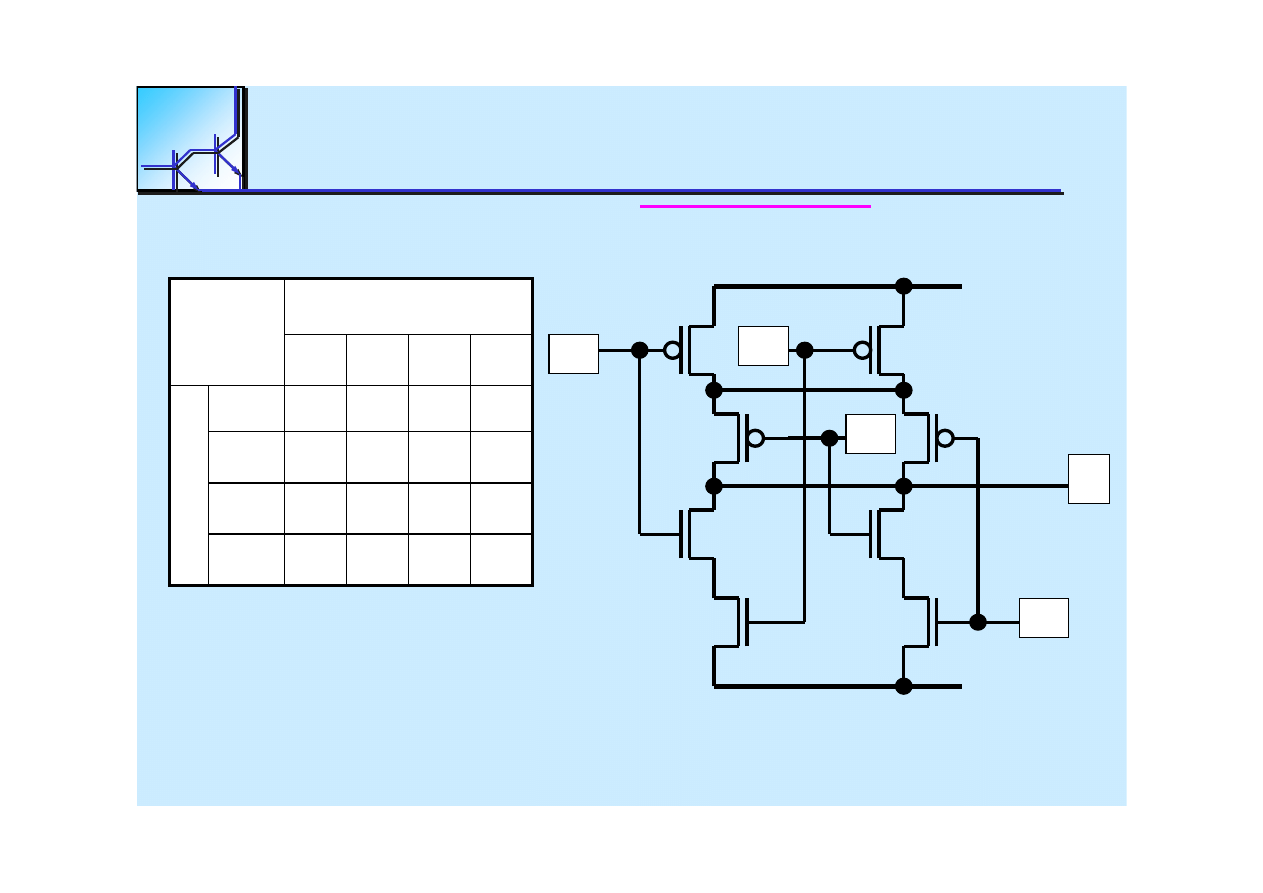
25 marca 2008
Cyfrowe układy kombinacyjne
56
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
Inverted
Inverted
function
function
: F = (A
: F = (A
•
•
B) + (C
B) + (C
•
•
D)
D)
V
V
SS
SS
V
V
DD
DD
F
F
A
A
PMOS
PMOS
NMOS
NMOS
B
B
C
C
D
D
Circuit consists
Circuit consists
8
8
Transistors
Transistors
F
F
CD
CD
00
00
01
01
11
11
10
10
A
A
B
B
0 0
0 0
1
1
1
1
0
0
1
1
0 1
0 1
1
1
1
1
0
0
1
1
1 1
1 1
0
0
0
0
0
0
0
0
10
10
1
1
1
1
0
0
1
1
NMOS: F
NMOS: F
’
’
= AB + CD
= AB + CD
PMOS: F = A
PMOS: F = A
’
’
C
C
’
’
+A
+A
’
’
D
D
’
’
+B
+B
’
’
C
C
’
’
+B
+B
’
’
D
D
’
’
=
=
= C
= C
’
’
(A
(A
’
’
+B
+B
’
’
)+D
)+D
’
’
(A
(A
’
’
+B
+B
’
’
) = (A
) = (A
’
’
+B
+B
’
’
)(C
)(C
’
’
+D
+D
’
’
)
)
=(AB)
=(AB)
’
’
*(CD)
*(CD)
’
’
=AB+CD
=AB+CD
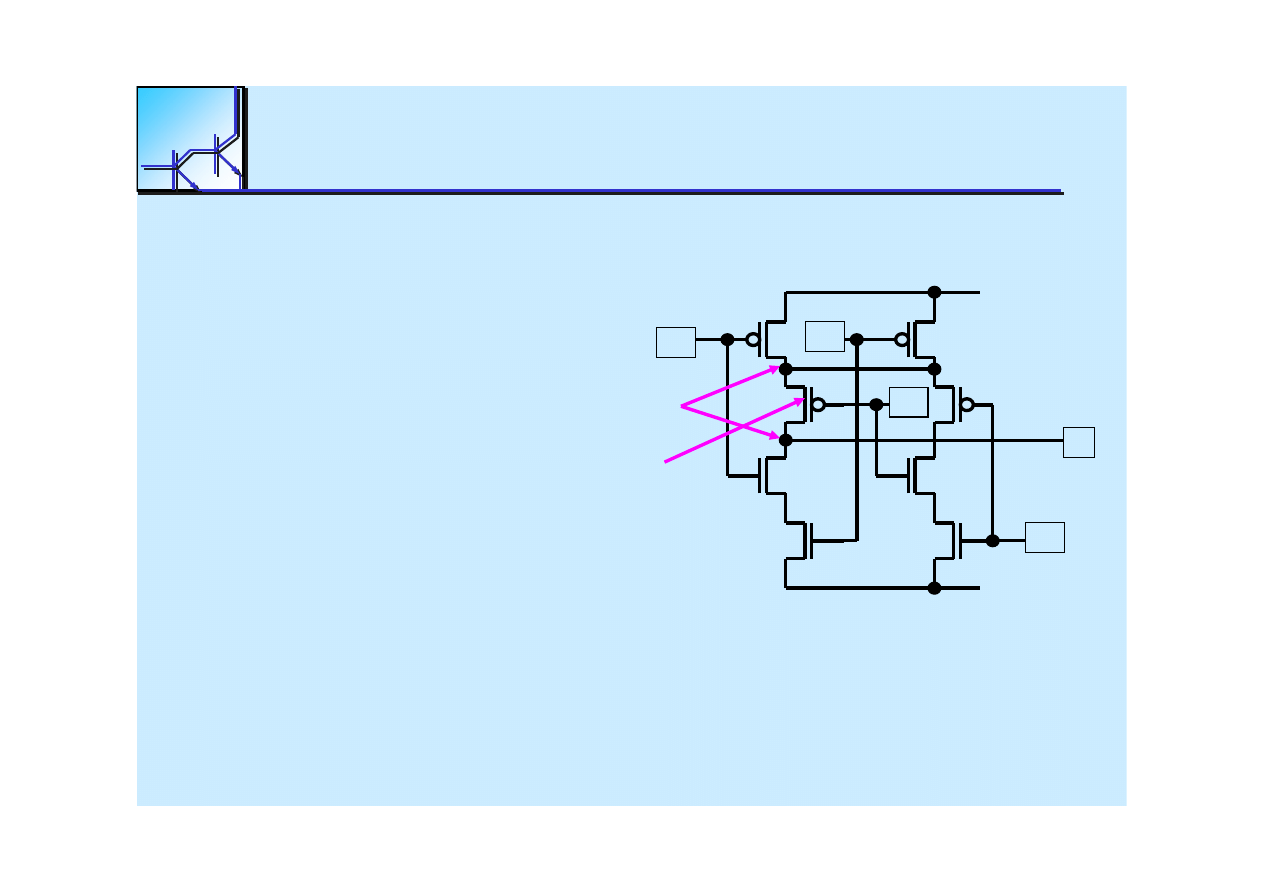
25 marca 2008
Cyfrowe układy kombinacyjne
57
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
Inverted
Inverted
function
function
: F = (A
: F = (A
•
•
B) + (C
B) + (C
•
•
D)
D)
Non
Non
-
-
inverting
inverting
function
function
need
need
extra
extra
inverter
inverter
at the output
at the output
F = (A
F = (A
•
•
B) + (C
B) + (C
•
•
D) ==>
D) ==>
F
F
= (A
= (A
•
•
B) + (C
B) + (C
•
•
D)
D)
Function
Function
A
A
B
B
C
C
D
D
F
F
Function
Function
A
A
B
B
C
C
D
D
F
F
Not F
Not F
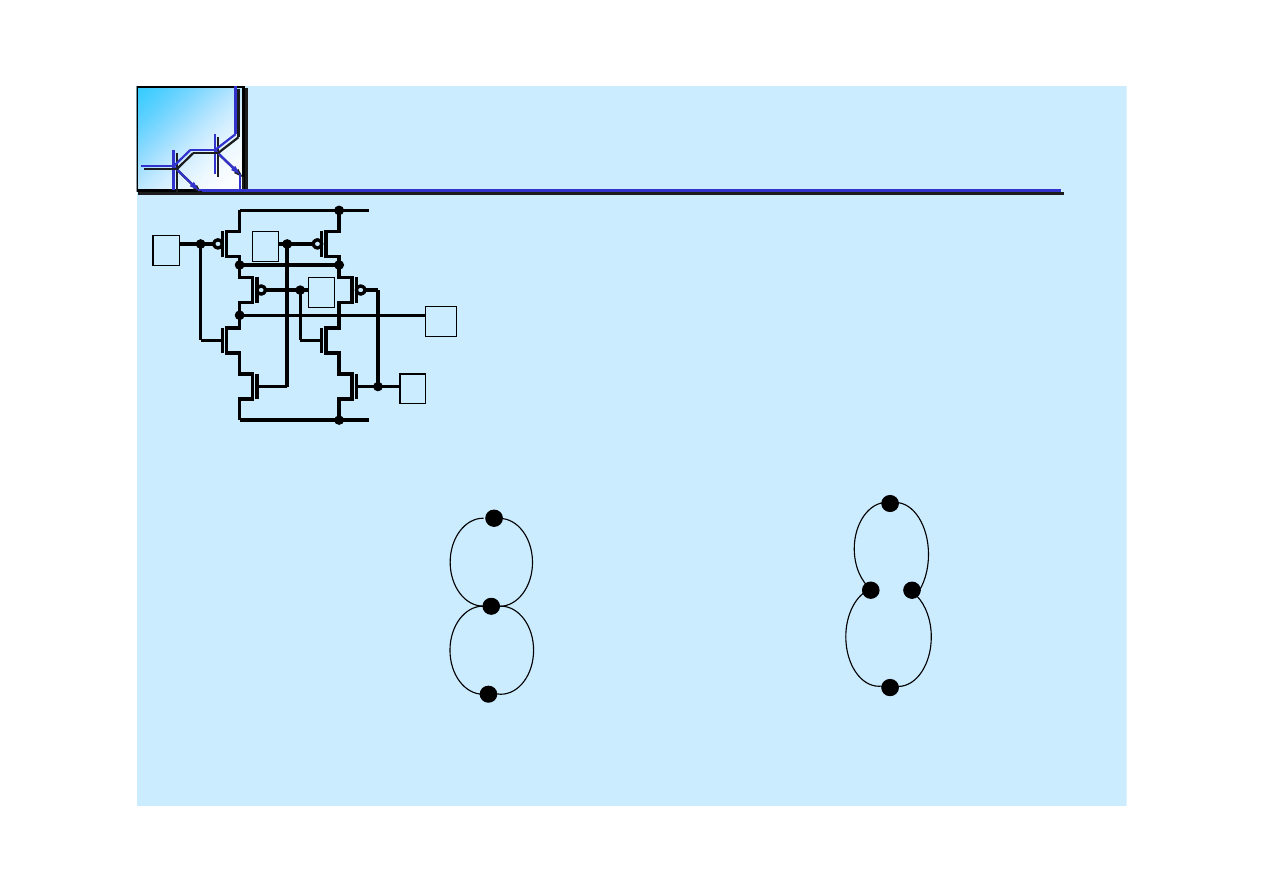
25 marca 2008
Cyfrowe układy kombinacyjne
58
The
Complex
Gate
- Euler Path
The
The
Complex
Complex
Gate
Gate
-
-
Euler Path
Euler Path
V
V
SS
SS
V
V
DD
DD
F
F
A
A
PMOS
PMOS
NMOS
NMOS
B
B
C
C
D
D
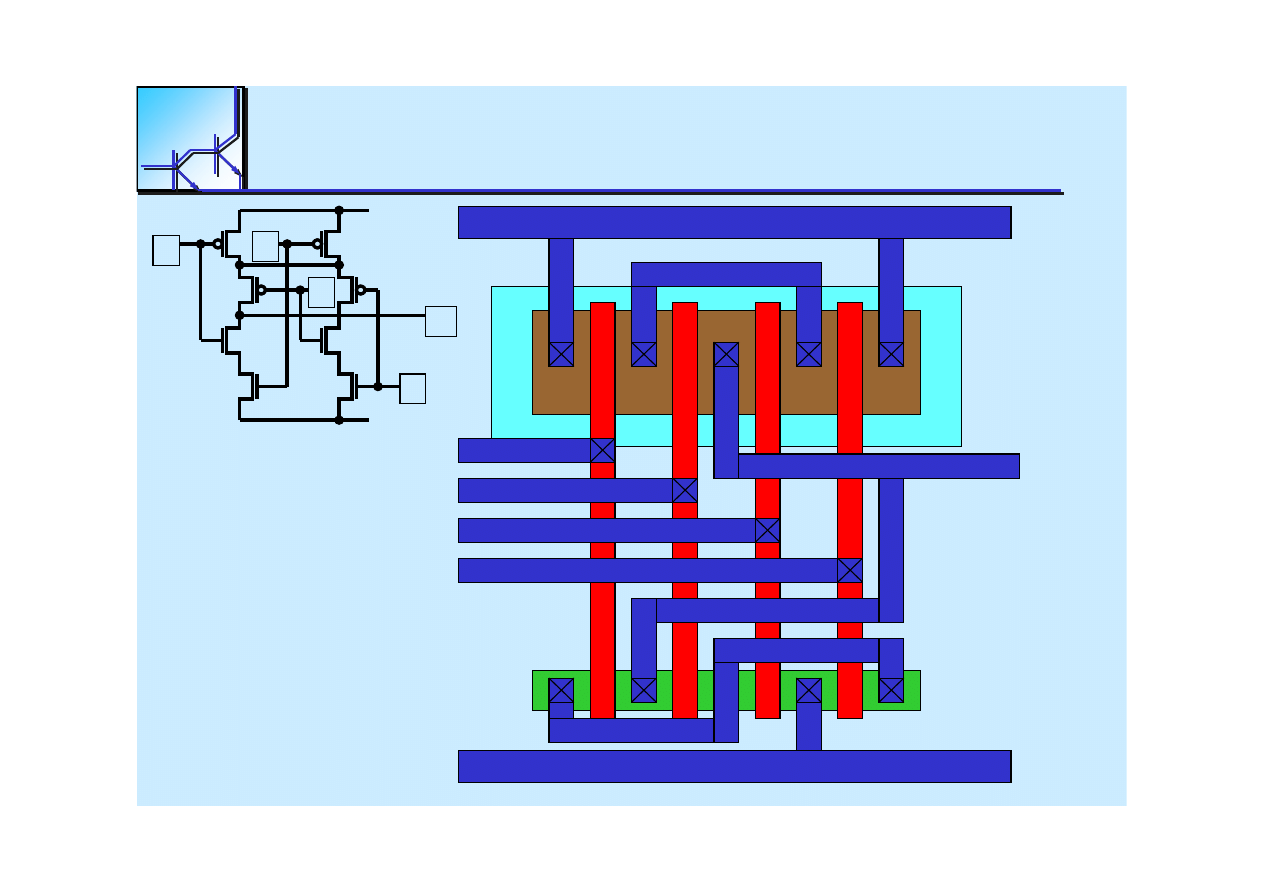
Euler path consists:
Euler path consists:
•
•
Nodes
Nodes
are source and drain connections
•
•
Branch
Branch
are transistors
Branches mirror the series-parallel connection of the transistors in the
circuit.
Two graphs for nMOS
and pMOS
have to be created
Node
Node
Branch
Branch
Euler graphs allow to find way of layout design without
Euler graphs allow to find way of layout design without
breaks
breaks
25 marca 2008
Cyfrowe układy kombinacyjne
59
The
Complex
Gate
- Euler Path
The
The
Complex
Complex
Gate
Gate
-
-
Euler Path
Euler Path
V
V
SS
SS
V
V
DD
DD
F
F
A
A
PMOS
PMOS
NMOS
NMOS
B
B
C
C
D
D
Algorithm for Gate designed without
Algorithm for Gate designed without
breaks:
breaks:
•
•
Find all Euler paths that cover the graph
Find all Euler paths that cover the graph
•
•
Find a
Find a
pMOS
pMOS
and
and
nMOS
nMOS
Euler path that have
Euler path that have
identical labeling (ordering of gate labels)
identical labeling (ordering of gate labels)
•
•
If is not found
If is not found
–
–
break the gate in minimum
break the gate in minimum
number of places to achieve identical labeling in
number of places to achieve identical labeling in
each piece of gate
each piece of gate
PMOS
PMOS
Logic
Logic
NMOS
NMOS
Logic
Logic
V
V
SS
SS
V
V
DD
DD
A
A
B
B
C
C
D
D
F
F
A
A
B
B
C
C
D
D
F
F
A
A
→
→
C
C
→
→
D
D
→
→
B
B
A
A
→
→
C
C
→
→
D
D
→
→
B
B
≡
≡
Paths:
Paths:
ACDB
ACDB
ADCB
ADCB
ABCD
ABCD
BDCA
BDCA
BCDA
BCDA
…………
…………
Paths:
Paths:
ACDB
ACDB
ABDC
ABDC
BACD
BACD
BDCA
BDCA
…………
…………
25 marca 2008
Cyfrowe układy kombinacyjne
60
The
Complex
Gate
The
The
Complex
Complex
Gate
Gate
V
V
SS
SS
V
V
DD
DD
F
F
A
A
PMOS
PMOS
NMOS
NMOS
B
B
C
C
D
D
V
V
DD
DD
A
A
B
B
F
F
V
V
ss
ss
D
D
C
C
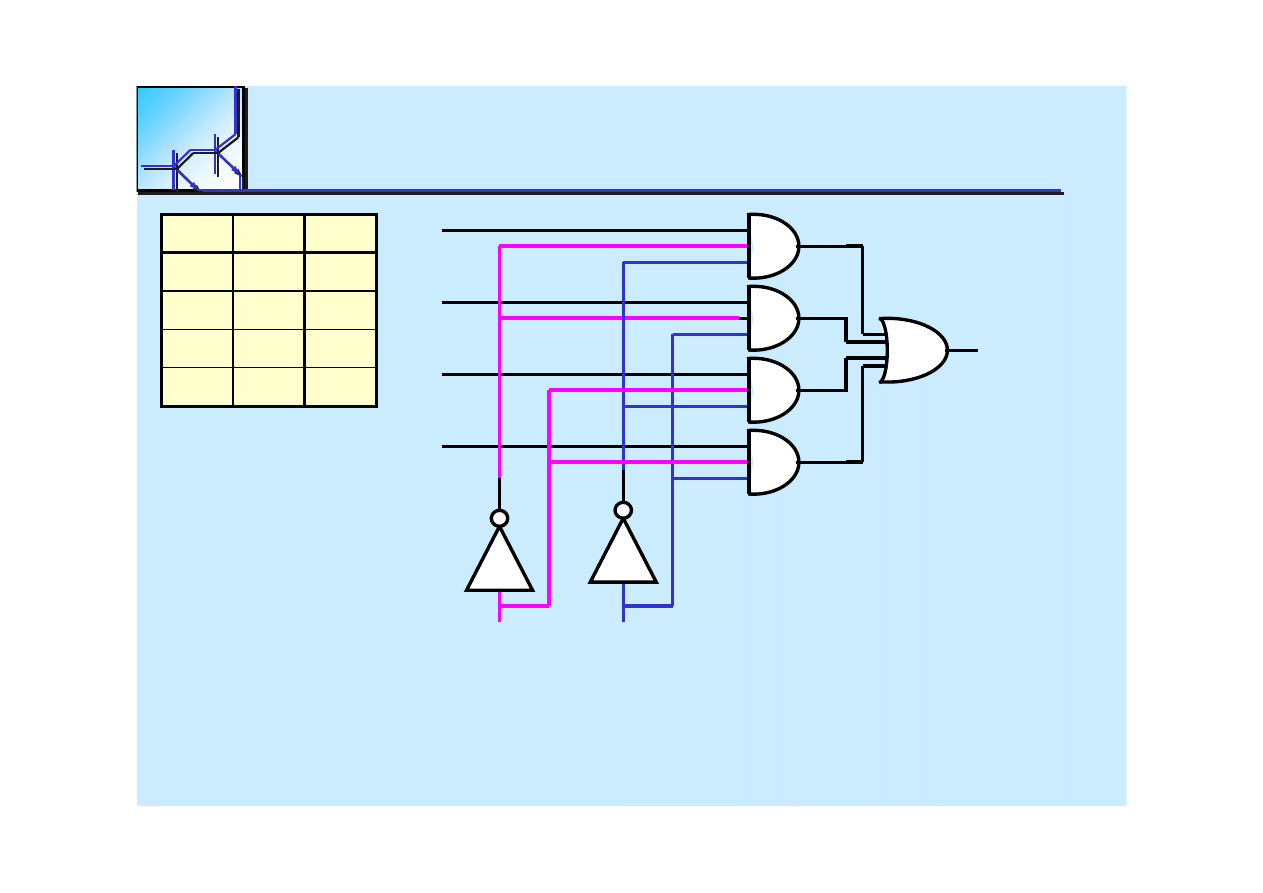
A C D B
A C D B
25 marca 2008
Cyfrowe układy kombinacyjne
61
Multiplexery
i demultipleksery
Multiplexery
Multiplexery
i demultipleksery
i demultipleksery
Cyfrowe
układy
kombinacyjne
Cyfrowe
Cyfrowe
uk
uk
ł
ł
ady
ady
kombinacyjne
kombinacyjne
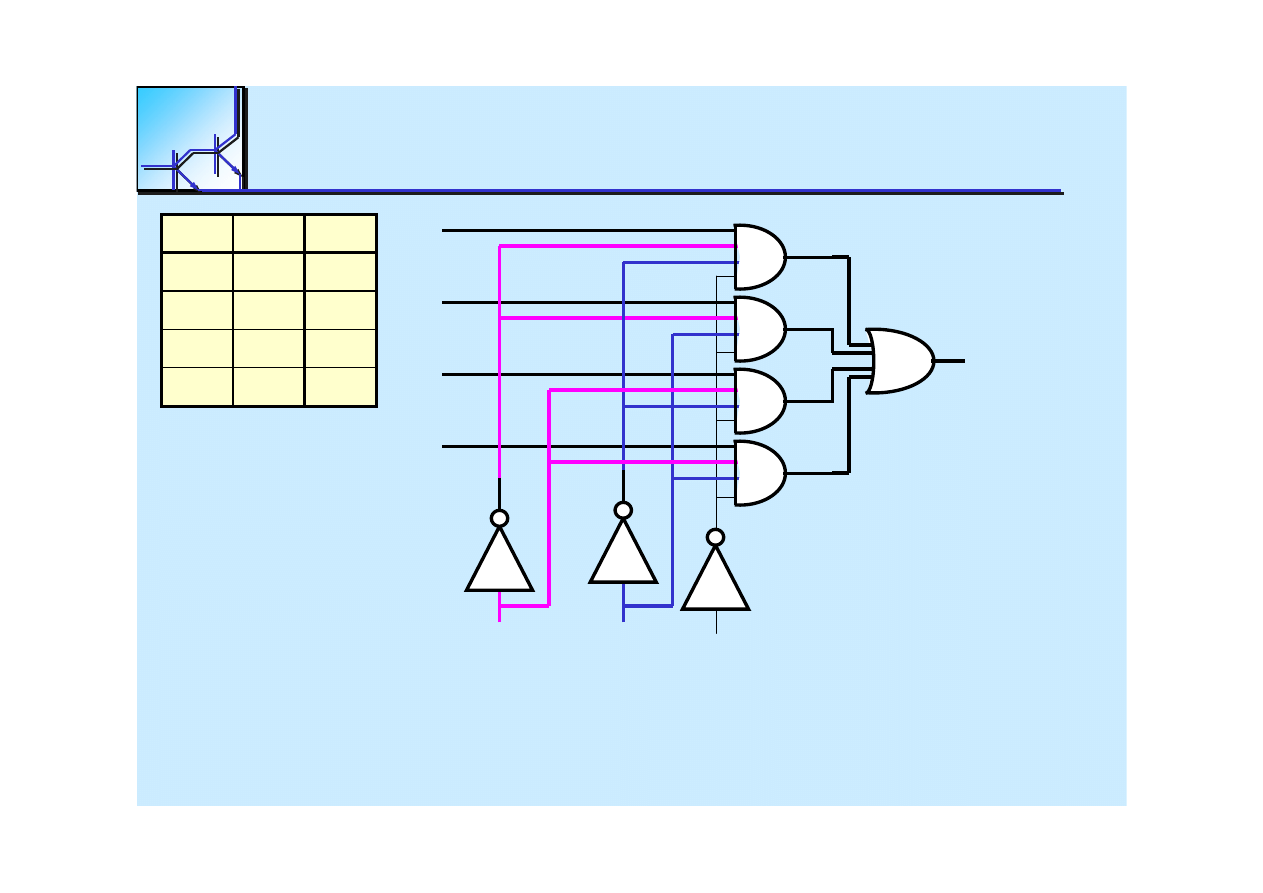
25 marca 2008
Cyfrowe układy kombinacyjne
62
Multipleksery
Multipleksery
Multipleksery
Umo
Umo
ż
ż
liwiaj
liwiaj
ą
ą
wyb
wyb
ó
ó
r i przes
r i przes
ł
ł
anie na wyj
anie na wyj
ś
ś
cie sygna
cie sygna
ł
ł
u z jednego z
u z jednego z
N wej
N wej
ść
ść
Numer wej
Numer wej
ś
ś
cia jest okre
cia jest okre
ś
ś
lany przez stan wej
lany przez stan wej
ść
ść
adresowych
adresowych
(steruj
(steruj
ą
ą
cych) S0, S1 ....
cych) S0, S1 ....
Z uwagi na naturalny kod binarny stosowany do okre
Z uwagi na naturalny kod binarny stosowany do okre
ś
ś
lenia
lenia
adresu, liczba wej
adresu, liczba wej
ść
ść
jest zwi
jest zwi
ą
ą
zana z liczb
zana z liczb
ą
ą
wej
wej
ś
ś
c
c
steruj
steruj
ą
ą
cych
cych
zale
zale
ż
ż
no
no
ś
ś
ci
ci
ą
ą
:
:
N = 2
N = 2
n
n
D0
D0
D1
D1
D2
D2
D3
D3
S1 S0
S1 S0
Out
Out
25 marca 2008
Cyfrowe układy kombinacyjne
63
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1
S1
S0
S0
OUT
OUT
0
0
0
0
D0
D0
0
0
1
1
D1
D1
1
1
0
0
D2
D2
1
1
1
1
D3
D3
S1
S1
D0
D0
D1
D1
D2
D2
D3
D3
S0
S0
Out
Need (n + 1)
Need (n + 1)
-
-
input AND gates for selection and a 2
input AND gates for selection and a 2
n
n
-
-
input
input
OR gate to
OR gate to
get the output.
get the output.
25 marca 2008
Cyfrowe układy kombinacyjne
64
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1
S1
S0
S0
OUT
OUT
0
0
0
0
D0
D0
0
0
1
1
D1
D1
1
1
0
0
D2
D2
1
1
1
1
D3
D3
S1
S1
D0
D0
D1
D1
D2
D2
D3
D3
S0
S0
Out
Dodatkowe wej
Dodatkowe wej
ś
ś
cie
cie
enable
enable
pozwala zablokowa
pozwala zablokowa
ć
ć
stan wyj
stan wyj
ś
ś
cia
cia
multipleksera
multipleksera
En
En
25 marca 2008
Cyfrowe układy kombinacyjne
65
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1
S1
S0
S0
OUT
OUT
0
0
0
0
D0
D0
0
0
1
1
D1
D1
1
1
0
0
D2
D2
1
1
1
1
D3
D3
Dodatkowe wej
Dodatkowe wej
ś
ś
cie
cie
enable
enable
pozwala zablokowa
pozwala zablokowa
ć
ć
stan wyj
stan wyj
ś
ś
cia
cia
multipleksera
multipleksera
D0
D0
D1
D1
D8
D8
Out
Out
S1 S2 S3
S1 S2 S3
En
En
25 marca 2008
Cyfrowe układy kombinacyjne
66
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1
S1
S0
S0
OUT
OUT
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
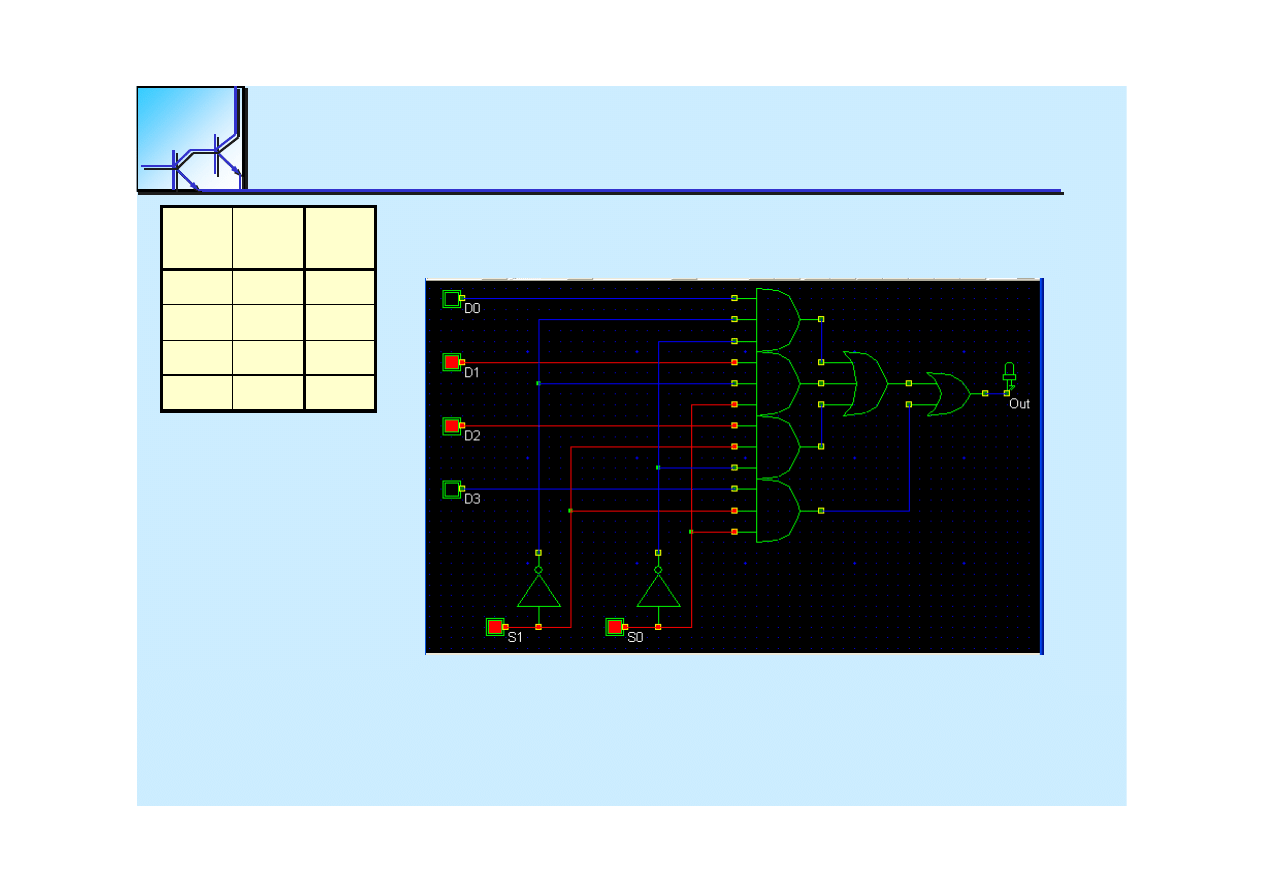
MUX with n select lines can be used to implement any
MUX with n select lines can be used to implement any
boolean
boolean
function of n variables by directly connecting the
function of n variables by directly connecting the
data inputs to
data inputs to
„
„
1
1
”
”
or
or
„
„
0
0
”
”
Multiplexer
Multiplexer
D0
D0
D1
D1
D2
D2
D3
D3
S1 S0
S1 S0
Out
Out
0
0
1
1
1
1
0
0
25 marca 2008
Cyfrowe układy kombinacyjne
67
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1
S1
S0
S0
OUT
OUT
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
25 marca 2008
Cyfrowe układy kombinacyjne
68
The
Multiplexer
as AND Gate
The
The
Multiplexer
Multiplexer
as AND
as AND
Gate
Gate
S1
S1
S0
S0
OUT
OUT
0
0
0
0
0
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
1
1
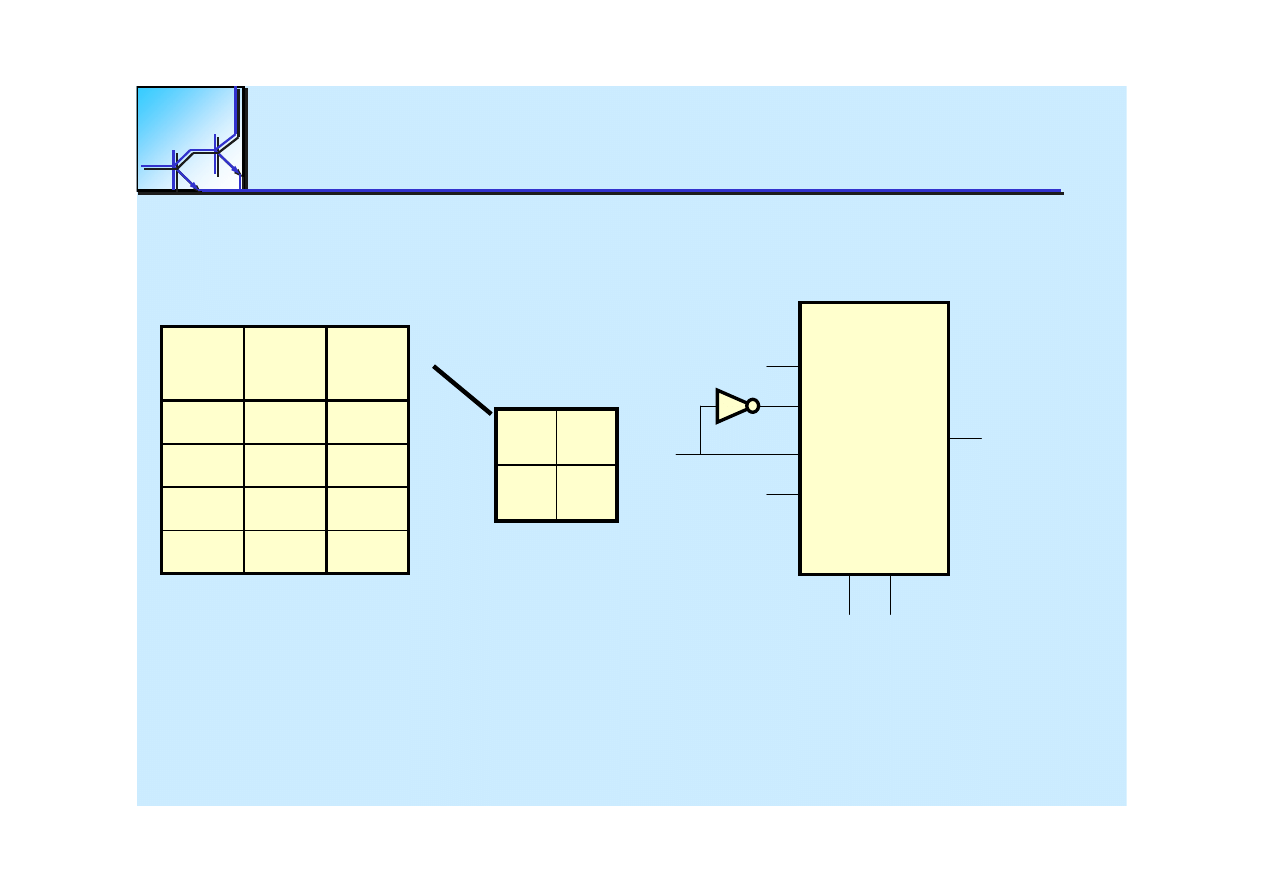
MUX with n select lines can be used to implement any
MUX with n select lines can be used to implement any
boolean
boolean
function of n variables by directly connecting the
function of n variables by directly connecting the
data inputs to
data inputs to
„
„
1
1
”
”
or
or
„
„
0
0
”
”
Multiplexer
Multiplexer
D0
D0
D1
D1
D2
D2
D3
D3
x y
x y
z
z
0
0
0
0
0
0
1
1
x
x
z
z
y
y
≡
≡
25 marca 2008
Cyfrowe układy kombinacyjne
69
The
Multiplexer
as OR Gate
The
The
Multiplexer
Multiplexer
as OR
as OR
Gate
Gate
S1
S1
S0
S0
OUT
OUT
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
MUX with n select lines can be used to implement any
MUX with n select lines can be used to implement any
boolean
boolean
function of n variables by directly connecting the
function of n variables by directly connecting the
data inputs to
data inputs to
„
„
1
1
”
”
or
or
„
„
0
0
”
”
Multiplexer
Multiplexer
D0
D0
D1
D1
D2
D2
D3
D3
x y
x y
z
z
0
0
1
1
1
1
1
1
≡
≡
x
x
z
z
y
y
25 marca 2008
Cyfrowe układy kombinacyjne
70
The
Multiplexer
The
The
Multiplexer
Multiplexer
F
F
F
F
Use a 4
Use a 4
to
to
1 MUX to implement:
1 MUX to implement:
F
F
=
=
x
x
’
’
y
y
’
’
z + xyz
z + xyz
’
’
+
+
yz
yz
= x
= x
’
’
⋅
⋅
1
1
⋅
⋅
0 + x
0 + x
⋅
⋅
0
0
⋅
⋅
1 + 0
1 + 0
⋅
⋅
0
0
0
0
= x
= x
’
’
⋅
⋅
0
0
⋅
⋅
1 + x
1 + x
⋅
⋅
1
1
⋅
⋅
0 + 1
0 + 1
⋅
⋅
1
1
1
1
= x
= x
’
’
⋅
⋅
0
0
⋅
⋅
0 + x
0 + x
⋅
⋅
1
1
⋅
⋅
1 + 1
1 + 1
⋅
⋅
0
0
x
x
= x
= x
’
’
⋅
⋅
1
1
⋅
⋅
1 + x
1 + x
⋅
⋅
0
0
⋅
⋅
0 + 0
0 + 0
⋅
⋅
1
1
x
x
’
’
S1=
S1=y
y
S0=
S0=z
z
0
0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
25 marca 2008
Cyfrowe układy kombinacyjne
71
The
Multiplexer
The
The
Multiplexer
Multiplexer
S1=
S1=y
y
S0=
S0=z
z
F
F
0
0
0
0
0
0
0
0
1
1
x
x
’
’
1
1
0
0
x
x
1
1
1
1
1
1
Use a 4
Use a 4
to
to
1 MUX to implement:
1 MUX to implement:
F
F
=
=
x
x
’
’
y
y
’
’
z + xyz
z + xyz
’
’
+
+
yz
yz
Multiplexer
Multiplexer
D0
D0
D1
D1
D2
D2
D3
D3
S1 S0
S1 S0
Out
Out
0
0
x
x
1
1
y z
y z
F
F
I
I
t is possible to generate any function of (n+1) variables with
t is possible to generate any function of (n+1) variables with
a 2
a 2
n
n
to
to
1 MUX, and an INVERTER
1 MUX, and an INVERTER
S0
S0
S1
S1
0
0
1
1
0
0
0
0
x
x
’
’
1
1
x
x
1
1
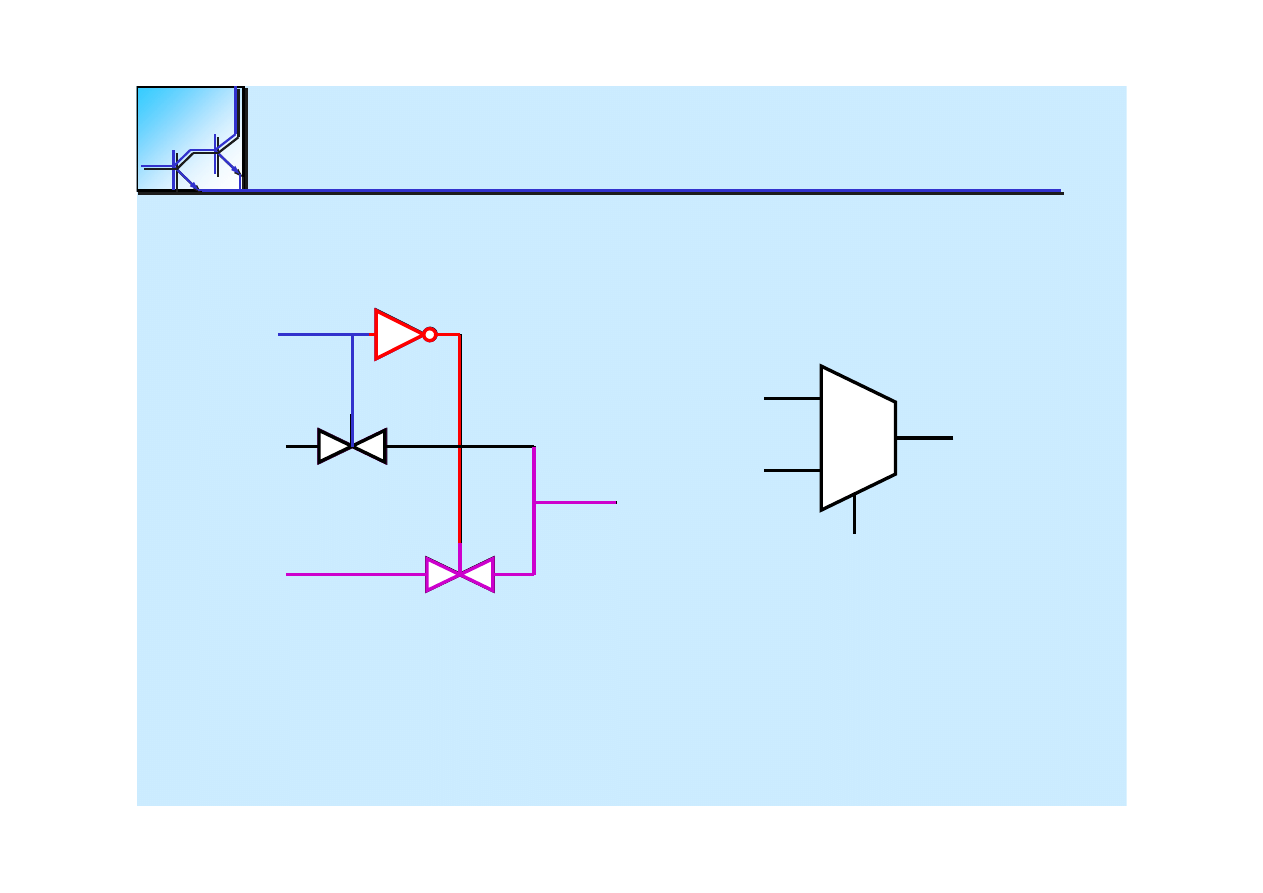
25 marca 2008
Cyfrowe układy kombinacyjne
72
The
Multiplexer
The
The
Multiplexer
Multiplexer
The main component of the multiplexer is transmission gate
The main component of the multiplexer is transmission gate
In
In
Out
Out
En
En
In
In
Out
Out
En
En
D0
D0
D1
D1
Out
Out
Sel
Sel
Multiplexer
Multiplexer
2
2
to 1
to 1
MUX
MUX
D0
D0
D1
D1
S
S
el
el
Out
Out
==
==
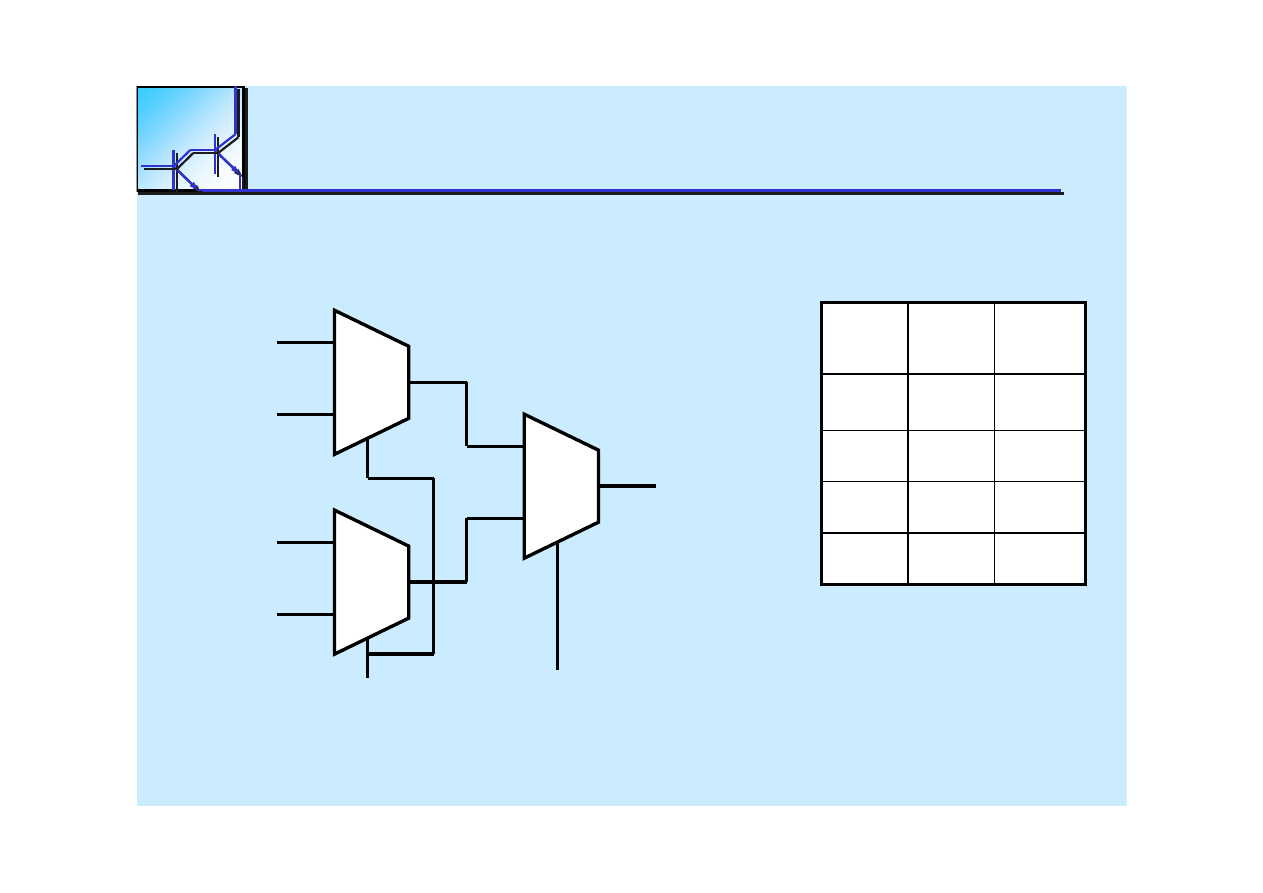
25 marca 2008
Cyfrowe układy kombinacyjne
73
The
Multiplexer
The
The
Multiplexer
Multiplexer
A
A
B
B
C
C
D
D
F
F
S1
S1
S
S
0
0
Multiplexer 4 to 1
Multiplexer 4 to 1
S1
S1
S
S
0
0
F
F
0
0
0
0
D
D
0
0
1
1
C
C
1
1
0
0
B
B
1
1
1
1
A
A
MUX
MUX
D0
D0
D1
D1
S
S
el
el
Out
Out
MUX
MUX
D0
D0
D1
D1
S
S
el
el
Out
Out
MUX
MUX
D0
D0
D1
D1
S
S
el
el
Out
Out
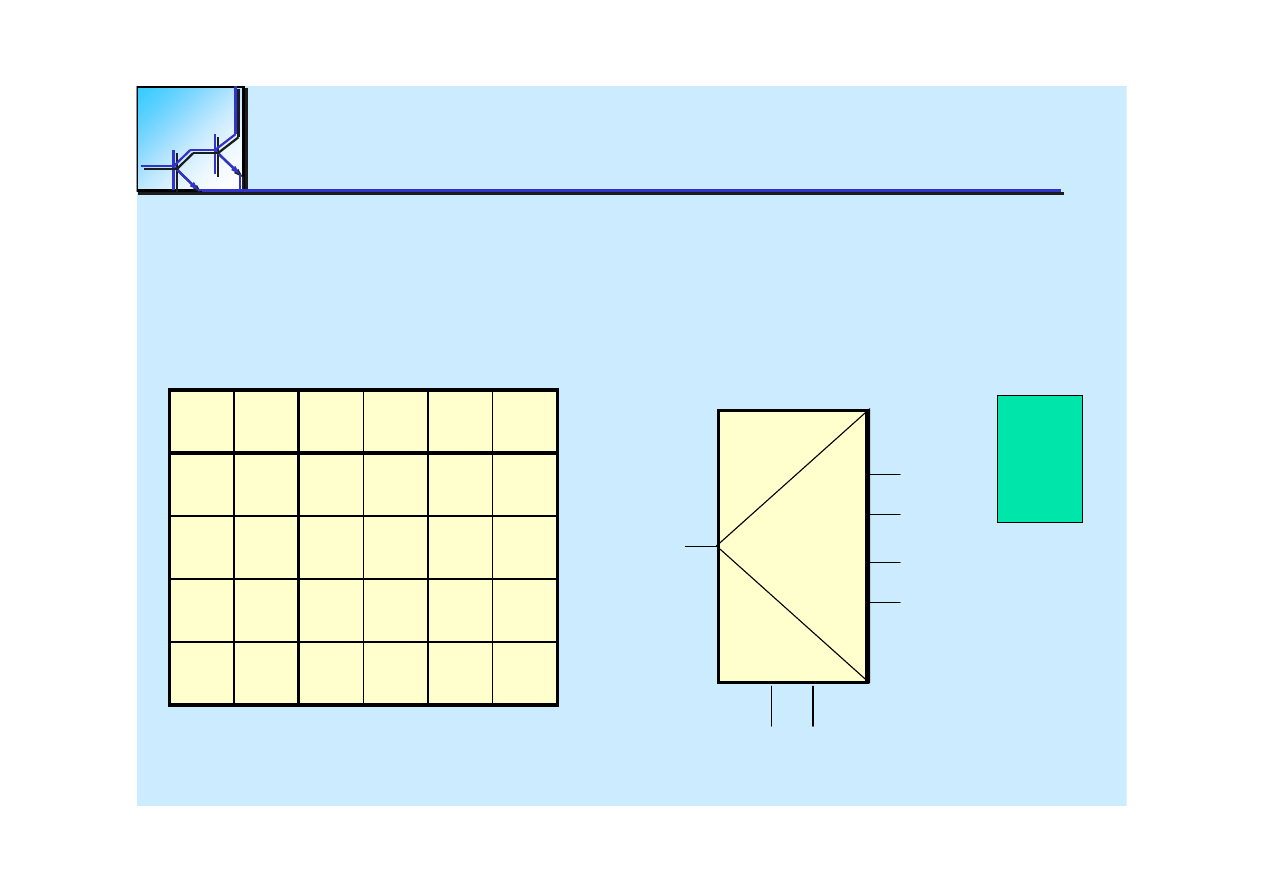
25 marca 2008
Cyfrowe układy kombinacyjne
74
The
Multiplexer
4 to 1
The
The
Multiplexer
Multiplexer
4 to 1
4 to 1
00 10 01 11
00 10 01 11
S1
S1
S
S
0
0
F
F
0
0
0
0
D
D
0
0
1
1
B
B
1
1
0
0
C
C
1
1
1
1
A
A
A
A
B
B
C
C
D
D
S1
S1
S0
S0
F
F
25 marca 2008
Cyfrowe układy kombinacyjne
75
Demultiplekser
Demultiplekser
Demultiplekser
Umo
Umo
ż
ż
liwiaj
liwiaj
ą
ą
wyb
wyb
ó
ó
r i przes
r i przes
ł
ł
anie sygna
anie sygna
ł
ł
u z wej
u z wej
ś
ś
cia do jednego z N
cia do jednego z N
wyj
wyj
ść
ść
Numer wyj
Numer wyj
ś
ś
cia jest okre
cia jest okre
ś
ś
lany przez stan wej
lany przez stan wej
ść
ść
asresowych
asresowych
(steruj
(steruj
ą
ą
cych)
cych)
S1
S1
S0
S0
D3
D3
D2
D2
D1
D1
D0
D0
0
0
0
0
0
0
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
0
0
1
1
1
1
Z
Z
0
0
0
0
0
0
Demultiplexer
Demultiplexer
D0
D0
D1
D1
D2
D2
D3
D3
S1 S0
S1 S0
Z
Z
In
In
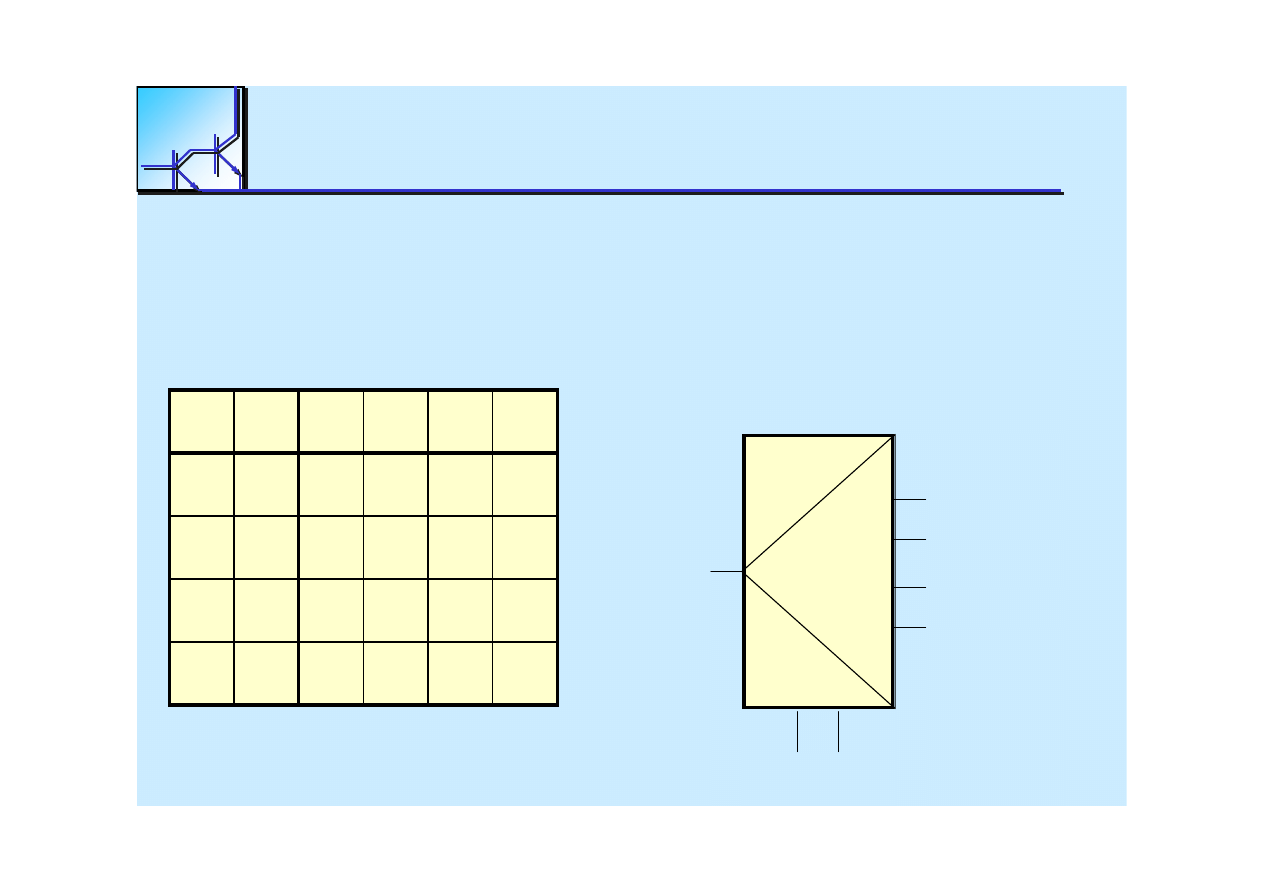
25 marca 2008
Cyfrowe układy kombinacyjne
76
Demultiplekser
Demultiplekser
Demultiplekser
Stosowane jako dekodery z naturalnego kodu binarnego na kod
Stosowane jako dekodery z naturalnego kodu binarnego na kod
„
„
1 z N
1 z N
”
”
Liczba wyj
Liczba wyj
ść
ść
jest zwi
jest zwi
ą
ą
zana z liczb
zana z liczb
ą
ą
wej
wej
ść
ść
steruj
steruj
ą
ą
cych
cych
zale
zale
ż
ż
no
no
ś
ś
ci
ci
ą
ą
: N = 2
: N = 2
n
n
S1
S1
S0
S0
D3
D3
D2
D2
D1
D1
D0
D0
0
0
0
0
0
0
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
0
0
1
1
1
1
Z
Z
0
0
0
0
0
0
Demultiplexer
Demultiplexer
D0
D0
D1
D1
D2
D2
D3
D3
S1 S0
S1 S0
Z
Z
In
In
25 marca 2008
Cyfrowe układy kombinacyjne
77
Demultiplekser
Demultiplekser
Demultiplekser
S1
S1
S0
S0
D3
D3
D2
D2
D1
D1
D0
D0
0
0
0
0
0
0
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
1
1
0
0
0
0
Z
Z
0
0
0
0
1
1
1
1
Z
Z
0
0
0
0
0
0
S1
S1
D0
D0
D1
D1
D2
D2
D3
D3
S0
S0
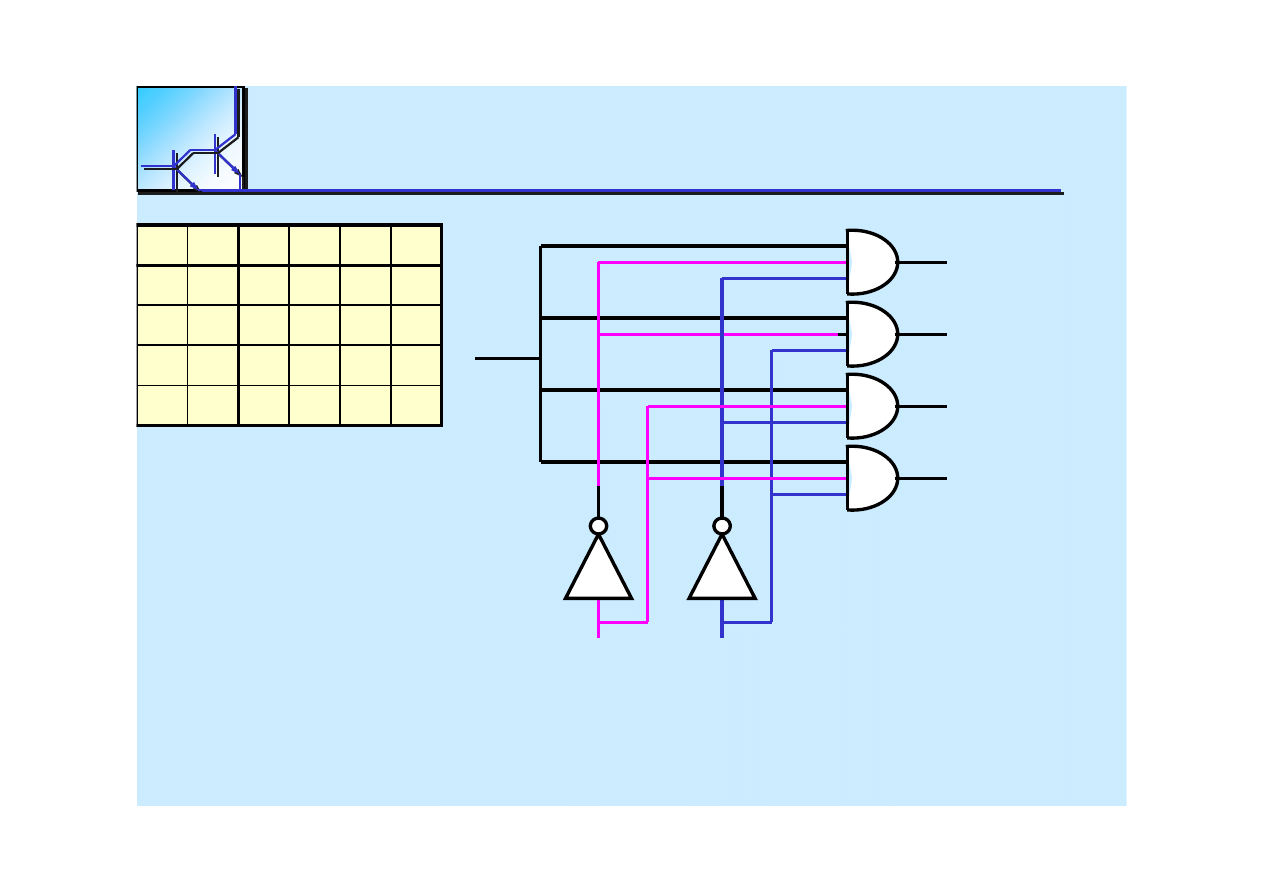
Need (n + 1)
Need (n + 1)
-
-
input AND gates for selection
input AND gates for selection
to
to
get
get
the
the
2
2
n
n
-
-
outputs
outputs
Z
Z
25 marca 2008
Cyfrowe układy kombinacyjne
78
Demultiplekser
Demultiplekser
Demultiplekser
Po podaniu odpowiedniego sygna
Po podaniu odpowiedniego sygna
ł
ł
u na wej
u na wej
ś
ś
cie demultipleksera na wyj
cie demultipleksera na wyj
ś
ś
ciach s
ciach s
ą
ą
dost
dost
ę
ę
pne realizacje wszystkich
pne realizacje wszystkich
minterm
minterm
ó
ó
w
w
1
1
a b c
a b c
a
a
’
’
b
b
’
’
c
c
’
’
a
a
’
’
b
b
’
’
c
c
a
a
’
’
bc
bc
’
’
a
a
’
’
bc
bc
ab
ab
’
’
c
c
’
’
ab
ab
’
’
c
c
abc
abc
’
’
abc
abc
z
z
25 marca 2008
Cyfrowe układy kombinacyjne
79
Kodery i dekodery,
konwertery kodów
Kodery i dekodery,
Kodery i dekodery,
konwertery kod
konwertery kod
ó
ó
w
w
Cyfrowe
układy
kombinacyjne
Cyfrowe
Cyfrowe
uk
uk
ł
ł
ady
ady
kombinacyjne
kombinacyjne
25 marca 2008
Cyfrowe układy kombinacyjne
80
The
Decoder
The
The
Decoder
Decoder
•
•
n inputs
n inputs
is
is
decoded
decoded
into
into
2
2
n
n
outputs
outputs
X1
X1
X2
X2
Decoder
Decoder
D0
D0
D1
D1
D2
D2
D3
D3
En
En
25 marca 2008
Cyfrowe układy kombinacyjne
81
The
Decoder
The
The
Decoder
Decoder
•
•
n inputs
n inputs
is
is
decoded
decoded
into
into
2
2
n
n
outputs
outputs
•
•
Each output represents a
Each output represents a
minterm
minterm
of an n variable function. The output
of an n variable function. The output
that corresponds to the
that corresponds to the
minterm
minterm
that appears on the inputs is asserted
that appears on the inputs is asserted
(low
(low
or high depending on the particular decoder), all other outputs
or high depending on the particular decoder), all other outputs
are
are
deasserted
deasserted
.
.
•
•
Some decoders have enable inputs. If the enable is not asserted,
Some decoders have enable inputs. If the enable is not asserted,
all
all
outputs are inactive.
outputs are inactive.
x1
x1
x0
x0
En
En
D3
D3
D2
D2
D1
D1
D0
D0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
x
x
x
x
0
0
0
0
0
0
0
0
0
0
D
3
= Enx
0
x
1
D
2
= Enx
0
’x
1
D
1
= Enx
0
x
1
’
D
0
= Enx
0
’x
1
’
D
D
3
3
= Enx
= Enx
0
0
x
x
1
1
D
D
2
2
= Enx
= Enx
0
0
’
’
x
x
1
1
D
D
1
1
= Enx
= Enx
0
0
x
x
1
1
’
’
D
D
0
0
= Enx
= Enx
0
0
’
’
x
x
1
1
’
’
25 marca 2008
Cyfrowe układy kombinacyjne
82
The
Decoder
The
The
Decoder
Decoder
x0
x1
En
D0
D1
D2
D3
Decoder
Decoder
En
x0
D0
D1
D2
D3
x1
D
3
= Enx
0
x
1
D
2
= Enx
0
’x
1
D
1
= Enx
0
x
1
’
D
0
= Enx
0
’x
1
’
D
D
3
3
= Enx
= Enx
0
0
x
x
1
1
D
D
2
2
= Enx
= Enx
0
0
’
’
x
x
1
1
D
D
1
1
= Enx
= Enx
0
0
x
x
1
1
’
’
D
D
0
0
= Enx
= Enx
0
0
’
’
x
x
1
1
’
’
25 marca 2008
Cyfrowe układy kombinacyjne
83
The
Decoder
The
The
Decoder
Decoder
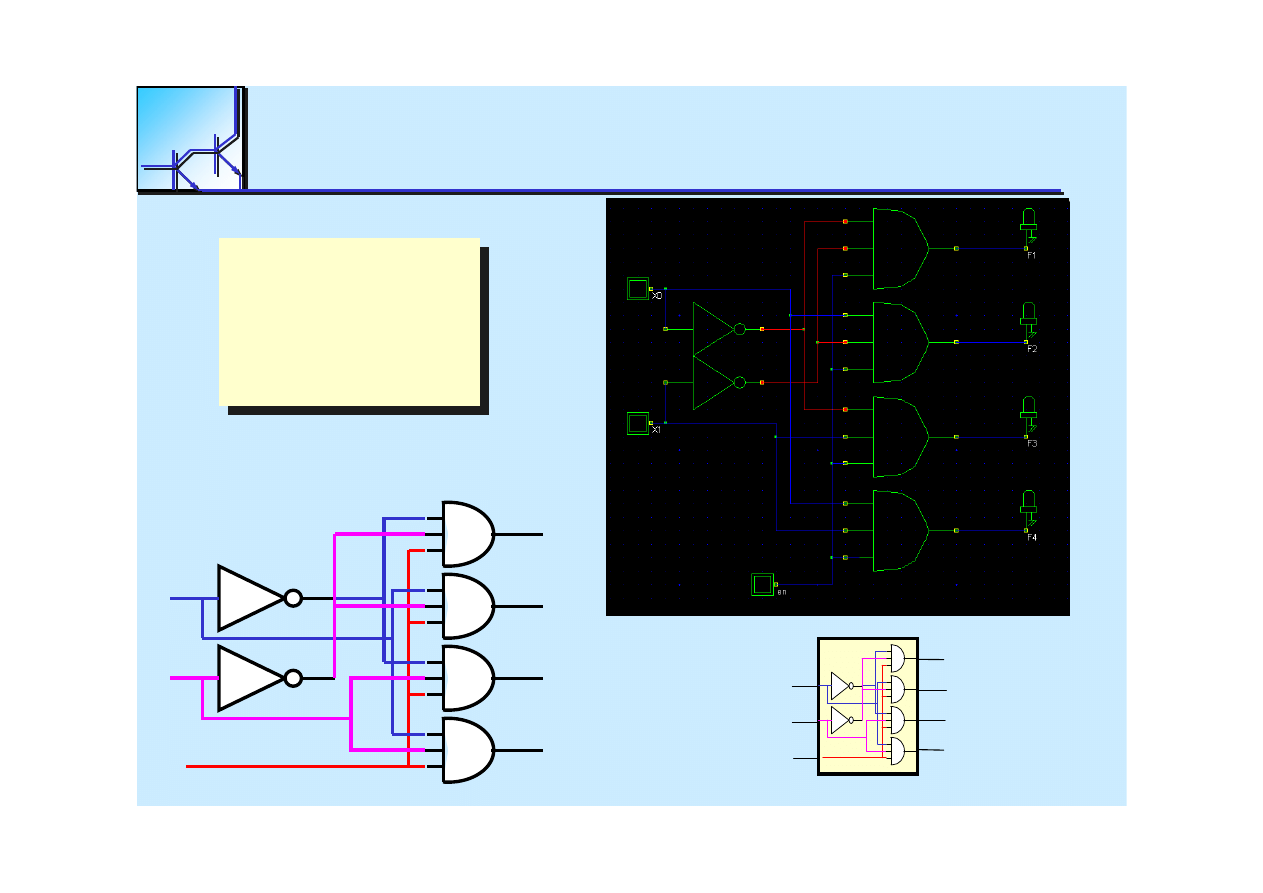
Decoders can be used to implement logic functions
Decoders can be used to implement logic functions
Dec
Dec
En
x0
D0
D1
D2
D3
x1
x1
x1
x0
x0
F1
F1
F2
F2
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
0
0
1
1
F1
F1
F2
F2
25 marca 2008
Cyfrowe układy kombinacyjne
84
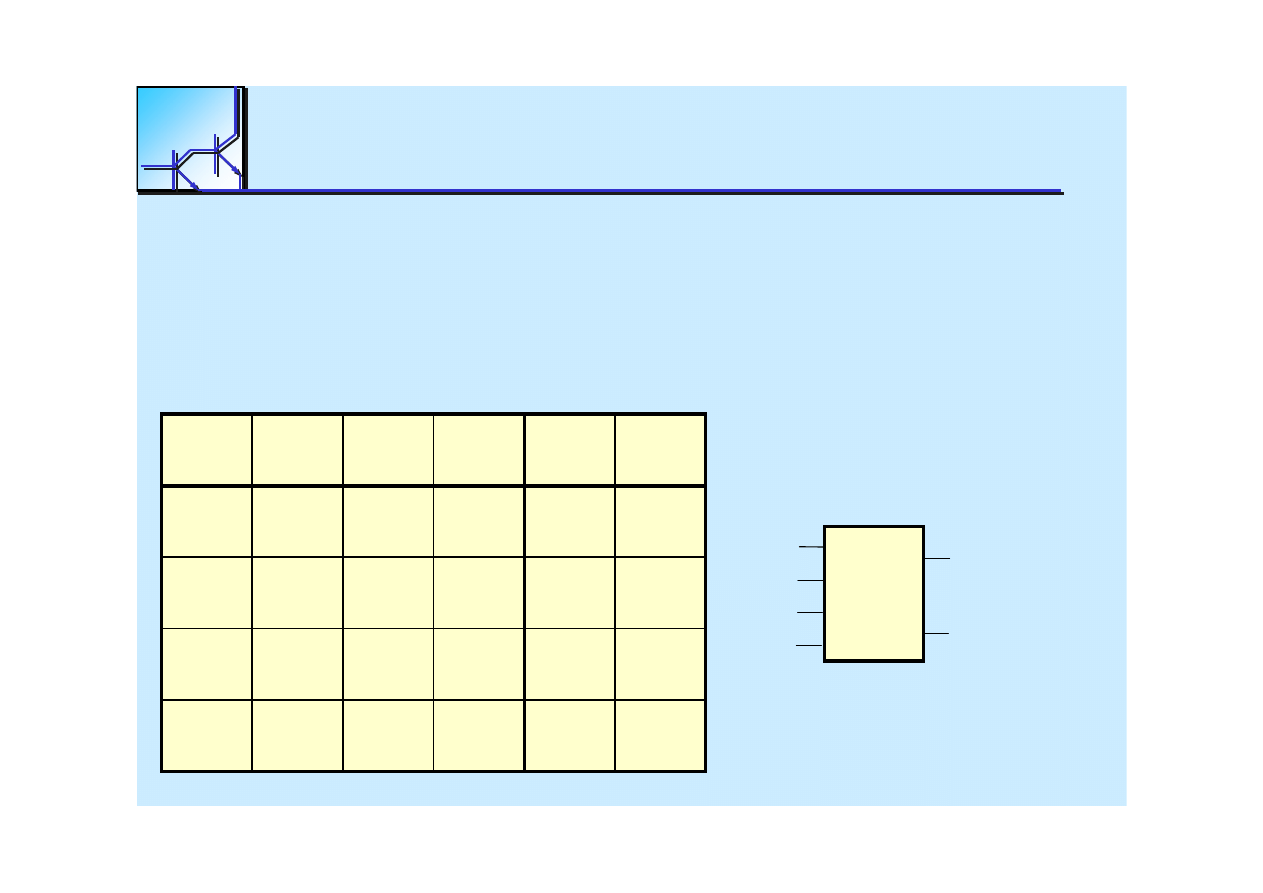
4 bit Decoder
4 bit
4 bit
Decoder
Decoder
A large size decoder can be constructed by cascading
A large size decoder can be constructed by cascading
smaller decoders
smaller decoders
with enable
with enable
lines to form a decoder tree
lines to form a decoder tree
En
x0
D0
D1
D2
D3
x1
A
A
B
B
C
C
D
D
En
En
Out
Out
0
0
0
0
0
0
0
0
1
1
m0
m0
0
0
0
0
0
0
1
1
1
1
m1
m1
0
0
0
0
1
1
0
0
1
1
m2
m2
0
0
0
0
1
1
1
1
1
1
m3
m3
0
0
1
1
0
0
0
0
1
1
m4
m4
0
0
1
1
0
0
1
1
1
1
m5
m5
0
0
1
1
1
1
0
0
1
1
m6
m6
0
0
1
1
1
1
1
1
1
1
m7
m7
1
1
0
0
0
0
0
0
1
1
m8
m8
1
1
0
0
0
0
1
1
1
1
m9
m9
1
1
0
0
1
1
0
0
1
1
m10
m10
1
1
0
0
1
1
1
1
1
1
m11
m11
1
1
1
1
0
0
0
0
1
1
m12
m12
1
1
1
1
0
0
1
1
1
1
m13
m13
1
1
1
1
1
1
0
0
1
1
m14
m14
1
1
1
1
1
1
1
1
1
1
m15
m15
x
x
x
x
x
x
x
x
0
0
none
none
A
A
B
B
En
x0
D0
D1
D2
D3
x1
En
x0
D0
D1
D2
D3
x1
En
x0
D0
D1
D2
D3
x1
En
x0
D0
D1
D2
D3
x1
C
C
D
D
m0
m0
m1
m1
m2
m2
m3
m3
m4
m4
m5
m5
m6
m6
m7
m7
m8
m8
m9
m9
m10
m10
m11
m11
m12
m12
m13
m13
m14
m14
m15
m15
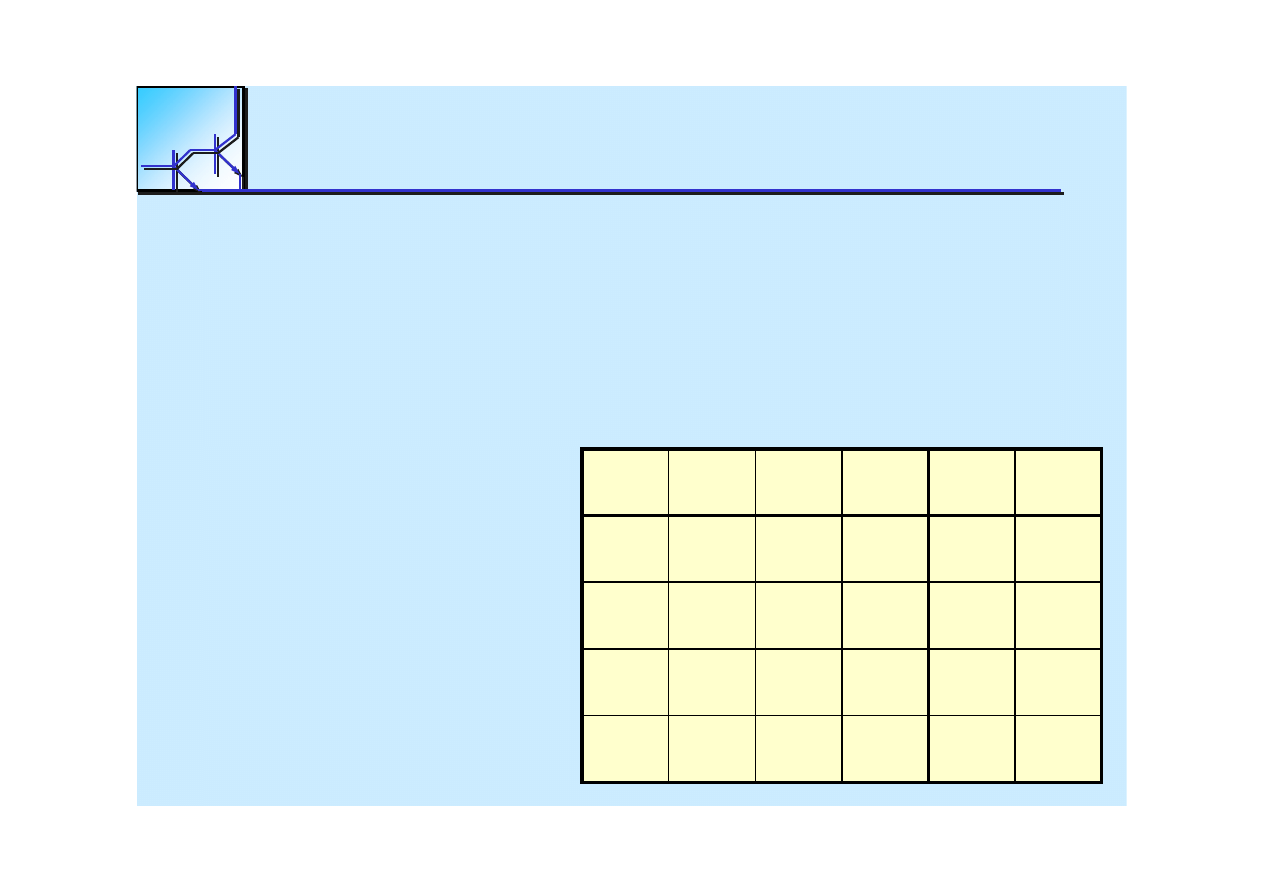
25 marca 2008
Cyfrowe układy kombinacyjne
85
The
Encoder
The
The
Encoder
Encoder
Encoder
Encoder
x0
D0
D1
D2
D3
x1
Encoder is opposite of decoder.
Encoder is opposite of decoder.
Its output has fewer bits
Its output has fewer bits
than the
than the
input code.
input code.
Binary Encoder:
Binary Encoder:
input:
input:
1
1
-
-
out
out
-
-
of
of
-
-
2
2
n
n
code
code
output:
output:
n
n
-
-
bit
bit
binary
binary
code
code
D3
D3
D2
D2
D1
D1
D0
D0
x1
x1
x0
x0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
0
1
1
1
1
25 marca 2008
Cyfrowe układy kombinacyjne
86
The
Encoder
The
The
Encoder
Encoder
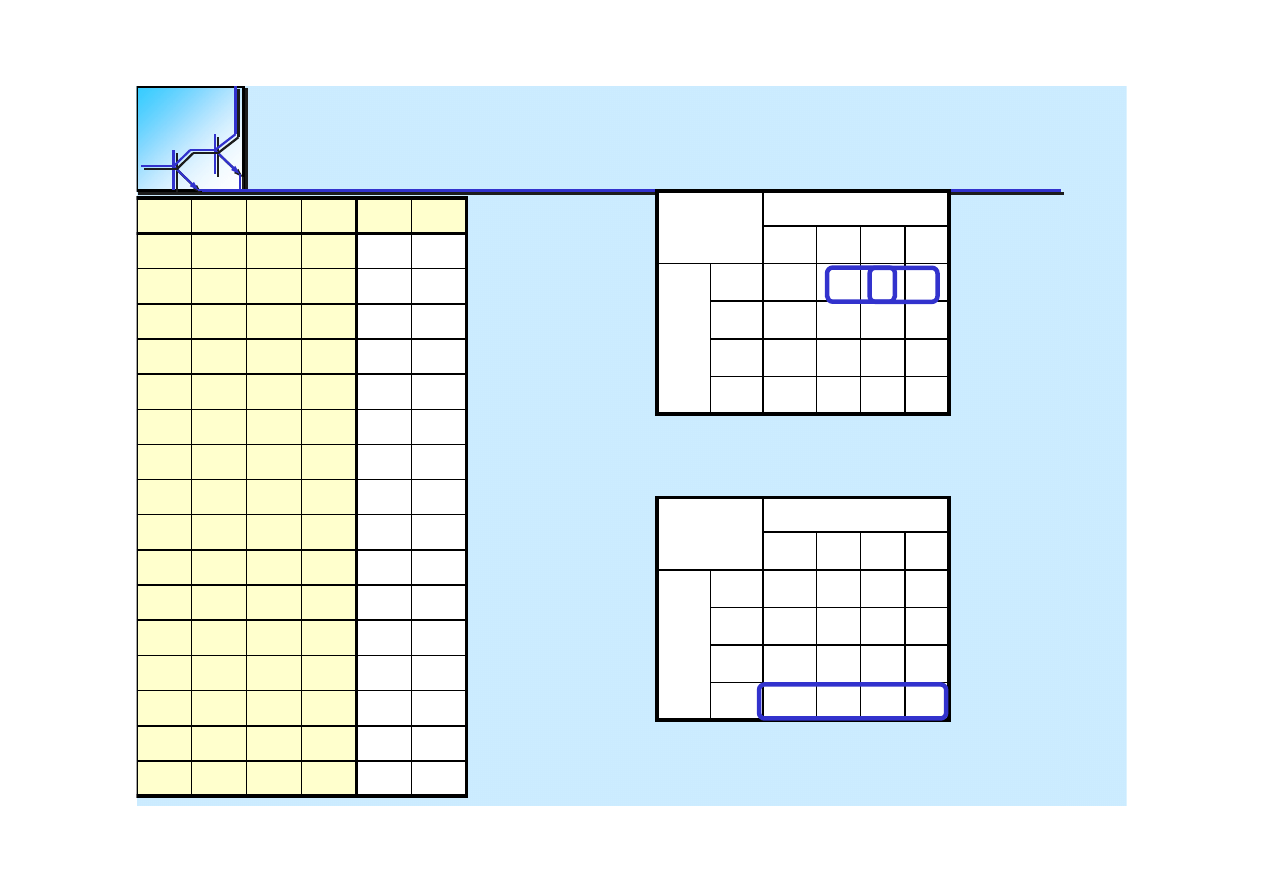
Priority Encoder:
Priority Encoder:
Consider a system with 2
Consider a system with 2
n
n
devices, each of which
devices, each of which
indicates
indicates
a request for service.
a request for service.
-
-
a binary encoder can be used to determine the requesting device
a binary encoder can be used to determine the requesting device
if and
if and
only if at most one input is asserted at a time.
only if at most one input is asserted at a time.
D0
D0
D1
D1
D2
D2
D3
D3
x1
x1
x0
x0
1
1
X
X
X
X
X
X
0
0
0
0
0
0
1
1
X
X
X
X
0
0
1
1
0
0
0
0
1
1
X
X
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
-
-
multiple requests at a time can
multiple requests at a time can
be handled by assigning priority
be handled by assigning priority
to the
to the
input lines, so that when
input lines, so that when
multiple requests are asserted,
multiple requests are asserted,
the en
the en
cod
cod
ing
ing
device produces
device produces
the number of the highest
the number of the highest
-
-
priority requestor
priority requestor
-
-
a priority
a priority
encoder
encoder
25 marca 2008
Cyfrowe układy kombinacyjne
87
X
X
1
1
D
D
3
3
D
D
2
2
00
00
01
01
11
11
10
10
D
D
1
1
D
D
0
0
00
00
0
0
1
1
1
1
1
1
01
01
0
0
0
0
0
0
0
0
11
11
0
0
0
0
0
0
0
0
10
10
0
0
0
0
0
0
0
0
The
Encoder
The
The
Encoder
Encoder
D
D
0
0
D
D
1
1
D
D
2
2
D
D
3
3
x
x
1
1
x
x
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
1
1
1
1
0
0
1
1
1
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
0
1
1
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
X
X
1
1
= D
= D
0
0
’
’
D
D
1
1
’
’
D
D
3
3
+ D
+ D
0
0
’
’
D
D
1
1
’
’
D
D
2
2
X
X
0
0
= D
= D
0
0
’
’
D
D
2
2
’
’
D
D
3
3
+ D
+ D
0
0
’
’
D
D
1
1
X
X
0
0
D
D
3
3
D
D
2
2
00
00
01
01
11
11
10
10
D
D
1
1
D
D
0
0
00
00
0
0
0
0
0
0
1
1
01
01
0
0
0
0
0
0
0
0
11
11
0
0
0
0
0
0
0
0
10
10
1
1
1
1
1
1
1
1
25 marca 2008
Cyfrowe układy kombinacyjne
88
The
Encoder
The
The
Encoder
Encoder
Encoder
Encoder
x0
D0
D1
D2
D3
x1
D
D
0
0
D
D
1
1
D
D
2
2
D
D
3
3
x
1
x
0
x
1
= D
0
’D
1
’D
3
+ D
0
’D
1
’D
2
x
0
= D
0
’D
2
’D
3
+ D
0
’D
1
x
x
1
1
= D
= D
0
0
’
’
D
D
1
1
’
’
D
D
3
3
+ D
+ D
0
0
’
’
D
D
1
1
’
’
D
D
2
2
x
x
0
0
= D
= D
0
0
’
’
D
D
2
2
’
’
D
D
3
3
+ D
+ D
0
0
’
’
D
D
1
1
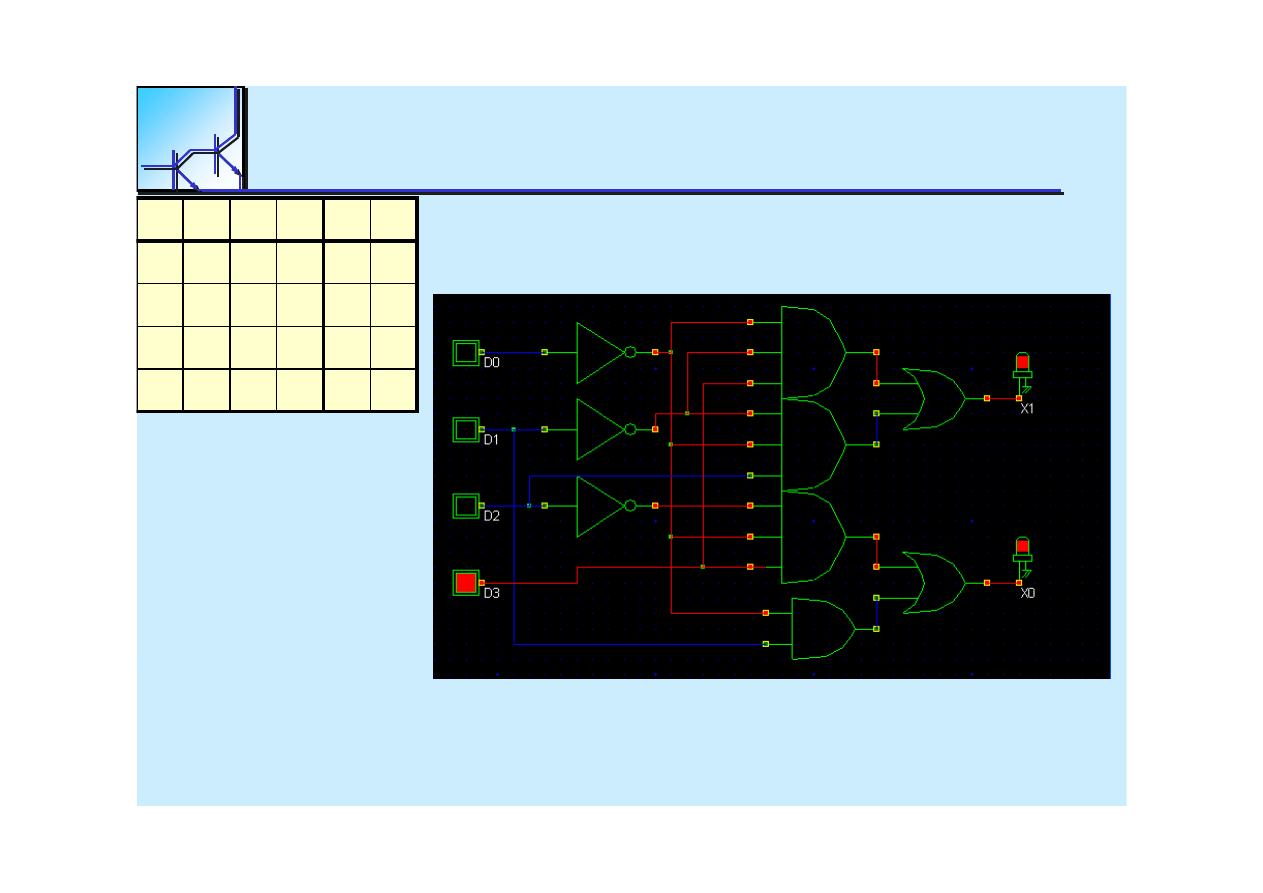
25 marca 2008
Cyfrowe układy kombinacyjne
89
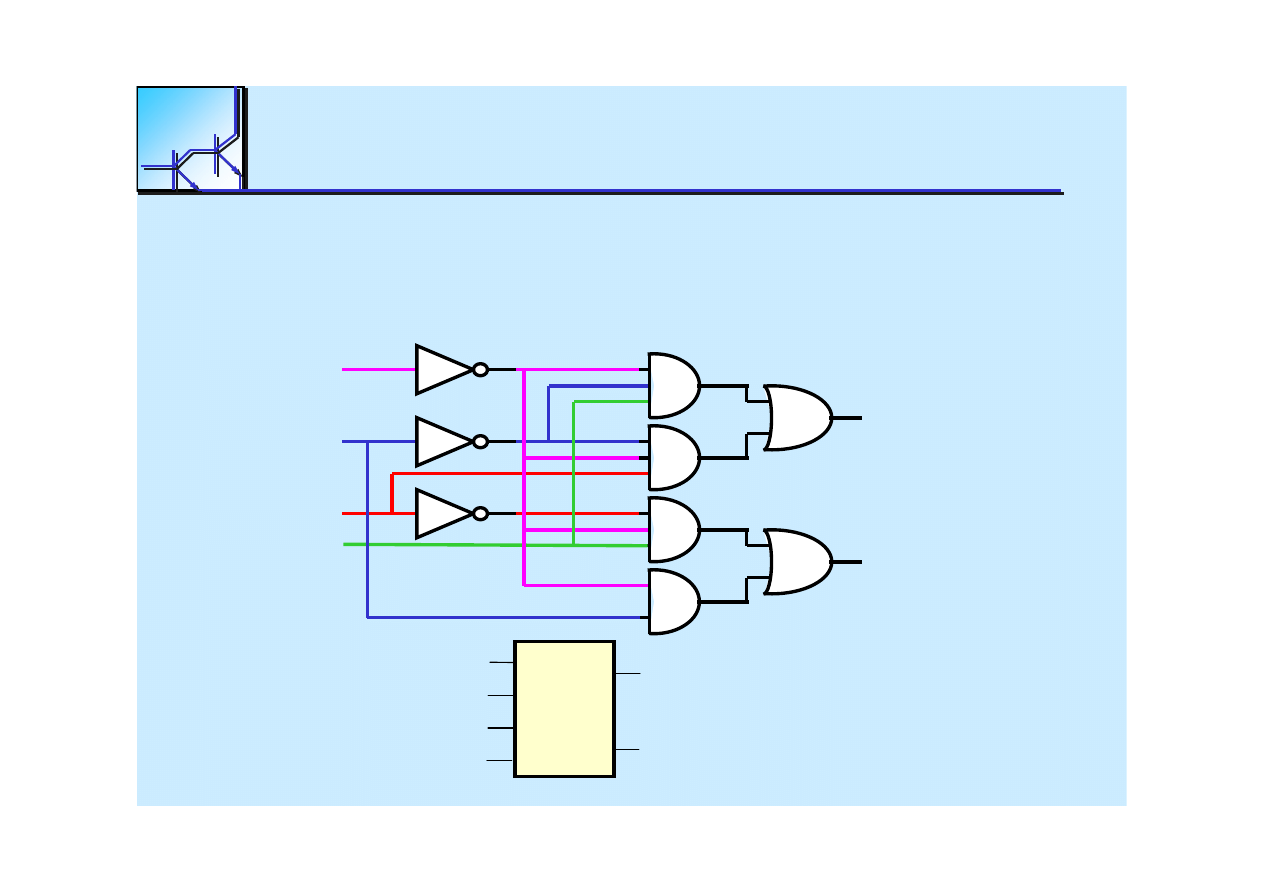
The
Encoder
The
The
Encoder
Encoder
D0
D0
D1
D1
D2
D2
D3
D3
x1
x1
x0
x0
1
1
X
X
X
X
X
X
0
0
0
0
0
0
1
1
X
X
X
X
0
0
1
1
0
0
0
0
1
1
X
X
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
25 marca 2008
Cyfrowe układy kombinacyjne
90
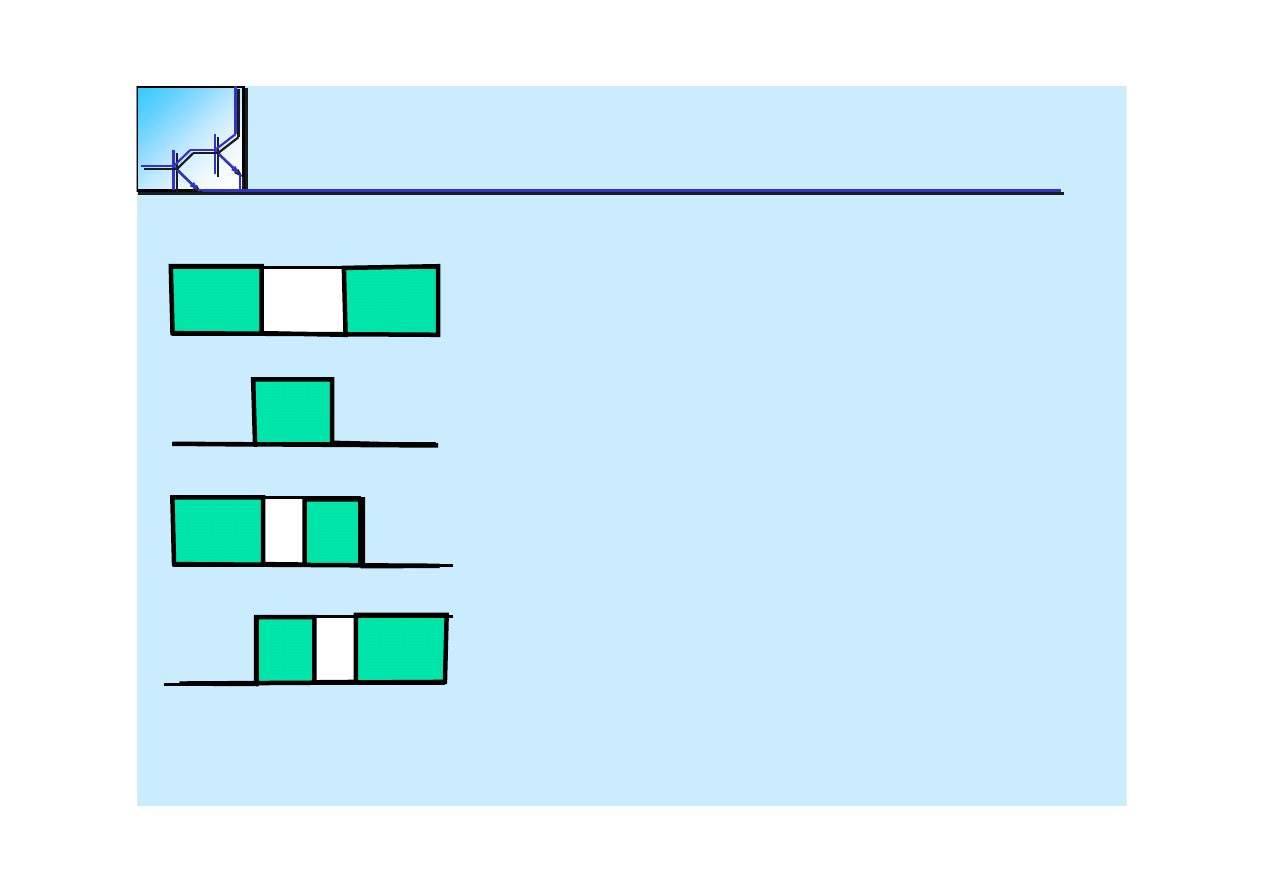
Hazard
Hazard
Hazard
Cyfrowe
układy
kombinacyjne
Cyfrowe
Cyfrowe
uk
uk
ł
ł
ady
ady
kombinacyjne
kombinacyjne
25 marca 2008
Cyfrowe układy kombinacyjne
91
Hazard
Hazard
Hazard
Kr
Kr
ó
ó
tkie zak
tkie zak
ł
ł
ó
ó
cenie impulsowe na wyj
cenie impulsowe na wyj
ś
ś
ciu uk
ciu uk
ł
ł
adu podczas proces
adu podczas proces
ó
ó
w
w
przej
przej
ś
ś
ciowych
ciowych
Hazard funkcjonalny
Hazard funkcjonalny
-
-
powstaje na skutek jednoczesnej zmiany
powstaje na skutek jednoczesnej zmiany
dw
dw
ó
ó
ch lub wi
ch lub wi
ę
ę
cej sygna
cej sygna
ł
ł
ó
ó
w wej
w wej
ś
ś
ciowych propaguj
ciowych propaguj
ą
ą
cych drogami o
cych drogami o
r
r
ó
ó
ż
ż
nych op
nych op
ó
ó
ź
ź
nieniach (trudny do eliminacji
nieniach (trudny do eliminacji
Hazard logiczny
Hazard logiczny
–
–
pojedyncza zmiana sygna
pojedyncza zmiana sygna
ł
ł
u na wej
u na wej
ś
ś
ciu propaguje
ciu propaguje
drogami o r
drogami o r
ó
ó
ż
ż
nych op
nych op
ó
ó
ź
ź
nieniach (eliminowanie przez dodanie
nieniach (eliminowanie przez dodanie
nadmiarowych element
nadmiarowych element
ó
ó
w w uk
w w uk
ł
ł
adzie)
adzie)
Hazard krytyczny
Hazard krytyczny
-
-
wyst
wyst
ę
ę
puje w uk
puje w uk
ł
ł
adach asynchronicznych.
adach asynchronicznych.
25 marca 2008
Cyfrowe układy kombinacyjne
92
Typy Hazardu
Typy Hazardu
Typy Hazardu
Hazard statyczny
Hazard statyczny
„
„
w jedynkach
w jedynkach
”
”
Hazard statyczny
Hazard statyczny
„
„
w zerach
w zerach
”
”
Hazard dynamiczny 1
Hazard dynamiczny 1
Î
Î
0
0
Hazard dynamiczny 0
Hazard dynamiczny 0
Î
Î
1
1
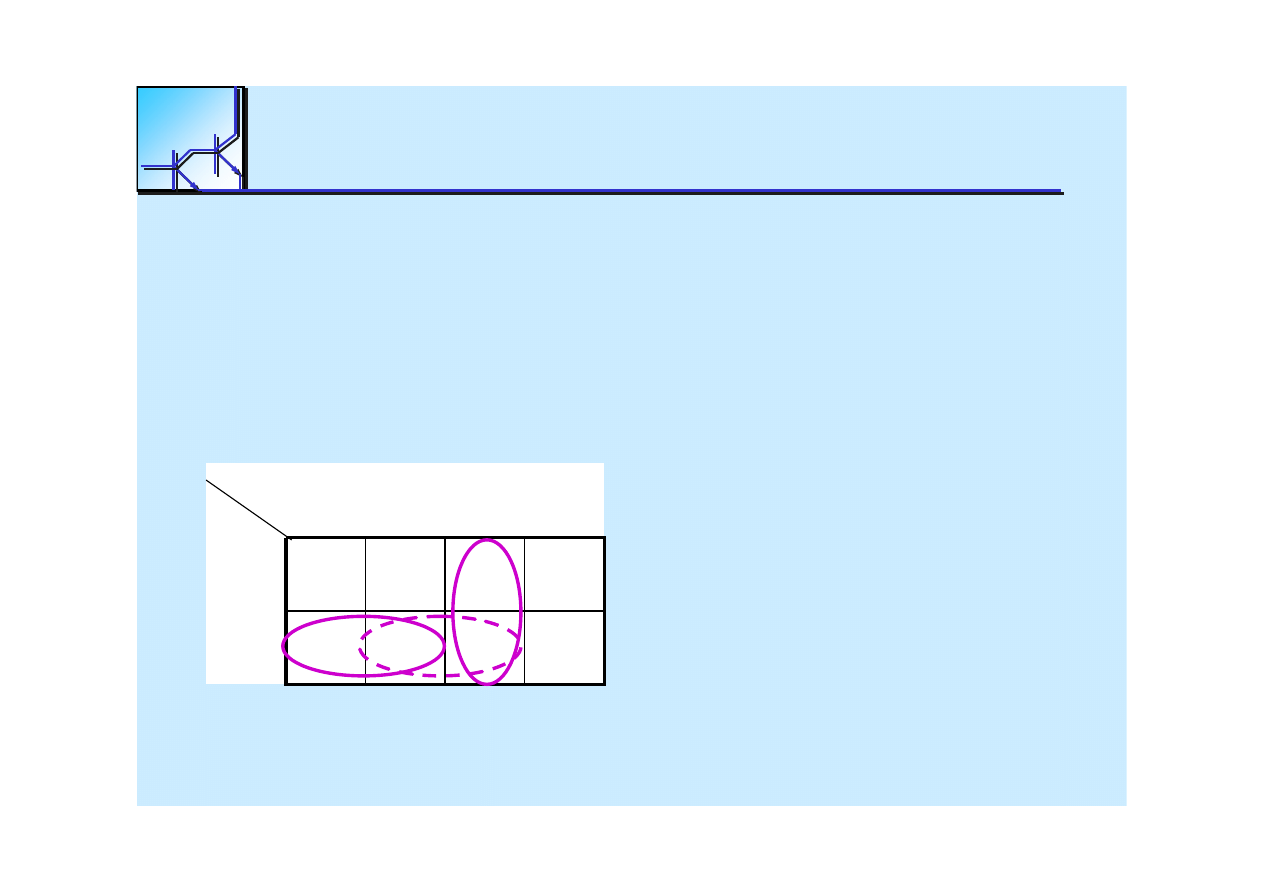
25 marca 2008
Cyfrowe układy kombinacyjne
93
Hazard statyczny
Hazard statyczny
Hazard statyczny
Hazard statyczny mo
Hazard statyczny mo
ż
ż
e wyst
e wyst
ą
ą
pi
pi
ć
ć
, gdy cho
, gdy cho
ć
ć
by jeden sygna
by jeden sygna
ł
ł
jest przesy
jest przesy
ł
ł
any
any
dwoma drogami o r
dwoma drogami o r
ó
ó
ż
ż
nych op
nych op
ó
ó
ź
ź
nieniach, prowadz
nieniach, prowadz
ą
ą
cymi do jednej bramki.
cymi do jednej bramki.
Mo
Mo
ż
ż
liwo
liwo
ść
ść
wyst
wyst
ą
ą
pienia hazardu mo
pienia hazardu mo
ż
ż
na wykry
na wykry
ć
ć
na siatce
na siatce
Karnaugh
Karnaugh
, je
, je
ż
ż
eli
eli
forma boolowska jest reprezentowana przez stykaj
forma boolowska jest reprezentowana przez stykaj
ą
ą
ce si
ce si
ę
ę
grupy,
grupy,
odpowiadaj
odpowiadaj
ą
ą
ce
ce
implikantom
implikantom
prostym. Stykanie si
prostym. Stykanie si
ę
ę
takich grup wskazuje na
takich grup wskazuje na
obecno
obecno
ść
ść
hazardu. Aby unikn
hazardu. Aby unikn
ąć
ąć
hazardu, nale
hazardu, nale
ż
ż
y wprowadzi
y wprowadzi
ć
ć
dodatkow
dodatkow
ą
ą
bramk
bramk
ę
ę
reprezentuj
reprezentuj
ą
ą
c
c
ą
ą
dodatkowy
dodatkowy
implikant
implikant
.
.
x
x
2
2
x
x
1
1
x
x
0
0
00
00
01
01
11
11
10
10
0
0
0
0
0
0
1
1
0
0
1
1
1
1
1
1
1
1
0
0
F = X
F = X
2
2
X
X
1
1
+ X
+ X
0
0
X
X
’
’
2
2
F = X
F = X
2
2
X
X
1
1
+ X
+ X
0
0
X
X
’
’
2
2
+ X
+ X
0
0
X
X
1
1
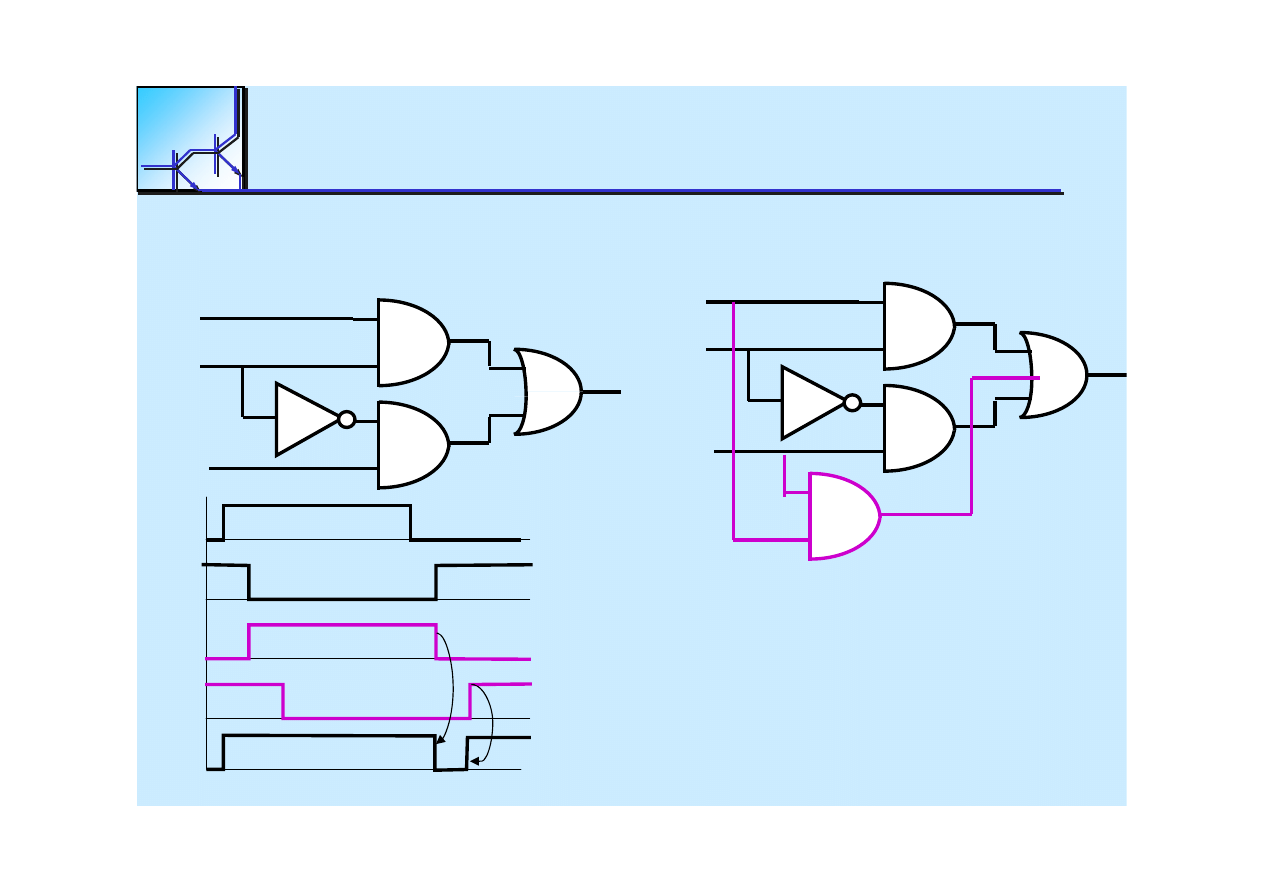
25 marca 2008
Cyfrowe układy kombinacyjne
94
Hazard statyczny
Hazard statyczny
Hazard statyczny
F = X
F = X
2
2
X
X
1
1
+ X
+ X
0
0
X
X
’
’
2
2
F = X
F = X
2
2
X
X
1
1
+ X
+ X
0
0
X
X
’
’
2
2
+ X
+ X
0
0
X
X
1
1
y
y
1
1
z
z
y
y
2
2
y
y
X
X
1
1
X
X
2
2
X
X
0
0
X
X
2
2
Y
Y
Y
Y
1
1
Y
Y
2
2
Z
Z
y
y
1
1
z
z
y
y
2
2
y
y
X
X
1
1
X
X
2
2
X
X
0
0
Przy X
Przy X
0
0
= X
= X
1
1
= 1 impuls hazardu
= 1 impuls hazardu
zostaje wyeliminowany
zostaje wyeliminowany
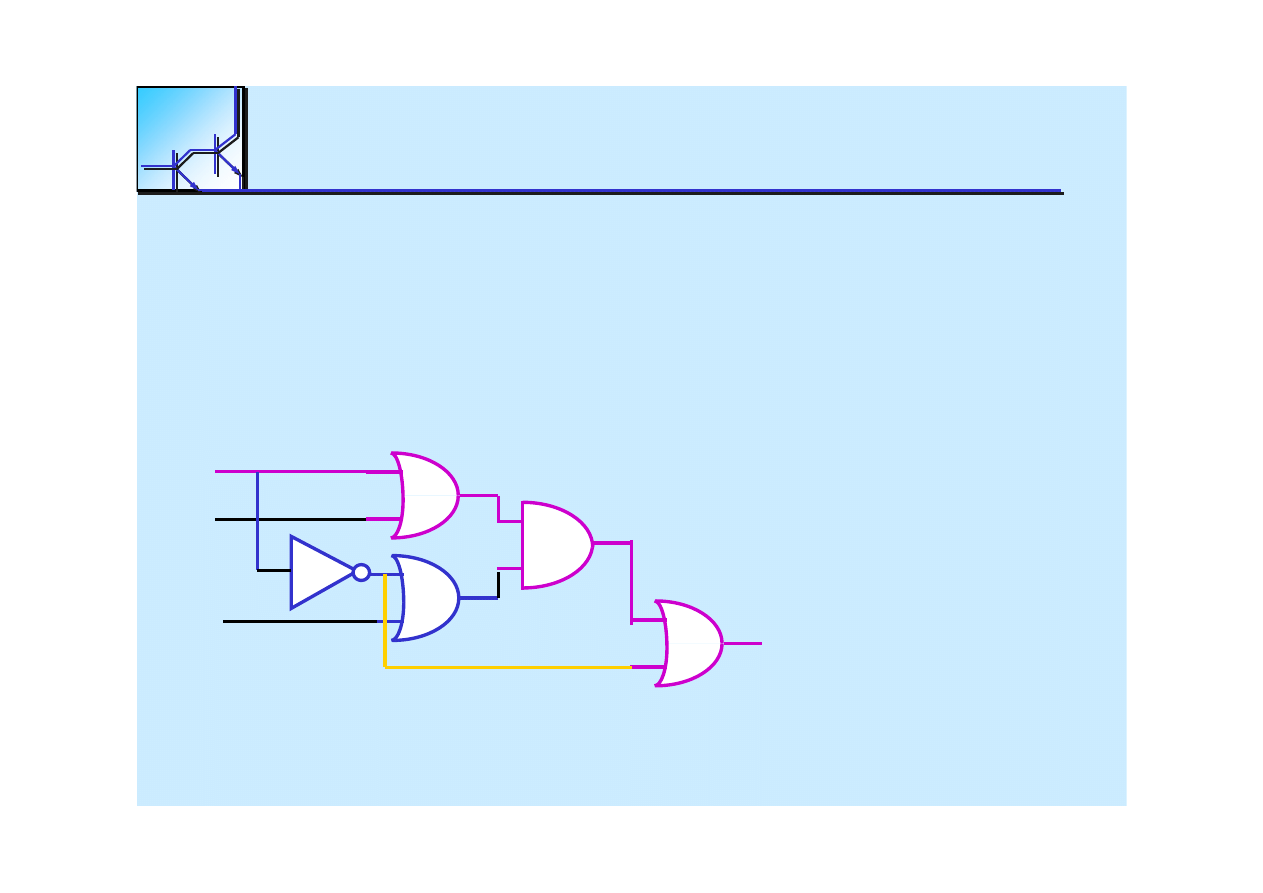
25 marca 2008
Cyfrowe układy kombinacyjne
95
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
W uk
W uk
ł
ł
adach wielopoziomowych mo
adach wielopoziomowych mo
ż
ż
na zaobserwowa
na zaobserwowa
ć
ć
zjawisko hazardu
zjawisko hazardu
dynamicznego. Polega ono na pojawieniu si
dynamicznego. Polega ono na pojawieniu si
ę
ę
na wyj
na wyj
ś
ś
ciu uk
ciu uk
ł
ł
adu impulsu
adu impulsu
szpilkowego bezpo
szpilkowego bezpo
ś
ś
rednio po zmianie poziom
rednio po zmianie poziom
ó
ó
w logicznych z 0 na 1 lub 1 na 0.
w logicznych z 0 na 1 lub 1 na 0.
Hazard dynamiczny mo
Hazard dynamiczny mo
ż
ż
e wyst
e wyst
ą
ą
pi
pi
ć
ć
, gdy cho
, gdy cho
ć
ć
by jeden sygna
by jeden sygna
ł
ł
jest przesy
jest przesy
ł
ł
any
any
do wyj
do wyj
ś
ś
cia trzema drogami o r
cia trzema drogami o r
ó
ó
ż
ż
nych op
nych op
ó
ó
ź
ź
nieniach.
nieniach.
y
y
1
1
y
y
2
2
y
y
3
3
X
X
1
1
X
X
2
2
X
X
0
0
y
y
4
4
z
z
X
X
1
1
Î
Î
Y
Y
2
2
Î
Î
Y
Y
4
4
Î
Î
Z
Z
X
X
1
1
Î
Î
Y
Y
1
1
Î
Î
Y
Y
3
3
Î
Î
Y
Y
4
4
Î
Î
Z
Z
X
X
1
1
Î
Î
Y
Y
1
1
Î
Î
Z
Z
25 marca 2008
Cyfrowe układy kombinacyjne
96
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
y
y
1
1
y
y
2
2
y
y
3
3
X
X
1
1
X
X
2
2
= 0
= 0
X
X
0
0
= 0
= 0
y
y
4
4
z
z
X
X
1
1
Î
Î
Y
Y
2
2
Î
Î
Y
Y
4
4
Î
Î
Z
Z
X
X
1
1
Î
Î
Y
Y
1
1
Î
Î
Y
Y
3
3
Î
Î
Y
Y
4
4
Î
Î
Z
Z
X
X
1
1
Î
Î
Y
Y
1
1
Î
Î
Z
Z
X
X
1
1
Y
Y
1
1
Y
Y
2
2
Y
Y
3
3
Y
Y
4
4
Z
Z
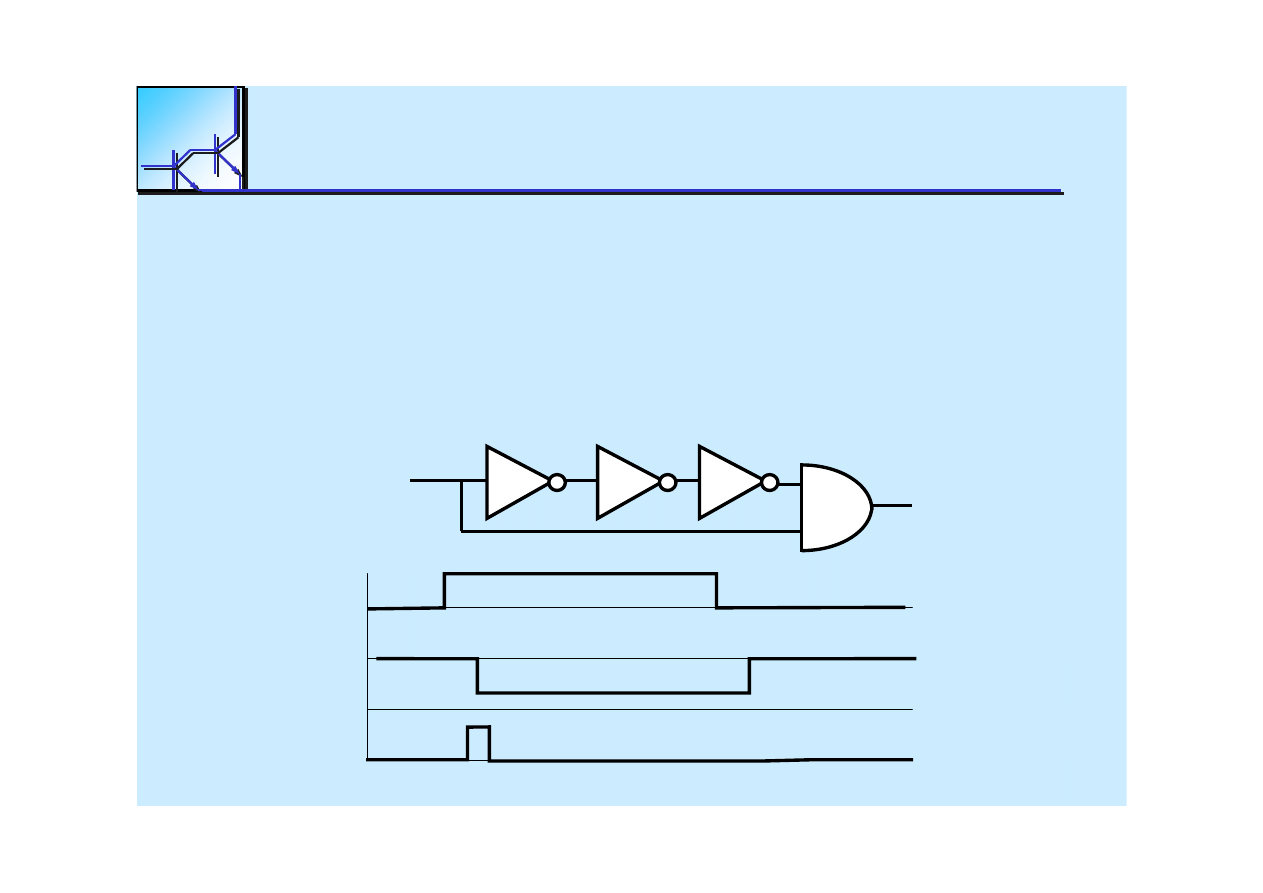
25 marca 2008
Cyfrowe układy kombinacyjne
97
Hazard
Hazard
Hazard
Uk
Uk
ł
ł
ady generuj
ady generuj
ą
ą
ce hazard s
ce hazard s
ą
ą
r
r
ó
ó
wnie
wnie
ż
ż
celowo wykorzystywane w praktyce.
celowo wykorzystywane w praktyce.
S
S
ą
ą
stosowane jako uk
stosowane jako uk
ł
ł
ady detektor
ady detektor
ó
ó
w pocz
w pocz
ą
ą
tku i ko
tku i ko
ń
ń
ca impulsu wej
ca impulsu wej
ś
ś
ciowego.
ciowego.
Do uzyskania impuls
Do uzyskania impuls
ó
ó
w wyj
w wyj
ś
ś
ciowych o po
ciowych o po
żą
żą
danej szeroko
danej szeroko
ś
ś
ci zwi
ci zwi
ę
ę
ksza si
ksza si
ę
ę
op
op
ó
ó
ź
ź
nienie jednego z tor
nienie jednego z tor
ó
ó
w sygna
w sygna
ł
ł
u wej
u wej
ś
ś
ciowego przez po
ciowego przez po
łą
łą
czenie kaskadowe
czenie kaskadowe
dodatkowych
dodatkowych
inwerter
inwerter
ó
ó
w
w
lub bramek.
lub bramek.
Sa
Sa
to tzw. Uk
to tzw. Uk
ł
ł
ady logicznego r
ady logicznego r
ó
ó
ż
ż
niczkowania.
niczkowania.
y
y
1
1
z
z
X
X
1
1
Y
Y
1
1
Z
Z
X
X
1
1
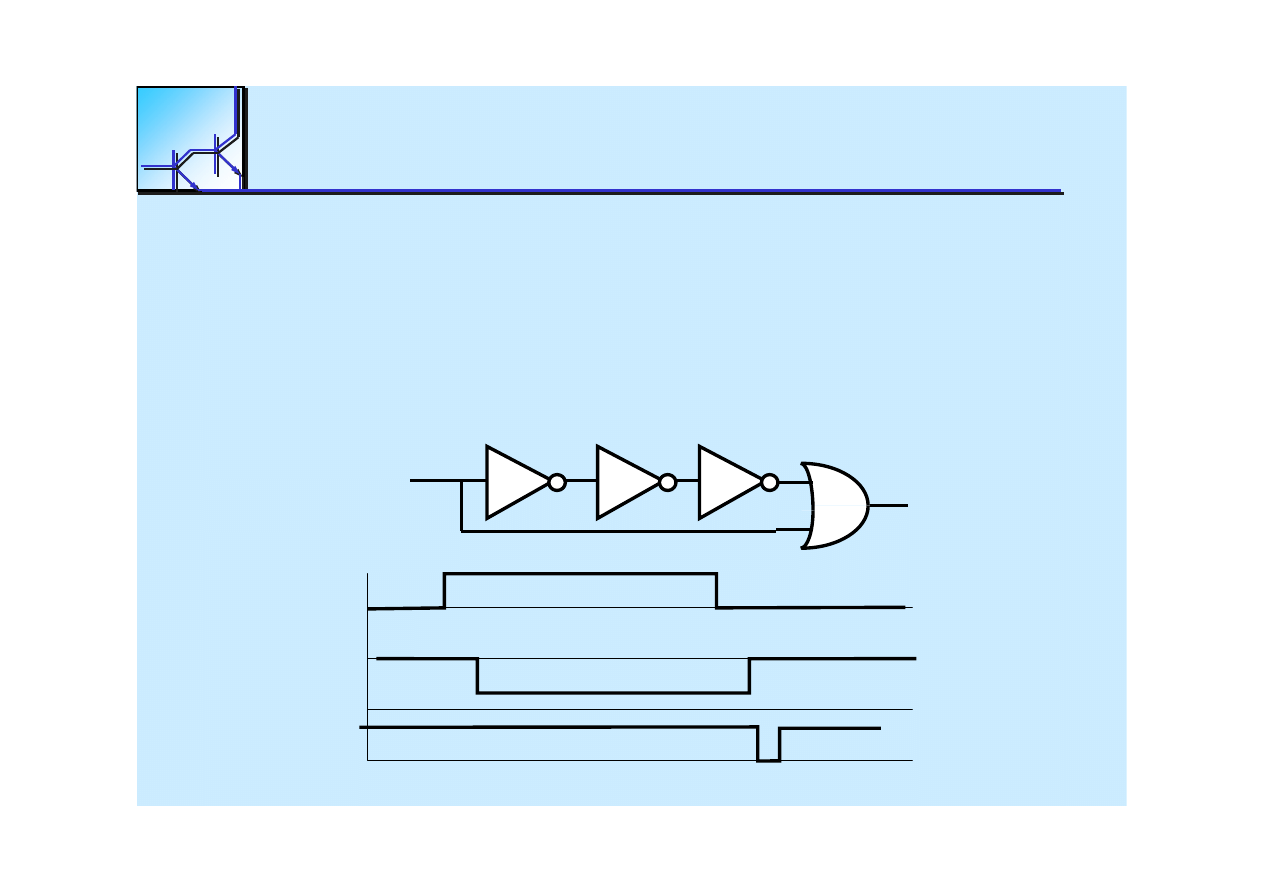
25 marca 2008
Cyfrowe układy kombinacyjne
98
Hazard
Hazard
Hazard
Uk
Uk
ł
ł
ady
ady
generujace
generujace
hazard s
hazard s
ą
ą
r
r
ó
ó
wnie
wnie
ż
ż
celowo wykorzystywane w praktyce.
celowo wykorzystywane w praktyce.
S
S
ą
ą
stosowane jako uk
stosowane jako uk
ł
ł
ady detektor
ady detektor
ó
ó
w
w
poczatku
poczatku
i ko
i ko
ń
ń
ca impulsu wej
ca impulsu wej
ś
ś
ciowego.
ciowego.
Do uzyskania impuls
Do uzyskania impuls
ó
ó
w wyj
w wyj
ś
ś
ciowych o po
ciowych o po
żą
żą
danej szeroko
danej szeroko
ś
ś
ci zwi
ci zwi
ę
ę
ksza si
ksza si
ę
ę
op
op
ó
ó
ż
ż
nienie
nienie
jednego z tor
jednego z tor
ó
ó
w sygna
w sygna
ł
ł
u wej
u wej
ś
ś
ciowego przez po
ciowego przez po
łą
łą
czenie kaskadowe
czenie kaskadowe
dodatkowych
dodatkowych
inwerter
inwerter
ó
ó
w
w
lub bramek.
lub bramek.
Sa
Sa
to tzw. Uk
to tzw. Uk
ł
ł
ady logicznego r
ady logicznego r
ó
ó
ż
ż
niczkowania.
niczkowania.
X
X
1
1
Y
Y
1
1
Z
Z
X
X
1
1
y
y
1
1
z
z
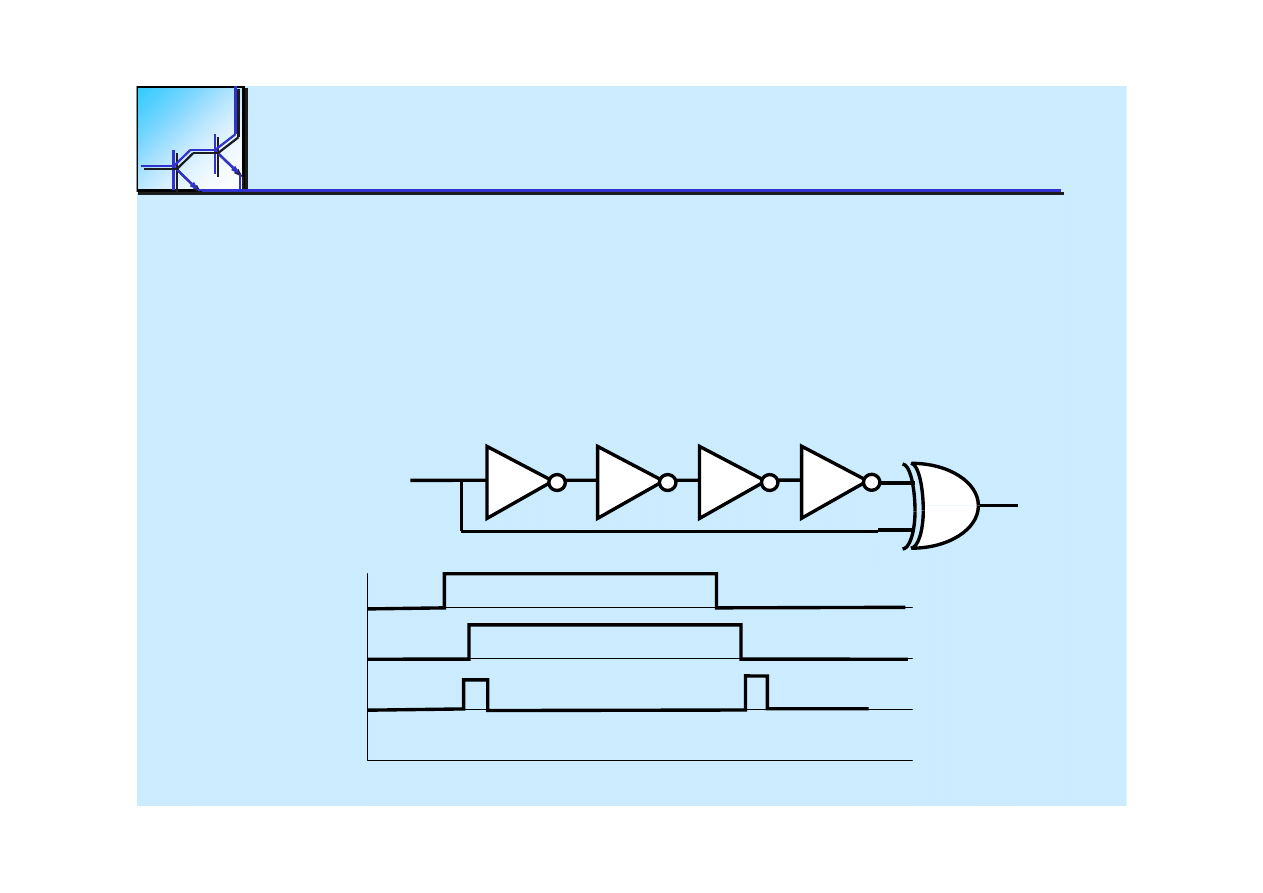
25 marca 2008
Cyfrowe układy kombinacyjne
99
Hazard
Hazard
Hazard
Uk
Uk
ł
ł
ady generuj
ady generuj
ą
ą
ce hazard s
ce hazard s
ą
ą
r
r
ó
ó
wnie
wnie
ż
ż
celowo wykorzystywane w praktyce.
celowo wykorzystywane w praktyce.
S
S
ą
ą
stosowane jako uk
stosowane jako uk
ł
ł
ady detektor
ady detektor
ó
ó
w pocz
w pocz
ą
ą
tku i ko
tku i ko
ń
ń
ca impulsu wej
ca impulsu wej
ś
ś
ciowego.
ciowego.
Do uzyskania impuls
Do uzyskania impuls
ó
ó
w wyj
w wyj
ś
ś
ciowych o po
ciowych o po
żą
żą
danej szeroko
danej szeroko
ś
ś
ci zwi
ci zwi
ę
ę
ksza si
ksza si
ę
ę
op
op
ó
ó
ź
ź
nienie jednego z tor
nienie jednego z tor
ó
ó
w sygna
w sygna
ł
ł
u wej
u wej
ś
ś
ciowego przez po
ciowego przez po
łą
łą
czenie kaskadowe
czenie kaskadowe
dodatkowych
dodatkowych
inwerter
inwerter
ó
ó
w
w
lub bramek.
lub bramek.
Sa
Sa
to tzw. Uk
to tzw. Uk
ł
ł
ady logicznego r
ady logicznego r
ó
ó
ż
ż
niczkowania.
niczkowania.
X
X
1
1
Y
Y
1
1
Z
Z
X
X
1
1
y
y
1
1
z
z
Document Outline
- Slajd numer 1
- Slajd numer 2
- Slajd numer 3
- CMOS Inverter
- Inverter
- Slajd numer 10
- Noise Margins
- Slajd numer 12
- Dynamic Behaviour
- Dynamic Behaviour
- Slajd numer 15
- Capacitance Sources
- Capacitance Calculations
- Slajd numer 18
- Czas propagacji
- Czas propagacji
- Czas propagacji
- Czas propagacji w układach kombinacyjnych
- Czas propagacji w układach kombinacyjnych
- Propagation Delay of Combinational Circuits
- Inverter Propagation Delay
- Propagation Delay of Combinational Circuits
- Propagation Delay of Combinational Circuits
- Slajd numer 28
- Dynamic Power Consumpsion
- Direct-Path Currents Power Consumpsion
- Static Power Consumpsion
- Contents
- The NAND Gate
- The NAND Gate
- The NOR Gate
- The 3 Input NOR Gate
- The AND Gate
- Enable input case
- The 3 State Inverter
- The 3 State Inverter
- The Transmission Gate
- The Transmission Gate
- The Complex Gate
- The Complex Gate – gate level design
- The Complex Gate – gate level design
- The Complex Gate
- The Complex Gate
- The Complex Gate
- The Complex Gate
- The Complex Gate - Euler Path
- The Complex Gate - Euler Path
- The Complex Gate
- Slajd numer 61
- Multipleksery
- The Multiplexer
- The Multiplexer
- The Multiplexer
- The Multiplexer
- The Multiplexer
- The Multiplexer as AND Gate
- The Multiplexer as OR Gate
- The Multiplexer
- The Multiplexer
- The Multiplexer
- The Multiplexer
- The Multiplexer 4 to 1
- Demultiplekser
- Demultiplekser
- Demultiplekser
- Demultiplekser
- Slajd numer 79
- Slajd numer 90
- Slajd numer 91
- Slajd numer 92
- Slajd numer 93
- Slajd numer 94
- Slajd numer 95
- Slajd numer 96
- Slajd numer 97
- Slajd numer 98
- Slajd numer 99
Wyszukiwarka
Podobne podstrony:
Uklady kombinacyjne
układy kombinacyjne, Studia, semestr 4, Elektronika II, cw2
uklady kombinacyjne
Sprawozdanie - Uklady Kombinacyjne, Studia, semestr 4, Elektronika II, Elektr(lab)
Sprawozdanie Złożone układy kombinacyjne
multiplekserPP, Polibuda, IV semestr, SEM IV, Elektronika i Energoelektronika. Laboratorium, 10. Ukł
układy kombinacyjne, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, Elektryczny, Teo
Układy kombinacyjne oparte na elektronicznych układach TTL
Cyfrowe układy kombinacyjne
Zadania 2, układy kombinacyjne
08 Złożone układy kombinacyjneid 7323 ppt
układy kombinacyjne, mechanika, BIEM- POMOCE, automatyka i sterowanie
Układy kombinowane
E6Cyfrowe uklady kombinacyjne
multiplekser, Polibuda, IV semestr, SEM IV, Elektronika i Energoelektronika. Laboratorium, 10. Układ
06 Bramki logiczne i układy kombinacyjneid 6179 ppt
Elektroniczne układy analogowe i cyfrowe, Układy kombinacyjne
203 uklady kombinacyjne - kodery i dekodery, Politechnika Wrocławska - Materiały, logika ukladow cyf
więcej podobnych podstron