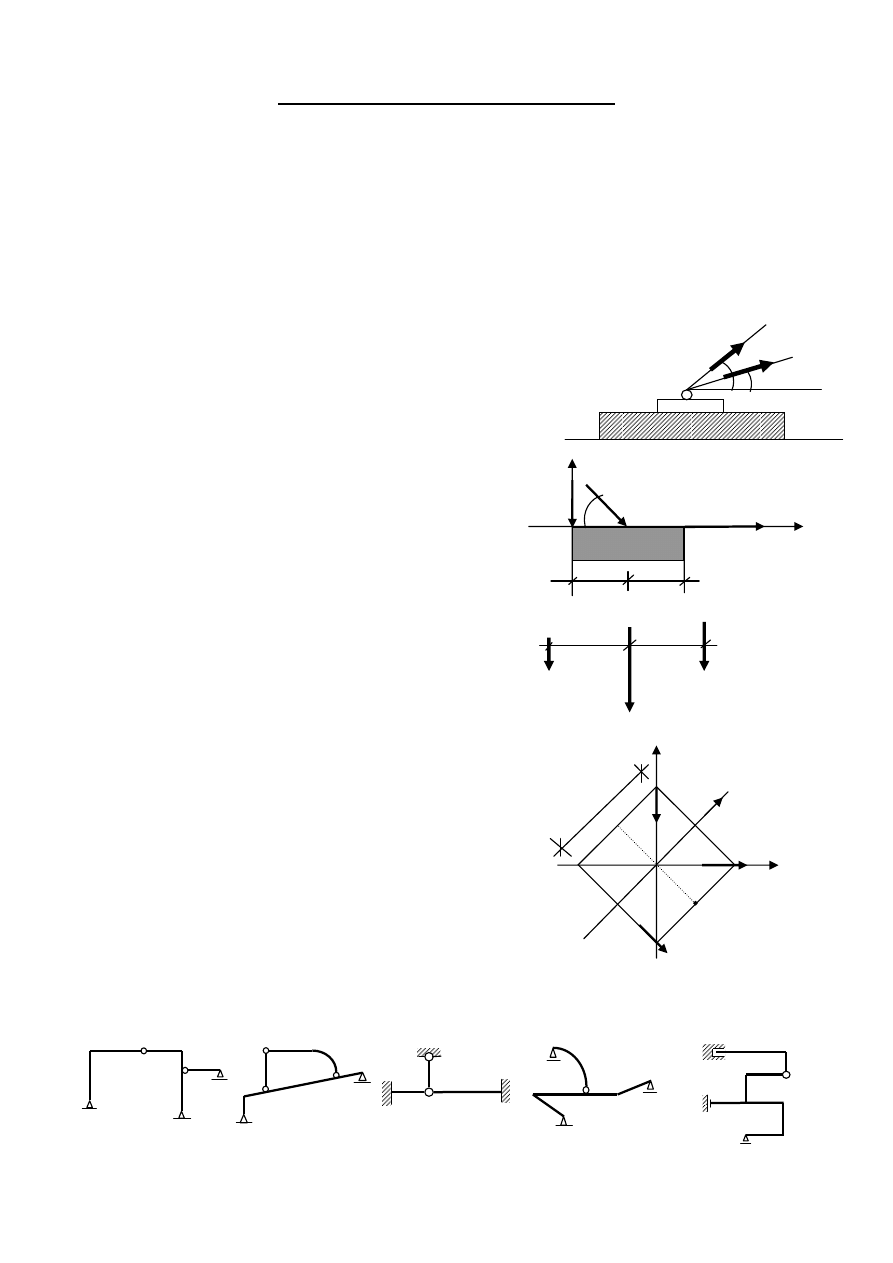
LISTA ZADAŃ Z MECHANIKI OGÓLNEJ

A. RACHUNEK WEKTOROWY

Zad. 1A Dane są wektory: a = i + 3j + 5k ; b = 4i – j + 6k . Oblicz sumę wektorów e = a + b oraz kosinusy
kątów, jakie tworzy wektor e z osiami układu ( kosinusy kierunkowe ).
Zad. 2A Dane są wektory: a = i + 3j + 5k ; b = 4i – j + 6k . Sprawdzić prostopadłość i równoległość tych
wektorów.
Zad. 3A Wyznacz długość i cosinusy kierunkowe iloczynu wektorowego OA x OB znając współrzędne
punktów A = (1, 2, 3 ), B = (-2, -3, 2 ). Punkt „O” jest początkiem układu współrzędnych.
Zad. 4A Dane są wektory: a = i + 3j + 5k ; b = 4i – j + 6k ; c = 2i + 2j + 7k ; d = 3i + 4j +4k. Znaleźć kąty
między wektorami: < ( a , c ) ; < (b , d )
Zad. 5A Obliczyć:

a) Ia x bI wiedząc, że IaI = 1, IbI = 5 oraz a ◦ b = -3
b) b ◦ c jeżeli a ◦ b = 0; a x c = 0; ( a ≠ 0 )

B. UKŁADY SIŁ NA PŁASZCZYŹNIE

P

2

Zad. 1B Wyznacz wypadkową dwóch sił P

1

= 20 kN i P

2

= 50 kN

β

α

P

1

działających na fundament w punkcie A odpowiednio pod
kątem α= 30

0

i β= 45

0

do poziomu (rys.1).

(rys.1)

Zad. 2B Wyznacz wypadkową układu sił działających na tarczę. y
Dane: P

1

= 100 kN, P

2

= 200 kN α

2

= 45

0

, P

3

= 50 kN P

1

P

2

(rys. 2 )
α

2

P

3

x

2 2
(rys. 2 )

Zad. 3B

Wyznaczyć wypadkową W ( wartość i linię działania )

układu trzech sił równoległych. Wartości sił wynoszą 50 cm 40 cm
P

1

= 10 kN, P

2

= 40 kN , P

3

= 15 kN. ( rys. 3 )

P

1

P

2

P

3

( rys. 3 )
Zad. 4B

Oblicz: x

2

a) sumę rzutów sił na osie układu współrzędnych x

1

, x

2

, F

1

= 15kN

b) sumę rzutów sił na oś l o wersorze e

l

.( rys. 4 ) e

l

a=4,0 m
Zad. 5B Oblicz:
a) sumę momentów statycznych F

2

= 30kN

wszystkich sił wzgl. pkt A,
b ) sumę momentów statycznych x

1

wszystkich sił wzgl. osi x

3

. ( rys. 4 ) A

F

3

=20kN ( rys. 4 )

C. ANALIZA STATYCZNA

Polecenie dla wszystkich zadań: zbadaj statyczną wyznaczalność przedstawionych układów prętowych.
Narysuj układy sił czynnych i biernych.

Zad. 1C Zad. 2C Zad. 3C Zad. 4C Zad. 5C

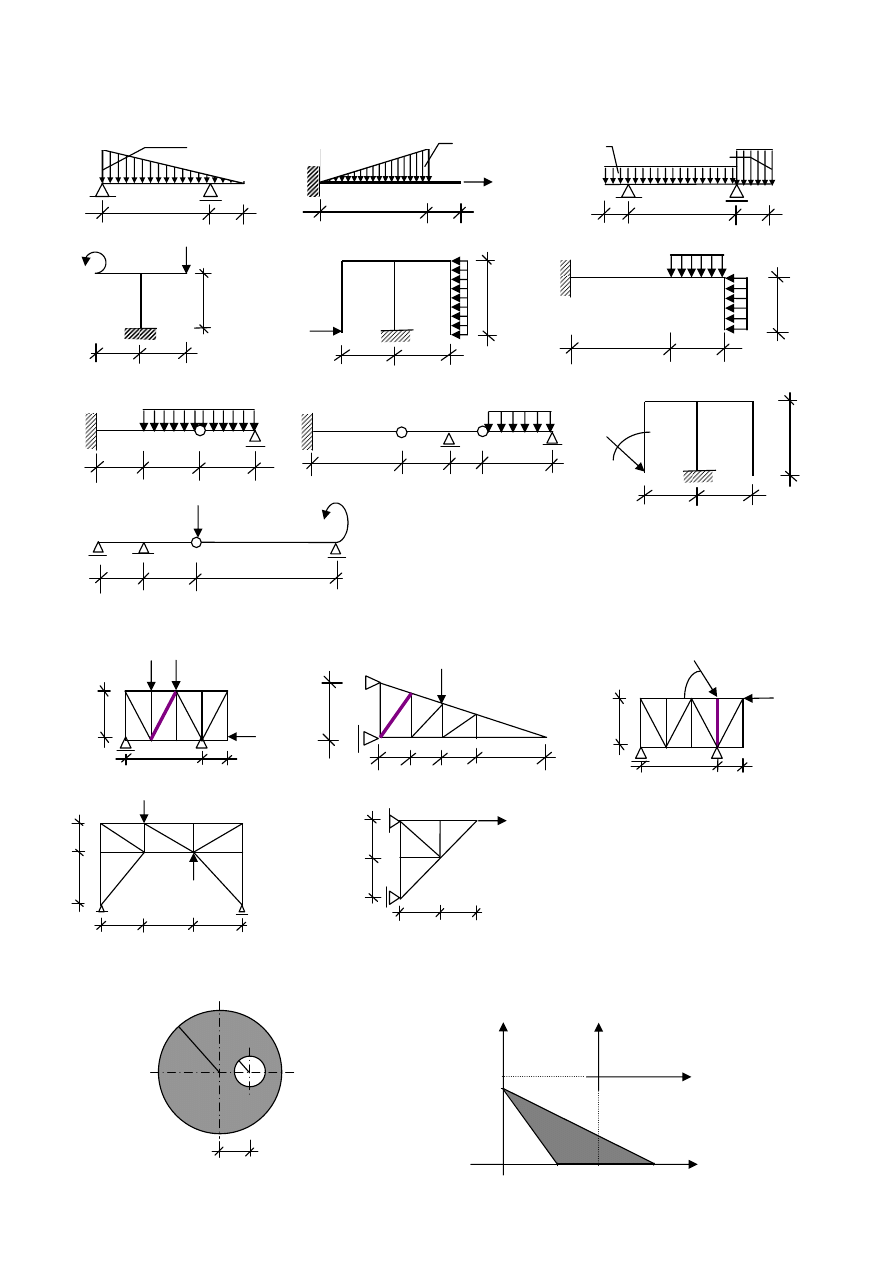
D. OBLICZANIE REAKCJI

Polecenie dla wszystkich zadań: oblicz reakcje podporowe w przedstawionych belkach, ramach.
Zad. 1D Zad. 2D Zad. 3D





Zad. 4D Zad. 5D Zad. 6D








Zad. 7D Zad. 8D Zad. 9D






Zad. 10D





E. KRATOWNICA

Polecenie dla zadań 1E, 2E, 3E : wyznacz siły w zaznaczonych prętach kratownic z poniższych zadań.
Zad. 1E Zad. 2E Zad. 3E







Polecenie dla zadań 4E, 5E : wskaż pręty zerowe ( uzasadnij słownie ).
Zad. 4E Zad. 5E








F. CHARAKTERYSTYKI PÓL FIGUR PŁASKICH

Zad. 1F Wyznaczyć środek ciężkości Zad. 2F Dla figury przedstawionej na rysunku wyznaczyć:
dla figury przedstawionej poniżej. - środek ciężkości ,
- momenty bezwładności wzgl. osi x

1

, y

1.

6

2 2

M=10kNm

4

P=20kN

3 3

q=4kN/m

q=3kN/m




2

4 2

q=2kN/m



2 3 2

q=2kN/m.



4 2 1 3

4
30

0

P=20kN

3 3

P=12kN M=8kNm




4 4 8

3 x 2 2

4

P

1

=10kN P

1

=10kN

P

2

=4kN

P=20kN


5

1 1 1 2

P

2

=2kN

3 x 2 2

4

P

1

=20kN

60

0

P
a


a

a a

P

a


b P


c c c

r

1

=10cm

r

2

=2cm

5,0

y y

1

8 x

1

7

0 5 8 12 x

6

2

2

4

2

6

2

q=4 kN/m

P=10kN

q=4 kN/m

P=10kN

q=2 kN/m

q=2 kN/m

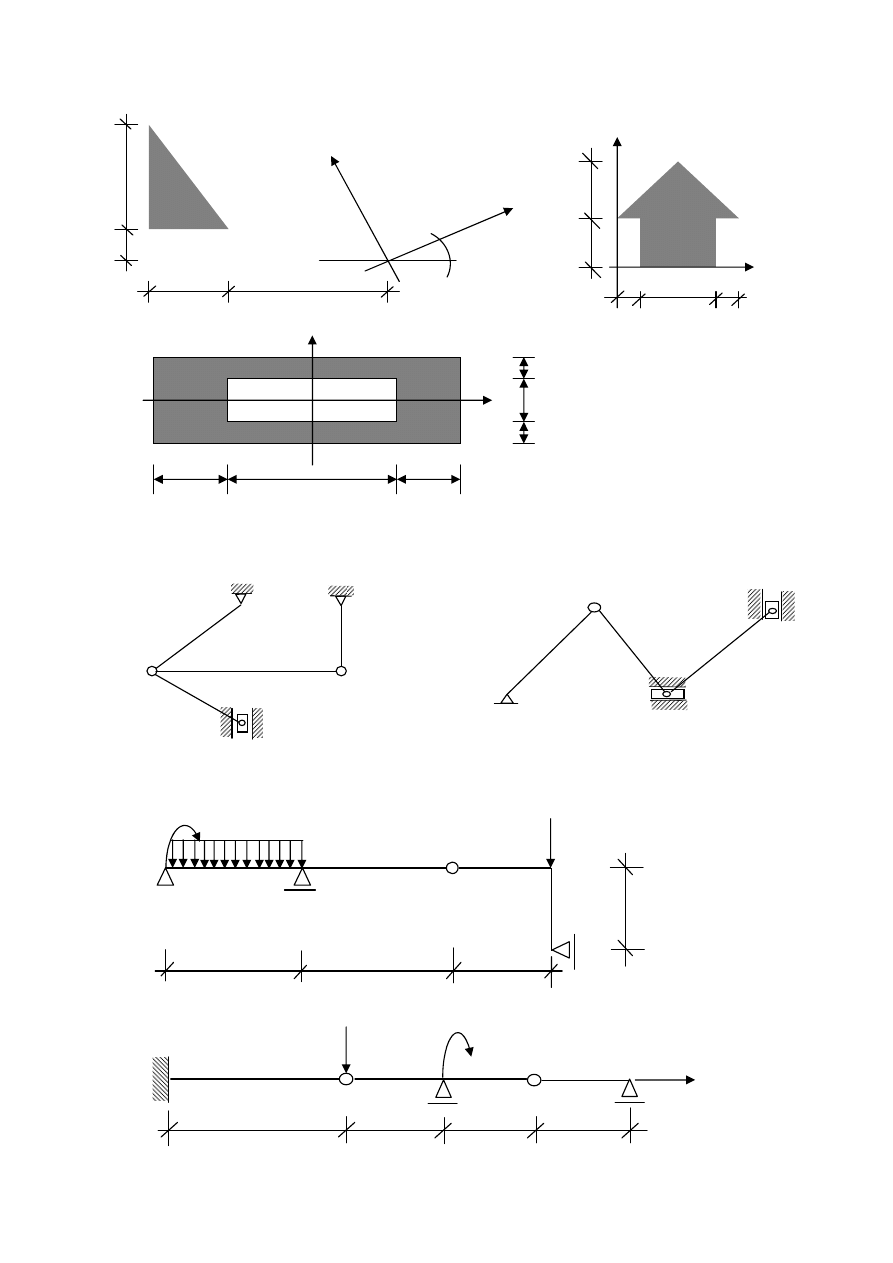
Zad. 3F Oblicz momenty bezwładności względem Zad.4F Wyznaczyć położenie osi centralnych,
osi x i y figury przedstawionej na rysunku. dla których moment dewiacji jest
ekstremalny.

Zad. 5F Znaleźć takie „d” , aby I

I

= I

II

.

G. KINEMATYKA UKŁADÓW GEOMETRYCZNIE ZMIENNYCH

Wyznacz plan biegunów układów i narysuj nieskończenie mały ruch układu.

Zad. 1G Zad. 2G












H. ZASADA PRACY WIRTUALNEJ PRZY WIRTUALNYM STANIE PRZEMIESZCZEŃ

Oblicz reakcje podporowe w belkach stosując powyższą zasadę.
Zad. 1H









Zad. 2H

y
6


x

3
30

0

4 10

x

y

6

6

8

1

1

2

2

d

10

4

4

y

x

120 kNm 20 kN/m. 100kN

1,5


4 2 3 [m]

15kN 20kNm
2kN


4 2 3 2 [m]