PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE
INSTYTUT NAUK TECHNICZNYCH

Laboratorium Mechaniki Płynów

Ćwiczenie 3

Pomiar oporu ciśnieniowego profilu kołowego

Opracował: dr inż. Dariusz Mika

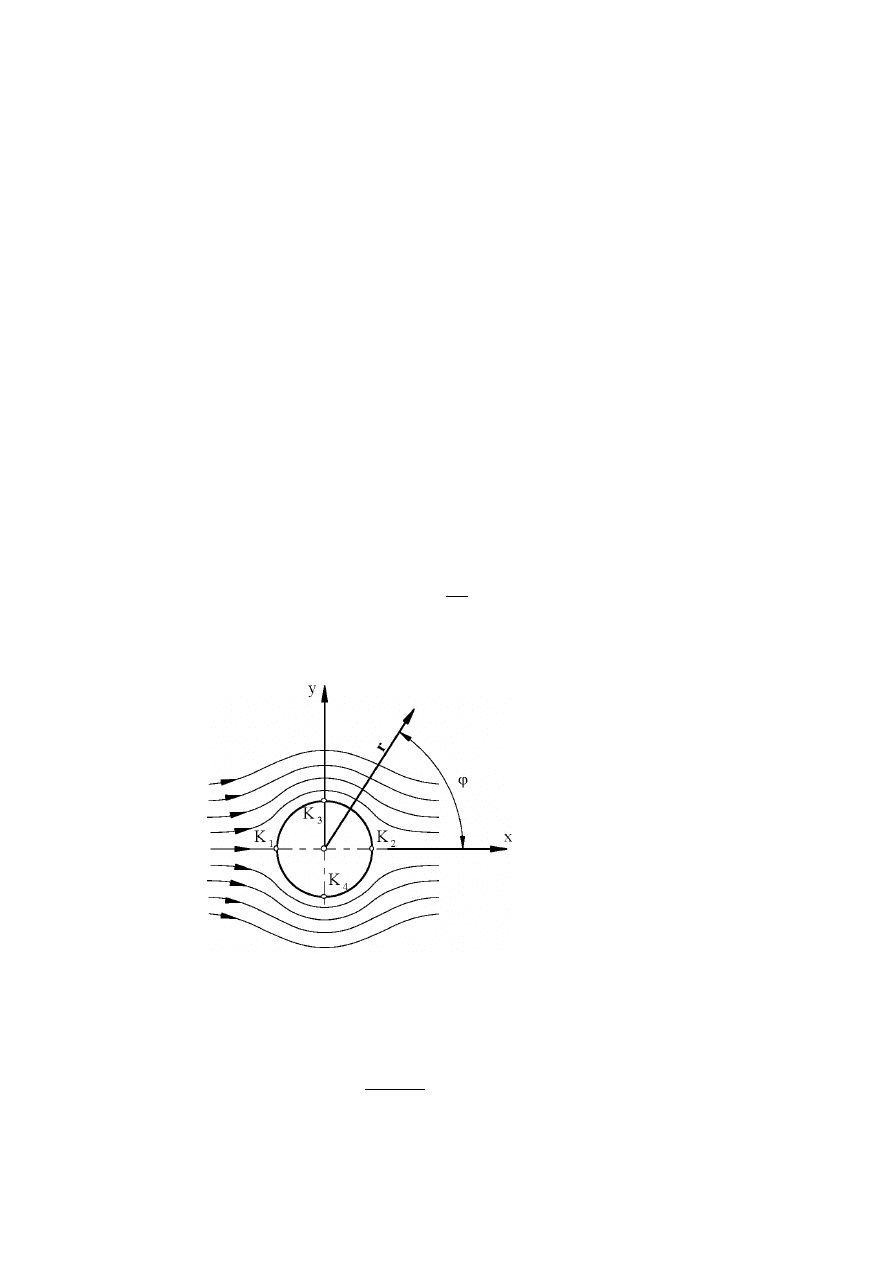
1. Wprowadzenie teoretyczne.

Na ciało (opływane lub poruszające się w płynie lepkim) działają siły ciśnienia i

naprężeń stycznych. Podczas opływu płynem nielepkim naprężenia styczne nie występują.

Opływ walca jest przykładem płaskiego opływu osiowo-symetrycznego, o osi

normalnej do kierunku strugi. W celu porównania zakładamy początkowo potencjalny opływ
walca o promieniu R i długości l (przy czym l/R >> 1) płasko-równoległą strugą płynu
nielepkiego. Przepływ taki otrzymuje się przez superpozycję przepływu równoległego i
dipola. Prędkość płynu nielepkiego na powierzchni walca,

v = - 2v

x

sin φ (1)

jest zawsze skierowana stycznie. Prędkość przepływu jest różna od zera we wszystkich

punktach powierzchni walca, oprócz tzw. punktów krytycznych (punktów spiętrzenia), które
odpowiadają kątom p = 0 i p = π ( punkty K

1

i K

2

na rys. 1.). Po stronie napływowej prędkość

przepływu rośnie, a ciśnienie maleje, po stronie spływowej, odwrotnie.

Gdy znane jest pole prędkości, można na podstawie równania Bernoulliego wyznaczyć

pole ciśnień i otrzymujemy wówczas zależność

)

sin

4

1

(

2

2

2















v

p

p

(2)

w której



p

,



v

są wartościami odnoszącymi się do przepływu niezakłóconego.

Rys. 1. Potencjalny opływ profilu kołowego.

Stosunek różnicy ciśnień do ciśnienia dynamicznego strugi niezakłóconej, zwany

współczynnikiem ciśnienia





2

2

sin

4

1

2

/













v

p

p

C

p

(3)

nie zależy on zatem od wymiarów geometrycznych walca ani parametrów przepływu strugi, a
jedynie jest funkcją kąta φ (rys. 2a - linia przerywana). Osiąga on wartość maksymalną w
punktach krytycznych K

1

i K

2

, a minimalną w punktach K

3

i K

4

. Symetryczny rozkład ciśnień

względem obu osi, wzdłużnej i poprzecznej do kierunku przepływu powoduje, że wypadkowa
siła działająca na opływane ciało jest równa zeru.

Jeżeli walec opływany jest płynem lepkim, pola prędkości i ciśnień w napływowej

(przedniej) stronie walca są na ogół zbliżone do pól obliczanych dla opływu potencjalnego,
ale po stronie spływowej (tylnej) występuje wyraźna rozbieżność między opływem nielepkim
i lepkim (rys. 1 i 2). Również doświadczenia wskazują, że każde ciało opływane strugą płynu
lepkiego znajduje się pod działaniem znacznych sił oporu. Te rozbieżności można wyjaśnić
na podstawie teorii warstwy przyściennej.

Z analizy wzoru (3) wynika, że w przedziale 0 < p < π/2 gradient ciśnienia jest ujemny,

natomiast w przedziale π /2 < p < π - dodatni. Ten rozkład ciśnienia sugeruje, że po stronie
spływowej walca może wystąpić oderwanie strugi w przekroju O-O (rys. 3). Położenie
przekroju O-O zależy od charakteru przepływu w warstwie przyściennej. Dla laminarnej
warstwy przyściennej to oderwanie, zwane dalej oderwaniem laminarnym, występuje
wcześniej (rys. 3a), a dla warstwy turbulentnej - zwane oderwaniem turbulentnym - później
(rys. 3b). Linie prądu rzeczywistego (lepkiego) opływu walca do przekroju oderwania
pokrywają się w przybliżeniu z liniami prądu przepływu potencjalnego, a od przekroju
oderwania biegną równolegle do kierunku prędkości strugi napływającej. Na liniach
rozgraniczających obszar oderwania od przepływu potencjalnego panuje w przybliżeniu stała
prędkość, a zatem ciśnienia też będą stałe. Również w warstwie przyściennej, w kierunku
normalnym do powierzchni opływanej, ciśnienia na tych liniach nie ulegają zmianie, a zatem
w całym obszarze panuje stałe ciśnienie.

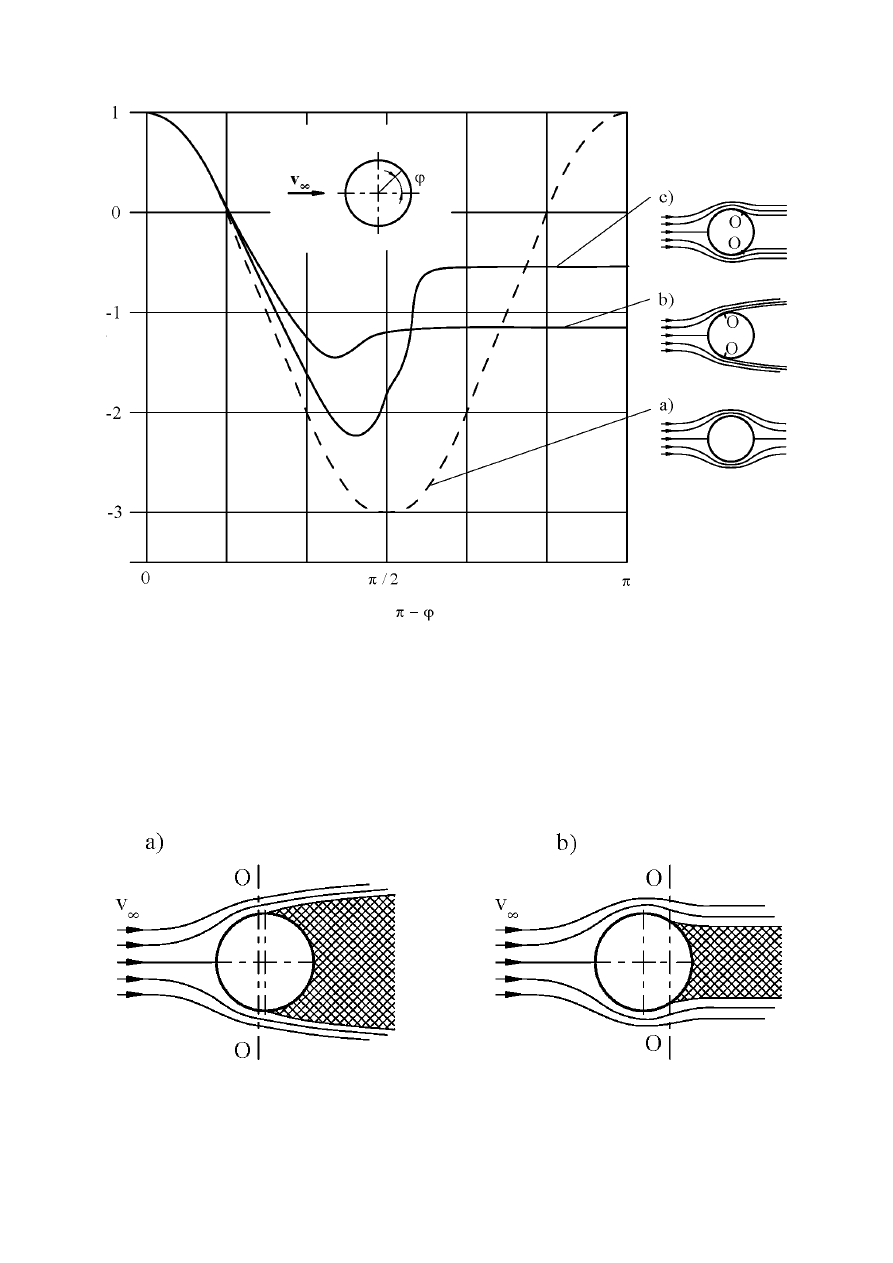
c

p

Rys. 2. Rozkład współczynnika ciśnienia na obwodzie walca: a) opływ potencjalny, b)

opływ z oderwaniem laminarnej warstwy przyściennej, c) opływ z oderwaniem turbulentnej

warstwy przyściennej

Rys. 3. Rzeczywisty opływ walca: a) z oderwaniem laminarnym, b) z oderwaniem

turbulentnym

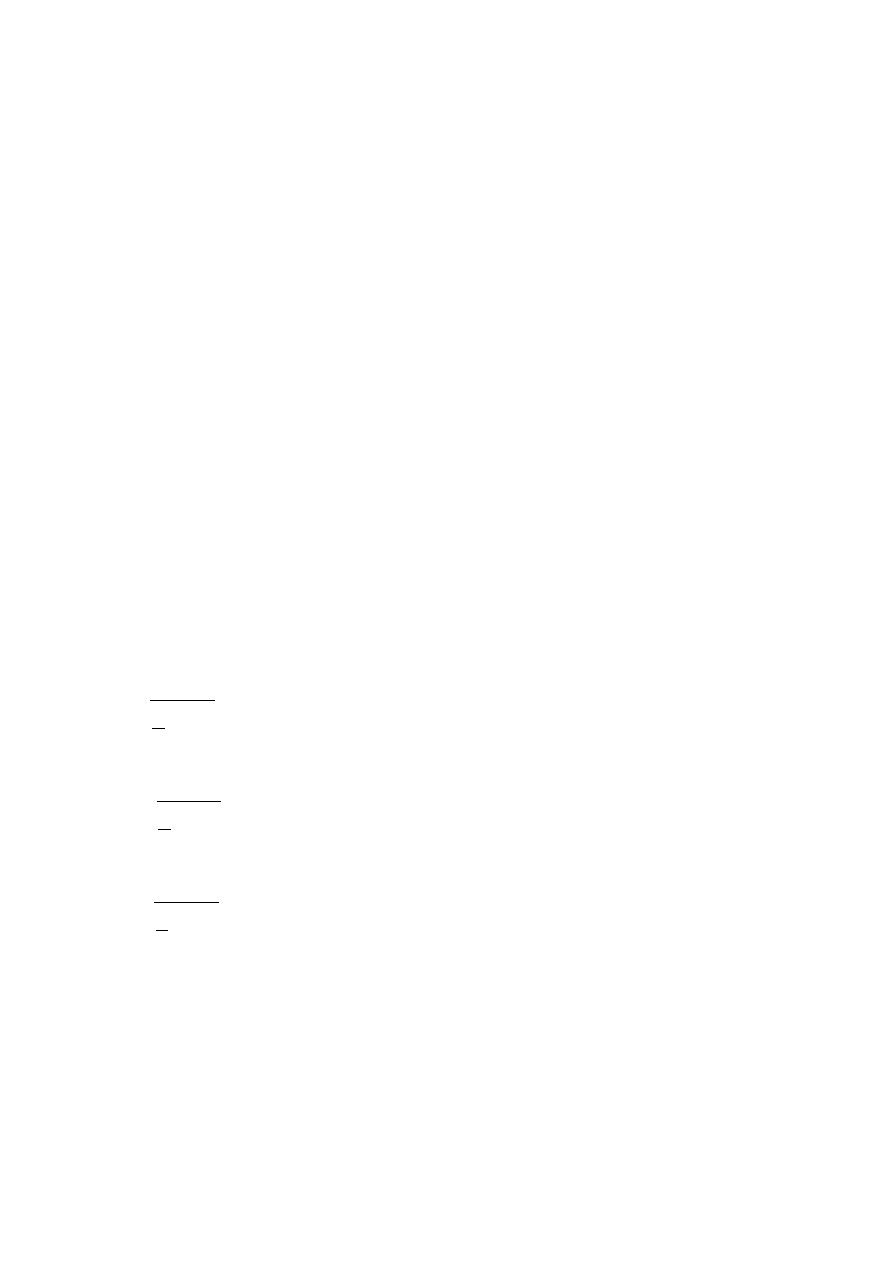
Jeżeli, w przypadku rzeczywistych rozkładów ciśnienia, obliczymy siłę działającą w

kierunku osi x, to przekonamy się, że siła oporu ciśnieniowego











0

cos

2

d

Rp

P

(4)

jest większa od zera. Wynika to z tego, że w tylnej części walca, zwłaszcza w obszarze

oderwania, ciśnienia są dużo mniejsze niż w części przedniej i wobec tego nie równoważą się
one tak, jak w przepływie potencjalnym. Z analizy rozkładów ciśnienia wynika, że opór
ciśnieniowy jest tym większy, im większy jest obszar oderwania, a więc w przepływie z
oderwaniem laminarnym opór ten jest większy niż w przepływie z oderwaniem turbulentnym.

Całkowita siła oporu składa się z oporu ciśnieniowego i oporu tarcia

t

c

P

P

P





(5)

Odnosząc poszczególne składniki powyższego równania do

)

(

2

/

1

2

A

v





przy czym A jest

polem przekroju charakterystycznego ciała opływanego, otrzymamy zależność

xt

xp

x

c

c

c





(6)

w której:

A

v

P

c

x

2

2

1







- współczynnik oporu profilowego,

A

v

P

c

c

xp

2

2

1







- współczynnik oporu ciśnieniowego,

A

v

P

c

t

xt

2

2

1







- współczynnik oporu tarcia.

Opór tarcia jest proporcjonalny do gradientu prędkości w kierunku normalnym do

opływanej powierzchni; jest więc stosunkowo mały w przepływie laminarnym, a znacznie
większy w turbulentnym. Zmiana charakteru przepływu wywołuje więc znaczne zmiany
wartości oporu ciśnieniowego i oporu tarcia. W opływach ciał, w których występują wyraźne
obszary oderwania, decydujący wpływ na opór całkowity wywiera opór ciśnieniowy i
przeciwnie, w opływach tzw. ciał aerodynamicznych, w których nie ma oderwania albo
występuje na znikomej powierzchni, decydującą rolę odgrywają opory tarcia.

2. Cele ćwiczenia

Celem ćwiczenia jest wyznaczenie rozkładu ciśnień (naprężeń normalnych) na profilu

kołowym, wyznaczenie siły oraz współczynnika oporu ciśnieniowego (części wsp. oporu
profilowego), która od togo rozkładu ciśnienia pochodzi.

3. Zadania

a) wyznaczyć rzeczywisty rozkład współczynnika ciśnienia c

p

na profilu

kołowym,

b) na podstawie otrzymanych wyników obliczyć wartość siły oporu

ciśnieniowego oraz współczynnik oporu ciśnieniowego dla badanego
profilu.

4. Przebieg ćwiczenia.

Ćwiczenie przeprowadzane jest z wykorzystaniem tunelu aerodynamicznego

edukacyjnego Aerolab typu otwartego. Profil ćwiczeniowy należy umieścić w sekcji testowej
tunelu (stosowanie do instrukcji obsługi tunelu). Profil ćwiczeniowy posiada 24 otwory
testowe rozmieszczone równomiernie na kołowym przekroju poprzecznym profilu. Od
każdego otworu wyprowadzony jest wężyk elastyczny. Drugie końce wężyków należy
połączyć z odpowiednimi gałązkami (kanałami) multi-manometru będącego wyposażeniem
tunelu. Drugie gałązki manometru są otwarte do atmosfery w związku z tym manometr
mierzy różnicę ciśnienia na profilu i ciśnienia atmosferycznego (Δp(β)=p(β)-p

0

)).

5. Opracowanie wyników pomiaru.

Wskazania manometru dają różnicę ciśnień między ciśnieniem panującym na profilu w

wybranym punkcie określonym szerokością kątową p(β) a ciśnieniem atmosferycznym, czyli
wartości

Δp(β)=p(β)-p

0

(7)

podciśnień i nadciśnień panujących na profilu.

Na podstawie wskazań multimanometru dla poszczególnym otworów, otrzymamy

rozkład wartości różnic p(β) - p

0

dla 24 punktów pomiarowych na obwodzie profilu, czyli

Δp(β). Należy pamiętać o odpowiedniej konwencji znakowej odczytywania wysokości
słupków cieczy w manometrach. Wysokości powyżej przyjętego poziomu zerowego bierzemy
ze znakiem (-) (podciśnienie w stosunku do ciśnienia atmosferycznego) natomiast wysokości
poniżej poziomu zerowego ze znakiem (+) (nadciśnienie). Aby odnieść otrzymane wyniki do
ciśnienia statycznego przepływu niezakłóconego



p

należy do otrzymanych wyników dodać

różnicę ciśnień pomiędzy ciśnieniem atmosferycznym a ciśnieniem statycznym sekcji

testowej tunelu

























p

p

p

p

p

p

p

p

p

)

(

)

(

)

(

)

(

)

(

0

0

0







. Różnicę

tych ciśnień odczytujemy korzystając z sondy Prandtla umieszczonej w sekcji testowej tunelu

1

0





P

p

. Za pomocą sondy Prandtla wyznaczamy dodatkowo ciśnienie dynamiczne przepływu

niezakłóconego q.

Z uwagi na fakt, że na wielkości ciśnień w poszczególnych punktach profilu wpływają

takie wielkości, jak rodzaj otaczającego profil ośrodka - jego gęstość i prędkość, przyjęło się
w aerodynamice takie rozkłady przedstawiać w formie bezwymiarowej tzw. współczynników
ciśnienia C

p

, gdzie wartości poszczególnych ciśnień są odniesiono do wartości ciśnienia dy-

namicznego q panującego w strumieniu w czasie pomiarów (zależność (3)):

q

p

p

c

p







Odkładając

na

przekroju

profilu, wzdłuż promienia, odcinki
odpowiadające (po uwzględnieniu
podziałki)

pomierzonym

w

poszczególnych

punktach

wielkościom C

p

,

w

konwencji:

nadciśnienie do środka okręgu,
podciśnienie

na

zewnątrz,

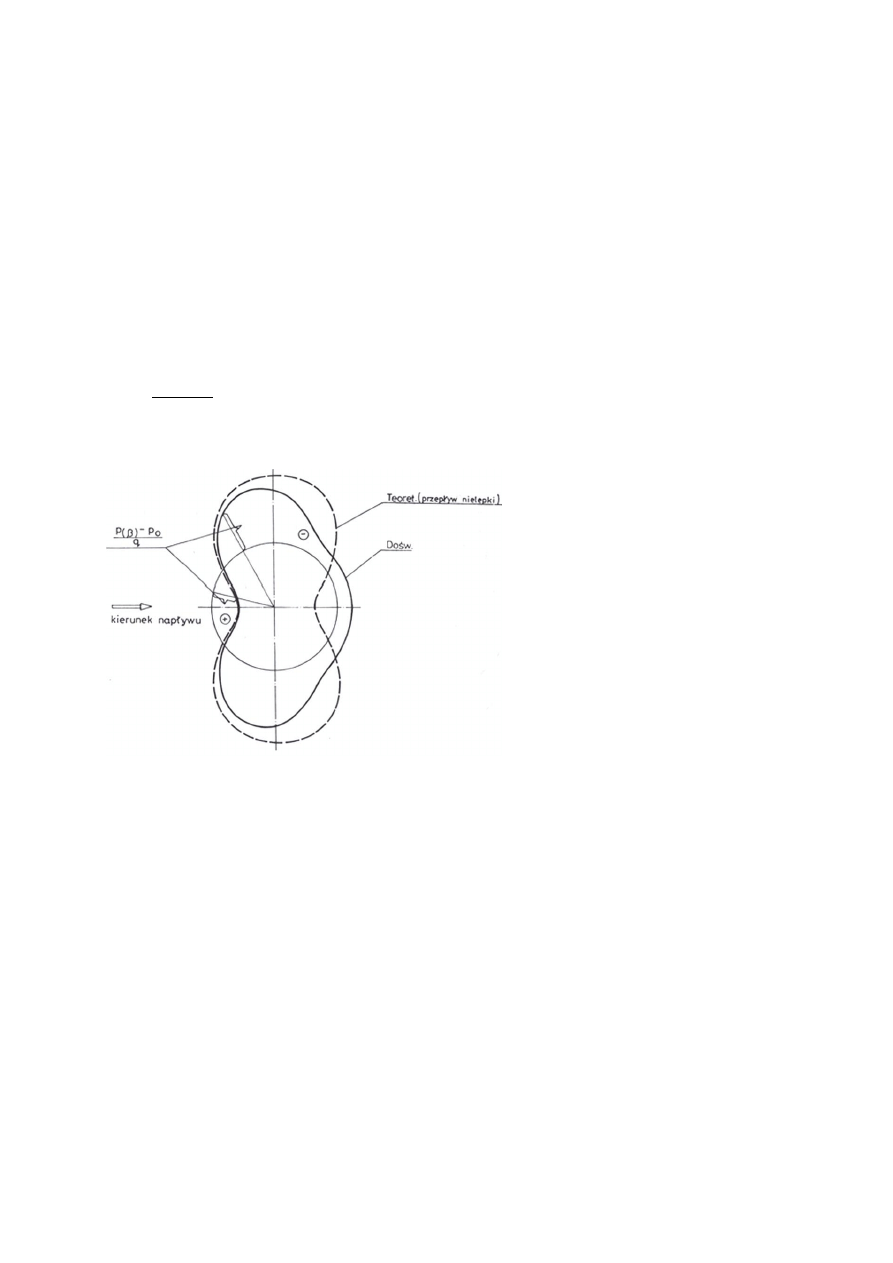
otrzymamy graficzny obraz rozkładu
C

p

(β) (rys. 4) równoznaczny z

rozkładem ciśnień rzeczywistych.

Rys. 4. Teoretyczny (nielepki) oraz rzeczywisty

rozkład współczynnika ciśnienia na profilu
kołowym.

Przedstawiając zależność teoretyczną na C

p

(wzór (3)) w przyjętej wyżej konwencji

widać, że jest on symetryczny względem obu charakterystycznych osi: pionowej i poziomej
(rys. 4) nie sugeruje to zatem powstania między płynem a profilem jakiejkolwiek reakcji.

Sugestia ta stoi w wyraźnej sprzeczności z intuicyjnym wyczuwaniem rzeczywistości

przez obserwatora (paradoks d'Alamberta), a po porównaniu z doświadczeniem zwraca
uwagę, jak istotny wpływ na kształtowanie obrazu rozpatrywanego zjawiska mają siły
lepkości, nie uwzględnione w analizie.

Niesymetryczny rozkład ciśnień rzeczywistych względem osi walca prostopadłej do

kierunku przepływu (rys. 4) jest przyczyną, że po zsumowaniu składowych poziomych
naporów elementarnych otrzymamy niezerową wypadkową tych naporów, równoległą do

kierunku przepływu. Siłę na profilu działającą w tym kierunku przyjęło się w aerodynamice
nazywać siłą oporu ciśnienia. Z uwagi na symetrię rozkładu ciśnienia względom osi poziomej
profilu, nie wystąpi oczywiście reakcja prostopadła do kierunku przepływu - siła nośna, gdyż
wypadkowa elementarnych naporów rzutowanych na ten kierunek jest równa zeru.

Przykładowo, do analizy weźmy lewą połówkę profilu (walca) z rysunku 4. Rachunek

przeprowadzimy zakładając, że rozpatrywany element walca posiada długość (w kierunku
prostopadłym do płaszczyzny rysunku) równą jedności.

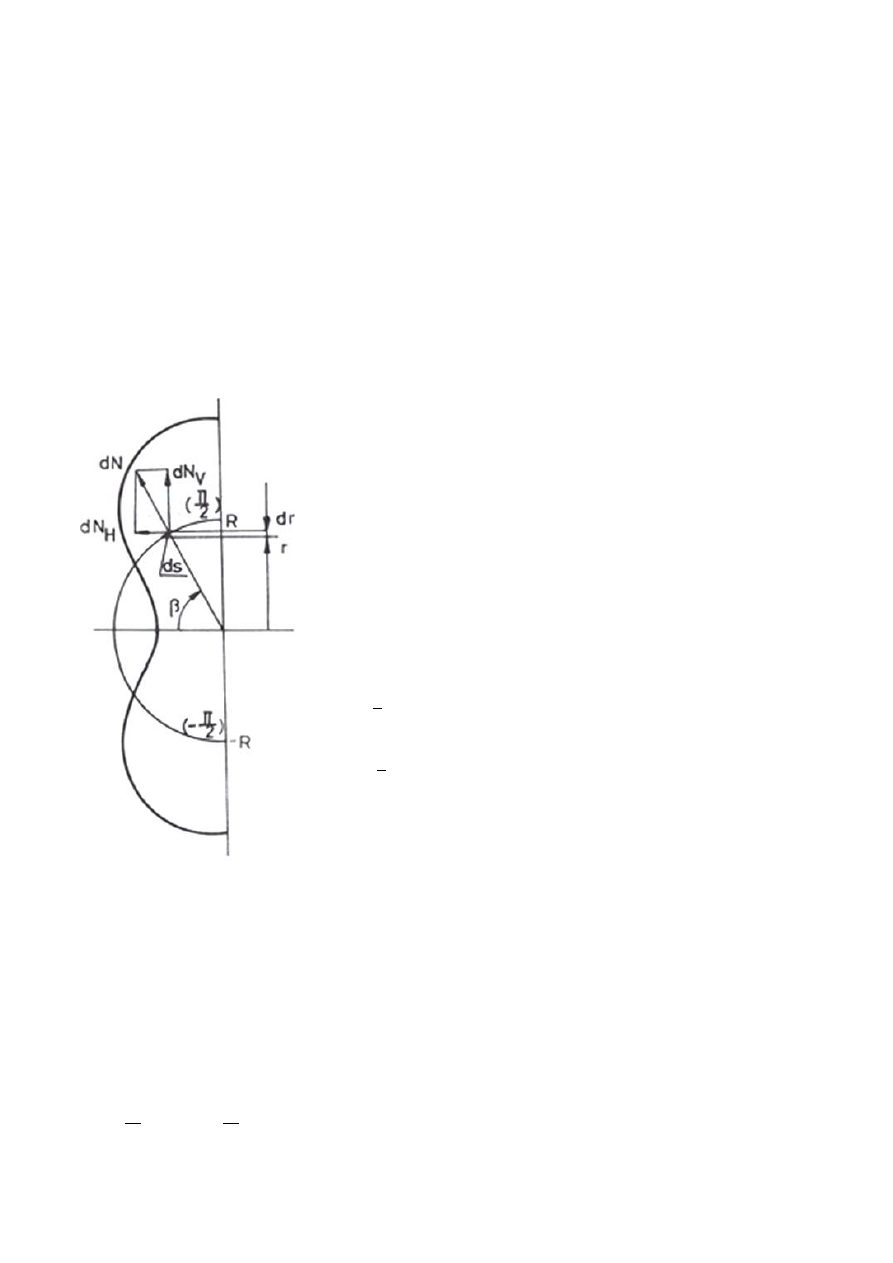
Usytuowanie składowych elementarnych naporu oraz informacje dotyczące

współrzędnych punktu ich przyłożenia podano na rys. 5. Otrzymamy:

Elementarna siła parcia:

l

ds

p

dN





)

(



(8)

gdzie: l - długość profilu w kierunku prostopadłym do

płaszczyzny rysunku.

Jeżeli przyjmiemy l=1, to składowa pozioma elementarnej

siły parcia:







cos

)

(

cos









ds

p

dN

dN

H

(9)

Całkowita składowa pozioma siły parcia dla lewej połówki

walca będzie:







2

2

cos

)

(









ds

p

N

HL

gdzie: ds=Rdβ (10)

Układ współrzędnych, w którym wyprowadzono powyższą

zależność, jest o tyle niewygodny, że wymaga całkowania wzdłuż
łuku, komplikując obliczenie całki

Możemy się jednak tej niedogodności pozbyć, zmieniając układ współrzędnych jak

niżej:

Z rys. 5 widać, że przyrost promienia dr jest równy rzutowi łuku na kierunek promienia:

dr = ds cosβ

Wprowadzając tę zmienną pod znak całki oraz zmieniając granice całkowania

odpowiednio:

R







2



i

R



2



Rys. 5

Rys. 5.

otrzymamy:







R

R

HL

dr

r

p

N

)

(

(11)

Zapis jest równoważny poprzedniemu z różnicą, że pod znakiem całki występuje

funkcja zmian ciśnienia w

zależności od r, a nie, jak poprzednio od β . Jest ona łatwa, jak się

później okaże, do określenia i scałkowania.

Całkowita siła pozioma równa będzie algebraicznej sumie składowych dla lewej i

prawej połówki walca:

HP

HL

H

N

N

N





(12)

z uwagi na to, że wskutek obciążenia powierzchni walca ciśnieniem otoczenia p

Q

,

całkowite siły: pozioma i pionowa pochodzące od stałego p

0

są równe zeru, czyli:

0









































P

R

R

L

R

R

dr

p

dr

p

(13)

łącząc (10), (11), (12), możemy napisać:

0

)

)

(

(

)

)

(

(















































P

R

R

L

R

R

H

dr

p

r

p

dr

p

r

p

N

(14)

W ostatniej postaci równania, pod znakiem całki, mamy zależne od promienia r

wartości różnic ciśnień mierzone na stanowisku przy pomocy multi-manometru.

Gdybyśmy mieli określony matematyczną funkcją przebieg





p

r

p )

(

w przedziale od

-R do R dla obu połówek walca, to równanie (14) pozwala na obliczenie wypadkowej siły N

H

.

Ponieważ określenie matematyczne takiej funkcji na podstawie pomiarów rozkładu





p

r

p )

(

jest, poza skomplikowaniem, obarczone błędem przybliżeń, proponuje się dla określenia N

H

prostszą, graficzną metodę całkowania.

Metoda ta sprowadza się do wyznaczenia graficznego przebieg





p

r

p )

(

na podstawie

pomierzonego i przedstawionego na wykresie (rys. 4) przebiegu p





p

r

p )

(

.

Sposób postępowania podano na rys.6 .

Rozkłady





p

r

p )

(

określono oddzielnie dla obu połówek (rys. 6 b i c), Odcinek -R, R

oznacza średnicę profilu (walca) wzdłuż której, odpowiednio, każdej wartości r równej Rsinβ
przyporządkowano odcinek obrazujący wartość:











p

p

p

r

p

)

(

)

(



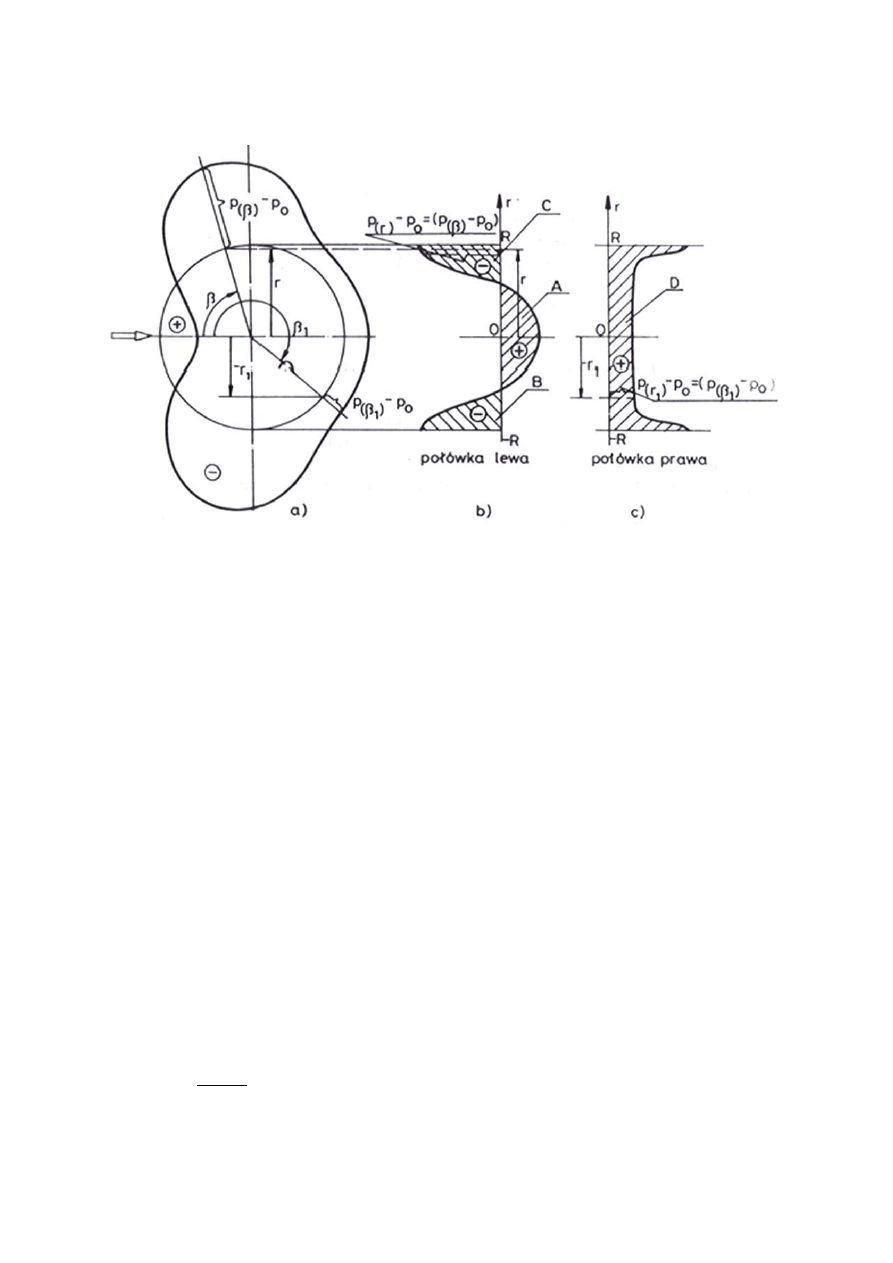
wzięty z wykresu rozkładu ciśnień pomierzonych w funkcji β (rys. 6a).

Rys. 6. Sposób graficznego całkowania ciśnienia wzdłuż obwodu walca.

W myśl geometrycznej interpretacji wartości całki, wartość z równania (14) jest równa

sumie pól zawartych między funkcją podcałkową a osią r w granicach od -R do R. Jeżeli
oznaczymy te pola jak na rys.6 literami A, B, C i D i przyjmiemy kierunek napływu jako
kierunek dodatni dla zwrotów składowych poziomych naporów elementarnych, to otrzy-
mamy:

- dla lewej połówki: pole A w obrębie nadciśnień, zwroty zgodne, znak "+", pola B i C

w obrębie podciśnień, zwroty przeciwne (rys. 6), znak "-",

- dla prawej połówki: pole D, znajdujące się w obrębie podciśnień, jak pola B i C na

połówce lewej, ale wskutek odmiennie zorientowanej powierzchni zwroty składowych
poziomych naporów elementarnych mają znak "+".

Otrzymamy więc:





P

R

H

k

k

C

B

D

A

N

)

(

)

(









(15)

k

R

k

P

są podziałkami, jakie uwzględniliśmy, przedstawiając wielkości





p

r

p )

(

oraz R

w postaci graficznej.

Przykładowo: 1 MPa w rzeczywistości jest równoważny 10 cm na wykresie. Wówczas:

cm

MPa

k

P

10

1



Planimetrując więc poszczególne pola, dodając według (15) do siebie

i

uwzględniając

podziałki, otrzymamy wartość jednostkowej siły poziomej N

H

, równoważnej jednostkowej

sile oporu aerodynamicznego profilu p

x

, wymuszonej rozkładem ciśnień. Równanie (14)

możemy napisać również w nieco odmiennej postaci, wprowadzając pod znak całki funkcję
zmian współczynnika ciśnienia C

P

(r) :

x

P

R

R

L

R

R

H

P

dr

q

p

r

p

dr

q

p

r

p

q

N

































































)

(

)

(

(16)

Zapis ten upoważnia nas, przy tworzeniu graficznym wykresów rozkładów ciśnień (rys.

6 ) do korzystania bezpośredniego z wykonanego wykresu rozkładów C

p

(β) (rys. 4). Trzeba

tylko pamiętać, że z operacji tej otrzymamy rozkład C

P

(r) i zależność (15) przyjmie postać:





x

Cp

R

H

P

k

k

C

B

D

A

q

N













)

(

)

(

(17)

gdzie k

Cp

jest podziałką przyjętą dla współczynnika ciśnienia.

Wybór sposobu obliczenia N

H

pozostawia się do dyspozycji studenta.

Znając wielkość siły P

x

, możemy określić współczynnik oporu (ciśnienia) dla tego

profilu.

Jak wiadomo:

2

2

v

F

c

P

c

x





gdzie: c

x

- współczynnik oporu (ciśnienia),

F- powierzchnia profilu, w naszym przypadku jednostkowa, równa

1

2



R

.

2

2

v



-

ciśnienie dynamiczne strumienia; w naszym przypadku odczytane z

monitora tunelu i oznaczono przez q.

Tak więc współczynnik oporu będzie równy:

Rq

N

c

H

xp

2



(18)

Literatura

1.

Kabsch K, H. Szewczyk: Mechanika Płynów, Oficyna Wydawnicza Politechniki Wrocławskiej,
Wrocław 2001

2.

Bukowski J, Kijkowski P.: Kurs mechaniki płynów, PWN, Warszawa 1980

Zadanie do wykonania:

1. Wyznaczyć rozkład współczynnika ciśnienia C

P

(lub rozkład na profilu

ćwiczeniowym

2. Na podstawie otrzymanych wyników pomiaru wyznaczyć siłę oporu ciśnieniowego
N

H

oraz współczynnik oporu ciśnieniowego c

xp.

Średnica profilu ćwiczeniowego 2R=10 [cm]
Ciśnienie dynamiczne

:

.........

025

,

0

2

1









P

z

g

q



;

..........

025

,

0

1

0

0

1

0



















P

P

z

g

p

p

p



;

1

0





P

z

-

wysokość słupa cieczy manometru odpowiadająca różnicy ciśnienia

atmosferycznego i ciśnienia statycznego sekcji testowej.

2

1





P

z

- różnica wysokości słupa cieczy manometrycznej odpowiadająca różnicy

ciśnień wskazywanej przez rurkę Prandtla.

Tabela ćwiczeniowa:

Lp.

β

[°]

z



[cale]

1

0

025

,

0

)

(















P

p

z

g

p

p





[Pa]

q

p

p

C

P







)

(



r=Rsin β

[m]



2

sin

4

1





e

PTeoretycn

C

1.

2.

3.

4.

5.

6.

Państwowa Wyższa Szkoła Zawodowa w Chełmie

Laboratorium

Mechaniki Płynów

Laboratorium mechaniki płynów, ćwiczenie nr 3

Temat ćwiczenia: „Pomiar oporu ciśnieniowego profilu kołowego”

Imię i nazwisko

Grupa

Semestr/rok akademicki

Prowadzący

Data wykonania ćwiczenia/godz.

Ocena

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.