Analityka Medyczna zaliczenie wykładów z Biofizyki. Wersja A

Łącznie 33 pkt.

4 styczeń 2012 r.

1. (1 pkt.) Wyjaśnij pojęcie: podstawowa wielkość fizyczna.

Podstawowe wielkości fizyczne tworzą zbiór wzajemnie niezależnych wielkości fizycznych za pomocą któ-
rych oraz przy pomocy odpowiednich wzorów definicyjnych można zdefiniować wszystkie pozostałe wielko-
ści fizyczne.

2. (2 pkt.) Wyraź opór naczyniowy





3

kPa s

2,5

dm

w



3

Pa s

.

m

Obliczenia krok po kroku.





















6

3

1

3

3

kPa s

1000Pa s

Pa s

2,5

2,5

2,5 10

dm

(10 m)

m

. Po 1 pkt za zamianę jednostek i 1 pkt za wynik.

3. (5 pkt.) Oblicz hematokryt Φ























gdzie

krwinek

krwi

V

Φ

V

krwi, jeżeli wiadomo, że objętość krwinek wynosi

(39  5) m, a objętość krwi ma wartość (97  7) cm

3

(1 pkt). Oblicz błąd pomiaru hematokrytu metodą

logarytmiczną (obliczenia wykonaj krok po kroku: wzór na błąd pomiaru 1 pkt, obliczenie błędu – pra-
widłowe zaokrąglanie wyników pośrednich i dobry wynik 1 pkt, zaokrąglenie błędu 1 pkt, zaokrąglenie
wyniku i zapis końcowy wyniku 1 pkt).











3

3

(39

5)cm ,

(97

7)cm oraz

krwinek

krwinek

krwi

krwi

V

V

V

Φ

V

(1 pkt) Zatem:











  

 











Δ

Δ

Δ

krwinek

krwi

krwinek

krwi

V

V

Φ

Φ

V

V

(1 pkt)











 



 

 





 















5

7

Δ

0,402

0,402 0,128

0,0722

0,0805

39

97

Φ

(1 pkt)

Zaokrąglenie błędu

 

Δ

0,081

Φ

(1 pkt) zaokrąglenie wyniku





0,402061

0,402

Φ

i zapis wyniku





(0,402

0,081).

Φ

(1 pkt).

4. (3 pkt.) Jakich trzeba użyć podstawień, aby zlinearyzować następująca zależność:  



2

5

10,

y

x

gdzie

zmienną niezależną jest x, a zmienną zależną y (1 pkt.). Narysuj wykres ilustrujący tę zależność w no-
wym układzie współrzędnych (1 pkt.). Jaką wartość ma współczynnik kierunkowy uzyskanej linii w tym
nowym układzie współrzędnych (1 pkt).

Właściwe podstawienie, to 

Y

y oraz 

2

X

x 1 pkt. z podstawienie.

2

Zadanie 4. (1 pkt. za poprawny rysunek opis osi i początek wykresu).

Współczynnik kierunkowy jest równy

 5

k

(1 pkt).

5. (3 pkt.) Substancje zmniejszające napięcie powierzchniowe wody – jak się nazywają i jakie posiadają

właściwości (2 pkt.). Dlaczego zmniejszają napięcie powierzchniowe wody (1 pkt.).

To surfaktanty. Są amfifilowe (mają jedną końcówkę hydrofobową i drugą hydrofilową) (2 pkt.).
Na powierzchni wody zakotwiczają się hydrofilowym zakończeniem, co zakłóca oddziaływani miedzy czą-
steczki wody i prowadzi o obniżenia napięci powierzchniowego (1 pkt.).

6. (3 pkt.) Dyfuzja – opisz na czym polega to zjawisko (1 pkt); podaj i objaśnij prawo Ficka (1 pkt); od cze-

go zależy wartość współczynnika dyfuzji (1 pkt.)?

Dyfuzja to spontaniczny, samoistny przepływ substancji z miejsca, gdzie jej stężenie jest większe do miejsca,

gdzie jest mniejsze (1 pkt). Prawo Ficka

  

Δ

Δ

Δ

Δ

n

c

D S

t

x

(1 pkt). Opis Δn liczba moli substancji rozpuszczonej

dyfundująca w czasie Δt przez powierzchnię S przy gradiencie stężenia

Δ
Δ

c
x

, D oznacza współczynnik dyfuzji

(5 pkt.). Współczynnik dyfuzji





  

6

k T

D

π η r

zależy od temperatury T, lepkości rozpuszczalnika η oraz pro-

mienia r cząsteczki rozpuszczonej (1 pkt.).

7. (2 pkt.) Oblicz wartość współczynnika dyfuzji rozpuszczonych w cieczy cząsteczek, których średnia dro-

ga swobodna w tej cieczy wynosi 0,03 nm, a ich średnia prędkość w danej temperaturze wynosi
10

4

cm/s. Wzór (1 pkt), przeliczenie jednostek, obliczenia i odpowiedź (1 pkt).

Wzór



  

1

3

D

v

(1 pkt), przeliczenie jednostek 10

4

cm/s = 100 m/s, obliczenia, 0,03 nm = 3·10

−11

m:







   

 





2

11

9

1

1

m

100 3 10

10

3

3

s

D

v

(1 pkt).

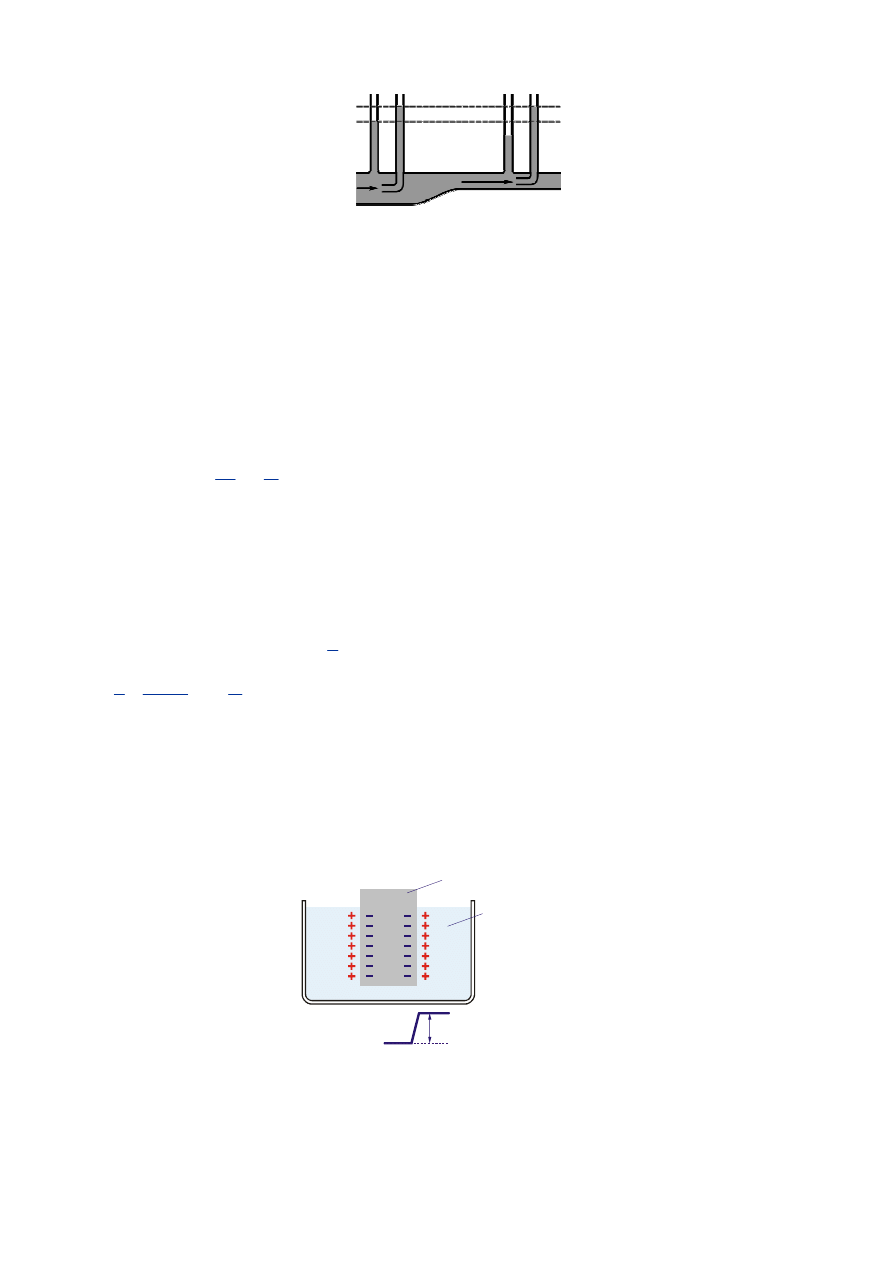
8. (2 pkt.) W naczyniu pokazanym na rysunku płynie ciecz doskonała w kierunku zaznaczonym strzałkami.

Wyjaśnij w oparciu o prawo Bernoullego (napisz i objaśnij to prawo 1 pkt), dlaczego poziomy cieczy
w rurkach 2 i 4 są takie same? (1 pkt).

y

x

2

0

3

Rysunek do zadania 8.

Prawo to mówi, że ciśnienie całkowite jest stałe w każdym miejscu naczynia (1 pkt), w którym płynie ciecz
doskonała. Rurki 2 i 4 pokazują ciśnienia całkowite, stąd poziomy cieczy są w nich jednakowe (1 pkt).

9. (3 pkt.) Ciśnienie tętnicze krwi – zmierzone w tętnicy promieniowej młodego i zdrowego człowieka –

waha się w granicach od 80 mmHg do 120 mmHg; wyraź ciśnienie skurczowe tego człowieka w jed-
nostkach układu SI (gęstość rtęci jest równa 13,6 g/cm

3

, przyspieszenie grawitacyjne 10 m/s

2

). Wzór

i przeliczenie danych (2 pkt), wynik (1 pkt)

   







3

2

kg

m

13600

10

0,120 m 16320 Pa

m

s

p

ρ g h

wzór (1 pkt), przeliczenie odpowiednich (1 pkt) danych

(1 pkt), wynik i jednostka (1 pkt).

10. (2 pkt.) Wypadkowa wartość biernych sił sprężystych w ściankach naczynia krwionośnego o promieniu

R = 3 mm i długości  równej 12 cm ma wartość F = 9 N. Oblicz napięcie sprężyste w ścianach naczynia.

Napięcie sprężyste definiujemy

F

T 



(1 pkt). Zatem napięcie sprężyste wynosi w tym wypadku

 





9N

N

75

0,12m

m

F

T

(przeliczenie i wynik 1 pkt.).

11. (4 pkt.) Potencjał elektrodowy – co to jest (1 pkt)? Jak powstaje w przypadku metali nieszlachetnych

(2 pkt.)? Wzór na jego wartość i opis (1 pkt).

Płytka wykonana z metalu Me zanurzona w roztworze zawierającym jony tego metalu Me

+z

stanowi tzw.

elektrodę (rys.).

Zadanie 11.

Wartość potencjału elektrodowego ΔV

e

to różnica potencjałów pomiędzy metalem i roztworem (1 pkt):





Δ

.

e

Me

J

V

V

V

V

Me

ΔV

e

V

j

Me

roztwór zawierający
jony metalu Me

+z

elektroda z metalu Me

1

2

3

4

4

Po zanurzeniu metalu w roztworze jego jonów, atomy metalu o dużej prężności roztwórczej (metale nieszla-
chetne, np. potasowce, wapniowce, Zn) utleniają się, a powstałe jony (kationy) metalu dyfundują do roz-
tworu, pozostawiając w metalu swoje elektrony walencyjne. W rezultacie metal zaczyna ładować się ujem-
nie, a roztwór dodatnio.

Pojawiająca się różnica potencjałów zaczyna inicjować proces redukcji jonów Me

+z

zawartych w roztworze,

które skutek oddziaływań elektrostatycznych zaczynają osadzać się na powierzchni metalu.

Gdy różnica potencjałów osiągnie taką wartość, że oba procesy przebiegają z jednakową szybkością, to od
tego momentu wspominana różnica potencjałów nie ulega już zmianie. Istniejąca w tym stanie różnica po-
tencjałów elektrycznych pomiędzy metalem i roztworem nazywa się potencjałem elektrodowym ΔV

e

.

Procesy zachodzące wtedy na elektrodzie opisuje równanie:





 









utlenianie

z

redukcja

Me

Me

z e

gdzie: Me, Me

+z

− odpowiednio atom i kation metalu,

z

− wartościowość kationu,

e

−

− elektron.

W przypadku elektrody z metalu szlachetnego (o małej prężności roztwórczej, np. Cu, Ag, Au), na początku
po zanurzeniu płytki przeważa proces osadzania się kationów metalu roztworu na elektrodzie i ich redukcja
(przyłączanie elektronów walencyjnych) i ładowanie elektrody ładunkiem dodatnim, co sprzyja procesowi
utleniania atomów metalu i przechodzeniu jonów metalu do ujemnie naładowanego roztworu, tak długo aż
procesy nie osiągną tej samej szybkości. (2 pkt.)

Wartość potencjału elektrodowego ΔV

e

jest określona wzorem Nernsta:





 







0

Δ

Δ

ln

e

Me

J

j

R T

V

V

V

V

c

z F

gdzie: R

− stała gazowa,

T

− temperatura bezwzględna,

F

− stała Faradaya,

c

j

− stężenie kationów metalu w roztworze,

z

− wartościowość kationu,

ΔV

0

− potencjał standardowy elektrody, czyli potencjał elektrody zanurzonej w roztworze o stęże-

niu kationów równym 1 kmol/m

3

(1 pkt).

12. (3 pkt.) Co to jest potencjał spoczynkowy komórki (np. nerwowej) (1 pkt). Rozkład jonów Cl

−

wewnątrz

i na zewnątrz neuronu (0,5 pkt.); Określ kierunki transportu dyfuzyjnego (wywołanego różnicą stężeń),
elektrycznego (wywołanego różnicą potencjałów elektrycznych) i transportu aktywnego jonów chloru
w stanie spoczynku przez błonę komórki nerwowej (1,5 pkt.).

Potencjał spoczynkowy to różnica potencjałów pomiędzy wnętrzem komórki i jej zewnętrzem, gdy komórka
jest niepobudzona (1 pkt).

W tabeli zebrano wartości stężeń wybranych jonów wewnątrz, c

W

i na zewnątrz, c

Z

komórek mięśniowych

zwierząt stałocieplnych.

Rodzaj jonów

c

W

mmol/

c

Z

mmol/

c

Z

/c

W

Na

+

12

145

12:1

K

+

155

4

1:39

Inne kationy

0

5

Cl

−

4

120

32:1

B

−

155

−

Inne aniony

8

34

1:4

5

Zmierzony potencjał spoczynkowy: −90 mV

Wystarczyło jednak podać, że chloru jest dużo w płynie śródkomórkowym, a mało w cytoplazmie (0,5 pkt.).

Transport dyfuzyjny dokomórkowy (0,5 pkt.).

Transport elektryczny odkomórkowy (0,5 pkt.).

Transport aktywny bark (0,5 pkt.).