Analityka Medyczna zaliczenie wykładów z Biofizyki. Wersja B

Łącznie 33 pkt.

4 styczeń 2012 r.

1. (2 pkt.) Co to jest błąd systematyczny pomiaru? Co trzeba zrobić, aby rozstrzygnąć, czy dany pomiar

obarczony jest błędem systematycznym? (1 pkt) W jaki sposób można oszacować wartość błędu sys-
tematycznego (1 pkt)?

Błąd systematyczny to ciągły, o stałym nasileniu błąd pomiaru.

Jeżeli kilkukrotnie, w tych samych warunkach wykona się pomiar tej samej wielkości fizycznej i jeśli otrzy-
mane wyniki nie różnią się od siebie o więcej niż błąd wskazania przyrządu pomiarowego, to w takim przy-
padku mówimy o błędzie systematycznym (1 pkt).

Najważniejszym jego składnikiem jest błąd wskazania przyrządu pomiarowego, pozostałe jego składniki
trudno jest oszacować. Trzeba analizować wpływ każdego kroku pomiarowego na wynik. Często okazuje się,
że błąd wskazania jest dojmujący i on stanowi zasadniczy składnik błędu systematycznego (1 pkt).

2. (2 pkt.) Zaokrąglij prawidłowo błąd pomiaru (1 pkt) i zmierzoną wartość (1 pkt), wyjaśniając zasady za-

okrąglania: A = 2,8963698276598 [A] i ΔA = ±0,08978967 [A].

Błąd zaokrąglamy do pierwszej cyfry znaczącej do góry (chyba, że..) ΔA = ±0,09 [A] (1 pkt).

Wynik zaokrąglamy do ostatniego miejsca dziesiętnego błędu, tutaj setnych, czyli A = 2,90 [A] (1 pkt).

3. (5 pkt.) Oblicz stałą naczynia pomiarowego C służącego do pomiaru przewodności elektrycznej krwi,

jeżeli wiadomo, że ciecz wzorcowa ma przewodność właściwą γ = (0,74  0,07) 

−1



m

−1

, a jej opór

równa się R = (260  5) , przy czym C = γ·R (1 pkt). Wymień metody szacowania błędu wielkości zło-
żonej (1 pkt). Jedną z nich, krok po kroku (nazwa metody, odpowiedni wzór/wzory lub bez wzoru, ra-
chunki (2 pkt.), końcowy zapis błędu i wyniku (1 pkt)) oszacuj błąd pomiaru stałej naczynia pomiaro-
wego w rozpatrywanym przypadku.

Wartość

1

1

0,74

260 Ω

192,4

Ω m

m

C

γ R

  







(1 pkt).

Metody: (a) liczba cyfr znaczących, (b) najmniej korzystnego przypadku i (c) metoda logarytmiczna (1 pkt)

Metoda logarytmiczna:

Δ

Δ

Δ

γ

R

C

C

γ

R









  



















1

7

5

1

1

1

Δ

192

192

0,0946

0,0192

192

0,114

21,9

m

74

260

m

m

m

C







 





 





 



 















Ostatecznie

1

Δ

22

m

C  

(za wzór i obliczenia 2 pkt.)

Końcowy zapis:

1

(192

22)

m

C 



(1 pkt).

2

4. (3 pkt.) Jakich trzeba użyć podstawień, aby zlinearyzować następująca zależność:  



5 e

10,

x

y

gdzie

zmienną niezależną jest x, a zmienną zależną y (1 pkt.). Narysuj wykres ilustrujący tę zależność w no-
wym układzie współrzędnych (1 pkt.). Jaką wartość ma współczynnik kierunkowy uzyskanej linii w tym
nowym układzie współrzędnych (1 pkt).

Właściwe podstawienie, to 

Y

y oraz

e

x

X 

1 pkt. z podstawienie.

Zadanie 4. (1 pkt. za poprawny rysunek opis osi i początek wykresu).

Współczynnik kierunkowy jest równy

 5

k

(1 pkt).

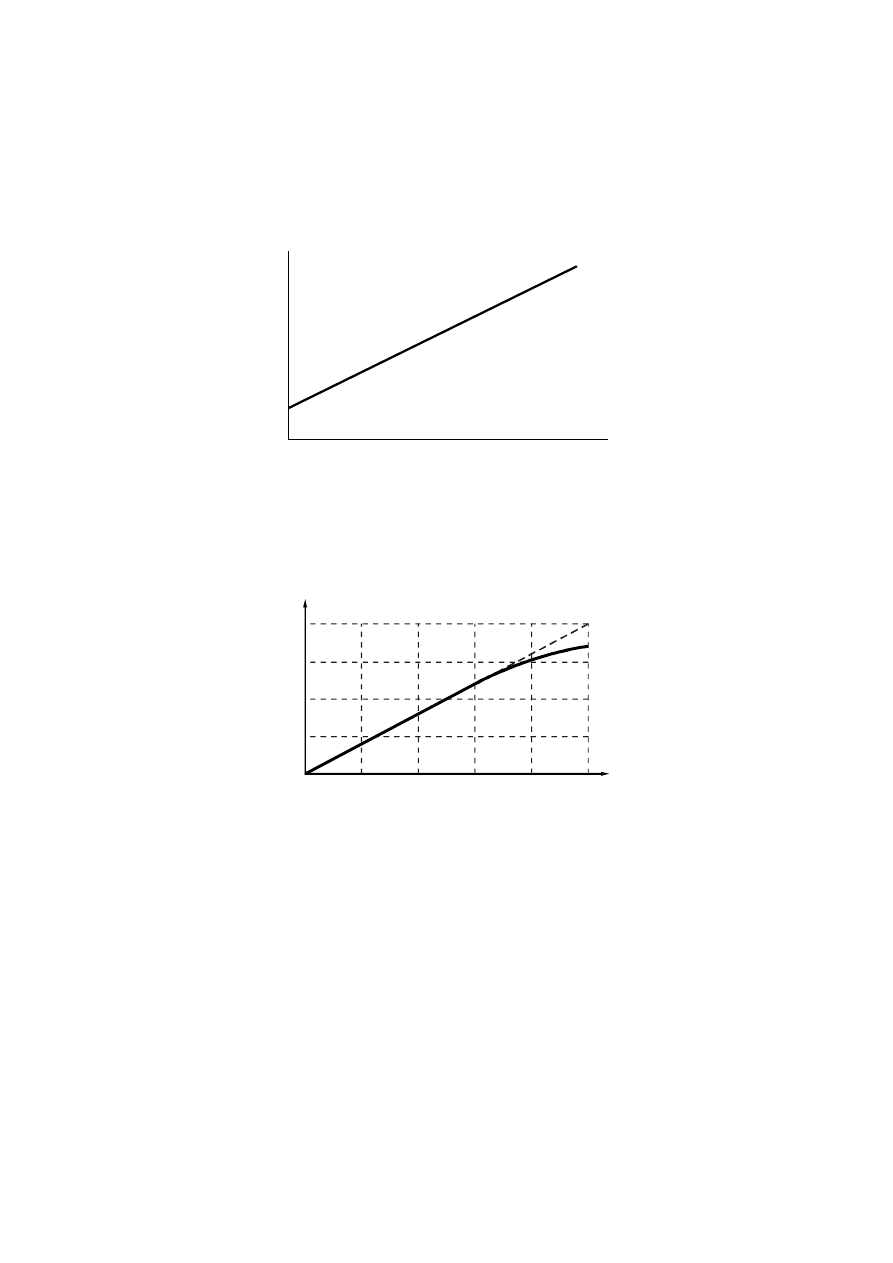
5. (2 pkt.) Na rysunku pokazano wykres zależności szybkości dyfuzji od stężenia.

Czy badany proces był zgodny jest z prawem Ficka w całym zakresie zmian gradientu stężenia? Odpo-
wiedź uzasadnij (1 pkt).

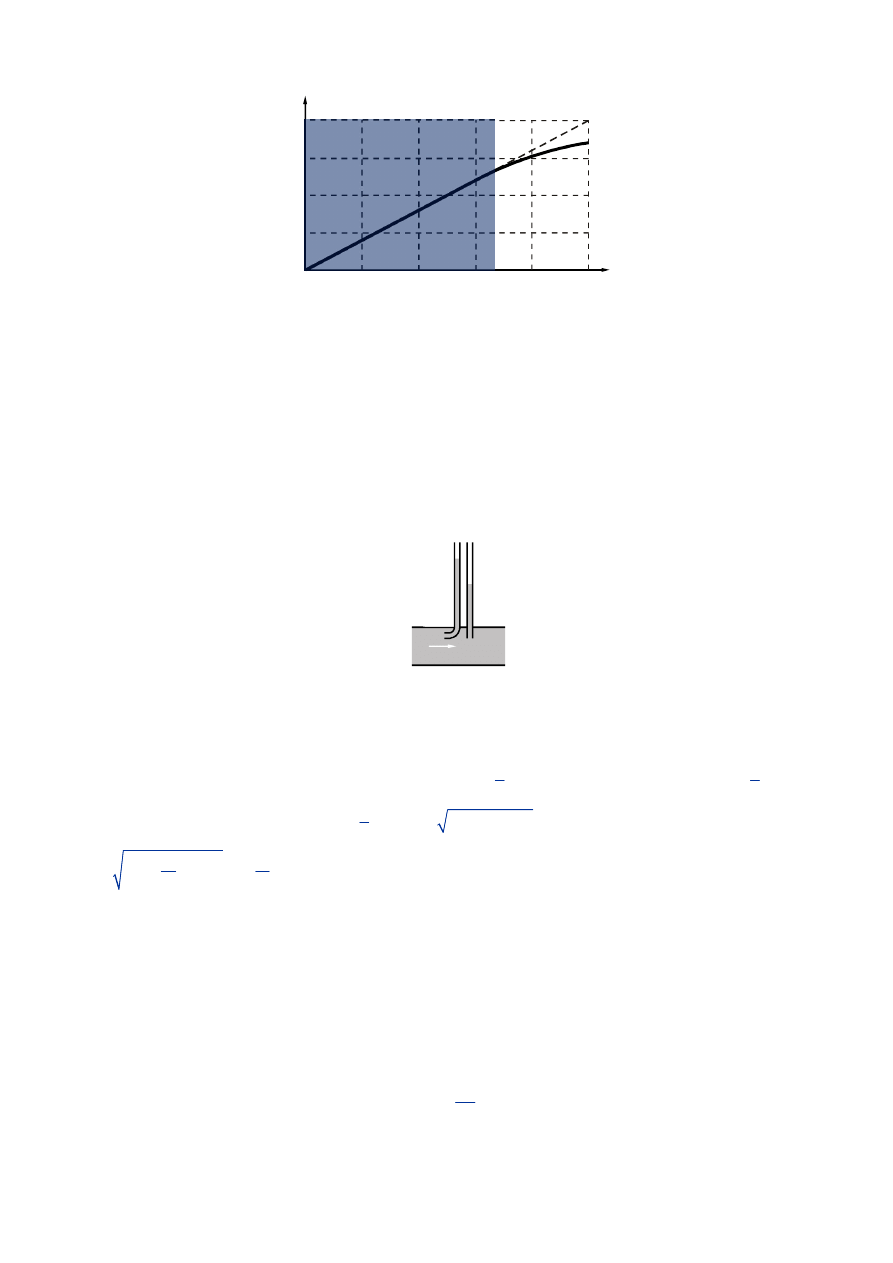
Jeśli nie był, to w jakim zakresie zmian gradientu stężenia było spełnione prawo Ficka? (zaznacz na ry-
sunku) (0,5 pkt.)
Zaznacz w jakim zakresie gradientu stężenia współczynnik dyfuzji był stały? (zaznacz na rysunku) (0,5
pkt.)

Nie był, ponieważ nie w całym zakresie gradientów stężenia szybkość dyfuzji była wprost proporcjonalna do
gradientu stężenia (wykres nie w całym zakresie gradientu stężeń jest liniowy) (1 pkt).
Poniżej zaznaczono zakres te zakresy (są one takie same) (1 pkt).

y

e

x

0

0

sz

yb

ko

ść

d

yf

u

zj

i

gradient stężenia

3

6. (2 pkt.) Wymień funkcje jakie pełni w naszym organizmie układ krążenia.

Są to funkcje transportowe; krew transportuje substancje pokarmowe i tlen do miejsc zapotrzebowania
i odprowadza produkty przemiany materii, dwutlenek węgla i ciepło. Ponadto przenosi hormony, enzymy,
jony i przeciwciała. (2 pkt.)

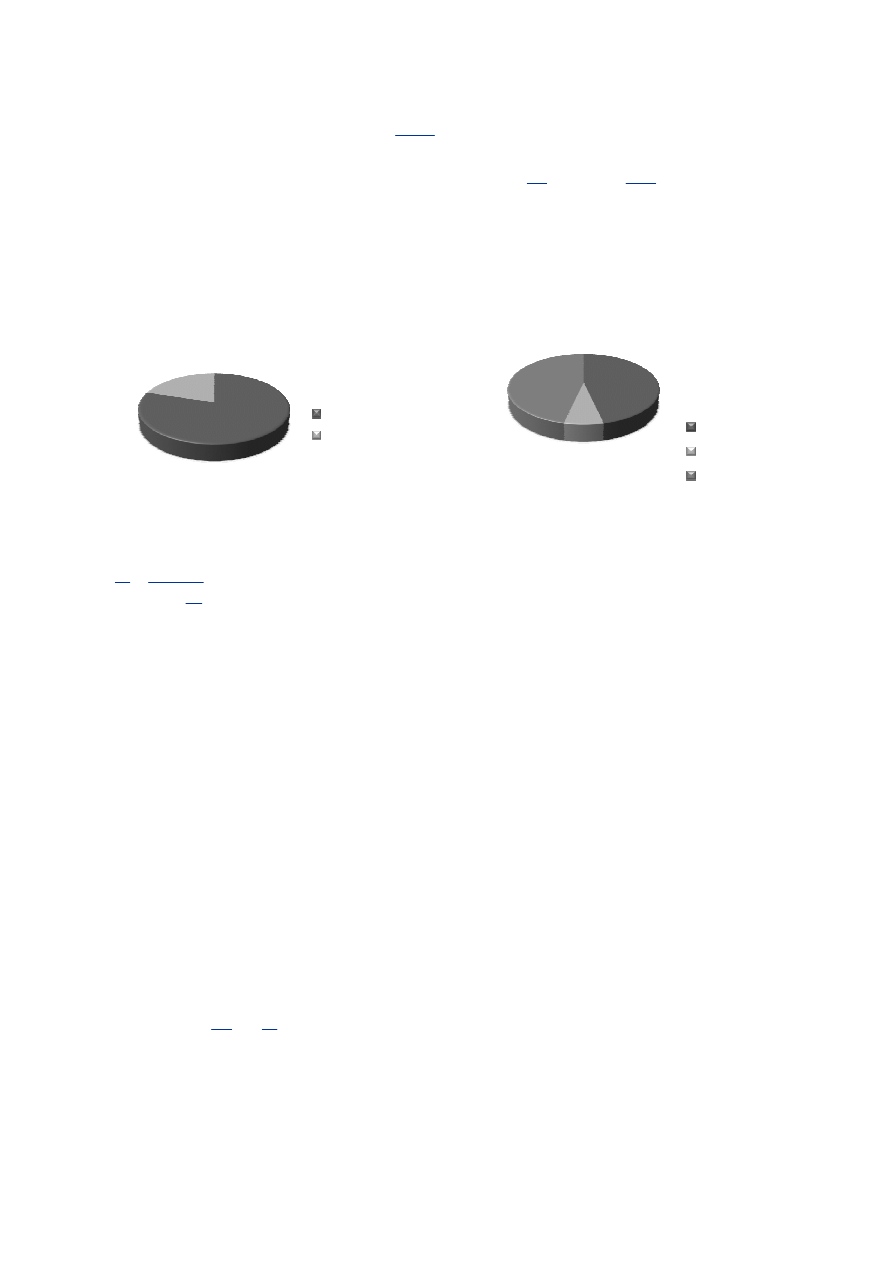
7. (3 pkt.) Rysunek ilustruje fragment układu hydraulicznego, w którym płynie ciecz nielepka (doskonała).

Niech h

1

wynosi 60 cm, a h

2

- 40 cm, a przyspieszenie grawitacyjne 10 m/s

2

. Oblicz prędkość v przepły-

wu cieczy.

Rysunek do zadania 7.

Manometr 1 wskazuje ciśnienie całkowite

1

,

c

p

ρ g h

  

a 2 – statyczne

2

.

s

p

ρ g h

  

(1 pkt.). Różnica tych

ciśnień





1

2

c

s

p

p

ρ g h

h

   



to ciśnienie dynamiczne

2

1

,

2

d

p

ρ v



 

(1 pkt) czyli:





2

1

2

1

.

2

ρ g h

h

ρ v

 





 

Po przekształceniu mamy:









2

1

2

1

2

1

2

2

g h

h

v

v

g h

h







  

 



2

m

m

2 10

0,2 m

2

s

s

v 







(1 pkt)

8. (4 pkt.) Prawo Hagena-Poiseuille'a – kiedy jest spełnione, co ono głosi (1 pkt)? Zdefiniuj opór naczy-

niowy (1 pkt), wyjaśnij, od jakich wielkości fizycznych on zależy (1 pkt), jaka jest jego jednostka miary
w układzie SI (1pkt)?

Prawo Hagena-Poiseuille'a mówi, że jeśli w sztywnym cylindrycznym naczyniu płynie laminarnie lepka i nie-
ściśliwa ciecz to strumień objętości Q płynącej cieczy jest wprost proporcjonalny do różnicy ciśnień Δp na
końcach rurki

Δ .

Q

p



(1 pkt).

Opór naczyniowy R zdefiniowany jest następująco:

Δ

.

p

R

Q



( 1pkt)

0

sz

yb

ko

ść

d

yf

u

zj

i

gradient stężenia

h

2

h

1

v

4

W przypadku cylindrycznej o promieniu r, sztywnej rurki o długości , w której laminarnie płynie ciecz o lep-

kości η, jej opór naczyniowy wyraża wzór:

4

8

.

η

R

π r

 







(1 pkt).

Z definicji oporu naczyniowego wynika jego jednostka miary:

3

Δ

Pa s

[ ]

.

m

p

R

R

Q









( 1pkt)

9. (4 pkt.) Oblicz objętość krwi zgromadzonej w żyłach małego krążenia u człowieka o masie 65 kg. Załóż,

że 7% masy człowieka stanowi masa krwi, a jej gęstość ma wartość 1060 kg/m

3

. Wykorzystaj dane z

poniższego diagramu.

Rozkład krwi w krążeniu.

Rozkład krwi w krążeniu płucnym

Masa krwi ma wartość:

65 kg 0,07

4,55 kg

m 





(1 pkt), jej objętość obliczymy ze wzoru:

4,55 kg

4,29

kg

1,06

m

V

d











(1 pkt).

Z diagramów wynika, ze w małym krążeniu jest 20% krwi z czego w jego żyłach (100 – 46 – 7 = 47) 47%, za-
tem w żyłach małego krążenia objętość krwi wynosi:

4,29 0,2 0,47

0,403

żmk

V











 (2 pkt.).

10. (2 pkt.) Jaka wielkość fizyczna jest taka sama w równolegle połączonych oporach naczyniowych R

1

i R

2

?

Jak można obliczyć zastępczy opór naczyniowy w przypadku równolegle połączonych naczyń o oporach
R

1

i R

2

?

Gdy opory włączone są równoległe, to przez każdy z nich płynie strumień cieczy (zazwyczaj różny), ale pod wpływem tej
samej różnicy ciśnień, a odwrotność ich oporu zastępczego jest równa sumie odwrotności oporów w ten sposób połą-
czonych. (2 pkt.)

11. (2 pkt.) Średnie ciśnienie, ponad ciśnienie atmosferyczne, krwi w aorcie jest równe 13,5 kPa, gęstość

krwi wynosi 1080 kg/m

3

. Oblicz ciśnienie krwi w tętnicy głowy na wysokości 60 cm ponad sercem. Ci-

śnienie atmosferyczne wynosi 1013 hPa, przyspieszenie grawitacyjne 10 m/s

2

.

Ciśnienie w tętnicy głowy jest mniejsze od ciśnienia w aorcie o ciśnienie hydrostatyczne słupa krwi o wyso-
kości 0,6 m, czyli:

3

2

kg

m

1080

10

0,6 m

6480 Pa.

m

s

p

d g h

   







(1 pkt)

Zatem jego wartość jest o

13500 Pa 6480 Pa

7020 Pa





wyższe od ciśnienia atmosferycznego. (1 pkt).

12. (2 pkt.) Ruchliwość jonów: definicja i od czego zależy jej wartość?

80%

Obwodowe
Płucne

7%

46%

Układ tętniczy

Kapilary

Układ żylny

5

Prędkości unoszenia v, czyli szybkość z jaką jony przemieszczają się pod wpływem pola elektrycznego o natę-
żenia E, (nie mieszać z szybkością z jaką te jony się poruszają) jest wprost proporcjonalna do wartości natę-
żenia tego pola, a stosunek tych wielkości nazywa się ruchliwością u:

.

v

u

E



(1 pkt)

Wg wzoru Einsteina:

6

q

u

π r η



  

ruchliwość u cząstki zależy od jej ładunku q, promienia r i lepkości środowiska η. (1 pkt).
Jeśli skojarzyć ten wzór z wzorem Einsteina-Stokesa dotyczącym współczynnika dyfuzji D, to otrzymamy:

,

B

k T

D

u

q



 

gdzie oznaczenia są nam już znane