Ćwiczenie 3

Modelowanie implantów - endoprotez stawu biodrowego

Cel

ćwiczenia: analiza charakterystyki odkształceniowo-naprężeniowej trzpieni endoprotez

wykonanych z różnych materiałów z wykorzystaniem modelu numerycznego (MES).

Alloplastyka stawu biodrowego należy do dość powszechnie przeprowadzanych

operacji. Każdego roku na świecie wykonuje się ok. 800 tys. implantacji endoprotez, w Polsce
wartość ta wynosi ok. 15 tys. Ze względu na zwiększającą się urazowość życia, rośnie liczba
stosowanych endoprotez u ludzi młodych. Jednak pomimo wielu nowych rozwiązań
konstrukcyjnych, wciąż niejednokrotnie dochodzi do różnorakich powikłań pooperacyjnych
prowadzących do konieczności przeprowadzenia powtórnej operacji. Powikłania wynikają
przede wszystkim z braku powiązań kryteriów klinicznych z kryteriami biomechanicznymi.
Wciąż trwają poszukiwania nowych rozwiązań materiałowych i konstrukcyjnych w oparciu o
badania eksperymentalne prowadzone na modelach fizycznych, numerycznych, na
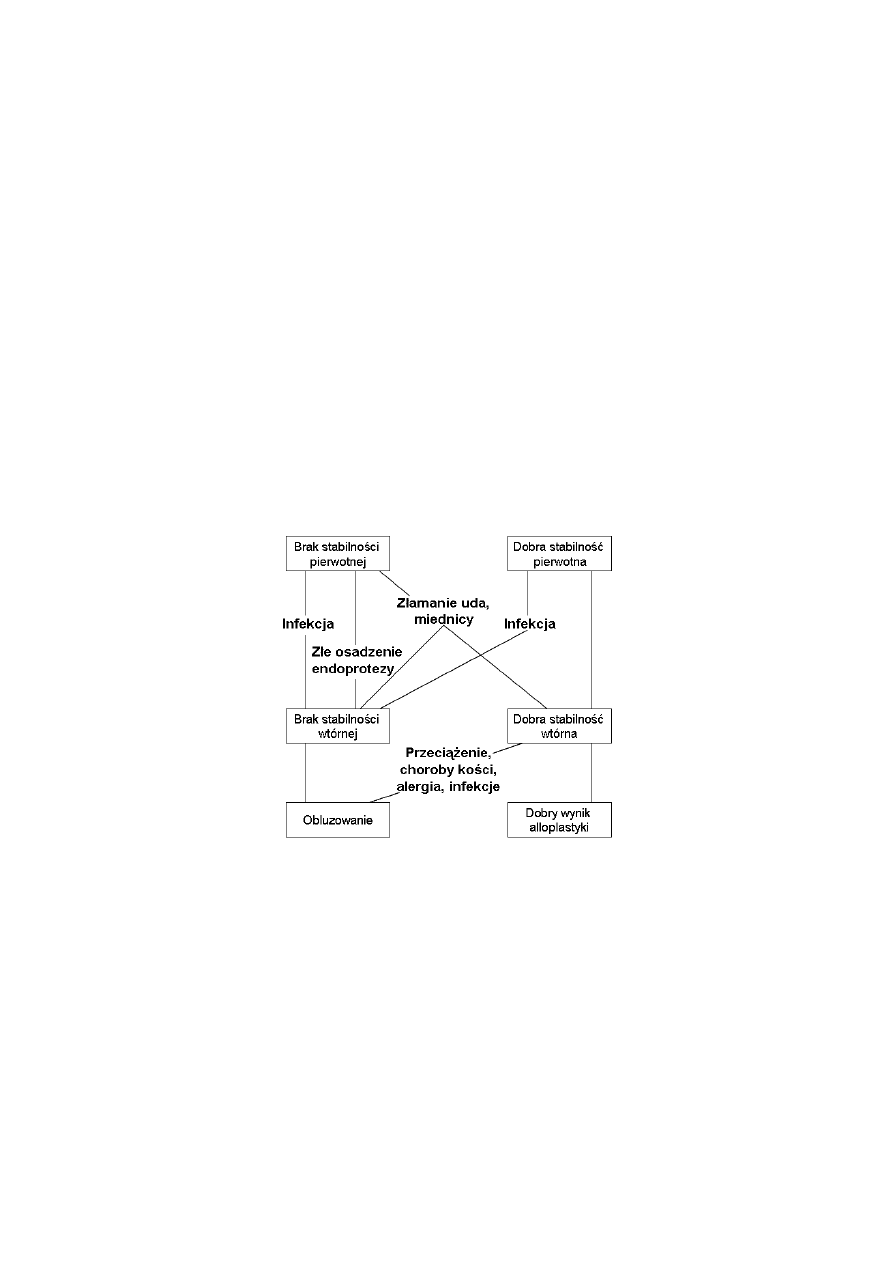
zwierzętach, a w końcowym etapie w badaniach klinicznych (Rys. 1.1). Badania numeryczne
pozwalają na określenie pełnych warunków biomechanicznej stabilności implantu, a przez to
na stworzenie podstaw fizycznych określających wybór danego rozwiązania endoprotezy.

Rys. 1.1 Kliniczne kryteria alloplastyki stawu biodrowego [2]

Budowa stawu biodrowego

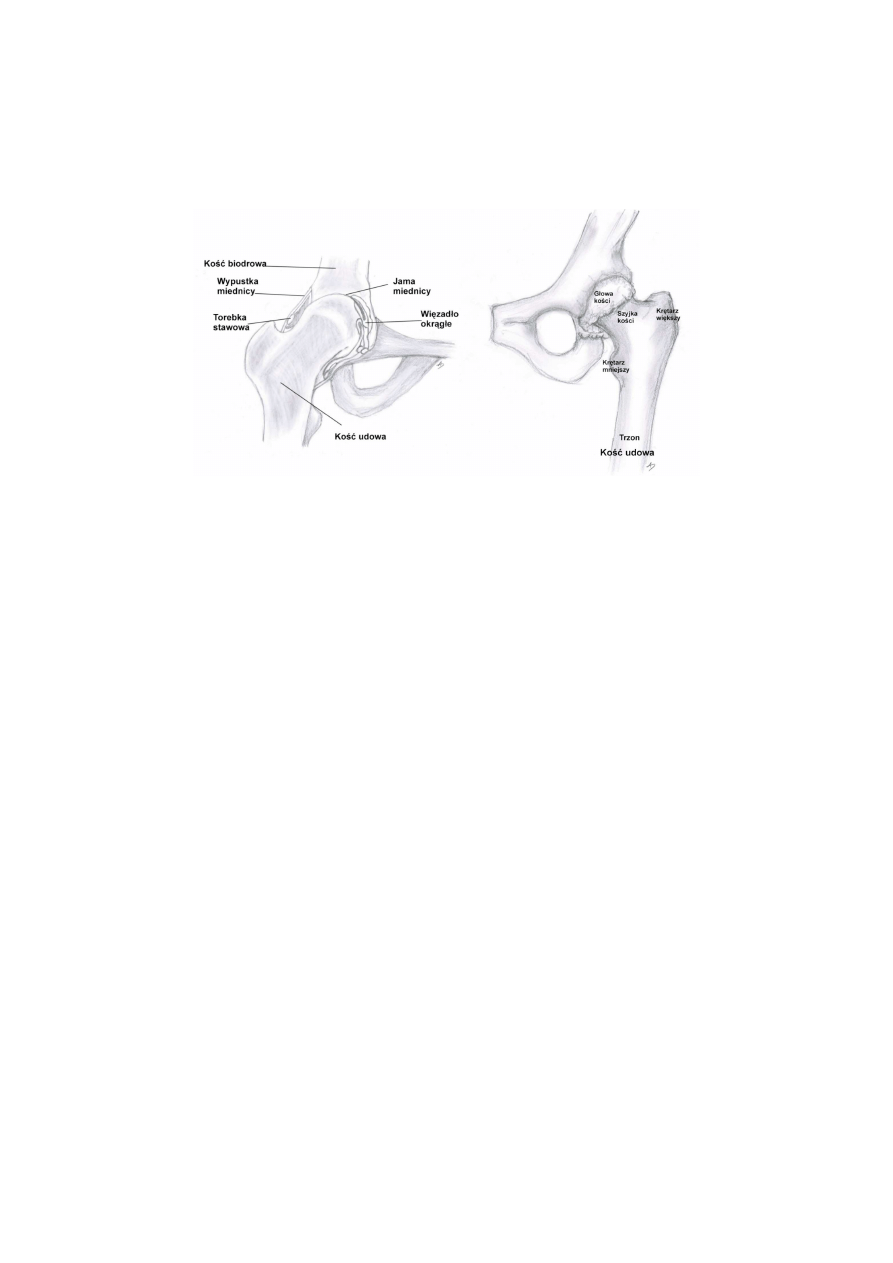
Staw biodrowy jest stawem kulistym panewkowatym złożonym z głowy kości udowej

i panewki stawowej (Rys. 1.2). Panewka stanowi półkoliste zagłębienie w kości miedniczej o
kształcie i wielkości odpowiadającym rozmiarom i kulistej budowie głowy kości udowej.
Skośnie ustawiona szyjka łączy głowę kości udowej z jej trzonem. Głowę kości udowej
pokrywa chrząstka o maksymalnej grubości w strefie obciążenia 3-4mm, a cały staw otacza
torebka stawowa. Chrząstka charakteryzuje się znaczną sprężystością i odpornością na
działanie obciążeń dynamicznych, dzięki czemu stanowi sprężystą ochronę kostnych części
stawu i umożliwia równomierny rozkład obciążeń na powierzchniach stawowych. Kość
udowa jest jednym z podstawowych elementów biorących udział w przenoszeniu obciążeń w
obrębie biodra (Rys. 1.2). Należy ona do kości długich. Nasada kości udowej zbudowana jest
z istoty gąbczastej i odpowiada za przenoszenie naprężeń ściskających i rozciągających.

Trzon kości udowej jest zbudowany z istoty zbitej, ma kształt rury wytrzymałej na obciążenia

osiowe i zginające, a jego wnętrze wypełnia szpik kostny.

Połączenie warstwy

powierzchniowej o wysokiej wytrzymałości i twardości ze sprężystością warstwy
wewnętrznej (istota gąbczasta) i miękkim szpikiem kostnym wypełniającym wnętrze rury
nadaje kości udowej efekt wysokiej wytrzymałości i sprężystości, równocześnie umożliwiając
tym samym przenoszenie wysokich naprężeń.

Rys. 1.2 Budowa stawu biodrowego i kości udowej

Staw biodrowy dzięki swojej budowie charakteryzuje się rozległą skalą ruchu. W

układzie trójosiowym do podstawowego zakresu ruchu stawu biodrowego zalicza się:
– zgięcie i wyprost w płaszczyźnie czołowej (osie poprzeczne);
– odwodzenie i przywodzenie kończyn w płaszczyźnie strzałkowej przednio-tylnej;
– przyśrodkową i zewnętrzną rotację w osi pionowej (długa oś kończyny podczas

wyprostu);

Staw biodrowy dzięki odpowiedniej budowie kostnych części stawu i ich współpracy ze
złożonym układem mięśni i więzadeł jest przystosowany do przenoszenia dużych obciążeń
statyczno-dynamicznych. Równocześnie jest on jednym z najbardziej eksploatowanych
stawów nośnych i w związku z tym jest w dużym stopniu narażony na zmiany
przeciążeniowo-zwyrodnieniowe.
Do najczęstszych przyczyn uszkodzeń stawu biodrowego należą zmiany zwyrodnieniowe,
zużycie się poszczególnych części stawu (głównie jako wynik tarcia) lub też w wyniku urazu.
Wartość i charakter powstających w kości udowej naprężeń i odkształceń zależy w dużym
stopniu od kształtu i ustawienia kości udowej w układzie kostnym człowieka. W anatomicznie
prawidłowo ukształtowanym stawie biodrowym dorosłego człowieka występują następujące
zależności:
– kąt

szyjkowo-trzonowy

wynosi

125-128°

(kąt

utworzony

przez

oś

szyjki

i trzonu kości udowej);

– kąt przodoskręcenia szyjki wynosi 12° (kąt zawarty między płaszczyzną szyjki i głowy a

płaszczyzną styczną do powierzchni tylnej obu kłykci kości udowej);

– zanurzenie głowy kości udowej w panewce wynosi 2/3 jej obwodu, a jej środek

odpowiada dokładnie środkowi panewki (zapewnia to kontakt obu powierzchni oraz
równomierny rozkład sił w obszarach przylegania głowy do dna i ścian panewki.

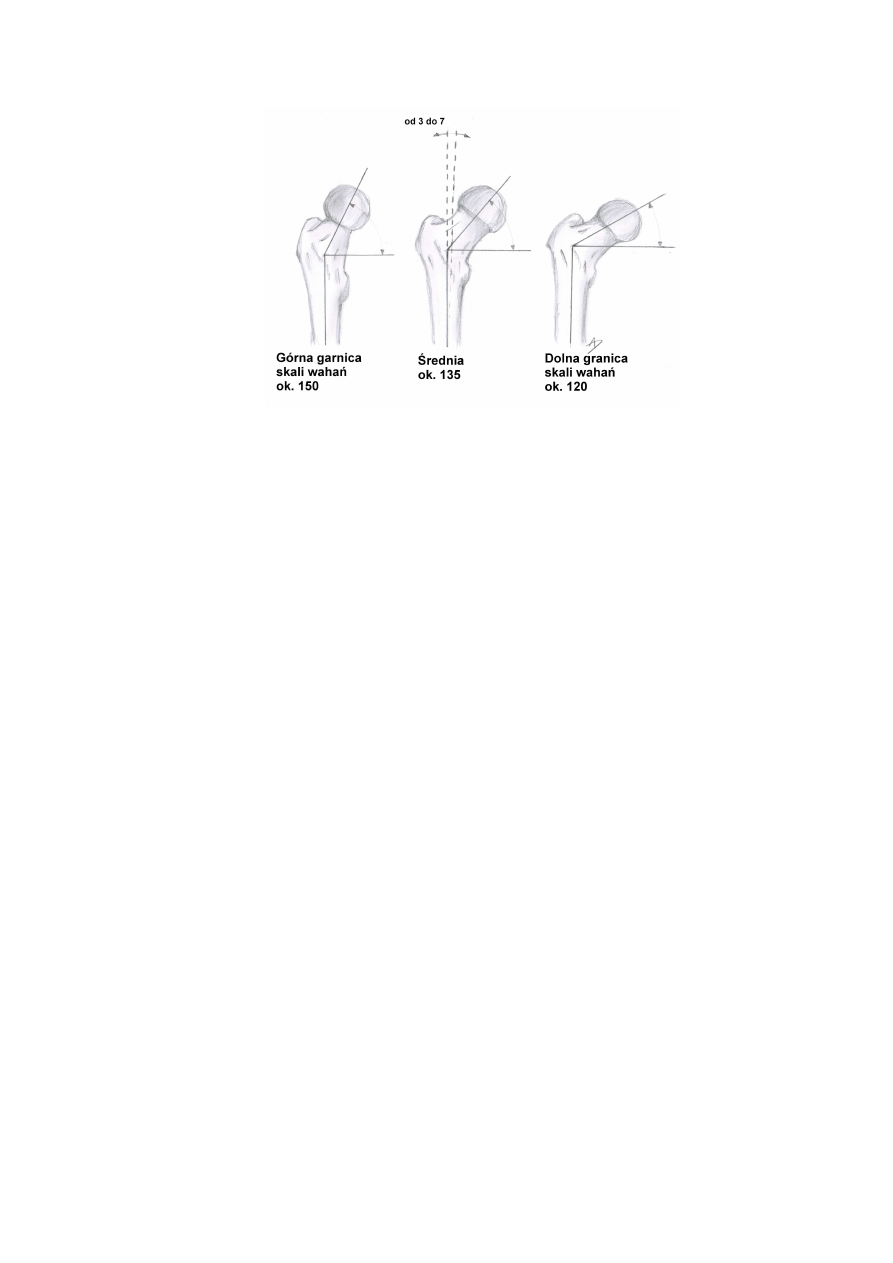
Rys. 1.3 Kąt szyjkowo-trzonowy kości udowej

Zmiany w obrębie kształtu kości udowej następują samoczynnie wraz ze wzrostem

człowieka. Kąt szyjkowo-trzonowy kształtuje się od 150° u noworodka, do 120° w wieku
starszym (Rys. 1.3). Podobnie kąt przodoskręcenia szyjki ulega zmianie, wzrastając wraz z
wiekiem od zerowego w okresie niemowlęcym. Wszelkie odchylenia od wartości podanych
kątów, bądź też niedorozwój panewki lub zniekształcenie głowy kości udowej oznaczają
zaburzenia zborności stawu. Jest to przyczyną pogorszenia warunków jego pracy, a tym
samym sprzyja rozwojowi zmian zwyrodnieniowych. W stanach chorobowych (np. krzywica,
zmiękczenie kości) kąt szyjkowo-trzonowy może ulegać zmianom w szerokim zakresie. Jeśli
ulega zmniejszeniu (nawet do 90º) mamy do czynienia z biodrem szpotawym, przy znacznym
zwiększeniu (strome ustawienie szyjki) mówi się o biodrze koślawym. Podobnie może
dochodzić do zaburzenia kąta przodoskręcenia szyjki, gdzie w przypadkach krańcowych
odchylenie do przodu osiąga wartość 37º, natomiast do tyłu 25º.

W przypadku zaawansowanych zmian zwyrodnieniowych stawu biodrowego,

uszkodzeń lub złamań w obrębie głowy lub szyjki kości udowej, niejednokrotnie, zwłaszcza
w podeszłym wieku, jedynym rozwiązaniem jest alloplastyka stawu biodrowego, tzn.
zastąpienie uszkodzonego stawu endoprotezą. Do najczęstszych i jednoznacznych wskazań do
alloplastyki stawu biodrowego należą:
– artroza główki;
– złamania kości;
– choroba nowotworowa;
– martwica kości;

Alloplastyka stawu biodrowego

Endoproteza stawu biodrowego jest implantem, który zastępuje częściowo

(endoproteza częściowa) lub całkowicie (endoproteza całkowita – łącznie z panewką)
zniszczony, naturalny staw biodrowy. Jej zadaniem jest przejęcie na stałe funkcji naturalnego
stawu, czyli przenoszenie ciężaru górnej części ciała z miednicy na kość kończyny dolnej
oraz zapewnienie kończynie dolnej pełnego zakresu ruchów. Budowę endoprotezy stawu
biodrowego wraz z podstawowymi parametrami wymiarowania endoprotez uwzględnianymi
przy ich projektowaniu przedstawia Rys. 1.4.

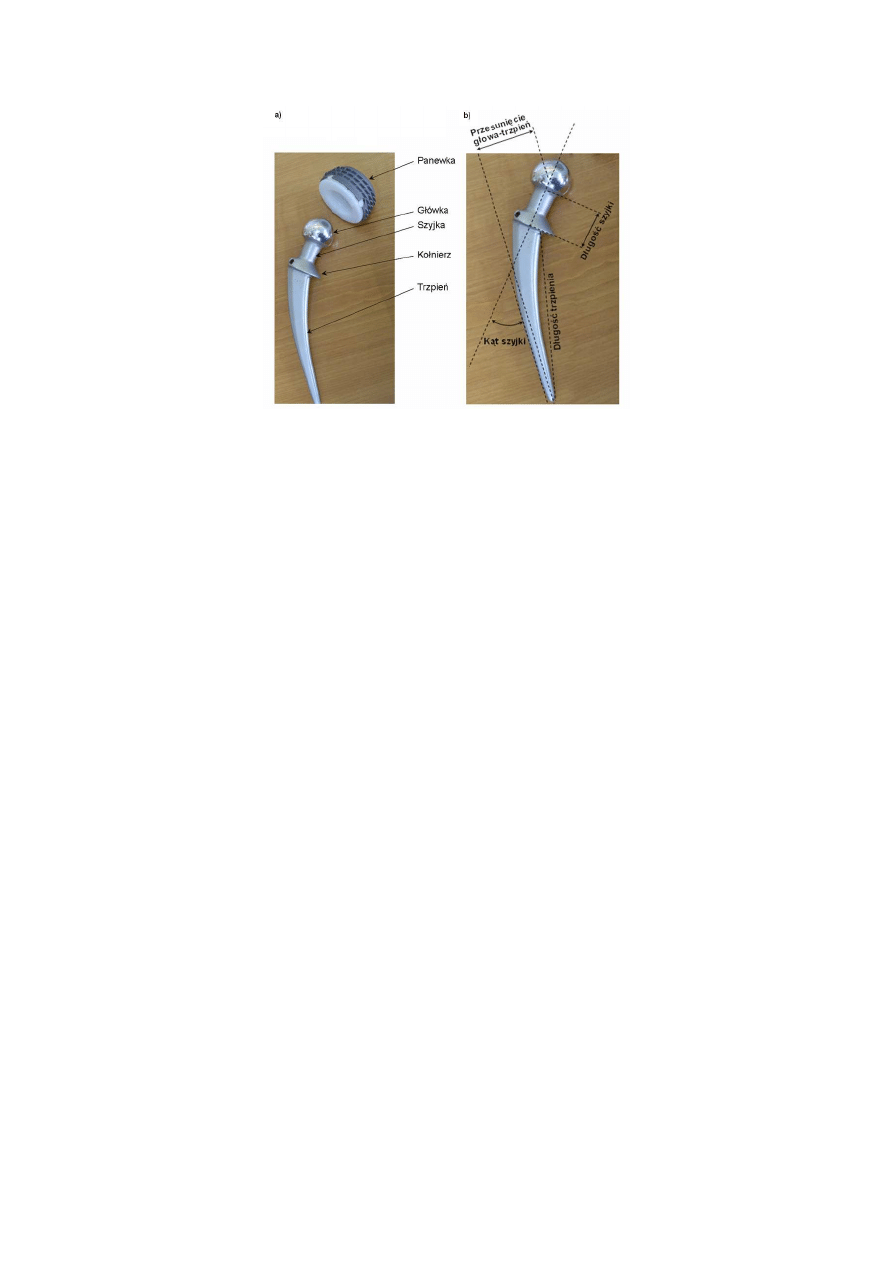
Rys. 1.4 Endoproteza stawu biodrowego: a) budowa, b) podstawowe parametry wymiarowania

Endoprotezoplastyka stawu biodrowego w pierwszym etapie polega na odcięciu i

usunięciu główki operowanej kości udowej. Następnie kanał kostny jest czyszczony i
kształtowany. Do tak przygotowanego kanału kostnego wprowadza się trzpień endoprotezy.
Jeśli schorzenie wymaga wszczepienia endoprotezy całkowitej przeprowadza się również
frezowanie panewki w miednicy i implantację panewki endoprotezy.

Poprawne funkcjonowanie endoprotezy jest możliwe pod warunkiem jej

odpowiedniego zamocowania w kości. Obluzowanie endoprotezy prowadzi do powikłań i
konieczności jej wymiany. Zasadniczym podziałem w alloplastyce, wynikającym ze sposobu
mocowania endoprotezy, jest rozróżnienie endoprotez cementowych i bezcementowych (Rys.
1.5). Wszczepienie endoprotez cementowych jest realizowane z zastosowaniem cementu
kostnego (PMMA). Polimeryzacja cementu PMMA zachodzi w ciele pacjenta (in situ).
Towarzyszy jej wzrost temperatury sprzyjający obumieraniu sąsiadujących tkanek, co stanowi
podstawowe ograniczenie tego typu cementu. Do wad cementu PMMA zalicza się także
możliwość depolimeryzacji oraz silniejszą więź na granicy kość-cement niż cement-implant,
co z kolei przy konieczności usunięcia endoprotezy utrudnia oczyszczenie tkanki kostnej z
cementu. Zastosowanie endoprotez bezcementowych pozwala na uniknięcie wymienionych
problemów. Trzpień w tym przypadku wprowadza się ciasno do kanału kostnego.
Stabilne zamocowanie implantu w kanale kostnym jest realizowane przez wytworzenie
uprzednio warstwy porowatej na całości lub części powierzchni trzpienia (wielkość porów
otwartych 100-200µm), bądź też przez naniesienie warstw bioaktywnych (hydroksyapatyt,
bioszkło), które umożliwiają przerośnięcie powierzchni endoprotezy przez tkankę kostną.
Stosuje się również różnego rodzaju profilowanie powierzchni trzpienia mające zapewnić
jego pierwotną stabilizację.

Ze względu na różnorodność rozwiązań konstrukcyjnych wyodrębnić można

również podział endoprotez na kołnierzowe i bezkołnierzowe. Obecność kołnierza ma
zabezpieczać przed wgłębianiem się endoprotezy do wnętrza trzonu kości udowej.
Przykładem endoprotezy kołnierzowej jest przedstawiona endoproteza Wellera (Rys. 1.4).
Stanowi ona starsze rozwiązanie jednak do dziś jest jedną z częściej wszczepianych
endoprotez w Polsce. Przykłady endoprotez bezkołnierzowych pokazuje Rys. 1.5, są to
endoprotezy typu Bi-Metric produkowane przez firmę Biomet. Od kilkunastu lat powszechnie
stosowane są również endoprotezy bezcementowe kołnierzowe Parchofera-Möncha i
Mittelmeiera. Nowszym rozwiązaniem firmy Aesculap są endoprotezy BiContact w wersji
cementowej i bezcementowej.

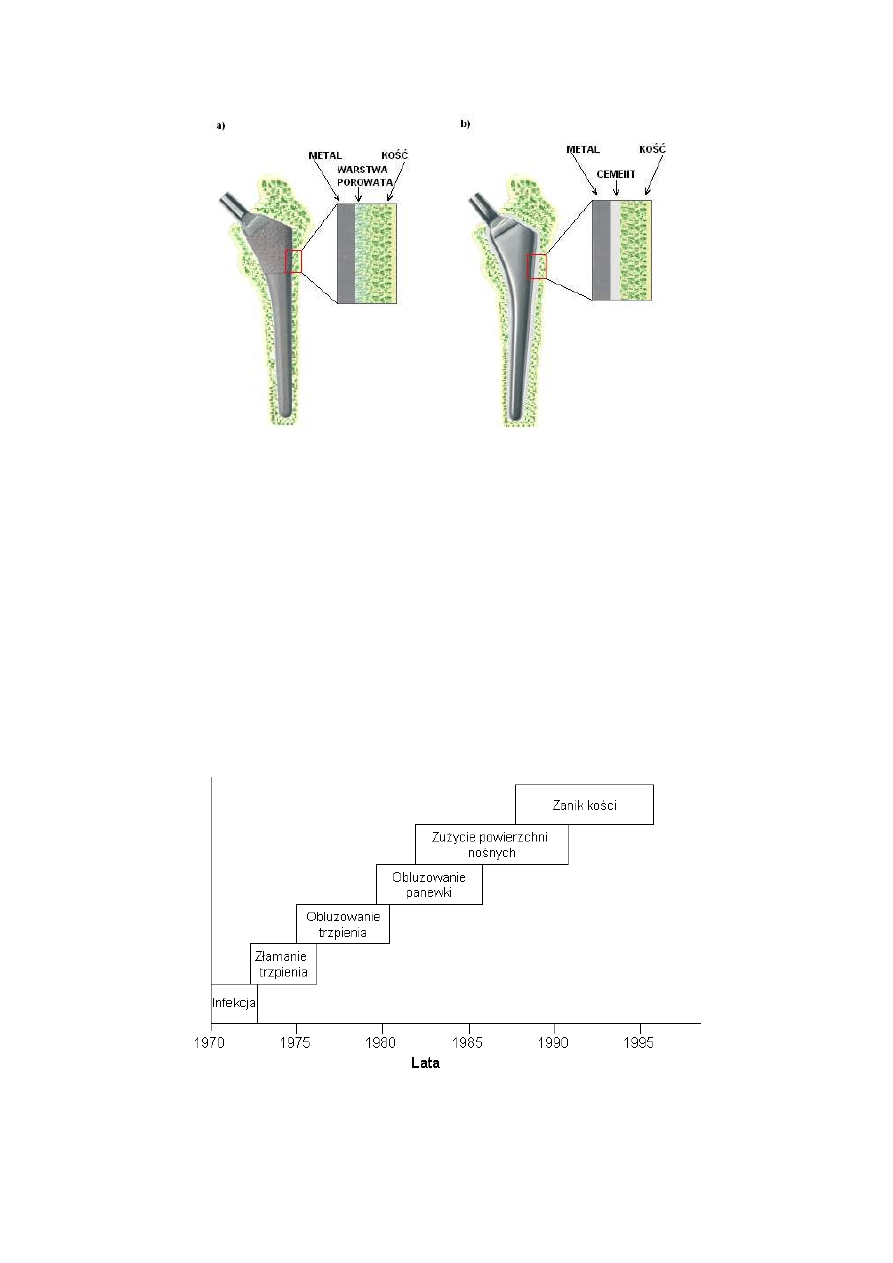
Rys. 1.5 Rodzaje endoprotez: a) bezcementowa z porowatym pokryciem, b) cementowa

Pierwotnie stosowane endoprotezy w całości wykonane były z jednego materiału.

Unowocześnieniem konstrukcji było oddzielne mocowanie główki, co ułatwia wszczepienie
implantu i poprawia jego trwałość. Materiały stosowane na główki endoprotez to stopy
metali, Al

2

O

3

, ZrO

2

. Najlepsze efekty przynosi zastosowanie główek ceramicznych, z uwagi

na wysoką gładkość i twardość materiału, zapewniające wysoką odporność na ścieranie.
Ś

cieralność polietylenowej panewki przez główkę metalową wynosi ok. 0,1mm w ciągu roku,

natomiast przez główkę ceramiczną poniżej 0,1mm. Na szybkość ścierania ma również
wpływ waga pacjenta, jego tryb życia oraz rodzaj polietylenu. Obecnie najbardziej oporny na
ś

cieranie jest polietylen nowej generacji typu "cross-linking". Dobrą parę trącą stanowią

również ceramiczna główka i ceramiczna panewka.

Intensywny rozwój endoprotezoplastyki rozpoczął się w latach 60-tych ubiegłego

stulecia od opracowania przez Charnleya endoprotezy całkowitej ze stopu Cr-Co-Mo.
Stopniowo pojawiały się nowe rozwiązania konstrukcyjne pozwalające na rozwiązanie
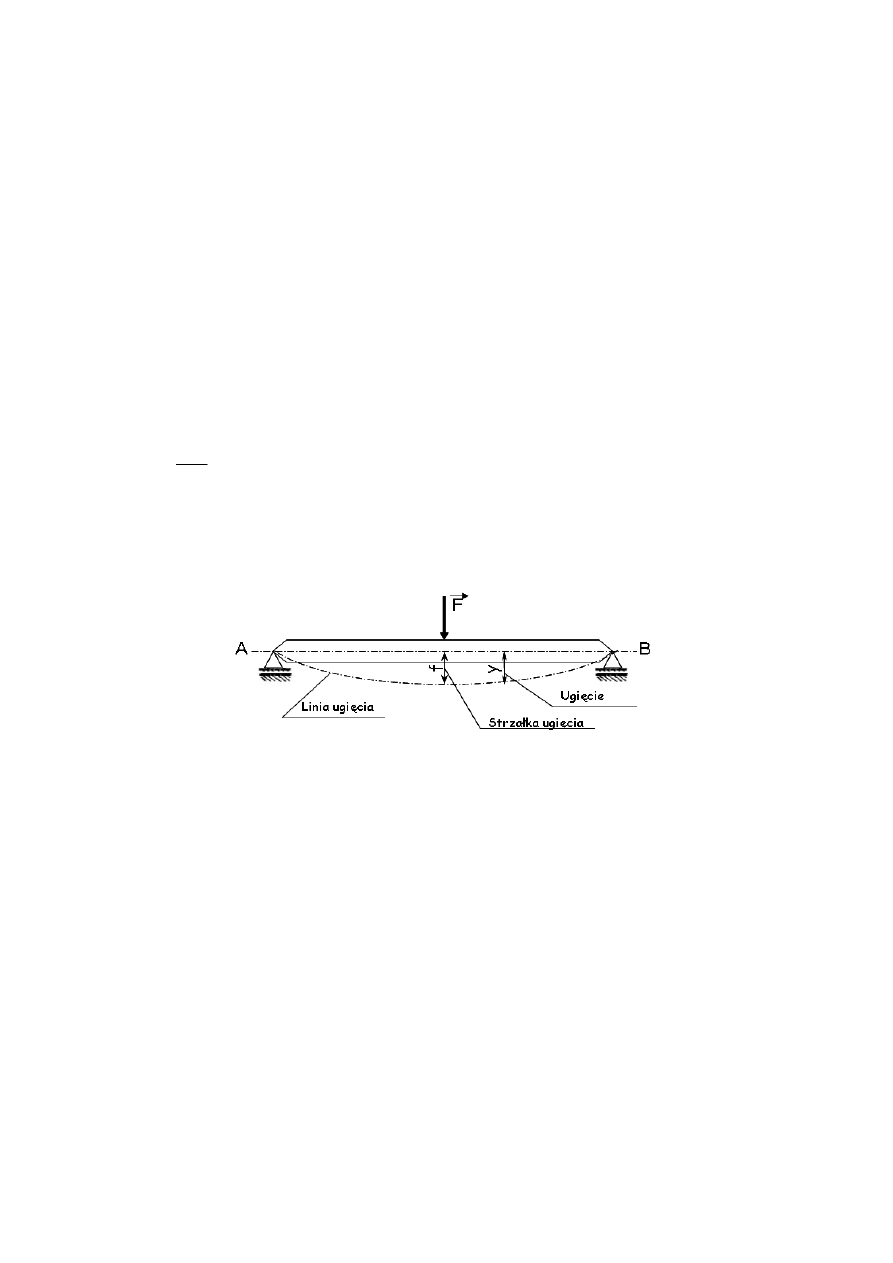
podstawowych problemów w alloplastyce stawu biodrowego (Rys. 1.6).

Rys. 1.6 Kolejność rozwiązywania problemów w endoprotezoplastyce w latach 1970-1995 [6]

Kolejnym zagadnieniem związanym z alloplastyką stawu biodrowego jest

zapewnienie właściwych relacji naprężeniowo-odkształceniowych w układzie kość-implant.
Zbyt wysoki moduł Younga trzpienia endoprotezy powoduje zmniejszenie obciążenia kości, a
tym samym prowadzi do jej zaniku i obluzowania implantu. Związane jest to z faktem, że
prawidłowy wzrost i przebudowa kości odbywa się wyłącznie w warunkach obciążeń.
Równocześnie zbyt niski moduł Younga trzpienia w stosunku do kości może spowodować
zbyt duże odkształcenia, a przez to wzajemne przemieszczenia uniemożliwiające
przerośnięcie powierzchni implantu kością. Do charakterystyki zachowania materiałów pod
wpływem działania obciążeń często stosuje się pojęcie sztywności giętnej (sztywność
zginania, sztywność na zginanie). Do wyznaczenia sztywności giętnej wykorzystuje się
założenie, że trzpień endoprotezy jest belką (Rys. 1.7). Podczas jej punktowego obciążania
następuje ugięcie belki w kierunku prostopadłym do osi poziomej, a maksymalną wartość
przemieszczenia środka ciężkości przekroju nazywamy strzałką ugięcia. Ugięcie można
opisać wzorem:

EI y’’ = - M

g

Gdzie:

y’’ = (

2

2

dx

y

d

) – opisuje promień krzywizny osi trzpienia w funkcji odległości

od głowy protezy;
x – odległość od środka belki;
EI – sztywność giętna belki, stanowi iloczyn modułu Younga i momentu
bezwładności przekroju;
M

g

– moment gnący.

Rys. 1.7 Schemat zginania belki

Niekorzystne relacje naprężeniowo-odkształceniowe wynikają z zastosowania na

trzpienie endoprotez materiałów metalicznych (Cr-Co-Mo, tytan i jego stopy). Ich przewagą
jest przede wszystkim wysoka wytrzymałość, jednak do podstawowych wad należą zbyt
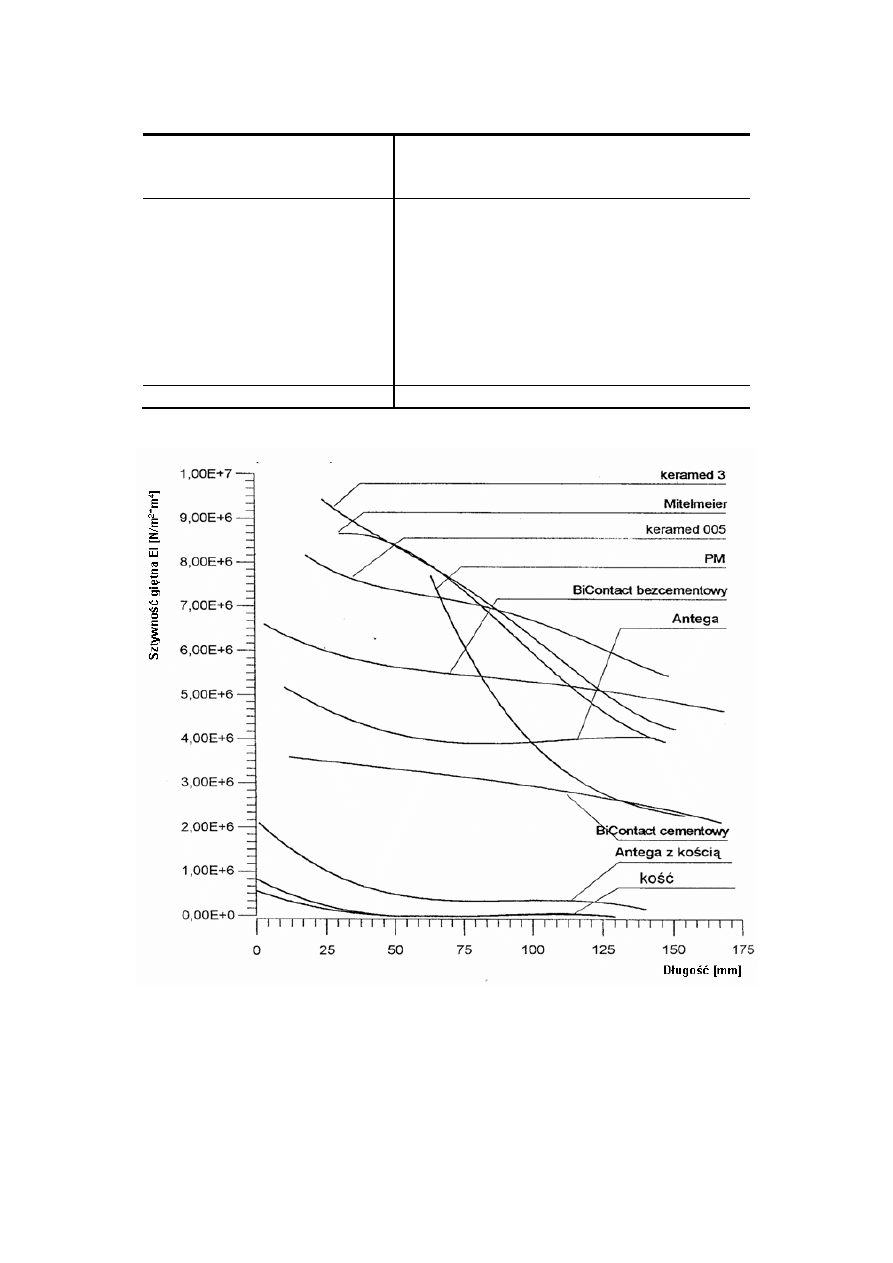
wysoki moduł Younga i korozyjność (Tab. 1). Porównanie rozkładu sztywności giętnej
endoprotez metalowych o różnych rozwiązaniach konstrukcyjnych przedstawia Rys. 1.8.
Równoczesne zapewnienie wysokiej wytrzymałości i sprężystości jest możliwe do uzyskania
jedynie w przypadku materiałów kompozytowych. Materiałem mogącym spełnić powyższe
wymogi jest kompozyt węgiel-węgiel. W ostatnich latach firma Man-Ceramics wprowadziła
do produkcji endoprotezę, w której trzpień i panewkę wykonano kompozytu z włóknami
węglowymi, brak jest natomiast informacji na temat wyników implantacji. Jednym z
nowszych rozwiązań jest endoproteza Isoelastic, w której cienki trzpień pokryto warstwą
tworzywa sztucznego o mniejszej sztywności.

Innym czynnikiem wpływającym na relacje odkształceniowo-naprężeniowe układu

implant-kość jest długość trzpienia. Wpływa ona na wielkość stref przenoszenia obciążeń z
trzpienia na kość. Z ostatnich badań wynika, iż krótsze trzpienie dają korzystniejszy rezultat.
Jedno ze starszych rozwiązań zastosowania endoprotezy krótkotrzpieniowej przedstawia Rys.
1.9. W tym przypadku, wprowadzono zewnętrzną śrubę kostną zabezpieczającą docisk
endoprotezy w kanale kostnym. Jednak zastosowanie śruby bocznej nie sprawdziło się ze
względu na jej wysuwanie się z kości prowadzące do wyrywania płytki.

Tab. 1 Właściwości wybranych materiałów implantacyjnych

Rys. 1.8 Porównanie rozkładu sztywności giętnej trzpieni endoprotez oraz części bliższej kości udowej

Materiał

Wytrzymałość

na rozciąganie

[MPa]

Moduł

Younga

[GPa]

Współczynn

ik

Poissona

Stal 316L

275-1240

210

0,3

Tytan

240-785

110

0,3

Stopy tytanu

850-1120

110

0,3

Stopy kobaltu

630-1790

200

0,3

Al

2

O

3

250

390

0,25

Kompozyt węgiel-węgiel 1D

800-1350

70

0,2

Kompozyt węgiel-węgiel 2D

200-600

30

0,25

Kompozyt węgiel-węgiel 3D

70-250

10

-

Ż

ywice epoksydowe

50-90

4

0,37

Ko

ść zbita

130

20

-

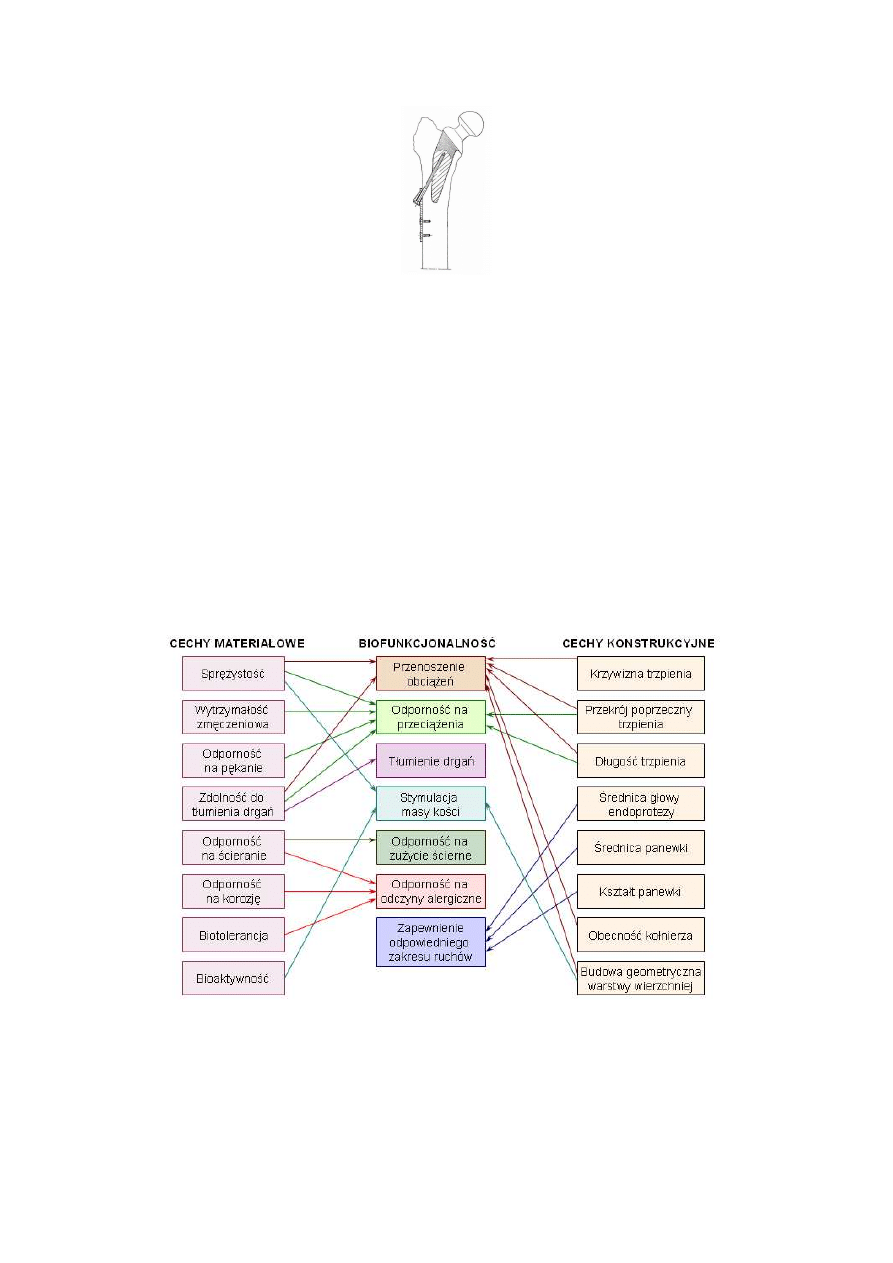
Rys. 1.9 Endoproteza krótkotrzpieniowa z dodatkowym mocowaniem śrubowym

Najważniejsze wymagania stawiane materiałom na endoprotezy oraz ich relacje z

biofunkcjonalnością i konstrukcją endoprotezy przedstawia Rys. 1.10.

Wciąż aktualne problemy w endoprotezoplastyce stawu biodrowego związane są ze

spełnieniem następujących warunków:
– biozgodność materiałów;
– wysoka wytrzymałość statyczna i zmęczeniowa;
– sprężystość zbliżona do sprężystości kości;
– odporność na ścieranie pary trącej główka-panewka;
– mocne złącze kość-implant, możliwość samofiksacji;
– równomiernie rozłożony kontakt implantu z kością w celu uniknięcia miejscowej

koncentracji naprężeń;

– zapewnienie możliwości łatwego wszczepienia endoprotezy;
– personalizacja implantów: dostosowanie kształtu endoprotezy i przenoszonych obciążeń

do warunków anatomicznych, stanu kości, struktury i ukształtowania mięśni.

Rys. 1.10 Związek między cechami materiałowymi i konstrukcyjnymi a biofunkcjonalnością endoprotez

Badania symulacyjne trzpieni endoprotez stawu biodrowego

Badania numeryczne z zastosowaniem metody elementów skończonych (MES)

pozwalają na ocenę warunków biomechanicznych różnych materiałów przeznaczonych na
trzpienie endoprotez, a przez to umożliwiają przewidywanie zarówno przebiegu, jak i
rezultatów implantacji. Dają pełny opis trójwymiarowych rozkładów odkształceń i naprężeń,
prowadząc tym samym do osiągnięcia kompromisu między sztywnością a wytrzymałością
trzpieni. Zastosowanie metod numerycznych pozwala na uzyskanie złożonych modeli
obciążania poszczególnych elementów stawu biodrowego z uwzględnieniem większości grup
mięśniowych biorących udział w przenoszeniu obciążeń i ruchu kończyny dolnej. Proces
projektowania endoprotezy powinien składać się z kilku etapów. Pierwszym z nich jest
analiza kształtowo-wymiarowa elementów kostnych stawu biodrowego. Przydatna jest tu
przede wszystkim tomografia komputerowa. W obrazie tomograficznym wyodrębnia się
interesujące obszary, wyznacza granice kości korowej i określa w układzie odniesienia
współrzędne punktów opisujących te granice. Dane te są przetwarzane w programie
komputerowym i służą do dostosowania modelu geometrycznego projektowanej endoprotezy
do anatomii kości udowej. Na tej podstawie ustalany jest kształt i wymiary endoprotezy.
Gotowy model pozwala na przeprowadzenie analizy odkształceniowo-naprężeniowej dla
różnych materiałów przez wprowadzenie ich parametrów mechanicznych do programu.
Umożliwia to wytypowanie materiału pozwalającego na optymalną współpracę implantu z
kością.

Zadania do wykonania

Analiza relacji naprężeniowo-odkształceniowych trzpieni endoprotez dla trzech

różnych materiałów (stal 316L, tytan, kompozyty węgiel-węgiel) oraz przy różnych
długościach trzpienia na podstawie symulacji komputerowych.

WYKONANIE ĆWICZENIA

Należy wyznaczyć charakterystyki sztywności giętnej oraz ocenić wartości

przemieszczeń, rozkład odkształceń i naprężeń trzpieni endoprotez dla 4 materiałów: stali
316L, tytanu, kompozytu węgiel-węgiel 1D i 2D. Przedmiotem badań jest endoproteza
starszego typu, główka jest połączona sztywno z trzpieniem, cała proteza jest wykonana z
jednego materiału. Etapy tworzenia modelu geometrycznego endoprotezy przedstawia
załącznik A. Stosowany w ćwiczeniu model endoprotezy został opracowany na Politechnice
Wrocławskiej w Zakładzie Inżynierii Biomedycznej i Mechaniki Eksperymentalnej. Badania
symulacyjne należy wykonać przy pomocy programu ANSYS zgodnie z załączoną przy
stanowisku instrukcją obsługi. Zamocowanie endoprotezy zostało zamodelowane poprzez
odebranie trzech stopni swobody wszystkim węzłom znajdującym się na powierzchni głowy.
Prostopadle do osi trzpienia została przyłożona siła o wartości 10N. Model obciążenia
przedstawia Rys. 1.11.

Rys. 1.11 Model obciążenia endoprotezy z zaznaczonymi punktami pomiarowymi

Całość ćwiczenia obejmuje następujące kroki:
1.

Wybór materiału, dla którego chcemy wykonać obliczenia - dokonuje się tego poprzez
wpisanie w pliku źródłowym modułu Younga i wartości współczynnika Piossona
wybranego materiału. Wartości te zostały podane w tab.1.

2.

Wyznaczenie 20 punktów równomiernie rozmieszczonych na górnej powierzchni
trzpienia endoprotezy (kierunek X) zgodnie z Rys. 1.11.

3.

Obliczenie wartości przemieszczeń wyznaczonych punktów w kierunku Y.

4.

Pomiar długości trzpienia endoprotezy.

5.

Analiza przemieszczeń występujących w endoprotezie podczas jej obciążania.

6.

Ocena rozkładu naprężeń i odkształceń w endoprotezie podczas jej obciążania.

OPRACOWANIE WYNIKÓW

1. Na podstawie obliczonych przez program wartości przemieszczeń punktów
znajdujących się na górnej powierzchni trzpienia endoprotezy w kierunku Y należy
wyznaczyć wartości sztywności giętnej trzpieni. W tym celu należy skorzystać ze wzoru:

EI=[Fl/(6Uy)]*[x

2

(3-x/l)] [(N/m

2

)*m

4

]

gdzie:
EI

– sztywność giętna belki;

F[N] – wartość siły działającej prostopadle do trzpienia;
l[m] – długość trzpienia;
Uy [m] – wartości przemieszczeń w kierunku osi Y(wartość bezwzględna);
x=|x

A

-k| [m], gdzie:

x

A

– odległość wybranego punktu od głowy endoprotezy;

k

– całkowita długość endoprotezy.

Wzór ten otrzymano po scałkowaniu poniższej zależności, opisującej endoprotezę jako belkę
jednostronnie zamocowaną, która jest poddawana zginaniu:

EIy’’ = -M(x)

gdzie:
E

– moduł sprężystości podłużnej (moduł Younga);

I

– moment bezwładności przekroju;

M(x) – moment gnący w funkcji długości trzpienia.
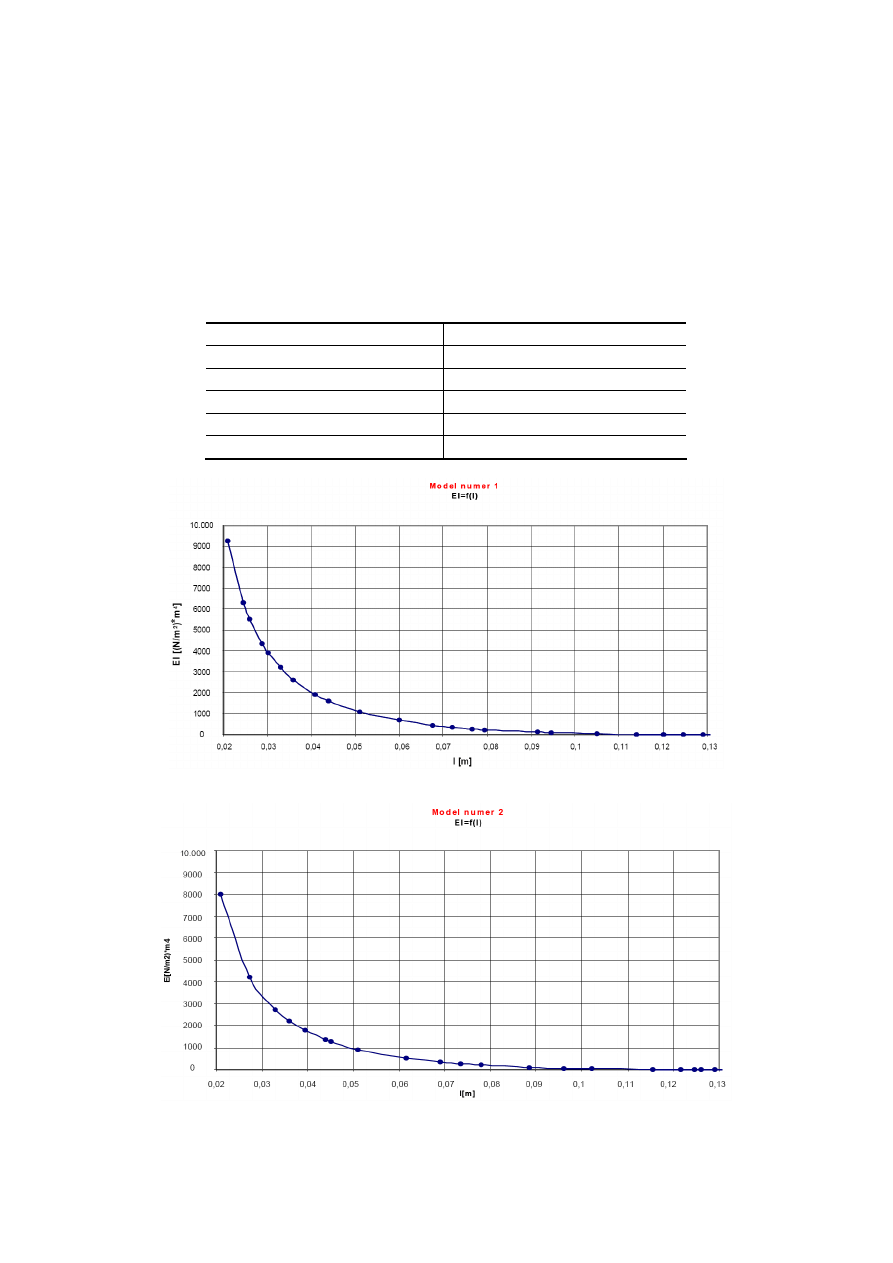
2. Następnie wyznaczyć charakterystyki sztywności giętnej w formie graficznej,
jako zależności EI (l).
3. Przeprowadzić analizę sztywności giętnej endoprotezy oraz analizę

wyznaczonych

w

programie

ANSYS

rozkładów

naprężeń

i

odkształceń

dla badanych materiałów. Na podstawie uzyskanych wyników zaproponować
optymalny materiał na wykonanie endoprotezy.

4. Na podstawie dołączonych charakterystyk sztywności giętnej endoprotezy

stalowej otrzymanych dla różnych długości trzpieni (Rys. 1.12-1.16), przeprowadzić
analizę wpływu długości trzpienia na sztywność giętną endoprotezy.

Charakterystyki sztywno

ści giętnej pięciu modeli stworzonych ze stali austenitycznej przy

ró

żnej długości trzpieni

Tab. 2 Długości trzpieni w poszczególnych modelach

Model

Długo

ść trzpienia [mm]

M1

129

M2

126

M3

123

M4

120

M5

117

Rys. 1.12Sztywność giętna trzpieni stalowych o długości 129mm

Rys. 1.13 Sztywność giętna trzpieni stalowych o długości 126mm

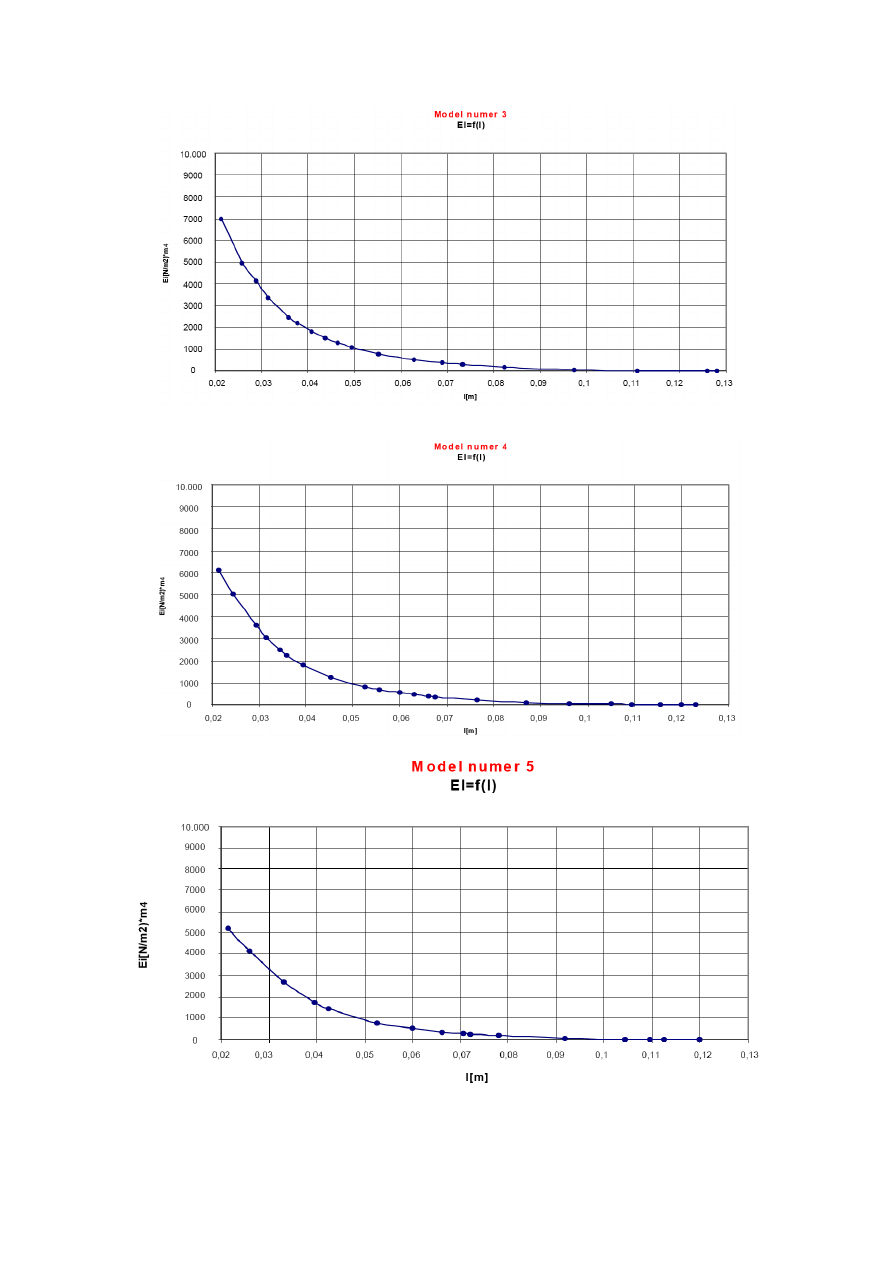
Rys. 1.14 Sztywność giętna trzpieni stalowych o długości 123mm

Rys. 1.15 Sztywność giętna trzpieni stalowych o długości 120mm

Rys. 1.16 Sztywność giętna trzpieni stalowych o długości 117mm

Zał

ącznik A. Etapy tworzenia modelu geometrycznego endoprotezy

Tworzenie modelu geometrycznego endoprotezy przebiegało w dwóch etapach. W

pierwszym etapie stworzono model głowy i szyjki, w drugim etapie powstał trzpień. Model
geometryczny projektowanej endoprotezy oraz jej parametry przedstawia Rys. 1.8 a,b,c.

Tworzenie modelu głowy i szyjki endoprotezy obejmowało wyrysowanie niepełnego

okręgu o wyliczonym kącie, który stanowi połowę przekroju głowy endoprotezy. Następnie
wyznaczono punkty opisujące geometrię półprzekroju i połączono je liniami. Do stworzenia
górnego łuku zastosowano polecenie spline, łuk przy kołnierzu stworzono łącząc trzy punkty
poleceniem ltan (Rys. 1.20a). Następnie za pomocą polecenia al, stworzono powierzchnię z
obszaru opisanego liniami. Powierzchnię obrócono wokół wysokości poleceniem vrota i w
ten sposób powstała objętość głowy i szyjki (Rys. 1.17).

Trzpień endoprotezy składa się z poprzecznych przekrojów (Rys. 1.18). Etapy

tworzenia pojedynczego przekroju obejmowały:
–

tworzenie dwóch okręgów;

–

połączenie punktów na okręgach liniami;

–

usunięcie wewnętrznych linii;

–

tworzenie powierzchni z obszaru ograniczonego liniami.

Po stworzeniu pojedynczego przekroju przesunięto układ współrzędnych, obrócono go

o obliczony kąt i stworzono kolejne powierzchnie. Obliczony kąt między głową a trzpieniem
endoprotezy wynosi 131

°

. Dlatego też kąt o który obrócono układ współrzędnych od

położenia prostopadłego w stosunku do osi symetrii głowy i szyjki do położenia
prostopadłego w stosunku do osi trzpienia, wynosi 49

°

(Rys. 1.18b). Przekroje połączono

linią za pomocą polecenia spline. Następnie, za pomocą polecenia al, z linii należących do
dwóch sąsiadujących przekrojów oraz odcinków linii łączących je, stworzono nieplanarne
powierzchnie (Rys. 1.19).

Objętość

trzpienia

stworzono

z

obszarów

ograniczonych

otrzymanymi

powierzchniami nieplanarnymi i przekrojami (Rys. 1.20). Dzięki użyciu polecenia spline
zastosowano polecenia vglue, all aby uwspólnić wszystkie powierzchnie i punkty w całym
modelu. W ten sposób otrzymano model geometryczny endoprotezy (Rys. 1.21).

Model dyskretny - typ elementu dyskretnego

Podział modelu na siatkę elementów skończonych wykonano w oparciu

o trójwymiarowy element typu TETRA (Rys. 1.24). Jest to element czworościenny
o 10 węzłach. Każdy węzeł posiada trzy stopnie swobody. Czworościany są bardzo często
stosowanymi elementami trójwymiarowymi, zwłaszcza przy tworzeniu modeli o
skomplikowanej, niesymetrycznej geometrii. Dzięki użyciu takiego elementu uzyskać można
łatwość modyfikacji siatki i zmianę jej gęstości. Można również dzielić poszczególne
objętości modelu osobno. Ze względu na to, że obliczenia z użyciem elementu są mniej
dokładne niż w przypadku elementów typu BRICK (nie spełnia on wszystkich kryteriów przy
aproksymacji funkcją kształtu), należy użyć mniejszych elementów i stworzyć gęstszą siatkę.
Elementy nie mogą być jednak zbyt małe, gdyż uzyskanie zbyt dużej ich ilości wydłuża
znacznie czas potrzebny na obliczenia. Poleceniem esize ustalono wielkość elementu. Dzięki
użyciu smrtsize wyeliminowano nieprawidłowe elementy, których wielkości w
newralgicznych miejscach program dobrał sam, niezależnie od zadeklarowanych przez
użytkownika wielkości.

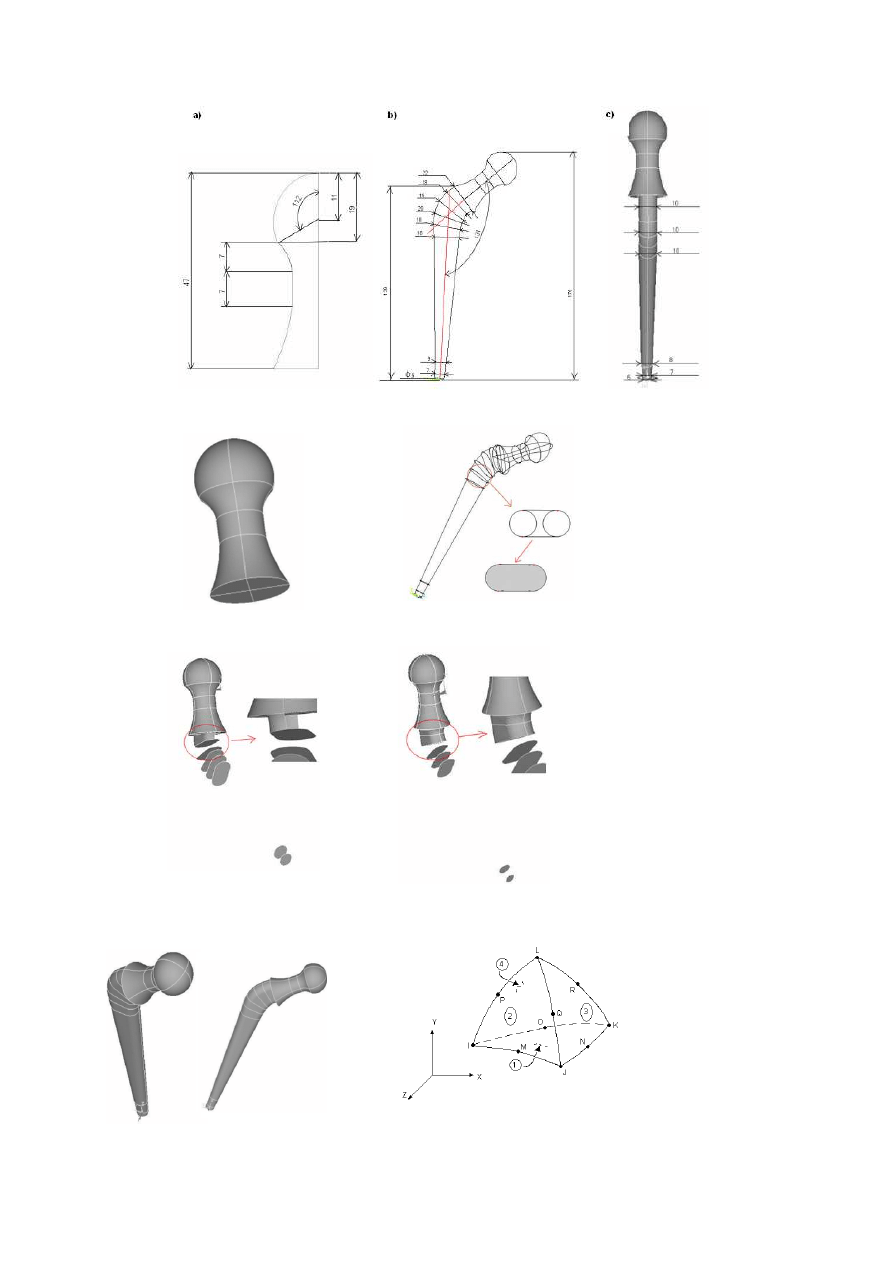
Rys. 1.18 Endoproteza: a) głowa i szyjka, b) przekrój, c) widok tylny połowa przekroju

Rys. 1.19 Głowa i szyjka endoprotezy

Rys. 1.20 Przekroje tworzące trzpień

Rys. 1.21 Tworzenie powierzchni trzpienia

Rys. 1.22 Tworzenie objętości trzpienia

Rys. 1.23 Gotowy model geometryczny

Rys. 1.24 Element typu TETRA, 10-cio węzłowy