ROZDZIAŁ 9

INNE TESTY ISTOTNOŚCI

Testy istotności stanowią obszerną grupę najczęściej stosowanych i charakteryzujących się
prostotą testów statystycznych. W poprzednim rozdziale poznaliśmy dwie najważniejsze
grupy testów - testy istotności pomiędzy średnimi dla prób zależnych i niezależnych.
Obecnie w krótki i syntetyczny sposób poznamy inne. Będą to testy:

1. Test dla dwóch współczynników korelacji

2. Test dla dwóch wskaźników struktury (procentów)
3. Test dla jednej i dwóch średnich (po raz drugi)

Omówimy je poniżej, ilustrując prostymi przykładami, a następnie zobaczymy, jak
analizować to w programie STATISTICA.

Ad 1
Test ten pozwala na porównanie istotności statystycznej różnic pomiędzy dwoma
współczynnikami korelacji Pearsona.

171

Przy założeniu prawdziwości hipotezy zerowej opisywana statystyka ma rozkład zbliżony
do rozkładu normalnego

(N(0,1)).

tlHHHHHH^HflHHHHHflMBHHH

Przykład 1
Załóżmy, że badamy korelację między aktywnością dwóch enzymów w populacji chorych
na niewydolność krążenia i w populacji ludzi pozbawionych tej dolegliwości. W wyniku

Przystępny kurs statystyki

eksperymentu przeprowadzonego w dwóch losowo wybranych próbach A i B liczebność
próby i współczynnik korelacji przyjmują następujące wartości:

n

1

= 10, r

1

= -0,23 dla próby A (zdrowi)

n

2

= 20, r

2

= -0,55 dla próby B (chorzy)

Chcemy na poziomie istotności α = 0,05 zweryfikować hipotezę, że współczynnik korelacji
w populacji chorych jest istotnie większy od współczynnika korelacji tych enzymów
w populacji ludzi pozbawionych tej dolegliwości. Obliczamy wartość testu U dla podanych
wartości i otrzymujemy U = -0,8555. Z tablic dla poziomu istotności α = 0,05 odczytujemy
(przy hipotezie alternatywnej H

1

: r

1

< r

2

)

wartość krytyczną u

α

= -1,64.

Ponieważ U = -0,8555 < u

α

= -1,64 wiec brak podstaw do odrzucenia hipotezy

zerowej o braku

różnic współczynników korelacji w badanych populacjach.

Badając dwie populacje ze względu na cechę niemierzalną, musimy często sprawdzać
hipotezę, że wskaźniki struktury (procenty) są w obu populacjach takie same. Test podany
niżej pozwala na zweryfikowanie tej hipotezy w oparciu o wyniki dwu dużych prób.
W zależności od postaci hipotezy alternatywnej, rozpatrujemy obszar krytyczny
dwustronny albo też jednostronny. Sprawdzianem hipotezy jest test:

Ad 3
Testy tu występujące pozwalają na obliczenie:

• poziomu istotności (komputerowy) dla różnicy pomiędzy średnią z próby

a średnią z populacji;

Ad 2

172

Inne testy istotności

• poziomu istotności (komputerowy) dla różnicy pomiędzy dwiema średnimi

z dwóch prób.

Drugi z testów był przez nas dokładnie omawiany w poprzednim rozdziale. Narzędzie
obecne umożliwia przeprowadzenie tej samej analizy, gdy nie mamy konkretnych danych,
a tylko średnie i odchylenia standardowe z porównywanych grup. Konkretne przykłady
zostaną pokazane poniżej.

I. A jak to się liczy w programie STATISTICA

W programie STATISTICA do obliczania takich testów służy opcja Inne Testy istotności
w module PODSTAWOWE STATYSTYKI I TABELE. Po wybraniu tej opcji
i naciśnięciu OK (lub po dwukrotnym kliknięciu na nazwie opcji) otwiera się okno Inne
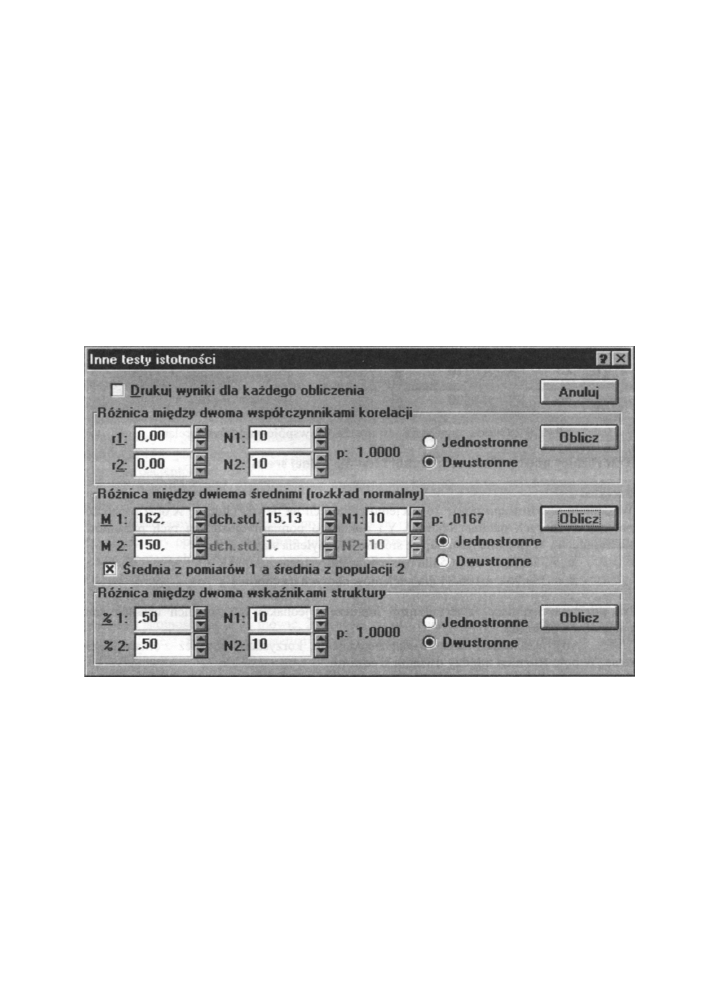
testy istotności jak na rysunku poniżej.

Rys. 9.1 Okno dialogowe - Inne testy istotności

Kolejne pola w oknie Inne testy istotności (rysunek powyżej) poświęcone są omawianym
powyżej testom. Idąc kolejno są to testy:

1. Test dla dwóch współczynników korelacji;

2. Test różnicy między dwiema średnimi i test dla jednej średniej;
3. Test dla dwóch wskaźników struktury (procentów).

Na konkretnych przykładach przedstawionych poniżej pokażemy, jak pracujemy z tymi
testami.

173

Przystępny kurs statystyki

Test dla dwóch współczynników korelacji

Przykład 1 ciąg dalszy
Jak rozwiązać przedstawione w przykładzie 1 zagadnienie, korzystając z omawianego
okna. W polu Różnica między dwoma współczynnikami korelacji

* wprowadzamy konkretne dane z prób (tak jak na rysunku poniżej),
* wybieramy opcję Jednostronne lub dwustronne (w zależności od hipotezy

alternatywnej),

* naciskamy przycisk Oblicz.

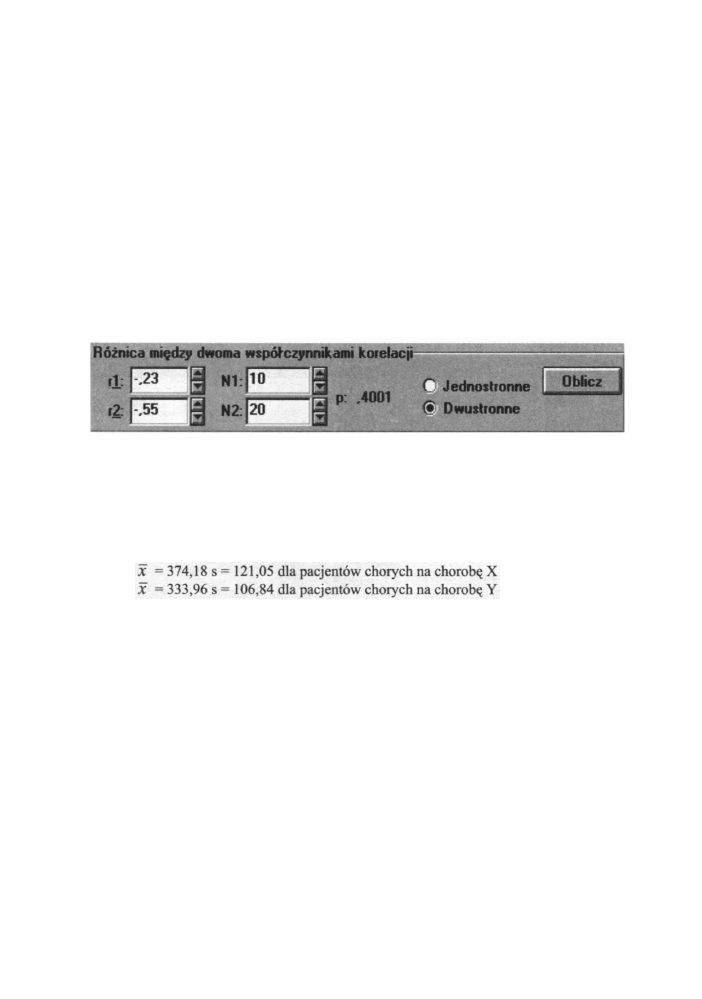
Obliczony zostanie komputerowy poziom istotności p = 0,401 (rysunek poniżej),
potwierdzający naszą poprzednią interpretację o braku podstaw do odrzucenia hipotezy
zerowej.

Na poziomie istotności zweryfikujmy hipotezę o jednakowych średnich czasach snu
pacjentów z obu grup.

Aby rozwiązać przedstawione zagadnienie, korzystamy również z omawianego

okna. W polu Różnica między dwiema średnimi:

* wprowadzamy konkretne dane z prób (tak jak na rysunku poniżej),
* wybieramy opcję Jednostronne lub Dwustronne (w zależności od hipotezy

alternatywnej),

* naciskamy przycisk Oblicz.

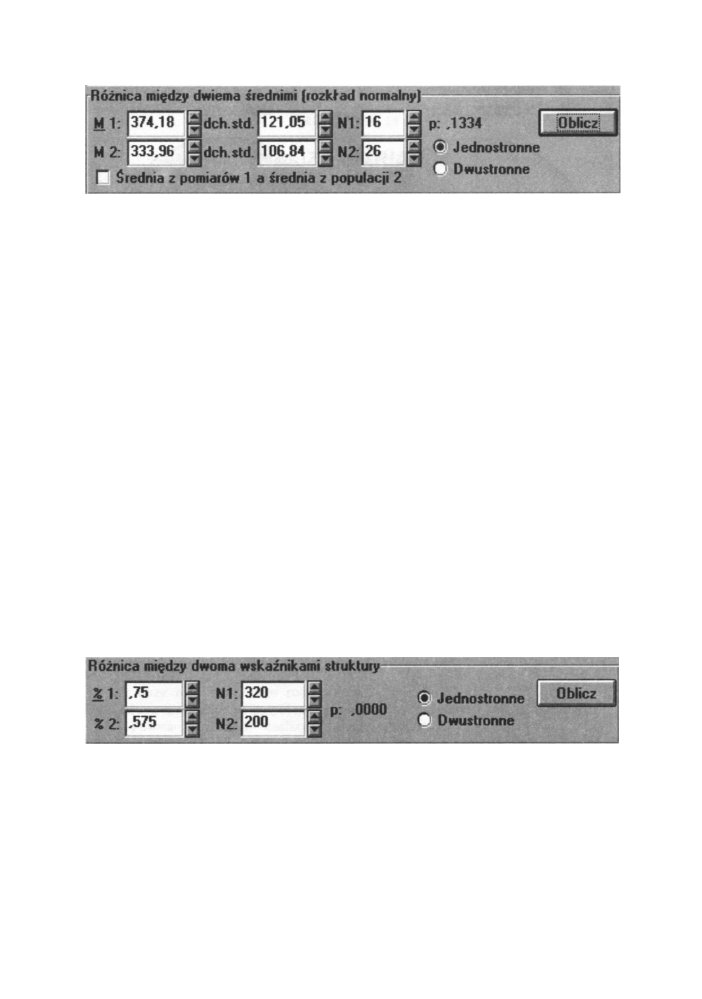
Obliczony zostanie komputerowy poziom istotności p= 0,134 (rysunek poniżej). Brak
podstaw do odrzucenia hipotezy zerowej o jednakowych średnich czasach snu pacjentów
z obu grup.

174

Rys. 9.2 Okno z wynikami test dla dwóch współczynników korelacji

Test różnicy między dwiema średnimi i test dla jednej średniej

Przykład 2
W szpitalu wylosowano próbę 16 pacjentów chorych na pewną chorobę X oraz próbę 26
pacjentów chorych na inną chorobę Y i dokonano pomiaru czasu snu tych pacjentów
(w minutach). Wyliczono następujące średnie i odchylenia standardowe:

Inne testy istotności

Rys. 9.3 Okno z wynikami test różnicy między dwoma średnimi

Wybranie opcji Średnia z pomiarów 1 a średnia z populacji 2 umożliwia znalezienie
poziomu istotności dla różnicy między średnią z próby a średnią z populacji. Jest to tzw.
testowanie hipotezy o wartości przeciętnej. Przykładowy wynik takiej analizy pokazano na
rysunku 9.1.

Różnica między dwoma wskaźnikami struktury

Przykład 3
Badano wpływ nowego leku na poprawę stanu zdrowia chorych na cukrzycę. W tym celu
320 wylosowanym chorym podano ten lek i u 240 chorych stwierdzono po ustalonym
okresie leczenia powrót poziomu cukru do normy. Natomiast w drugiej 200 osobowej
grupie chorych, gdzie leczono tradycyjnymi lekami, stwierdzono powrót poziomu cukru do
normy u 115 pacjentów. Zweryfikujmy hipotezę o większym procencie wyzdrowień
w grupie pacjentów leczonych nowym lekiem.

Aby rozwiązać przedstawione zagadnienie korzystamy również z omawianego

okna. W polu Różnica między dwoma wskaźnikami struktury:
* wprowadzamy konkretne dane z prób (tak jak na rysunku poniżej),
* wybieramy opcję Jednostronne lub Dwustronne (w naszym przypadku jednostronne,

bo hipoteza alternatywna ma postać H

1

: p

1

>

p

2

) ,

* naciskamy przycisk Oblicz.

Obliczony zostanie poziom istotności p = 0,000 (rysunek poniżej). Przy dowolnie małym
poziomie istotności możemy mówić, że procent wyzdrowień w grupie pacjentów leczonych
nowym lekiem jest istotnie statystycznie większy niż procent wyzdrowień w grupie
z tradycyjną metodą leczenia.

Rys. 9.4 Okno z wynikami test dla dwóch wskaźników struktury

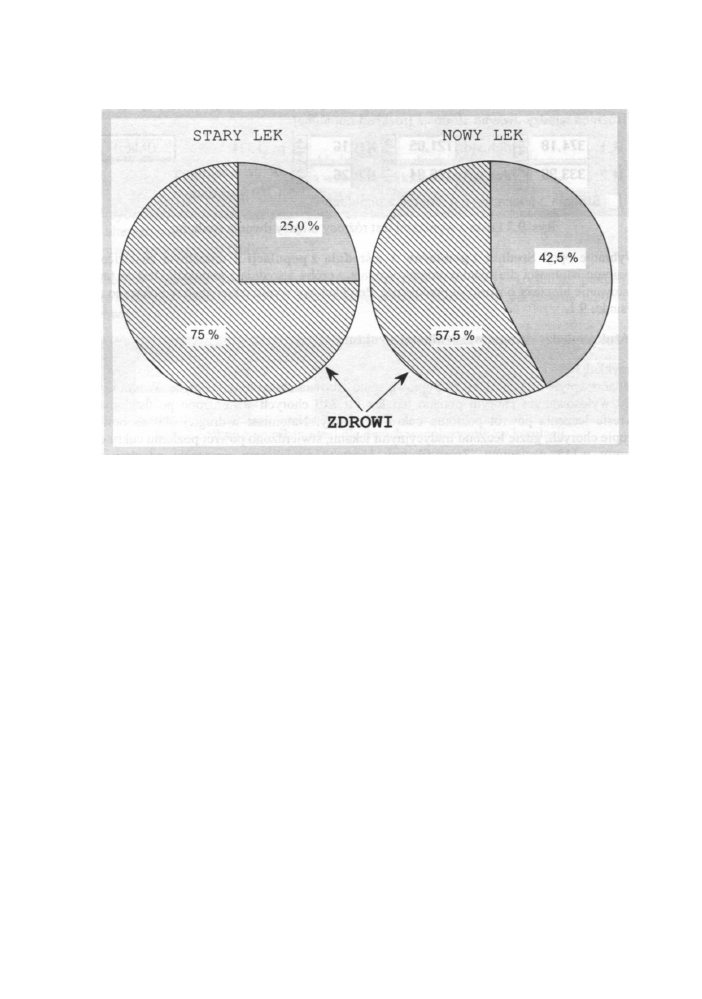
Sytuację tę ilustruje poniższy rysunek:

175

Przystępny kurs statystyki

Rys. 9.5 Okno z interpretacją graficzną dla danych z przykładu 3

Obliczone wyniki statystycznych analiz możemy automatycznie wydrukować (wysłać do
pliku lub okna raportów - w zależności od ustawień w oknie dialogowym Układ
strony/Wyjścia), o ile wybraliśmy opcję - Drukuj wyniki dla każdego obliczenia.

176