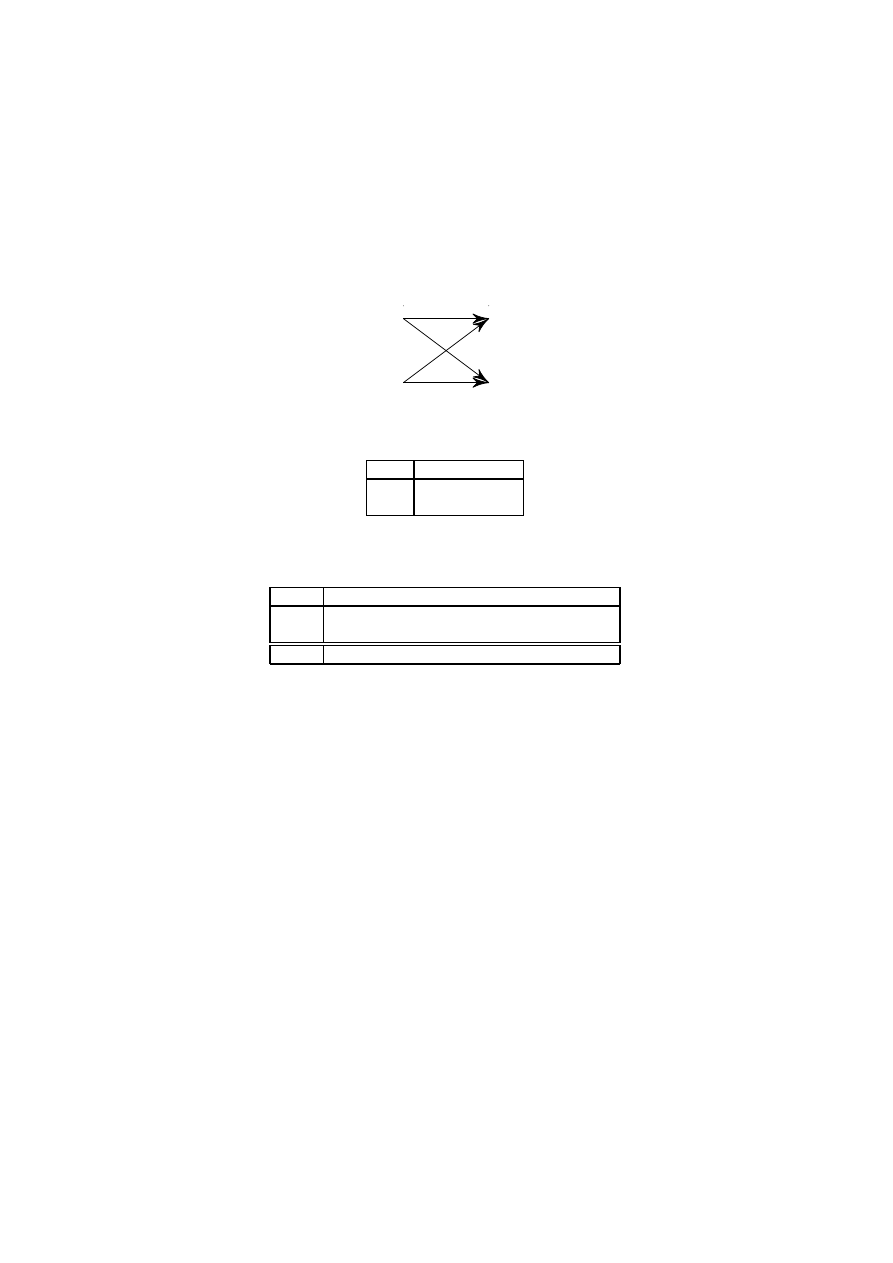
Transmisja w binarnym kanale symetrycznym

Wartości (0, 1) zmiennej X pojawiają się na wejściu binarnego kanału syme-

trycznego z prawdopodobieństwami { α , 1−α }. Kanał przekłamuje te wartości
z prawdopodobieństwem µ (zob. rys).

1

0

1

0

X

Y

µ

µ

1

− µ

1

− µ

Z rysunku znajdujemy rozkład prawdopodobieństwa warunkowego P (Y |X):

X

|Y

0

1

0

1 − µ

µ

1

µ

1 − µ.

Korzystając ze wzoru p(y, x) = p(y|x)p(x) obliczamy rozkład prawdopodobień-
stwa łącznego P (Y |X):

X

|Y

0

1

0

α

(1 − µ)

αµ

1

(1 − α)µ

(1 − α)(1 − µ)

P

(Y )

α

(1 − µ) + (1 − α)µ

αµ

+ (1 − α)(1 − µ)

Sumując w kolumnach po wartościach zmiennej X dostajemy rozkład prawdo-
podobieństw zmiennej Y : P (Y ) = {α(1 − µ) + (1 − α)µ, αµ + (1 − α)(1 − µ)}.
Aby uniknąć operowania na długich, nieprzyjemnych wzorach i stowarzyszo-
nym z tym większym prawdopodobieństwem popełnienia błędu wprowadzamy
oznaczenie s = α + µ − 2αµ. Wówczas P (Y ) = {s, 1 − s} i od razu dostajemy
niepewność związaną z tą zmienną:

H

(Y ) = −[s log s + (1 − s) log(1 − s)] = H(s)

. Niepewność warunkową H(Y |X) wyliczamy ze wzoru:

H

(Y |X) = P (X = 0)H(Y |X = 0) + P (X = 1)H(Y |X = 1)

= α[−(1 − µ) log 1 − µ − µ log µ] + (1 − α)[−µ log µ − (1 − µ) log 1 − µ]

= −(1 − µ) log 1 − µ − µ log µ = H(µ).

Policzmy do kompletu niepewność źródła:

H

(X) = −[α log α + (1 − α) log (1 − α)] = H(α).

Jak widać, niepewność źródła zależy tylko od prawdopodobieństw pojawiania
się jego symboli, niepewność warunkowa zależy tylko od właściwości kanału, a
niepewność związana ze zmienną Y , tj. z obserwacją symboli na wyjściu kanału,
zależy zarówno od prawdopodobieństw symboli ze źródła, jak i od właściwości
kanału.

Znając H(Y ) i H(Y |X) możemy policzyć informację wzajemną miedzy wyjściem
i wejściem kanału:

I

(X; Y ) = H(Y ) − (Y |X) = H(s) − H(µ).

Aby stąd wyznaczyć przepustowość kanału, musimy znaleźć maksimum tego
wyrażenia ze względu na rozkłady prawdopodobieństw ze źródła. Od α zależy
tylko H(s) i wiemy, że przyjmuje wartość maksymalną równą jedności przy
s

=

1
2

. Widzimy więc, że przepustowość symetrycznego kanału binarnego wynosi

C

= 1 − H(µ)

i jest osiągana przy

1
2

= α + µ − 2αµ lub 2α(1 − 2µ) = 1 − 2µ.

Stąd dostajemy α =

1
2

. Zatem zgodnie z oczekiwaniami widzimy, że przepusto-

wość kanału symetrycznego jest osiągana przy jednorodnym rozkładzie prawdo-
podobieństw symboli ze źródła.

2