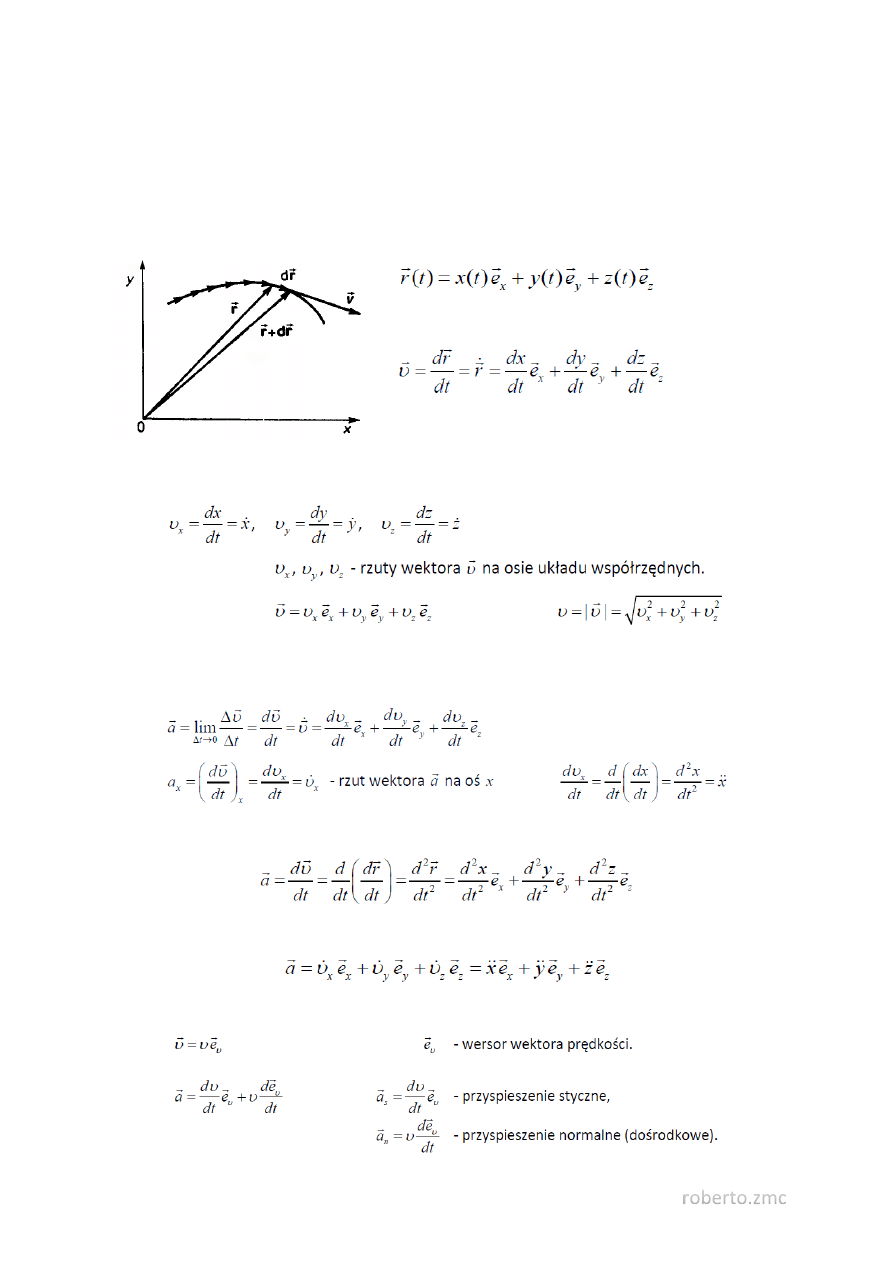
Opracowanie pytań na Egzamin z Fizyki I
Inżynieria biomedyczna
2013/2014
(na podstawie materiałów wykładowych dr hab. Józefa Kuśby)
1. Prędkość punktu materialnego.
Poruszający się punkt materialny zakreśla w przestrzeni pewną linię, którą nazywamy torem.
Prędkość υ
⃗
punktu materialnego definiuje się, jako:
Prędkość punktu materialnego jest to wielkość wektorowa, charakteryzująca szybkość przemieszczania
się cząstki po torze, a także uwzględniająca kierunek i zwrot ruchu cząstki w każdej chwili czasu.
2. Przyspieszenie punktu materialnego.
Przyspieszeniem cząstki nazywamy szybkość zmian wektora υ
⃗⃗⃗
.
Przyspieszenie jest pochodną wektora prędkości albo drugą pochodną wektora położenia
Wyrażenie wektora przyspieszenia poprzez rzuty:
3. Prędkość i przyspieszenie w ruchu obrotowym.
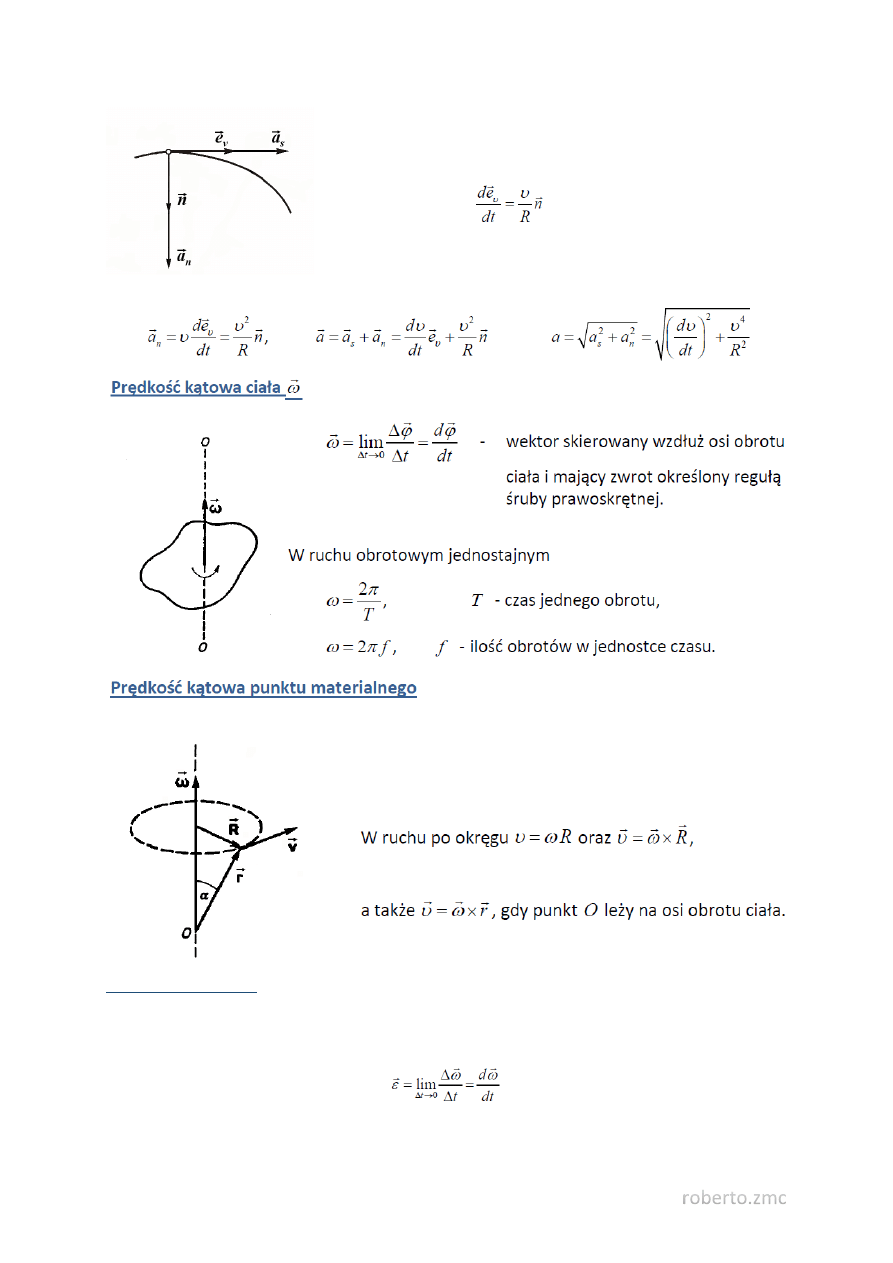
𝑛⃗ - wersor prostopadły do 𝑒
υ
( a tym samym do υ
⃗ ) o zwrocie
wskazującym kierunek zakrzywiania się toru.
Można pokazać, że
R - promień krzywizny toru. Promień krzywizny toru w danym punkcie
jest równy promieniowi okręgu, który ma krzywiznę równą krzywiźnie
toru w tym punkcie. Stąd:
Przyspieszenie kątowe
Wektor 𝜔
⃗⃗ może się zmieniać zarówno z powodu zmian prędkości obrotów ciała wokół osi (zmiany
modułu wektora 𝜔
⃗⃗ ), jak i z powodu obracania się samej osi w przestrzeni (zmiany kierunku wektora 𝜔
⃗⃗ )
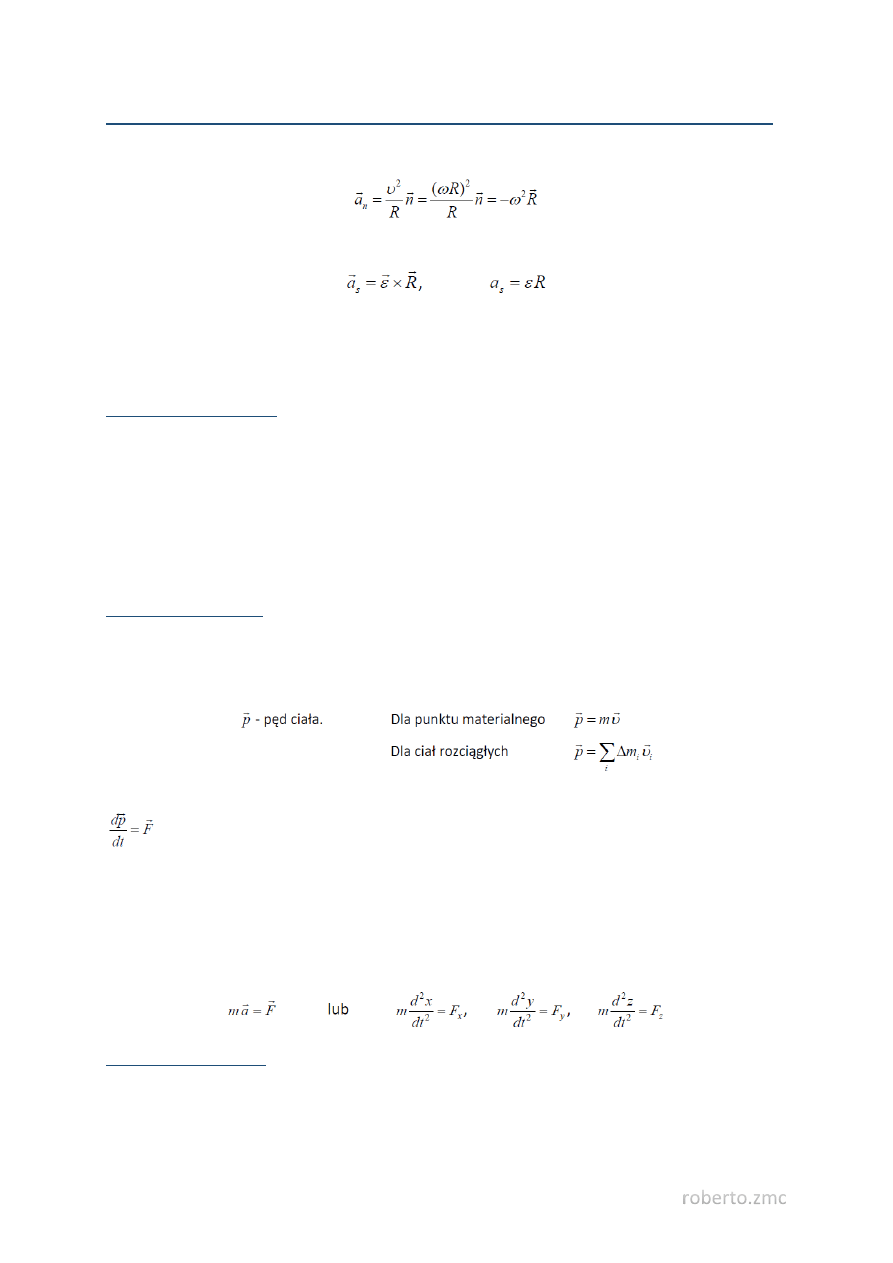
Przyspieszenie normalne i styczne punktu materialnego w ruchu po okręgu (wokół nieruchomej osi)
Przyspieszenie normalne (dośrodkowe)
Przyspieszenie styczne
4. Prawa dynamiki Newtona.
Podstawą mechaniki klasycznej (newtonowskiej) są trzy prawa dynamiki sformułowane przez Newtona
(1687 r.)
Pierwsze prawo Newtona
Każde ciało znajduje się w stanie spoczynku lub ruchu jednostajnego prostoliniowego, dopóki
działanie ze strony innych ciał nie zmieni tego stanu.
Układ odniesienia, w którym jest słuszne pierwsze prawo Newtona, nazywamy układem inercjalnym.
Każdy układ odniesienia poruszający się względem danego układu inercjalnego ruchem jednostajnym
po linii prostej jest także układem inercjalnym.
Układem inercjalnym jest np. heliocentryczny układ odniesienia.
Drugie prawo Newtona
Działanie innych ciał na dane ciało powoduje jego przyspieszenie. Jednakowe działanie po-woduje u
różnych ciał różne przyspieszenia. Ciała można, więc charakteryzować za pomocą własności nazywanej
bezwładnością, której miarą jest masa ciała m.
Szybkość zmiany pędu ciała równa jest sile działającej na ciało.
- drugie prawo Newtona, a jednocześnie dynamiczne równanie ruchu ciała.
Dynamiczne równanie ruchu (różniczkowe równanie ruchu) - Równanie różniczkowe, określające
szybkość zmian pewnych wielkości fizycznych (np. prędkości, położenia), jako funkcję aktualnego stanu
układu. Przez równanie ruchu najczęściej rozumiemy drugą zasadę dynamiki Newtona, zapisaną w
postaci równania różniczkowego.
Gdy masa pozostaje stała w czasie, wtedy możemy napisać:
Trzecie prawo Newtona
Każde działanie jednych ciał na drugie ma charakter wzajemnego oddziaływania:, jeżeli ciało 1 działa
na ciało 2 z siłą 𝐹
21
, to ciało 2 działa na ciało 1 z siłą 𝐹
12
.
Siły, którymi działają na siebie oddziaływujące ciała, są równe, co do wartości i kierunku, lecz
przeciwne, co do zwrotu.
𝐹
21
= −𝐹
12
Uwaga: siły 𝐹
21
i 𝐹
12
przyłożone są do różnych ciał.
Trzecie prawo Newtona przestaje być słuszne dla prędkości zbliżonych do prędkości światła υ ≈ 𝑐. W
ramach mechaniki newtonowskiej przyjmuje się, że prędkość rozchodzenia się za-burzenia pola jest
nieskończona, a trzecie prawo Newtona jest zawsze słuszne.
5. Nieinercjalne układy odniesienia, siły bezwładności.
Prawa Newtona są spełnione tylko w inercjalnych układach odniesienia.
Dany układ odniesienia jest nieinercjalny, gdy:
- porusza się względem układu inercjalnego z pewnym przyspieszeniem,
- wiruje względem układu inercjalnego.
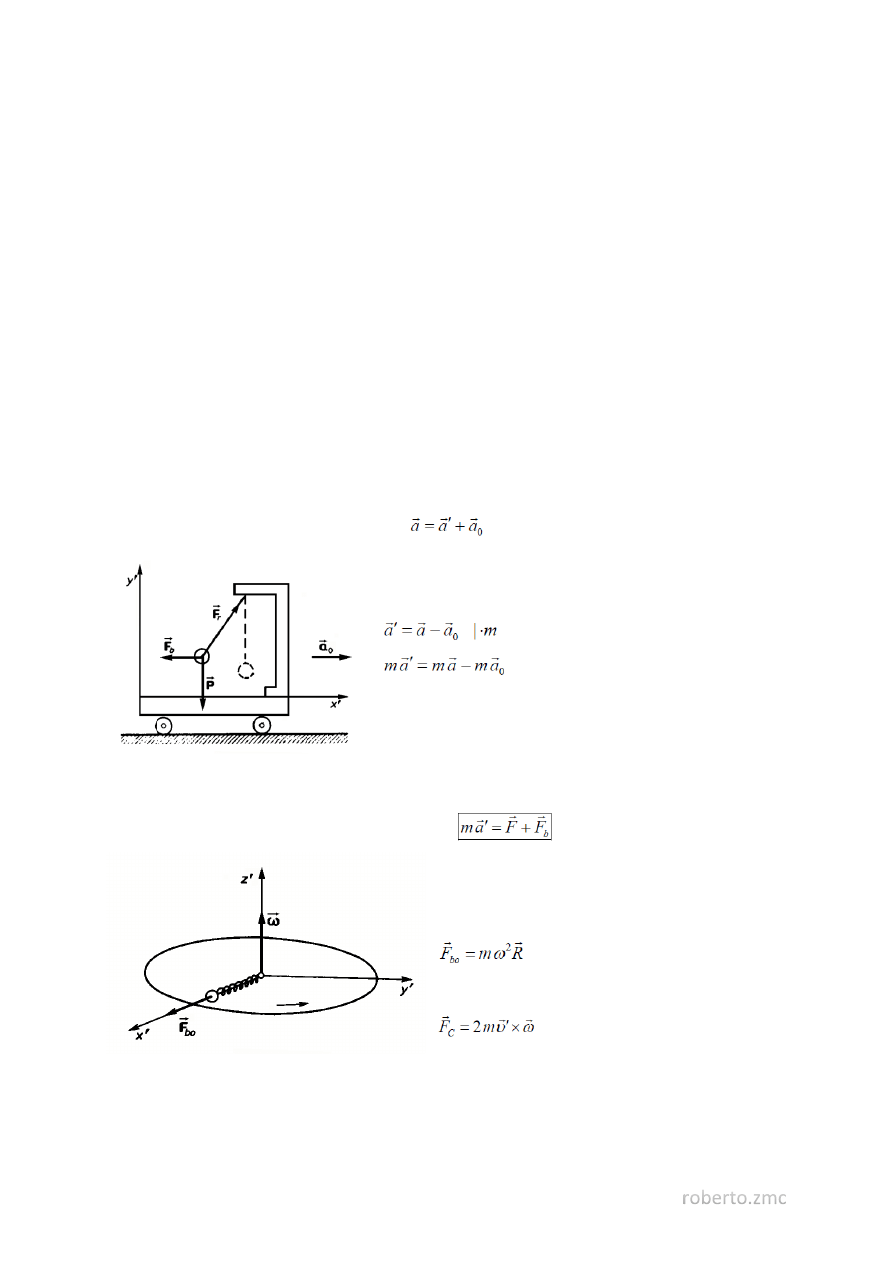
W przypadku postępowego ruchu przyspieszonego mamy:
𝑎 jest przyspieszeniem ciała względem zewnętrznego układu
inercjalnego, 𝑎 ′ - względem poruszającego się z
przyspieszeniem 𝑎
0
układu nieinercjalnego (wózka)
Zgodnie z drugą zasadą dynamiki 𝑚𝑎 = 𝐹 . Składnik −𝑚𝑎
0
oznaczymy, jako 𝐹
𝑏
, i nazwiemy siłą
bezwładności. Siła bezwładności jest siłą pozorną, gdyż nie można wskazać ciała, od którego pochodzi.
Drugie prawo Newtona w układzie nieinercjalnym:
W układzie obracającym się występują dwie siły
bezwładności:
- siła odśrodkowa
- siła Coriolisa
Siły bezwładności nie wynikają z działania na dane ciało innych ciał, tak jak siły np. sprężystości,
grawitacyjne, tarcia itd., ale są uwarunkowane własnościami układu odniesienia, w którym
analizowane są zjawiska mechaniczne. Dlatego siły bezwładności nazywane są siłami fikcyjnymi, albo
pozornymi.
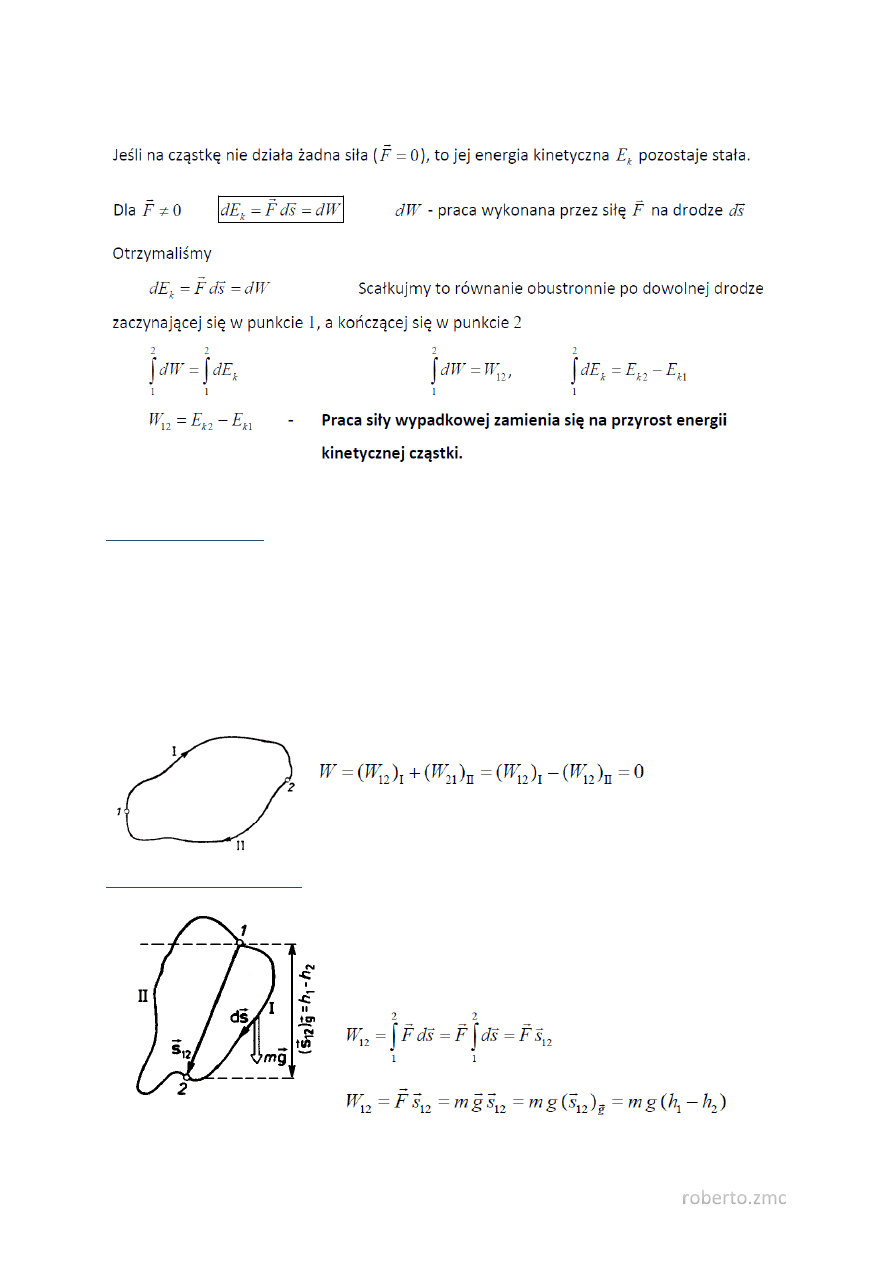
6. Energia kinetyczna cząstki, a praca sił działających na cząstkę.
7. Siły zachowawcze i ich praca.
Pole sił zachowawczych
Jeżeli w każdym punkcie przestrzeni cząstka jest poddana działaniu innych ciał, to mówimy, że cząstka
znajduje się w polu sił.
Pole stacjonarne - Pole, które nie zmienia się w czasie.
Pole zachowawcze - Pole stacjonarne, w którym praca wykonana nad cząstką przez siły pola zależy
tylko od początkowego i końcowego położenia cząstki, nie zależy natomiast od drogi, po której porusza
się cząstka.
Praca sił zachowawczych na drodze zamkniętej jest równa zeru.
Zachowawczość siły ciężkości
Siła ciężkości jest siłą zachowawczą. W ograniczonym obszarze
przestrzeni można przyjąć, że siła ta ma w dowolnym punkcie tę
samą wartość, ten sam kierunek i ten sam zwrot. Praca wykonana
przez siły pola na drodze od punktu 1 do punktu 2 wynosi
𝑊
12
nie zależy od kształtu toru łączącego punkty 1 i 2,a więc 𝐹 jest tu siłą zachowawczą.
Można pokazać, że siłą zachowawczą jest również każda siła centralna
8. Zależność między siłą, a energią potencjalną.
Energia potencjalna cząstki w polu sił
W zachowawczym polu sił każdej cząstce umieszczonej w dowolnym punkcie pola można przypisać
wartość pewnej funkcji 𝐸
𝑝
(𝑥, 𝑦, 𝑧), taką, że praca sił pola przy przeniesieniu tej cząstki z punktu 1 do
punktu 2 równa jest ubytkowi tej funkcji (przyrostowi ze znakiem minus):
Energia potencjalna określona jest z dokładnością do pewnej nieznanej stałej addytywnej
Znając siły pola możemy określić tylko różnice energii potencjalnej cząstki w poszczególnych punktach
pola, ale nie wartości bezwzględne tej energii.
Zależność sił pola od energii potencjalnej
Znając postać funkcji 𝐸
𝑝
(𝑥, 𝑦, 𝑧) dla danej cząstki można określić siłę, która działa na cząstkę w każdym
punkcie pola. Ponieważ dla dowolnych dwóch punktów 1 i 2 mamy
więc zachodzi
lub inaczej
Siła zachowawcza jest równa gradientowi energii potencjalnej ze znakiem minus.
9. Zasada zachowania energii mechanicznej.
W polu sił zachowawczych całkowita energia mechaniczna E cząstki zdefiniowana,
jako jest taka sama w każdym punkcie tego pola.
Prawo zachowania energii mechanicznej
Całkowita energia mechaniczna układu ciał, na które działają tylko siły zachowawcze, jest stała.
10. Zasada zachowania pędu układu cząstek.
Prawo zachowania pędu
Pęd odosobnionego układu punktów materialnych jest stały. Pęd jest stały również w przypadku
układu nieodosobnionego, o ile wypadkowa sił zewnętrznych jest równa zeru.
11. Zasada zachowania momentu pędu układu cząstek.
Można pokazać, że
Pochodna po czasie momentu pędu jest równa sumie momentów sił zewnętrznych.
Przy braku momentów sił zewnętrznych
Prawo zachowania momentu pędu
Moment pędu odosobnionego układu cząstek jest stały. Moment pędu jest stały również dla układu
nieodosobnionego, o ile całkowity moment sił zewnętrznych jest równy zeru.
12. Zderzenia ciał.
Ciała zderzające się ze sobą ulegają odkształceniom. To powoduje, że w punkcie zetknięcia narasta
szybko duża siła kontaktowa. Siła ta powoduje zmianę kierunku i wartości względnej prędkości obu
ciał.
Zderzenie sprężyste (elastyczne) - Zderzenie, w którym energia mechaniczna ciał nie przechodzi w
inne, niemechaniczne postacie energii. Zwroty i kierunki prędkości ciał po zderzeniu określone są przez
prawo zachowania pędu i prawo zachowania energii mechanicznej.
Zderzenie niesprężyste (nieelastyczne) - Zderzenie, w którym energia kinetyczna ciał całkowicie lub
częściowo zamienia się na energię wewnętrzną. Wzrost energii wewnętrznej ciał zazwyczaj sprowadza
się do podwyższenia ich temperatury.
Zderzenie całkowicie niesprężyste (doskonale nieelastyczne) - Zderzenie, w którym następuje
największa możliwa strata energii kinetycznej, tj. zderzenie, którego produkty mają najmniejszą
możliwą energię kinetyczną umożliwiającą im spełnienie zasady zachowania pędu. Po takim zderzeniu
ciała poruszają się z jednakową prędkością, albo spoczywają.
Zderzenie centralne - Zderzenie dwóch ciał, w którym ich wektory prędkości (przed i po zderzeniu) leżą
na tej samej prostej przechodzącej przez środek masy tych ciał. W wyniku zderzenia centralnego
następuje największa możliwa zmiana pędu.
Całkowicie niesprężyste zderzenie dwóch cząstek tworzących układ odosobniony
Podczas zderzenia niesprężystego w nieobecności sił zewnętrznych zachowany jest całkowity pęd
cząstek. Część energii kinetycznej przechodzi w ciepło, a więc całkowita energia mechaniczna cząstek
nie jest zachowana
Centralne, sprężyste zderzenie jednorodnych i nieobracających się kul, tworzących układ odosobniony
Podczas zderzenia sprężystego w nieobecności sił zewnętrznych zachowany jest całkowity pęd cząstek
i ich całkowita energia kinetyczna.
Zachowanie energii:
Zachowanie pędu:
Po wstawieniu (***) do (*) mamy
Otrzymaliśmy:
13. Pole grawitacyjne. Energia potencjalna ciała w polu grawitacyjnym.
Prawo powszechnego ciążenia (prawo grawitacji)
Dwa punkty materialne o masach m
1
i m
2
przyciągają się wzajemnie siłą proporcjonalną do iloczynu
ich mas i odwrotnie proporcjonalną do kwadratu ich odległości r.
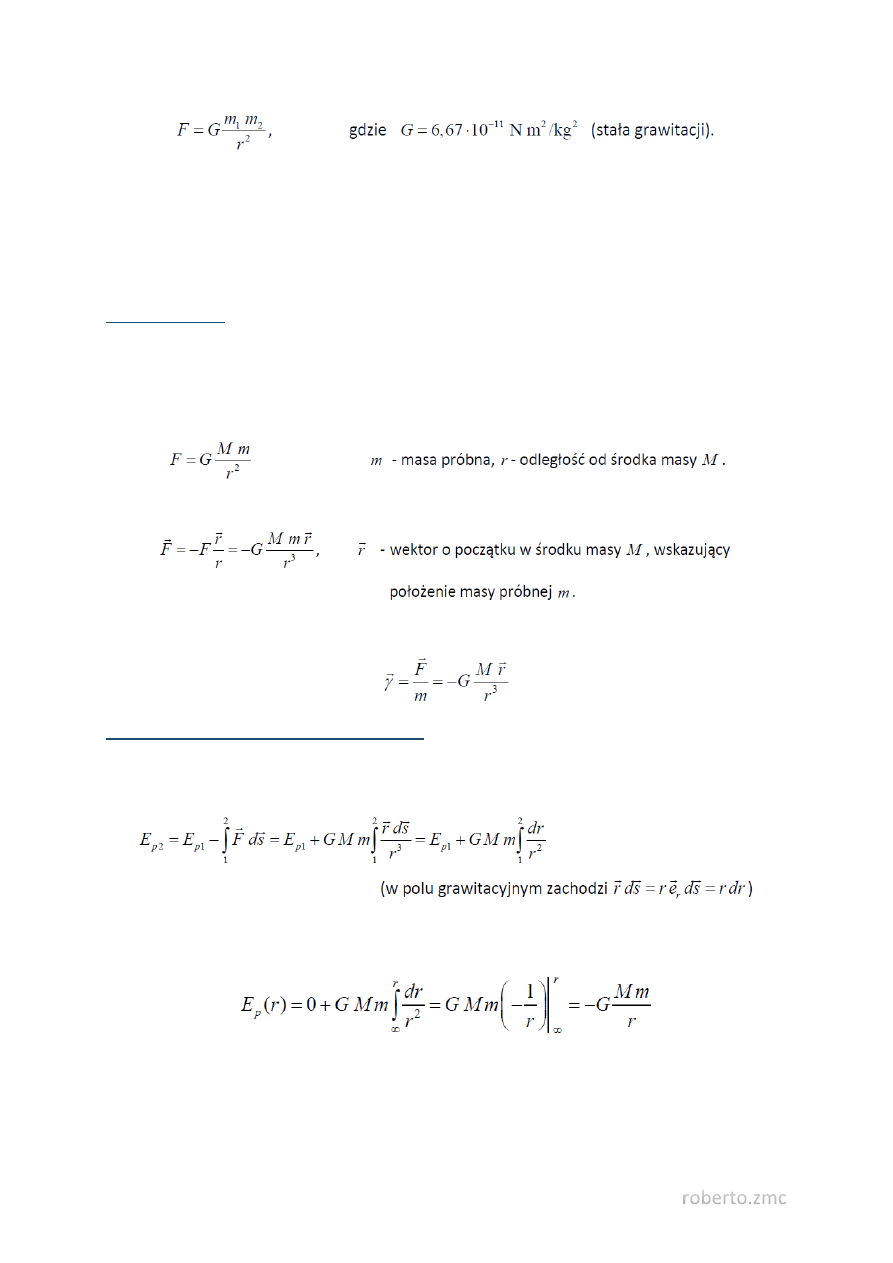
Ciała rozciągłe o skończonych rozmiarach traktujemy, jako układy punktów materialnych. Siły
przyciągania między takimi ciałami oblicza się przez całkowanie prawa powszechnego ciążenia dla
punktów materialnych. Można udowodnić, że
Jednorodne ciała kuliste oraz ciała złożone z jednorodnych koncentrycznych warstw kulistych
przyciągają się tak, jak punkty materialne umieszczone w ich środkach.
Pole grawitacyjne
Jest to pole sił przyciągania grawitacyjnego w przestrzeni otaczającej masę M. Jeśli masa M jest
punktem materialnym, jednorodnym ciałem kulistym, lub ciałem złożonym z jednorodnych
koncentrycznych warstw kulistych, to pole grawitacyjne wytwarzane przez masę M opisane jest
wyrażeniem
Pole grawitacyjne masy M można opisać wektorowo
Natężenie pola grawitacyjnego - Stosunek siły działającej na masę próbną do wartości tej masy.
Energia potencjalna ciała w polu grawitacyjnym
Pole grawitacyjne jest polem zachowawczym, dlatego można określić energię potencjalną ciał
znajdujących się w tym polu.
Zazwyczaj przyjmujemy, że energia potencjalna ciała m znajdującego się nieskończenie dużej odległości
od masy M jest równa zeru. Stąd mamy
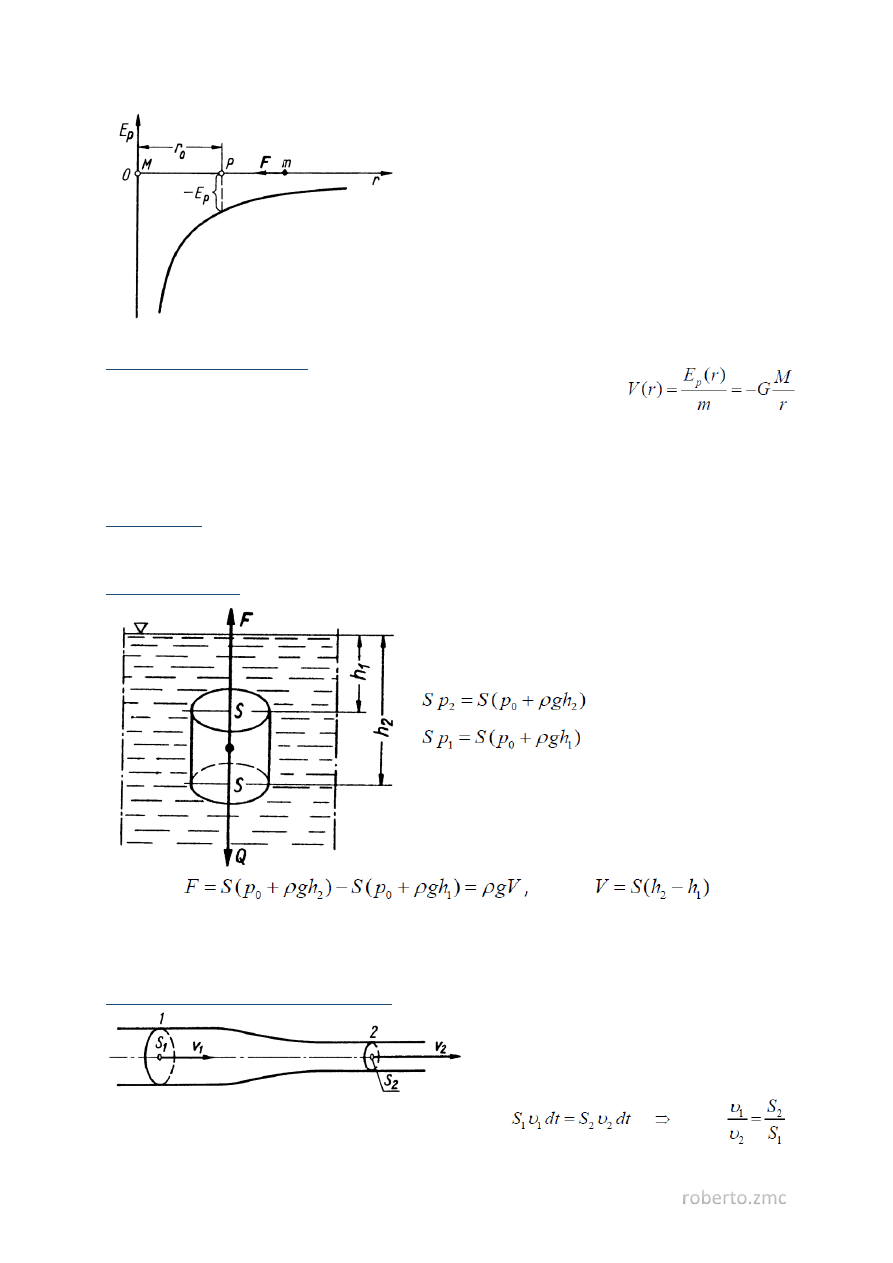
Energia potencjalna masy próbnej m jest ujemna i rośnie
w miarę oddalania się od masy M, osiągając wartość
zero w nieskończoności.
Potencjał pola grawitacyjnego
Jest to stosunek energii potencjalnej masy próbnej m do wartości tej masy.
Potencjał określa energię potencjalną w odległości r od środka masy M przypadającą na jednostkę
masy próbnej i wyraża się w J/kg.
14. Prawa Pascala i Archimedesa.
Prawo Pascala
Ciśnienie zewnętrzne wywierane na płyn jest przenoszone we wszystkich kierunkach jednakowo.
Prawo Archimedesa
Siły działające na boczne ścianki cylindra są skierowane
prostopadle do ścianek i znoszą się. Siły działające na
dolną i górną powierzchnię:
Siła wypadkowa:
Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy.
15. Równanie ciągłości strugi cieczy. Prawo Bernoulliego.
Równanie ciągłości dla cieczy nieściśliwych
Załóżmy, że przepływ jest stacjonarny. Przez
przekrój "1" i "2" w czasie dt przepływają te
same objętości cieczy.
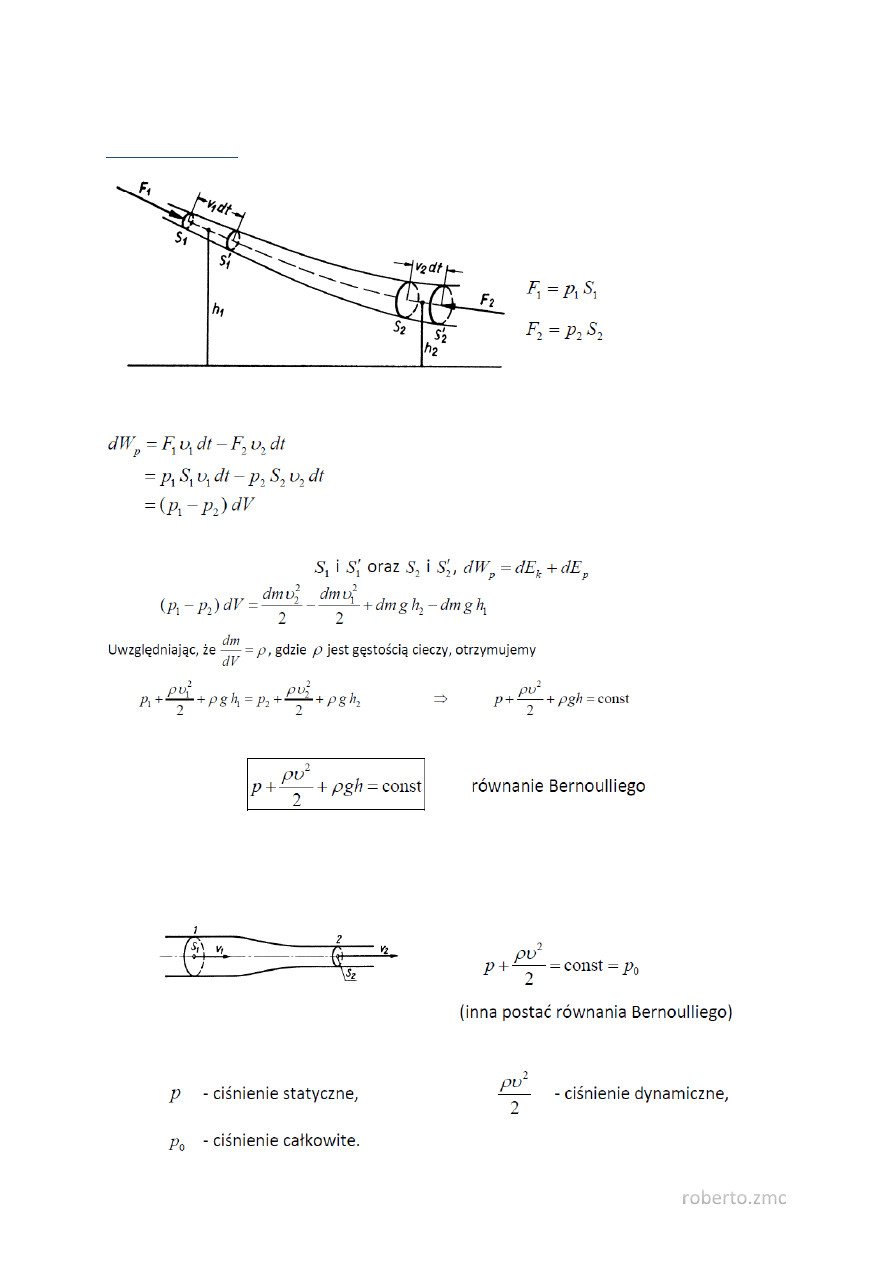
Prędkości cieczy w strudze są odwrotnie proporcjonalne do powierzchni przekrojów strugi.
Prawo Bernoulliego
Załóżmy, że przepływ cieczy doskonałej
(w której nie występują siły lepkości)
następuje od przekroju S
1
do przekroju
S
2
. Siły parcia:
Obliczmy pracę sił parcia w odcinku czasu dt
W nieobecności sił lepkości praca ta równa jest zmianie energii kinetycznej i potencjalnej mas dm cieczy
zawartej między przekrojami
, czyli
Ogólnie możemy więc napisać
Suma ciśnienia oraz energii kinetycznej i potencjalnej jednostki objętości ustalonego przepływu
cieczy doskonałej jest wielkością stałą.
W przypadku pomijalnie małych zmian wysokości przepływu zachodzi:
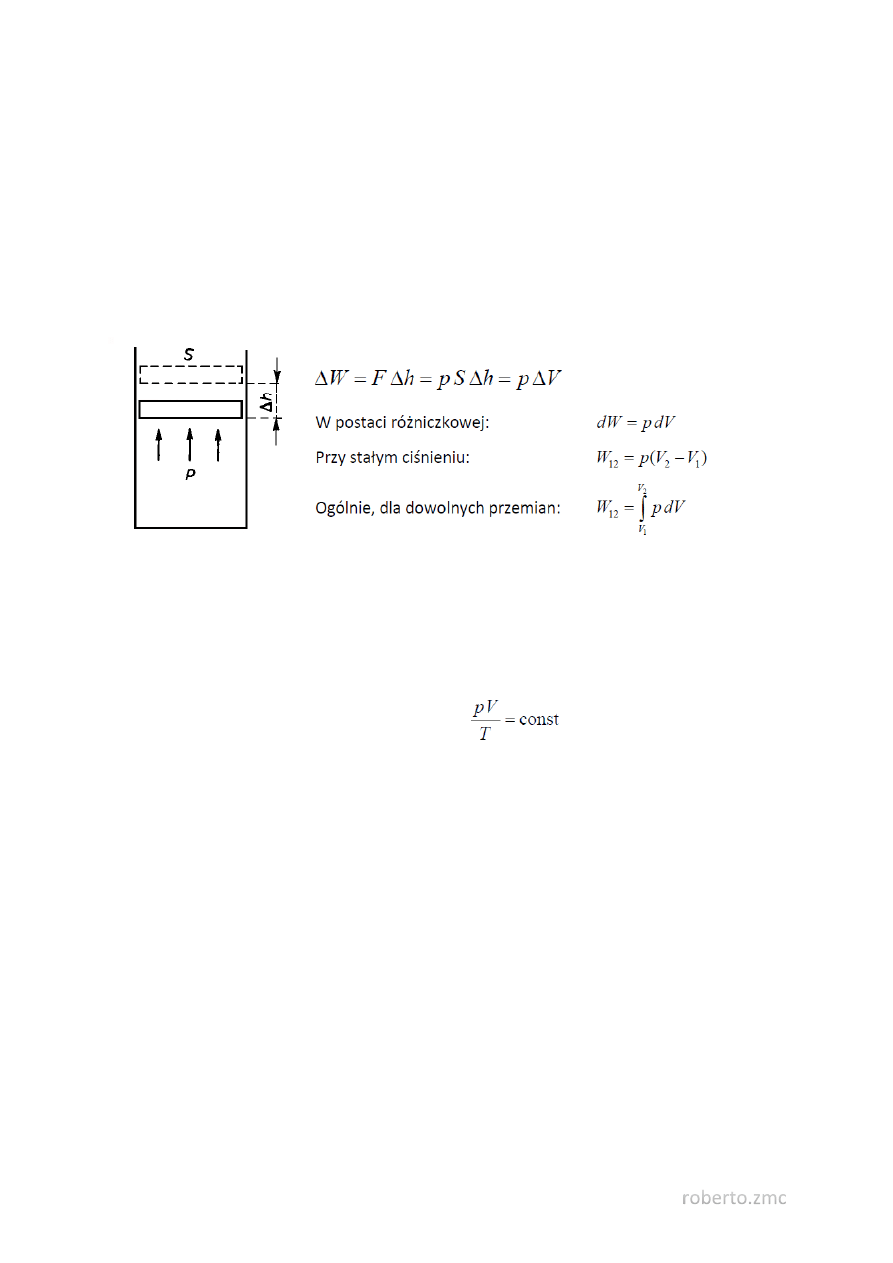
16. Pierwsza zasada termodynamiki.
Pierwsza zasada termodynamiki
Ciepło dostarczone do układu jest zużywane na przyrost energii wewnętrznej tego układu i na
wykonywanie przez układ pracy nad ciałami zewnętrznymi.
W postaci różniczkowej pierwsza zasada termodynamiki zapisywana jest, jako
𝑑𝑄 = 𝑑𝑈 + 𝑑𝑊
17. Praca wykonana przez ciało w przypadku zmiany objętości.
Infinitezymalne przesunięcie tłoka o Δh odpowiada pracy:
18. Równanie gazu doskonałego.
Stan gazu doskonałego jest określony przez trzy parametry:
p - ciśnienie, V - objętość, T - temperatura.
Badania doświadczalne, a także rozważania teoretyczne pokazują, że w przypadku gazu doskonałego
parametry te łączy prosty związek.
Równanie gazu doskonałego (równanie Clapeyrona):
Prawo Avogadra - W warunkach, scharakteryzowanych przez te same wartości parametrów p i T, mol
każdego gazu zajmuje tę samą objętość.
19. Pojemność cieplna.
Otrzymujemy stąd, że dla ciała o dowolnej masie m zachodzi
20. Przemiany gazu doskonałego.
Spośród wielu możliwych przemian gazu doskonałego na wyróżnienie zasługują przemiany, w których
- oprócz równania stanu - spełniony jest dodatkowy warunek określający rodzaj przemiany
Przykładem przemiany adiabatycznej może być sprężanie i rozprężanie gazu przy rozchodzeniu się w
gazie fali dźwiękowej, w odniesieniu do małych objętości.
21. Ruch cieplny cząsteczek - ciśnienie gazu.
22. Średnia energia ruchu postępowego cząsteczek.
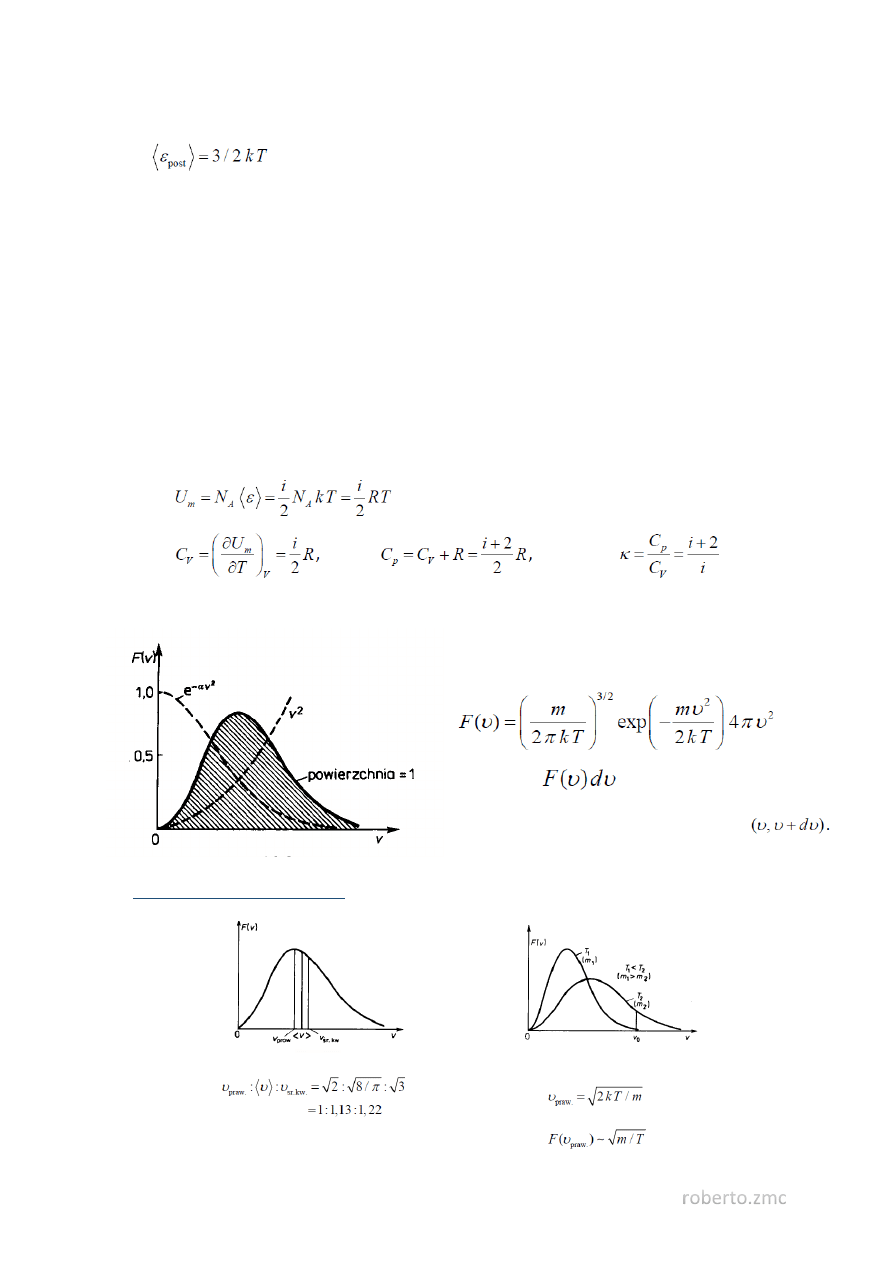
23. Zasada ekwipartycji energii.
Wynik
wiąże się z prawem ekwipartycji energii (zasadą równego rozkładu energii
na stopnie swobody cząsteczek):
Na każdy rodzaj ruchu (stopień swobody) przypada - średnio - taka sama energia kinetyczna 1/2kT.
Liczbą stopni swobody układu mechanicznego - Jest to liczba niezależnych współrzędnych, za pomocą
których może być opisane położenie układu.
Punkt materialny ma trzy stopnie swobody (do opisu jego położenia w przestrzeni potrzebne są trzy
współrzędne).
Układ N punktów materialnych, które nie są ze sobą sztywno związane ma 3N stopni swobody. Każde
sztywne wiązanie między dwoma punktami zmniejsza liczbę stopni swobody o jeden.
24. Energia wewnętrzna, ciepło molowe cząsteczek gazu doskonałego.
Cząsteczki gazu doskonałego nie oddziałują ze sobą. Stąd
25. Rozkład Maxwella, średnia i najbardziej prawdopodobna prędkość cząsteczek.
F(υ) - funkcja rozkładu prędkości cząsteczek gazu.
Rozkład Maxwella
Wyrażenie
ma znaczenie
prawdopodobieństwa tego, że dana cząsteczka
ma moduł prędkości zawarty w przedziale
Właściwości rozkładu Maxwella
Średnie prędkości cząsteczek gazu
Prędkość najbardziej prawdopodobna
26. Wzór barometryczny, rozkład Boltzmanna.
Wzór barometryczny
n - liczba cząstek w jednostce objętości (koncentracja
cząstek).
Rozkład Boltzmanna
Rozkład Boltzmanna jest to rozkład koncentracji cząsteczek w dowolnym potencjalnym polu sił, o ile
mamy do czynienia ze zbiorem jednakowych cząstek poruszających się chaotycznym ruchem cieplnym.
Liczba cząstek 𝑑𝑁
𝑥,𝑦,𝑧
w elemencie objętości 𝑑𝑉 = 𝑑𝑥𝑑𝑦𝑑𝑧
27. Entropia, a prawdopodobieństwo termodynamiczne.
Prawdopodobieństwo termodynamiczne, Ω (waga statystyczna) - Liczba różnych mikrostanów
odpowiadająca danemu makrostanowi.
Prawdopodobieństwo termodynamiczne nie jest wielkością addytywną. Aby to pokazać, weźmy pod
uwagę układ składający się z dwóch praktycznie nieoddziaływujących ze sobą podukładów. Mamy
Wielkością addytywną jest ln Ω. Jako wielkość charakteryzującą stan wprowadza się więc entropię
układu zdefiniowaną, jako
𝑆 = 𝑘𝑙𝑛Ω
(k – stała Boltzmanna)
Główne właściwości entropii (wynikające z właściwości prawdopodobieństwa termodynamicznego)
Entropia jest ilościową miarą stopnia cząsteczkowego chaosu w układzie.
28. Związek przyrostu entropii z ilością ciepła dostarczonego do układu.
Zmiana entropii w procesie odwracalnym, a ciepło dostarczone do układu
Fizyka statystyczna pokazuje, że w dowolnym procesie odwracalnym zachodzi
Zmiany entropii układu w procesach nieodwracalnych
Jeśli ilość ciepła dQ jest doprowadzana do układu w procesie nieodwracalnym, to entropia układu
wzrasta zarówno w wyniku dostarczania ciepła, jak i w wyniku nieodwracalności samej przemiany.
Wówczas
Podczas przemiany nieodwracalnej temperatura układu nie jest określona. Symbol T oznacza tu więc
temperaturę termostatu, od którego dany układ pobiera ciepło dQ. Ogólnie
W temperaturze zera bezwzględnego prawdopodobieństwo termodynamiczne stanu układu zmierza
do jedności.
Twierdzenie Nernsta (trzecia zasada termodynamiki)
Jeśli temperatura ciała dąży do zera bezwzględnego, to entropia ciała dąży do zera.
29. Równanie ruchu harmonicznego prostego.
Ruch okresowy - Ruch, który powtarza się w regularnych odstępach czasu.
Ruch harmoniczny - Szczególny przypadek ruchu okresowego, w którym położenie obiektu zmienia się
jak funkcja sinus lub cosinus. W takim ruchu obiekt wykonuje drgania harmoniczne.
Ruch harmoniczny prosty - Ruch, w którym poza siłą harmoniczną nie występują żadne inne siły (np.
tarcia, lub inne siły zewnętrzne zależne od położenia lub prędkości danego obiektu.
Równanie ruchu harmonicznego prostego
Ogólne rozwiązanie równania niejednorodnego jest równe sumie ogólnego rozwiązania
odpowiedniego równania jednorodnego i dowolnego rozwiązania szczególnego równania
niejednorodnego.
30. Składanie drgań harmonicznych.
Składanie drgań równoległych
Mamy dwa drgania składowe:
Założymy, że A
1
> 0 i A
2
> 0.
Drganie wypadkowe dane jest równaniem
Złożenie dwóch drgań równoległych o dowolnych amplitudach można analizować używając metody
wektorowej lub metody wskazów.
Diagram wektorowy.
Z twierdzenia cosinusów
Jeśli ɷ
1
≠ ɷ
2
, to amplituda A zmienia się w czasie. Występuje wtedy modulacja amplitudy.
Z diagramu wektorowego widać również, że
Dodawanie drgań prostopadłych
Weźmy pod uwagę drganie punktu materialnego będące wynikiem nałożenia się dwóch drgań
harmonicznych odpowiednio wzdłuż osi x i y.
- równanie toru w postaci parametrycznej
Położenie tego punktu może być opisane wektorem
31. Równanie fali płaskiej.
Fala płaska - Fala, która może być opisana tylko jedną składową wektora prędkości, np. υ
x
= υ
f
i jedną
współrzędną przestrzenną, np. x. Powierzchnia stałej fazy fali płaskiej jest płaszczyzną.
32. Fala stojąca a fala biegnąca.
Fala stojąca powstaje w wyniku nałożenia się dwóch ciągów falowych o jednakowych częstościach,
jednakowych amplitudach, ale biegnących w przeciwnych kierunkach.
33. Prędkość fazowa fal podłużnych w ciele stałym.
34. Prędkość fal akustycznych w gazach.
W tym przypadku deformacja ośrodka polega na zmianie objętości. Można przyjąć, że przemiany
towarzyszące propagacji fali akustycznej w gazie są przemianami adiabatycznymi opisanymi
równaniem Poissona 𝑝𝑉
𝜅
= 𝑐𝑜𝑛𝑠𝑡
W wyniku zróżniczkowania równania Poissona mamy
Aby odnieść się do skończonych zmian ciśnienia i objętości scałkujmy obustronnie to ostatnie równanie
w granicach odpowiednio od 𝑝 do 𝑝 + 𝛥𝑝 i od 𝑉 do V+𝛥𝑉
Biorąc pod uwagę, że w przypadku najgłośniejszych dźwięków amplituda drgań nie przewyższa 1mmHg
przy ciśnieniu atmosferycznym rzędu 10
3
mmHg i, że związane z tym względne zmiany objętości są
również bardzo niewielkie, możemy napisać
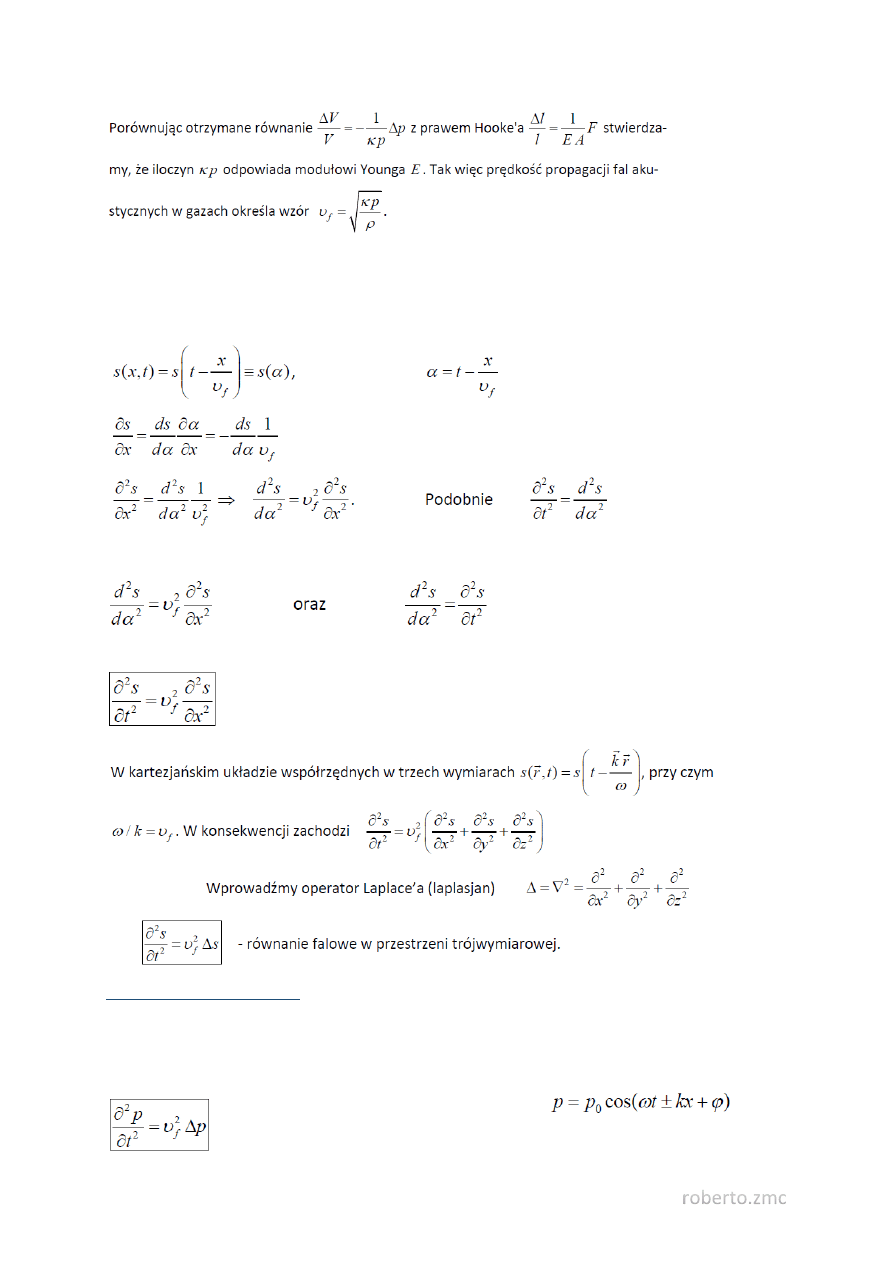
35. Równanie falowe.
Weźmy równanie dowolnego zaburzenia o charakterze periodycznym, lub nawet nieperiodycznym (np.
pojedynczy impuls)
Otrzymaliśmy
Stąd wynika, że
- równanie falowe (jednowymiarowe), równanie różniczkowe ruchu falowego.
Równanie falowe w akustyce
W przypadku fal akustycznych można pokazać, że równanie falowe odnosi się nie tylko do zmian
położenia drgających cząstek ośrodka, ale również do zmian tzw. ciśnienia akustycznego p (lokalnego
odchylenia od ciśnienia średniego)
W przypadku harmonicznych fal dźwiękowych
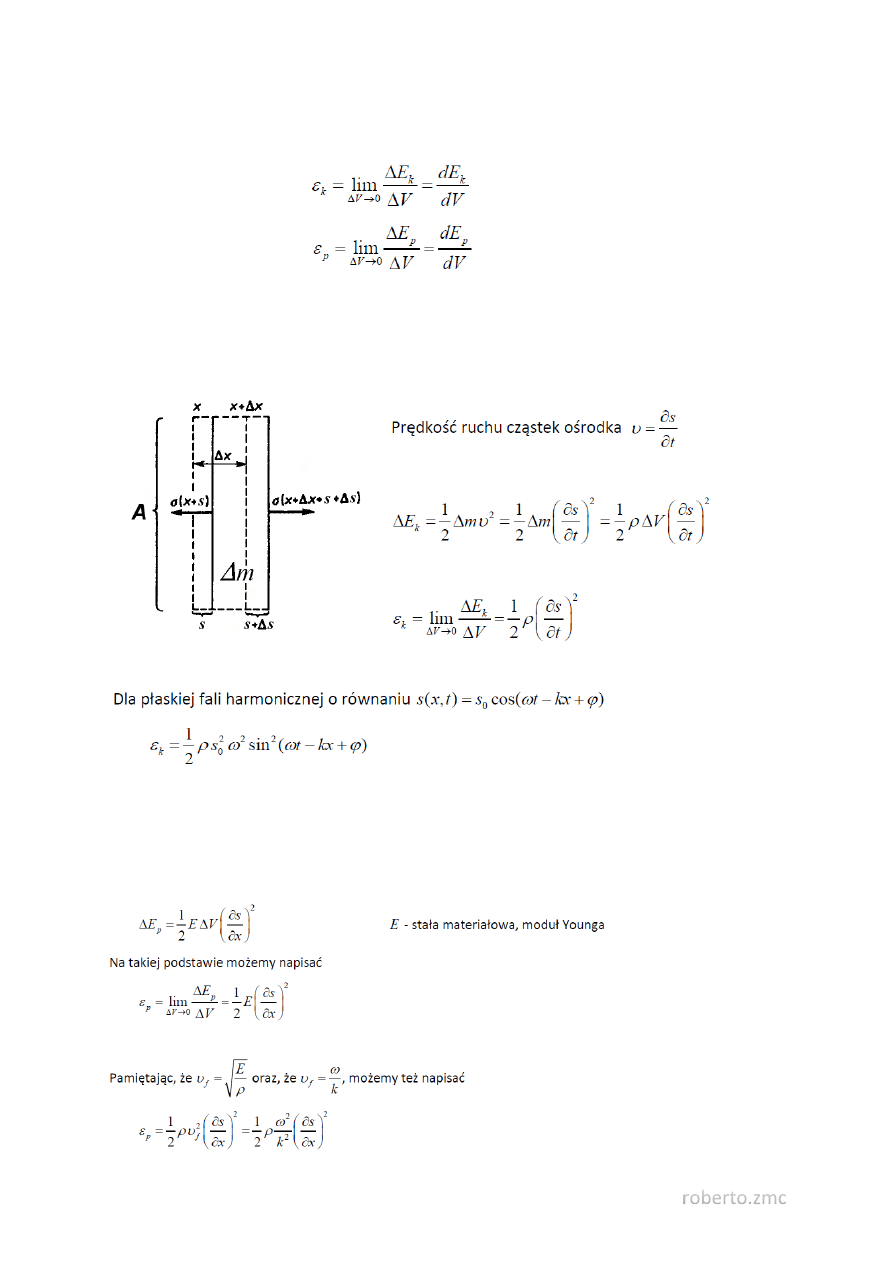
36. Gęstość energii fali.
Jest to ilość energii ruchu falowego zawarta w jednostce objętości ośrodka
Gęstość energii kinetycznej
Gęstość energii potencjalnej
37. Gęstość energii kinetycznej fali podłużnej.
Weźmy pod uwagę prostopadłą do kierunku ruchu podłużnej płaskiej fali 𝑠 = 𝑠(𝑥, 𝑡) warstwę ośrodka
o masie 𝛥𝑚 i o grubości 𝛥𝑥 w nieobecności ruchu falowego
38. Gęstość energii potencjalnej fali podłużnej.
W obecności ruchu falowego warstwa ośrodka o masie 𝛥𝑚 i początkowej grubości 𝛥𝑥 ciągle w wyniku
zewnętrznych naprężeń zmienia swoją grubość. Można pokazać, że z tymi odkształceniami wiąże się
energia potencjalna
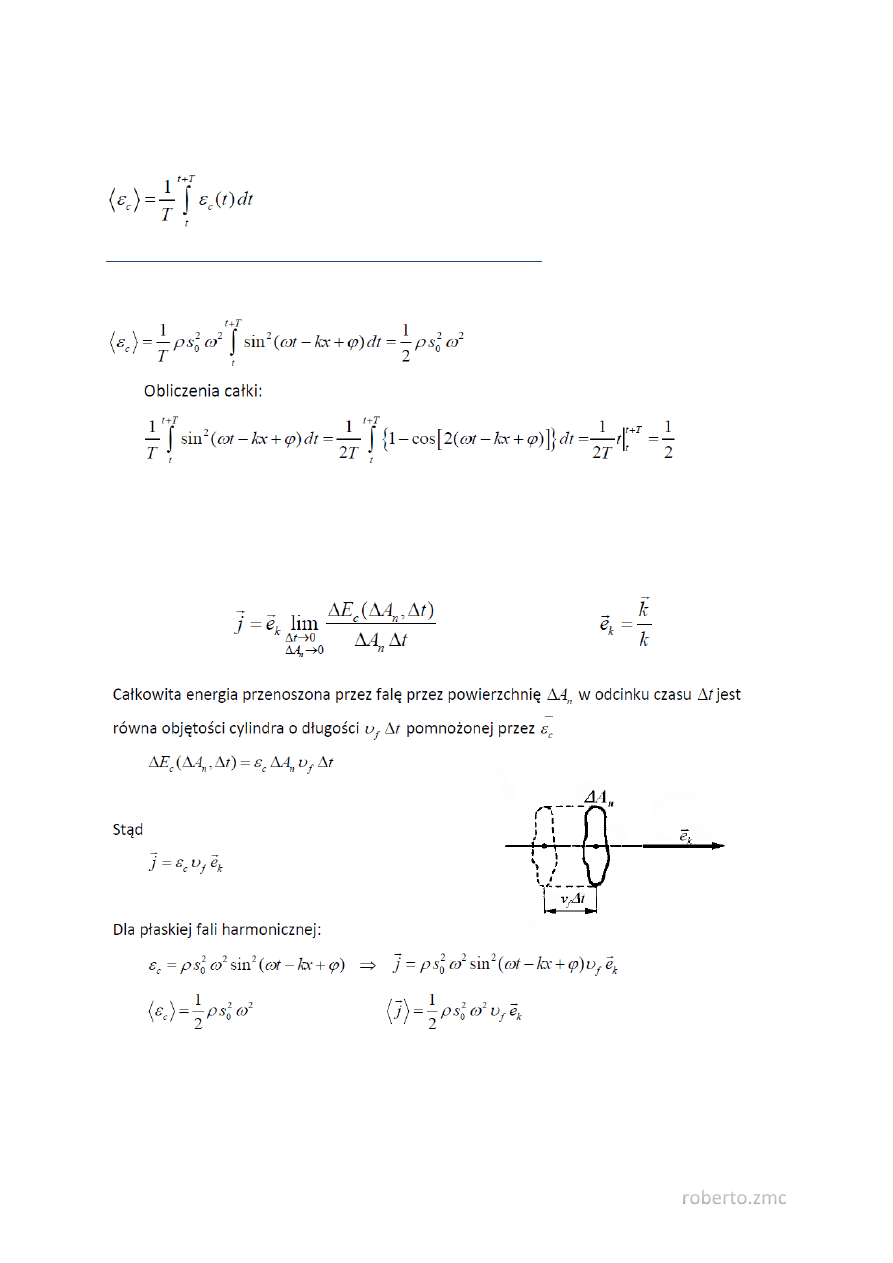
39. Średnia gęstość energii ruchu falowego.
Średnią (całkowitą) gęstość energii ruchu falowego oblicza się z równania
Średnia gęstość energii ruchu falowego płaskiej fali harmonicznej
Dla płaskiej fali harmonicznej
40. Wektor gęstości strumienia energii fali.
Jest to wektor (Poyntinga - Umowa) o kierunku zgodnym z kierunkiem rozchodzenia się fali i o długości
równej całkowitej ilości energii przenoszonej przez falę przez jednostkową powierzchnię prostopadłą
do kierunku rozchodzenia się fali w jednostce czasu.
41. Strumień energii fali. Natężenie fali.
Strumień energii fali
Natężenie fali
Jest to średnia ilość całkowitej energii przenoszonej przez falę przez jednostkową powierzchnię
prostopadłą do kierunku rozchodzenia się fali w jednostce czasu
Dla fali biegnącej o jednej częstości
Stąd dla płaskiej fali harmonicznej
42. Główne parametry ośrodka przenoszącego fale sprężyste.
Gęstość ośrodka - Gęstość ośrodka w danym punkcie jest granicą stosunku masy do objętości,
gdy objętość obejmuje coraz mniejsze obszary przestrzenne zawierające dany punkt.
Moduł sprężystości podłużnej (moduł Younga) - Moduł
Younga E jest hipotetycznym naprężeniem (F/A), które
wystąpiłoby przy dwukrotnym wydłużeniu próbki materiału
(𝛥𝑙 = 𝑙), przy założeniu, że jej przekrój (A) nie ulegnie zmianie.
Moduł sprężystości poprzecznej (moduł Kirchhoffa) - Moduł sprężystości poprzecznej
τ ma znaczenie przy takich odkształceniach ośrodka jak ścinanie lub skręcanie.
43. Impedancja falowa.
Weźmy dla uproszczenia pod uwagę falę płaską poruszającą się w dodatnim kierunku osi x
Rozważmy np. falę podłużną w ciele stałym
Stąd
Znaczy to, że w tej fali w każdej chwili prędkość cząstek ośrodka (𝜕𝑠/𝜕𝑡) jest wprost proporcjonalna
do działającego naprężenia. Stałym współczynnikiem proporcjonalności jest impedancja falowa
Przy tym samym naprężeniu cząstki w ośrodkach o małej impedancji falowej poruszają się szybciej niż
cząstki ośrodkach o dużej impedancji falowej.
Podobne rozważania można przeprowadzić dla fal w gazach i dla fal poprzecznych w ciele stałym.
Ogólnie impedancję falową możemy przedstawić wyrażeniem
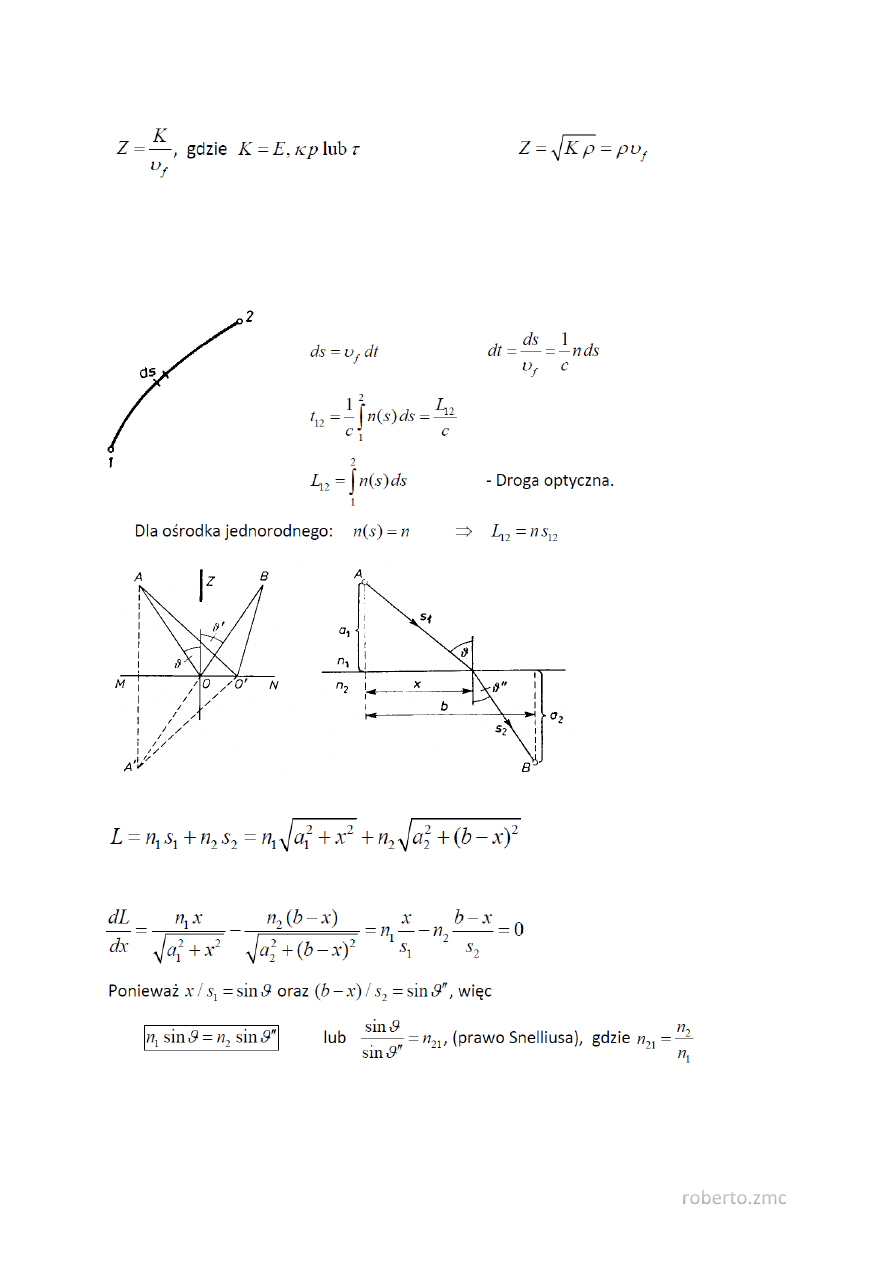
oraz równoważnie
44. Zasada Fermata, a prawa odbicia i załamania.
Światło rozchodzi się po takiej drodze, która wymaga najkrótszego czasu (zasada Fermata,
sformułowana w połowie XVII wieku).
Z zasady Fermata wynikają
prawa odbicia i załamania
światła.
Przy odbiciu (lewy rysunek)
każda droga typu AO’B jest
dłuższa od drogi AOB.
Przy załamaniu (prawy rysunek) droga optyczna dowolnego promienia jest równa:
Droga ekstremalna wynika z zależności:
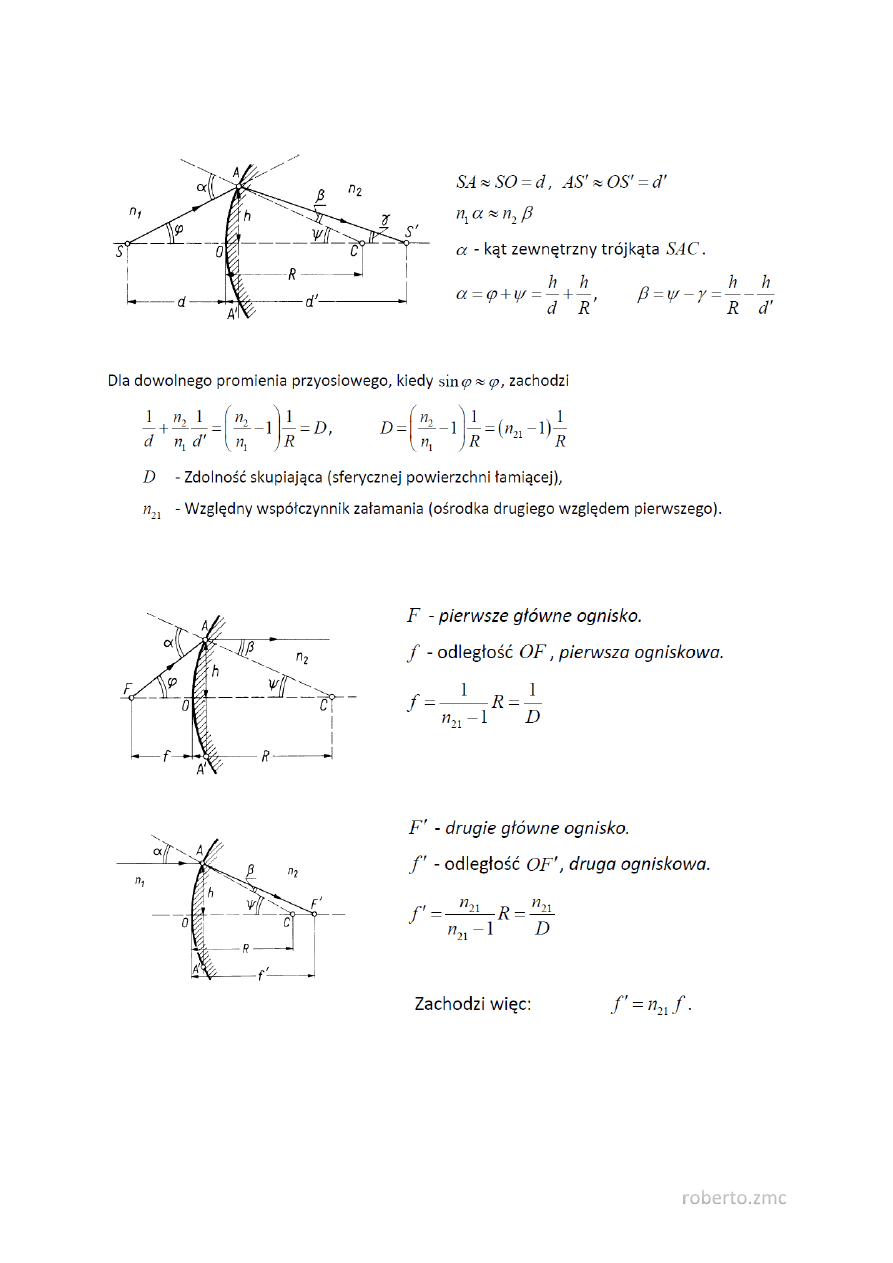
45. Załamania światła na powierzchni sferycznej.
Oś optyczna - Prosta przechodząca przez środek krzywizny powierzchni sferycznej.
Wszystkie promienie przyosiowe wychodzące z punktu S skupiają się w jednym punkcie S′. Punkt S′ jest
obrazem punktu S.
46. Równanie soczewki cienkiej.
Soczewka cienka - Soczewka, której grubość jest znacznie mniejsza od promieni krzywizny powierzchni
ograniczających soczewkę.
Stosując podobne rozważania jak dla pojedynczej powierzchni sferycznej można pokazać, że dla
promieni przyosiowych przechodzących przez cienką soczewkę słuszne jest następujące równanie
soczewki cienkiej
47. Światło, jako fala EM.
Fala elektromagnetyczna powstaje w otoczeniu ładunków elektrycznych poruszających się ruchem
przyspieszonym. Jest złożeniem zmiennego pola elektrycznego i magnetycznego.
48. Superpozycja fal świetlnych.
49. Spójność światła.
Spójność czasowa - Spójność drgań wywołanych przez falę w tym samym punkcie przestrzeni w
różnych momentach czasu. Spójność czasowa jest tym większa im wiązka światła jest bardziej
monochromatyczna.
Spójność przestrzenna - Spójność drgań wywołanych przez falę w różnych punktach powierzchni
falowej.
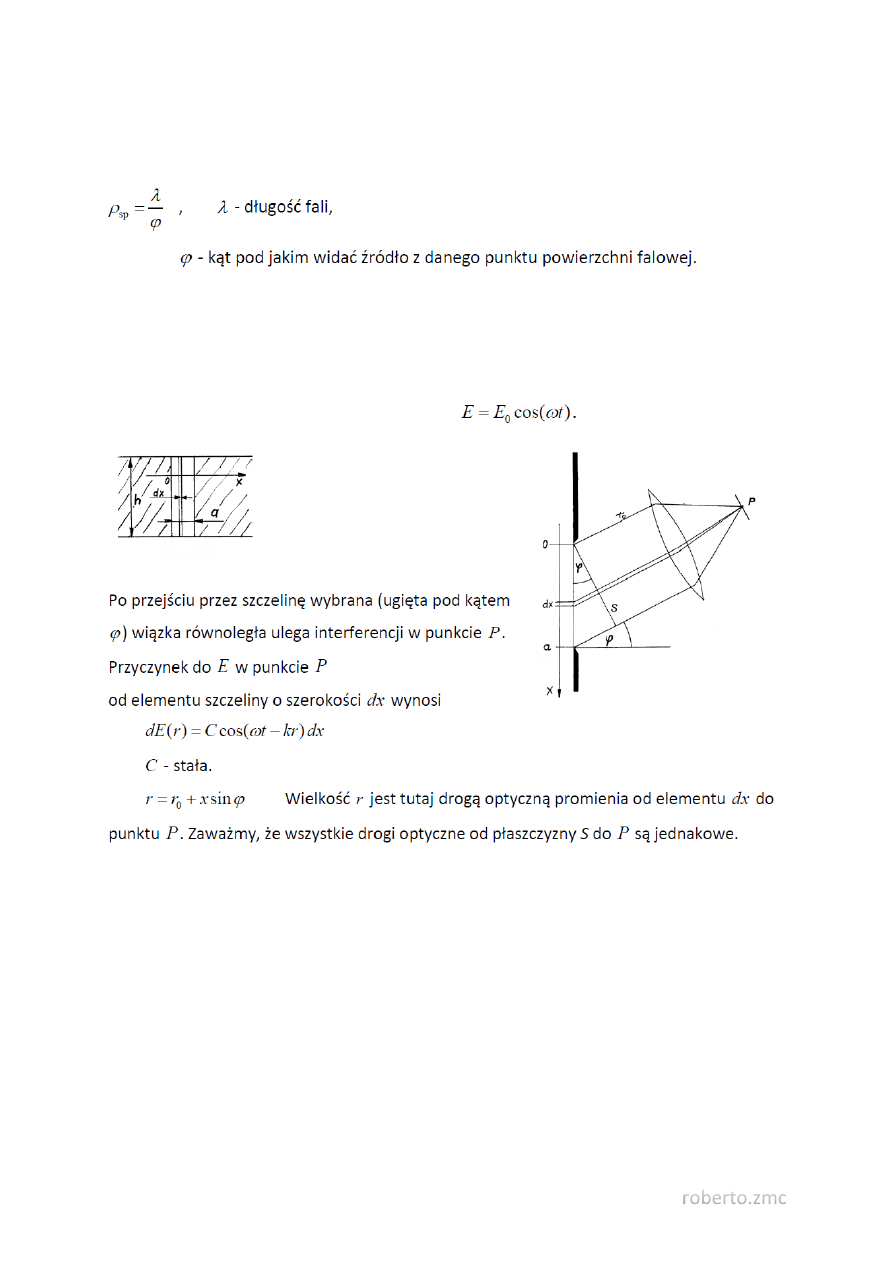
Dla źródeł konwencjonalnych spójność przestrzenna związana jest ze skończonymi rozmiarami
przestrzennymi źródła. Promień spójności 𝜌
𝑠𝑝
obszaru spójności w danym punkcie po-wierzchni
falowej.
50. Dyfrakcja Fraunhofera na pojedynczej szczelinie.
Dyfrakcja - Zespół zjawisk powstających podczas rozchodzenia się światła w ośrodku z ostrymi
niejednorościami, związanych z odchyleniami od praw optyki geometrycznej.
Rozważmy przejście światła przez szczelinę o szerokości a i wysokości h. Załóżmy, że w płaszczyźnie
szczeliny pole elektryczne opisane jest wyrażeniem
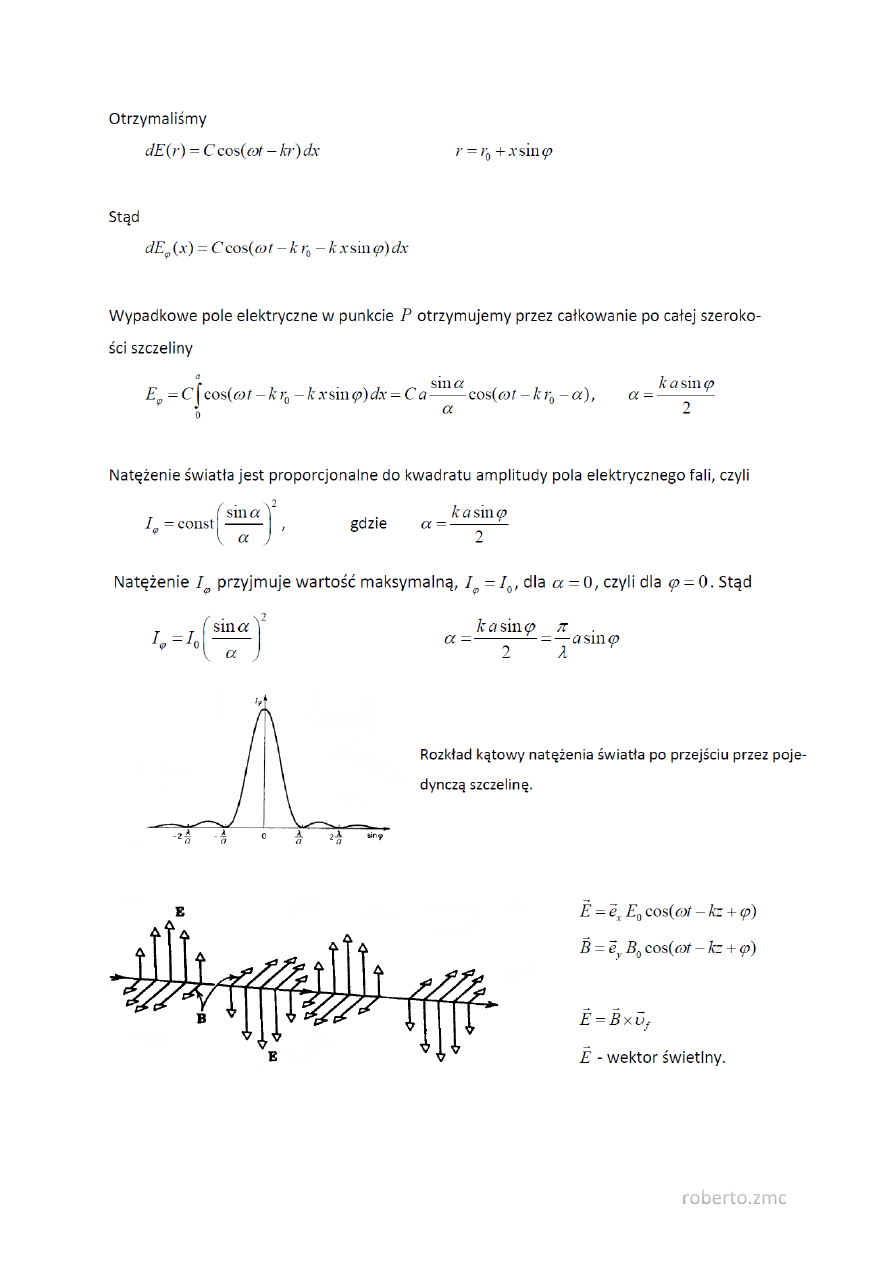
51. Polaryzacja światła.
Światło naturalne - Światło, w którym drgania wektora świetlnego w różnych kierunkach szybko i w
sposób nieuporządkowany zamieniają się wzajemnie (światło zdepolaryzowane).
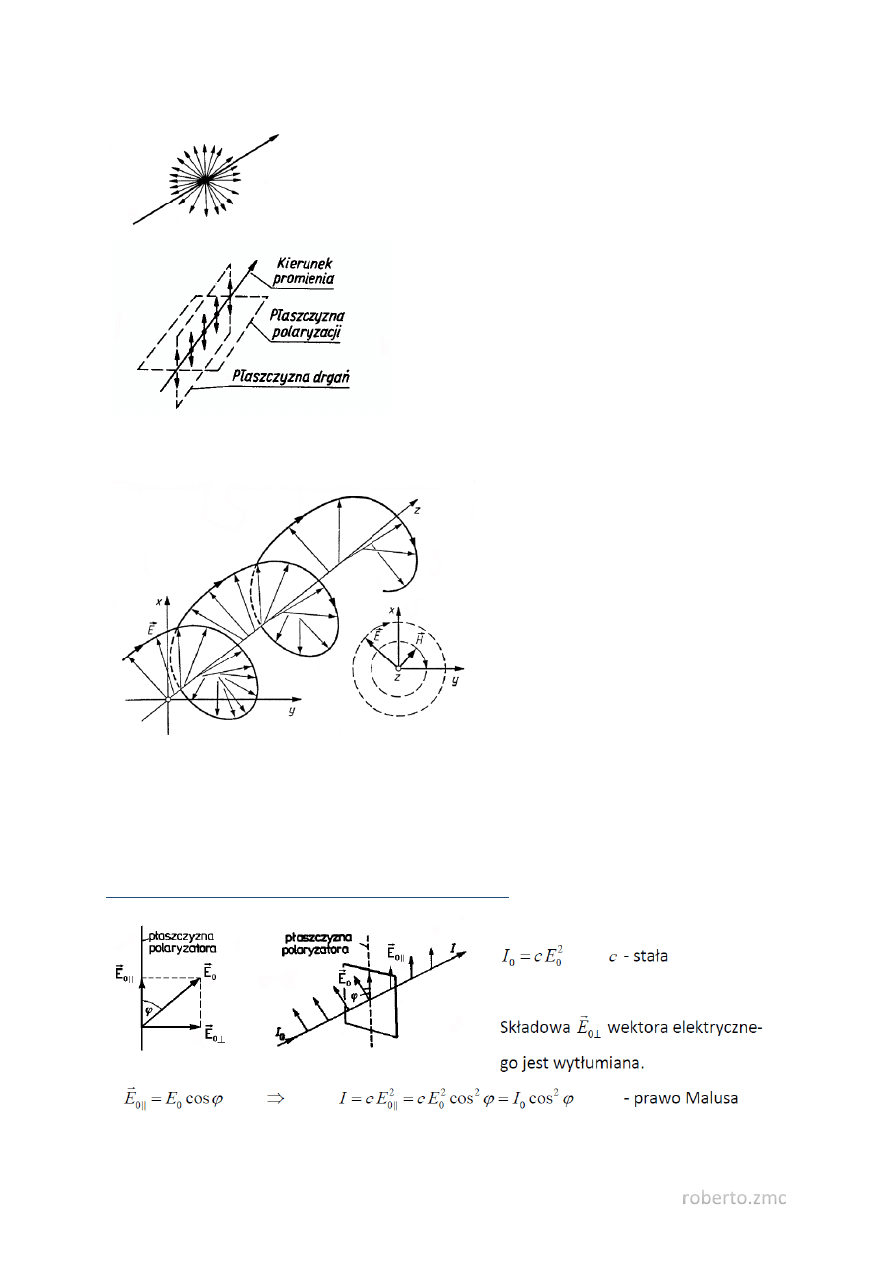
Światło spolaryzowane - Światło, w którym drgania wektora
świetlnego są w jakiś sposób uporządkowane.
Polaryzacja liniowa - Rodzaj polaryzacji, kiedy drgania wektora
świetlnego zachodzą tylko w jednej przechodzącej przez promień
płaszczyźnie.
Ilustracja polaryzacji liniowej. Strzałki przedstawiają
kierunek drgań wektora elektrycznego. W nowszej litera-
turze często płaszczyzną polaryzacji nazywana jest
płaszczyzna drgań.
Polaryzacja eliptyczna - Rodzaj polaryzacji, kiedy w
ustalonej płaszczyźnie prostopadłej do kierunku
rozchodzenia się fali wektor 𝐸⃗ obraca się wokół
promienia, a koniec wektora 𝐸⃗ opisuje elipsę.
Polaryzacja kołowa - Rodzaj polaryzacji eliptycznej, kiedy koniec wektora 𝐸⃗ opisuje okrąg.
Polaryzacja
eliptyczna
(kołowa)
jest
prawoskrętna, kiedy względem kierunku
przeciwnego do biegu promienia (dla
obserwatora
patrzącego
naprzeciw
promienia) wektor 𝐸⃗ obraca się zgodnie z
kierunkiem ruchu wskazówek zegara. W
przypadku
przeciwnym
polaryzacja
eliptyczna (kołowa) jest lewoskrętna.
Światło spolaryzowane częściowo - Światło, w którym drgania o jednym kierunku przeważają nad
drganiami we wszystkich pozostałych kierunkach.
52. Przejście światła przez polaryzator.
Polaryzator - Przyrząd służący do wydzielenia światła o polaryzacji liniowej ze światła naturalnego lub
częściowo spolaryzowanego.
Przejście światła liniowo spolaryzowanego przez polaryzator
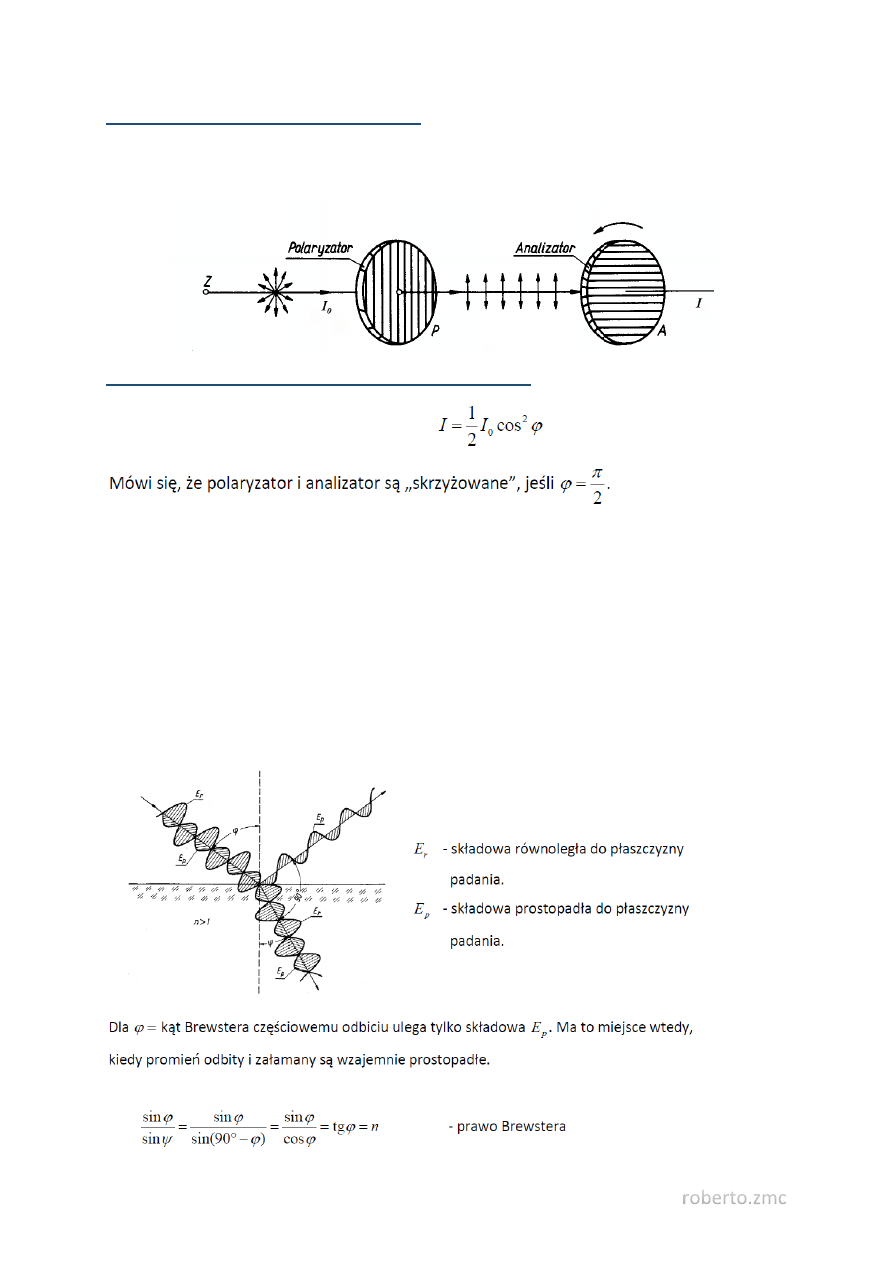
Przejście światła naturalnego przez polaryzator
Natężenie światła związane ze składowymi wektorów 𝐸⃗ równoległymi do płaszczyzny polaryzatora
stanowi połowę całkowitego natężenia 𝐼
0
, stąd w tym przypadku
Przejście światła naturalnego przez układ dwóch polaryzatorów
53. Zjawiska fizyczne wykorzystywane w polaryzatorach.
− Polaryzacja światła przy odbiciu od dielektryków.
− Dwójłomność (podwójne załamanie światła). Wykorzystanie właściwości niektórych kryształów,
polegającej na rozszczepianiu przechodzącego przez nie promieniowania na dwie wiązki o wzajemnie
prostopadłych polaryzacjach.
− Dichroizm. Wykorzystanie właściwości niektórych materiałów polegającej na różnym pochłanianiu
światła, w zależności od jego polaryzacji.
54. Prawo Brewstera.
55. Przekształcenie Galileusza, zasada względności Galileusza.
56. Postulaty Einsteina. Przekształcenia Lorentza.
Inercjalny układ odniesienia - Jest to układ odniesienia, w którym wolny od oddziaływań zewnętrznych
punkt materialny znajduje się w stanie spoczynku lub porusza się ruchem jednostajnym
prostoliniowym.
Postulaty Einsteina
Zasada względności Einsteina
Wszystkie prawa przyrody są takie same we wszystkich inercjalnych układach odniesienia.
lub
Równania wyrażające prawa przyrody są niezmiennicze względem przekształceń współrzędnych i
czasu, wynikających z przejścia z jednego inercjalnego układu odniesienia do drugiego.
Zasada stałości prędkości światła
Prędkość światła w próżni jest taka sama we wszystkich inercjalnych układach odniesienia i nie
zależy od ruchu źródeł i odbiorników światła.
Prędkość światła w próżni jest prędkością graniczną. Żaden sygnał, żadne działanie jednego ciała na
drugie nie może rozchodzić się z prędkością większą od prędkości światła w próżni. Jest to również
prawo przyrody, a więc zgodnie z zasadą względności ta prędkość graniczna powinna być taka sama
we wszystkich inercjalnych układach odniesienia.
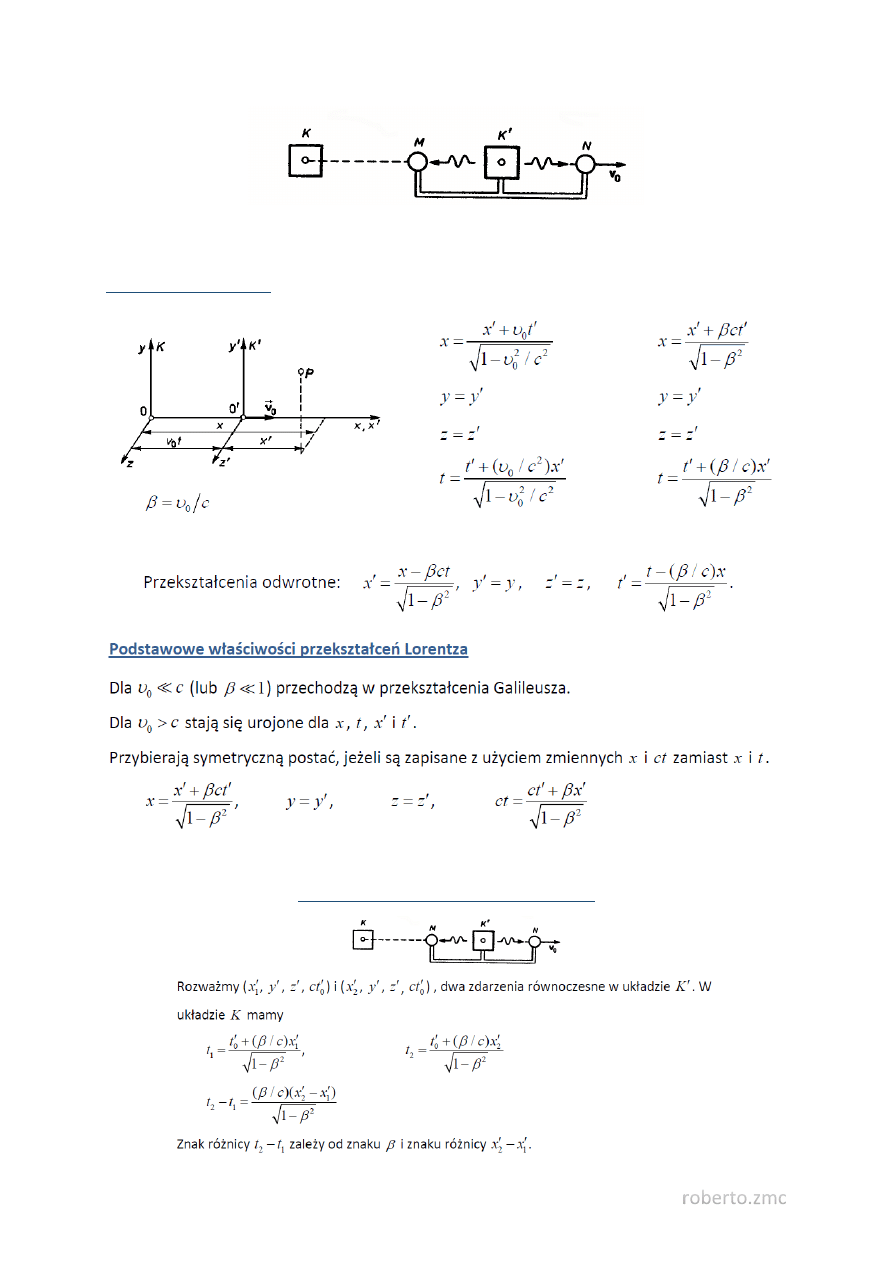
Dwa zdarzenia jednoczesne w jednym układzie odniesienia mogą nie być jednoczesne w innym
układzie odniesienia.
Przekształcenia Lorentza
57. Jednoczesność zdarzeń w różnych układach odniesienia.
KONSEKWENCJE PRZEKSZTAŁCEŃ LORENTZA
Dwa przestrzennie rozdzielone zdarzenia równoczesne w jednym układzie odniesienia nie są
równoczesne w innym układzie odniesienia.
58. Długość ciał w różnych układach odniesienia.
Zjawisko Fitzgeralda-Lorentza
Poruszające się ciała skracają swoje rozmiary w kierunku ruchu, przy czym skrócenie to jest tym
większe im większa jest prędkość tego ruchu.
Wymiary ciał w kierunkach prostopadłych do 𝜐
0
pozostają niezmienione.
59. Odstęp czasu między zdarzeniami zachodzącymi w tym samym punkcie przestrzeni.
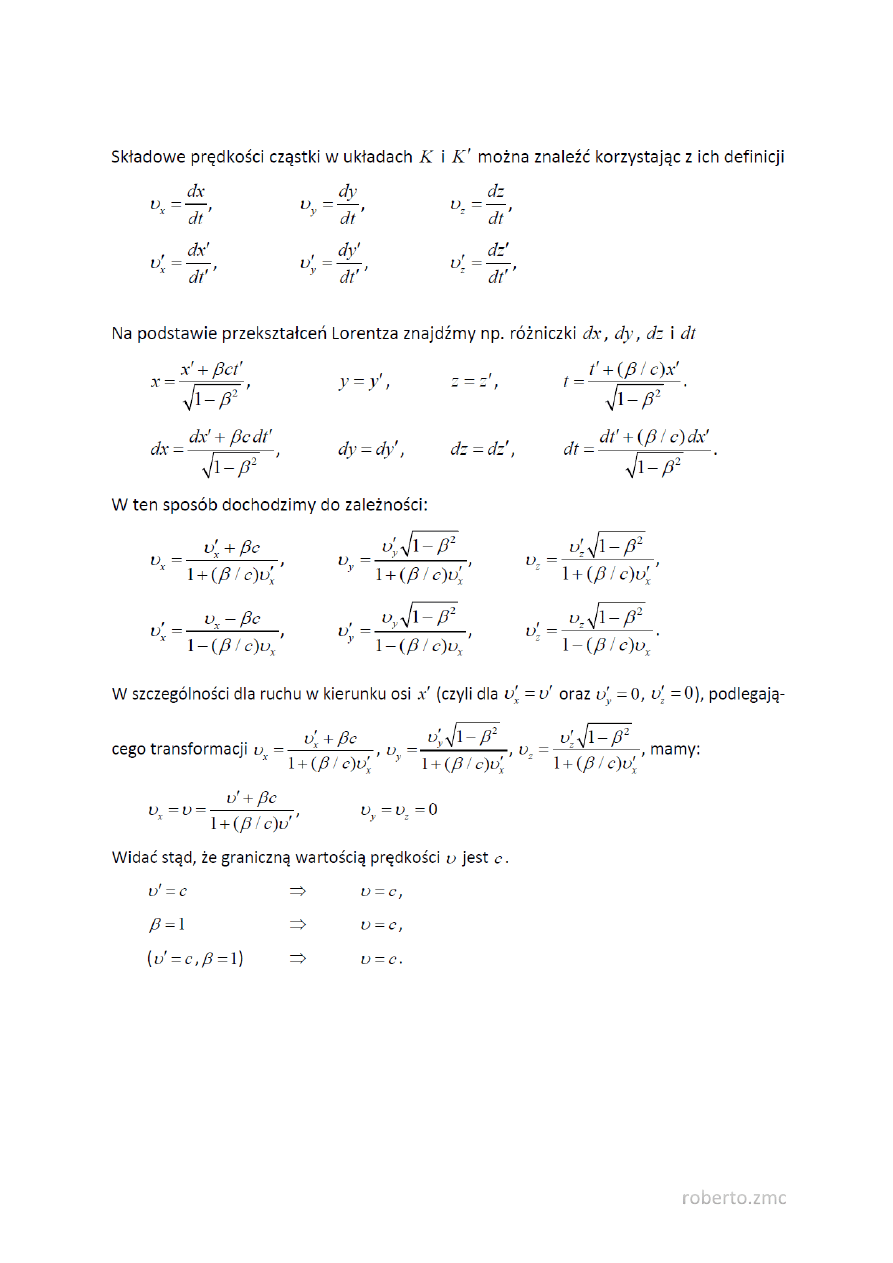
60. Przekształcanie prędkości w mechanice relatywistycznej.
61. Relatywistyczna energia kinetyczna cząstki.
62. Relatywistyczna zależność między pędem i energią.
