
Zmiany, Poprawki, Uwagi
UKD 624.014.2:624.04
POLSKA NORMA
Numer: PN-90/B-03200
Tytuł: Konstrukcje stalowe - Obliczenia statyczne i
projektowanie
Grupa ICS: 91.080.10
SPIS TRE
Ś
CI
1. WST
Ę
P
1.1. Przedmiot normy
1.2. Zakres stosowania normy
1.3. Dokumentacja projektowa
1.4. Podstawowe oznaczenia
1.4.1. Cechy geometryczne
1.4.2. Obci
ąż
enia, siły przekrojowe, no
ś
no
ść
1.4.3. Napr
ęż
enia i wytrzymało
ść
1.4.4. Współczynniki
1.4.5. Indeksy i inne oznaczenia
2. MATERIAŁY I WYROBY
2.1. Stal. Stałe materiałowe i cechy mechaniczne
2.2. Liny i druty stalowe
2.3.
Ś
ruby
2.4. Nity
2.5. Elektrody
2.6. Atestowanie materiałów
3. ZASADY PROJEKTOWANIA
3.1. Postanowienia ogólne
3.1.1. Metoda wymiarowania
3.1.2. Obci
ąż
enia
3.1.3. Współczynnik konsekwencji zniszczenia
3.1.4. Wytrzymało
ść
obliczeniowa stali
3.1.5. Wytrzymało
ść
w zło
ż
onym stanie napr
ęż
enia
3.2. Obliczenia statyczne i badania konstrukcji
3.2.1. Model obliczeniowy konstrukcji
3.2.2. Siły przekrojowe i przemieszczenia konstrukcji
3.2.3. Badania atestacyjne
3.3. Stany graniczne u
ż
ytkowania - warunki sztywno
ś
ci
3.3.1. Zasady ogólne
3.3.2. Ugi
ę
cia belek i elementów obudowy
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 1

3.3.3. Przemieszczenia poziome konstrukcji
3.3.4. Podniesienie wykonawcze
3.3.5. Drgania
3.4. No
ś
no
ść
konstrukcji ze wzgl
ę
du na zm
ę
czenie materiału
3.5. Wpływ temperatury
3.5.1. Działanie ró
ż
nicy temperatur. Przerwy dylatacyjne
3.5.2. Wła
ś
ciwo
ś
ci stali
3.6. Ochrona konstrukcji przed korozj
ą
i ogniem
4. ELEMENTY KONSTRUKCJI
4.1. Postanowienia ogólne
4.1.1. Zło
ż
ony stan napr
ęż
enia
4.1.2. Osłabienie elementu otworami na ł
ą
czniki
4.1.3. Klasyfikacja przekrojów
4.2. Stateczno
ść
miejscowa
4.2.1. Zasady ogólne
4.2.2.
Ś
cianki
ś
ciskane,
ś
ciskane mimo
ś
rodowo lub zginane
4.2.3.
Ś
cianki
ś
cinane
4.2.4.
Ś
rodniki pod obci
ąż
eniem skupionym
4.2.5.
Ś
rodniki w zło
ż
onym stanie napr
ęż
enia
4.2.6.
Ż
ebra usztywniaj
ą
ce
4.3. Elementy rozci
ą
gane
4.3.1. Postanowienia ogólne
4.3.2. No
ś
no
ść
elementów rozci
ą
ganych osiowo
4.4. Elementy
ś
ciskane
4.4.1. Postanowienia ogólne
4.4.2. No
ś
no
ść
obliczeniowa przekroju przy osiowym
ś
ciskaniu
4.4.3. Smukło
ść
wzgl
ę
dna pr
ę
ta przy wyboczeniu
4.4.4. Współczynnik wyboczeniowy
4.4.5. No
ś
no
ść
(stateczno
ść
) elementów
ś
ciskanych osiowo
4.5. Elementy zginane
4.5.1. Postanowienia ogólne
4.5.2. No
ś
no
ść
obliczeniowa przekroju przy jednokierunkowym zginaniu
4.5.3. Smukło
ść
wzgl
ę
dna przy zwichrzeniu
4.5.4. Współczynnik zwichrzenia
4.5.5. No
ś
no
ść
(stateczno
ść
) elementów jednokierunkowo zginanych
4.5.6. No
ś
no
ść
elementów dwukierunkowo zginanych lub zginanych i rozci
ą
ganych
4.6. Elementy
ś
ciskane i zginane
4.6.1. Zasady ogólne - parametry stateczno
ś
ci
4.6.2. No
ś
no
ść
(stateczno
ść
) elementów
ś
ciskanych i zginanych
4.7. Elementy wielogał
ę
ziowe
4.7.1. Zasady ogólne
4.7.2. Smukło
ść
zast
ę
pcza
4.7.3. Przewi
ą
zki i skratowania
5. UKŁADY KONSTRUKCYJNE - STATECZNO
ŚĆ
OGÓLNA
5.1. Zasady i wymagania ogólne
5.2. Podparcia boczne elementów
ś
ciskanych
5.3. St
ęż
enia dachowe
5.4. Układy ramowe (szkieletowe)
5.4.1. Ogólny podział ram
5.4.2. Parametr niedoskonało
ś
ci
5.4.3. Wska
ź
nik wra
ż
liwo
ś
ci na efekty II rz
ę
du
5.4.4. Zasady oblicze
ń
statycznych
5.5. Stateczno
ść
poło
ż
enia
6. POŁ
Ą
CZENIA
6.1. Postanowienia ogólne
6.2. Poł
ą
czenia na
ś
ruby, nity i sworznie
6.2.1. Kategorie poł
ą
cze
ń
6.2.2. Wymagania konstrukcyjne
6.2.3. No
ś
no
ść
obliczeniowa ł
ą
czników
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 2

6.2.4. Obliczanie i wymiarowanie poł
ą
cze
ń
6.3. Poł
ą
czenia spawane
6.3.1. Ogólne wymagania i zalecenia
6.3.2. Wymiary obliczeniowe i wymagania konstrukcyjne
6.3.3. Obliczanie i wymiarowanie poł
ą
cze
ń
6.4. Poł
ą
czenia bez
ż
ebrowe
6.4.1. Zasady ogólne
6.4.2. Poł
ą
czenia spawane belek ze słupami
6.5. Oparcie i ło
ż
yska belek
6.6. Styki i podstawy słupów
7. POSTANOWIENIA PRZEJ
Ś
CIOWE
ZAŁ
Ą
CZNIKI
Zał
ą
cznik 1. Parametry stateczno
ś
ci elementów konstrukcji
Zał
ą
cznik 2. Warto
ś
ci pomocnicze do obliczania poł
ą
cze
ń
ś
rubowych
Zał
ą
cznik 3. Zasady sprawdzania no
ś
no
ś
ci konstrukcji ze wzgl
ę
du na zm
ę
czenie materiału (wysokocyklowe)
Zał
ą
cznik 4. Obliczanie i projektowanie konstrukcji z uwzgl
ę
dnieniem plastycznej rezerwy no
ś
no
ś
ci
Zał
ą
cznik 5. Belki podsuwnicowe
INFORMACJE DODATKOWE
1. WST
Ę
P
1.1. Przedmiot normy. Przedmiotem normy jest obliczanie i projektowanie konstrukcji stalowych.
1.2. Zakres st osowania norm y. Norm
ę
nale
ż
y stosowa
ć
pr zy opracowywaniu dokumentacji technicznej
konstrukcji budowlanych, których projektowanie nie jest przedmiotem osobnych norm.
1.3. Dokumentacja projektowa powinna by
ć
opracowana zgodnie z PN-90/B-03000 oraz PN-64/B-01043.
1.4. Podstawowe oznaczenia
1.4.1. Cechy geometryczne
a - wielko
ść
geometryczna liniowa (rozstaw, odległo
ść
),
a - grubo
ść
obliczeniowa spoiny,
b, b
e
- szeroko
ść
, szeroko
ść
współpracuj
ą
ca,
c - odległo
ść
, wymiar strefy docisku,
d, d
0
-
ś
rednica,
ś
rednica otworu,
e - mimo
ś
ród,
h - wysoko
ść
,
i - promie
ń
bezwładno
ś
ci,
l - długo
ść
, rozpi
ę
to
ść
,
l
0
- długo
ść
obliczeniowa,
l
e
- długo
ść
wyboczeniowa,
r - promie
ń
zaokr
ą
glenia,
t - grubo
ść
ś
cianki, blachy,
A, A
n
- pole przekroju brutto, netto,
A
e
- pole współpracuj
ą
cej cz
ęś
ci przekroju w stanie nadkrytycznym,
A
v
- pole cz
ęś
ci przekroju czynnej przy
ś
cinaniu,
I - moment bezwładno
ś
ci,
S - moment statyczny,
W - wska
ź
nik wytrzymało
ś
ci przekroju.
W
e
- wska
ź
nik wytrzymało
ś
ci przekroju współpracuj
ą
cego,
W
pl
- wska
ź
nik oporu plastycznego przy zginaniu,
,
- smukło
ść
pr
ę
ta, smukło
ść
wzgl
ę
dna,
- wzgl
ę
dna smukło
ść
płytowa.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 3

1.4.2. Obci
ąż
enia, siły przekrojowe, no
ś
no
ść
F - obci
ąż
enie, siła (ogólnie),
F
Rj
- no
ś
no
ść
obliczeniowa poł
ą
czenia zakładkowego,
H - siła pozioma,
M, M
R
- moment zginaj
ą
cy, no
ś
no
ść
obliczeniowa przekroju przy zginaniu,
M
Rj
- no
ś
no
ść
obliczeniowa poł
ą
czenia przy zginaniu,
N, N
R
- siła podłu
ż
na, no
ś
no
ść
obliczeniowa przekroju: przy
ś
ciskaniu N
Rc
, przy rozci
ą
ganiu N
Rt
,
N
Rj
- no
ś
no
ść
obliczeniowa poł
ą
czenia doczołowego przy rozci
ą
ganiu,
P, P
R
- siła skupiona, no
ś
no
ść
obliczeniowa
ś
rodnika pod obci
ąż
eniem skupionym,
S, S
R
- siła przypadaj
ą
ca na ł
ą
cznik, no
ś
no
ść
obliczeniowa ł
ą
cznika,
V, V
R
- siła poprzeczna, no
ś
no
ść
obliczeniowa przekroju przy
ś
cinaniu.
1.4.3. Napr
ęż
enia i wytrzymało
ść
σ
- napr
ęż
enia normalne,
τ
- napr
ęż
enia styczne,
R
e
- specyfikowana przez producenta (normowa) granica plastyczno
ś
ci,
R
m
- specyfikowana przez producenta wytrzymało
ść
na rozci
ą
ganie,
f
yk
- wytrzymało
ść
charakterystyczna stali odpowiadaj
ą
ca wyra
ź
nej lub umownej granicy plastyczno
ś
ci,
f
d
- wytrzymało
ść
obliczeniowa stali,
f
dT
- wytrzymało
ść
obliczeniowa stali w podwy
ż
szonej temperaturze,
∆σ
,
∆τ
- zakres zmienno
ś
ci napr
ęż
e
ń
normalnych, stycznych,
∆σ
R
,
∆τ
R
- wytrzymało
ść
zm
ę
czeniowa (ogólnie).
1.4.4. Współczynniki
α
- współczynnik warunków pracy (ogólnie),
β
- współczynnik momentu zginaj
ą
cego,
γ
f
- współczynnik obci
ąż
enia,
γ
s
- współczynnik materiałowy,
µ
- współczynnik długo
ś
ci wyboczeniowej, współczynnik tarcia,
ϕ
- współczynnik wyboczeniowy,
ϕ
L
- współczynnik zwichrzenia,
ϕ
p
- współczynnik niestateczno
ś
ci miejscowej,
ψ
- współczynnik redukcyjny no
ś
no
ś
ci obliczeniowej przekroju.
1.4.5. Indeksy i inne oznaczenia
d, k - obliczeniowy, charakterystyczny,
c, t, v, b -
ś
ciskanie, rozci
ą
ganie,
ś
cinanie, docisk,
f, w, s - pas (półka),
ś
rodnik,
ż
ebro,
j - poł
ą
czenie,
R - graniczny w sensie no
ś
no
ś
ci obliczeniowej,
cr - krytyczny w sensie klasycznej teorii stateczno
ś
ci,
pl - plastyczny,
x, y, z - wzgl
ę
dem osi X, wzgl
ę
dem osi Y, wzgl
ę
dem osi Z,
i - kolejny, i = 1,2 ... ; i = x lub y,
min, max - najmniejszy, najwi
ę
kszy,
red - zredukowany,
||, ⊥
- równoległy, prostopadły,
∆
- przyrost, ró
ż
nica, składnik poprawkowy,
Σ
- suma.
2. MATERIAŁY I WYROBY
2.1. Stal. Stałe materiałowe i cechy mechaniczne
a) Kształtowniki, rury, blachy, pr
ę
ty stalowe i odlewy staliwne nale
ż
y przyjmowa
ć
wg norm hutniczych i aktualnych
program ów produkcji, dobieraj
ą
c gatunek stali ( skład chemiczny) oraz jej wła
ś
ciwo
ś
ci mechaniczne, technologiczne
i eksploatacyjne odpowiednio do rodzaju i przeznaczenia elementu konstrukcyjnego.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 4
Konstrukcje spawane nale
ż
y projektowa
ć
ze stali spawalnej. Konstrukcje przeznaczone do eksploatacji w
warunkach sprzyjaj
ą
cych kruchemu p
ę
kaniu nale
ż
y projektowa
ć
ze stali o odpowiedniej udarno
ś
ci gwarantowanej
atestem.
b) Stałe materiałowe stali nale
ż
y przyjmowa
ć
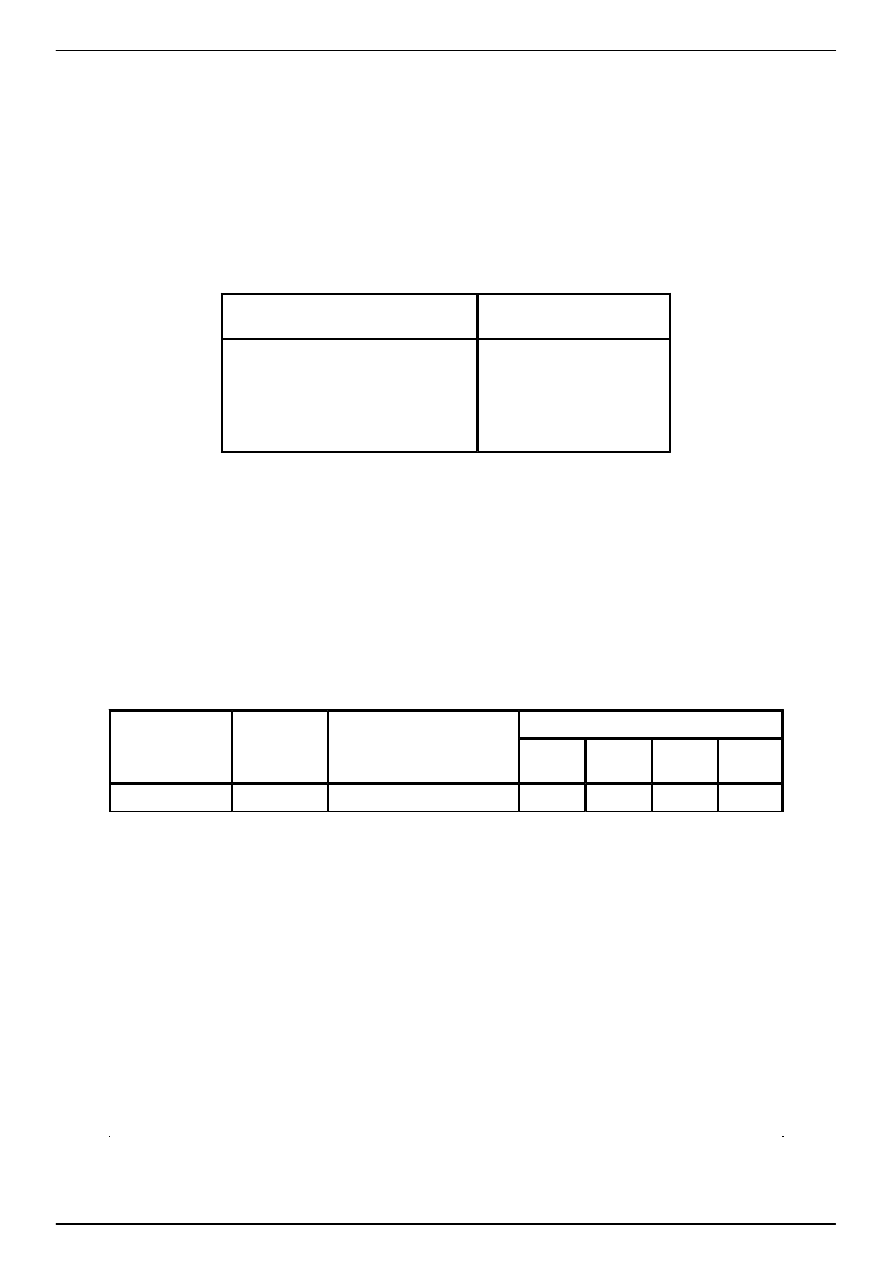
wg tabl. 1.
Tablica 1
Stała materiałowa
Warto
ść
charakterystyczna
Współczynnik spr
ęż
ysto
ś
ci podłu
ż
nej
Współczynnik spr
ęż
ysto
ś
ci poprzecznej
Współczynnik Poissona
Współczynnik rozszerzalno
ś
ci cieplnej
liniowej
G
ę
sto
ść
masy
E = 205 GPa
G = 80 GPa
v = 0,30
ε
T
= 12 × 10
-6
/°C
ρ
= 7850 kg/m
3
Współczynniki oporu tarcia w ło
ż
yskach podporowych nale
ż
y przyjmowa
ć
w zale
ż
no
ś
ci od rodzaju i sposobu
przygotowania powierzchni:
- przy
ś
lizganiu powierzchni płaskich
µ
= 0,2 ÷ 0,3,
- przy
ś
lizganiu powierzchni krzywej po płaskiej
µ
= 0,1 ÷ 0,2,
- przy toczeniu
µ
= 0,03.
c) Wła
ś
ciwo
ś
ci stali nale
ż
y przyjmowa
ć
wg norm przedmiotowych. Dla najcz
ęś
ciej stosowanych gatunków stali,
minimalne wg norm hutniczych warto
ś
ci cech mechanicznych R
e
, R
m
i A
5
podano w tabl. 2.
Tablica 2
Rodzaj stali
Znak stali
Rodzaj wyrobu, grubo
ś
ci
1)
, t
mm
Wła
ś
ciwo
ś
ci mechaniczne
R
e min
MPa
min R
m
MPa
A
5 min
%
f
d
MPa
1
2
3
4
5
6
7
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 5
Stal niestopowa
konstrukcyjna wg
PN-88/H-84020
StOS
Blachy,
kształtowniki,
pr
ę
ty, rury
t
≤
16
16<t
≤
40
195
185
315
23
22
175
165
St3SX,
St3SY, St3S,
St3V, St3W
t
≤
16
16<t
≤
40
40<t
≤
100
235
225
215
375
26
25
23
215
205
195
St4VX,
St4VY, St4V,
St4W
t
≤
16
16<t
≤
40
255
245
410
24
23
235
225
Stal niskostopowa
wg PN-86/H-
84018
18G2, 18G2A
t
≤
16
16<t
≤
30
30<t
≤
50
355
345
335
490
22
305
295
285
18G2AV
2)
t
≤
16
16<t
≤
30
30<t
≤
50
440
430
420
560
18
370
360
350
Stal
trudnordzewiej
ą
ca
wg PN-83/H-
84017
10HA
walcowane
na zimno
315
440
24
275
10H, 10HA
walcowane
na gor
ą
co
345
470
22
290
12H1JA,
12PJA
10HNAP
3)
walcowane
na zimno
355
490
22
290
10HAV
walcowane
na gor
ą
co
390
510
20
310
Stal do produkcji
rur
4)
wg PN-89/H-
84023/07
R
rury walcowane lub ci
ą
gnione
nie okre
ś
la si
ę
165
R35
235
345
25
210
R45
255
440
21
225
12X
rury zgrzewane
205
330
26
180
Staliwo wg PN-
85/H-83152
L400
odlewy staliwne grupy II
250
400
25
225
L450
260
450
22
235
L500
320
500
18
280
1)
Dla kształtowników walcowanych miarodajna jest
ś
rednia grubo
ść
półki (stopki).
2)
Podane w tablicy warto
ś
ci dotycz
ą
kategorii wytrzymało
ś
ciowej E440.
3)
Stal 10HNAP jest walcowana na gor
ą
co.
4)
Rury walcowane lub ci
ą
gnione s
ą
produkowane tak
ż
e ze stali 18G2A, a zgrzewane ze stali St3S i 18G2A.
2.2. Liny i druty stalowe. Rodzaje, gatunki i wła
ś
ciwo
ś
ci mechaniczne drutów i lin stalowych do konstrukcji
spr
ęż
onych nale
ż
y przyjmowa
ć
wg PN-71/M-80014 i PN-71/M-80236, a pozostałych lin - wg PN-68/M-80200 i PN-
92/M-80201.
Dla drutów oraz lin wst
ę
pnie przeci
ą
gni
ę
tych mo
ż
na przyjmowa
ć
nast
ę
puj
ą
ce współczynniki spr
ęż
ysto
ś
ci:
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 6

- dla drutów i wi
ą
zek drutów równoległych
E = 195 GPa,
- dla lin skr
ę
conych zamkni
ę
tych
E = 165 GPa,
- dla lin z rdzeniem stalowym
E = 145 GPa,
- dla lin z rdzeniem niemetalowym
E = 125 GPa.
2.3.
Ś
ruby dokładne,
ś
redniodokładne i zgrubne z łbem sze
ś
ciok
ą
tnym nale
ż
y stosowa
ć
wg PN-85/M-82101, a w
uzasadnionych pr zypadkach - wg PN- 85/M- 82105; nakr
ę
tki i podkładki (zwykłe, spr
ęż
yste, klinowe, twarde) - wg
norm przedmiotowych.
2.4. Nity z łbem kulistym, płaskim lub soczewkowym nale
ż
y stosowa
ć
wg norm przedmiotowych. Wła
ś
ciwo
ś
ci
mechaniczne i odchyłki wymiarów nale
ż
y przyjmowa
ć
wg PN-79/M-82903.
2.5. Elektrody oraz inne materiały do spawania nale
ż
y stosowa
ć
wg norm przedmiotowych odpowiednio do
gatunku stali, metody i warunków spawania.
2.6. Atestowanie materiałów. Materiały i wyroby budowlane o jako
ś
ci innej ni
ż
katalogowa powinny m ie
ć
wymagane parametry potwierdzone atestem. W technicznie uzasadnionych przypadkach nale
ż
y
żą
da
ć
atestu
potwierdzaj
ą
cego jako
ść
katalogow
ą
.
3. ZASADY PROJEKTOWANIA
3.1. Postanowienia ogólne
3.1.1. Metoda wymiarowania. Wymiarowanie konstr ukcji nale
ż
y przeprowadza
ć
metod
ą
stanów granicznych wg
PN-76/B-03001
, rozró
ż
niaj
ą
c:
- stany graniczne no
ś
no
ś
ci (i obci
ąż
enia obliczeniowe) oraz
- stany graniczne u
ż
ytkowania (i obci
ąż
enia charakterystyczne).
Przy wymiarowaniu konstrukcji nale
ż
y wykaza
ć
,
ż
e we wszystkich mo
ż
liwych do przewidzenia przypadkach
projektowych, w fazach realizacji i eksploatacji, spełnione s
ą
warunki no
ś
no
ś
ci i sztywno
ś
ci konstrukcji.
3.1.2. Obci
ąż
enia. Rodzaje, war to
ś
ci, współczynniki i kombinacje obci
ąż
e
ń
nale
ż
y ustala
ć
wg
PN-82/B-02000
oraz
innych norm i przepisów wła
ś
ciwych ze wzgl
ę
du na przedmiot projektowania.
3.1.3. Współczynnik konsekwencji zniszczenia
γ
n
nale
ż
y przyjmowa
ć
jako m no
ż
nik do obci
ąż
e
ń
obliczeniowych
w zale
ż
no
ś
ci od rodzaju, wielko
ś
ci i przeznaczenia konstrukcji, z uwzgl
ę
dnieniem strat materialnych i zagro
ż
enia
ż
ycia ludzkiego w przypadku ewentualnej awarii.
Je
ś
li inne przepisy nie stanowi
ą
inaczej, ani te
ż
nie przeprowadza si
ę
specjalnej analizy probabilistycznej, to dla
konstrukcji no
ś
nych w budownictwie powszechnym nale
ż
y przyjmowa
ć
γ
n
= 1.
3.1.4. Wytrzymało
ść
obliczeniow
ą
stali nale
ż
y przyjmowa
ć
wg tabl. 3.
Tablica 3
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 7
Wytrzymało
ść
obliczeniowa stali
Definicja
1)
Rozci
ą
ganie,
ś
ciskanie i przy
zginaniu w kształtownikach,
rurach, pr
ę
tach i blachach
Ś
cinanie w elementach jw.
Docisk powierzchni płaskich
Docisk skupiony wg Hertza
Rozci
ą
ganie w ci
ę
gnach o
wysokiej wytrzymało
ś
ci
(R
m
≥
880 MPa)
1)
Obliczone warto
ś
ci mo
ż
na zaokr
ą
gli
ć
do 5 MPa.
2)
Dla gatunków stali nie uj
ę
tych w tabl. 2 wytrzymało
ść
obliczeniow
ą
ustala si
ę
indywidualnie, dziel
ą
c wytrzymało
ść
charakterystyczn
ą
f
yk
przez współczynnik materiałowy
γ
s
.
Je
ś
li nie przeprowadzono odpowiednich bada
ń
, to nale
ż
y przyjmowa
ć
f
yk
= R
emin
oraz:
γ
s
= 1,15 - dla stali R
e
≤
355 MPa,
γ
s
= 1,20 - dla stali 355<R
e
≤
460 MPa,
γ
s
= 1,25 - dla stali 460<R
e
≤
590 MPa.
3)
W przypadku ło
ż
ysk z liczb
ą
wałków wi
ę
ksz
ą
ni
ż
2 nale
ż
y zmniejszy
ć
warto
ść
f
dbH
o 100 MPa.
4)
W przypadku ci
ę
gien wiotkich równomiernie wyt
ęż
onych na odcinku
dłu
ż
szym ni
ż
30 m nale
ż
y uwzgl
ę
dnia
ć
redukcj
ę
wytrzymało
ś
ci
obliczeniowej wskutek statystycznego efektu skali.
3.1.5. Wytrzymało
ść
w zło
ż
onym stanie napr
ęż
enia nale
ż
y sprawdza
ć
wg wzoru
(1)
w którym
σ
y
,
σ
z
,
τ
- składowe napr
ęż
enia normalne i styczne w płaskim stanie napr
ęż
enia.
3.2. Obliczenia statyczne i badania konstrukcji
3.2.1. M odel obliczeniowy konstrukcji powinien odwzorowywa
ć
wszystkie istotne parametry i czynniki maj
ą
ce
wpływ na zachowanie si
ę
konstrukcji w rozpatrywanym stanie granicznym tj.: obci
ąż
enia i oddziaływania,
wła
ś
ciwo
ś
ci m ateriału, cechy geom etryczne oraz sztywno
ść
(podatno
ść
) elementów, poł
ą
cze
ń
i wi
ę
zi podporowych
(st
ęż
e
ń
).
Stopie
ń
zło
ż
ono
ś
ci modelu obliczeniowego powinien by
ć
uzasadniony z punktu widzenia wa
ż
no
ś
ci zadania
projektowego.
3.2.2. Siły przekrojowe i przemieszczenia konstrukcji nale
ż
y wyznacza
ć
metodami mechaniki budowli wg teor ii I
rz
ę
du, a w uzasadnionych przypadkach ( np. p. 5.4.4) - wg teorii II r z
ę
du przy zało
ż
eniu spr
ęż
ystego modelu
materiału.
W przypadkach okr e
ś
lonych w zał
ą
czniku 4 mo
ż
na uwzgl
ę
dnia
ć
w obliczeniach plastyczn
ą
redystrybucj
ę
napr
ęż
e
ń
i
sił przekrojowych oraz zwi
ą
zan
ą
z ni
ą
plastyczn
ą
rezerw
ę
no
ś
no
ś
ci konstrukcji.
Gdy zastosowanie analizy obliczeniowej jest utrudnione lub jej wyniki wzbudzaj
ą
w
ą
tpliwo
ść
, to siły przekrojowe i
przemieszczenia nale
ż
y wyznacza
ć
na podstawie bada
ń
do
ś
wiadczalnych.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 8
3.2.3. Badania atestacyjne. Konstrukcje lub elementy konstrukcji szczególnego typu lub pr zeznaczenia, w tym
konstrukcje prototypowe przeznaczone do seryjnej produkcji, powinny by
ć
poddane próbom obci
ąż
enia.
3.3. Stany graniczne u
ż
ytkowania - warunki sztywno
ś
ci
3.3.1. Zasady ogólne
a) Sprawdzenie konstrukcji ze wzgl
ę
du na stany graniczne u
ż
ytkowania ma na celu niedopuszczenie do
nadm iernych ugi
ęć
, przemieszcze
ń
i drga
ń
, utrudniaj
ą
cych lub uniemo
ż
liwiaj
ą
cych pr awidłow
ą
eksploatacj
ę
obiektu.
b) Do oblicze
ń
nale
ż
y przyjmowa
ć
warto
ś
ci charakterystyczne obci
ąż
e
ń
(
γ
f
= 1).
c) Przy obliczaniu ugi
ęć
i przemieszcze
ń
konstrukcji nie uwzgl
ę
dnia si
ę
:
- współczynników dynamicznych,
- osłabienia elementów otworami na ł
ą
czniki,
- obci
ąż
enia stałego w przypadku konstrukcji z podniesieniem wykonawczym,
- wzrostu przemieszcze
ń
spowodowanego efektami II rz
ę
du.
d) Graniczne ugi
ę
cia belek podsuwnicowych podano w Zał
ą
czniku 5.
e) Graniczne ugi
ę
cia i przemieszczenia konstrukcji nie uj
ę
tych w normie nale
ż
y przyjmowa
ć
wg norm
przedmiotowych.
3.3.2. Ugi
ę
cia belek i elementów obudowy (swobodnie podpartych, ci
ą
głych i utwierdzonych) nie powinny
przekracza
ć
ugi
ęć
granicznych podanych w tabl. 4.
Tablica 4
Elementy konstrukcji
Ugi
ę
cie graniczne
1)
Elementy stropów, podestów i pomostów:
- główne belki stropowe (podci
ą
gi),
- inne belki stropowe i w klatkach
schodowych,
- płyty stalowe i kratki pomostowe
l
/
350
2)
l
/
250
3)
l
/
150
D
ź
wigary dachowe (kratowe i pełno
ś
cienne)
l
/
250
Elementy obudowy:
- płatwie, rygle, słupki
- ramy i szczebliny okien
- blacha fałdowa
l
/
200
4)
l
/
200
l
/
150
5)
Nadpro
ż
a okien i bram
l
/
500
1)
l oznacza rozpi
ę
to
ść
elementu lub podwójny wysi
ę
g wspornika.
2)
Dodatkowe wymagania wg 3.3.5a).
3)
W stropach otynkowanych lub obci
ąż
onych
ś
cianami wra
ż
liwymi na
zarysowanie ugi
ę
cie od obci
ąż
e
ń
zmiennych długotrwałych nie powinno
przekracza
ć
l
/
350
.
4)
Przy obudowie z blachy fałdowej i rozpi
ę
to
ś
ci ł
≤
6 m mo
ż
na przyj
ąć
l
/
150
.
5)
Je
ś
li specjalne wymagania ze wzgl
ę
du na odwodnienie dachu nie
stanowi
ą
inaczej.
Gdy rozpi
ę
to
ś
ci i obci
ąż
enia prz
ę
seł ró
ż
ni
ą
si
ę
nie wi
ę
cej ni
ż
o 20%, to ugi
ę
cia belek ci
ą
głych o stałym przekroju
mo
ż
na przyjmowa
ć
jak dla belki swobodnie podpartej, ze współczynnikiem redukcyjnym, który dla prz
ę
seł
skrajnych (
ś
rodkowych) wynosi:
0,5(0,2) - przy obci
ąż
eniu stałym oraz
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 9

0,75(0,6) - przy obci
ąż
eniu zmiennym.
W przypadku belek obetonowanych, a tak
ż
e belek monolitycznie zespolonych z płytami stropowym i mo
ż
na
uwzgl
ę
dnia
ć
w obliczeniach współprac
ę
belki stalowej z betonem. Je
ś
li nie przeprowadza si
ę
dokładnej analizy, to
ugi
ę
cia belki stalowej mo
ż
na zmniejszy
ć
o 20%.
3.3.3. Przemieszczenia poziome konstrukcji nie powinny przekracza
ć
:
a) w układach jednokondygnacyjnych (bez suwnic):
- przy obudowie wra
ż
liwej na p
ę
kanie:
h
/
250
,
- w pozostałych przypadkach:
h
/
150
,
gdzie h - wysoko
ść
kondygnacji;
b) w układach wielokondygnacyjnych: h
i
/
500
,
gdzie h
i
- poziom rygla (stropu) rozpatrywanej kondygnacji wzgl
ę
dem wierzchu fundamentów.
3.3.4. Podniesienie wykonawcze nale
ż
y stosowa
ć
w d
ź
wigarach dachowych o rozpi
ę
to
ś
ci 30 m i wi
ę
kszej
(m niejszej w uzasadnionych przypadkach), przyjm uj
ą
c przeciwstr załk
ę
monta
ż
ow
ą
nie mniejsz
ą
ni
ż
suma ugi
ęć
od
obci
ąż
enia stałego i połowy obci
ąż
enia zmiennego.
Podniesienia wykonawczego mo
ż
na nie stosowa
ć
w d
ź
wigarach z krzywoliniowym (załamanym) pasem dolnym lub
ze
ś
ci
ą
giem mi
ę
dzy podporami.
3.3.5. Drgania
a) Cz
ę
stotliwo
ść
drga
ń
własnych konstrukcji stropu w pom ieszczeniach u
ż
yteczno
ś
ci publicznej (wolnych od
ś
cian
działowych) o rozpi
ę
to
ś
ci l > 12 m powinna wynosi
ć
co najmniej 5 Hz. Warunku tego mo
ż
na nie sprawdza
ć
, gdy
ugi
ę
cie konstrukcji od kombinacji obci
ąż
e
ń
długotrwałych nie przekracza 10 mm.
b) Ró
ż
nica cz
ę
stotliwo
ś
ci drga
ń
wzbudzonych i drga
ń
własnych konstrukcji nara
ż
onych na oddziaływania typu
harmonicznego powinna wynosi
ć
co najmniej 25% cz
ę
stotliwo
ś
ci drga
ń
własnych.
c) Budynki nara
ż
one na drgania przekazywane przez podło
ż
e, nale
ż
y projektowa
ć
z uwzgl
ę
dnieniem postanowie
ń
PN-85/B-02170
.
3.4. No
ś
no
ść
konstrukcji ze wzgl
ę
du na zm
ę
czenie materiału nale
ż
y dodatkowo sprawdza
ć
w przypadku
obci
ąż
e
ń
dynamicznych wielokrotnie zmiennych.
Zasady obliczania konstrukcji oraz warunki no
ś
no
ś
ci zm
ę
czeniowej elementów i poł
ą
cze
ń
przy obci
ąż
eniach
wysokocyklowych podano w zał
ą
czniku 3.
3.5. Wpływ temperatury
3.5.1. Działanie ró
ż
nicy temperatur. Przerwy dylatacyjne
a) W pr ojektowaniu konstrukcji nale
ż
y uwzgl
ę
dnia
ć
wpływ temperatury pochodzenia technologicznego, a w
uzasadnionych przypadkach wpływ temperatury pochodzenia klimatycznego wg
PN-86/B-02015
.
b) Je
ś
li nie przeprowadza si
ę
dokładnej analizy wg ww. normy, to dla konstrukcji eksploatowanych w krajowych
warunkach klimatycznych m o
ż
na przyjmowa
ć
obliczeniow
ą
r ó
ż
nic
ę
tem peratur
∆
T
0
=
ą
30°C w stosunku do
umownej temperatury scalania konstrukcji T
0
= 10°C.
c) W przypadku jednokondygnacyjnych układów szkieletowych mo
ż
na pomija
ć
w obliczeniach statycznych wpływ
temperatury pochodzenia klimatycznego, je
ś
li spełnione s
ą
nast
ę
puj
ą
ce warunki:
- długo
ść
obiektu lub jego oddylatowanej cz
ęś
ci (rozstaw dylatacji) nie przekracza:
150 m - w budynkach halowych,
120 m - w estakadach, a ponadto
- odległo
ść
mi
ę
dzy najdalszym i wzgl
ę
dem siebie podporami (st
ęż
eniami lub słupami) przenosz
ą
cymi siły poziome
w rozpatrywanym kierunku, jak równie
ż
odległo
ść
przerwy dylatacyjnej od najbli
ż
szego st
ęż
enia pionowego, nie
przekracza 60 m.
3.5.2. Wła
ś
ciwo
ś
ci stali. Je
ś
li temperatura eksploatacyjna konstrukcji T przekracza 70°C, to do oblicze
ń
nale
ż
y
przyjmowa
ć
zredukowan
ą
wytrzymało
ść
obliczeniow
ą
f
dT
, zredukowany pocz
ą
tkowy współczynnik spr
ęż
ysto
ś
ci E
T
oraz zredukowane współczynniki niestateczno
ś
ci
ϕ
T
. Warto
ś
ci te dla 70°
≤
T
≤
600°C mo
ż
na oblicza
ć
wg wzorów:
(2)
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 10
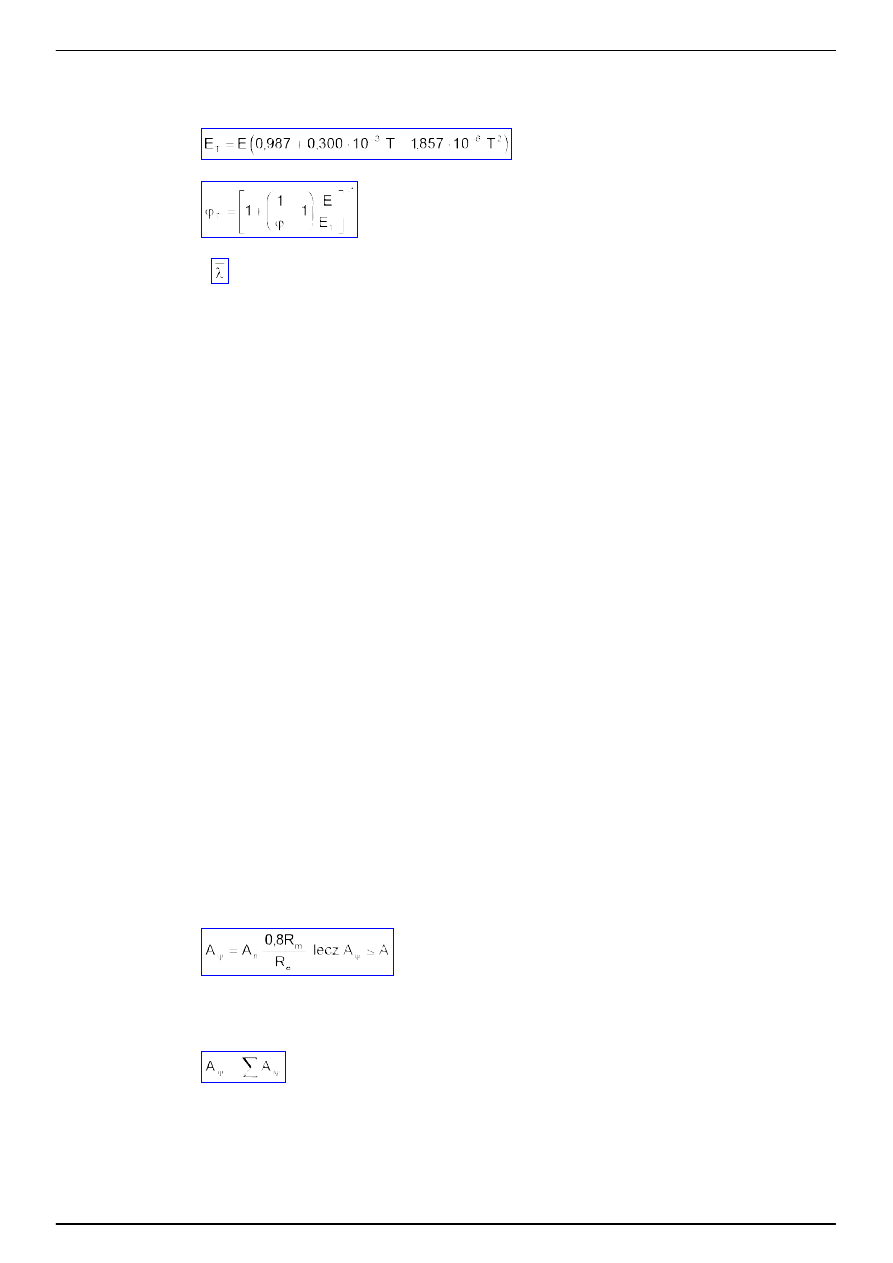
(3)
(4)
w których
ϕ
=
ϕ
(
) - odpowiedni współczynnik niestateczno
ś
ci dla sm ukło
ś
ci wzgl
ę
dnej, ustalonej przy nie
zmienionych warto
ś
ciach f
d
i E.
3.6. Ochrona konstrukcji przed korozj
ą
i ogniem
a) Zabezpieczenie konstrukcji przed korozj
ą
(przez dobór odpowiednich materiałów, rozwi
ą
za
ń
konstrukcyjnych,
powłok ochr onnych i ewentualnie naddatek grubo
ś
ci elementu) nale
ż
y projektowa
ć
stosownie do przewidywanego
okresu eksploatacji, stopnia agresywno
ś
ci korozyjnej
ś
rodowiska, a tak
ż
e warunków konserwacji i renowacji powłok
ochronnych.
b) W konstrukcjach nar a
ż
onych na bezpo
ś
rednie działanie czynników atm osferycznych grubo
ść
ś
cianek
kształtowników nie powinna by
ć
mniejsza ni
ż
3 mm, a elementy rurowe (je
ś
li ich wewn
ę
trzne powierzchnie nie s
ą
specjalnie zabezpieczone) powinny by
ć
szczelnie zamkni
ę
te. Wymagania te nie dotycz
ą
konstrukcji ze stali
trudnordzewiej
ą
cej.
W ka
ż
dym przypadku przez odpowiednie ukształtowanie konstrukcji, wypełnienie elementów lub specjalne otwory
nale
ż
y umo
ż
liwi
ć
odpływ wody opadowej.
c) W instrukcji zabezpieczenia przeciwkorozyjnego nale
ż
y okre
ś
li
ć
sposób przygotowania (stopie
ń
czysto
ś
ci)
powierzchni, rodzaj i grubo
ść
powłok ochronnych oraz warunki techniczne ich wykonania, odbioru i renowacji.
d) Zabezpieczenie konstrukcji pr zed ogniem przez czynne lub bierne
ś
rodki ochrony nale
ż
y pr ojektowa
ć
wg
specjalnych przepisów, stosownie do wymaganej klasy odporno
ś
ci ogniowej obiektu i poszczególnych elementów.
4. ELEMENTY KONSTRUKCJI
4.1. Postanowienia ogólne
4.1.1. Zło
ż
ony stan napr
ęż
enia. Je
ś
li inne przepisy nie stanowi
ą
inaczej, a w szczególno
ś
ci, gdy pocz
ą
tek
uplastycznienia materiału uto
ż
samia si
ę
ze stanem gr anicznym, to w przypadku elementów lub ich cz
ęś
ci b
ę
d
ą
cych
w zło
ż
onym stanie napr
ęż
enia nale
ż
y dodatkowo sprawdzi
ć
warunek (1).
4.1.2. Osłabienie elementu otworami na ł
ą
czniki
a) Je
ś
li wska
ź
nik osłabienia przy rozci
ą
ganiu (
ψ
ot
),
ś
ciskaniu (
ψ
oc
) lub
ś
cinaniu (
ψ
ov
) jest mniejszy od jedno
ś
ci, to
odpowiednio do stanu napr
ęż
enia nale
ż
y dodatkowo sprawdzi
ć
warunki no
ś
no
ś
ci podane w tabl. 5.
b) Wska
ź
nik osłabienia
ψ
oc
ma zastosowanie wtedy, gdy w strefie
ś
ciskanej elementu wyst
ę
puj
ą
otwory
powi
ę
kszone (tabl. 14) lub nie wypełnione ł
ą
cznikami; w pozostałych przypadkach przyjmuje si
ę
ψ
oc
= 1.
c) Napr
ęż
enia w rozpatrywanej, osłabionej cz
ęś
ci elementu nale
ż
y oblicza
ć
jak w przypadku elem entów nie
osłabionych - na podstawie cech geometrycznych przekroju brutto.
d) Sprowadzone pole przekroju przy rozci
ą
ganiu A
ψ
oblicza si
ę
nast
ę
puj
ą
co:
- dla elementu pojedynczego (
ś
cianki, blachy)
(5)
gdzie A
n
- pole najmniejszego płaskiego lub łamanego przekroju netto; rys. 13; A
n
= min(A
1
, A
2
),
- dla elementu zło
ż
onego (kształtownika)
(6)
przy czym A
i
ψ
- wg wzoru (5).
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 11
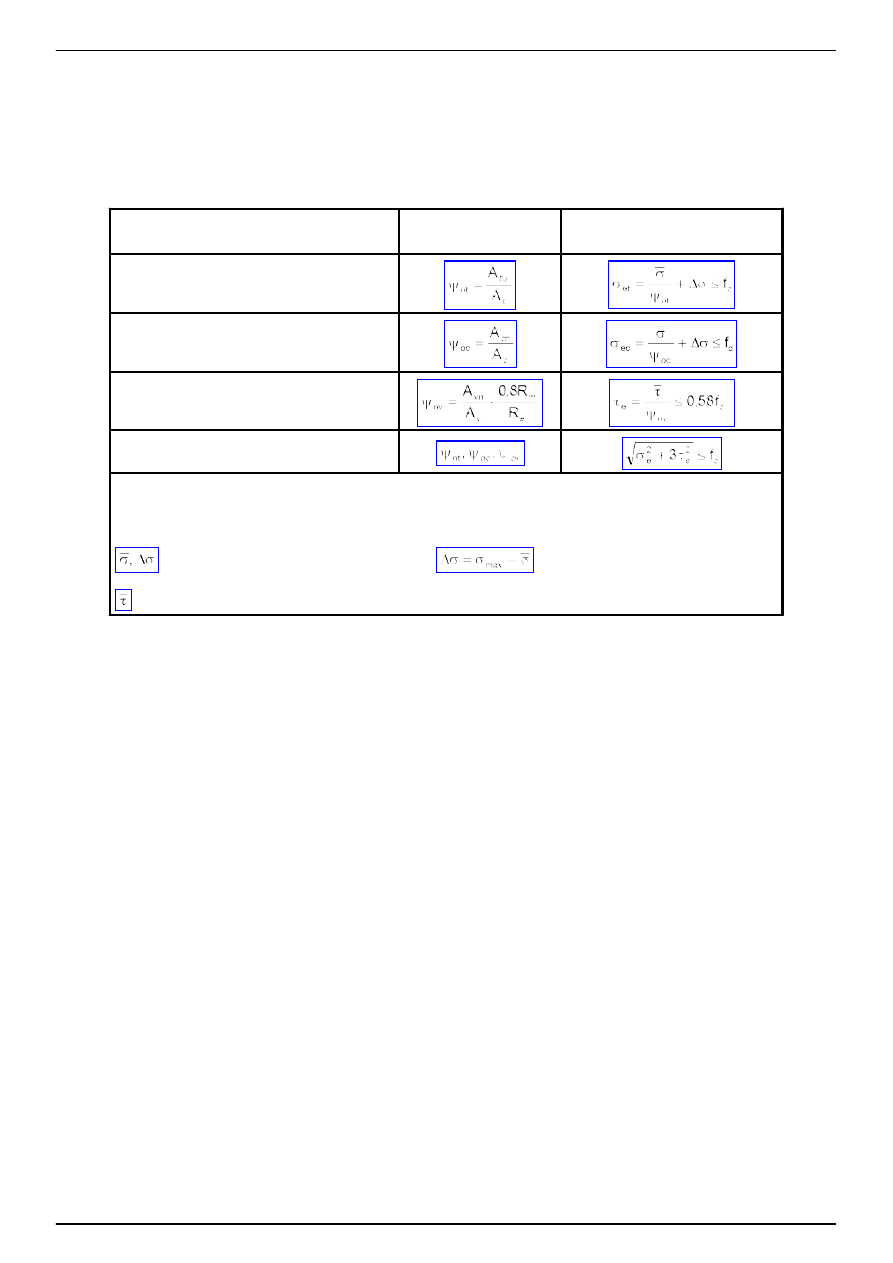
Tablica 5
Stan napr
ęż
enia w rozpatrywanej cz
ęś
ci
(
ś
ciance) osłabionej otworami
Wska
ź
nik osłabienia
Warunek no
ś
no
ś
ci
Rozci
ą
ganie równomierne (
∆σ
= 0) lub
mimo
ś
rodowe
Ś
ciskanie równomierne (
∆σ
= 0) lub
mimo
ś
rodowe (por. poz. b)
Ś
cinanie
Zło
ż
ony stan napr
ęż
enia
Oznaczenia:
A
t
,A
t
ψ
- pole przekroju cz
ęś
ci rozci
ą
ganej brutto, sprowadzone,
A
c
,A
cn
- pole przekroju cz
ęś
ci
ś
ciskanej brutto, netto,
A
v
,A
vn
- pole cz
ęś
ci przekroju czynnej przy
ś
cinaniu brutto, netto (tabl. 7),
- napr
ęż
enia normalne
ś
rednie i od zginania (
) obliczone na podstawie cech
geometrycznych przekroju brutto,
-
ś
rednie napr
ęż
enie styczne (
τ
= V/A
v
).
W przypadku kształtowników osłabienie otworami rozpatruje si
ę
dla ka
ż
dej (i-tej)
ś
cianki indywidualnie, a nast
ę
pnie
wyznacza si
ę
sumaryczne pole przekroju.
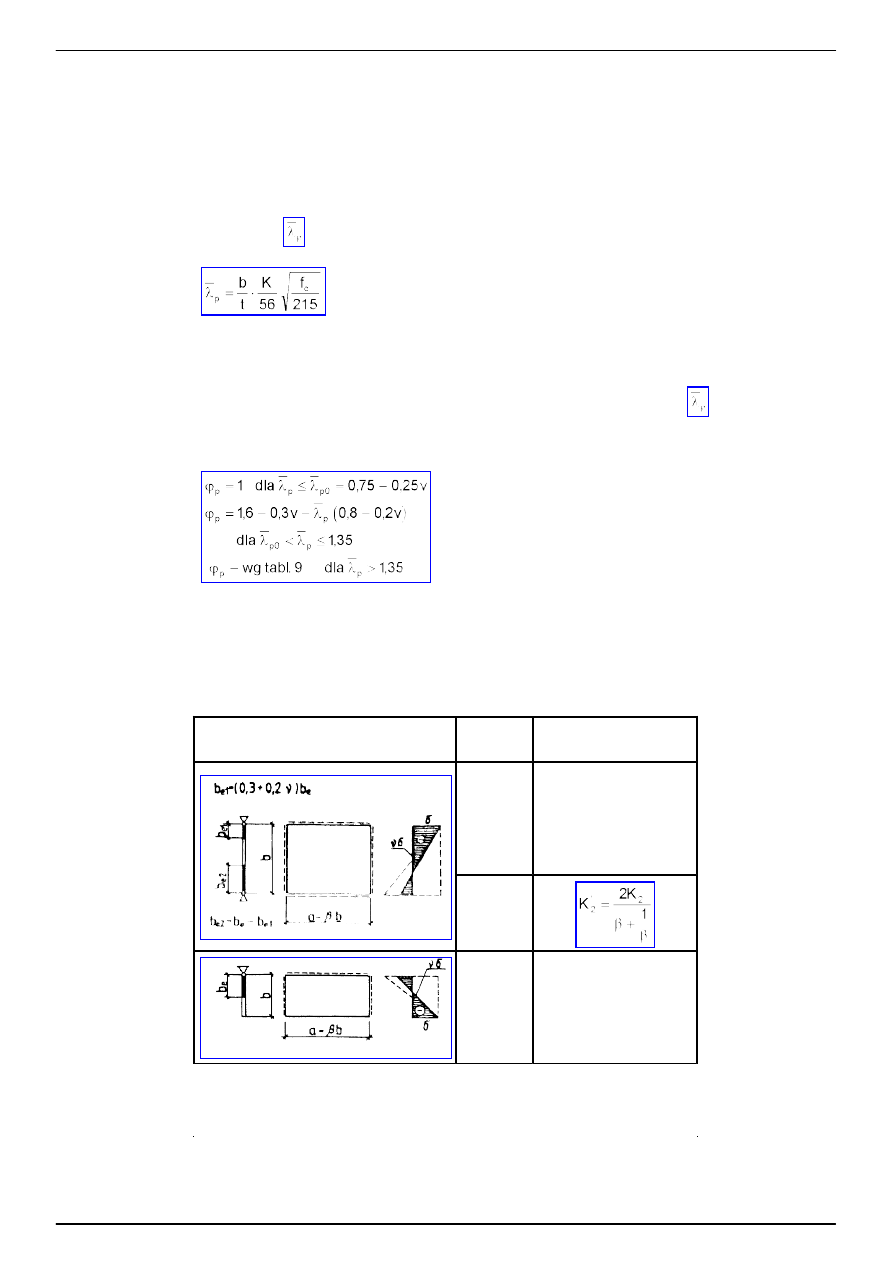
4.1.3. Klasyfikacja przekrojów
Klasa 1. Przekr oje klasy 1 mog
ą
osi
ą
gn
ąć
no
ś
no
ść
uogólnionego przegubu plastycznego, a w stanie pełnego
uplastycznienia przy zginaniu wykazuj
ą
zdolno
ść
do obrotu, niezb
ę
dn
ą
do plastycznej redystrybucji mom entów
zginaj
ą
cych.
Klasa 2. Przekroje klasy 2 mog
ą
osi
ą
gn
ąć
no
ś
no
ść
uogólnionego przegubu plastycznego, lecz wskutek miejscowej
niestateczno
ś
ci plastycznej wykazuj
ą
ograniczon
ą
zdolno
ść
do obrotu, uniemo
ż
liwiaj
ą
c
ą
r edystrybucj
ę
mom entów
zginaj
ą
cych.
Tablica 6
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 12
Poz.
Podparcie
ś
cianki -
miarodajna
szeroko
ść
b
Obci
ąż
enie
ś
cianki -
rozkład napr
ęż
e
ń
Graniczna smukło
ść
ś
cianki
dla przekroju klasy
1
2
3
4
a)
33
ε
39
ε
42
ε
66
ε
78
ε
105
ε
b)
9
ε
10
ε
14
ε
-
c)
1)2)
23
ε
25
ε
28
ε
65
ε
71
ε
105
ε
d)
1)
ś
ciskanie lub zginanie
50
ε
2
70
ε
2
100
ε
2
- wg tabl. 8 (dla spr
ęż
ystych rozkładów napr
ęż
e
ń
)
1)
Dla rur walcowanych na gor
ą
co obowi
ą
zuj
ą
warto
ś
ci podane w poz. a).
2)
Dotyczy przekrojów elementów pr
ę
towych.
Klasa 3. Przekroje klasy 3 charakter yzuj
ą
si
ę
tym ,
ż
e ich no
ś
no
ść
jest uwarunkowana pocz
ą
tkiem uplastycznienia
strefy
ś
ciskanej (
σ
c
max
≤
f
d
).
Klasa 4. Przekroje klasy 4 trac
ą
no
ś
no
ść
pr zy najwi
ę
kszych napr
ęż
eniach
ś
ciskaj
ą
cych (lub
ś
rednich
ś
cinaj
ą
cych)
mniejszych ni
ż
granica plastyczno
ś
ci.
Klas
ę
przekroju tj. stopie
ń
odporno
ś
ci elementu na m iejscow
ą
utrat
ę
stateczno
ś
ci nale
ż
y ustala
ć
wg tabl. 6, w
zale
ż
no
ś
ci od warunków podparcia, rozkładu napr
ęż
e
ń
i smukło
ś
ci
ś
cianek (
b
/
t
).
Przekroje elementów, których
ś
cianki nie spełniaj
ą
warunków smukło
ś
ci dla klasy 3 lub warunków smukło
ś
ci przy
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 13
ś
cinaniu, podanych w tabl. 7, zalicza si
ę
do klasy 4, która obejm uje przekroje elementów wra
ż
liwych na miejscow
ą
utrat
ę
stateczno
ś
ci w stanie spr
ęż
ystym.
Tablica 7
Kształtownik - typ przekroju
Pole przekroju
czynnego przy
ś
cinaniu sił
ą
V
i
1)
Warunek
smukło
ś
ci
2)
1)
Podane wzory obowi
ą
zuj
ą
, gdy siła poprzeczna (lub jej składowa) V
i
działa w kierunku równoległym do
ś
cianek (
ś
rodników) tworz
ą
cych
przekrój czynny A
v
.
2)
Je
ś
li spełniony jest odpowiedni warunek smukło
ś
ci, gdzie
to
ś
cianka kształtownika jest odporna na miejscow
ą
utrat
ę
stateczno
ś
ci przy czystym
ś
cinaniu (
ϕ
pv
= 1).
3)
W przypadku kształtowników walcowanych mo
ż
na przyjmowa
ć
h
w
= h, gdzie h - wysoko
ść
kształtownika.
4)
W przypadku
ś
rodników u
ż
ebrowanych graniczn
ą
warto
ść
smukło
ś
ci
mo
ż
na okre
ś
li
ć
wg 4.2.3.
4.2. Stateczno
ść
miejscowa
4.2.1. Zasady ogólne
a) Poni
ż
sze postanowienia dotycz
ą
pełno
ś
ciennych elementów konstrukcji, w których wyst
ę
puj
ą
ś
cianki płaskie,
wra
ż
liwe na m iejscow
ą
utrat
ę
stateczno
ś
ci. Do takich elementów zalicza si
ę
kształtowniki o przekroju klasy 4 oraz
ś
rodniki kształtowników spawanych, obci
ąż
one sił
ą
skupion
ą
.
b) Przy ustalaniu parametr ów stateczno
ś
ci nale
ż
y rozró
ż
nia
ć
kształtowniki o przekroju otwartym (walcowane,
spawane lub gi
ę
te) oraz kształtowniki o przekroju zamkni
ę
tym - rurowe lub skrzynkowe.
Pod poj
ę
ciem kształtownika rurowego nale
ż
y rozumie
ć
kształtownik zam kni
ę
ty o profilu wielobocznym,
zaokr
ą
glonych naro
ż
ach i stałej grubo
ś
ci
ś
cianek.
c) W pr zypadku elementów obci
ąż
onych statycznie mo
ż
na uwzgl
ę
dnia
ć
w obliczeniach stan nadkrytyczny
ś
cianek i
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 14
towarzysz
ą
cy mu wzrost no
ś
no
ś
ci obliczeniowej przekroju. Konstrukcje z kształtowników gi
ę
tych, w których
uwzgl
ę
dnia si
ę
pełny stan nadkrytyczny nale
ż
y oblicza
ć
i projektowa
ć
wg specjalnych przepisów.
4.2.2.
Ś
cianki
ś
ciskane,
ś
ciskane mimo
ś
rodowo lub zginane w swojej płaszczy
ź
nie
4.2.2.1. No
ś
no
ść
w stanie krytycznym
a) Smukło
ść
wzgl
ę
dn
ą
ś
cianki
nale
ż
y oblicza
ć
wg wzoru
(7)
w którym:
b, t - szeroko
ść
i grubo
ść
ś
cianki wg tabl. 6,
K - współczynnik podparcia i obci
ąż
enia
ś
cianki wg tabl. 8.
b) Współczynniki niestateczno
ś
ci
ϕ
p
nale
ż
y przyjmowa
ć
w zale
ż
no
ś
ci od sm ukło
ś
ci wzgl
ę
dnej
, wg tabl. 9, z
wyj
ą
tkiem kształtowników skrzynkowych i rurowych z napr
ęż
eniami spawalniczymi, dla których obowi
ą
zuj
ą
zale
ż
no
ś
ci:
gdzie
ν
- stosunek napr
ęż
e
ń
ś
rednich do najwi
ę
kszych napr
ęż
e
ń
ś
ciskaj
ą
cych w rozpatrywanej
ś
ciance (tabl. 8).
Tablica 8
Schemat podparcia i obci
ąż
enia
ś
cianki
Zakres
wa
ż
no
ś
ci
Współczynnik K
β
> 1
0
≤
ν
≤
1
_ _ _ _ _ _
_
ν
≤
0
K
2
= 0,4 + 0,6
ν
_ _ _ _ _ _ _
K
2
= 0,4/(1-
ν
)
β
< 1
0,5
≤
ν
≤
1
β
≥
1,6
0
≤
ν
≤
1
K
1
= 2,2 + 0,8
ν
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 15
β
≥
1
β < 1
Tablica 9
Smukło
ść
wzgl
ę
dna
Współczynniki niestateczno
ś
ci miejscowej
1)
ϕ
p
ϕ
pe
(
σ
c
= f
d
)
≤
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55
2,60
2,65
2,70
1
0,956
0,911
0,870
0,834
0,800
0,740
0,687
0,640
0,598
0,560
0,526
0,495
0,467
0,441
0,418
0,397
0,377
0,359
0,342
0,327
0,312
0,299
0,286
0,275
0,264
0,254
0,244
0,235
0,227
0,219
0,211
0,204
0,197
0,191
0,185
0,179
0,173
0,168
0,163
1
0,956
0,911
0,870
0,834
0,800
0,769
0,741
0,715
0,691
0,669
0,649
0,629
0,611
0,594
0,578
0,563
0,549
0,536
0,523
0,511
0,500
0,489
0,479
0,469
0,459
0,450
0,442
0,434
0,426
0,418
0,411
0,404
0,397
0,391
0,384
0,378
0,372
0,367
0,361
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 16
2,75
2,80
2,85
2,90
2,95
3,00
0,159
0,154
0,150
0,146
0,142
0,138
0,356
0,351
0,346
0,341
0,337
0,332
1)
Równania krzywych
c) Warunek stateczno
ś
ci
ś
cianki w jednoosiowym stanie napr
ęż
enia jest okre
ś
lony nast
ę
puj
ą
co
(9)
gdzie
σ
c
- najwi
ę
ksze napr
ęż
enia
ś
ciskaj
ą
ce w rozpatrywanej
ś
ciance.
4.2.2.2. Cechy przekroju w stanie nadkrytycznym
a) Szeroko
ść
współpracuj
ą
c
ą
ś
cianki b
e
w stanie nadkrytycznym mo
ż
na oblicza
ć
wg wzoru
(10)
Współczynnik niestateczno
ś
ci
ϕ
pe
nale
ż
y przyjmowa
ć
wg tabl. 9, z wyj
ą
tkiem kształtowników skrzynkowych i
rurowych z napr
ęż
eniami spawalniczymi, dla których obowi
ą
zuj
ą
zale
ż
no
ś
ci:
(11)
gdzie
ν
- jak we wzorze (8).
b) Je
ś
li najwi
ę
ksze napr
ęż
enia
ś
ciskaj
ą
ce
σ
c
w przekroju współpracuj
ą
cym s
ą
ogr aniczone do warto
ś
ci mniejszej
ni
ż
f
d
, to mo
ż
na zamiast
ϕ
pe
przyjmowa
ć
(12)
c) Przekrój współpracuj
ą
cy elementu w stanie nadkrytycznym ustala si
ę
okr e
ś
laj
ą
c wielko
ść
i rozm ieszczenie
odcinków szeroko
ś
ci współpracuj
ą
cej b
e
jego poszczególnych
ś
cianek (tabl. 8). Dla tak zredukowanego przekroju
oblicza si
ę
miarodajne cechy geometryczne, a w szczególno
ś
ci jego pole A
e
≤
A oraz wska
ź
nik wytrzymało
ś
ci W
e
≤
W.
W przypadku
ś
ciskania ze zginaniem m o
ż
na pr zyjmowa
ć
pole A
e
ustalone jak przy równomiernym
ś
ciskaniu, a
wska
ź
nik W
e
- ustalony jak przy czystym zginaniu.
Je
ś
li
ś
rodek ci
ęż
ko
ś
ci przekroju współpracuj
ą
cego (ustalonego przy zało
ż
eniu równomiernego
ś
ciskania) jest
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 17
przesuni
ę
ty wzgl
ę
dem poło
ż
enia pierwotnego o wielko
ść
e, to nale
ż
y uwzgl
ę
dnia
ć
w obliczeniach dodatkowe
zginanie momentem
∆
M = Ne.
4.2.2.3. Współczynnik redukcyjny
ψ
no
ś
no
ś
ci obliczeniowej przekroju jest okre
ś
lony nast
ę
puj
ą
co:
- w stanie krytycznym
(13)
- w stanie nadkrytycznym
(14)
- w stanie nadkr ytycznym ograniczonym (p. 4.2.2.2 b), tj. gdy napr
ęż
enia
σ
c
w przekroju współpracuj
ą
cym
ś
cianki
podpieranej (o najwi
ę
kszej smukło
ś
ci
) s
ą
ograniczone do warto
ś
ci wynikaj
ą
cej ze stanu krytycznego
ś
cianki
podpieraj
ą
cej (
σ
c
=
ϕ
p
f
d
, gdzie
ϕ
p
dla
).
(15)
Dla kształtowników, w których wyst
ę
puj
ą
wył
ą
cznie
ś
cianki jednostronnie usztywnione (tj. dla k
ą
towników,
teowników i elementów o przekroju krzy
ż
owym), a tak
ż
e dla innych kształtowników nara
ż
onych na obci
ąż
enia
wielokrotnie zmienne lub udarowe nale
ż
y przyjmowa
ć
ψ
wg wzoru (13).
W pzostałych przypadkach mo
ż
na i zaleca si
ę
przyjmowa
ć
ψ
wg wzoru (15).
4.2.3.
Ś
cianki
ś
cinane. No
ś
no
ść
obliczeniowa przekroju przy
ś
cinaniu sił
ą
poprzeczn
ą
V jest okre
ś
lona wzorem
(16)
w którym:
ϕ
p
ν
- współczynnik niestateczno
ś
ci przy
ś
cinaniu:
(17)
- smukło
ść
wzgl
ę
dna, któr
ą
nale
ż
y oblicza
ć
wg wzoru (7), przyjmuj
ą
c miarodajn
ą
szeroko
ść
ś
cianki b równ
ą
rozstawowi usztywnie
ń
podłu
ż
nych oraz współczynnik K = K
ν
wg tabl. 8.
A
ν
- pole przekroju czynnego przy
ś
cinaniu wg tabl. 7.
4.2.4.
Ś
rodniki pod obci
ąż
eniem skupionym. No
ś
no
ść
obliczeniow
ą
ś
r odnika obci
ąż
onego sił
ą
skupion
ą
P
nale
ż
y oblicza
ć
wg wzoru
(18)
w którym:
k
c
- współczynnik, który nale
ż
y oblicza
ć
nast
ę
puj
ą
co:
- gdy siła działa stacjonarnie (rys. 1)
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 18
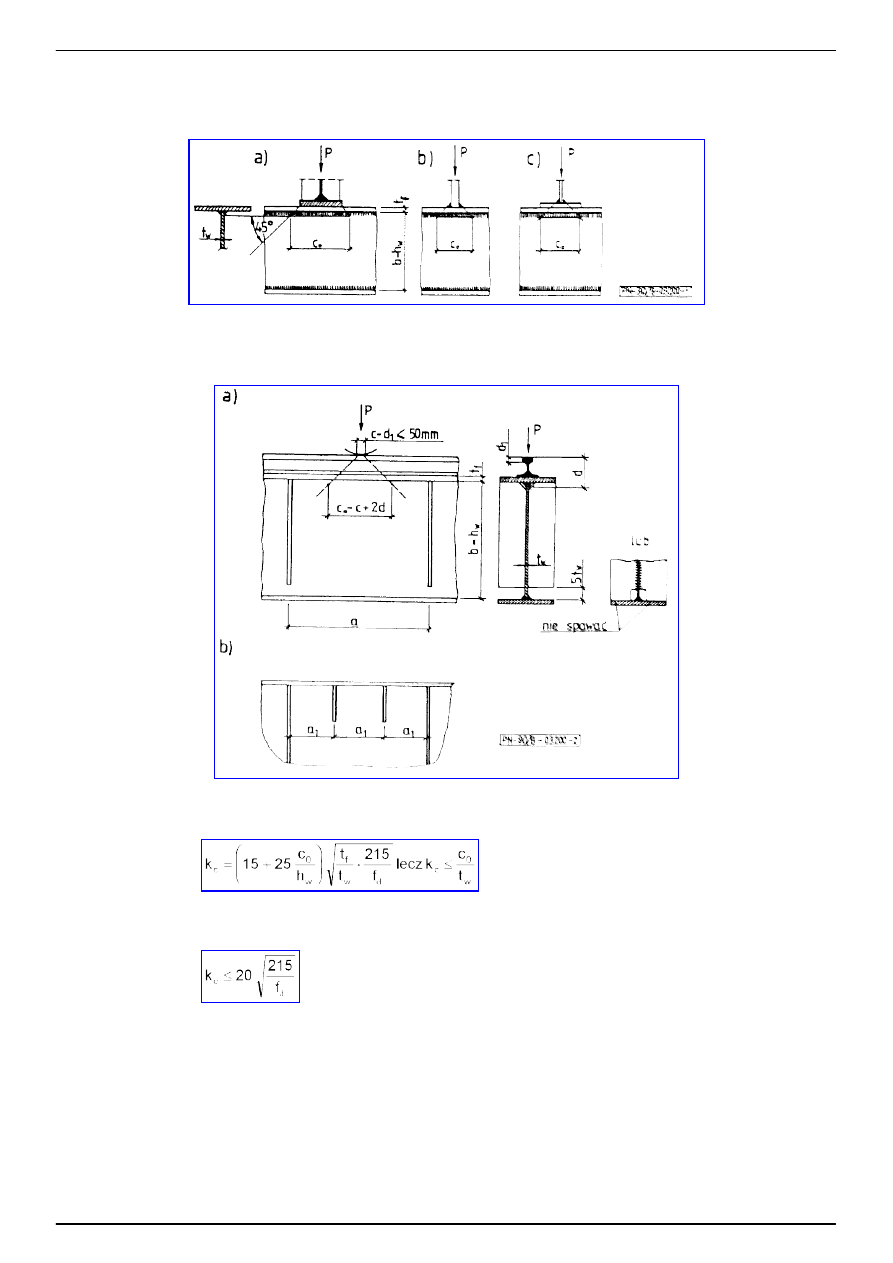
Rys. 1
Rys. 2
(19)
- gdy siła mo
ż
e zmienia
ć
poło
ż
enie wzdłu
ż
belki (rys. 2a) powinien by
ć
dodatkowo spełniony warunek
(20)
przy czym w przypadku dodatkowego usztywnienia
ś
rodnika
ż
ebrami krótkimi (rys. 2b) o rozstawie a
1
< 2c
0
i
długo
ś
ci równej
2
/
3
szeroko
ś
ci strefy
ś
ciskanej, mo
ż
na przyjmowa
ć
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 19
(21)
Je
ś
li napr
ęż
enia
ś
ciskaj
ą
ce
σ
c
w
ś
rodniku, skierowane wzdłu
ż
styku z pasem s
ą
wi
ę
ksze ni
ż
0,5f
d
to nale
ż
y
przyjmowa
ć
no
ś
no
ść
obliczeniow
ą
zredukowan
ą
(22)
gdzie
η
c
- współczynnik redukcyjny, który dla
0,5f
d
<
σ
c
≤
f
d
wynosi
(23)
W przypadku
ś
rodników o przekroju klasy 4 obowi
ą
zuje warunek (24).
4.2.5.
Ś
rodniki w zło
ż
onym st anie napr
ęż
enia. Stateczno
ść
ś
rodników obci
ąż
onych w ogólnym przypadku siłami
N
w
, M
w
, V i P nale
ż
y sprawdza
ć
wg wzoru
(24)
w którym:
N
Rw
, M
Rw
- no
ś
no
ść
obliczeniowa
ś
rodnika pr zy
ś
ciskaniu, przy zginaniu; w przypadku obci
ąż
e
ń
statycznych i braku
siły skupionej (P = 0) mo
ż
na przyjmowa
ć
no
ś
no
ść
w stanie nadkrytycznym,
ϕ
p
- współczynnik niestateczno
ś
ci
ś
cianki wg 4.2.2,
P
Rc
- wg wzoru (18),
V
R
- wg wzoru (16).
Przy sprawdzaniu stateczno
ś
ci
ś
rodników z
ż
ebram i krótkim i (rys. 2b), nie uwzgl
ę
dnia si
ę
ż
eber krótkich, a we
wzorze (24) nale
ż
y przyj
ąć
P = 0.
4.2.6.
Ż
ebra usztywniaj
ą
ce
4.2.6.1. Zalecenia konstrukcyjne
a)
Ż
ebra usztywniaj
ą
ce (rys. 3) projektuje si
ę
z płaskowników lub kształtowników, jako jednostronne lub
dwustronne, spawane lub nitowane.
Rys. 3
b)
Ż
ebra poprzeczne stosuje si
ę
w miejscach działania znacznych obci
ąż
e
ń
skupionych, na podporach, w strefach
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 20
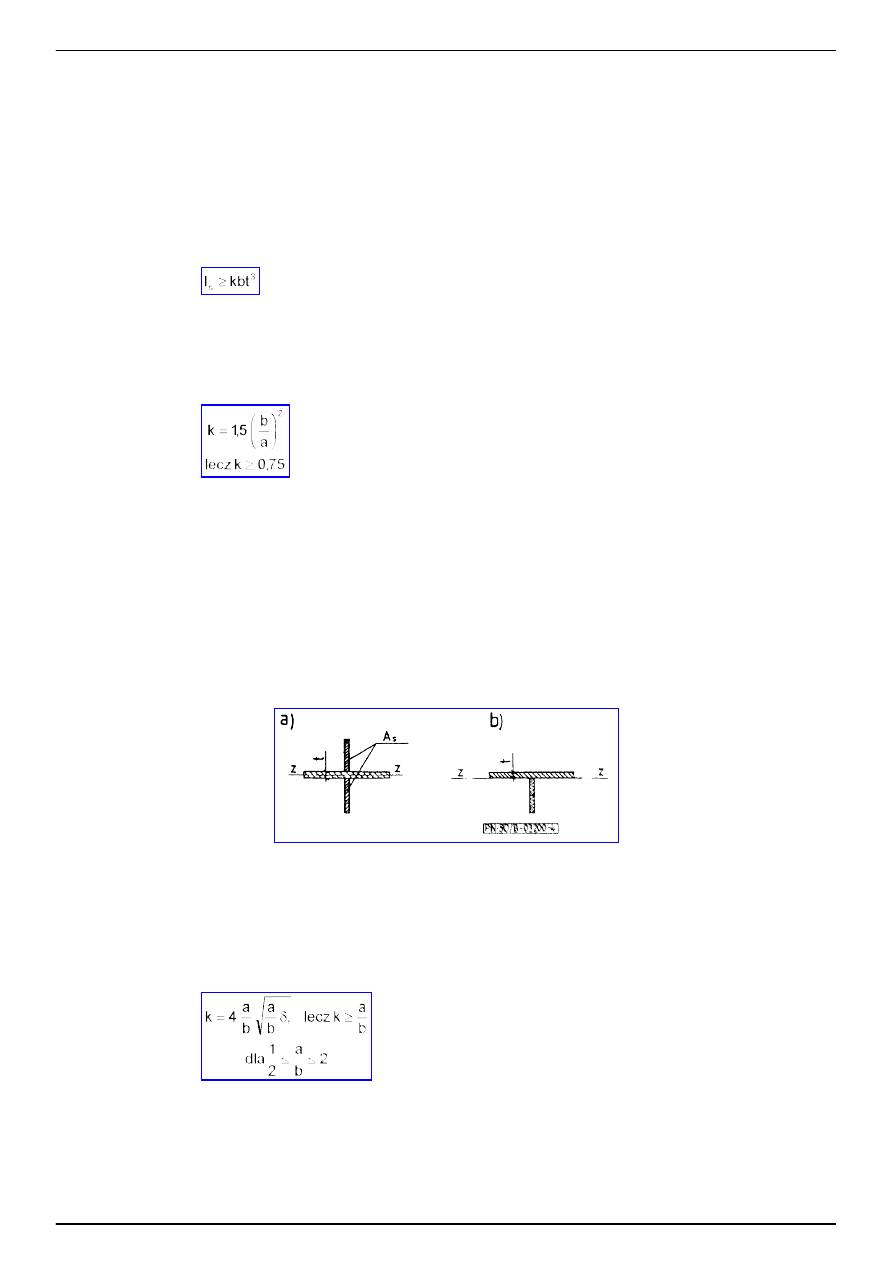
w
ę
złów sztywnych, a tak
ż
e w innych miejscach, gdy zachodzi potrzeba dodatkowego usztywnienia smukłych
ś
cianek.
c) Rozstaw
ż
eber poprzecznych w prz
ę
słach belek o przekroju klasy 4 nie powinien by
ć
wi
ę
kszy ni
ż
podwójna
wysoko
ść
ś
rodnika.
d)
Ż
ebra podłu
ż
ne stosuje si
ę
w przypadku bardzo smukłych
ś
rodników, lokalnie - w
ś
ciskanych strefach belek i na
całej długo
ś
ci w elementach
ś
ciskanych (słupach).
4.2.6.2.
Ż
ebra poprzeczne powinny spełnia
ć
warunek sztywno
ś
ci
(25)
gdzie:
I
s
- m oment bezwładno
ś
ci przekroju
ż
ebr a wzgl
ę
dem osi w płaszczy
ź
nie
ś
r odkowej
ś
rodnika - w przypadku
ż
ebra
dwustronnego (rys. 4a) lub wzgl
ę
dem osi w płaszczy
ź
nie styku - w przypadku
ż
ebra jednostronnego (rys. 4b).
k - współczynnik okre
ś
lony wzorem
(26)
a - rozstaw
ż
eber,
b, t - szeroko
ść
i grubo
ść
ś
cianki usztywnionej.
Gdy uwzgl
ę
dnia si
ę
no
ś
no
ść
nadkrytyczn
ą
ś
cianki, to nale
ż
y dodatkowo sprawdzi
ć
no
ś
no
ść
ż
ebra, traktuj
ą
c je jak
swobodnie podpart
ą
(przez pasy) belk
ę
, obci
ąż
on
ą
w płaszczy
ź
nie prostopadłej do
ś
cianki:
- obci
ąż
eniem równomiernie rozło
ż
onym, równowa
ż
nym 2% siły
ś
ciskaj
ą
cej w
ś
ciance,
- siłam i skupionymi (w m iejscach skrzy
ż
owania
ż
eber) o warto
ś
ciach równych 2% odpowiednich sił w
ż
ebrach
podłu
ż
nych.
Ż
ebr a podporowe or az
ż
ebra pod sił
ę
skupion
ą
wymiaruje si
ę
jak pr
ę
ty
ś
ciskane przy długo
ś
ci wyboczeniowej
l
e
= 0,8h
w
, gdzie h
w
- wysoko
ść
ś
rodnika. W przypadku obci
ąż
e
ń
statycznych m o
ż
na uwzgl
ę
dnia
ć
w obliczeniach
cz
ęść
współpracuj
ą
c
ą
ś
rodnika o szeroko
ś
ci 30t
w
.
Rys. 4
4.2.6.3.
Ż
ebra podłu
ż
ne powinny mie
ć
przekrój klasy nie wy
ż
szej ni
ż
3 or az odpowiedni
ą
sztywno
ść
, któr
ą
dobiera
si
ę
z warunku (25), przyjmuj
ą
c wła
ś
ciwe dla
ż
eber podłu
ż
nych współczynniki k.
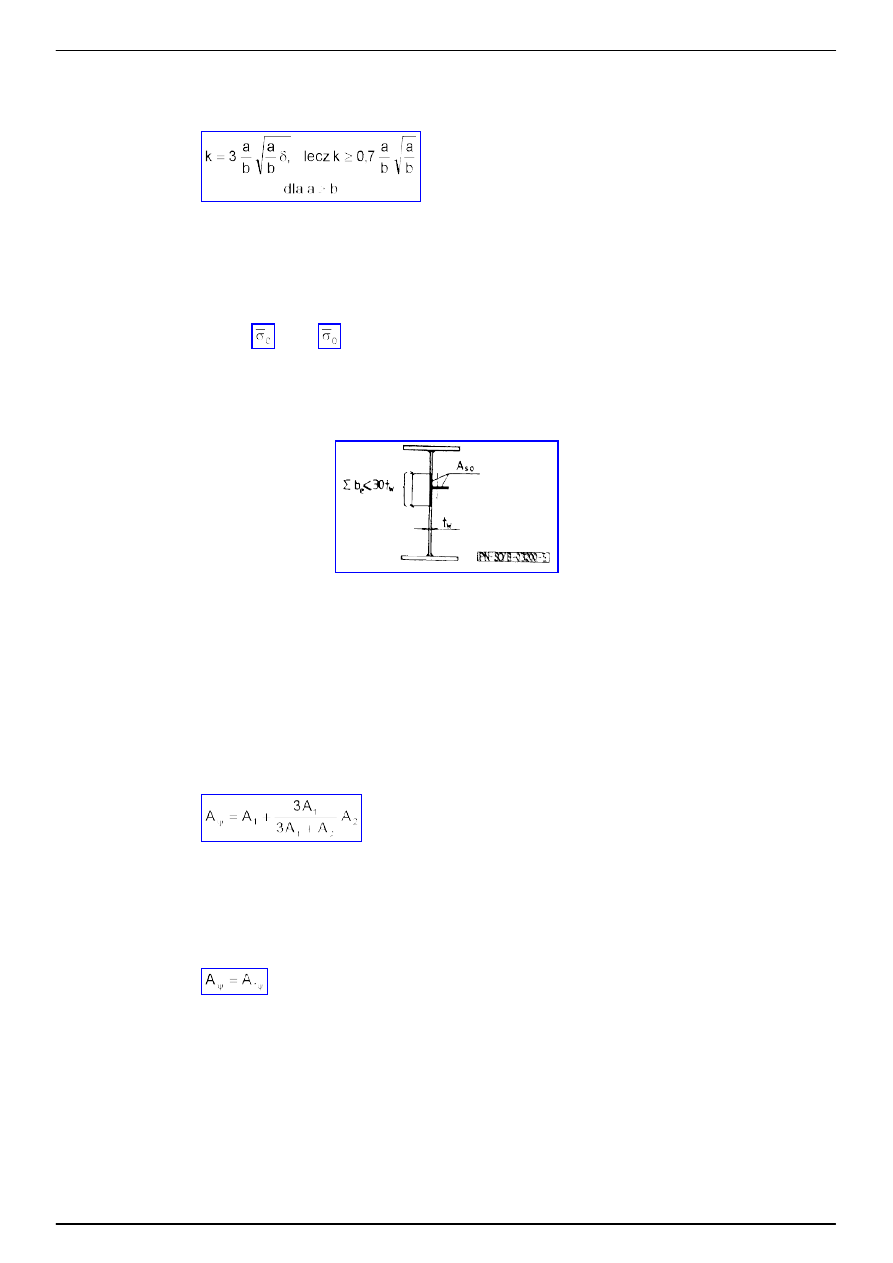
Dla
ż
eber usztywniaj
ą
cych
ś
rodnik belki zginanej (r ys. 3b) w odległo
ś
ci b
1
= (0,25 ÷ 0,33) b od pasa
ś
ciskanego
mo
ż
na przyjmowa
ć
(27)
a dla
ż
eber usztywniaj
ą
cych
ś
ciank
ę
ś
ciskan
ą
w połowie jej szeroko
ś
ci.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 21
(28)
gdzie
δ
- stosunek pola przekroju
ż
ebra do pola przekroju
ś
cianki usztywnionej (
ś
rodnika), przy czym:
0,05
≤
δ
= A
s
/bt
≤
0,20.
Gdy uwzgl
ę
dnia si
ę
stan nadkrytyczny
ś
cianki, to nale
ż
y dodatkowo sprawdzi
ć
stateczno
ść
ż
ebr a w płaszczy
ź
nie
prostopadłej do
ś
cianki przyjmuj
ą
c do oblicze
ń
:
- obliczeniowe pole przekroju
ż
ebra A
s0
= A
s
+
Σ
b
e
t
w
(rys. 5),
- długo
ść
wyboczeniow
ą
, równ
ą
rozstawowi
ż
eber poprzecznych lub st
ęż
e
ń
bocznych elementu,
- obci
ąż
enie sił
ą
N
0
= A
s0
, gdzie
-
ś
rednie napr
ęż
enie w przekroju A
s0
.
Ż
ebr a dwustronne, a tak
ż
e jednostronne zachowuj
ą
ce ci
ą
gło
ść
na skrzy
ż
owaniach z
ż
ebrami popr zecznymi oblicza
si
ę
jak pr
ę
ty
ś
ciskane osiowo. Przy braku ci
ą
gło
ś
ci
ż
eber jednostronnych nale
ż
y przyjm owa
ć
,
ż
e siła działa w
płaszczy
ź
nie
ś
rodkowej
ś
cianki.
Rys. 5
4.3. Elementy rozci
ą
gane
4.3.1. Postanowienia ogólne
a) W przypadku pr
ę
tów projektowanych jako osiowo rozci
ą
gane mo
ż
na pomija
ć
zginanie wywołane ci
ęż
arem
własnym, je
ś
li rzut poziomy długo
ś
ci pr
ę
ta nie przekracza 6 m.
b) Zam ocowane mimo
ś
rodowo pr
ę
ty pojedyncze: k
ą
towniki zamocowane jednym ramieniem, ceowniki
zam ocowane
ś
rodnikiem oraz teowniki zamocowane półk
ą
mo
ż
na traktowa
ć
jak osiowo obci
ąż
one pod warunkiem,
ż
e do oblicze
ń
przyjmuje si
ę
sprowadzone pole przekroju A
ψ
okre
ś
lone wzorem
(29)
w którym:
A
1
- pole pr zekroju cz
ęś
ci przylgowej kształtownika: brutto - w przypadku poł
ą
czenia spawanego, netto - w
przypadku poł
ą
czenia
ś
rubowego lub nitowego;
A
2
- pole przekroju cz
ęś
ci odstaj
ą
cej kształtownika.
W przypadku poł
ą
czenia na jeden ł
ą
cznik nale
ż
y przyjmowa
ć
(30)
gdzie A
1
ψ
- sprowadzone pole przekroju cz
ęś
ci przylgowej kształtownika obliczone wg wzoru (5).
c) W przypadku obci
ąż
e
ń
dynamicznych obowi
ą
zuje ograniczenie smukło
ś
ci pr
ę
ta:
λ
≤
250 - dla pr
ę
tów kratownic,
λ
≤
350 - dla ci
ę
gien bez wst
ę
pnego naci
ą
gu.
d) No
ś
no
ść
elementów rozci
ą
ganych mimo
ś
rodowo nale
ż
y sprawdza
ć
wg 4.5.6.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 22

4.3.2. No
ś
no
ść
elementów rozci
ą
ganych osiowo nale
ż
y sprawdza
ć
wg wzoru
(31)
przy czym w przypadku elementów osłabionych otworami na ł
ą
czniki (p. 4.1.2d) lub zamocowanych mimo
ś
rodowo
(p. 4.3.1b) obowi
ą
zuje warunek
(32)
gdzie A
ψ
- sprowadzone pole przekroju.
4.4. Elementy
ś
ciskane
4.4.1. Postanowienia ogólne
a) W przypadku pr
ę
tów projektowanych jako osiowo
ś
ciskane mo
ż
na pomija
ć
zginanie wywołane ci
ęż
arem
własnym, je
ś
li iloczyn smukło
ś
ci wzgl
ę
dnej pr
ę
ta w płaszczy
ź
nie pionowej i rzutu poziomego jego długo
ś
ci nie
przekracza 6 m.
b) Zamocowane mim o
ś
rodowo pr
ę
ty skratowania, okre
ś
lone w 4.3.1b) m o
ż
na uwa
ż
a
ć
za osiowo
ś
ciskane, pr zy
czym dodatkowo powinien by
ć
spełniony warunek (32), w którym A
ψ
- wg wzoru (29).
c) Osłabienie elementu otworami na ł
ą
czniki nale
ż
y uwzgl
ę
dnia
ć
wg 4.1.2.
d) Smukło
ść
pr
ę
ta powinna spełnia
ć
warunek
λ
≤
250.
e) No
ś
no
ść
elementów
ś
ciskanych mimo
ś
rodowo nale
ż
y sprawdza
ć
wg 4.6.
4.4.2. No
ś
no
ść
obliczeniowa przekroju przy osiowym
ś
ciskaniu N
Rc
jest okre
ś
lona nast
ę
puj
ą
co:
(33)
przy czym
- dla przekrojów klasy 1, 2 i 3 przyjmuje si
ę
ψ
= 1
- dla przekrojów klasy 4 przyjmuje si
ę
ψ
- wg 4.2.2.3.
4.4.3. Smukło
ść
wzgl
ę
dna pr
ę
ta przy wyboczeniu
jest okre
ś
lona wzorem
(34)
w którym N
cr
- siła krytyczna wg klasycznej teorii stateczno
ś
ci przy wyboczeniu gi
ę
tnym, skr
ę
tnym lub gi
ę
tno-
skr
ę
tnym; odpowiednie wzory do obliczania N
cr
podano w zał
ą
czniku 1, rozdz. 3.
Smukło
ść
wzgl
ę
dn
ą
pr
ę
ta prostego o stałym przekroju przy wyboczeniu gi
ę
tnym mo
ż
na oblicza
ć
wg wzorów:
(35)
lub w przypadku przekroju klasy 4 (
ψ
< 1)
(36)
w których:
λ
- smukło
ść
pr
ę
ta (stosunek długo
ś
ci wyboczeniowej l
e
do wła
ś
ciwego promienia bezwładno
ś
ci przekroju)
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 23
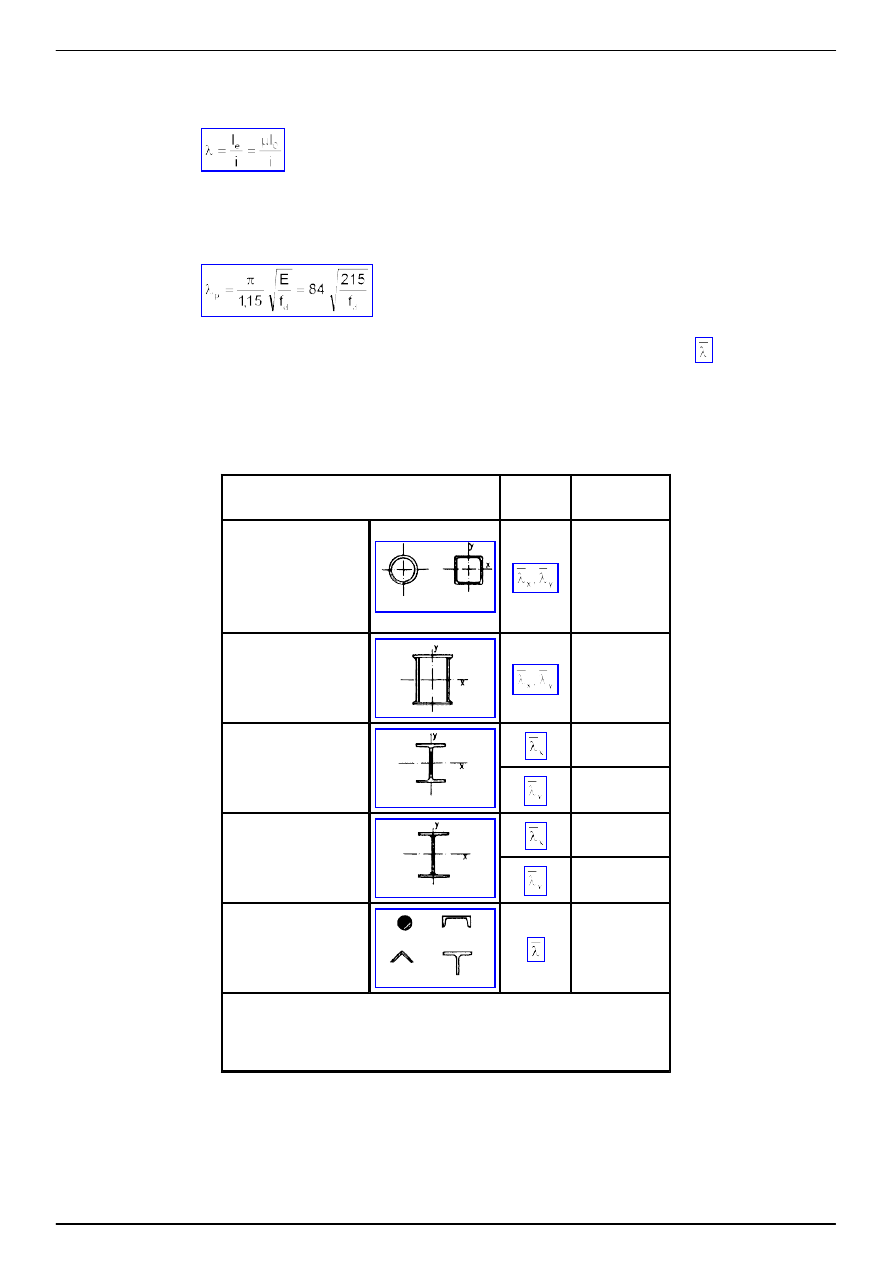
(37)
µ
- współczynnik długo
ś
ci wyboczeniowej, który mo
ż
na przyjmowa
ć
(wyznacza
ć
) wg zał
ą
cznika 1,
l
0
- długo
ść
obliczeniowa pr
ę
ta mierzona w osiach podpór (st
ęż
e
ń
) lub mi
ę
dzy teoretycznymi w
ę
złami konstrukcji,
λ
p
- smukło
ść
porównawcza:
(38)
4.4.4. Współczynnik wyboczeniowy
ϕ
nale
ż
y przyjmowa
ć
w zale
ż
no
ś
ci od smukło
ś
ci wzgl
ę
dnej
z tabl. 11 wg
odpowiedniej krzywej wyboczeniowej ustalonej na podstawie tabl. 10.
Tablica 10
Element - technologia wytwarzania,
przekrój
Smukło
ść
wzgl
ę
dna
Krzywa
wyboczeniowa
Rurowy okr
ą
gły lub
prostok
ą
tny
- bez napr
ęż
e
ń
spawalniczych
- z napr
ęż
eniami
spawalniczymi
a
b
Skrzynkowy -
spawany
1/
z blach lub
kształtowników
b (a)
Dwuteowy walcowany
2/
a (b)
b (c)
Dwuteowy spawany
1)
b (a)
c (b)
Inne elementy o
przekroju pełnym lub
otwartym
c
1)
Kształtownikom poddanym wy
ż
arzaniu odpr
ęż
aj
ą
cemu mo
ż
na
przyporz
ą
dkowa
ć
krzywe podane w nawiasach.
2)
Dwuteownikom szerokostopowym (h/b
≤
1,2) nale
ż
y
przyporz
ą
dkowa
ć
krzywe podane w nawiasach.
Tablica 11
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 24

Smukło
ść
wzgl
ę
dna
Współczynniki niestateczno
ś
ci ogólnej
ϕ
,
ϕ
L
(wg krzywej
1)
)
a
0
(n = 2,5)
a (n = 2)
b (n = 1,6)
c (n = 1,2)
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55
2,60
2,65
1,000
1,000
1,000
1,000
1,000
1,000
0,999
0,998
0,996
0,993
0,988
0,981
0,970
0,957
0,940
0,918
0,893
0,863
0,831
0,795
0,758
0,720
0,681
0,643
0,607
0,571
0,538
0,506
0,477
0,449
0,423
0,399
0,377
0,356
0,337
0,319
0,302
0,287
0,273
0,259
0,247
0,235
0,225
0,214
0,205
0,196
0,188
0,180
0,173
0,166
0,159
0,153
0,147
0,142
1,000
1,000
1,000
1,000
0,999
0,998
0,996
0,993
0,987
0,980
0,970
0,957
0,941
0,921
0,898
0,872
0,842
0,811
0,777
0,742
0,707
0,672
0,637
0,603
0,570
0,539
0,509
0,481
0,454
0,430
0,406
0,384
0,364
0,345
0,327
0,310
0,295
0,280
0,267
0,254
0,243
0,231
0,221
0,211
0,202
0,194
0,186
0,178
0,171
0,164
0,158
0,152
0,146
0,141
1,000
1,000
1,000
0,999
0,996
0,993
0,987
0,979
0,968
0,954
0,937
0,918
0,895
0,869
0,841
0,811
0,780
0,747
0,714
0,681
0,648
0,616
0,585
0,555
0,526
0,499
0,473
0,448
0,425
0,403
0,382
0,363
0,345
0,328
0,312
0,297
0,282
0,269
0,257
0,245
0,234
0,224
0,214
0,205
0,197
0,189
0,181
0,174
0,167
0,161
0,155
0,149
0,144
0,139
1,000
0,999
0,997
0,991
0,983
0,971
0,956
0,938
0,916
0,892
0,865
0,837
0,807
0,776
0,744
0,713
0,681
0,650
0,619
0,590
0,561
0,534
0,507
0,482
0,459
0,436
0,415
0,394
0,375
0,357
0,340
0,324
0,309
0,295
0,282
0,269
0,257
0,246
0,236
0,226
0,216
0,208
0,199
0,191
0,184
0,177
0,170
0,164
0,158
0,152
0,147
0,141
0,137
0,132
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 25
2,70
2,75
2,80
2,85
2,90
2,95
3,00
0,137
0,132
0,127
0,123
0,119
0,115
0,111
0,136
0,131
0,127
0,122
0,118
0,114
0,110
0,134
0,129
0,125
0,120
0,117
0,113
0,109
0,127
0,123
0,119
0,115
0,112
0,108
0,105
1)
Współczynnik
ϕ
jest parametryczn
ą
funkcj
ą
smukło
ś
ci wzgl
ę
dnej:
, gdzie n - uogólniony
parametr imperfekcji.
4.4.5. No
ś
no
ść
(stateczno
ść
) elementów
ś
ciskanych osiowo nale
ż
y sprawdza
ć
wg wzoru
(39)
w którym:
N
Rc
- no
ś
no
ść
obliczeniowa przekroju wg 4.4.2,
ϕ
- współczynnik wyboczeniowy:
ϕ
= min
ϕ
(
) - wg 4.4.4.
W przypadku pr
ę
tów o przekroju otwartym : monosymetrycznym , punktowo sym etrycznym (np. krzy
ż
owym) lub
niesym etrycznym, oprócz wyboczenia gi
ę
tnego, nale
ż
y bra
ć
równie
ż
pod uwag
ę
mo
ż
liwo
ść
wyboczenia gi
ę
tno-
skr
ę
tnego lub skr
ę
tnego, obliczaj
ą
c stosown
ą
smukło
ść
wg wzoru (34). Mo
ż
na nie sprawdza
ć
stateczno
ś
ci gi
ę
tno-
skr
ę
tnej pr
ę
tów z kształtowników walcowanych.
4.5. Elementy zginane
4.5.1. Postanowienia ogólne
a) Elem enty zginane wzgl
ę
dem jednej z dwu głównych osi bezwładno
ś
ci przekroju uwa
ż
a si
ę
za zginane
jednokierunkowo.
b) Je
ś
li obci
ąż
enie poprzeczne elem entu przy zginaniu jednokierunkowym lub dwukierunkowym (uko
ś
nym) działa
mim o
ś
rodowo wzgl
ę
dem osi
ś
rodków
ś
cinania, to nale
ż
y dodatkowo uwzgl
ę
dnia
ć
w obliczeniach skr
ę
canie
elementu, lub stosowa
ć
odpowiednie zabezpieczenie konstrukcyjne (st
ęż
enie) w celu przeniesienia momentów
skr
ę
caj
ą
cych.
Mo
ż
na pomija
ć
w obliczeniach wpływ drugorz
ę
dnego skr
ę
cania w przypadku kształtowników o przekroju
zamkni
ę
tym.
c) No
ś
no
ść
elementów zginanych wzgl
ę
dem osi najwi
ę
kszej bezwładno
ś
ci przekroju (X) nale
ż
y sprawdza
ć
z
uwzgl
ę
dnieniem mo
ż
liwo
ś
ci utraty płaskiej postaci zginania, czyli zwichrzenia.
Mo
ż
na przyj
ąć
,
ż
e s
ą
konstrukcyjnie zabezpieczone przed zwichrzeniem:
- elementy, których pas
ś
ciskany jest st
ęż
ony sztywn
ą
tarcz
ą
;
- dwuteowniki walcowane, gdy spełniony jest warunek
(40)
gdzie:
l
1
- r ozstaw st
ęż
e
ń
bocznych pasa
ś
ciskanego lub odległo
ść
mi
ę
dzy przekrojam i zabezpieczonym i przed obrotem i
przemieszczeniem bocznym,
i
y
- promie
ń
bezwładno
ś
ci przekroju wzgl
ę
dem osi Y,
β
- wg tabl. 12, poz. a), jak dla elementu o długo
ś
ci l
0
= l
1
;
- elementy rurowe i skrzynkowe, gdy spełniony jest warunek
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 26
(41)
gdzie:
l
1
- jak we wzorze (40),
b
0
- osiowy rozstaw
ś
rodników.
d) Rozpi
ę
to
ść
obliczeniow
ą
belek l
0
nale
ż
y przyjmowa
ć
równ
ą
osiowemu rozstawowi podpór (ło
ż
ysk), a przy
oparciu powierzchniowym lub zamocowaniu w
ś
cianach - równ
ą
:
1,05l - w przypadku belek dwustronnie podpartych lub zamocowanych,
1,025l - w przypadku wsporników lub skrajnych prz
ę
seł belek ci
ą
głych,
przy czym l
0
≥
l + 0,5h, gdzie l - odległo
ść
w
ś
wietle mi
ę
dzy
ś
cianam i lub mi
ę
dzy ło
ż
yskiem a
ś
cian
ą
, h - wysoko
ść
belki.
e) No
ś
no
ść
ś
rodników pod obci
ąż
eniem skupionym nale
ż
y sprawdza
ć
wg 4.2.4, a w przypadku kształtowników
walcowanych - wg 6.5.
f) Osłabienie elementu otworami na ł
ą
czniki nale
ż
y uwzgl
ę
dnia
ć
wg 4.1.2.
g) Przy wymiarowaniu elementów zginanych nale
ż
y spełni
ć
odpowiednie warunki sztywno
ś
ci podane w 3.3.2.
4.5.2. No
ś
no
ść
obliczeniowa przekroju przy jednokierunkowym zginaniu M
R
jest okre
ś
lona nast
ę
puj
ą
co:
a) dla przekrojów klasy 1 i 2,
(42)
gdzie:
α
p
- obliczeniowy współczynnik r ezerwy plastycznej przekroju przy zginaniu wg zał
ą
cznika 4, rozdz. 2; współczynnik
α
p
> 1 m o
ż
na stosowa
ć
w przypadku elem entów obci
ąż
onych statycznie i zginanych w płaszczy
ź
nie symetrii
przekroju; w pozostałych przypadkach nale
ż
y przyj
ąć
α
p
= 1;
W - wska
ź
nik wytrzymało
ś
ci pr zekroju przy zginaniu spr
ęż
ystym dla najbardziej oddalonej od osi oboj
ę
tnej kraw
ę
dzi
ś
ciskanej (W
c
) lub rozci
ą
ganej (W
t
); W = min (W
c
, W
t
);
b) dla przekrojów klasy 3 (
ψ
= 1) i 4 (
ψ
< 1)
(43)
gdzie:
ψ
- współczynnik redukcyjny wg 4.2.2.3,
α
p
- jak we wzorze (42),
c) w przypadku pojedynczych ceowników walcowanych, zginanych w płaszczy
ź
nie
ś
rodnika lub do niego
równoległej, wpływ drugorz
ę
dnego skr
ę
cania mo
ż
na uwzgl
ę
dnia
ć
w sposób przybli
ż
ony pr zyjmuj
ą
c no
ś
no
ść
obliczeniow
ą
zredukowan
ą
wg wzoru
(44)
w którym:
V - siła poprzeczna w rozpatrywanym przekroju,
V
R
- no
ś
no
ść
obliczeniowa przekroju przy
ś
cinaniu wg wzoru (47),
e - mimo
ś
ród obci
ąż
enia poprzecznego (płaszczyzny zginania) wzgl
ę
dem
ś
rodka
ś
cinania przekroju, pr zy czym e
≤
b,
t
w
- grubo
ść
ś
rodnika,
b, t
f
- szeroko
ść
i
ś
rednia grubo
ść
półki.
d) je
ś
li w przekroju wyst
ę
puje siła poprzeczna V > V
0
, gdzie V
0
- jak ni
ż
ej, to nale
ż
y przyjmowa
ć
no
ś
no
ść
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 27
obliczeniow
ą
zredukowan
ą
M
R, v
, któr
ą
mo
ż
na oblicza
ć
nast
ę
puj
ą
co:
- w przypadku bisymetrycznych przekrojów dwuteowych klasy 1 i 2, zginanych wzgl
ę
dem osi najwi
ę
kszej
bezwładno
ś
ci, gdy V > V
0
= 0,6V
R
,
(45)
- w pozostałych przypadkach, gdy V > V
0
= 0,3V
R
,
(46)
gdzie:
I
(v)
- moment bezwładno
ś
ci cz
ęś
ci przekroju czynnej przy
ś
cinaniu wzgl
ę
dem osi oboj
ę
tnej,
I - moment bezwładno
ś
ci całego przekroju.
Je
ś
li spełniony jest odpowiedni warunek smukło
ś
ci z tabl. 7, to no
ś
no
ść
obliczeniow
ą
przy
ś
cinaniu V
R
mo
ż
na
oblicza
ć
wg wzoru
(47)
W przeciwnym razie obowi
ą
zuje wzór (16).
e) w przypadku dwuteowników hybrydowych (f
df
> f
dw
) no
ś
no
ść
obliczeniow
ą
przekroju mo
ż
na oblicza
ć
wg wzorów:
- przy zginaniu (wzgl
ę
dem osi X)
(48)
gdzie:
M
R,f
- no
ś
no
ść
obliczeniowa przekroju zło
ż
onego z pasów (f
d
= f
df
)
M
R,w
- no
ś
no
ść
obliczeniowa przekroju
ś
rodnika (f
d
= f
dw
)
- przy
ś
cinaniu ze zginaniem
(49)
gdzie:
V
R
- wg wzoru (16),
W - wska
ź
nik wytrzymało
ś
ci całego przekroju.
4.5.3. Smukło
ść
wzgl
ę
dna przy zwichrzeniu
.
a) Smukło
ść
jest okre
ś
lona wzorem
(50)
gdzie M
cr
- moment krytyczny wg klasycznej teorii stateczno
ś
ci; odpowiednie wzory do obliczania M
cr
podano w
zał
ą
czniku 1, rozdz. 3.
b) Smukło
ść
elementów o bisymetr ycznym przekroju dwuteowym, swobodnie podpartych w sposób widełkowy
(tj. bez mo
ż
liwo
ś
ci obrotu wokół osi pr
ę
ta) i obci
ąż
onych momentam i na podporach, mo
ż
na wyznacza
ć
wg wzoru
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 28
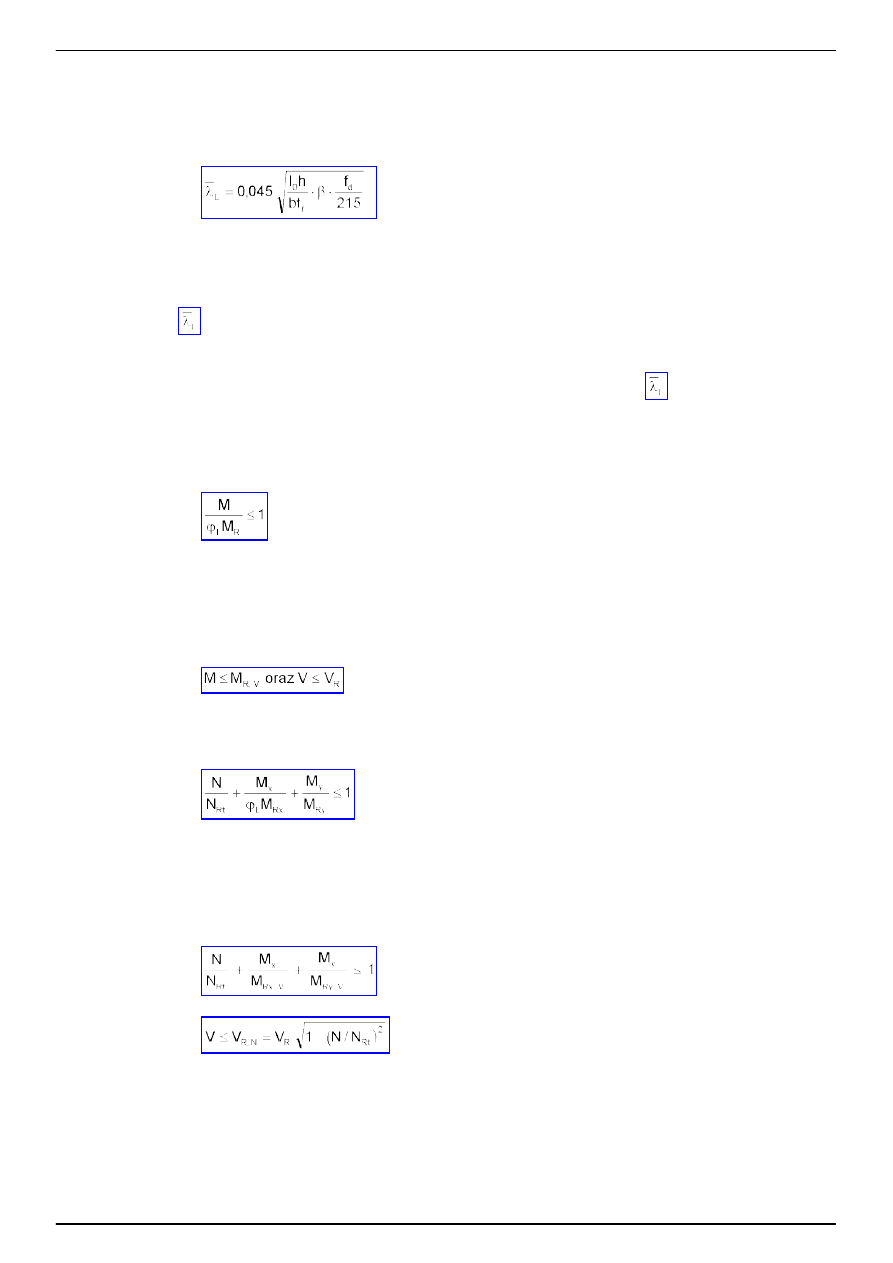
przybli
ż
onego
(51)
gdzie:
l
0
, h - rozpi
ę
to
ść
, wysoko
ść
elementu,
b, t
f
- szeroko
ść
, grubo
ść
pasa (półki),
β
- wg tabl. 12, poz. a).
c) Smukło
ść
ceowników walcowanych, podpartych i obci
ąż
onych jak w poz. b) mo
ż
na wyznacza
ć
wg wzoru
(51), zwi
ę
kszaj
ą
c otrzyman
ą
warto
ść
o 25%.
4.5.4. Współczynnik zwichrzenia
ϕ
L
nale
ż
y przyjm owa
ć
zale
ż
nie od smukło
ś
ci wzgl
ę
dnej
z tabl. 11, przy czym
dla elem entów walcowanych oraz elementów spawanych w sposób zmechanizowany - wg krzywej niestateczno
ś
ci
a
0
, natomiast w pozostałych przypadkach - wg krzywej a.
4.5.5. No
ś
no
ść
(stateczno
ść
) elementów jednokierunkowo zginanych nale
ż
y sprawdza
ć
wg wzoru
(52)
gdzie:
M
R
- no
ś
no
ść
obliczeniowa przekroju przy zginaniu wg 4.5.2,
ϕ
L
- współczynnik zwichr zenia wg 4.5.4; dla elementów zginanych wzgl
ę
dem osi najmniejszej bezwładno
ś
ci
przekroju, a tak
ż
e elementów zabezpieczonych przed zwichrzeniem (p. 4.5.1c) przyjmuje si
ę
ϕ
L
= 1.
W przekrojach, w których wyst
ę
puje siła poprzeczna (V > V
0
, p. 4.5.2d) powinny by
ć
spełnione warunki:
(53)
4.5.6. No
ś
no
ść
elementów dwukierunkowo zginanych lub zginanych i rozci
ą
ganych nale
ż
y sprawdza
ć
wg
wzoru
(54)
w którym:
N
Rt
- no
ś
no
ść
obliczeniowa przekroju przy rozci
ą
ganiu wg wzoru (31),
M
R
,
ϕ
L
- jak we wzorze (52).
Dodatkowe sprawdzenie no
ś
no
ś
ci przekrojów, w których wyst
ę
puje siła popr zeczna m o
ż
na przeprowadza
ć
wg
wzorów:
(55)
(56)
gdzie M
R,V
- no
ś
no
ść
obliczeniowa przekroju przy zginaniu ze
ś
cinaniem wg 4.5.2d).
4.6. Elementy
ś
ciskane i zginane
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 29
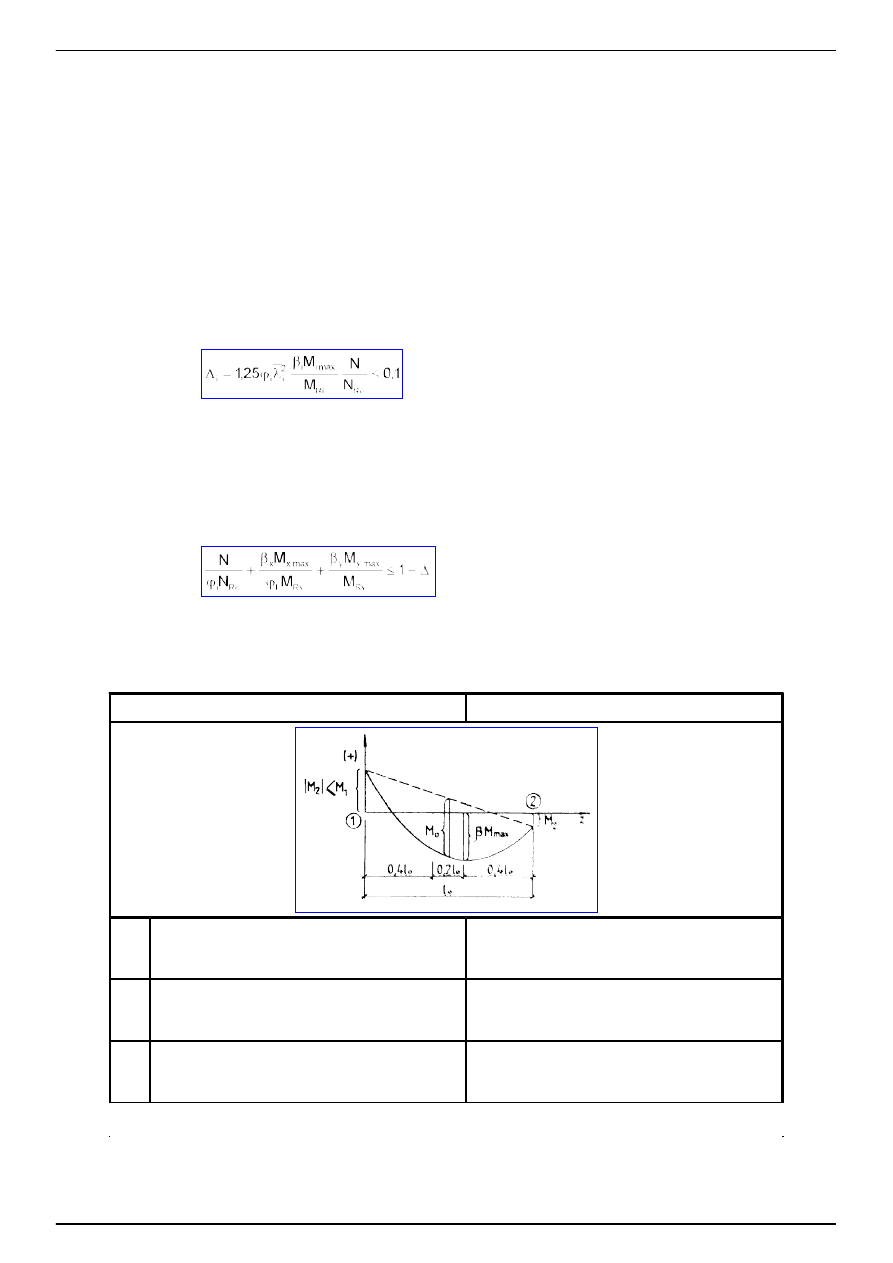
4.6.1. Zasady ogólne - parametry stateczno
ś
ci
a) Przy projektowaniu elementów
ś
ciskanych i zginanych obowi
ą
zuj
ą
ogólne postanowienia podane w 4.4.1 i 4.5.1.
b) Poni
ż
sze zasady dotycz
ą
elementów pełno
ś
ciennych o stałym przekr oju dowolnej klasy, obci
ąż
onych w ogólnym
przypadku sił
ą
podłu
ż
n
ą
N i momentami zginaj
ą
cymi M
x
i M
y
, działaj
ą
cym i odpowiednio wzgl
ę
dem osi najwi
ę
kszej
(X) i najmniejszej (Y) bezwładno
ś
ci przekroju.
c) No
ś
no
ść
obliczeniow
ą
przekroju (N
Rc
, M
Rx
, M
Ry
) oraz współczynniki niestateczno
ś
ci (
ϕ
,
ϕ
L
) nale
ż
y ustala
ć
jak w
przypadkach prostych stanów obci
ąż
enia -
ś
ciskania lub jednokierunkowego zginania.
d) Warto
ś
ci
β
M
max
nale
ż
y ustala
ć
wg tabl. 12, w zale
ż
no
ś
ci od warunków podparcia w rozpatrywanej płaszczy
ź
nie
wyboczenia oraz sposobu obci
ąż
enia pr
ę
ta (wykresu momentów) na odcinku równym jego długo
ś
ci obliczeniowej
l
0
.
e) Składnik poprawkowy
∆
i
nale
ż
y oblicza
ć
wg wzoru
(57)
w któr ym wielko
ś
ci z indeksem i = x lub y odpowiadaj
ą
zawsze r ozpatrywanej płaszczy
ź
nie wyboczenia - wzgl
ę
dem
osi X lub Y.
4.6.2. No
ś
no
ść
(stateczno
ść
) elementów
ś
ciskanych i zginanych
a) Stateczno
ść
elementów o przekroju co najmniej m onosymetrycznym
ś
ciskanych i zginanych jednokierunkowo
lub dwukierunkowo nale
ż
y sprawdza
ć
wg wzoru
(58)
Tablica 12
Warunki podparcia i sposoby obci
ąż
enia pr
ę
ta
Warto
ść
β
M
max
a)
Pr
ę
t o w
ę
złach wzajemnie poprzecznie
nieprzesuwnych (µ
≤
1), obci
ąż
ony momentami w
w
ę
złach podporowych (M
0
= 0)
β
M
max
= 0,55M
1
+ 0,45M
2
lecz
β
≥
0,4
b)
Pr
ę
t o w
ę
złach wzajemnie poprzecznie
przesuwnych (µ > 1), jednostronnie lub
dwustronnie utwierdzony
β
M
max
= M
1
+ 0,15M
2
1)
lecz
β
≤
1
c)
Pr
ę
t podparty dwustronnie przegubowo (µ = 1),
obci
ąż
ony poprzecznie mi
ę
dzy w
ę
złami i
ewentualnie momentami w w
ę
złach podporowych
β
M
max
= max M (0,4l
0
≤
z
≤
0,6l
0
)
2)
lecz
β
≥
0,4
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 30
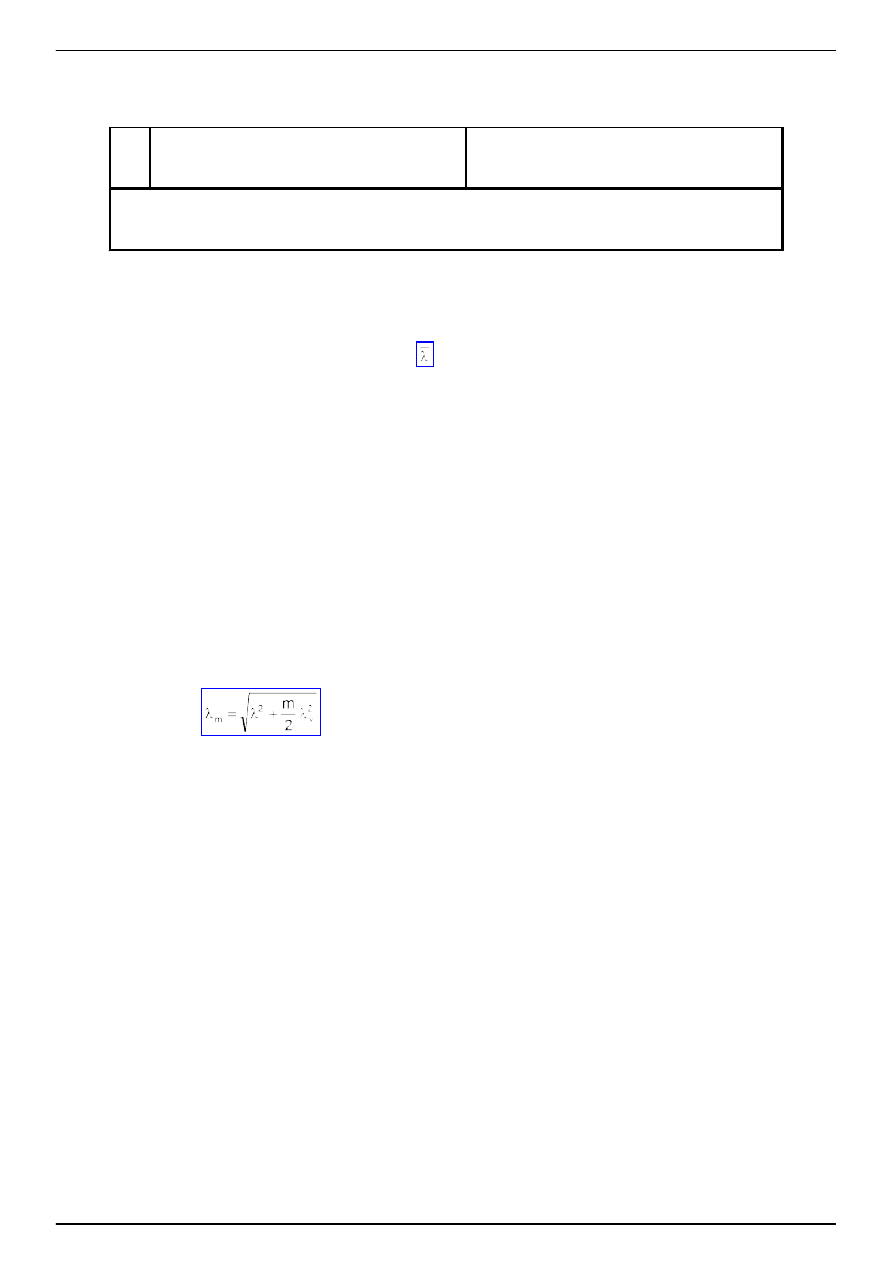
d)
W pozostałych przypadkach, gdy nie
przeprowadza si
ę
dokładnej analizy, nale
ż
y
przyjmowa
ć
β
M
max
= M
max
1)
Je
ś
li M
max
wyst
ę
puje mi
ę
dzy w
ę
złami podporowymi, a tak
ż
e dla wspornika nale
ż
y przyjmowa
ć
β
= 1.
2)
Warto
ść
β
M
max
przyjmuje si
ę
równ
ą
najwi
ę
kszej bezwgl
ę
dnej warto
ś
ci momentu w
ś
rodkowym przedziale
pr
ę
ta o długo
ś
ci 0,2l
0
.
W ogólnym przypadku powy
ż
szy warunek nale
ż
y sprawdzi
ć
dwukrotnie - dla
ϕ
x
i
ϕ
y
.
Przy jednokierunkowym zginaniu bez mo
ż
liwo
ś
ci zwichr zenia (
ϕ
L
= 1 lub M
x
= 0) przyjmuje si
ę
ϕ
i
w płaszczy
ź
nie
zginania.
W ka
ż
dym przypadku, gdy współczynnik
ϕ
i
> min
ϕ
(
), nale
ż
y dodatkowo sprawdzi
ć
warunek (39).
Je
ś
li
β
< 1 lub V > V
0
(p. 4.5.2d), to nale
ż
y ponadto sprawdzi
ć
warunek (54) oraz warunki no
ś
no
ś
ci przekroju (55) i
(56), przyjmuj
ą
c N
Rc
zamiast N
Rt
.
b) Stateczno
ść
gi
ę
tno-skr
ę
tn
ą
pr
ę
tów o przekroju otwartym bez osi symetr ii mo
ż
na sprawdza
ć
wg poz. a),
przyjmuj
ą
c we wzorze (58) zamiast
ϕ
L
współczynnik wyboczeniowy
ϕ
ustalony dla sm ukło
ś
ci
λ
1
= l
1
/i
y
, gdzie l
1
- jak
we wzorze (40).
4.7. Elementy wielogał
ę
ziowe
4.7.1. Zasady ogólne
a) Przy sprawdzaniu stateczno
ś
ci elementów wielogał
ę
ziowych ( rys. 6) nale
ż
y przyjmowa
ć
smukło
ść
zast
ę
pcz
ą
λ
m
i
okre
ś
lony dla niej współczynnik wyboczeniowy
ϕ
- wg krzywej niestateczno
ś
ci b lub wg krzywej wła
ś
ciwej dla
λ
, gdy
λ
m
=
λ
.
b) Je
ś
li
λ
m
>
λ
, to obowi
ą
zuj
ą
warunki no
ś
no
ś
ci jak dla elementów pełno
ś
ciennych o przekroju klasy 4 z tym,
ż
e do
oblicze
ń
nale
ż
y pr zyjmowa
ć
ψ
=
ϕ
1
lub (gdy przekrój gał
ę
zi jest klasy 4)
ψ
= min (
ϕ
1
,
ϕ
p
), gdzie:
ϕ
1
- współczynnik
wyboczeniowy ustalony dla pojedynczej gał
ę
zi,
ϕ
p
- współczynnik niestateczno
ś
ci miejscowej.
4.7.2. Smukło
ść
zast
ę
pcza elementu wielogał
ę
ziowego jest okre
ś
lona wzorem
(59)
gdzie:
λ
- sm ukło
ść
ustalona jak dla elementu pełno
ś
ciennego, m = 0, gdy rozpatr uje si
ę
wyboczenie wzgl
ę
dem osi
przecinaj
ą
cej materiał wszystkich gał
ę
zi (rys. 6 a/ i b);
λ
mx
=
λ
x
) lub
m - liczba gał
ę
zi w płaszczy
ź
nie przewi
ą
zek lub skratowania, równoległej do kierunku wyboczenia,
λ
v
- smukło
ść
postaciowa okre
ś
lona nast
ę
puj
ą
co:
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 31
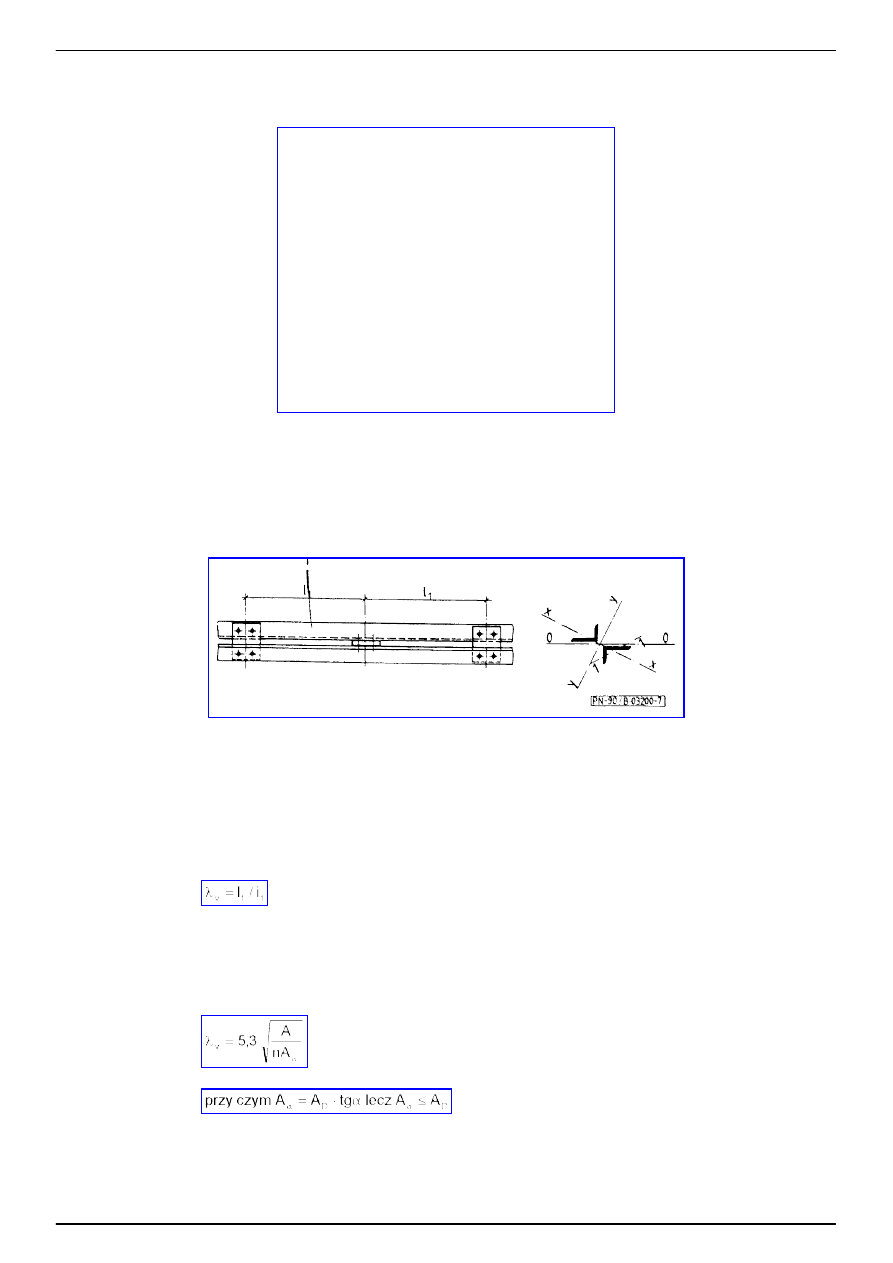
Rys. 6
Rys. 7
- dla elementów z przewi
ą
zkami (rys. 8a)
(60)
l
1
- odcinek r ówny osiowemu rozstawowi przewi
ą
zek, lecz nie wi
ę
kszy ni
ż
odst
ę
p mi
ę
dzy nimi zwi
ę
kszony o 100
mm,
i
1
- najmniejszy promie
ń
bezwładno
ś
ci przekroju gał
ę
zi;
- dla elementów kratowych (rys. 8 b) ÷ d)
(61)
(61)
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 32
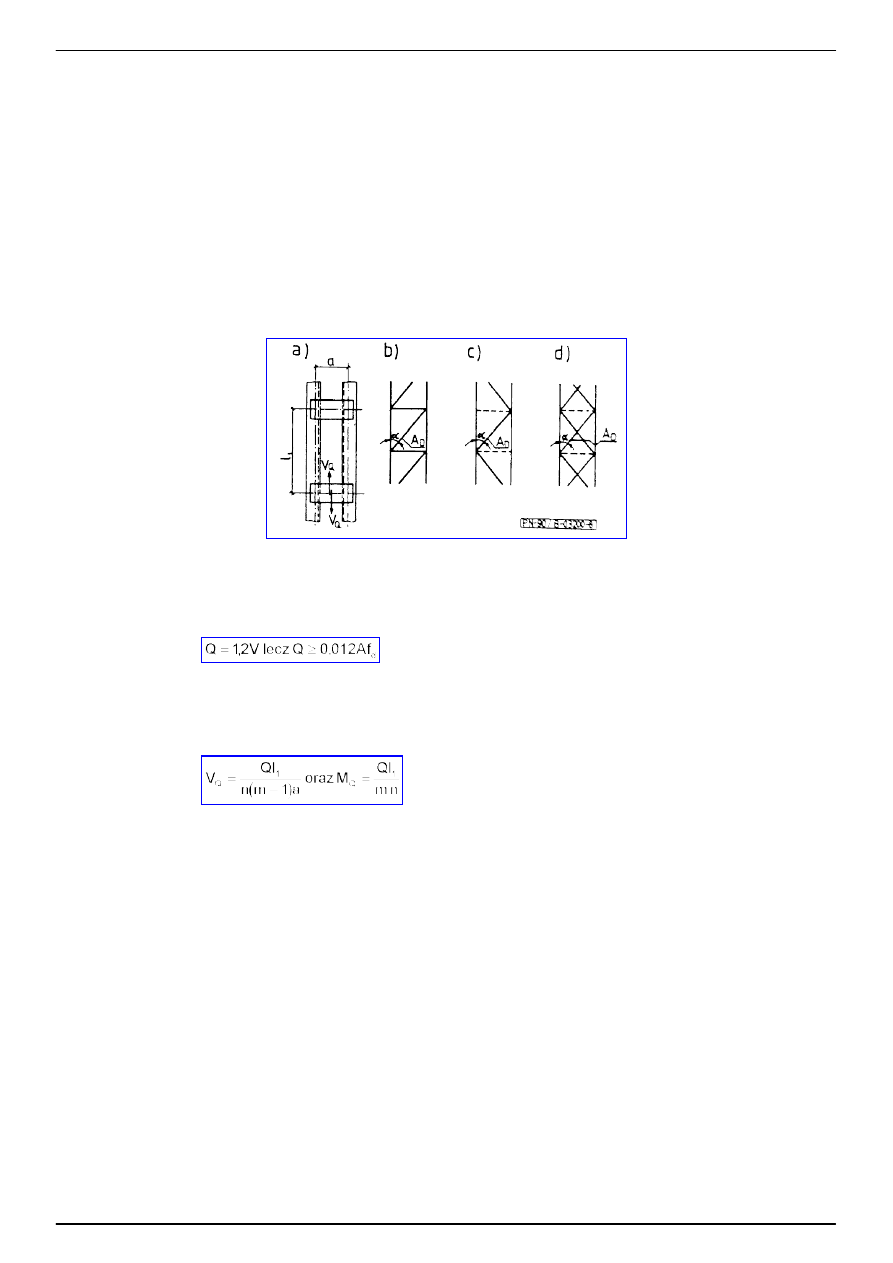
A - pole przekroju wszystkich gał
ę
zi,
n - liczba płaszczyzn skratowania w kierunku wyboczenia; dla elementów trójgraniastych (rys. 6 d) pr zyjmuje si
ę
n = 1,5,
A
D
- pole przekroju krzy
ż
ulca lub krzy
ż
ulców w przedziale skratowania,
α
- k
ą
t mi
ę
dzy osiami krzy
ż
ulca i gał
ę
zi.
W przypadku skratowania, jak na rys. 8b), smukło
ść
λ
v
nale
ż
y zwi
ę
kszy
ć
o 25%.
Pr
ę
ty zło
ż
one z dwóch k
ą
towników ustawionych krzy
ż
owo (rys. 7; l
1
/i
1
≤
60) nale
ż
y sprawdza
ć
na wyboczenie
wzgl
ę
dem osi X, przyjmuj
ą
c długo
ść
wyboczeniow
ą
l
ex
równ
ą
ś
redniej arytmetycznej długo
ś
ci wyboczeniowych w
płaszczyznach równoległych do ramion k
ą
towników.
W przypadku k
ą
towników nierównoramiennych mo
ż
na przyjmowa
ć
i
x
≅
0,8i
0
.
Rys. 8
4.7.3. Przewi
ą
zki i skratowania nale
ż
y wymiarowa
ć
na siły wynikaj
ą
ce z obci
ąż
enia sił
ą
poprzeczn
ą
Q
(62)
gdzie V - siła poprzeczna w elemencie wielogał
ę
ziowym od obci
ąż
enia zewn
ę
trznego.
Sił
ę
popr zeczn
ą
i moment w przewi
ą
zkach elementów dwugał
ę
ziowych (m = 2; r ys. 8a), a tak
ż
e wielogał
ę
ziowych
(m > 2) mo
ż
na oblicza
ć
wg wzorów:
(63)
w których:
n - liczba płaszczyzn przewi
ą
zek,
a, l
1
- rozstaw gał
ę
zi, rozstaw przewi
ą
zek.
Przewi
ą
zki nale
ż
y rozmieszcza
ć
regularnie przy niepar zystej liczbie przedziałów. Przewi
ą
zki po
ś
rednie powinny
mie
ć
szeroko
ść
b
≥
100 mm, a skrajne co najmniej 1,5b.
Poł
ą
czenia przewi
ą
zek lub pr
ę
tów skratowania z gał
ę
ziami projektuje si
ę
jako spawane, nitowe lub
ś
rubowe cierne;
wyj
ą
tkowo stosuje si
ę
poł
ą
czenia
ś
rubowe pasowane.
5. UKŁADY KONSTRUKCYJNE - STATECZNO
ŚĆ
OGÓLNA
5.1. Zasady i wymagania ogólne
a) Układy konstrukcyjne powinny mie
ć
zapewnion
ą
stateczno
ść
ogóln
ą
tj. zdolno
ść
do skutecznego
przeciwdziałania zm ianom kształtu i poło
ż
enia w warunkach realizacji i eksploatacji, a tak
ż
e przy r ozbudowie,
remontach i demonta
ż
u konstrukcji.
b) Stateczno
ść
ogóln
ą
mo
ż
na zapewni
ć
przez odpowiednie ukształtowanie (usztywnienie) konstrukcji, a w
przypadku układów, które nie s
ą
samostateczne lub wystarczaj
ą
co sztywne - przez odpowiedni system st
ęż
e
ń
stałych lub m onta
ż
owych. Jako st
ęż
enia m o
ż
na stosowa
ć
dodatkowe pr
ę
ty (zastrzały), skratowania, odci
ą
gi;
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 33

mo
ż
na tak
ż
e wykorzystywa
ć
w tym celu trzony
ż
elbetowe i sztywne tarcze tj. elementy stropów i
ś
cian, w tym
lekkiej obudowy z blach fałdowych.
c) Projektuj
ą
c st
ęż
enia nale
ż
y zapewni
ć
:
- przeniesienie na fundamenty wszelkich obci
ąż
e
ń
i oddziaływa
ń
poziomych,
- odpowiedni
ą
sztywno
ść
konstrukcji wymagan
ą
ze wzgl
ę
du na stan graniczny u
ż
ytkowania, jak r ównie
ż
ze wzgl
ę
du
na boczne podparcie (st
ęż
enie) elementów
ś
ciskanych i układów ramowych,
- odpowiednie warunki monta
ż
u i rektyfikacji konstrukcji na placu budowy.
d) Cz
ęś
ci konstrukcji oddzielone dylatacjam i powinny by
ć
st
ęż
one w sposób wzajemnie niezale
ż
ny. W przypadku
dylatacji termicznych nale
ż
y uwzgl
ę
dnia
ć
postanowienia 3.5.1.
5.2. Podparcia boczne elementów
ś
ciskanych
a) Element mo
ż
na uwa
ż
a
ć
za podpar ty (st
ęż
ony) nieprzesuwnie w kierunku bocznym prostopadłym do jego osi,
je
ś
li w miejscu podparcia jest on poł
ą
czony bezpo
ś
r ednio lub powi
ą
zany po
ś
rednio (za pom oc
ą
dodatkowych
pr
ę
tów) z konstrukcj
ą
sztywn
ą
i stateczn
ą
.
Za konstrukcj
ę
sztywn
ą
mo
ż
na uwa
ż
a
ć
układ tarczowy, tarczowopr
ę
towy lub pr
ę
towy (np. t
ęż
nik kratowy), je
ś
li
mo
ż
e on przenie
ść
dodatkowe siły boczne F
m
- wg wzoru (64) , a ponadto je
ś
li w warunkach działaj
ą
cych obci
ąż
e
ń
wzajemne przem ieszczenia s
ą
siednich punktów podparcia (w rozpatrywanym kierunku) nie przekraczaj
ą
1
/
200
odległo
ś
ci mi
ę
dzy nimi (rys. 9).
b) Podparcie
ś
ciskanych pasów d
ź
wigarów dachowych płatwiami lub innymi elementami mo
ż
na uwa
ż
a
ć
za
nieprzesuwne, je
ś
li ka
ż
de poł
ą
czenie w miejscu podparcia mo
ż
e przenie
ść
przypadaj
ą
c
ą
na nie sił
ę
F
0
- wg wzoru
(65), a elementy podpier aj
ą
ce wskutek ich zespolenia ze sztywnym pokryciem s
ą
konstrukcyjnie zabezpieczone
przed utrat
ą
stateczno
ś
ci w płaszczy
ź
nie połaci dachowej.
c) Je
ś
li boczne podparcie realizuje si
ę
w sposób po
ś
redni (r ys. 10), to ka
ż
dy pr
ę
t podpieraj
ą
cy jeden (m = 1) lub
po
ś
rednio wi
ę
cej (m > 1) elementów
ś
ciskanych powinien przenie
ść
i przekaza
ć
w kierunku st
ęż
enia stosown
ą
(zale
ż
n
ą
od liczby m) sił
ę
podłu
ż
n
ą
o warto
ś
ci równej
(64)
przy czym
(65)
gdzie:
N
c
- siła podłu
ż
na w słupie lub siła w pasie kratownicy (w miejscu podparcia) lub wypadkowa napr
ęż
e
ń
normalnych
w
ś
ciskanej strefie przekroju d
ź
wigara pełno
ś
ciennego (w miejscu podparcia),
A
c
- pole przekroju słupa, pasa
ś
ciskanego lub
ś
ciskanej strefy przekroju d
ź
wigara pełno
ś
ciennego.
Je
ś
li siła
ś
ciskaj
ą
ca w elemencie podpieranym (w słupie) jest stała (N
c
= const), a liczba po
ś
rednich punktów
podparcia jest wi
ę
ksza ni
ż
jeden, to do oblicze
ń
mo
ż
na przyjmowa
ć
siły boczne o warto
ś
ciach równych
(66)
gdzie:
l', l" - odległo
ś
ci rozpatrywanego punktu podparcia od s
ą
siednich punktów podparcia,
l - długo
ść
(rozpi
ę
to
ść
) elementu podpieranego.
5.3. St
ęż
enia dachowe
a) St
ęż
enia połaciowe poprzeczne nale
ż
y stosowa
ć
na całej szeroko
ś
ci dachu, co najmniej w dwóch skrajnych lub
przedskrajnych polach siatki podpór, a tak
ż
e w tych polach, w których wyst
ę
puj
ą
st
ęż
enia
ś
cian podłu
ż
nych.
b) St
ęż
enia podłu
ż
ne stosuje si
ę
w płaszczy
ź
nie połaci dachowej lub w poziomie pasów dolnych, gdy zachodzi
konieczno
ść
przeniesienia sił poziomych prostopadłych do
ś
cian podłu
ż
nych.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 34
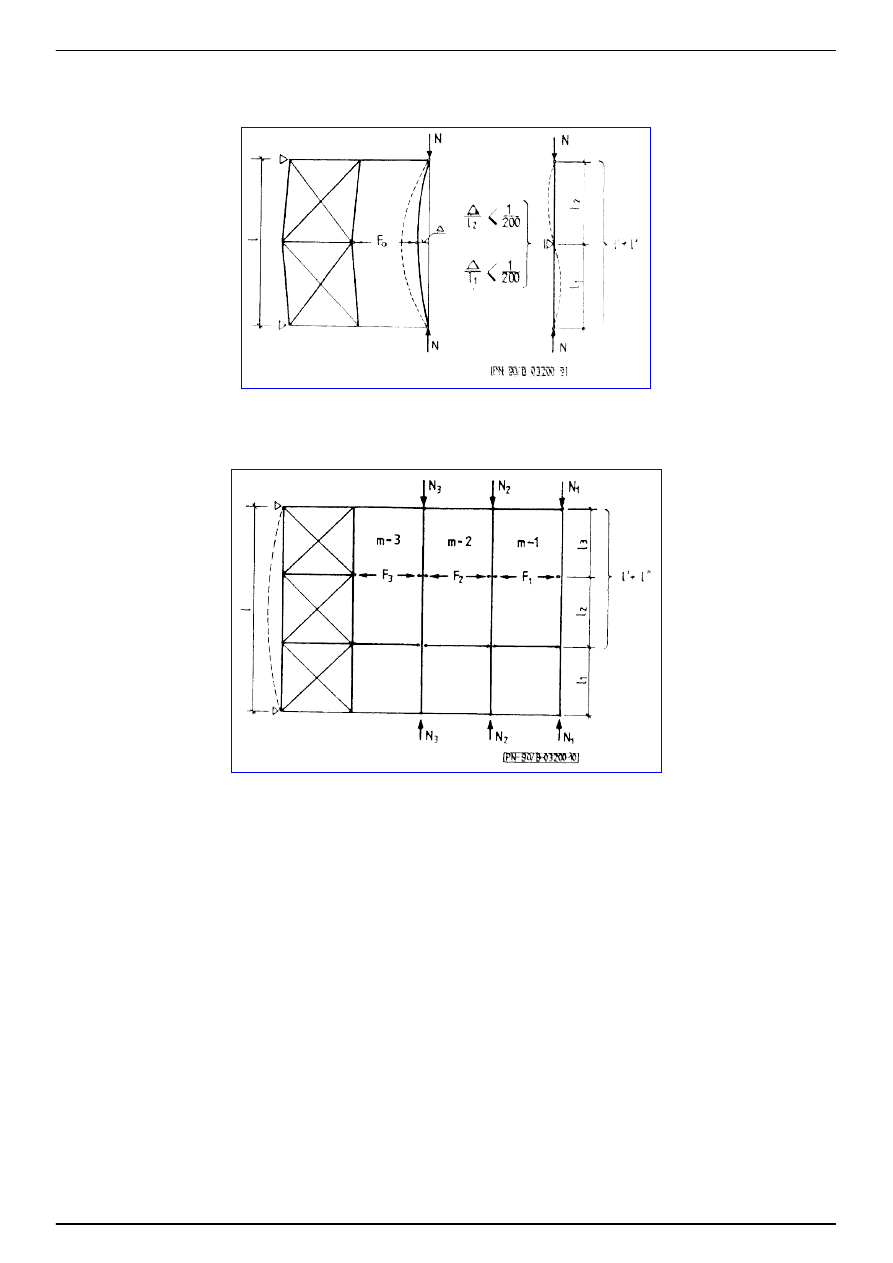
Rys. 9
Rys. 10
c) St
ęż
enia pionowe (skratowania mi
ę
dzy d
ź
wigarami) nale
ż
y stosowa
ć
co najmniej w tych polach, w których
wyst
ę
puj
ą
poprzeczne st
ęż
enia połaciowe, a w uzasadnionych przypadkach na całej długo
ś
ci dachu.
St
ęż
enia pionowe nale
ż
y rozmieszcza
ć
w
ś
rodku rozpi
ę
to
ś
ci d
ź
wigara lub g
ęś
ciej, a w przypadku d
ź
wigarów ze
słupkami podporowymi - równie
ż
w linii podpór. Rozstaw st
ęż
e
ń
, a tak
ż
e odległo
ść
najbli
ż
szego st
ęż
enia od linii
podpór nie powinna by
ć
wi
ę
ksza ni
ż
15 m.
Pasy gór ne d
ź
wigarów powinny by
ć
wzajemnie powi
ą
zane (st
ęż
one po
ś
rednio płatwiam i lub dodatkowym i pr
ę
tami
prostopadłymi) w płaszczyznach st
ęż
e
ń
pionowych lub g
ęś
ciej, gdy wymaga tego stateczno
ść
pasów.
W przypadku hal z suwnicami o ud
ź
wigu Q
≥
15 Mg, a tak
ż
e dachów bezpłatwiowych powy
ż
sze wymaganie
dotyczy równie
ż
pasów dolnych d
ź
wigarów kratowych.
5.4. Układy ramowe (szkieletowe)
5.4.1. Ogólny podział ram
a) Ram
ę
mo
ż
na uwa
ż
a
ć
za sztywno st
ęż
on
ą
w swojej płaszczy
ź
nie, czyli za układ o w
ę
złach nieprzesuwnych, je
ś
li
sztywno
ść
postaciowa układu "ram a + st
ęż
enie" (RS) jest co najmniej pi
ę
ciokrotnie wi
ę
ksza ni
ż
sztywno
ść
postaciowa ramy (R), tzn.:
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 35
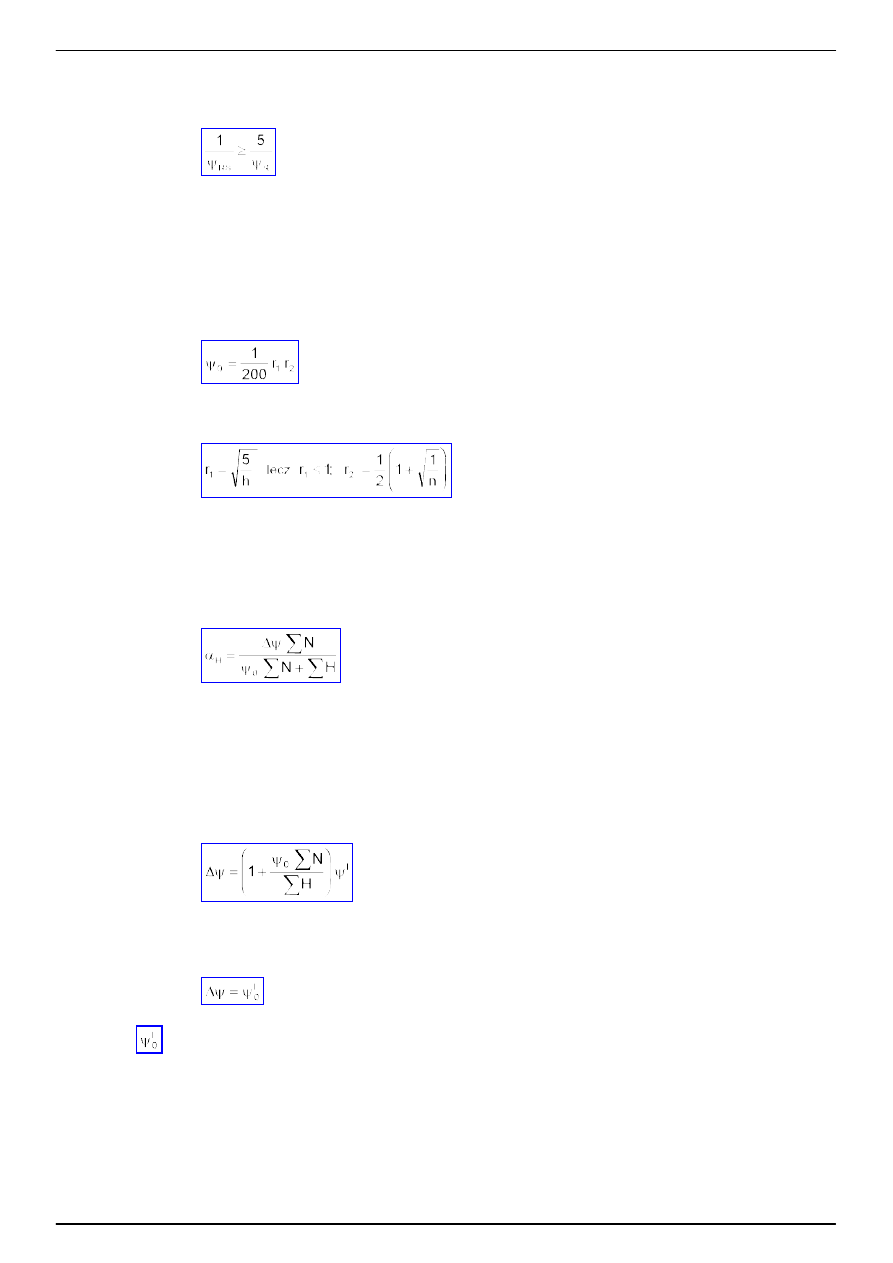
(67)
gdzie
ψ
RS
,
ψ
R
- odpowiednie warto
ś
ci przechyłu od poziomej siły jednostkowej; przechył nale
ż
y interpretowa
ć
jako
tangens k
ą
ta obrotu ci
ę
ciwy słupa mi
ę
dzy punktami podparcia.
b) Ramy samostateczne (tj ram y o w
ę
złach sztywnych, bez st
ęż
e
ń
), a tak
ż
e ramy podatnie st
ęż
one, gdy nie jest
spełniony warunek (67) nale
ż
y uwa
ż
a
ć
za układy o w
ę
złach przesuwnych.
5.4.2. Parametr niedoskonało
ś
ci
ψ
0
dla ram o prostok
ą
tnej lub zbli
ż
onej konfiguracji pr
ę
tów przyjmuje si
ę
w
postaci wst
ę
pnego przechyłu kondygnacji, okre
ś
lonego wzorem
(68)
gdzie:
h - wysoko
ść
kondygnacji, m,
n - liczba słupów danej kondygnacji w rozpatrywanej płaszczy
ź
nie.
5.4.3. Wska
ź
nik wra
ż
liwo
ś
ci na efekty II rz
ę
du
α
H
dotyczy wielokondygnacyjnych układów ramowych o w
ę
złach
przesuwnych (rys. 11), a jego warto
ść
nale
ż
y ustala
ć
dla ka
ż
dej kondygnacji nast
ę
puj
ą
co:
(69)
gdzie:
Σ
H - sumaryczne obci
ąż
enie poziome powy
ż
ej rozpatrywanej kondygnacji (siła poprzeczna od obci
ąż
enia
zewn
ę
trznego),
Σ
N - sumaryczne obci
ąż
enie pionowe przenoszone przez słupy rozpatrywanej kondygnacji,
ψ
0
- wst
ę
pny przechył rozpatrywanej kondygnacji obliczony wg wzoru (68),
∆ψ
- przyrost przechyłu spowodowany działaniem sił poziomych (H + H
o
).
Przyrost
∆ψ
mo
ż
na ustala
ć
wg zale
ż
no
ś
ci
(70)
gdzie
ψ
I
- przechył spowodowany działaniem sił H, obliczony wg teorii I rz
ę
du.
W przypadku braku zewn
ę
trznego obci
ąż
enia poziomego (
Σ
H = 0)
(71)
gdzie
- przechył spowodowany działaniem sił H
0
=
ψ
0
Σ
P, przy czym
Σ
P - oddziaływania pionowe rygli
rozpatrywanej kondygnacji.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 36
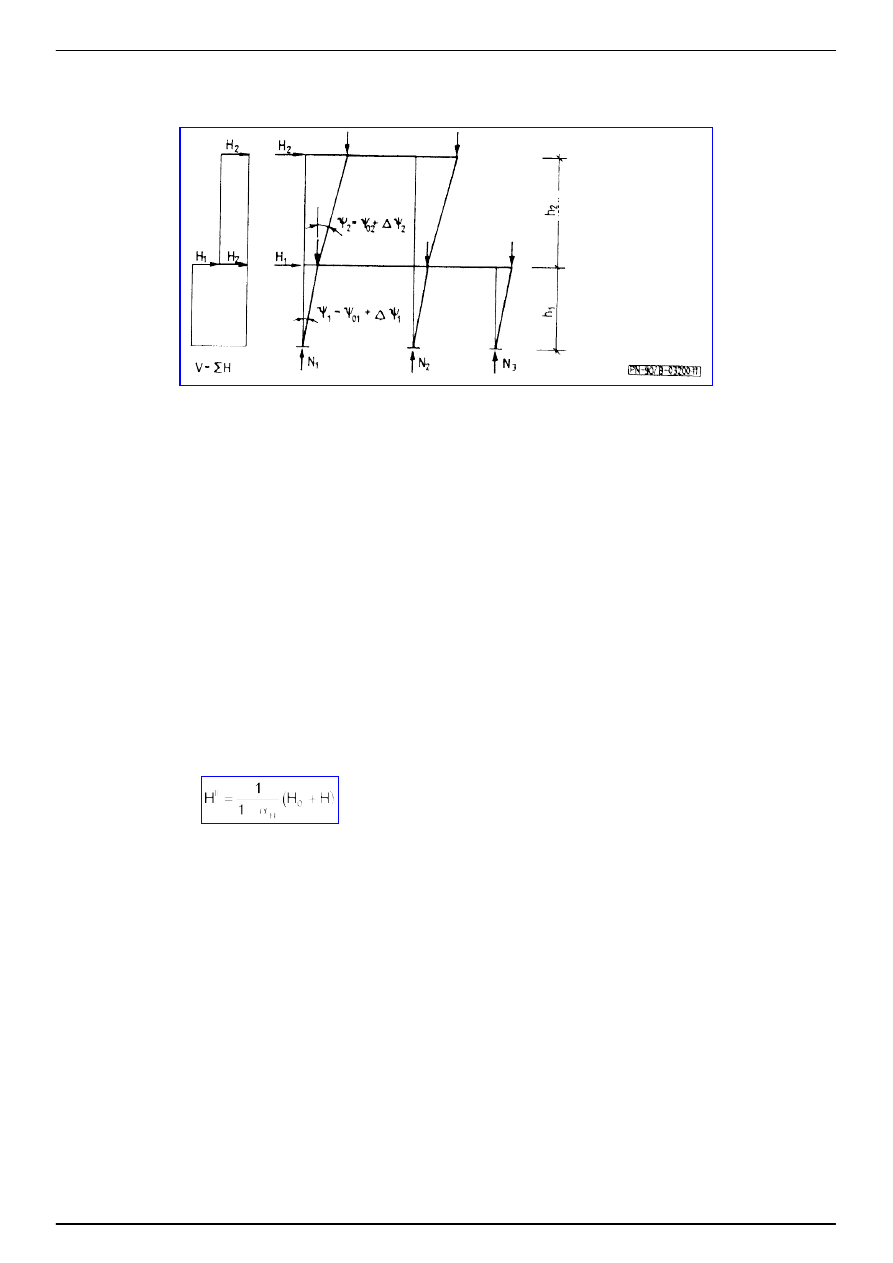
Rys. 11
Je
ś
li dla konstrukcji w stanie spr
ęż
ystym dla ka
ż
dej kondygnacji spełniony jest warunek
α
H
≤
0,1, to m o
ż
na przyj
ąć
,
ż
e układ nie jest wra
ż
liwy na efekty II rz
ę
du.
5.4.4. Zasady oblicze
ń
statycznych
a) Według teorii I rz
ę
du mo
ż
na oblicza
ć
:
- układy jednokondygnacyjne,
- układy wielokondygnacyjne sztywno st
ęż
one (p. 5.4.1 poz. a), a tak
ż
e
- układy niewra
ż
liwe na efekty II rz
ę
du (p. 5.4.3;
α
H
≤
0,1).
Je
ś
li wg teorii I rz
ę
du oblicza si
ę
ram y samostateczne lub st
ęż
one, które zawieraj
ą
(podpieraj
ą
za pomoc
ą
rygli)
słupy wahadłowe (rys. 12), to w obliczeniach nale
ż
y uwzgl
ę
dnia
ć
dodatkowe siły poziome H
0
spowodowane
wst
ę
pnym przechyłem słupów wahadłowych.
b) Według teorii II rz
ę
du nale
ż
y oblicza
ć
układy wielokondygnacyjne wra
ż
liwe na efekty II rz
ę
du (
α
H
≥
0,1), przy
czym je
ś
li wym iarowanie konstrukcji przeprowadza si
ę
na podstawie sił i m om entów II rz
ę
du z uwzgl
ę
dnieniem
wst
ę
pnych przechyłów
ψ
0
wg wzoru (68), to pr zy spr awdzaniu stateczno
ś
ci słupy takich układów mo
ż
na traktowa
ć
jak słupy układów o w
ę
złach nieprzesuwnych ze współczynnikiem długo
ś
ci wyboczeniowej
µ
≤
1.
c) Siły wewn
ę
trzne II rz
ę
du (zwi
ę
kszone w stosunku do sił I rz
ę
du wskutek przemieszcze
ń
poziomych układu)
mo
ż
na wyznacza
ć
w sposób przybli
ż
ony, przyjmuj
ą
c do oblicze
ń
wg teorii I rz
ę
du zast
ę
pcze (zwi
ę
kszone) siły
poziome H
II
, wyznaczone wg zale
ż
no
ś
ci:
(72)
gdzie:
α
H
- wska
ź
nik wra
ż
liwo
ś
ci wg wzoru (69),
H
0
- jak we wzorze (71),
H - siła pozioma od obci
ąż
enia zewn
ę
trznego na poziomie rozpatrywanej kondygnacji.
5.5. Stateczno
ść
poło
ż
enia
a) Sprawdzenie stateczno
ś
ci poło
ż
enia polega na wykazaniu,
ż
e konstrukcja lub jej cz
ęść
, traktowana jako ciało
sztywne, jest zabezpieczona przed przesuni
ę
ciem, uniesieniem lub wywróceniem.
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 37

Rys. 12
b) Stateczno
ść
poło
ż
enia jest zachowana, je
ś
li spełnione s
ą
warunki:
(73)
gdzie:
F
Rd
, M
Rd
- warto
ś
ci obliczeniowe wypadkowej siły biernej i momentu, przeciwdziałaj
ą
cych zmianie poło
ż
enia
(obrotowi):
F
Rd
= F
Rk
⋅
γ
f
; M
Rd
= M
Rk
⋅
γ
f
przy czym
γ
f
≤
0,9;
F
Sd
, M
Sd
- warto
ś
ci obliczeniowe działa
ń
czynnych;
F
Sd
= F
Sk
⋅
γ
f
; M
Sd
= M
Sk
⋅
γ
f
przy czym
γ
f
≥
1,1.
c) Je
ś
li warunki (73) nie s
ą
spełnione, to nale
ż
y stosowa
ć
specjalne zabezpieczenie w postaci st
ęż
e
ń
(zakotwie
ń
)
lub dodatkowego balastu.
Ci
ą
g dalszy normy
Zmiany, Poprawki, Uwagi
PN-90/B-03200/Az3, grudzie
ń
1995
PRZEDMOWA DO ZMIANY
Niniejsza zmiana jest trzeci
ą
zmian
ą
wprowadzon
ą
do PN-B-03200:1990 (PN-90/B-03200)
Zmiana ta nie uwzgl
ę
dnia tre
ś
ci poprzednich zmian.
Zmiany wprowadzone do normy w latach 1992 do 1994 zostały opublikowane w:
Biuletynie PKNMiJ nr 10/92,
Biuletynie PKNMiJ nr 13/93 (zmiana niepublikowana - tre
ść
zmiany wprowadzono do II wydania z 1994 r.).
Ostatnie wydanie normy jest dost
ę
pne w O
ś
rodku Informacji i Dokumentacji Biura Polskiego Kom itetu
Normalizacyjnego.
TRE
ŚĆ
ZMIANY
W rozdziale 7, tre
ść
postanowienia przej
ś
ciowego zmienia si
ę
nast
ę
puj
ą
co:
Dopuszcza si
ę
stosowanie PN-B-03200:1980 (PN-80/B-03200) do dnia 31 grudnia 1999 r. w takim zakresie, jak to
wynika z postanowie
ń
aktualnie obowi
ą
zuj
ą
cych norm odwołuj
ą
cych si
ę
do PN-B-03200:1980 (PN-80/B-03200).
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 38
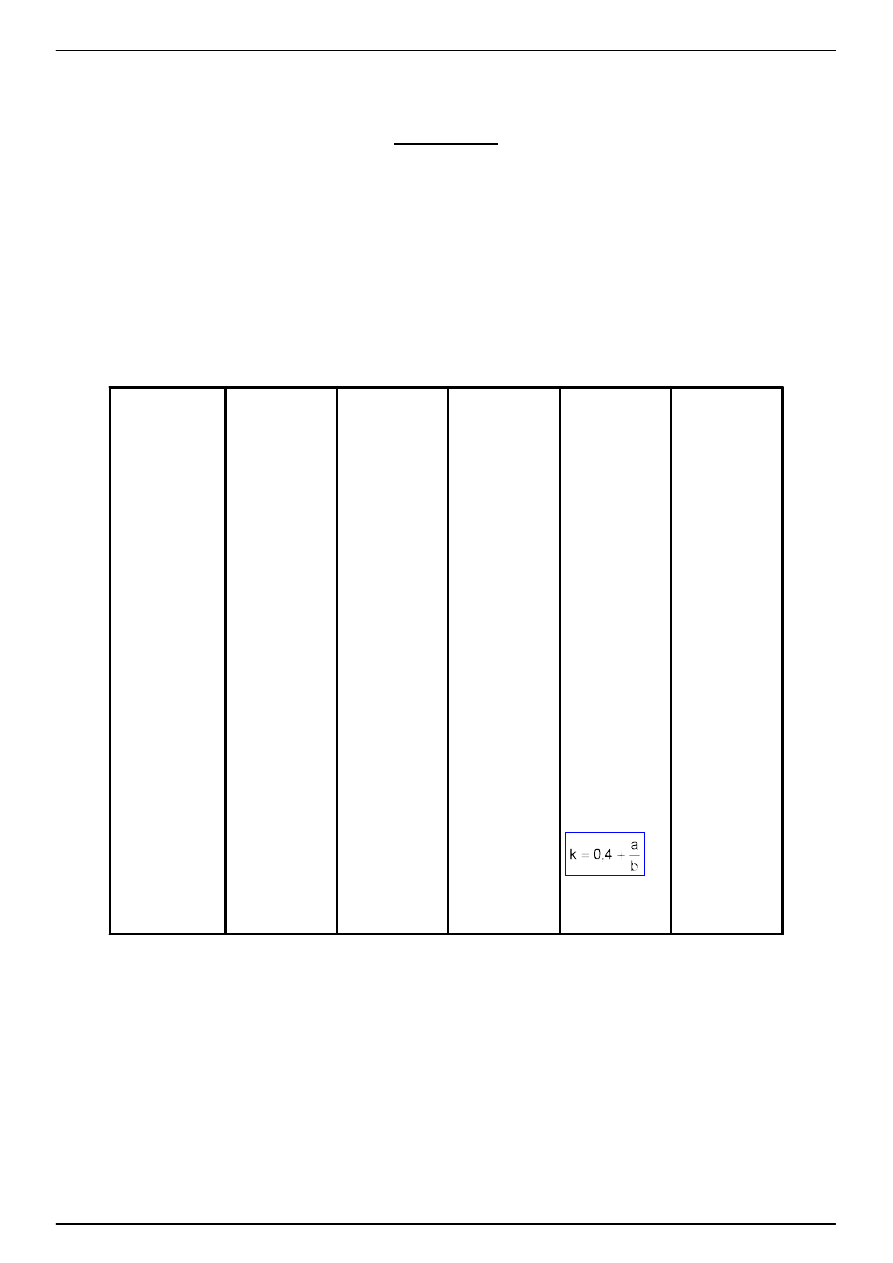
zmiana 1
92.07.29
5. PN-90/B-03200 Konstrukcje stalowe. Obliczenia statyczne i projektowe
0702
W rozdziale 7. POSTANOWIENIA PRZEJ
Ś
CIOWE zmienia si
ę
tre
ść
nast
ę
puj
ą
co:
Dopuszcza si
ę
stosowanie PN-80/B-03200 do dnia 31 grudnia 1995 r . w takim zakresie, jak to wynika z
postanowie
ń
aktualnie obowi
ą
zuj
ą
cych norm zwi
ą
zanych odwołuj
ą
cych si
ę
do PN-80/B-03200.
(Biuletyn PKNMiJ nr 10/92 poz. 48)
PN-B-
03200/AC2:1997
Konstrukcje
stalowe -
Obliczenia
statyczne i
projektowanie
Zał
ą
cznik 5
p.4.3 wzór (Z 5-
7) przy
współczynniku
1,4
INFORMACJE
DODATKOWE
odsyłacz
2)
;
2)
Patrz
INFORMACJE
DODATKOWE
p. 10
(tre
ść
odsyłacza
umieszcza si
ę
na dole strony
pod kresk
ą
)
Dopisuje si
ę
p.
10 o tre
ś
ci:
10. Komentarz
do wzoru (Z5-7)
Je
ś
li znany
(ustalony) jest
rozstaw
poprzeczny kół
w
ś
wietle a, to
we wzorze (Z5-
7) zamiast
współczynnika
1,4 (przy P)
mo
ż
na
przyjmowa
ć
warto
ść
gdzie:
b - szeroko
ść
pasa
1997-06-26
PN-90/B-03200
ASLAN - WYDAWNICTWA ELEKTRONICZNE
www.aslan.com.pl
Strona 39
Wyszukiwarka
Podobne podstrony:
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie(2)
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie(2)
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie(2)
PM 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie
PN 90 B 03200 Konstrukcje stalowe obliczenia i projektowanie
[norma]PN 83 B 03010 Ĺšciany oporowe Obliczenia statyczne i projektowanie
PN B 03150 2000 Konstrukcje drewniane Obliczenia statyczne i projektowanie
[norma]PN 83 B 03010 Ĺšciany oporowe Obliczenia statyczne i projektowanie
PN B 03204 2002 Konstrukcje stalowe Wieże i maszty Projektowanie i wykonanie
PN B 03215 1998 Konstrukcje Stalowe Polączenia Z Fundamentami Projektowanie I Wykonanie
PN B 03203 2000 Konstrukcje stalowe Zamknięcia hydrotechniczne Projektowanie i wykonanie
więcej podobnych podstron