1)

Sformułuj zasadę zachowania energii mechanicznej i ogólną zasadę zachowania energii.

Ogólne prawo zachowania energii

Δ E

k

+ Δ E

p

+ Q + Δ = 0

Suma energii kinetycznej, potencjalnej, energii cieplnej i innych rodzajów energii w układzie

zamkniętym jest zawsze stała. Z prawa tego wynika, że energia musi być przetwarzana z jednej

formy w drugą ale nie może powstawać z niczego i nie może ulec zniszczeniu.

Z prawa zachowania energii wynika, że dla dowolnego układu ciał całkowita energia mechaniczna

układu jest stała.

2)

Zdefiniuj pojęcia pracy, energii kinetycznej, energii potencjalnej i ciepła

Praca

- Zdefiniujmy pracę W wykonaną przez przyłożoną siłę F , rozpędzającą ciało o masie m,

na drodze Δ r jako

Praca wykonana nad ciałem swobodnym przez dowolnie przyło

ż

on

ą

sił

ę

jest równa

zmianie jego energii kinetycznej.

Energią kinetyczną

ciała nazywamy różnicę energii całkowitej i energii spoczynkowej:

ENERGIA POTENCJALNA

to zdolność do wykonania pracy lub do zwiększenia energii

kinetycznej.

CIEPŁO

-jeden z dwóch, obok pracy, sposobów przekazywania energii wewnętrznej układowi

termodynamicznemu. Jest to przekazywanie energii chaotycznego ruchu cząstek (atomów,

cząsteczek, jonów) w zderzeniach cząstek tworzących układy makroskopowe pozostające we

wzajemnym kontakcie; oznacza formę zmian energii, nie zaś jedną z form energii . Ciepło (jako

wielkość fizyczna) przepływa między ciałami, które nie znajdują się w równowadze termicznej

(czyli mają różne temperatury) i wywołuje zwykle zmianę temperatur ciał pozostających w

kontakcie termicznym. Kontakt termiczny jest warunkiem koniecznym przepływu ciepła

const

E

E

E

p

k

=

+

=

( )

r

F

r

F

r

F

W

r

r

r

r

∆

∆

=

∆

⋅

=

,

cos

∫

−

=

⋅

=

B

A

k

B

AB

m

m

r

d

F

W

2

2

2

1

2

1

ν

ν

r

r

(

)

2

0

0

c

m

m

E

E

E

k

−

=

−

=

E

mgh

mgx

m

=

=

+

2

2

1

ν

3)

Sformułuj zasadę zachowania pędu dla układu punktów materialnych.

Iloczyn całkowitej masy M układu i prędkości środka masy jest całkowitym pędem układu

punktów materialnych

Prawo zachowania pędu. Kiedy suma sił zewnętrznych działających na układ punktów

materialnych wynosi zero, to całkowity pęd układu pozostaje stały.

Wniosek: całkowity pęd układu może być zmieniony tylko przez siły zewnętrzne działające na

układ. Siły wewnętrzne będące równymi i przeciwnie skierowanymi wytwarzają równe i

przeciwne skierowane zmiany pędu, które się redukują. Pędy poszczególnych punktów układu

mogą ulegać zmianom, ale suma tych pędów jest stała, jeżeli na układ nie działają żadne siły

zewnętrzne

Równanie to jest równaniem wektorowym, odpowiada zatem trzem równaniom skalarnym. Stąd

prawo zachowania pędu dostarcza nam trzy warunki ruchu układu, do którego jest stosowane.

Prawo zachowania energii daje nam tylko jeden warunek ruchu, ponieważ jest równaniem

skalarnym. Prawo zachowania pędu jest prawem bardziej ogólnym i bardziej fundamentalnym niż

II prawo dynamiki Newtona, ponieważ obowiązuje również w fizyce atomowej i jądrowej, gdzie

nie obowiązuje mechanika Newtona.

4)

Sformułuj zasadę zachowania momentu pędu dla układu punktów materialnych i bryły sztywnej

W przypadku ruchu punktu materialnego dookoła osi obrotu związek między prędkością v a

prędkością kątową określa wzór

Kierunek v określa reguła śruby prawoskrętnej

Ostatnie równanie jest odpowiednikiem II zasady dynamiki Newtona dla ruchu obrotowego

punktu materialnego w ruchu po okręgu.

Widać, że sile F odpowiada moment siły M , masie m - moment bezwładności I, przyśpieszeniu a

- przyśpieszenie kątowe .

Moment siły działający na dowolny punkt materialny równy jest szybkości zmian wektora

momentu pędu tego punktu.

Zapis ostatniego równania dotyczy pojedynczego punktu materialnego. Jeśli chcemy obliczyć

całkowity moment pędu układu punktów względem dowolnego punktu obrotu, musimy dodać

wektorowo momenty pędu wszystkich punktów materialnych względem tego samego punktu

obrotu. W czasie całkowity moment pędu wszystkich punktów układu może się zmieniać w

wyniku zmian momentów sił wewnętrznych działających między tymi punktami oraz w wyniku

zmian momentów sił zewnętrznych działających na punkty materialne

Ciało sztywne jest szczególnym przypadkiem układu punktów materialnych, tzn. układem, dla

którego wzajemne odległości między punktami układu są stałe. Równanie powyższe stosuje się

również do ciała sztywnego. I oznacza teraz moment bezwładności bryły sztywnej

r

r

r

r

×

=

ω

v

M

F

r

r

r

r

=

×

∑

=

N

i

zew

F

dt

p

d

r

r

.

...

3

2

1

const

p

p

p

p

p

N

=

+

+

+

+

=

r

r

r

r

r

ε

ω

ω

r

r

r

r

I

dt

d

mr

r

dt

d

m

M

=

=

=

2

2

dt

L

d

M

zew

r

r

=

∑

ε

r

r

I

dt

L

d

=

moment pędu ciała sztywnego równa się iloczynowi momentu bezwładności i prędkości kątowej.

Jest to kolejna analogia do ruchu postępowego.

Gdy wypadkowy moment sił zewnętrznych działających na układ punktów materialnych wynosi

zero to całkowity moment pędu układu pozostaje stały. Jest to prawo zachowania momentu

pędu dla układu punktów. Dla układu N punktów całkowity moment pędu wynosi

Oznacza to, że momenty pędu poszczególnych punktów materialnych mogą się zmieniać, lecz ich

suma pozostaje stała zawsze, gdy wypadkowy moment sił zewnętrznych równa się zero. Jeżeli

układem punktów materialnych jest bryła sztywna, to prawo zachowania momentu pędu dla

bryły sztywnej przyjmuje postać

5)

Podaj ogólną definicję momentu bezwładności ciała

Moment bezwładności względem osi obrotu jest równy sumie iloczynów wszystkich mas

punktów materialnych i kwadratu ich odległości od osi obrotu. Określamy go wzorem

dla bryły sztywnej i

dla pkt. materialnego. W ruchu obrotowym moment

bezwładności odpowiada masie m w ruchu postępowym.

Jeżeli oznaczymy przez I

0

moment bezwładności ciała względem osi OO’ przechodzącej przez

środek masy R to moment bezwładności ciała I względem dowolnej osi AA’ równoległej do osi

przechodzącej przez środek masy i leżącej w tej samej płaszczyźnie:

. Zależność ta

nosi nazwę twierdzenia Steinera.

6)

Zdefiniuj ruch harmoniczny prosty, równanie różniczkowe, rozwiązanie i warunek rozwiązalności..

Ruchem harmonicznym prostym będziemy nazywali ruch punktu materialnego dookoła swojego

położenia równowagi pod wpływem siły, która jest proporcjonalna do wychylenia z położenia

równowagi:

Z 2 zasady dynamiki Newtona wiemy, że:

Po podstawieniu do ostatniego

równania wzoru na siłę harmoniczną otrzymamy:

Równanie to nazywamy

równaniem różniczkowym oscylatora harm. Prostego. Rozwiązaniem tego równania musi być

funkcja, której 2 pochodna równa się samej funkcji. Funkcja taką jest np. Funkcja cosα. Zapiszemy

ją w postaci

gdzie A-wielkość stałą, ()-faza ruchu, ψ-stała fazowa, ω-

częstotliwość kątowa.

Jeżeli do równania

podstawimy funkcję

i jej 2 pochodną

to otrzymamy warunek rozwiązywalności równania różniczkowego oscylatora

harmonicznego

.

7)

Sformułuj zasadę zachowania energii w ruchu harmonicznym

Przy maksymalnym wychyleniu energia K=0 energia U osiąga

maksimum U

max

+1/2kA

2

const

I

=

ω

r

ω

r

r

I

L

=

N

L

L

L

L

L

r

r

r

r

r

+

⋅⋅

⋅

+

+

+

=

3

2

1

W położeniu równowagi energia U=0 energia K osiaga max K

max

=1/2kA

2

, W pośrednich położeniach

energia kin i pot zmienia się tak, że ich suma zawsze jest równa.

8)

Podaj na czym polega zjawisko rezonansu mechanicznego

Rezonans mechaniczny to zjawisko polegające na przepływie energii pomiędzy kilkoma (najczęściej
dwoma) układami drgającymi. Warunkami koniecznymi do zajścia rezonansu mechanicznego są:

•

jednakowa lub zbliżona częstotliwość drgań własnych (lub swobodnych) układów,

•

istnienie mechanicznego połączenia między układami.

9)

Sformułuj wnioski wynikające z transformacji Lorentza

Założenia transformacji Lorentza:

•

Prędkośćświatła nie zależy od ruchu światła lub odbiornika czyli jest jednakowa we
wszystkich układach odniesienia, pozostawających w ruchu jednostajnym prostoliniowym
względem źródła;

•

Przestrzeń jest jednorodna i izotropowa;

•

Podstawowe prawa fizyki są identyczne dla każdej pary obserwatorów, znajdujących się
względem siebie w ruchu jednostajnym prostoliniowym;

Wnioski wynikające z transformacji Lorentza:

•

Prędkość swiatła jest niezminnicza względem transformacji Lorentza

•

Przekształcenie Lorentza daje wzajemną zależność przestrzeni i czasu

10)

Narysuj zależność masy, pędu i energii cząstki relatywistycznej w funkcji jej prędkości, wzory

11)

Sformułuj zasadę zachowania energii cząstki relatywistycznej, rozważ cztery przypadki

E = mc

2

+U = const – Zasada zach energii, gdy v ≠ 0 oraz U ≠ 0

E = mc

2

= const – zasada zach. En. Gdy v = 0 oraz U ≠ 0, masie m przypisuje się energię i energii

przypisuje się masę. Zatem energia i masa są równoważne, związek ten nosi nazwę ogólnego prawa

zachowania energii lub zasady równoważności masy i energii.

E = m

0

c

2

+ U = const – zas. Zach. En. Gdy v= 0 oraz U ≠ 0, jeżeli ciało jest w spoczynku, to obok energii

potencjalnej u przypisuje mu siępewną dodatkową ilość energii zwaną energią spoczynkową.

E = m

0

c

2

= const – zas. Zach. En. Gdy v = 0 oraz U = 0 , jeżeli ciało jest w spoczynku i nie znajduje się w

polu sił potencjalnych U przypisuje mu się energię spoczynkową.

12)

Sformułuj zasadę równoważności masy i energii oraz zasadę zachowania masy.

Wychodzimy od wzoru na pracę: Fds = mvdv + v

2

dm obliczamy różniczkę masy która po obliczeniach

przybiera postać:

Wyznaczamy iloczyn mvdv i podstawiamy go do wzoru na pracę po

czym otrzymujemy wzór w następującej postaci: Fds = (c

2

– v

2

)dm + v

2

dm + c

2

dm = d(mc

2

), zatem

praca ciała w układzie relatywistycznym jest równa różniczce iloczynu masy i prędkości światła.

Korzystając z wzoru:

i dokonując kolejnych obliczeń otrzymujemy zależność E = mc

2

+ U =

const.

Zasada zachowania masy: m = m

0

+ m

k

+ m

p

= const, ze wzoru wynika, że masa całkowita jest sumą

masy spoczynkowej, masy równoważnej energii kinetycznej i masy równoważnej energii potencjalnej.

13)

Zdefiniuj pojęcie temperatury gazu oraz cząstki w ujęciu kinetyczno-molekularnym.

Przez temperaturę gazu rozumiemy średnia energię kinetycznącząstek gazu w ich chaotycznym ruchu

postępowym.

Dla gazu:

Dla jednej cząsteczki

, gdzie k- jest stałą Boltzmanna. (…)

14)

Zdefiniuj strumień pola elektrycznego, prawo Gaussa, powierzchnię Gaussa

Miarą jest lini sił pola przypadająca na powierzchnię. Dla powierzchni zamkniętych strumień jest

dodatni, jeżeli linie sił są skierowane na zewnątrz powierzchni, a ujemny – jeżeli linie sił są

skierowane do wewnątrz powierzchni. Definicja strumienia pola elektrycznego dl a powierzchni

zamkniętej:

Φ

∑

°∆ n jest liczbą, na które została podzielona powierzchnia S. Sumowanie

pokazuje, że należy dodaćdo siebie wszystkie iloczyny skalarne dla wszystkich n kwadratów.

Dokładną def. Strumienia pola elektrycznego jest wartością graniczną ф

E

:

Φ

∑

°∆ oraz

Φ

∮

°

Powierzchnia Gaussa jest powierzchnią, która odzwierciedla geometryczny rozkład ładunków

zawartych wewnątrz tej powierzchni.

Związek pomiędzy strumieniem pola elektrycznego przechodzącego przez dowolną

powierzchnięzamkniętą a ładunkiem zamkniętym w jej wnętrzu podaje prawo Gaussa:

!

"

∮ °

# %!

"

Φ

#&, Prawo gaussa jest uogólnieniem wszystkich praw dla pola elektrostatycznego

15)

Zdefiniuj uogólnione prawo Gaussa dla dielektryków

Dla kondensatora z dielektrykiem istnieje zależność:

'

!

(

gdzie:

"

)

*

'

,

po podstawieniu

otrzymamy natężenie pola elektrycznego w dielektryku:

)

*

+

*

'

, podstawiamy otrzymaną

zależność do wzoru;

)

*

'

,

)-

*

'

,

, po przekształceniach otrzymamy wyażenie na indukowany

ładunek powierzchniowy:

#

-

#%1

/

*

0

& , Korzystając z otrzymanych zależności możemy

uogólnićprawo Gaussa:

!

"

∮ °

# #′ , (q-q’) jest ładunkiem wypadkowym, znajdującym się

wewnątrz powierzchni Gaussa. Po podstawieniu otrzymujemy:

!

"

∮ °

# # 21

/

*

0

3 #

/

4

0

,

Stąd po przekształceniu otrzymamy Uogólnione prawo Gaussa dla dielektryków

:

!

"

∮ !

(

°

#

16)

Zapisz prawa opisujące promieniowanie ciała doskonale czarnego

Prawo Wiena:

Prawo Plancka:

Prawo Stefana – Boltzmanna:

17)

Co to jest ciało doskonale czarne i jakie musi ono spełniać warunki

Jeżeli będziemy rozpatrywali wyidealizowane ciało ogrzane do pewnej temperatury, to zauważymy,
że:

właściwości emitowanego promieniowania nie zależą od rodzaju substancji pobudzanej do świecenia
oraz że emisja energetyczna promieniowania R zmienia się w prosty sposób z temperaturą.

niezależnie od temperatury ciało takie pochłania całą energię padającego promieniowania bez
względu na długość fali, czyli ma zdolność absorpcyjną równą jedności (A = 1).

Wyidealizowane ciało o takich właściwościach będziemy nazywali ciałem doskonale czarnym.

Najlepszym znanym odpowiednikiem w przyrodzie ciała doskonale czarnego jest czysta sadza, czerń
platynowa lub czarny aksamit.

18) Określ na czym polega efekt fotoelektryczny, podaj równanie fotonowe Einsteina

Efekt fotoelektryczny polega na tym, że promieniowanie o określonej długosci fali padające na

powierzchnię metalu wybija z niego elektrony.

Równanie fotonowe Einsteina:

, gdzie:

- energia fotonu, E

0

- praca wyjścia

elektronu na powierzchnięmetalu, K

max

- energia kinetyczna elektronu po opuszczeniu powierzchni

metalu.

19)

Określ na czym polega zjawisko Comptona, przedstaw graficznie zasady zachowania

Compton skierował wiązkę promieni rentgenowskich o dokładnie określonej długości fali na blok

grafitowy.

Chocia

ż

w wi

ą

zce padaj

ą

cej znajduje si

ę

promieniowanie tylko o długo

ś

ci fali

λλλλ

, to

rozpraszane promieniowanie rentgenowskie ma maksima przy dwóch długo

ś

ciach fali

λλλλ

i

λλλλ

'. Długo

ść

λλλλ

' jest przesuni

ę

ta w stosunku do długo

ś

ci

λλλλ

o wielko

ść

∆∆∆∆

λλλλ

.

To przesuni

ę

cie

∆∆∆∆

λλλλ

zwane jest

i zmienia wraz z k

ą

tem

przesuni

ę

ciem Comptona

rozpraszania

ϕϕϕϕ

.

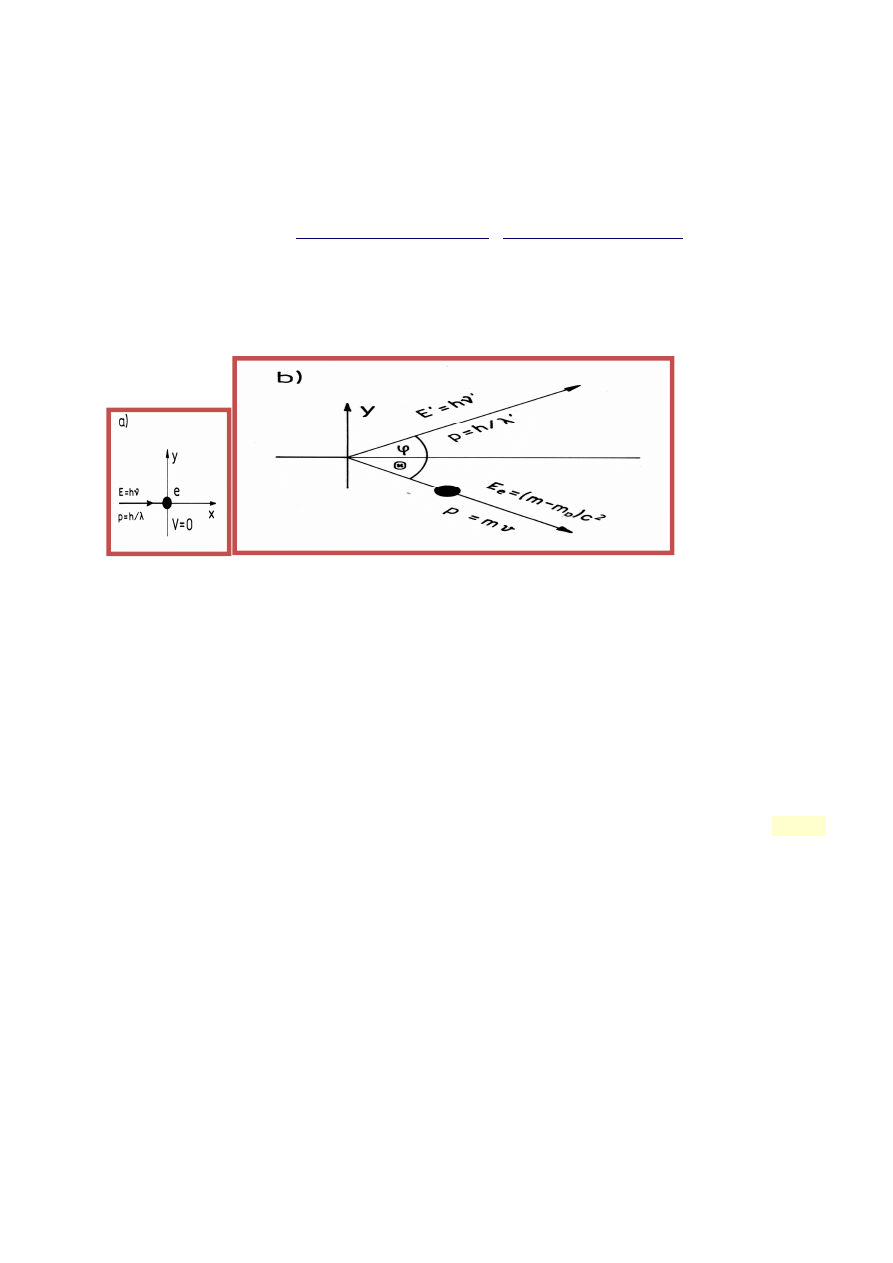
Compton wyja

ś

nił swoje do

ś

wiadczenie po zało

ż

eniu,

ż

e padaj

ą

ca wi

ą

zka promieni

rentgenowskich nie jest fal

ą

, lecz zbiorem fotonów o energii h

νννν

.

Poniewa

ż

padaj

ą

cy

foton o energii E = h

νννν

przekazuje cz

ęść

swojej energii elektronowi, z którym si

ę

zderza, wi

ę

c

foton rozpraszany musi mie

ć

energi

ę

ni

ż

sz

ą

(E' = h

νννν

’), czyli wi

ę

ksz

ą

długo

ść

λλλλ

'.

Elektron pocz

ą

tkowo znajduje si

ę

w stanie spoczynku i jest zupełnie swobodny

(a).

Zastosujmy do zderzenia prawo zachowania energii i prawo zachowania p

ę

du

(b).

Elektrony

mog

ą

mie

ć

pr

ę

dko

ś

ci porównywalne z pr

ę

dko

ś

ci

ą

ś

wiatła, stosujemy wi

ę

c do oblicze

ń

wyra

ż

enie relatywistyczne.

Suma energii fotonu i energii elektronu przed zderzeniem

(a)

jest równa energii fotonu i

energii elektronu odrzutu po zderzeniu

(b)

:

20)

W jaki sposób można eksperymentalnie wyznaczyć stałą Plancka

21)

Sformułuj postulaty Bohra i pojęcie orbitala

Orbital - Załóżmy, że elektron w atomie wodoru porusza się po kołowym orbitalu (orbicie) o
promieniu r, której środek znajduje się w miejscu jądra atomowego. Jądro atomowe jest tak ciężkie, że
skupia całą masę.

Postulaty Bohra
-elektron nie mo

ż

e kr

ąż

y

ć

po dowolnej orbicie (orbitalu), lecz tylko po takich orbitalach dla

których moment p

ę

du elektronu L jest wielokrotno

ś

ci

ą

stałej Plancka, podzielonej przez 2

π

-

atom absorbuje lub emituje energi

ę

w postaci kwantu h

ν

, przechodz

ą

c z jednego stanu

energetycznego atomu do drugiego j > i - emisja energii j < i - absorpcja energii

22)

Podaj zale

ż

no

ść

promienia atomu i energii od głównej liczby kwantowej i zasad

ę

odpowiednio

ś

ci

Ogólnie zasada odpowiedniości dotyczy relacji pomiędzy fizyką kwantową a klasyczną.
Fizyka klasyczna jest szczególnym przypadkiem fizyki kwantowej, stąd im wyższe wartości
liczb kwantowych tym większe zbliżenie (podobieństwo) z fizyką klasyczną. Składa się z następujących
części:

1. Przewidywania teorii kwantowej dotyczące zachowania się dowolnego układu

fizycznego muszą w granicy, w której liczby kwantowe określające stan układu stają
się bardzo duże, odpowiadać przewidywaniom fizyki klasycznej

2. Danej regule wyboru podlega cały zbiór wartości odpowiedniej liczby kwantowej.

Zatem wszystkie reguły wyboru, które niezbędne są do otrzymania wymaganej
odpowiedniości w granicy klasycznej stosują się także w granicy kwantowej.

(

)

2

0

c

m

m

h

h

−

+

′

=

ν

ν

h

n

L

=

i

j

E

E

h

−

=

ν

23)

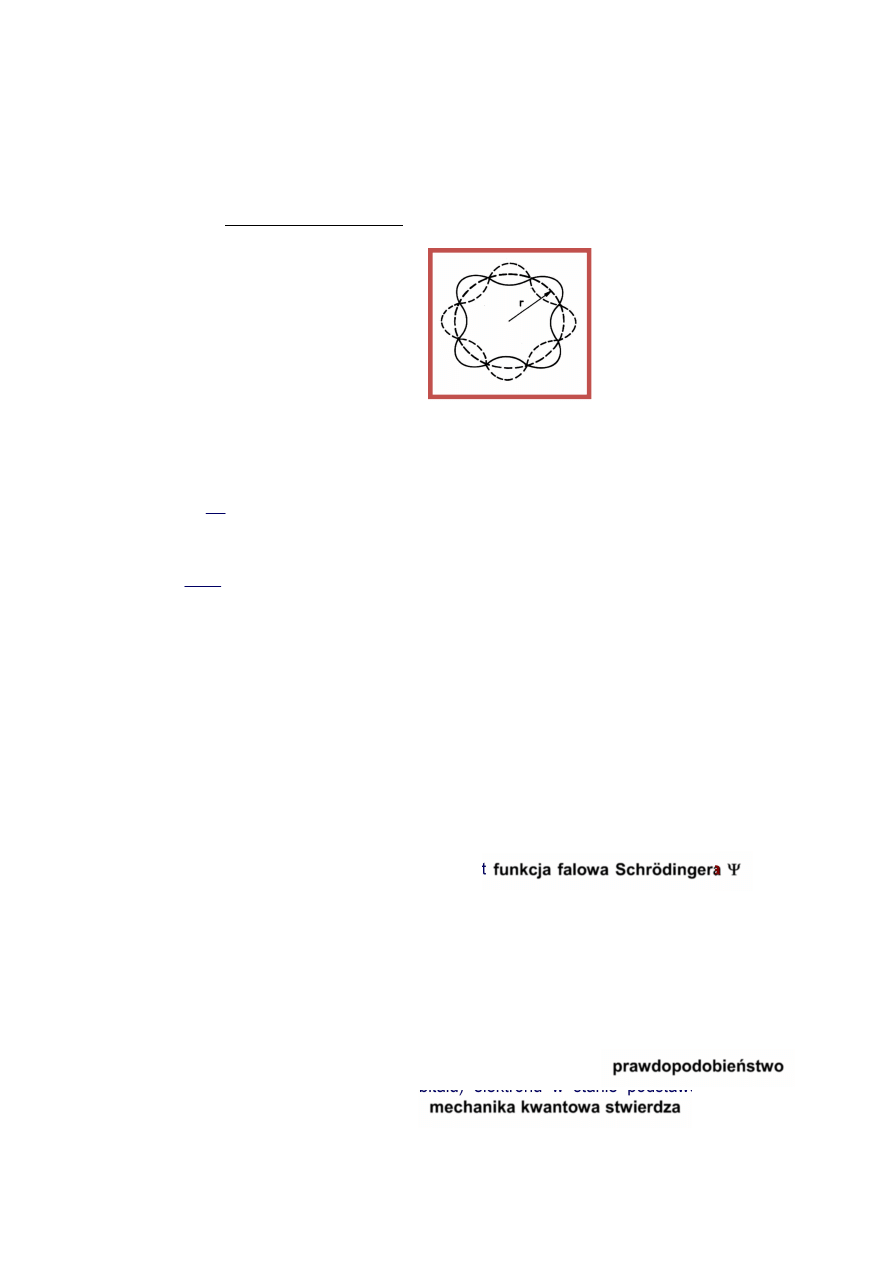
Wykaż słuszność warunku kwantyzacji Bohra w oparciu o fale de'Broglie

De Broglie ze swojej teorii fal materii potrafił wyprowadzić warunek kwantyzacji Bohra, dla momentu
pędu elektronu. Założył warunki brzegowe dla fal materii w atomie wodoru: długość fali

λλλλ

= h/p

została tak dobrana, aby orbita o promieniu r zawierała całkowitą liczbę fal materii.

Oznacza to, że na orbicie powstaje fala stojąca.

otrzymujemy następujące przekształcenia

Pojawia si

ę

zatem zgodno

ść

pomi

ę

dzy modelem atomu zaproponowanym przez Bohra a

faktem falowego charakteru materii. Elektron kr

ążą

cy wokół j

ą

dra nie promieniuje energii pod

warunkiem,

ż

e jego orbita zawiera całkowit

ą

liczb

ę

fal de Broglie'a zwi

ą

zanych z elektronem.

24) Sformułuj i skomentuj zasad

ę

nieoznaczono

ś

ci Heisenberga

25) Zdefiniuj i skomentuj poj

ę

cie funkcji falowej Schr

ő

dingera

Najwa

ż

niejsz

ą

wielko

ś

ci

ą

w mechanice falowej jest

funkcja falowa Schrödingera

Ψ

Ψ

Ψ

Ψ

, która

jest miar

ą

zaburzenia falowego fal materii. Born po raz pierwszy zasugerował,

ż

e kwadrat

funkcji falowej Schrödingera

Ψ

Ψ

Ψ

Ψ

2

w dowolnym ustalonym punkcie przedstawia miar

ę

prawdopodobie

ń

stwa, i

ż

cz

ą

stka znajduje si

ę

w pobli

ż

u tego punktu. Je

ż

eli wokół dowolnego

punktu w przestrzeni utworzymy element obj

ę

to

ś

ci

dV,

to

prawdopodobie

ń

stwo,

ż

e w danej

chwili cz

ą

steczka znajduje si

ę

w tym elemencie obj

ę

to

ś

ci wynosi

Ψ

2

dV.

Do mierzalnych wielko

ś

ci w mechanice kwantowej zaliczamy

prawdopodobie

ń

stwo.

Zamiast twierdzi

ć

,

ż

e promie

ń

orbity (orbitalu) elektronu w stanie podstawowym atomu

wodoru wynosi dokładnie mechanika kwantowa stwierdza,

ż

e warto

ść

ta

jest najbardziej prawdopodobna.

,...

,

,

gdzie

3

2

1

2

=

=

n

n

r

λ

π

p

h

n

r

=

π

2

π

2

h

n

rp

=

h

n

L

=

m

11

10

3

,

5

−

⋅

26)

Zapisz i skomentuj równane Schr

ő

dingera w postaci ogólnej

Jest to

ogólna posta

ć

równania Schrödingera

, gdzie funkcja falowa

Ψ

Ψ

Ψ

Ψ

(x,y,z,t) zale

ż

y od

współrz

ę

dnych i czasu. Aby rozwi

ą

za

ć

równanie Schrödingera, trzeba zna

ć

przebieg zmian

energii potencjalnej U(x,y,z,t), zale

ż

nej równie

ż

od współrz

ę

dnych i czasu.

Równanie to przedstawia zasad

ę

zachowania energii dla cz

ą

stki kwantowej, gdzie

człon odpowiadaj

ą

cy energii kinetycznej

człon odpowiadaj

ą

cy energii potencjalnej

człon odpowiadający energii całkowitej

27)

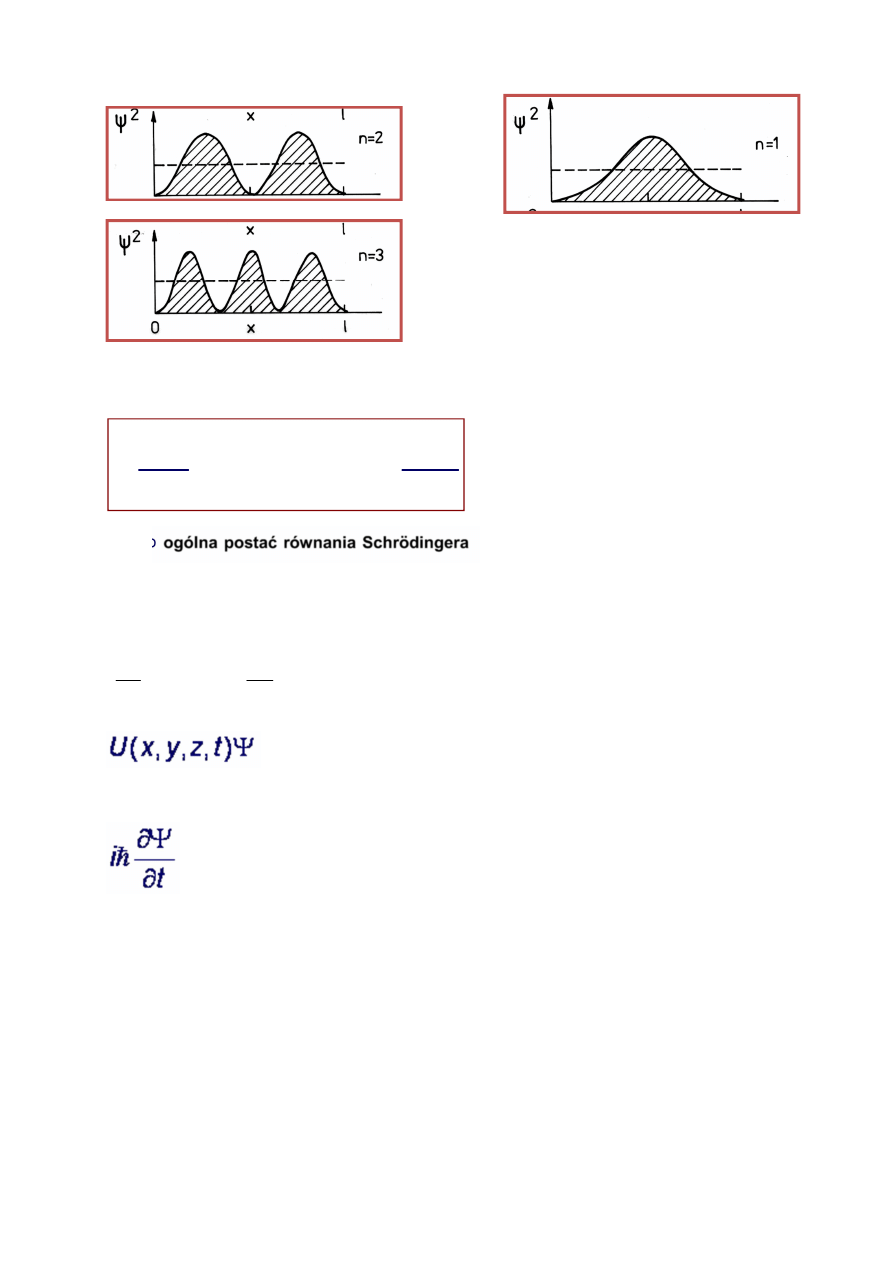
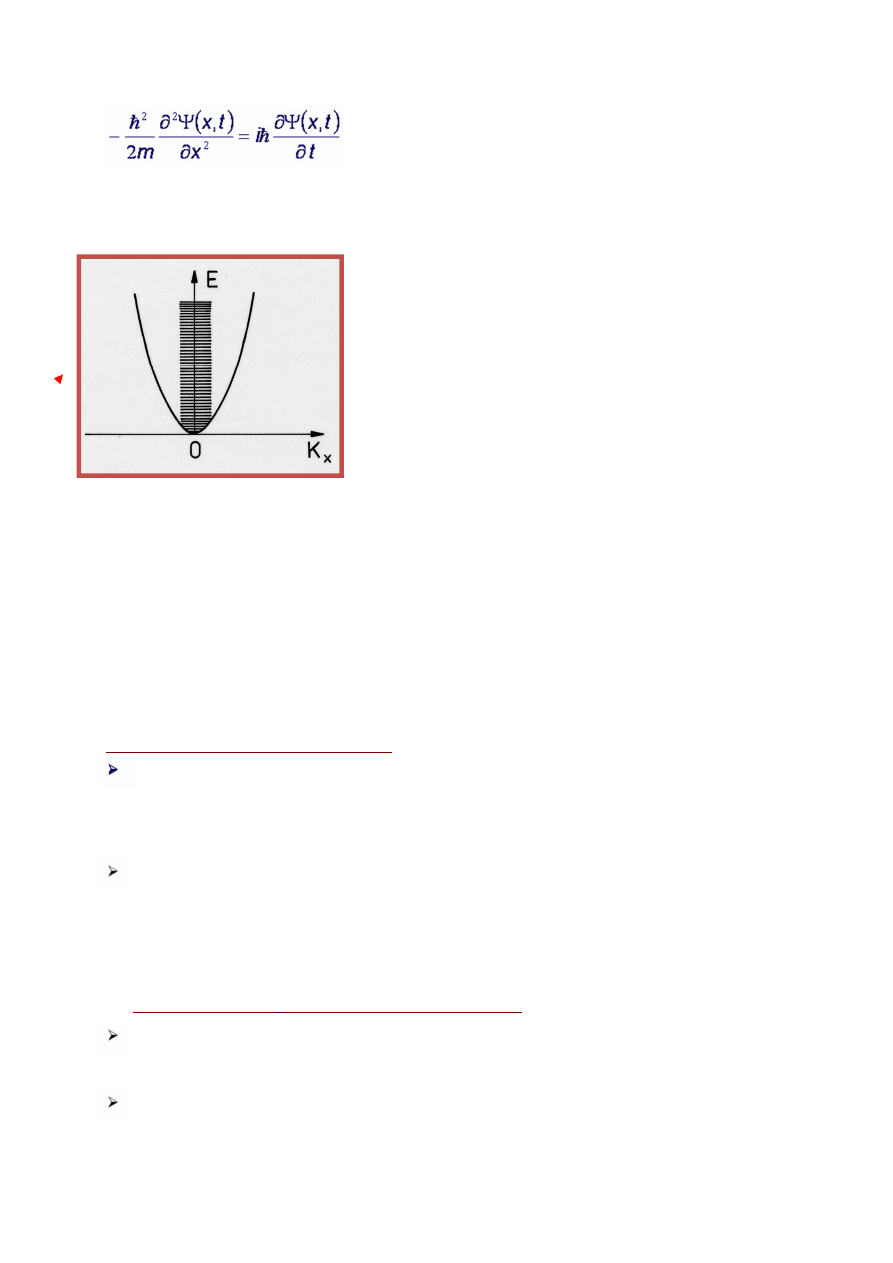
Zdefiniuj cząstkę swobodną i podaj jakie posiada widmo energetyczne.

Cząstka jest swobodna, jeżeli jej energia potencjalna równa się zeru.

Dla uproszczenia obliczeń zakładamy, że cząstka taka porusza się tylko w kierunku osi x, zatem

funkcja falowa tej cząstki będzie miała postać

, stąd równanie

Schrödingera przyjmie postać:

dt

d

i

U

m

Ψ

=

Ψ

+

∆Ψ

−

h

h

2

2

( )

t

x,

Ψ

=

Ψ

G

ę

sto

ść

prawdopodobie

ń

stwa

Ψ

Ψ

Ψ

Ψ

2

dt

d

i

U

m

Ψ

=

Ψ

+

∆Ψ

−

h

h

2

2

Rozwiązaniem tego równania jest funkcja falowa

28)

Jakie są założenia statystyki klasycznej i statystyk kwantowych

Metody statystyczne są stosowane do badania układów składających się z olbrzymiej liczby
cząsteczek (np. gaz doskonały).

Statystyka klasyczna Maxwella-Boltzmana:

Cz

ą

steczki gazu doskonałego s

ą

cz

ą

steczkami bardzo małymi, podlegaj

ą

prawom

mechaniki klasycznej; stan dowolnej cz

ą

steczki jest jednoznacznie okre

ś

lony

przez podanie współrz

ę

dnych poło

ż

enia i pr

ę

dko

ś

ci lub p

ę

dów

Cz

ą

steczki gazu odznaczaj

ą

si

ę

indywidualno

ś

ci

ą

, która pozwala odró

ż

ni

ć

dan

ą

cz

ą

steczk

ę

od innych; przestawienie miejscami dwóch cz

ą

steczek znajduj

ą

cych

si

ę

w ró

ż

nych stanach jest poł

ą

czone z przej

ś

ciem układu z jednego stanu do

drugiego

Dla

statystyk kwantowych

Bosego-Einsteina i Fermiego-Diraca

obowi

ą

zuj

ą

nast

ę

puj

ą

ce zało

ż

enia:

znaczenie fizyczne maj

ą

jedynie takie cz

ą

stki, których rozmiary komórek

elementarnych

nie s

ą

mniejsze od

ħ

3

wszystkie cz

ą

stki s

ą

identyczne, przestawienie dwóch cz

ą

stek miejscami nie

prowadzi do nowego stanu

( )

( )

t

i

e

x

t

x

ω

ψ

−

=

Ψ

,

widmo energetyczne
jest widmem ci

ą

głym