Przewodzenie prądu

Przewodzenie prądu

przez roztwory

przez roztwory

elektrolitów

elektrolitów

Konduktometria

Konduktometria

Przewodniki dzielimy na :

•

elektronowe

•

jonowe

W

przewodnikach elektronowych

nośnikiem prądu są

elektrony (czasem też dziury). Przepływowi ładunku
elektrycznego nie towarzyszy ruch masy, ani żadne reakcje
chemiczne. Przewodnictwo ich maleje ze wzrostem
temperatury. Należą tu metale i półprzewodniki.

W

przewodnikach jonowych

nośnikiem prądu są jony.

Przepływowi ładunku towarzyszy ruch masy i mogą zachodzić
reakcje chemiczne. Przewodnictwo ich rośnie wraz ze
wzrostem temperatury. Należą tu kryształy o budowie jonowej,
stopione sole, zjonizowane gazy i

roztwory elektrolitów

.

e

_

+

K

+

A

-

katoda anoda

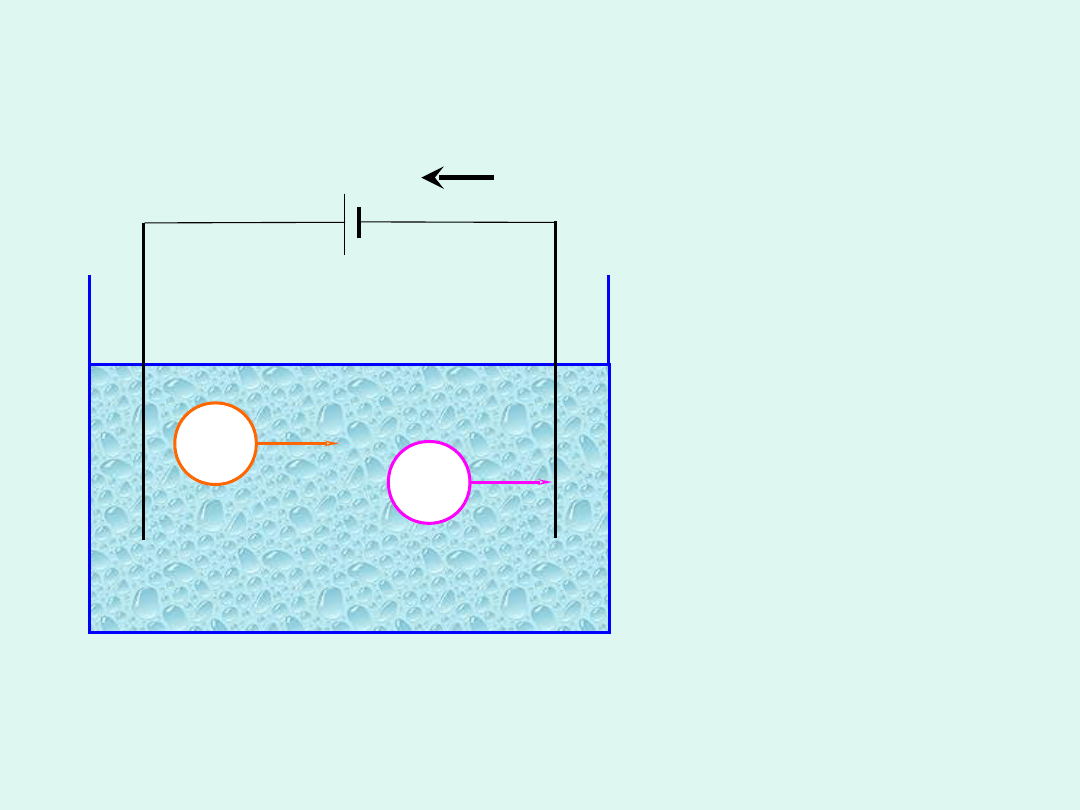
Elektroliza

K

e

K

→

+

+

A

e

A

→

−

−

Gdy przez roztwór
elektrolitu płynie prąd
stały, jony wędrują do
odpowiednich
elektrod, gdzie
ulegają rozładowaniu,
wydzielają się
rozmaite substancje.
Zjawisko to nosi
nazwę

elektrolizy

.

Prawa elektrolizy Faraday’a

I

Masa substancji wydzielonej na elektrodzie jest

wprost proporcjonalna do ładunku, jaki przepłynął
przez roztwór.

dla prądu stałego

II

Jeżeli przez roztwory przepłynął ten sam ładunek,

to masy dwu substancji wydzielonych na
elektrodach mają się do siebie jak ich współczynniki
elektrochemiczne.

q

k

m

⋅

=

t

I

k

m

⋅

⋅

=

const

q

gdy

k

k

m

m

2

1

2

1

=

=

Prawa Ohma

I

Natężenie prądu płynącego przez opornik jest

wprost
proporcjonal
ne do
napięcia.

II

Opór opornika jest wprost proporcjonalny do jego

długości, a
odwrotnie
proporcjonal
ny do jego
pola
przekroju
poprzeczneg
o do
kierunku
prądu.

R

I

U

R

U

I

⋅

=

=

A

l

R

ρ

=

ρ

– oporność (dawniej - opór właściwy) ;

l

– długość przewodnika ;

A

– pole przekroju poprzecznego, prostopadłego do kierunku

przepływu prądu

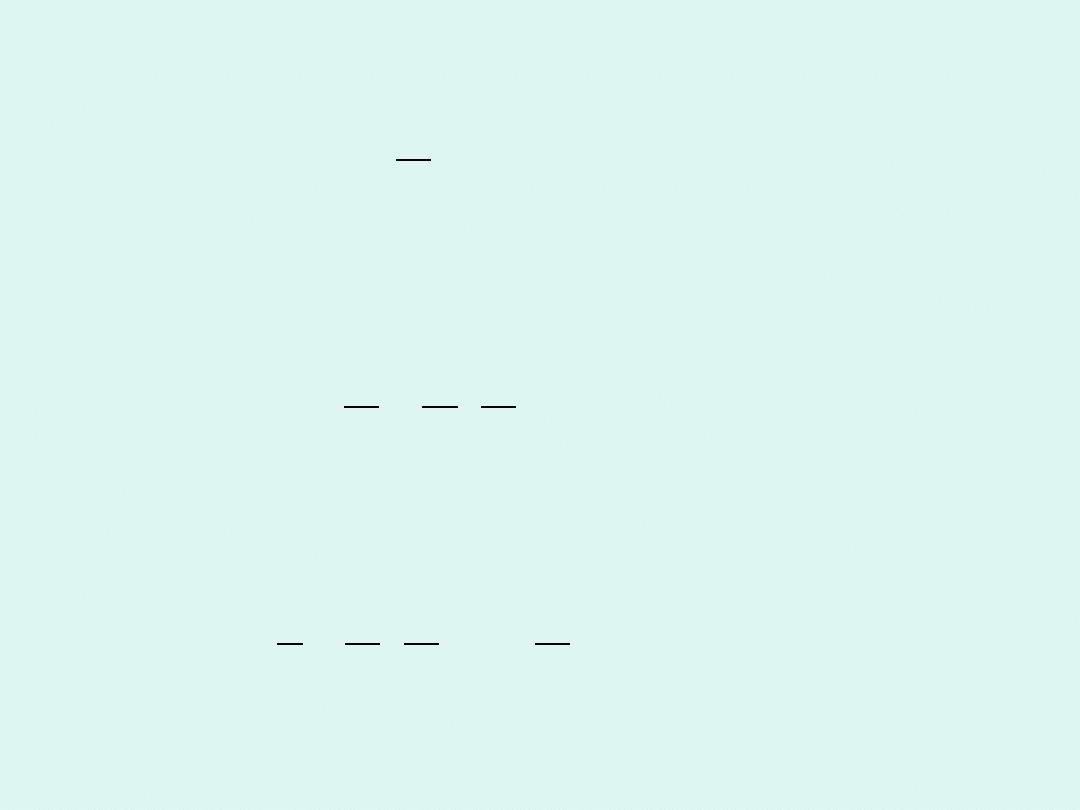
Przewodnictwo

Oporność

Przewodność (dawniej – przewodnictwo właściwe)

1

G

R

=

A

1 A

R

l

G l

ρ =

=

⋅

1

1 l

l

G

R A

A

κ =

=

⋅

=

⋅

ρ

jednostka [

Ω

-1

= S

]

jednostka [

Ω

-1

·m

-1

= S ·m

-1

]

jednostka [

Ω

·m

]

Przewodność elektrolityczna

(dawniej -

przewodnictwo właściwe elektrolitu) jest to
przewodnictwo roztworu elektrolitu zawartego
pomiędzy równoległymi elektrodami odległymi o
jednostkę (1 m) i polu przekroju poprzecznego
słupa

cieczy

zawartego

między

nimi

jednostkowym (1 m

2

), przy czym pole elektryczne

pomiędzy elektrodami jest jednorodne.

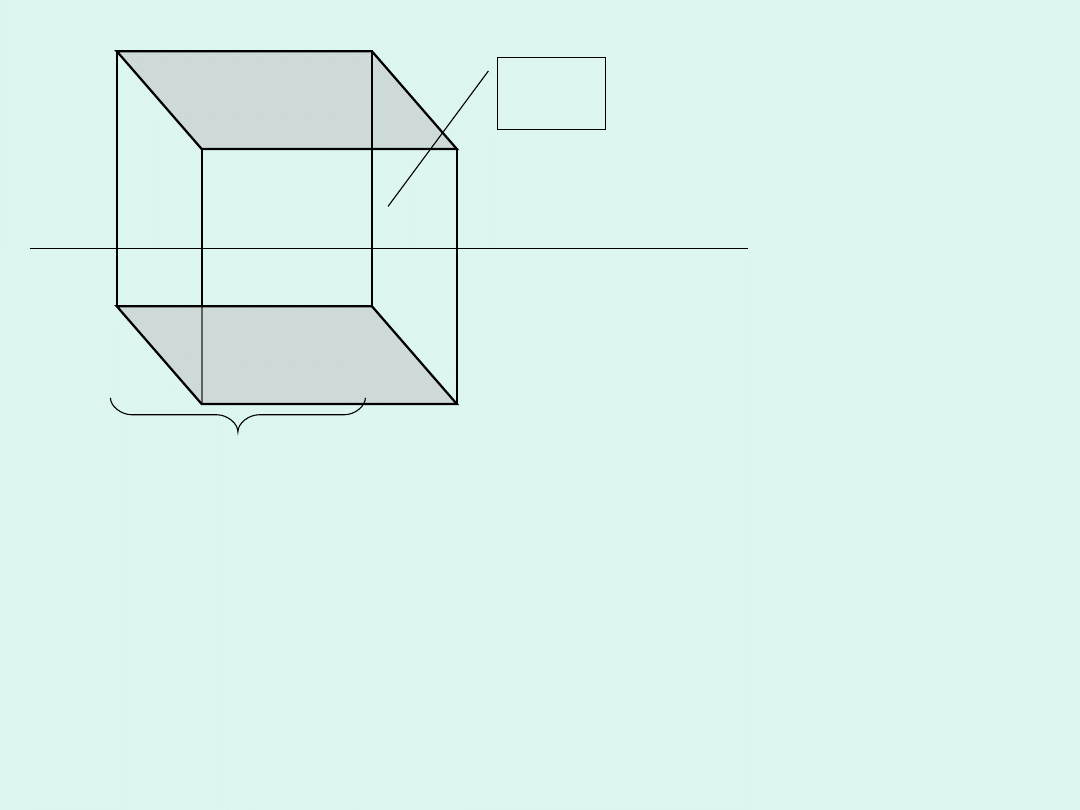
1 metr

1 m

2

kierunek
przepływu prądu

Jako przewodność elektrolityczną rozumiemy przewodnictwo
sześcianu o boku jednostkowym, zawierającego roztwór elektrolitu,
umieszczonego w jednorodnym polu elektrycznym.

Do pomiaru przewodności elektrolitycznej używany jest
zmodyfikowany

mostek Wheatstone’a

. Mostek ten jest zasilany

prądem zmiennym (zwykle o częstotliwości 1 kHz, aby :

•

zapobiec polaryzacji elektrod

•

zapobiec elektrolizie roztworu

W trakcie pomiarów naczynko konduktometryczne musi być
termostatowane, ponieważ przewodnictwo roztworów rośnie
silnie wraz ze wzrostem temperatury.

Ponieważ w zmiennym polu elektrycznym naczynko
konduktometryczne wykazuje pozorny opór pojemnościowy, to w
obwód włączony jest kondensator o zmiennej pojemności ,
kompensujący pojemność elektryczną naczynka.

~

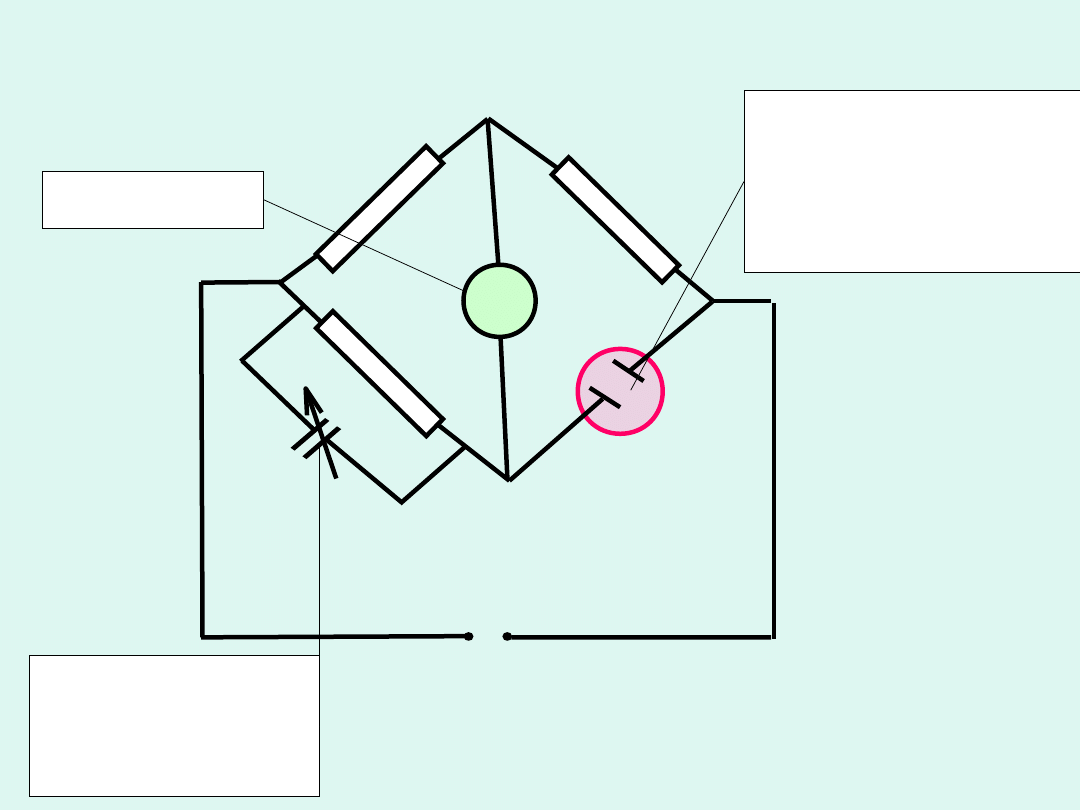
prąd zmienny o

częstotliwości 1000

Hz

naczyńko

konduktometryczne

(koniecznie musi być

termostatowane)

kondensator o

zmiennej

pojemności

galwanometr

A

D

C

B

C

2

R

x

R

3

R

2

R

1

C

x

G

Zmodyfikowany mostek Wheatstone’a

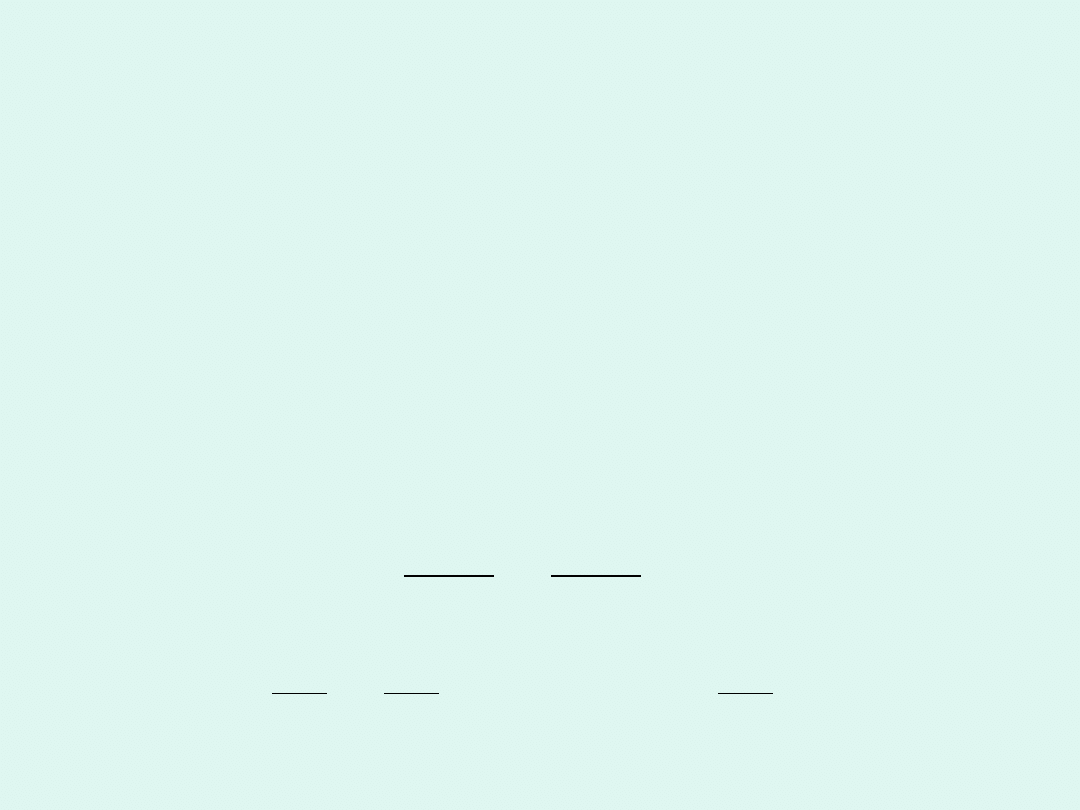
Aby zmierzyć opór naczynka napełnionego badanym roztworem
elektrolitu, należy tak dobrać opory

R

1

,

R

2

i

R

3

oraz pojemność

kondensatora

C

2

, aby mostek był w równowadze. Wówczas

potencjały w punktach

B

i

A

są jednakowe i nie płynie pomiędzy

nimi prąd elektryczny, co pokazuje nam galwanometr

G

.

x

3

2

1

I

I

i

I

I

=

=

B

A

1 1

3

3

2

2

x

x

V

V

I R

I R

I R

I R

=

⇓

=

=

I R

I R

I R
I R

R

R

R
R

R

R

R

R

x

x

x

x

1 1

2

2

3 3

1

2

3

3

2

1

=

=

⇒

=

Przykładowe sondy konduktometryczne (naczynka

konduktometryczne)

Ponieważ nie można określić parametrów geometrycznych elektrod (

l/A

)

oraz pole elektryczne w rzeczywistym naczynku nie jest jednorodne, to
pomiar przewodności elektrolitycznej wykonujemy jako pomiar
porównawczy. Stałą naczyńka ustalamy przez pomiar oporu naczynka
napełnionego wzorcowym roztworem elektrolitu.

G

k

R

k

G

R

k

G

k

R

k

x

x

x

wz

wz

wz

wz

wz

wz

wz

⋅

=

=

κ

κ

=

⋅

κ

=

⇒

⋅

=

=

κ

Przewodność elektrolityczna wzorcowych roztwo-

rów KCl

stężenie

[mol/dm

3

]

κ

w 18ºC [Sm

-1

]

κ

w 25ºC [Sm

-1

]

1

9,820

11,173

0,1

1,1192

1,2886

0,01

0,12227

0,14115

Przykłady zależności przewodności

elektrolitycznej od stężenia

H

2

S

O

4

N

aO

H

H

J

C

H

3

C

O

O

H

x

10

0

20

40

60

80

10

0

12

0

14

0

16

0

0

2

4

6

8

10

12

c

[m

o

l/

d

m

3

]

Można ją obliczyć z poniższego wzoru, przy czym stężenie
podstawiamy wyrażone w mol/m

3

.

jednostka [

Ω

-1

m

2

mol

-1

= S·m

2

mol

-1

]

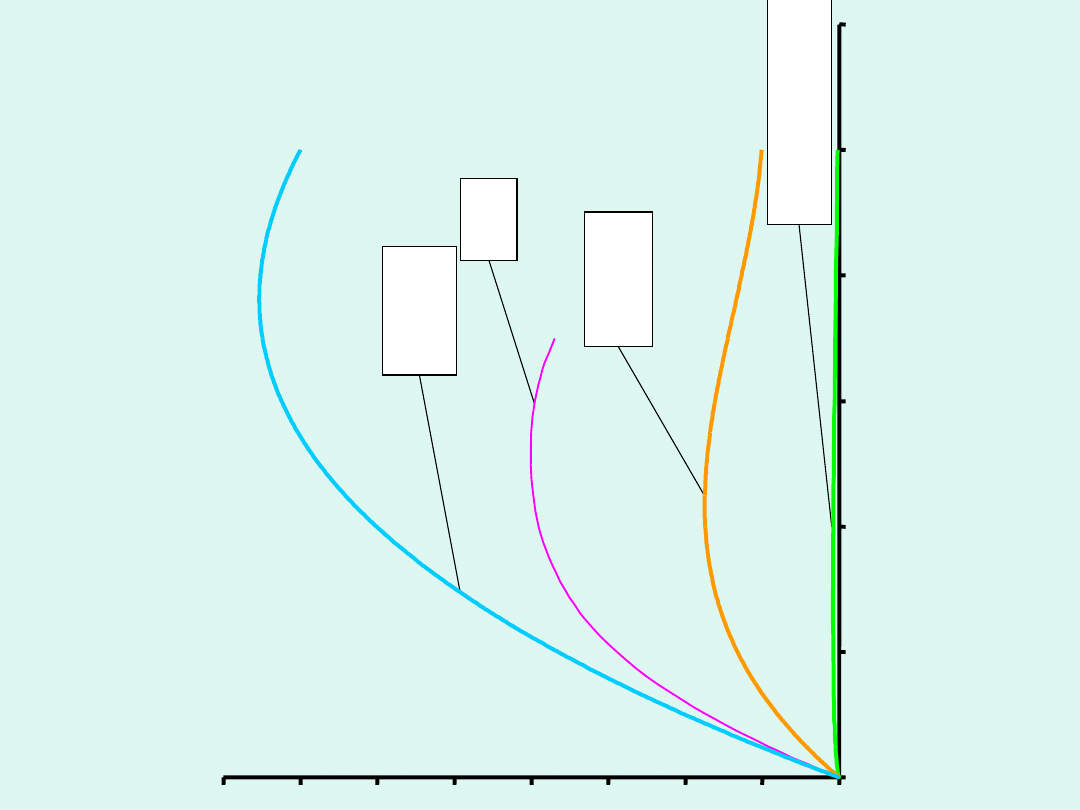
Przewodność molowa

Λ

(dawniej – przewodnictwo

molowe)

jest to przewodnictwo roztworu elektrolitu

zawartego pomiędzy równoległymi elektrodami
odległymi o jednostkę (1 m) i o takim polu przekroju
poprzecznego słupa cieczy zawartego między nimi, że
w tak utworzonej objętości zawarty jest jeden mol
elektrolitu, przy czym pole elektryczne pomiędzy
elektrodami jest jednorodne.

c

κ

=

Λ

1 metr

A

kierunek
przepływu prądu

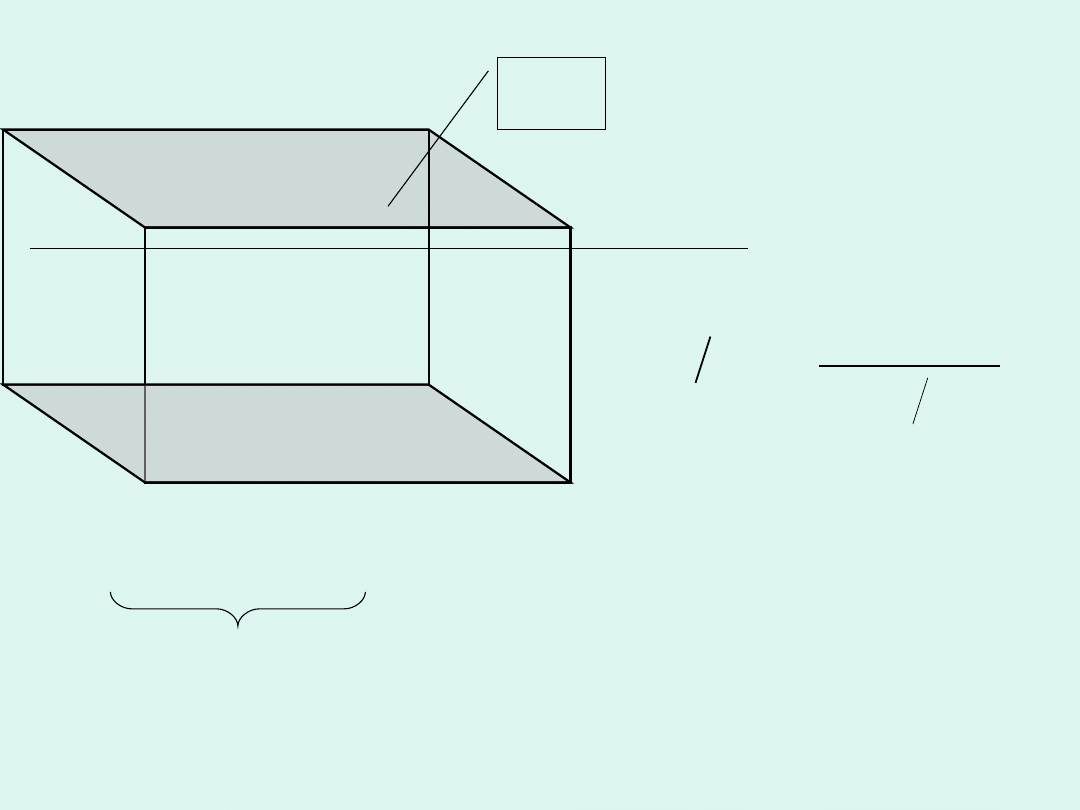
Jako przewodność molową rozumiemy
przewodnictwo

prostopadłościanu

zawierającego roztwór elektrolitu, o
jednostkowej grubości i takiej objętości,
że znajduje się w niej 1 mol elektrolitu,
umieszczonego w jednorodnym polu
elektrycznym.

3

3

1

1 A V m mol

c mol m





× =

=













Przewodność równoważnikowa

Λ

eqv

(dawniej –

przewodnictwo równoważnikowe) jest to przewodnictwo
roztworu elektrolitu zawartego pomiędzy równoległymi
elektrodami odległymi o jednostkę (1 m) i o takim polu
przekroju poprzecznego słupa cieczy zawartego między
nimi, że w tak utworzonej objętości zawarty jest jeden
gramorównoważnik elektrolitu, przy czym pole elektryczne
pomiędzy elektrodami jest jednorodne.

eqv

eqv

eqv

i

i

c

z

κ

Λ

=

Λ

Λ

=

ν

Dla mocnych elektrolitów przewodność molowa
zależy od stężenia w sposób, który można opisać

wzorem Kohlrascha

.

c

b

o

−

Λ

=

Λ

Λ

o

– graniczna przewodność molowa

b

– stała

Powyższy wzór jest słuszny dla roztworów o stężeniu
nie przekraczającym 0,01 mol/dm

3

.

Graniczna przewodność molowa

(równoważnikowa)

Λ

o

(

Λ

eqv,o

) to przewodność molowa (równoważnikowa) w

rozcieńczeniu nieskończenie wielkim (gdy stężenie dąży
do zera).

o

c 0

lim

→

Λ =

Λ

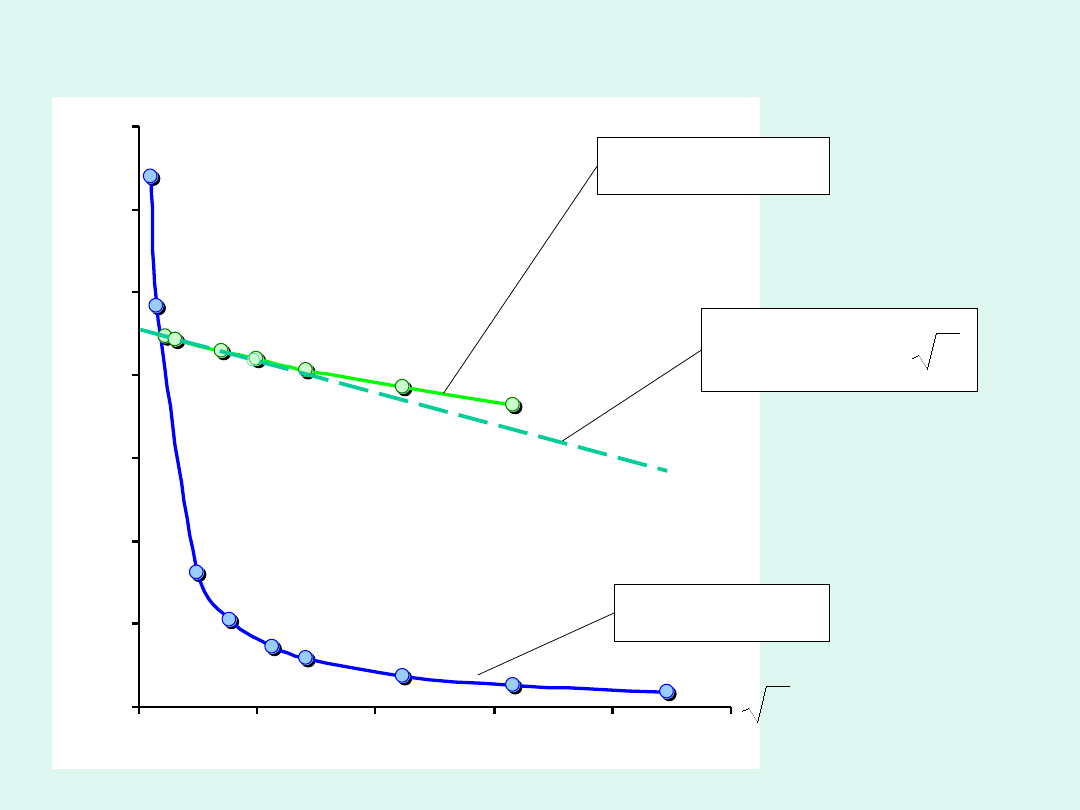
Dla mocnych elektrolitów

Λ

o

można wyznaczyć przez

ekstrapolację zależności podanej przez Kohlrauscha do
stężenia zerowego.

0

0.002

0.004

0.006

0.008

0.01

0.012

0.014

0

0.1

0.2

0.3

0.4

0.5

Λ

[Sm

2

mol

-1

]

Λ

o

CH

3

COOH

CH

3

COONa

[(mol/dm

3

)

1/2

]

c

c

b

o

−

Λ

=

Λ

Przykładowe zależności przewodności molowej od

pierwiastka ze stężenia

mocny elektrolit

słaby elektrolit

Jony w roztworze w polu elektrycznym wędrują
niezależnie od siebie, a przewodnictwo roztworu
elektrolitu jest sumą przewodnictw pochodzących
od poszczególnych jonów (kationów i anionów).

i

eqv,i

i

eqv

eqv,

eqv,

z

+ +

− −

+

−

Λ = ν λ + ν λ

λ

λ

=

Λ

= λ

+ λ

i

i

i

c

κ =

⋅ λ

∑

Prawo niezależnej wędrówki jonów

Kohlrauscha

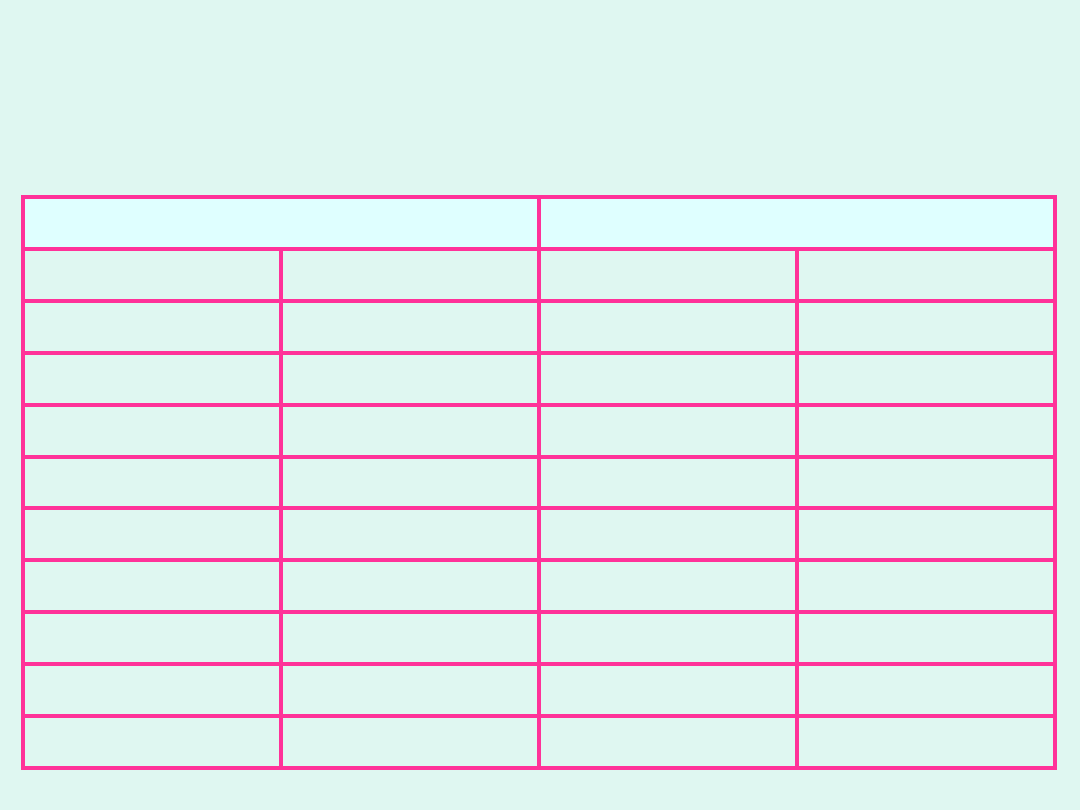
Przykładowe wartości granicznych przewodności równo-

ważnikowych jonów w temperaturze 25°C w roztworach

wodnych [

Ω

-1

m

2

mol

-1

]

kationy

aniony

H

+

349,65·10

-4

OH

-

198·10

-4

Na

+

50,08

·

10

-4

Cl

-

76,31

·

10

-4

K

+

73,48

·

10

-4

Br

-

78,1

·

10

-4

NH

4

+

73,5

·

10

-4

J

-

76,8

·

10

-4

Li

+

38,66

·

10

-4

NO

3

-

71,42

·

10

-4

1/2 Mg

2+

53,0

·

10

-4

CH

3

COO

-

40,9

·

10

-4

1/2 Ca

2+

59,47

·

10

-4

1/2 SO

4

2-

80,0

·

10

-4

1/2 Ba

2+

63,6

·

10

-4

1/2 CO

3

2-

69,3

·

10

-4

1/3 Al

3+

61

·

10

-4

1/3 Fe(CN)

6

3-

100,9

·

10

-4

1/3 Fe

3+

68

·

10

-4

C

10

H

21

SO

4

-

26

·

10

-4

F

el

F

η

Gdy jon porusza się ruchem jednostajnym, to siły działające
na niego się równoważą czyli siła oporu lepkiego jest równa
sile elektrycznej.

E

e

z

F

i

el

⋅

=

i

i

v

r

6

F

η

Π

=

η

i

i

i

i

i

i

el

r

6

e

z

E

v

v

r

6

eE

z

F

F

η

Π

=

η

Π

=

=

η

E

– natężenie pola elektrycznego ;

e

– ładunek elementarny ;

η

–

lepkość rozpuszczalnika ;

r

i

– promień jonu ;

v

i

– szybkość

poruszania się jonu

Ruchliwość jonu

Ruchliwość jonu

to szybkość poruszania się jonu w

polu elektrycznym o natężeniu jednostkowym.

E

v

u

i

i

=

jednostka [

m

2

/V·s

]

Ruchliwość jonu powiązana jest z przewodnością
równoważnikową jonu.

i

i

eqv

u

F

⋅

=

λ

,

Ruchliwość

jonu

zależy

jego

ładunku,

promienia

hydrodynamicznego czyli razem z jego warstwa solwatacyjną,
lepkości rozpuszczalnika, a pośrednio od temperatury, gdyż lepkość
cieczy maleje wraz ze wzrostem temperatury.

i

i

i

r

6

e

z

u

η

Π

=

W wodzie jony powstałe z jej autodysocjacji (H

+

i OH

-

) wyróżniają

się wysoką ruchliwością, co wskazuje, że ich mechanizm migracji
jest inny niż pozostałych jonów.

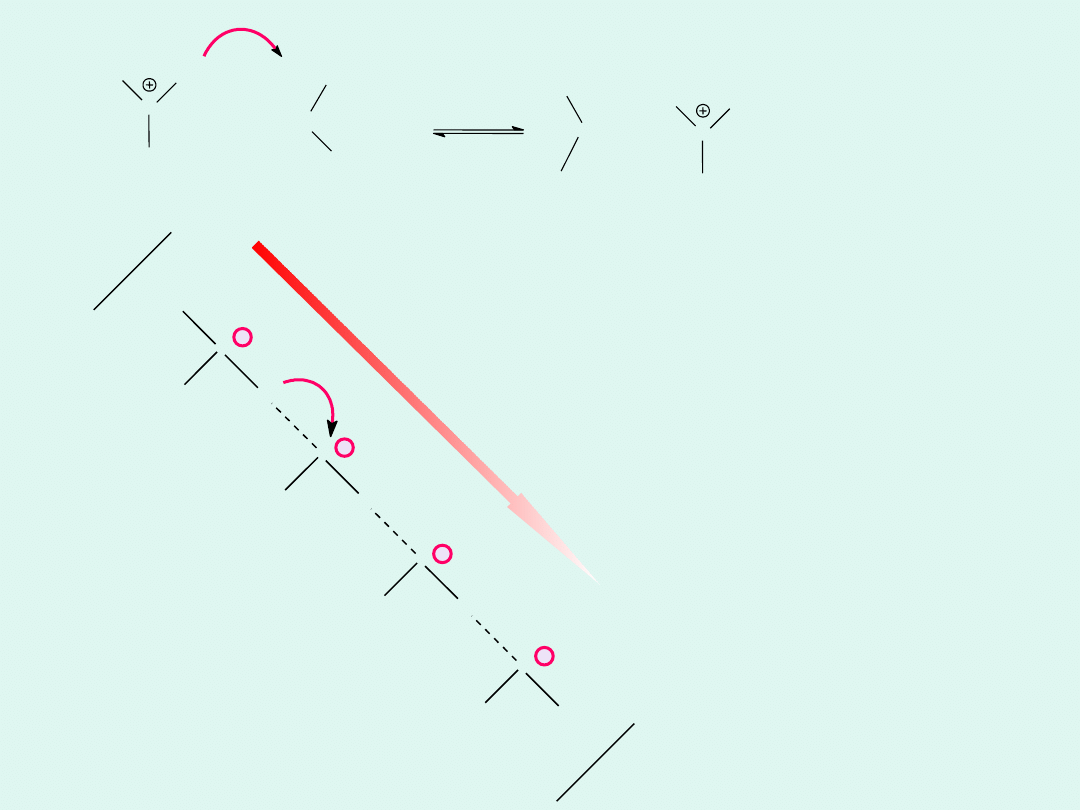
Mechanizm

łańcuchowy

transportu jonów

wodorowych w

wodzie

O

H

H

O

H

H

O

H

H

O

H

H

H

H

+

_

+

+

+

+

+

+

O

H

H

H

+

O

H

H

H

O

H

H

H

+

O

H

H

+

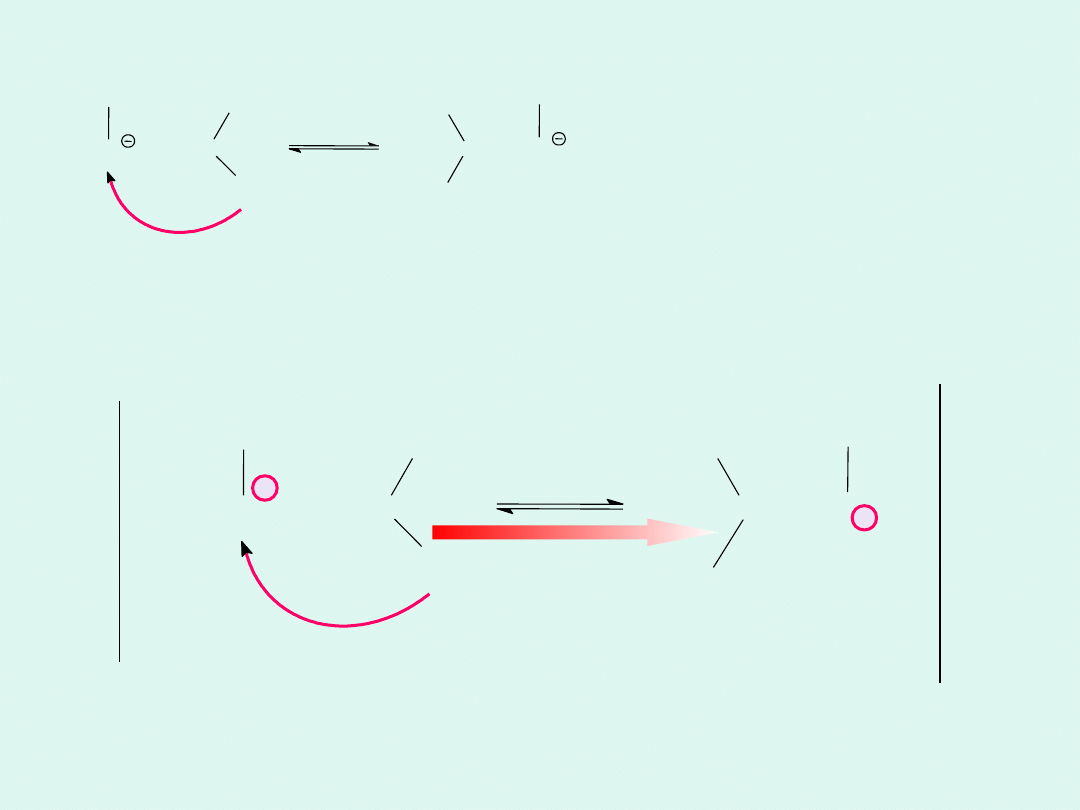
O

H

H

H

+

O

H

O

H

+

O

H

H

+

_

+

O

H

H

H

+

O

H

O

H

+

O

H

H

-

-

Mechanizm

transportu jonów

wodorotlenowych w

wodzie

Liczby przenoszenia jonów

Liczby przenoszenia jonu mówią, jaki ułamek ładunku został
przeniesiony przez jony danego znaku.

Liczba przenoszenia

jonu

to stosunek ładunku przeniesionego przez jony danego

znaku do całkowitego ładunku przeniesionego przez roztwór.

+

Q

Q

t

t

t

t

1

Q

Q

+

−

+

−

−

=

=

+

=

Znajomość liczb przenoszenia jest niezbędna do wyznaczenia
przewodności molowych (równoważnikowych) jonów.

eqv,

eqv,

eqv

eqv

t

t

t

t

+

−

+

−

+ +

− −

+

−

λ

λ

=

=

Λ

Λ

ν λ

ν λ

=

=

Λ

Λ

Metody wyznaczania liczb przenoszenia :

•

Metoda Hittorfa

•

Metoda ruchomej granicy

Żeby wyznaczyć przewodności równoważnikowe jonów należy
wyznaczyć przewodność równoważnikową elektrolitu i liczby
przenoszenia jonów w nim.

Wykorzystanie pomiarów

konduktometrycznych

•

Wyznaczanie iloczynu
rozpuszczalności soli trudno
rozpuszczalnych

•

Wyznaczanie iloczynu jonowego
wody

•

Wyznaczanie stałych dysocjacji
słabych elektrolitów

•

Miareczkowanie
konduktometryczne

Omawiane na
ćwiczeniach
rachunkowych
– obowiązuje do
egzaminu !

Miareczkowanie konduktometryczne polega na wyznaczaniu
punktu

równoważnikowego

pośrednio

poprzez

pomiar

przewodnictwa. W tym celu do próbki dodajemy porcjami
roztwór titranta i po każdym dodaniu mierzymy przewodnictwo
roztworu.

Podstawą metody jest prawo niezależnej wędrówki jonów
Kohlrauscha.

W czasie miareczkowania, na skutek zachodzącej reakcji
chemicznej zmienia się stężenie i rodzaj jonów w roztworze, co
powoduje zmiany przewodnictwa.

Metodę

miareczkowania

konduktometrycznego

można

wykorzystać

do

miareczkowań

kwasowo-zasadowych,

strąceniowych i kompleksometrycznych.

Miareczkowanie konduktometryczne

∑

λ

⋅

=

κ

i

i

i

c

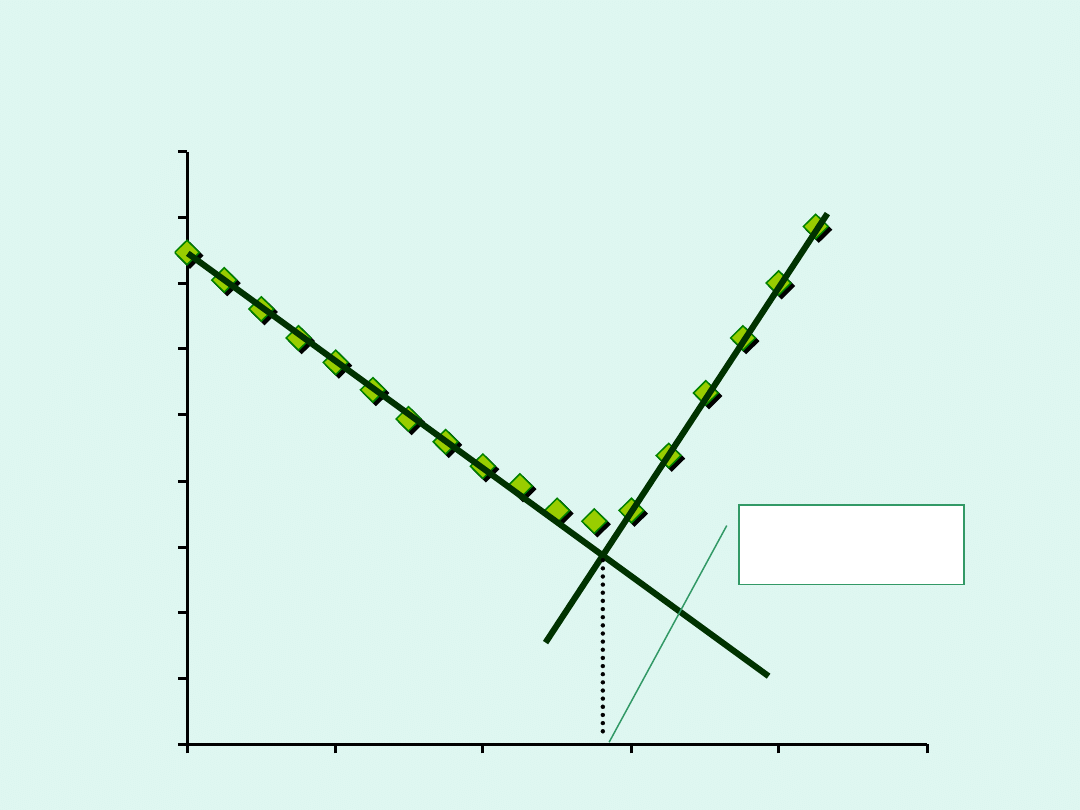
0

0,5

1

1,5

2

2,5

3

3,5

4

4,5

0

2

4

6

8

10

V

0,1 M HCl

[ml]

G [mS]

V

e qv

= 5,65 ml

Miareczkowanie mocnej zasady (NaOH) mocnym kwasem (HCl)

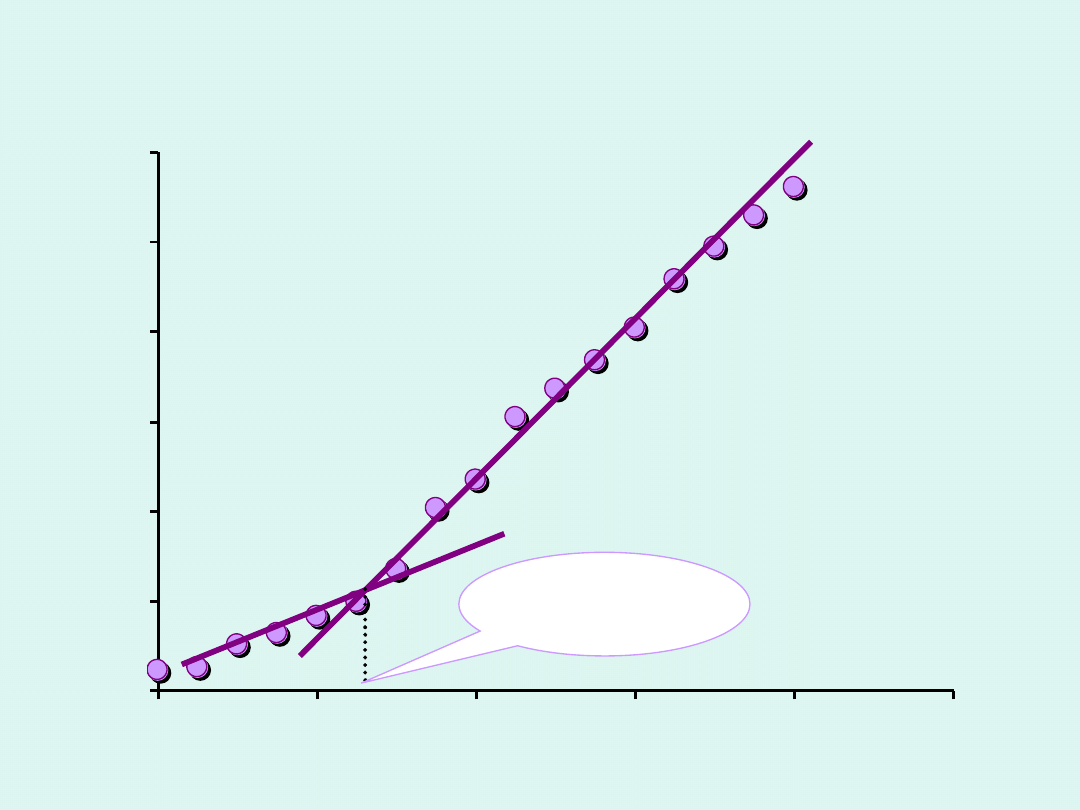
0

0.5

1

1.5

2

2.5

3

0

2

4

6

8

10

V

0,2 M NaOH

[ml]

G [mS]

V

eqv

=2,25 ml

Miareczkowanie słabego kwasu (CH

3

COOH) mocną zasadą

(NaOH)