1
PLANOWANIE I ANALIZA
EKSPERYMENTU
©2007 Paweł Możejko
Politechnika Gdańska, semestr zimowy, rok akademicki 2012/2013
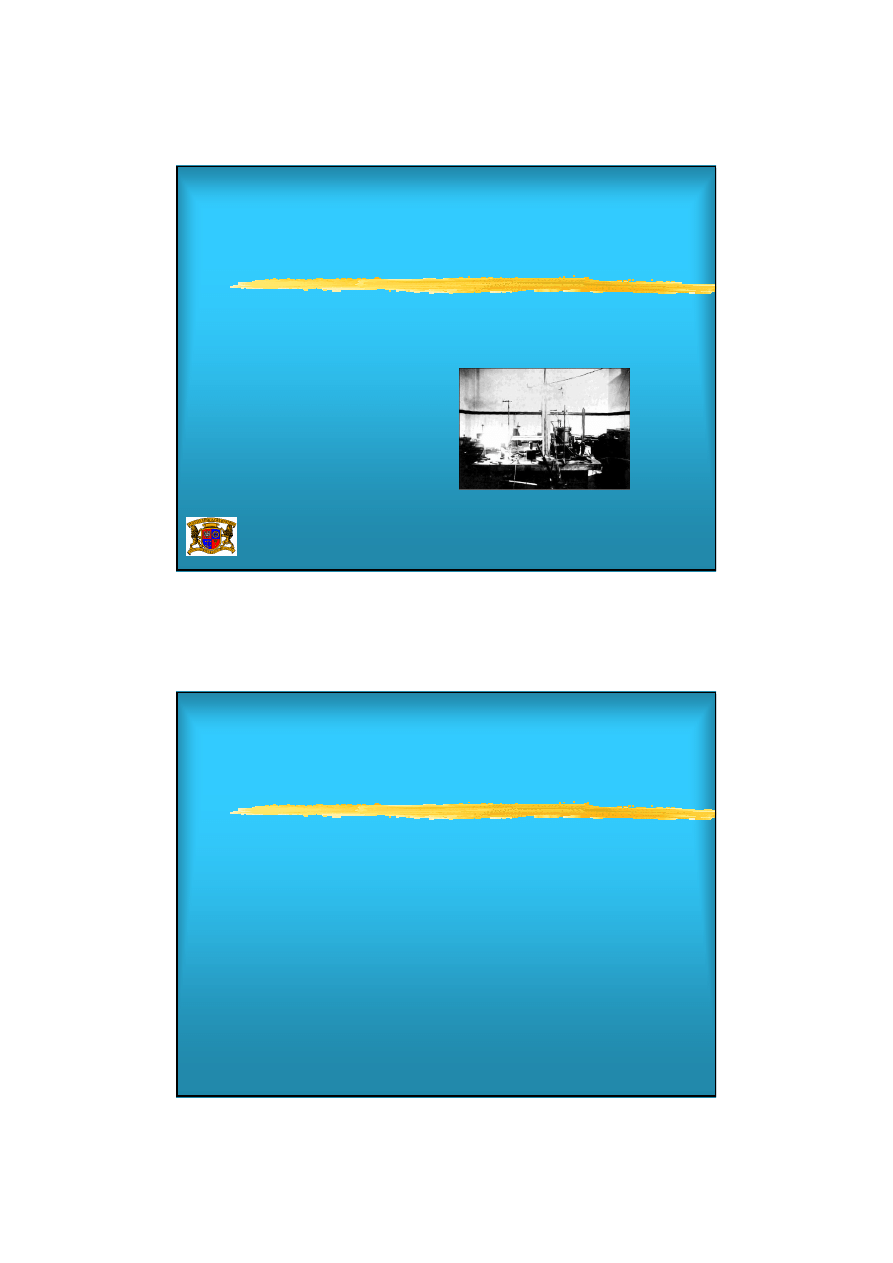
Aparatura Millikana do wyznaczenia ładunku elektronu
Wykład 3: Przenoszenie niepewności
PRZENOSZENIE NIEPEWNOŚCI
Niepewności w pomiarach bezpośrednich
Niepewności sumy i różnicy
Niepewności iloczynów i ilorazów
Niepewności wyrażenia potęgowego
Niezależne niepewności w sumie
Niepewności niezależne c.d.
Niepewności dowolnej funkcji jednej zmiennej
Ogólna reguła przenoszenia błędów
2
Niepewności w pomiarach bezpośrednich
źródło niepewności – odczyt skali oraz konieczność interpolacji
np. pomiędzy podziałkami miarki
Zagadnienie definicji – niepewności powstające ze względu na
nieprecyzyjne określenie dwóch punktów np. pomiar długości
wahadła fizycznego
Niepewności sumy i różnicy
W wyniku pomiarów bezpośrednich wyznaczamy wielkości
x
,
y
,…,
z
wraz odpowiadającymi im niepewnościami
δ
x
,
δ
y
, …,
δ
z
.
Zmierzone wartości
x
,
y
,…,
z
używamy do wyznaczenia szukanej
wielkości
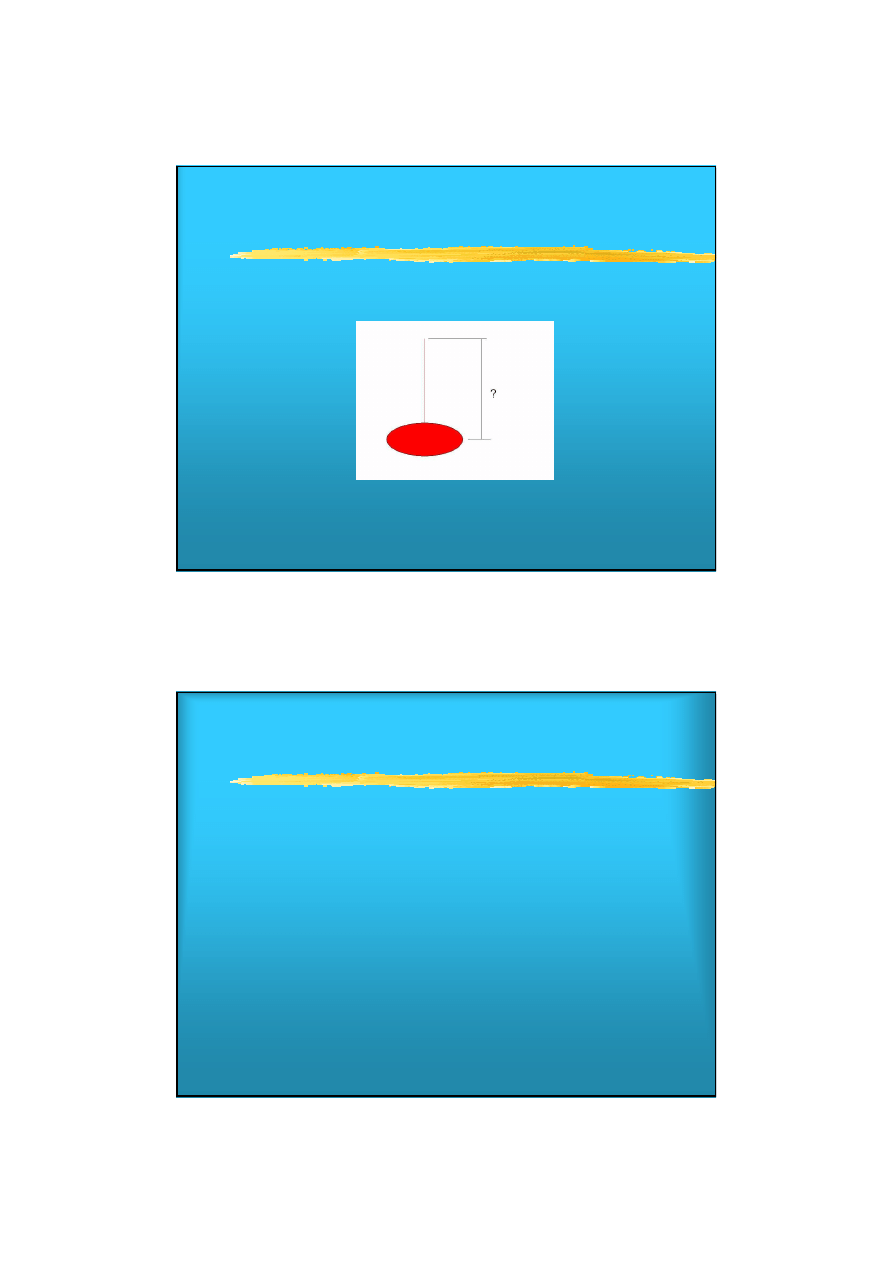
q=x+y+…+z-(u+…+w)
Ile wynosi niepewność
δ
q
wielkości
q
?
δ
q
≈
δ
x+
δ
y+…+
δ
z
+ δ
u
+...+ δ
u
3
Niepewności iloczynów i ilorazów
Jaką niepewnością obarczona jest wielkość
q
wyznaczona z
pomiarów bezpośrednich wielkości
x,y,…,z,u,…w
zmierzonych z
małymi niepewnościami
,
δ
y, …,
δ
z,
δ
u,…
δ
w
?
Niepewność względna wielkości
q
wynosi
w
u
z
x
q
⋅⋅
⋅
⋅⋅
⋅
=
w
w
u
u
z
z
y
y
x
x
q
q
δ
δ
δ
δ
δ
δ
+
+
+
+
+
+
≈
...
...
Niepewności iloczynów i ilorazów
Wielkość
x
wyznaczona jest z niepewnością
δ
x
używana jest do
obliczenia iloczynu
B jest wielkością stałą nie mającą żadnej niepewności tzn.
δΒ=0
Niepewność wielkości
q
wynosi
x
B
q
δ
δ
=
q = Bx,
4
Niepewności wyrażenia potęgowego
Wielkość
x
zmierzona z niepewnością
δ
x
,
jest używana do
obliczenia wyrażenia potęgowego
Niepewność względna jest
n
razy większa niż niepewność
x
n
x
q
=
x
x
n
q
q
δ
δ
=
Niepewności niezależne - niepewność
sumy i różnicy
Jeżeli niepewności,
δ
x
,…,
δ
z
,
δ
u
,…,
δ
w
wielkości zmierzonych
x
,…,
z
,
u
,…,
w
są niezależne i przypadkowe to niepewność obliczonej
wartości
q
jest pierwiastkiem z sumy kwadratów niepewności
początkowych:
Zachodzi:
)
...
(
...
w
u
z
x
q
+
+
−
+
+
=
2
2
2
2
)
(
...
)
(
)
(
...
)
(
w
u
z
x
q
δ
δ
δ
δ
δ
+
+
+
+
+
=
w
u
z
x
q
δ
δ
δ
δ
δ
+
+
+
+
+
≤
...
...
5
Niepewności niezależne -
niepewność iloczynu i ilorazu
Jeżeli niepewności,
dx
,…,
δ
z
,
δ
u
,…,
δ
w
wielkości
zmierzonych
x
,…,
z
,
u
,…,
w
są niezależne i przypadkowe
to niepewność obliczonej wartości
q
jest pierwiastkiem z sumy kwadratów początkowych
niepewności względnych:
Zachodzi:
w
u
z
x
q
⋅⋅
⋅
⋅⋅
⋅
=
w
w
u
u
z
z
x
x
q
q
δ
δ
δ
δ
δ
...
...
+
+
+
+
≤
2
2
2
2
...
...
+
+
+
+
+
≈
w
w
u
u
z
z
x
x
q
q
δ
δ
δ
δ
δ
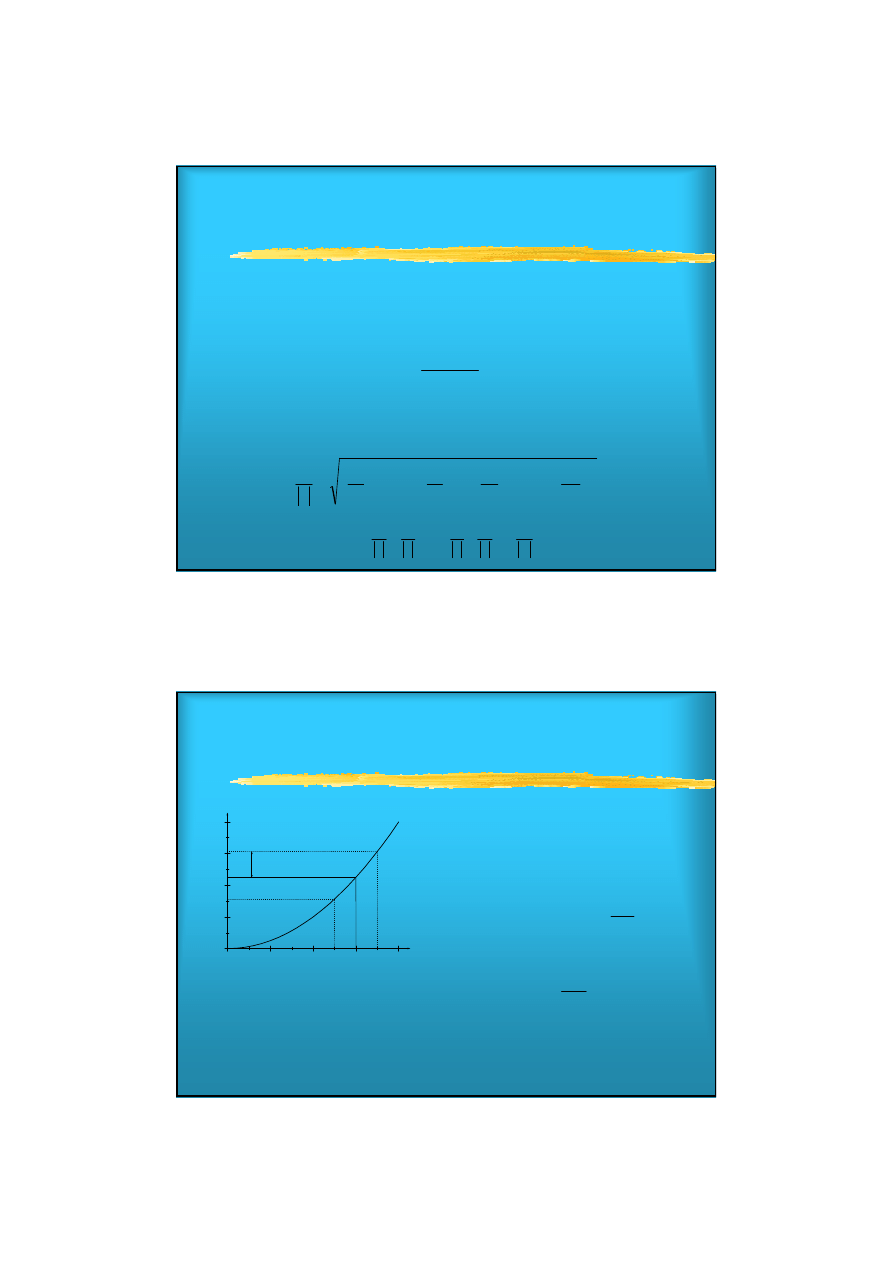
Niepewności dowolnej funkcji
jednej zmiennej
q(x)
δ
q
q
min
x
np
+
δ
x
x
np
-
δ
x
x
np
q
max
q
np
q
x
)
(
)
(
np
np
x
q
x
x
q
q
−
+
=
δ
δ
u
dx
dq
x
q
u
x
q
=
−
+
)
(
)
(
x
dx
dq
q
δ
δ
=
6
Niepewności dowolnej funkcji
jednej zmiennej
Jeżeli wielkość
x
jest zmierzona z niepewnością
δ
x
i
wykorzystywane do obliczenia wartości funkcji
q(x)
, to
niepewność
δ
q
jest równa:
x
x
q
q
δ
δ
d
d
=
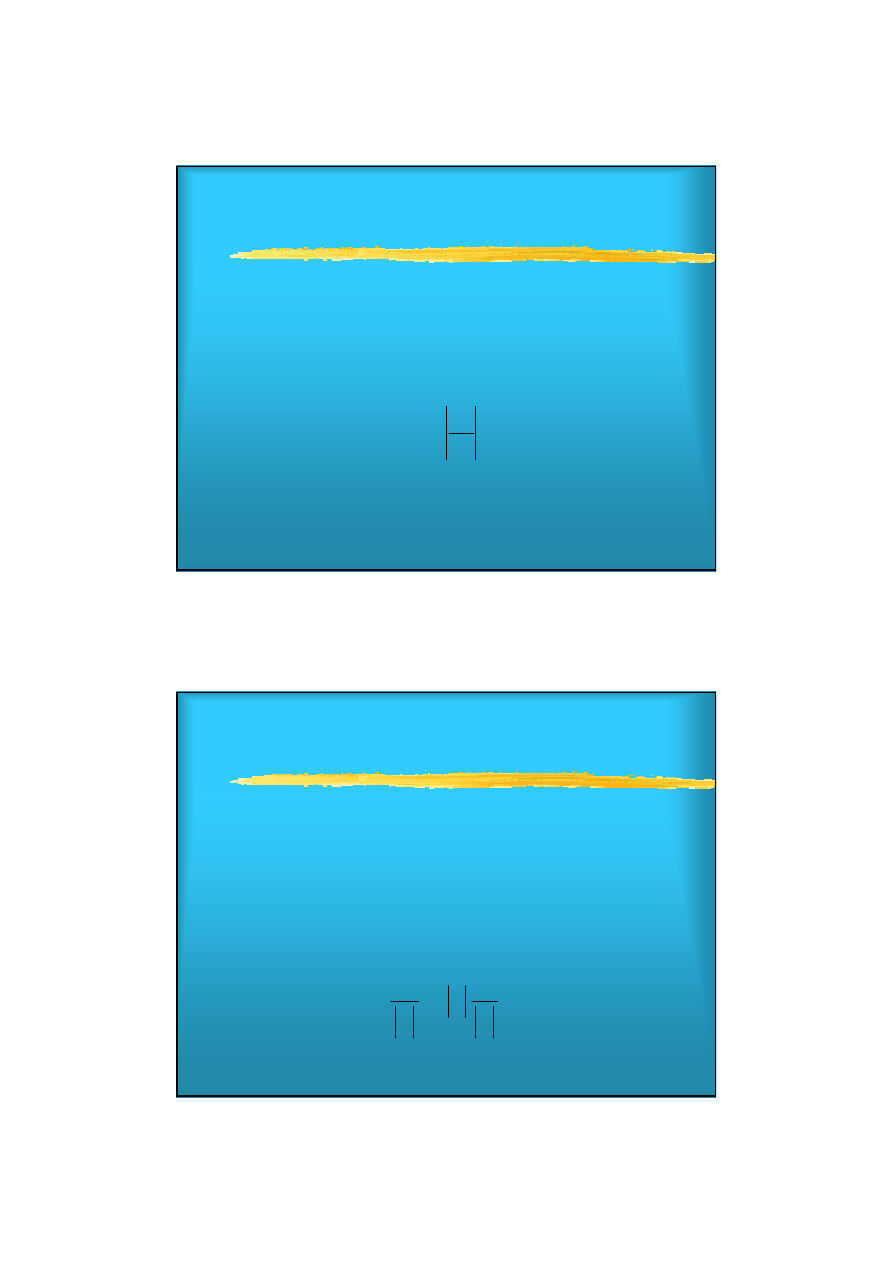
Niepewności dowolnej funkcji
jednej zmiennej
Niepewność wyrażenia potęgowego
Jeżeli
x
jest zmierzone z niepewnością
dx
i wykorzystywane do
obliczenia potęgi
q=x
n
(gdzie
n
jest ustaloną znaną liczbą), to
niepewność względna
q
jest równa:
x
x
n
q
q
δ
δ
=
7
Ogólna reguła przenoszenia błędów
Niepewność wartości funkcji wielu zmiennych
Załóżmy, że x,…,z zmierzone z niepewnościami
δ
x
,…,
δ
z
służą do
obliczenia wartości funkcji
q(x
,..,
z)
. Jeżeli niepewności
wyznaczenia
x
,..,
z
są niezależne i przypadkowe, to niepewność
wyznaczenia wartości funkcji
q
równa jest:
Zachodzi:
2
2
...
∂
∂
+
+
∂
∂
=
z
z
q
x
x
q
q
δ
δ
δ
z
z
q
x
x
q
q
δ
δ
δ
∂
∂
+
+
∂
∂
≤
...
Zadania na przyszłe wykłady
Jak uśredniać pomiary wykonywane seriami obarczone
różnymi niepewnościami statystycznymi
Uzasadnić w oparciu o rozkład normalny, że wartość
średnia jest najlepszym przybliżeniem wielkości
mierzonej wielokrotnie
Wyszukiwarka
Podobne podstrony:
piae wyklad2 12 13
piae wyklad1 12 13
INS LAB PEWN 4 12 13 id 214856 Nieznany
INS LAB PEWN 1 12 13 id 214853 Nieznany
piae wyklad4 12 13
piae wyklad2 12 13
piae wyklad2 12 13
PRZ OPI wyklad 3 v2 pdf id 4033 Nieznany
c3 19 12 2010 id 97134 Nieznany
cw 13 id 121763 Nieznany
mat fiz 2003 12 06 id 282350 Nieznany
36 13 id 36113 Nieznany (2)
7 13 id 44730 Nieznany (2)
Alkohole 13 id 58087 Nieznany (2)
więcej podobnych podstron