„URANIA — Post py Astronomii”
urania.pta.edu.pl/science.html
Poradnik Konstruktora Teleskopu
–
Oprawa lustra g ównego. Cz. III
1
OPRAWA LUSTRA G ÓWNEGO. CZ. III
Poprzednie uwagi i formu y dotyczy y zwierciad a
traktowanego jako p yta p askorównoleg a. Tak jednak
nie jest. Nasuwa si pytanie, jaki wp yw na rozk ad
masy w bryle zwierciad a ma wkl
jego czo owej
strony, podczas gdy strona tylna jest p aska i jak to
wp ywa na usytuowanie okr gów równowagi.
Wobec braku informacji na ten temat w dost pnej
literaturze, wspó autor artyku u T. Krzyt wyprowadzi
ogólne formu y matematyczne okre laj ce promienie
eq
r
okr gów równowagi, z uwzgl dnieniem
zag bienia i otworu w zwierciadle przy za
eniu, e
punkty podparcia s rozmieszczone wed ug metody
Hindle’a.
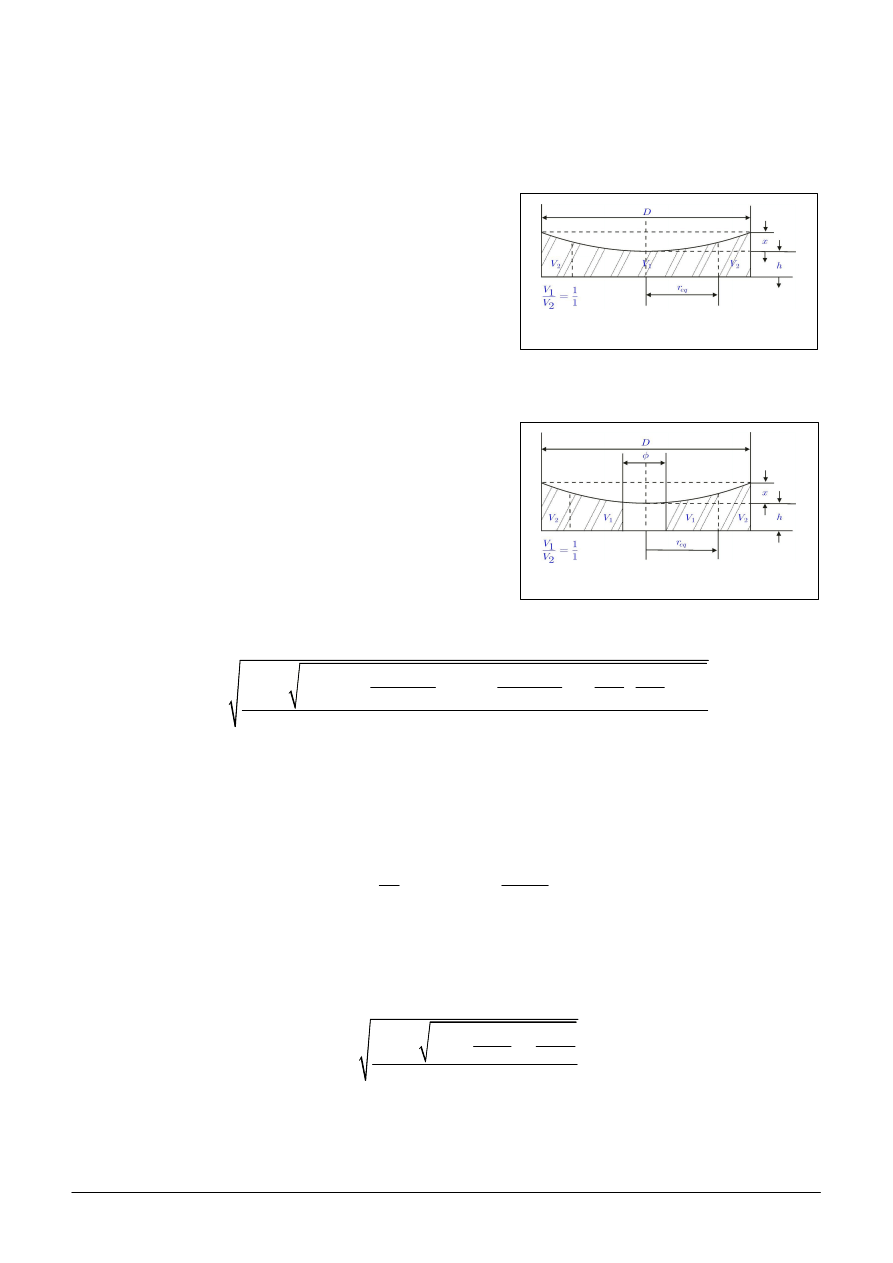
Bry a zwierciad a jest tu umownie dzielona na dyski
i torusy o takich wzajemnych stosunkach ich ci arów,
jak analogicznie powierzchnia p yty p askorównoleg ej
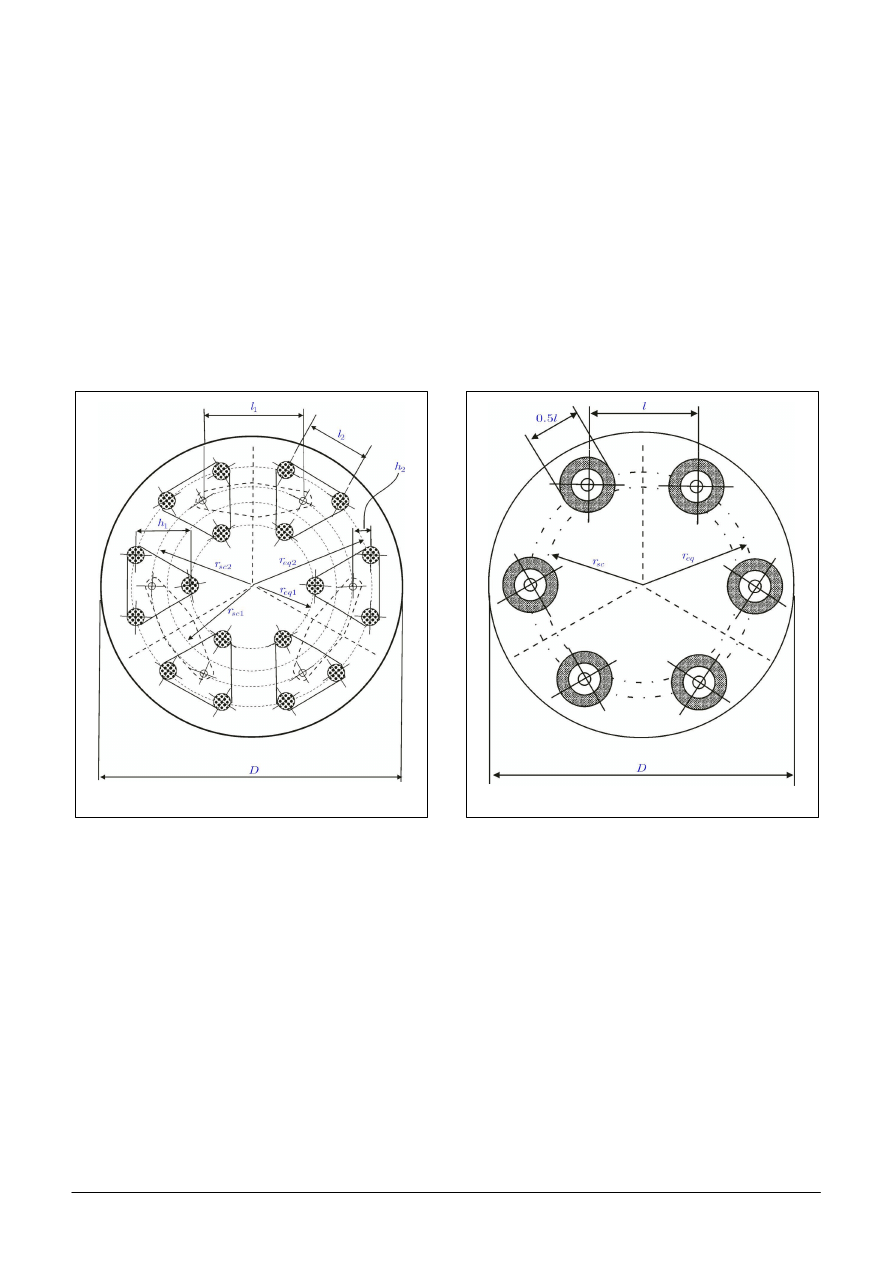
jest dzielona na odpowiednie pola (rys. 8).
Przy podparciu na 3 i 6 punktach
Dla zwierciad a z otworem, promie okr gu równowagi wynosi:
4
4
2
2
2
2
2
2
32
4
2
8
æ
ö
æ
ö
æ
ö
- F
- F
F
F
÷
÷
÷
ç
ç
ç
- +
+
+
+
+
÷
÷
÷
ç
ç
ç
÷
÷
÷
ç
ç
ç
è
ø
è
ø
è
ø
=
eq
D
D
k
k
h
h
k
hk
h
r
k
(1)
Gdzie:
D
— rednica zwierciad a
f — ogniskowa zwierciad a
x — zag bienie w rodku zwierciad a
h
— grubo zwierciad a w jego rodku
2
1
0,5
4
4
=
=
D
k
x
f
f
Symbol
,
f jak i
j
w poprzednich formu ach, oznacza rednic otworu centralnego w zwierciadle.
Grubo zwierciad a w jego rodku jest liczona tak, jak gdyby otworu nie by o (rys. 9).
Je li zwierciad o otworu nie posiada, to powy sza formu a (1) si upraszcza i ma nast puj
posta :
2 4
2
2
32
4
- +
+
+
=
eq
k D
khD
h
h
r
k
(2)
Rys. 8
Rys. 9
„URANIA — Post py Astronomii”
urania.pta.edu.pl/science.html
2
Poradnik Konstruktora Teleskopu
–
Oprawa lustra g ównego. Cz. III
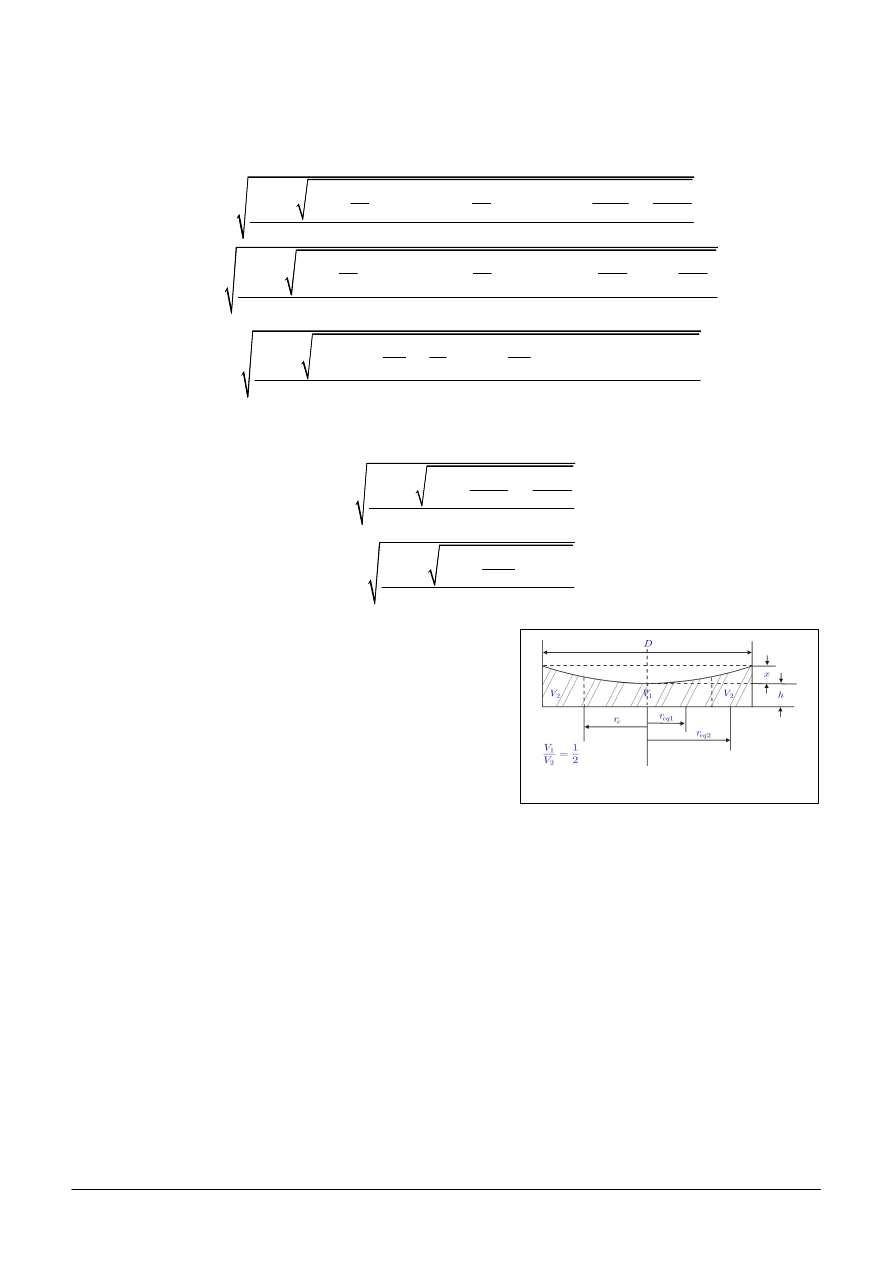
Podparcie w 9 i 18 punktach (rys. 10 i rys. 11) dla zwierciad a z otworem
Równania dla promieni okr gów równowagi s nast puj ce:
2
2 4
2
2
4
4
2
2
(
)
(
)
48
6
16
2
e
k
kh
k
hk
h
h
D
D
r
k
F
F
- +
+
- F +
- F +
+
=
(3)
2
2
2
2
4
4
2
2
1
(16
)
(4
)
32
4
2
8
æ
ö
F
F ÷
ç
- +
+
- F +
- F +
+
÷
ç
÷
çè
ø
=
e
e
eq
k
kh
k
k
h
h
r
r
H
r
k
(4)
4
4
2
2
2
2
2 4
2
2
2
32
2
4
æ
ö
æ
ö
÷
÷
ç
ç
- +
+
-
+
-
+
+
÷
÷
ç
ç
÷
÷
ç
ç
è
ø
è
ø
=
e
e
e
e
eq
D
r
D
h
h
k
hk
r
k r
khr
r
k
(5)
W przypadku zwierciad a bez otworu, wzory na promienie okr gów równowagi znacz co si
upraszczaj :
2 4
2
2
48
6
- +
+
+
=
e
k D
khD
h
h
r
k
(6)
2 4
2
2
1
2
- +
+
+
=
e
e
eq
k r
h
h
khr
r
k
(7)
Dla
2
eq
r
formu a jest taka sama, jak w przypadku
zwierciad a z otworem. Promie
,
eq
r
okre la granic
mi dzy umownymi cz ciami zwierciad a, wewn trzn
i zewn trzn , dla których stosunek ich ci arów ma si
jak 1:2.
Pos uguj c si powy szymi zale no ciami,
rozpatrzymy przyk ad nast puj cych trzech zwierciade
podpartych w 6 punktach:
1.
rednica
250
=
D
mm, ogniskowa
200
=
f
mm, grubo p yty przy kraw dzi
30 mm
Je li potraktujemy zwierciad o jako p yt p askorównoleg , to przy podparciu w 6
punktach,
eq
r
wyniesie
88.4
mm. Po uwzgl dnieniu zag bienia,
eq
r
zwi kszy si do
89.1mm.
2.
rednica
400
=
D
mm, ogniskowa
1600
=
f
mm, grubo przy kraw dzi
50mm
Analogicznie do poprzedniego przyk adu, w pierwszym przypadku
141.4
=
eq
r
mm, w
drugim
143.8
=
eq
r
mm.
3.
rednica
400
=
D
mm, ogniskowa
1600
=
f
mm, grubo przy kraw dzi
50mm, otwór w
zwierciadle o rednicy
60
F =
mm
Bez uwzgl dnienia zag bienia
143.0
=
eq
r
mm, a po jego uwzgl dnieniu
144.8
=
eq
r
mm.
Rys. 10
„URANIA — Post py Astronomii”
urania.pta.edu.pl/science.html
Poradnik Konstruktora Teleskopu
–
Oprawa lustra g ównego. Cz. III
3
Jak wida , ró nice s tu niewielkie. Je li grubo p yty zwierciad a jest znacz co wi ksza od
dopuszczalnej minimalnej, tak e istnieje spory zapas sztywno ci szk a, to wp yw zag bienia na
eq
r
mo na pomin
. Rzecz nabiera znaczenia przy zwierciad ach du ych, profesjonalnych teleskopów, w
których d
y si do tego, aby zwierciad o by o jak najl ejsze. Mo na te tylnej jego stronie nada
kszta t wypuk y o takiej krzywi nie, jak zag bienie czo owe, a wtedy problem przestanie istnie .
Rozpatruj c rzecz od strony konstrukcji mechanicznej, najprostszym jest podparcie 3 – punktowe.
Podpory s tu nieruchome, umieszczone na metalowej
ycie oprawy. Maj posta niewielkich, okr
ych
podk adek z twardej skóry, teflonu lub innego
liskiego, niespr
ystego materia u dopasowuj cego si
do p yty zwierciad a.
Pocz wszy od podparcia 6 – punktowego,
koniecznym staje si zastosowanie odpowiedniego
mechanizmu podpieraj cego. Najlepszym dla ma ych i
rednich rozmiarów zwierciade jest tak zwany system
Grubba, konstrukcja prosta i pewna w dzia aniu.
System ten jest stosowany przy zwierciad ach
dochodz cych nawet do rednicy
1 m, wykonanych z litej p yty szklanej.
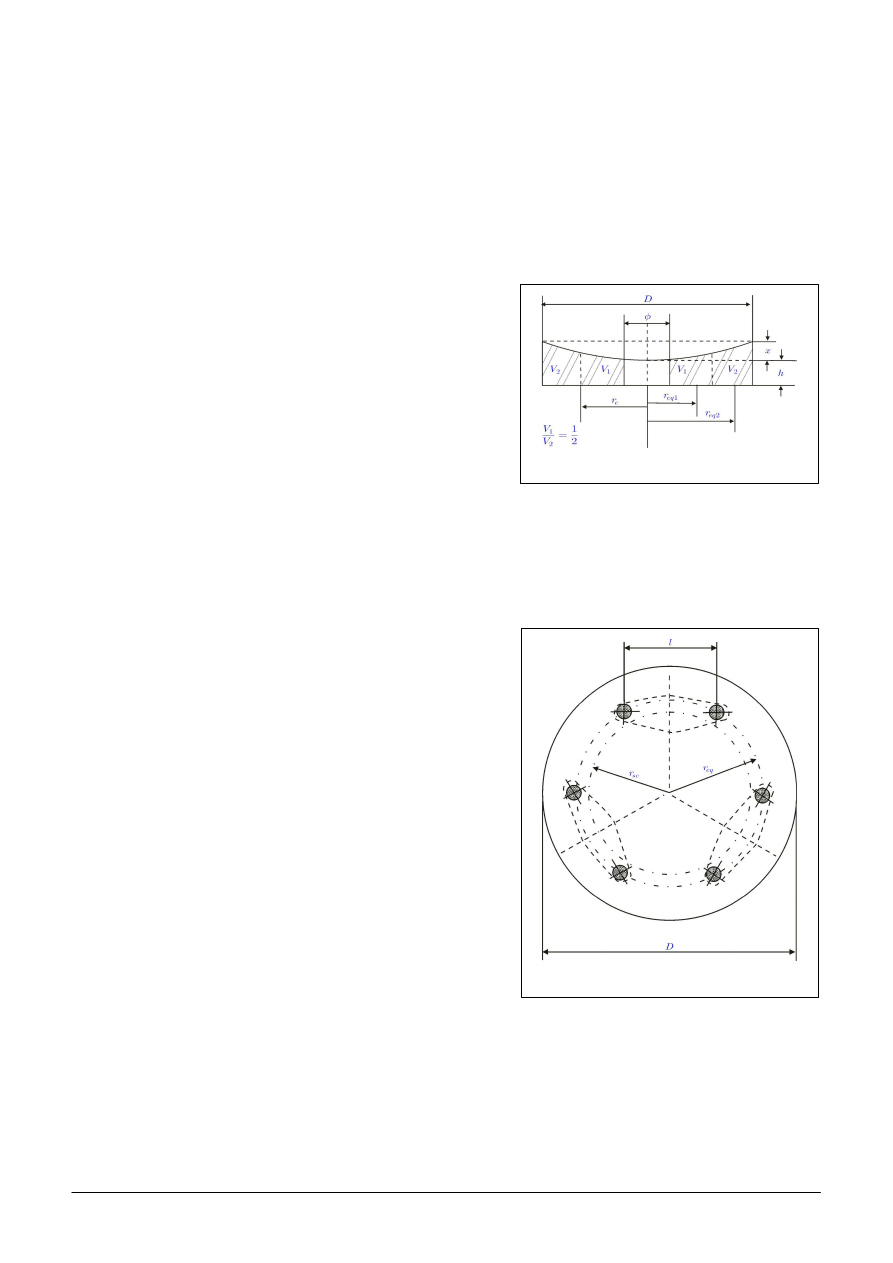
I tak, przy 6 punktach podparcia, punkty te s zgrupowane w 3 pary. S siednie punkty danej pary
umieszczone s na ko cach dwuramiennej symetrycznej d wigni, która w miejscu swojej osi obrotu
zamocowana jest do p yty oprawy. W ten sposób ci ar
zwierciad a poprzez d wignie opiera si na oprawie w 3
punktach (rys. 12).
W oprawie o 9 podporach, ka de 3 punkty podparcia
tworz ce trójk t równoramienny, umieszczone s na
rogach metalowego trójk ta, który swoim rodkiem
ci ko ci na podparciu kulowym, opiera si na p ycie
oprawy (rys. 13). Skoro s 3 takie trójk ty, to
zwierciad o spoczywaj ce na 9 samodopasowuj cych
si punktach podparcia, w ostateczno ci spoczywa na 3
podporach.
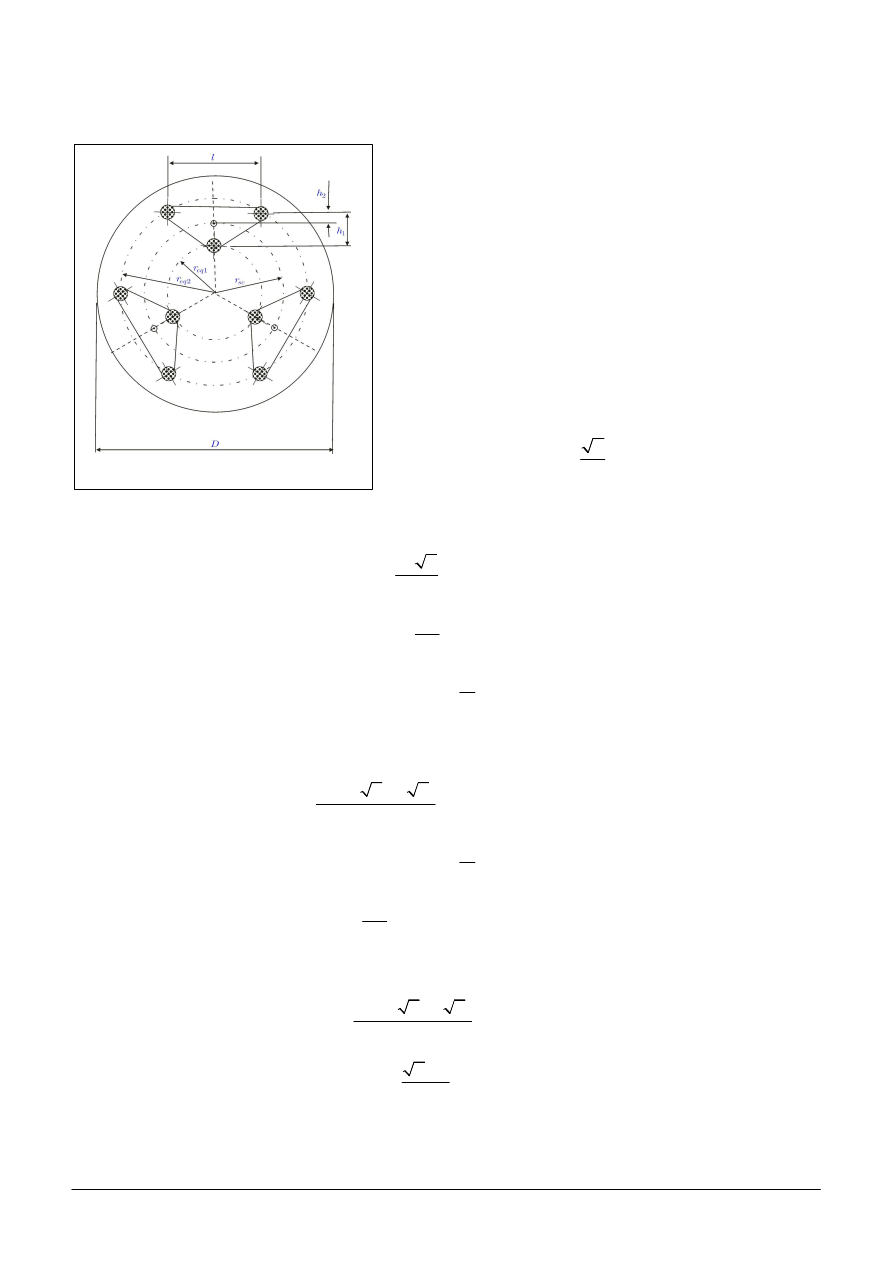
Osiemnastopunktowa oprawa jest swojego rodzaju
uk adem dwupi trowym, powsta ym z po czenia ze
sob mechanizmu opraw 6 – i 9 – punktowych. Jest tu
6 podporowych trójek tworz cych trójk ty
równoramienne. Punkty podparcia ka dej takiej trójki
usytuowane s na wierzcho kach metalowego trójk ta,
który w rodku swojej ci ko ci opiera si wahliwie
(na podparciu kulowym) na ko cu symetrycznej d wigni dwuramiennej (rys. 14). D wignie te poprzez
swoje osie obrotu, tak jak poprzednio, opieraj si na p ycie oprawy w 3 miejscach. I tak jak
poprzednio, ci ar zwierciad a jest równomiernie roz
ony na podtrzymuj cych go podparciach, które
same na bie co dopasowuj si do kszta tu p yty szklanej, natomiast ca
w ko cowym efekcie
Rys. 11
Rys. 12
„URANIA — Post py Astronomii”
urania.pta.edu.pl/science.html
4
Poradnik Konstruktora Teleskopu
–
Oprawa lustra g ównego. Cz. III
opiera si na 3 punktach, co jest idea em stateczno ci. Same punkty podparcia maj we wszystkich
powy szych oprawach t sam posta , co w oprawie 3 –
punktowej.
Oprócz wy ej wymienionych, stosowane jest te
poszerzone oparcie 6 – punktowe. Podpory maj tu
posta talerzyków wahliwie osadzonych na ko cach
wigni równoramiennej (rys. 15). Jest to w pewien
sposób rozwi zanie po rednie mi dzy podparciem 6 –, a
9 – punktowym.
Rozmieszczenie w
owych punktów konstrukcji
mechanicznej opraw, okre laj nast puj ce formu y:
Oparcie 6 punktowe (rys. 12)
(8)
Oparcie 9 punktowe (rys. 13)
2
1
1
1
3
, 0.866
2
×
=
=
-
=
× -
eq
eq
eq
l
l
r
h
r
l r
(9)
1
1
1
1
2
0.666
3
=
+
=
+
sc
eq
eq
h
r
r
r
h
(10)
1
2
3
= h
h
(11)
Oparcie 18 punktowe (rys. 14)
2
1
1
2
1
( 6
2)
0.966
4
×
+
=
-
=
-
eq
eq
eq
eq
r
h
r
r
r
(12)
1
2
3
= h
h
(13)
1
1
1
1
2
0.666
3
=
+
=
+
×
sc
eq
eq
h
r
r
r
h
(14)
1
2
=
sc
l
r
(15)
2
2
2
( 6
2)
0.517
2
×
-
=
=
×
eq
eq
r
l
r
(16)
1
1
1
3
0.866
2
×
=
=
×
sc
l
r
l
(17)
Rys. 13
3
, 0.866
2
eq
sc
eq
eq
l
r
r
r
r
=
=
=
×
„URANIA — Post py Astronomii”
urania.pta.edu.pl/science.html
Poradnik Konstruktora Teleskopu
–
Oprawa lustra g ównego. Cz. III
5
Je li promienie okr gów równowagi maj d ugo ci ustalone wed ug wskaza Yodera, to jak ju
by o wspomniane, warto ci
1
eq
r
i
sc
r
nie koresponduj tutaj ci le z geometri okre laj
equilibrium
pomi dzy polami wewn trz
.
sc
r
Przyj cie takiego ma ego odst pstwa powoduje, e przy
symetrycznym rozstawieniu zewn trznych punktów podparcia, trójk ty w 18 – punktowej oprawie s
równoboczne. Wp yw zag bienia w zwierciadle lub ewentualnego otworu w jego rodku jest
pomini ty.
Lucjan Newelski
Tomasz Krzyt
Rys. 14
Rys. 15
Document Outline
Wyszukiwarka
Podobne podstrony:
OPRAWA LUSTRA GŁÓWNEGO CZ 1
OPRAWA LUSTRA GŁÓWNEGO CZ 2
OPRAWA LUSTRA GŁÓWNEGO CZ 1
OPRAWA LUSTRA GŁÓWNEGO CZ 2
OPRAWA LUSTRA GŁÓWNEGO CZ 1
OPRAWA LUSTRA GŁÓWNEGO CZ 3
Oprawa lustra
Konstrukcja więźby dachowej nawy głównej kościoła ss wizytek w Warszawie, cz 2
Konstrukcja więźby?chowej nawy głównej kościoła ss wizytek w Warszawie, cz 4
Poziomy i podpoziomy, Poziomy główne dzieli się na poziomy główne organiczne, zawierające powyżej 20
Konstrukcja więźby dachowej nawy głównej kościoła ss wizytek w Warszawie, cz 4
Konstrukcja więźby?chowej nawy głównej kościoła ss wizytek w Warszawie, cz 3
Konstrukcja więźby dachowej nawy głównej kościoła ss wizytek w Warszawie, cz 3
Konstrukcja więźby?chowej nawy głównej kościoła ss wizytek w Warszawie, cz 2
Konstrukcja więźby dachowej nawy głównej kościoła ss wizytek w Warszawie, cz 2
więcej podobnych podstron