Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

Projekt nr 3

Charakterystyki aerodynamiczne samolotu

3.1 Uwagi wstępne

Wyznaczenie charakterystyk aerodynamicznych całego samolotu wymaga uwzględnienie sił
i momentów aerodynamicznych pochodzących od pozostałych (poza płatem) elementów
samolotu. Na wstępnym etapie analizy aerodynamiki samolotu wystarcza zwykle
uwzględnienie podzespołów największych pod względem wymiarów oraz tych, których
usytuowanie lub kształt generuje siły o znaczących wartościach. Do podzespołów tych należą:

 kadłub samolotu,
 usterzenie poziome i pionowe,
 gondole silnikowe i chłodnice zespołu napędowego,
 owiewki kabiny załogi,
 podwozie,
 zastrzały skrzydeł i stateczników,
 anteny,
 uzbrojenie zewnętrzne.

Badania na modelach samolotów pokazują, że z wystarczającą dokładnością siłę nośną, siłę
oporu i moment aerodynamiczny całego samolotu wyznaczyć można jako skalarne sumy sił
i momentu pochodzące od poszczególnych podzespołów:

Dzieląc obie strony powyższych sum odpowiednio przez

otrzymujemy wyrażenia na bezwymiarowe współczynniki aerodynamiczny sił i momentu:

Współczynniki C

xj

, C

zj

oraz C

mAj

są współczynnikami aerodynamicznymi poszczególnych

podzespołów samolotu, zaś S

j

jest polem powierzchni odniesienia a l

j

długością

charakterystyczną używanymi przy wyznaczaniu danego współczynnika. Opory podzespołów
samolotu innych niż płat nośny noszą nazwę oporów szkodliwych samolotu.

Dla celów niniejszych ćwiczeń projektowych współczynniki oporu podzespołów samolotu
(oprócz usterzenia poziomego) należy wyznaczyć dla kąta natarcia odpowiadającego zerowej
sile nośnej. Należy również pominąć wyznaczanie współczynników momentów podłużnych
podzespołów samolotu, zaś we współczynniku siły nośnej należy uwzględnić tylko składnik
od usterzenia poziomego.

Wyznaczane dalej współczynniki oporu i pola odniesienia poszczególnych podzespołów
samolotu – za wyjątkiem usterzenia poziomego - wpisujemy do tabeli obliczeniowej
(Tabela 3.1).

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-1

,

1







n

j

xj

x

P

P







n

j

zj

z

P

P

1

,







n

j

Ayj

Ay

M

M

1

;

,

*

*

*

2

1

2



V

S



a

c

V

S

*

*

*

*

2

1

2





,

*

1

S

S

C

C

n

j

j

xj

x







,

*

1

S

S

C

C

j

n

j

zj

z







.

*

*

*

1

a

j

j

n

j

mAj

mA

c

S

l

S

C

C







Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

3.2. Współczynniki oporu aerodynamicznego podzespołów samolotu

A. Kadłub
A.1 Kadłub opływowy
Badania szeregu kadłubów pokazały, że dla kadłubów opływowych, dobrze dopracowanych
aerodynamiczne (współczesne szybowce, samoloty sportowe z zakrytą kabiną i z silnikami
rzędowymi lub płaskimi, odrzutowce wojskowe, samoloty pasażerskie) współczynnik oporu
kadłuba dla kątów natarcia bliskich zeru można wyznaczyć z następującej zależności [7]:

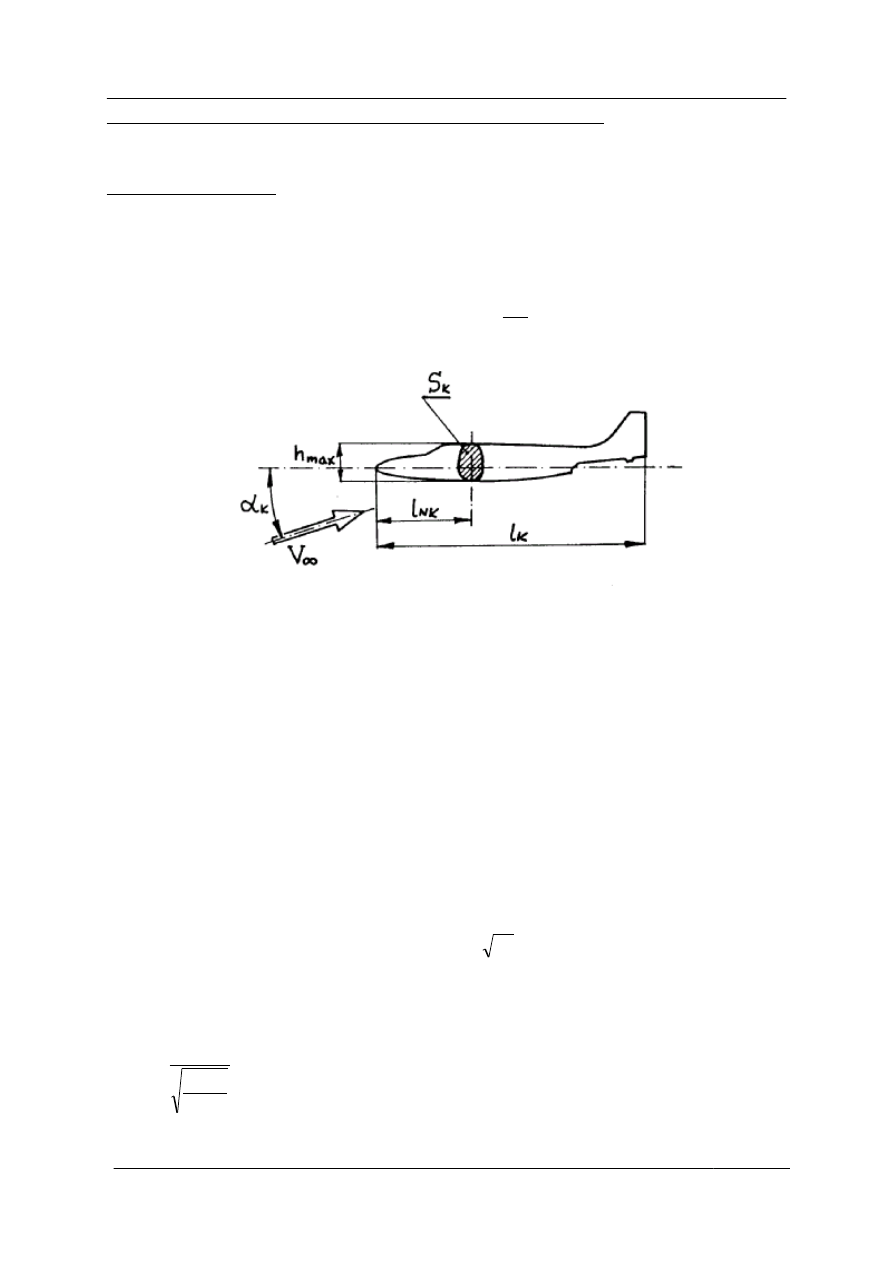
gdzie (oznaczenia wielkości geometrycznych według rys. 3.1):

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-2

(3.1)

,

*

*

*

k

ck

Ma

k

f

xk

S

S

c

C







,

*

*

85

.

2

k

k

ck

S

l

S



ck

S

-pole powierzchni zewnętrznej kadłuba omywanej przez powietrze; ze względu na
trudności obliczeniowe, jakie wystąpiłyby przy próbie obliczenia wartości tego pola
(brak dokładnych rysunków geometrii kadłuba), pole to wyznaczyć można
z przybliżonej zależności:

Ma



-współczynnik uwzględniający wpływ ściśliwości powietrza na opór kadłuba, dany
na rys. Z.69 jako funkcja liczby Macha Ma oraz wydłużenia nosowej części kadłuba


nk

,

k



-współczynnik uwzględniający wpływ kształtu kadłuba na opór, dany na rysunku
Z.68 [2] jako funkcja wydłużenia kadłuba



k

,

f

c

-współczynnik oporów tarcia wynikającego z omywania powierzchni kadłuba przez
powietrze; wyznaczyć go należy z rysunku Z.67 [2] dla liczby Reynoldsa kadłuba
Re

k

,

-pole maksymalnego przekroju czołowego kadłuba mierzone w płaszczyźnie
prostopadłej do osi geometrycznej kadłuba (osi symetrii bryły obrotowej najlepiej
przybliżającej kształt kadłuba),

k

S



k

k

k

S

l

*

4





-wydłużenie kadłuba,

Rys. 3.1.

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

- wydłużenie nosowej części kadłuba.

l

nk

- długość nosowej części kadłuba, równa odległości maksymalnego

przekroju czołowego kadłuba od nosa kadłuba.

Występujące w powyższych zależnościach liczby podobieństwa hydrodynamicznego
Reynoldsa Re

k

oraz Macha Ma są odpowiednio równe:

Uwaga: Wynik obliczeń współczynnika oporu kadłuba według zależności (3.1) zaleca się porównać z oporami
kadłubów podanych w [2].

A.2 Kadłub nieopływowy
Dla kadłubów nieopływowych, o pękatym kształcie lub z nieosłoniętym silnikiem
gwiaździstym, odkrytą kabiną należy oszacować współczynnik oporu C

xk

posługując się

rysunkami Z.35 i Z.36 [2] lub innymi źródłami wskazanymi przez prowadzącego
projektowanie, wybierając dane dla kadłuba najbardziej zbliżonego kształtem do kadłuba
samolotu analizowanego w projekcie.

A.3 Zakres wartości współczynnika Cx

k

Otrzymana wartość współczynnika Cx

k

nie powinny być mniejsze niż 0.06. Dla opływowych

kadłubów wypadać winna w przedziale od 0.08 do 0.15. Współczynniki oporów kadłubów
starych samolotów, z okresu 1910-1930, miały wartości od 0.1 do 0.3.

Uwaga: Pamiętać należy, jaka jest powierzchnia odniesienia dla współczynnika oporu kadłuba (jest ona
zdefiniowana w źródle danych o współczynniku oporu kadłuba). Zwykle jest to maksymalny przekrój czołowy
bryły kadłuba, łącznie z konturem silnika i owiewką kabiny.

B. Usterzenie poziome.

Opór aerodynamiczny usterzenia poziomego zależy od warunków równowagi podłużnej
samolotu ze względu na występowanie w nim składnika zależnego od kwadratu siły nośnej na
usterzeniu. Załóżmy, że samolot leci symetrycznym lotem poziomym ustalonym z prędkością

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-3

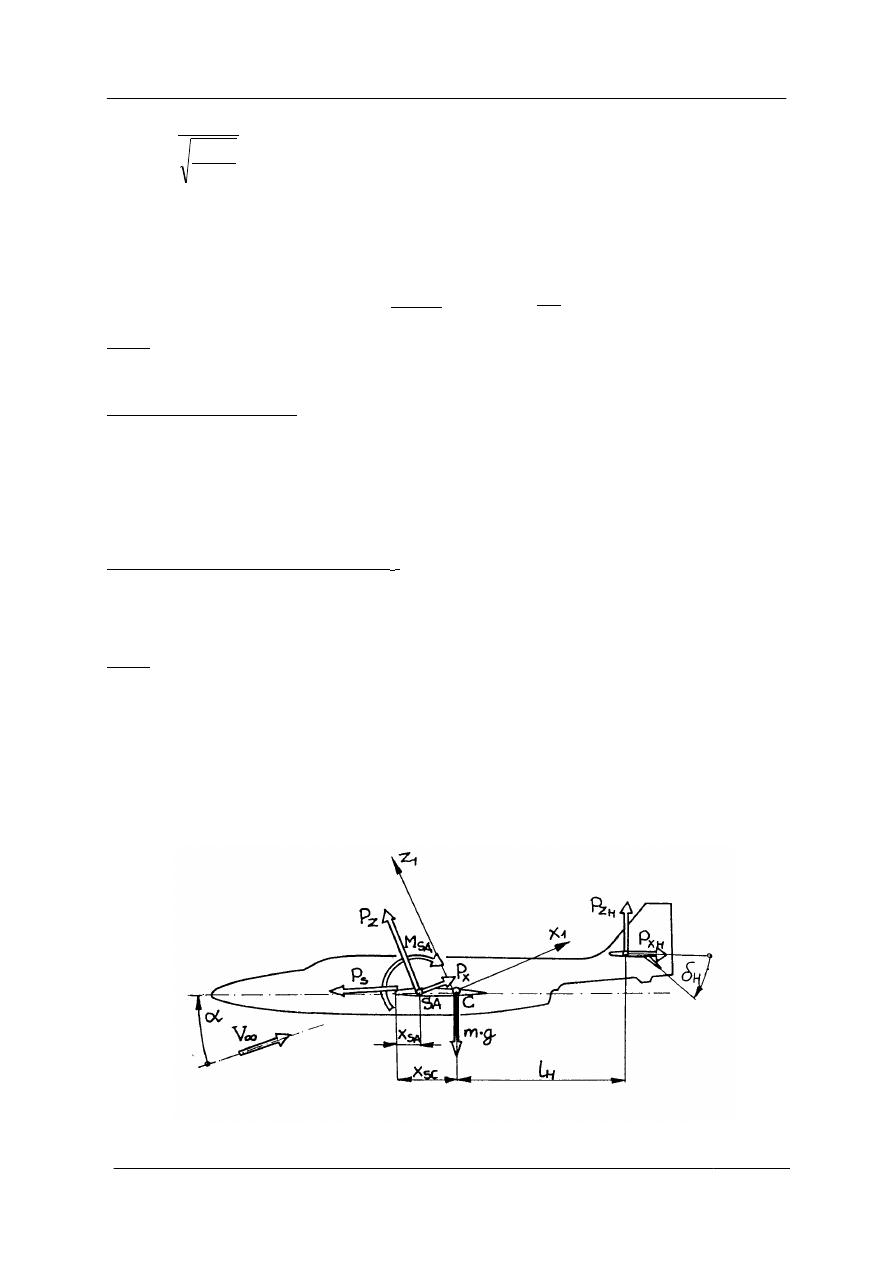
Rys. 3.2.

.

d

a

V

Ma





,

*

Re



k

k

l

V







k

nk

nk

S

l

*

4





Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

V

∞

. Równania równowagi podłużnej (równania sił względem osi x i z oraz równanie

momentów względem osi y) mają przybliżoną postać (rys.3.2, układ x

1

y

1

z

1

z początkiem

w środku masy C; przy rzutowaniu sil na osie Cx

1

y

1

z

1

przyjęto, że kąt natarcia α jest mały

i sinα = 0 oraz cos α =1):

Pz - m * g

= 0

}

Px - Ps

= 0

]>

(3.2)

M

S.A.

+ P

z

* ( x

S.C. -

x

S.A.

) - P

z H

.

* l

H

= 0

}

Ostatnie z równań równowagi (3.2) pozwoli wyznaczyć współczynnik siły nośnej na
usterzeniu wysokości Cz

H

, zapewniający równowagę. Biorąc pod uwagę, iż:

oraz dzieląc obustronnie trzecie z równań (3.2) przez

½**S*V



2

*c

a

otrzymujemy:

gdzie:

- współczynnik momentu podłużnego płata samolotu względem

środka aerodynamicznego płata,

- względne położenie środka aerodynamicznego płata,

- względne położenie środka masy samolotu,

- cecha objętościowa usterzenia poziomego,

- pole powierzchni i ramię usterzenia poziomego (por. rys. 3.2);

ramię usterzenia wysokości jest mierzone od środka masy
samolotu do środka aerodynamicznego usterzenia równolegle do
kierunku cięciwy płata;

- kwadrat stosunku średniej wartości prędkości opływu wokół

usterzenia

wysokości do wartości prędkości opływu

niezaburzonego (równy stosunkowi średniego ciśnienia
dynamicznego opływu na usterzeniu do ciśnienia dynamicznego
opływu niezaburzonego); przyjąć wartości:

•

0.98 dla usterzeń typu T (usterzenie poziome na
stateczniku pionowym),

•

0.90 dla usterzeń usytuowanych pod kadłubem,

•

0.85 dla usterzeń usytuowanych w osi kadłuba.

Ze związku (3.3) można już wyznaczyć wartość współczynnika Cz

H

zapewniającą

równowagę momentów podłużnych względem osi Cy

1

:

Wielkości geometryczne występujące w powyższych zależnościach można odczytać
z rysunków sylwetki samolotu. Położenie środka masy winno być podane w danych
technicznych samolotu. Jeżeli danych takich jest brak, to wielkość x

S.C.

/c

a

można założyć,

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-4

H

H

l

S ,

.

*

'

.

.

.

.

'

.

.

Cz

x

x

Cm

Cz

H

A

S

C

S

H

A

S

H











(3.4)

M

S . A .

=

1
2

∗

ρ∗S∗V

∞

2

∗

C

mS . A .

∗

c

a

,

P

x

=

1

2

∗

ρ∗S∗V

∞

2

∗

C

x .

,

P

z

=

1
2

∗

ρ∗S∗V

∞

2

∗

C

z .

,

x

S.C.

=

x

S.C.

c

a

.

.A

S

Cm

x

S.A.

=

x

S.A.

c

a

2

'

*

*

*



















V

V

c

S

l

S

H

a

H

H

H



2

















V

V

H

H

H

A

S

C

S

A

S

Cz

x

x

Cz

Cm

*

)

(

*

.

.

.

.

.

.

 







)

3

.

3

(

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

przyjmując np. wartość 0.28. Jako wartości współczynnika momentu podłużnego Cm

S.A.

oraz

położenie środka aerodynamicznego x

S.A.

można przyjąć takie, jak dla płata pomijając tym

samym wpływy pozostałych podzespołów samolotu. Pamiętać jednak przy tym należy, że jest
to postępowanie przybliżone i że w dalszych projektach poświęconych zagadnieniom
podłużnej równowagi, stateczności i sterowności wyznaczanie momentów podłużnych
samolotu wykonane zostanie znacznie dokładniej.
Współczynnik oporu usterzenia poziomego, analogicznie jak dla płata nośnego, wyznaczamy
ze związku:

gdzie :

C. Usterzenie pionowe
W locie symetrycznym usterzenie pionowe opływane jest symetrycznie, zaś ster kierunku nie
jest wychylony, zatem współczynnik oporu usterzenia pionowego nie zawiera oporu
indukowanego i wynosi (oznaczenia analogiczne jak dla usterzenia poziomego):

Uwaga. W przypadku braku danych o typie profili usterzeń poziomego i pionowego analizowanego
samolotu można przyjąć, że dla samolotów o prędkości maksymalnej lotu poziomego nie
przekraczającej 360 km/godz. jest to profil NACA 0012, zaś dla samolotów szybszych – profil
NACA 0009.
Polem powierzchni odniesienia S

V

jest – analogicznie do płata nośnego – pole rzutu obrysu usterzenia

pionowego na płaszczyznę symetrii samolotu.

D. Inne elementy samolotu
Wartości współczynników oporu pozostałych elementów samolotu należy wyznaczyć na
podstawie badań tunelowych modeli zamieszczonych np. w [2] rysunki Z.37 do Z.55.

Tabela 3.1

L.p.

Podzespół

Cx

j

S

j

Cx

j

*S

j

Źródło danych

1

Kadłub

2

Owiewka kabiny

3

Usterzenie pionowe

4

Podwozie

5

Owiewka silnika

6

Zewnętrzne zbiorniki paliwa

.....

.........

n

Cx

j

*S

j

Uwaga: w niektórych źródłach danych zamiast wartości współczynników oporu części samolotu oraz pola
powierzchni odniesienia związanej z tym współczynnikiem podane są wartości siły oporu P

x j

zmierzonej

w tunelu aerodynamicznym oraz informacje dotyczące pomiaru: prędkość lub ciśnienie dynamiczne

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-5





min



H

Cx

-minimalna wartość współczynnika oporu profilu usterzenia,

szcz

Cx



-przyrost współczynnika oporu profilowego wynikający z istnienia szczelin
między statecznikiem a sterem oraz między sterem a klapką wyważającą;
przyjąć wartość od 0.0040 do 0.0060;

H

H

H

eH

e

S

b

*

2





-wydłużenie usterzenia poziomego skorygowane o wpływ obrysu
usterzenia i szczelin między statecznikiem a sterem; wartość e

H

przyjąć równą od 0.7 (stateczniki o małym wydłużeniu) do 0.9.





,

*

2

min

eH

H

szcz

H

H

Cz

Cx

Cx

Cx















(3.5)





,

min

Vszcz

V

V

Cx

Cx

Cx









 

6

.

3

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

w przestrzeni pomiarowej tunelu oraz gęstość powietrza; w tym przypadku należy wyznaczyć tylko wartość C

x j

S

j

posługując się oczywistą zależnością

C

x j

⋅

S

j

=

P

x j

1
2

⋅⋅

V

2

.

3.3. Opory szkodliwe samolotu
Na podstawie danych zgromadzonych w Tabeli 3.1 wyznaczamy sumę

Cx

j

*S

j

, a na jej

podstawie minimalną wartość współczynnika oporów szkodliwych:

Wpływ kąta natarcia na opór szkodliwy samolotu uwzględnić można przyjmując
liniową zależność od współczynnika siły nośnej w postaci:

gdzie:

ζ - współczynnik proporcjonalności zamian oporów szkodliwych; do obliczeń

przyjąć wartości w zakresie od 6.0 dla samolotów o dobrze opracowanej
sylwetce (wojskowe samoloty odrzutowe, odrzutowe samoloty pasażerskie,
współczesne samoloty sportowe) do 3.0 (samoloty rolnicze, samoloty
wielozadaniowe z zastrzałami, podwieszeniami).

3.4 Współczynnik oporu kompletnego samolotu
Badania tunelowe modeli samolotu oraz badania samolotów w locie pokazują, że opór całego
samolotu zwykle bywa większy, niż suma oporów poszczególnych jego podzespołów.
Ów dodatkowy opór, będący wynikiem niekorzystnego oddziaływania podzespołów na siebie
nosi nazwę oporu interferencyjnego. Zjawisko to uwzględnić należy przyjmując zależność na
współczynnik oporu kompletnego samolotu w postaci:

gdzie:

Cx

’

p

- współczynnik oporu płata,

Cx

’

szk

- współczynnik oporów szkodliwych wg (3.8),

K

interf

- współczynnik wzrostu oporów na skutek interferencji aerodynamicznej;

przyjąć odpowiednio wartość:

•

0.02 dla odrzutowców

•

0.04 dla samolotów śmigłowych o dobrze dopracowanej sylwetce

•

0.06 do 0.15 dla pozostałych samolotów.

Obliczenia współczynnika oporu samolotu wykonać należy wykorzystując Tabelę 2.2
Projekt nr 2.

3.4 Współczynnik siły nośnej samolotu

Zgodnie z założeniami uwzględnić należy wpływ siły nośnej na usterzeniu wysokości na siłę
nośną całego samolotu. Współczynnik siły nośnej samolotu wyniesie zatem:

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-6

(3.8)

C

x szk

'

=



C

x szk



min

⋅



1

∣

C

z

∣





,





S

S

Cx

Cx

n

j

j

j

szk







1

min

*

 

7

.

3





erf

H

H

szk

p

K

Cx

S

S

Cx

Cx

Cx

int

'

'

1

*

*





















 

9

.

3

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

Obliczenia współczynnika siły nośnej na usterzeniu wysokości i dla całego samolotu
wykonać należy wykorzystując Tabelę 2.2 (Projekt nr 2).

3.5 Charakterystyki aerodynamiczne samolotu
Oprócz wartości współczynnika oporu i współczynnika siły nośnej obliczamy dodatkowo
dwie inne charakterystyki aerodynamiczne (wykorzystując również Tabelę 2.2):

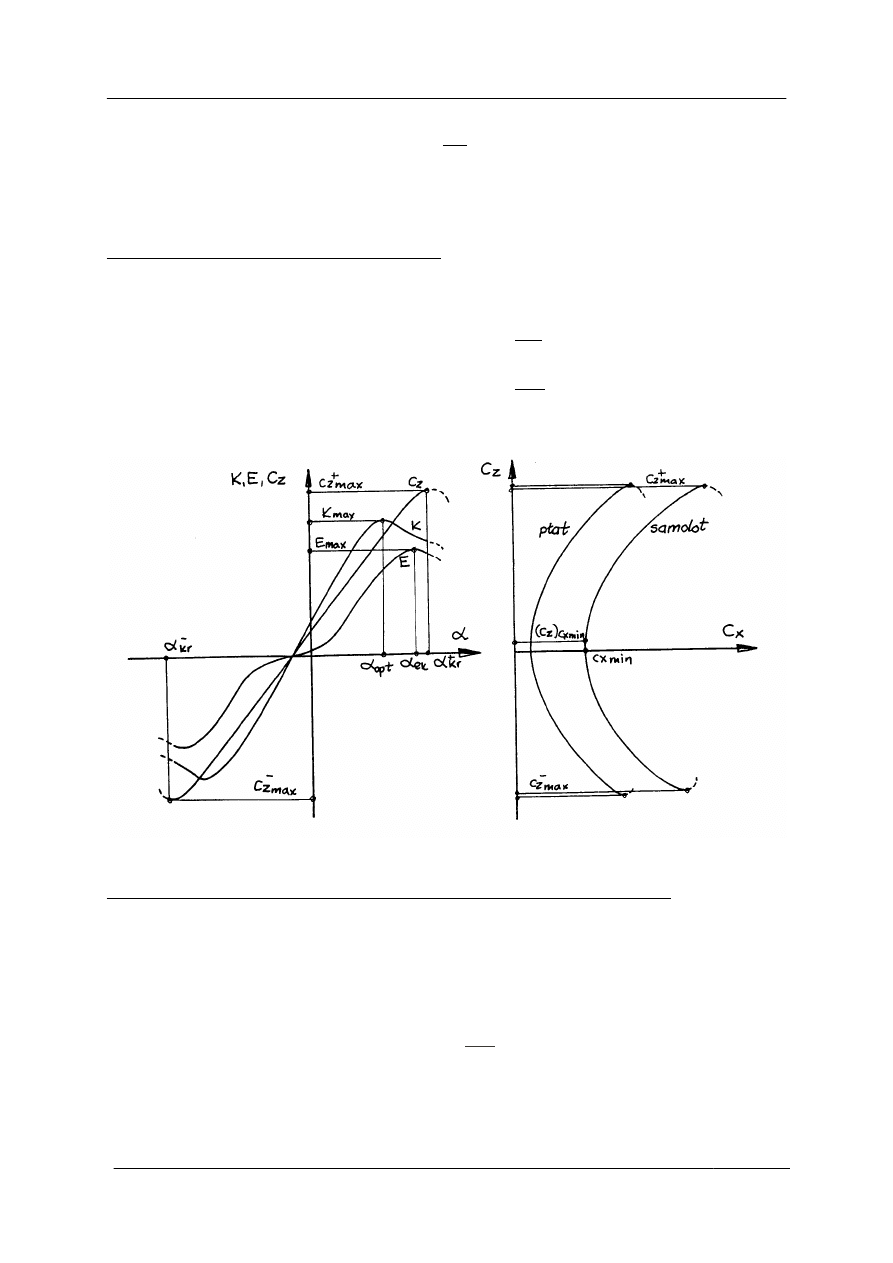
Wyniki obliczeń przedstawiamy na wykresach (rys. 3.3).

3.6 Aproksymacja charakterystyk aerodynamicznych. Biegunowa analityczna
W wielu przypadkach, szczególnie wtedy gdy należy szybko wykonać choćby mocno
przybliżone oszacowanie parametrów lotu samolotu, wykorzystuje się przybliżone zależności
na Cz(α), Cx(Cz) czy C

mB.H.

(Cz) w postaci możliwie prostych funkcji elementarnych.

Zależność współczynnika oporu aerodynamicznego samolotu od współczynnika siły nośnej
Cx(Cz) przyjmuje się w postaci niepełnego wielomianu drugiego stopnia (paraboli):

Zależność ta nosi nazwę biegunowej analitycznej. Wartości współczynników aproksymacji
Cx

0

oraz 1/(



e

) należy uzyskać drogą aproksymacji wyznaczonej w projektach 2 i 3

biegunowej „rzeczywistej” Cx(Cz).

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-7

-doskonałość aerodynamiczną

,

'

Cx

Cz

K



.

2

3

'

Cx

Cz

E



-aerodynamiczną funkcję energetyczną

Rys 3.3.

Cx=Cx

0



Cz

2

πΛ

e

,

*

'

H

H

Cz

S

S

Cz

Cz









10

.

3

(3.11)

Λ

e

=

1

π⋅

(

1

π⋅Λ

e

)

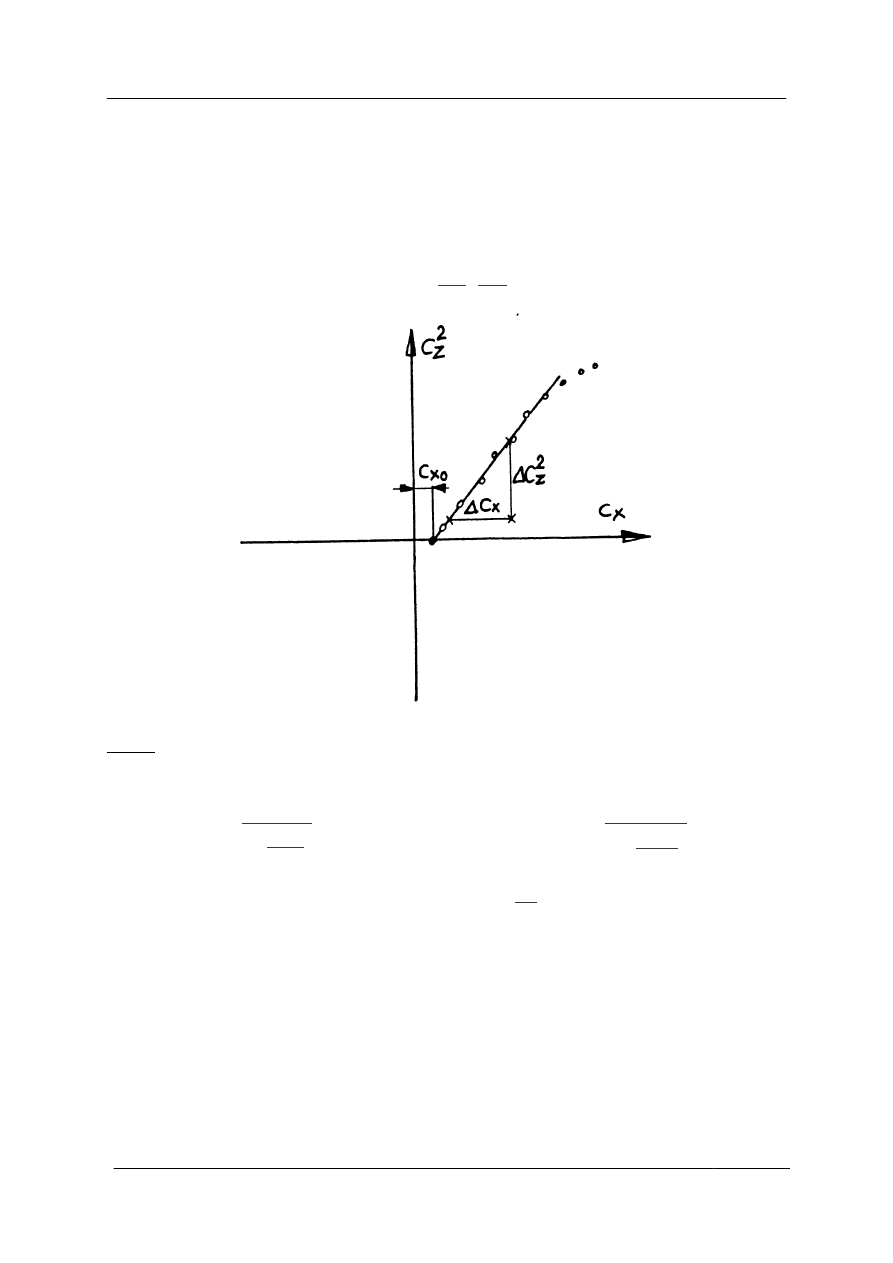
lub (dla metody wykreślno-rachunkowej)

Λ

e

=

1

π∗

(

ΔCx

ΔCz

2

)

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

Wyznaczanie zależności współczynnika momentu podłużnego samolotu C

mB.H.

od kąta

natarcia lub współczynnika siły nośnej wykracza poza zagadnienia osiągów samolotu i będzie
omawiana w drugiej części kursu Mechaniki Lotu.
Aproksymację dyskretnej funkcji Cx(Cz) można wykonać dowolną metodą korzystając
z kalkulatora programowanego i jego wbudowanych funkcji aproksymacji lub też
z mikrokomputera i odpowiedniego oprogramowania (patrz opis projektu nr 2, wyznaczanie
współczynnika a=dC

z

/dα dla profilu i dla płata nośnego). Można również skorzystać z nieco

mniej dokładnej metody wykreślno-rachunkowej, wykonując wykresy zależności Cx(Cz

2

)

(rys. 3.4) i odczytując z nich wartości Cx

0

i .

Uwaga: Otrzymane wartości współczynników aproksymacji należy sprawdzić.

Dla biegunowej analitycznej (3.10) współczynnik stojący przy C

z

2

należy sprawdzić obliczając wartość

wydłużenia efektywnego ze wzoru

i porównując ją z wydłużeniem geometrycznym

. Stosunek (nazywany współczynnikiem Oswalda)

winien znajdować się w zakresie od 0.7 do 0.98.

Współczynnik Cx

0

winien być niemal dokładnie równy wartości minimalnego współczynnika oporu samolotu

(Cx)

min

(por. Tab. 2.2 w Projekcie 2).

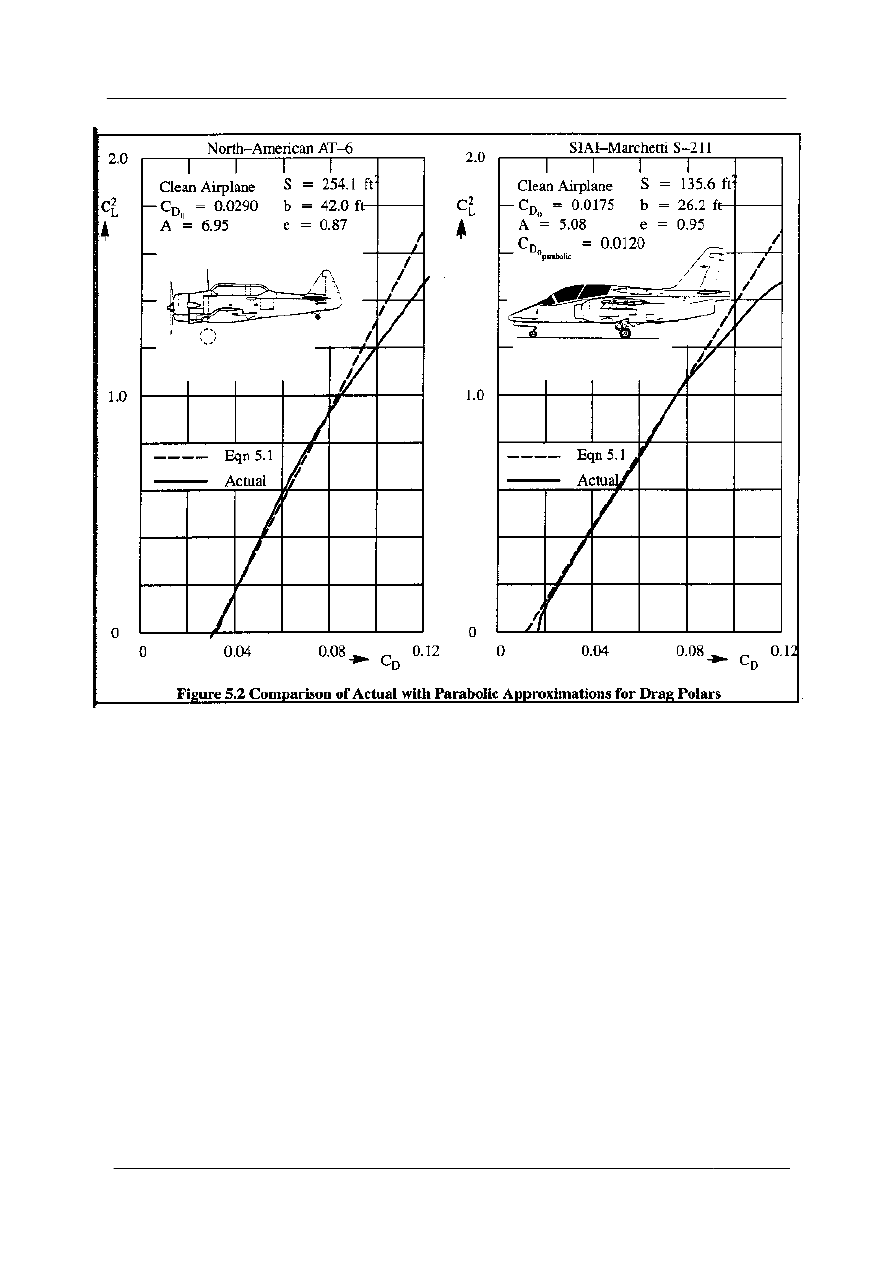
Dwa przykłady [10] ilustrujące wyniki wyznaczania biegunowej analitycznej oraz błędy
aproksymacji rzeczywistych zależności Cx(Cz) pokazano na rysunku 3.5.
Po wyznaczeniu współczynników zależności (3.11) należy sporządzić wykres biegunowej
analitycznej nanosząc ją na wykres wyznaczonej uprzednio dyskretnej biegunowej samolotu.
Istotne różnice między aproksymacją a funkcja dyskretną przy prawidłowo wykonanych
obliczeniach mogą występować jedynie w zakresie dużych kątów natarcia lub w pobliżu
Cz=0 (por. rys. 3.5).

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-8

Rys 3.4

1

π⋅Λ

e

=

ΔCx

Δ Cz

2

e =

Λ

e

Λ

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Mechaniki

[***]

Zbigniew Paturski - Przewodnik po projektach z Mechaniki Lotu , wydanie 5.2

III-9

Rys. 3.5