
DRGANIA
2.1. DRGANIA UKŁADÓW O JEDNYM
STOPNIU SWOBODY
© F.A. Dul 2009
DRGANIA WYMUSZONE
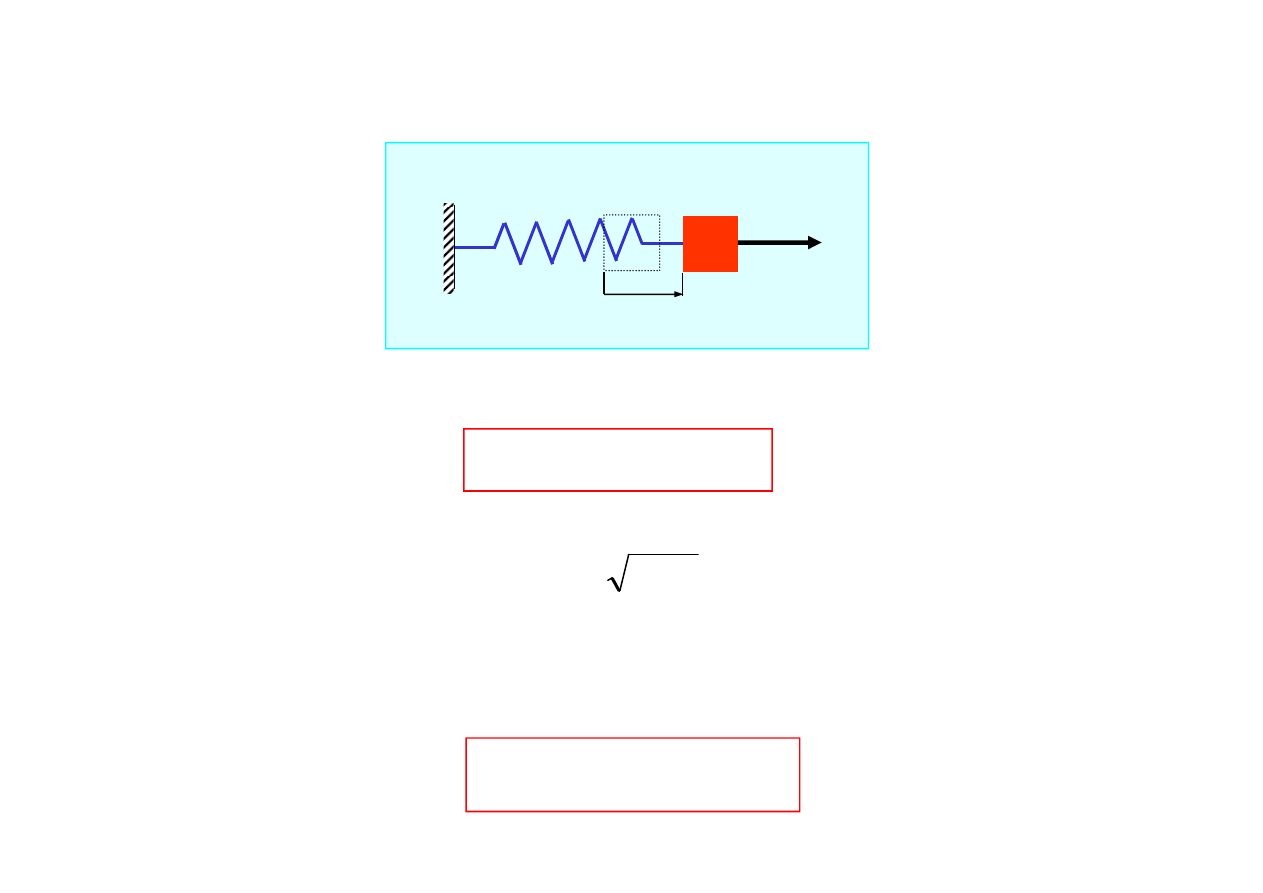
Siła wymuszaj
ą
ca
)
(t
F
Równanie ruchu
)
(t
F
kx
x
m
=
+
&
&
m
k
x(t)
F(t)
2.1.3. Drgania wymuszone nietłumione
)
1
.
3
.
1
.
2
(
© F.A. Dul 2009
Równanie ruchu
)
(t
F
kx
x
m
=
+
&
&
)
1
.
3
.
1
.
2
(
)
(
2
0
t
f
x
x
=
+
ω
&
&
Posta
ć
znormalizowana równania drga
ń
wymuszonych
Cz
ę
sto
ść
drga
ń
własnych układu jest równa
m
k /
0
=
ω
)
2
.
4
.
1
.
2
(
)
3
.
4
.
1
.
2
(
m
t
F
t
f
/
)
(
)
(
=
Wprowadzamy oznaczenie
)
4
.
4
.
1
.
2
(

2.1.3. Drgania wymuszone nietłumione
Je
ż
eli siła wymuszaj
ą
ca jest harmoniczna
)
5
.
4
.
1
.
2
(
)
sin(
)
(
0
t
F
t
F
Ω
=
)
sin(
0
2
0
t
f
x
x
Ω
=
+
ω
&
&
)
6
.
4
.
1
.
2
(
gdzie
Ω
Ω
Ω
Ω
jest cz
ę
sto
ś
ci
ą
siły wymuszaj
ą
cej, a F
0
- jej amplitud
ą
,
to równanie drga
ń
wymuszonych przybiera posta
ć
gdzie
f
0
= F
0
/ m
jest znormalizowan
ą
amplitud
ą
siły wymuszaj
ą
cej.
© F.A. Dul 2009
gdzie
f
0
= F
0
/ m
jest znormalizowan
ą
amplitud
ą
siły wymuszaj
ą
cej.
)
sin(
)
(
0
ϕ
ω
+
=
t
A
t
x
J
Rozwi
ą
zanie równania ruchu układu składa si
ę
z dwóch cz
ęś
ci:
- rozwi
ą
zania ogólnego równania jednorodnego
)
sin(
)
(
ε
+
Ω
=
t
B
t
x
N
- rozwi
ą
zania szczególnego równania niejednorodnego
)
7
.
4
.
1
.
2
(
)
8
.
4
.
1
.
2
(

Rozwi
ą
zanie równania drga
ń
wymuszonych ma zatem posta
ć
)
sin(
)
sin(
)
(
)
(
)
(
0
ε
ϕ
ω
+
Ω
+
+
=
+
=
t
B
t
A
t
x
t
x
t
x
N
J
)
9
.
4
.
1
.
2
(
Ruch układu jest zatem zło
ż
eniem (
superpozycj
ą
) dwóch ruchów:
- ruchu harmonicznego z cz
ę
sto
ś
ci
ą
siły wymuszaj
ą
cej
Ω
Ω
Ω
Ω
,
- ruchu harmonicznego z cz
ę
sto
ś
ci
ą
drga
ń
własnych układu
ω
0.
2.1.3. Drgania wymuszone nietłumione
Po podstawieniu (2.1.4.9) do równania (2.1.4.6) otrzymujemy
© F.A. Dul 2009
Po podstawieniu (2.1.4.9) do równania (2.1.4.6) otrzymujemy
)
sin(
)
sin(
)
(
0
2
2
0
t
f
t
B
Ω
=
+
Ω
Ω
−
ε
ω
2
2
0
0
Ω
−
=
ω
f
B
)
11
.
4
.
1
.
2
(
Je
ż
eli
Ω
Ω
Ω
Ω
≠ ω
0
to faza
εεεε
jest równa
za
ś
amplituda B jest równa
,
gdy
,
gdy
0
0
0
ω
π
ε
ω
ε
>
Ω
−
=
<
Ω
=
)
10
.
4
.
1
.
2
(
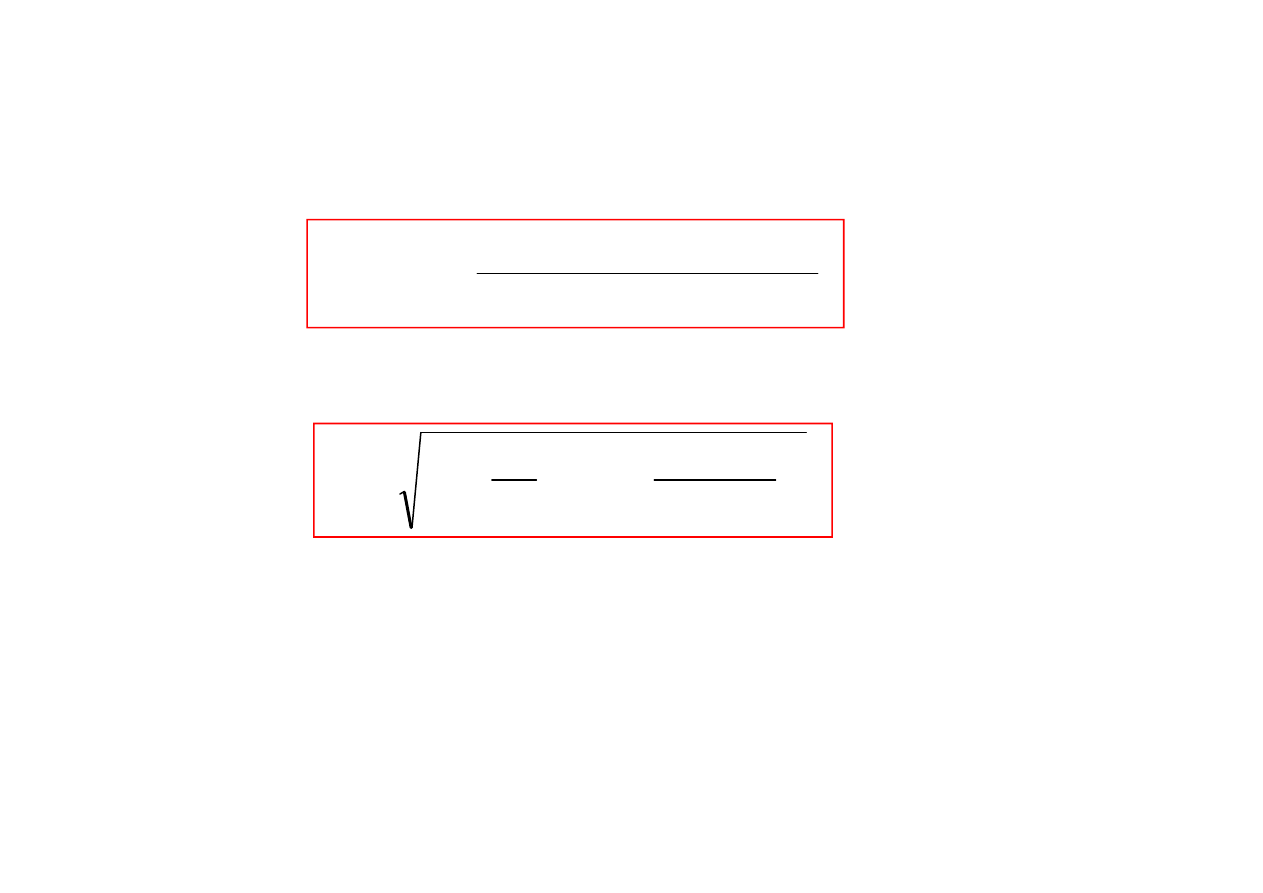
Stałe A oraz
ϕϕϕϕ
wyznaczamy z warunków pocz
ą
tkowych
2.1.3. Drgania wymuszone nietłumione
ε
ω
ω
ω
ϕ
cos
)v
(
)
(
tg
0
0
2
2
0
2
2
0
0
0
f
x
arc
Ω
−
Ω
−
Ω
−
=
Je
ż
eli
Ω
Ω
Ω
Ω ≠≠≠≠ ω
ωω
ω
0
to faza pocz
ą
tkowa
ϕϕϕϕ
jest równa
za
ś
amplituda
cos
1
ε
f
)
12
.
4
.
1
.
2
(
© F.A. Dul 2009
2
2
2
0
0
0
2
0
2
0
)
cos
v
(
1
Ω
−
Ω
−
+
=
ω
ε
ω
f
x
A
)
13
.
4
.
1
.
2
(
Gdy
f
0
= 0
to powy
ż
sze wzory redukuj
ą
si
ę
do wzorów dla drga
ń
swobodnych nietłumionych.
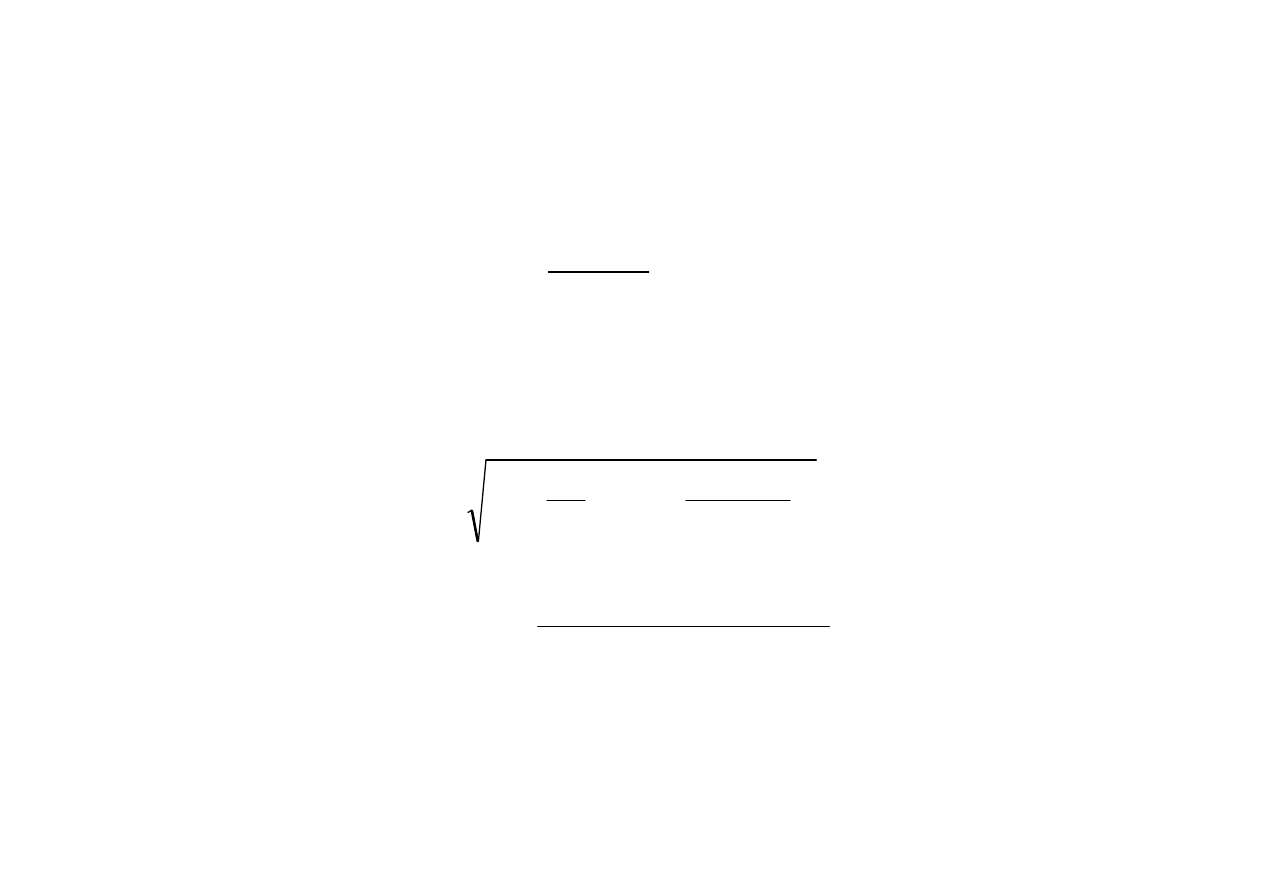
Zauwa
ż
my równie
ż
,
ż
e:
- ruch harmoniczny z cz
ę
sto
ś
ci
ą
siły wymuszaj
ą
cej
Ω
Ω
Ω
Ω
nie zale
ż
y od
warunków pocz
ą
tkowych,
- ruch harmoniczny z cz
ę
sto
ś
ci
ą
drga
ń
własnych układu
ω
0
zale
ż
y od
warunków pocz
ą
tkowych i siły wymuszaj
ą
cej,
2
2
0
0
Ω
−
=
ω
f
B
2.1.3. Drgania wymuszone nietłumione
© F.A. Dul 2009
- przy odpowiednim dobraniu warunków pocz
ą
tkowych ruch
z cz
ę
sto
ś
ci
ą
drga
ń
własnych układu
ω
0
nie wyst
ą
pi.
ε
ω
ω
ω
ϕ
cos
)v
(
)
(
tg
0
0
2
2
0
2
2
0
0
0
f
x
arc
Ω
−
Ω
−
Ω
−
=
2
2
2
0
0
0
2
0
2
0
)
cos
v
(
1
Ω
−
Ω
−
+
=
ω
ε
ω
f
x
A

Rozwa
ż
my ruch układu spowodowany wył
ą
cznie sił
ą
wymuszaj
ą
c
ą
Mo
ż
na zauwa
ż
y
ć
,
ż
e:
• drgania wymuszone s
ą
zgodne w fazie
z sił
ą
wymuszaj
ą
c
ą
,
)
sin(
)
(
2
2
0
0
ε
ω
+
Ω
Ω
−
=
t
f
t
x
)
14
.
4
.
1
.
2
(
,
gdy
0
0
ω
ε
<
Ω
=
)
15
.
4
.
1
.
2
(
• drgania wymuszone s
ą
w fazie przeciwnej
do siły wymuszaj
ą
cej,
⇒
Ω
=
)
sin(
)
(
0
t
F
t
F
2.1.3. Drgania wymuszone nietłumione
© F.A. Dul 2009
0
gdy
ω
π
ε
>
Ω
−
=
• drgania wymuszone s
ą
w fazie przeciwnej
do siły wymuszaj
ą
cej,
)
16
.
4
.
1
.
2
(

2.1.4. Rezonans
W przypadku, gdy cz
ę
sto
ść
siły wymuszaj
ą
cej jest równa cz
ę
sto
ś
ci drga
ń
własnych
0
ω
=
Ω
)
1
.
5
.
1
.
2
(
rozwi
ą
zanie równania niejednorodnego nie mo
ż
e by
ć
wyra
ż
one w postaci
)
sin(
)
(
t
B
t
x
N
Ω
=
±∞
→
⇒
→
Ω
B
0
ω
gdy
ż
amplituda B jest nieokre
ś
lona,
2
2
0
Ω
−
=
ω
f
B
© F.A. Dul 2009
±∞
→
⇒
→
Ω
B
0
ω
Z ogólnej teorii układów liniowych wynika,
ż
e rozwi
ą
zanie ma w takim
przypadku posta
ć
)
2
.
5
.
1
.
2
(
)
sin(
)
(
ε
+
Ω
=
t
Bt
t
x
N
)
sin(
)
cos(
2
0
t
f
t
B
Ω
=
+
Ω
Ω
ε
2
2
0
Ω
−
=
ω
B
Po podstawieniu (2.1.5.2) do równania ruchu (2.1.4.6) otrzymujemy
π
π
ε
ε
n
t
t
2
2
)
sin(
)
cos(
+
−
=
⇔
Ω
=
+
Ω
Z trygonometrii wiadomo,
ż
e
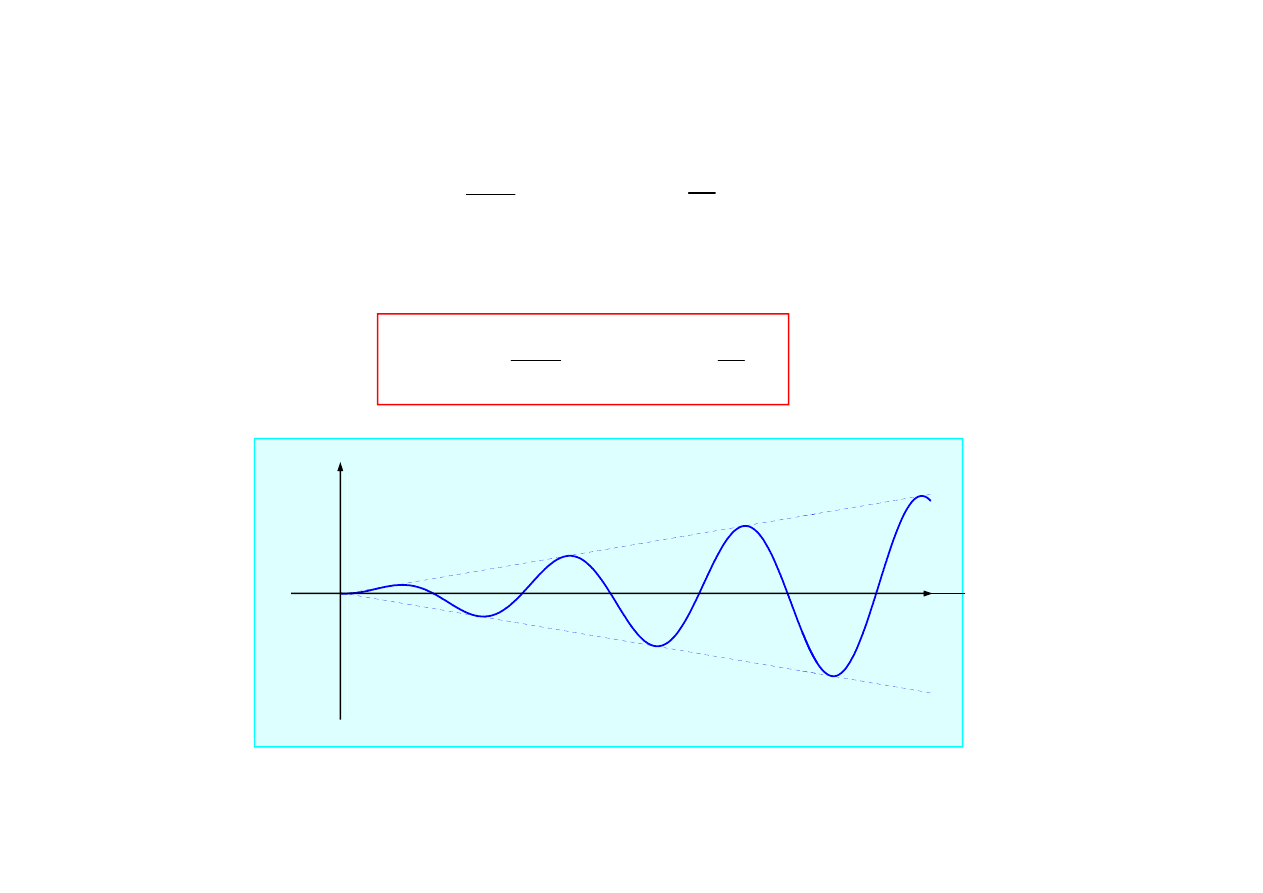
Amplituda i faza rozwi
ą
zania s
ą
zatem równe
Drgania opisane s
ą
wi
ę
c funkcj
ą
)
4
.
5
.
1
.
2
(
)
2
sin(
2
)
(
0
π
−
Ω
Ω
=
t
t
f
t
x
N
2.1.4. Rezonans
2
π
ε
−
=
Ω
=
2
0
f
B
)
3
.
5
.
1
.
2
(
© F.A. Dul 2009
Amplituda drga
ń
ro
ś
nie nieograniczenie.
x(t)
Bt
t
-Bt
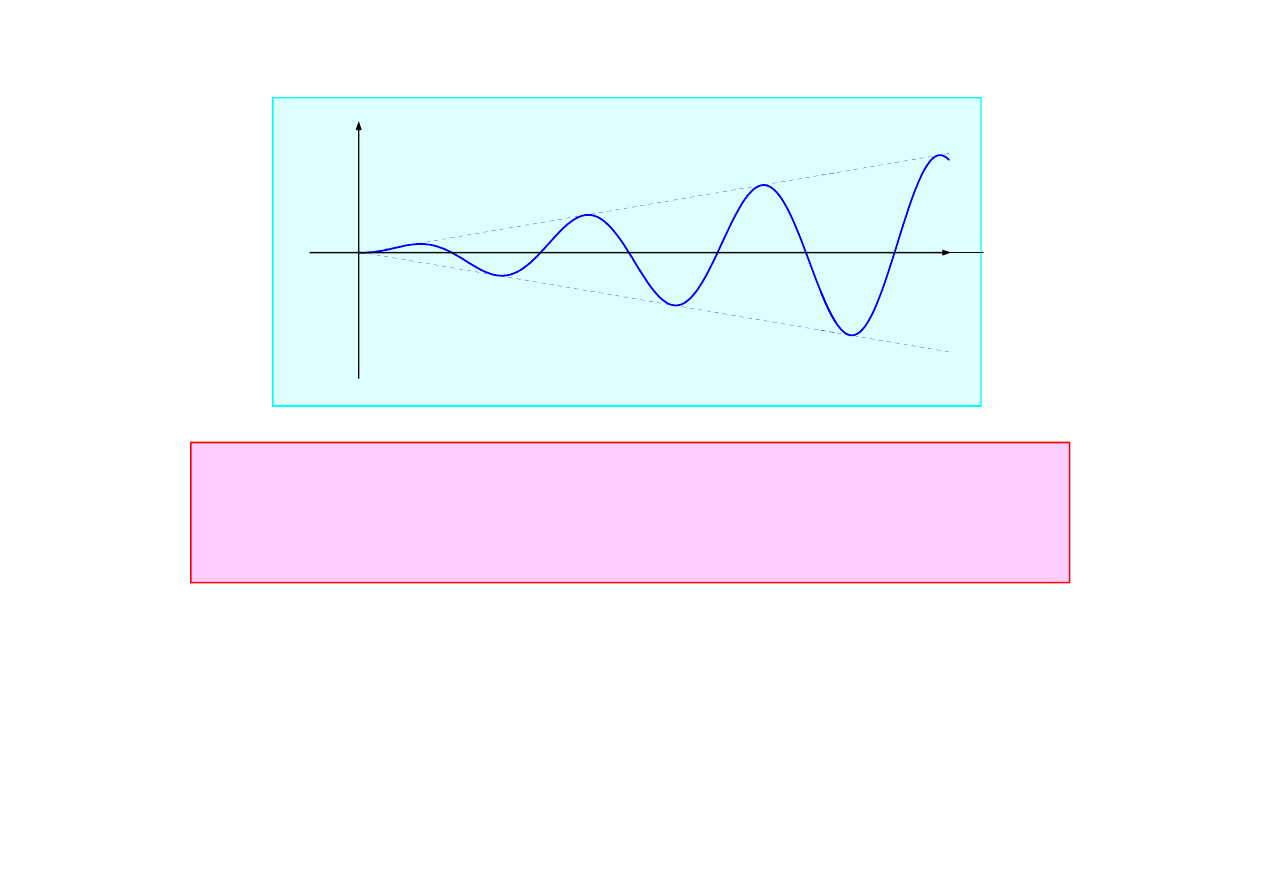
x(t)
Bt
t
-Bt
2.1.4. Rezonans
© F.A. Dul 2009
Zjawisko nieograniczonego wzrostu amplitudy drga
ń
wymuszonych sił
ą
okresow
ą
o cz
ę
sto
ś
ci równej cz
ę
sto
ś
ci
drga
ń
własnych układu nazywamy
rezonansem
.
•
amplituda drga
ń
ro
ś
nie nieograniczenie,
•
przemieszczenie jest opó
ź
nione w fazie w stosunku do siły o
π
/2,
•
przyczyn
ą
wzrostu amplitudy drga
ń
jest dostarczanie energii
do układu przez sił
ę
wymuszaj
ą
c
ą
.
Własno
ś
ci drga
ń
w rezonansie:
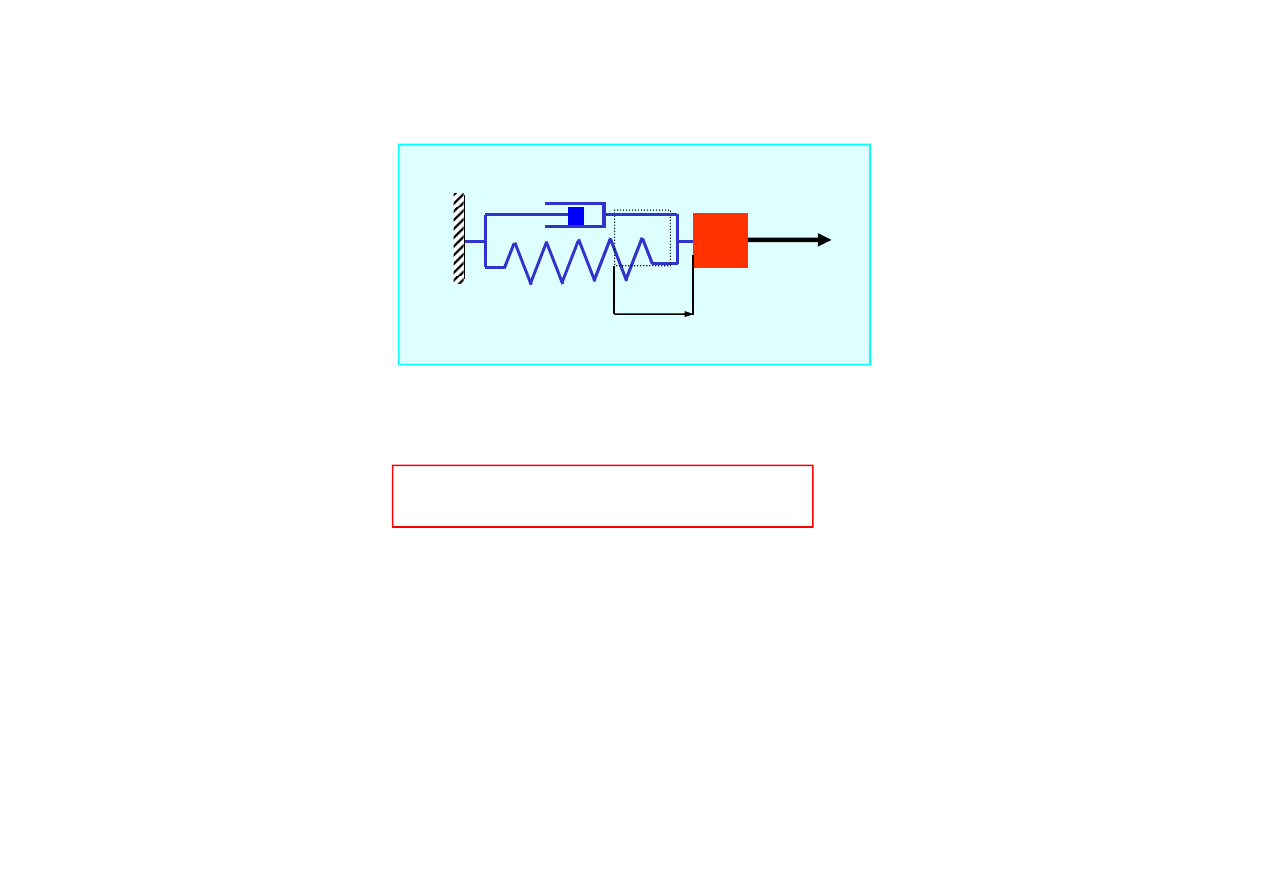
Równanie ruchu
F(t)
m
k
x(t)
c
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
)
(t
F
kx
x
c
x
m
=
+
+
&
&
&
Równanie ruchu
)
1
.
5
.
1
.
2
(
)
(
2
2
0
t
f
x
x
h
x
=
+
+
ω
&
&
&
)
2
.
5
.
1
.
2
(
Równanie ruchu w postaci znormalizowanej
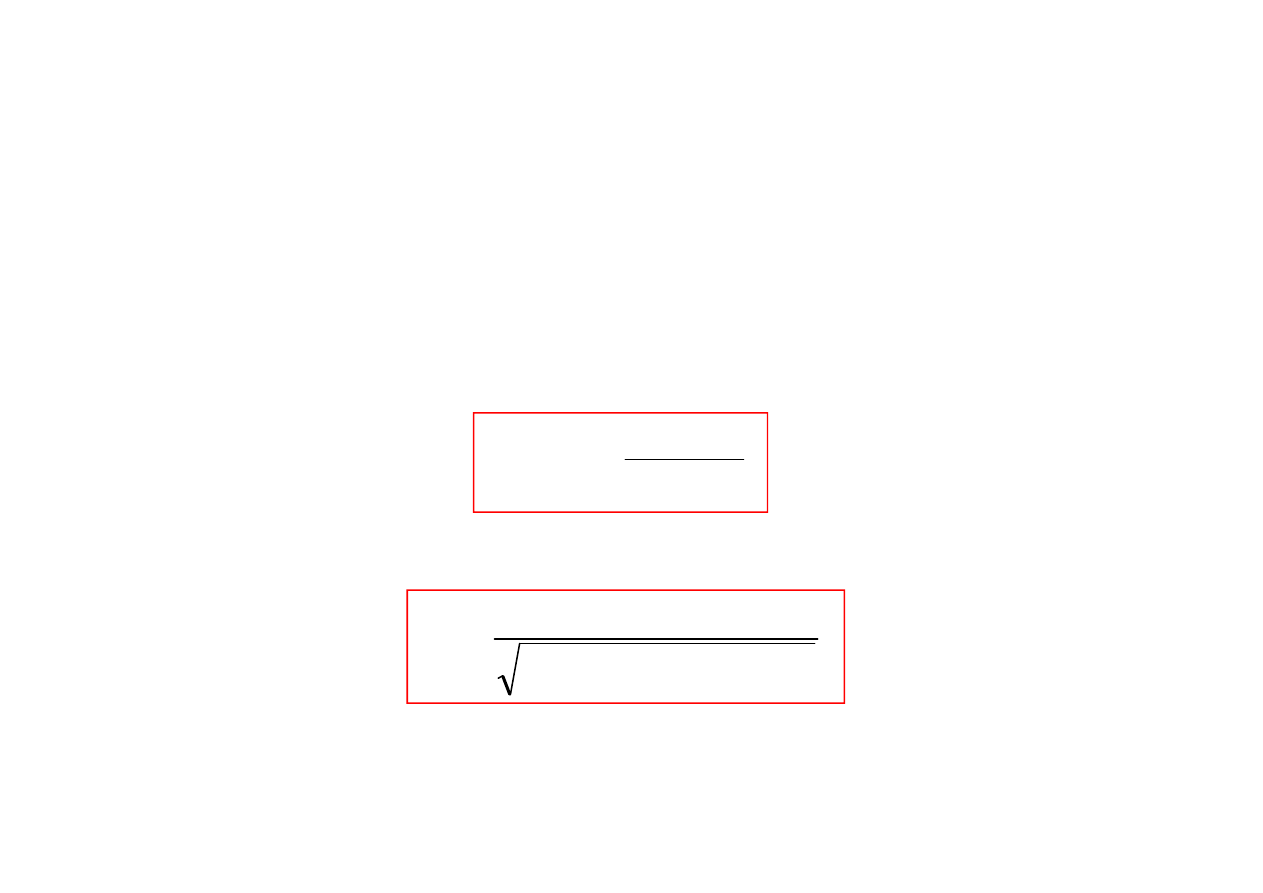
2.1.5. Drgania wymuszone tłumione
Drgania tłumione wymuszone sił
ą
harmoniczn
ą
Równanie ruchu układu z wymuszeniem sił
ą
harmoniczn
ą
)
sin(
2
0
2
0
t
f
x
x
h
x
Ω
=
+
+
ω
&
&
&
)
3
.
5
.
1
.
2
(
)
sin(
)
(
ε
+
Ω
=
t
B
t
x
Przewidujemy rozwi
ą
zanie szczególne równania w postaci
)
4
.
5
.
1
.
2
(
2
tg
Ω
−
=
ε
h
Opó
ź
nienie fazowe przemieszczenia w stosunku do siły wymuszaj
ą
cej
)
5
.
5
.
1
.
2
(
© F.A. Dul 2009
2
2
0
2
tg
Ω
−
Ω
−
=
ω
ε
h
)
5
.
5
.
1
.
2
(
2
2
2
2
2
0
0
4
)
(
Ω
+
Ω
−
=
h
f
B
ω
)
6
.
5
.
1
.
2
(
Amplituda drga
ń
wymuszonych jest zawsze ograniczona i równa
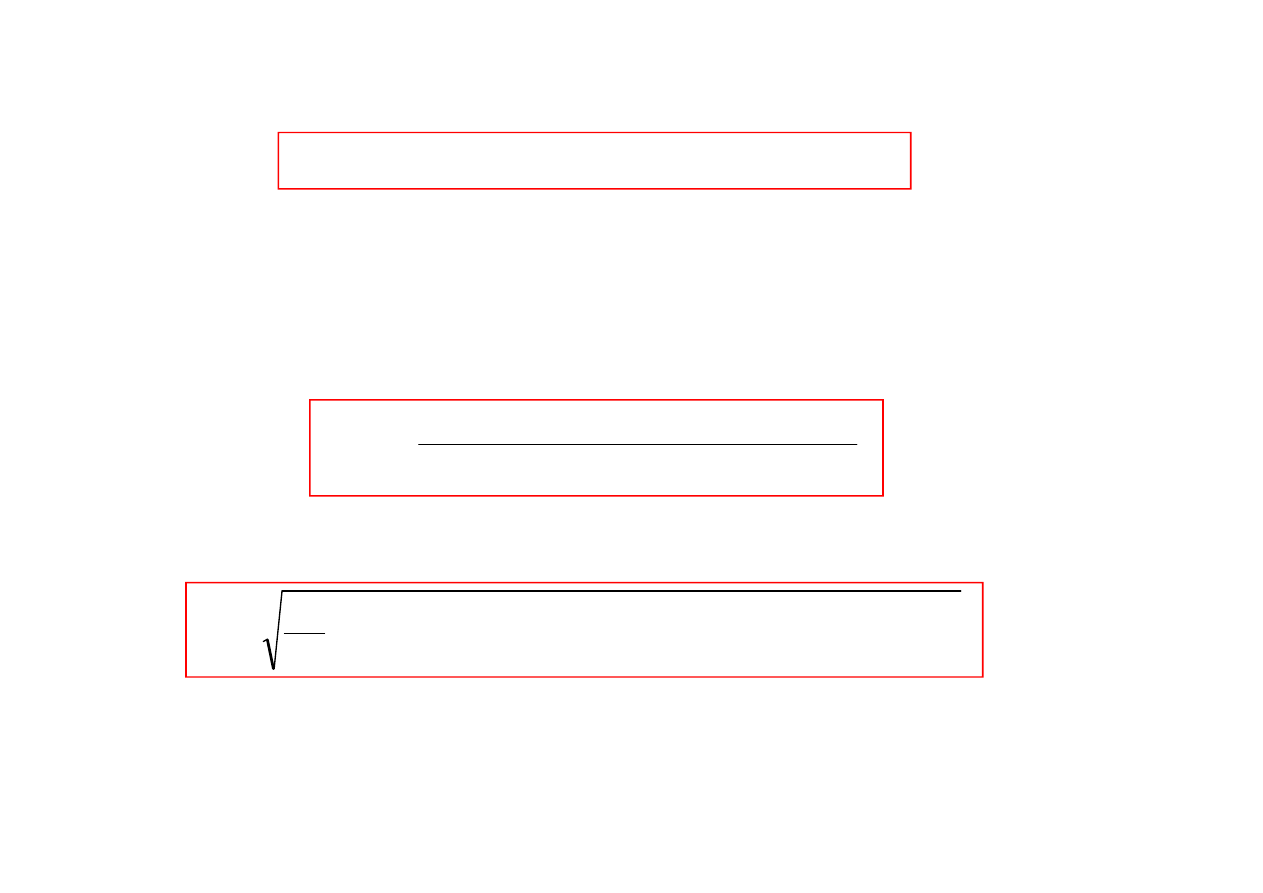
Rozwi
ą
zanie ogólne równania drga
ń
wymuszonych tłumionych ma posta
ć
)
sin(
)
sin(
)
(
ε
ϕ
ω
+
Ω
+
+
=
−
t
B
t
Ae
t
x
ht
0
)
0
(
x
x
=
0
)
0
(
v
=
x
&
Stałe A oraz
ϕϕϕϕ
wyznaczamy z warunków pocz
ą
tkowych
ε
ε
ω
ε
ω
ϕ
)
sin
(
0
B
x
tg
Ω
−
−
+
−
=
Faza drga
ń
wymuszonych tłumionych jest równa
)
7
.
5
.
1
.
2
(
)
8
.
5
.
1
.
2
(
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
ε
ε
ω
ϕ
cos
)
sin
(
v
0
0
B
B
x
h
tg
Ω
−
−
+
=
2
0
2
0
0
2
)
sin
(
]
cos
)
sin
(
[v
1
ε
ε
ε
ω
B
x
B
B
x
h
A
−
+
Ω
−
−
+
=
Amplituda drga
ń
wymuszonych tłumionych jest równa
)
8
.
5
.
1
.
2
(
)
9
.
5
.
1
.
2
(
Amplituda i faza drga
ń
wymuszonych tłumionych s
ą
zale
ż
ne zarówno
od warunków pocz
ą
tkowych jak i od siły wymuszaj
ą
cej.
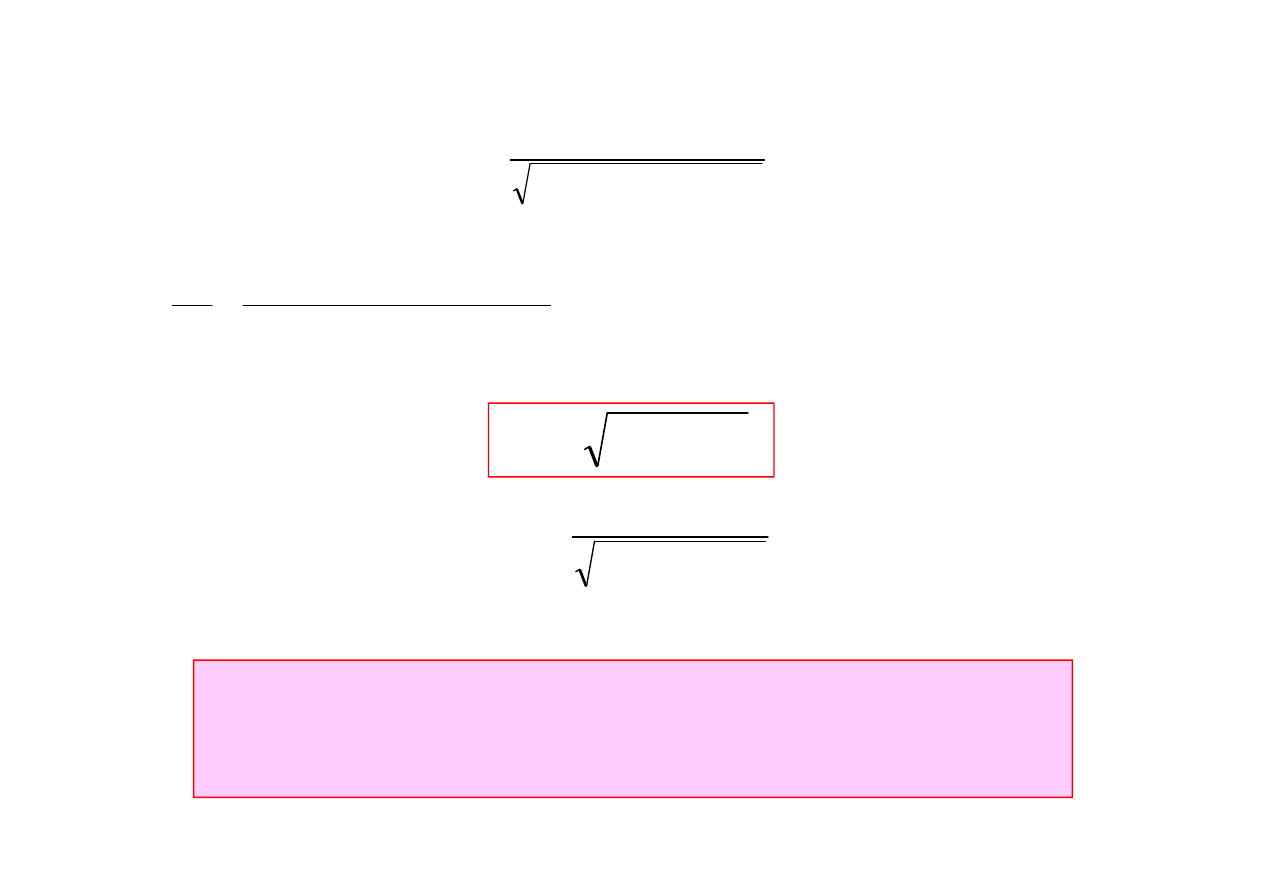
Maksimum amplitudy wyznaczymy z warunku
2
2
2
2
2
0
0
4
)
(
Ω
+
Ω
−
=
h
f
B
ω
Maksymalna warto
ść
amplitudy wyst
ą
pi dla cz
ę
sto
ś
ci siły wymuszaj
ą
cej
0
)
4
)
((
2
)
8
)
(
4
(
2
/
3
2
2
2
2
2
0
2
2
2
0
0
=
Ω
+
Ω
−
Ω
+
Ω
−
Ω
−
=
Ω
h
h
f
d
dB
ω
ω
0
2
)
(
2
2
2
0
=
+
Ω
−
−
⇒
h
ω
2
2
0
2h
−
=
Ω
ω
2.1.5. Drgania wymuszone tłumione
)
6
.
5
.
1
.
2
(
)
11
.
5
.
1
.
2
(
)
10
.
5
.
1
.
2
(
Wa
ż
ne pytanie: Kiedy amplituda drga
ń
jest najwi
ę
ksza?
© F.A. Dul 2009
Rezonansem nazywamy zjawisko gwałtownego wzrostu
amplitudy drga
ń
wymuszonych sił
ą
okresow
ą
o cz
ę
sto
ś
ci
bliskiej cz
ę
sto
ś
ci drga
ń
własnych układu.
0
2h
−
=
Ω
ω
)
(
4
2
2
0
2
0
max
h
h
f
B
−
=
ω
)
12
.
5
.
1
.
2
(
)
11
.
5
.
1
.
2
(
i jest równa
Definicja rezonansu dla układów swobodnych
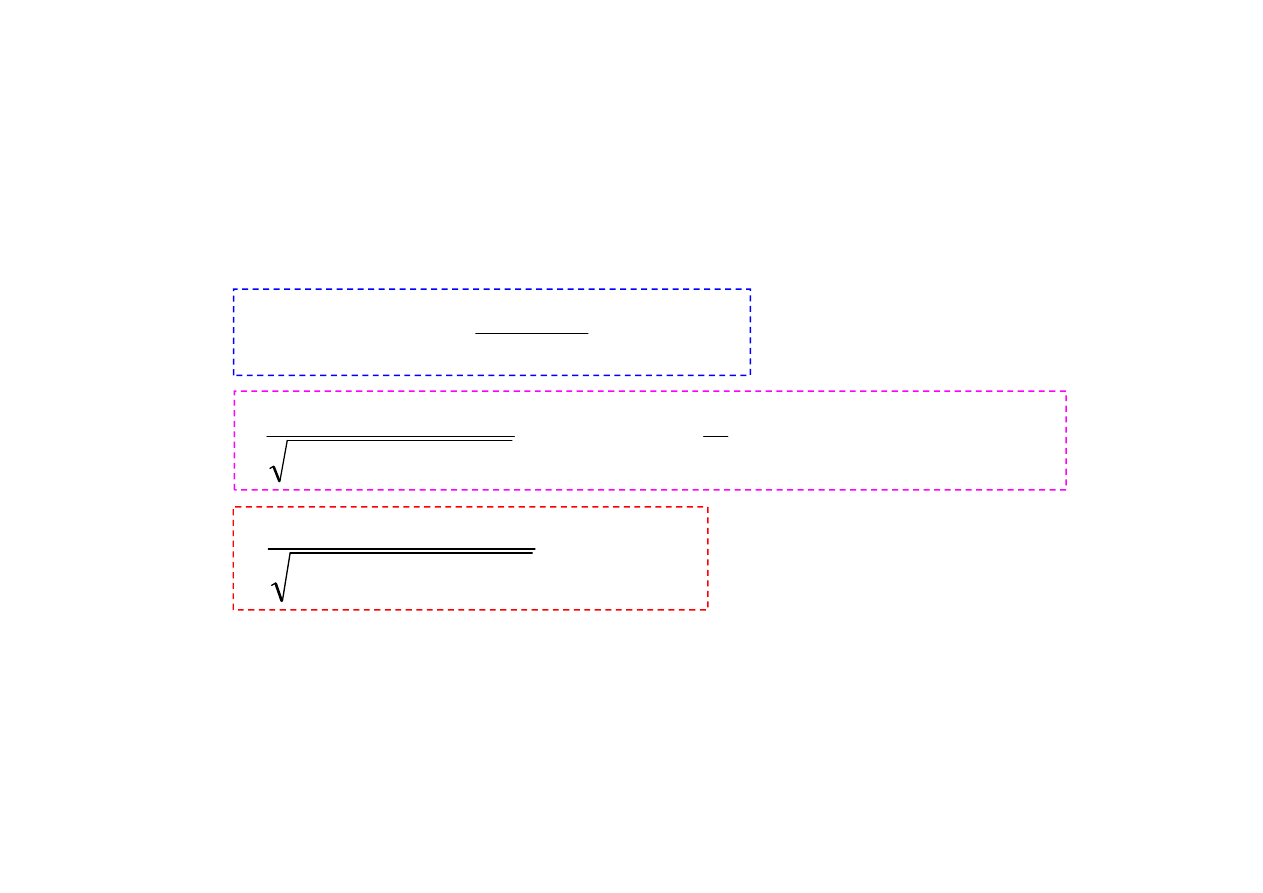
Rozwi
ą
zanie jest superpozycj
ą
trzech składników
1. Tłumienie podkrytyczne
0
ω
<
h
(a)
(b)
+
+
+
−
)
)
sin(
v
)
cos(
(
0
0
0
t
hx
t
x
e
ht
ω
ω
ω
+
Ω
−
+
Ω
+
Ω
−
+
−
]
)
sin(
)
cos
sin
(
1
)
cos(
sin
[
4
)
(
2
2
2
2
0
t
h
t
h
e
f
ht
ω
ε
ε
ω
ω
ε
ω
=
)
(t
x
2.1.5. Drgania wymuszone tłumione
Podobnie jak w przypadku układu swobodnego charakter ruchu zale
ż
y od
relacji pomi
ę
dzy cz
ę
sto
ś
ci
ą
drga
ń
swobodnych
ω
ωω
ω
0
a tłumieniem h
© F.A. Dul 2009
(
a) - drgania własne zale
ż
ne od warunków pocz
ą
tkowych,
(b)
(c)
(
b) - drgania z cz
ę
sto
ś
ci
ą
własn
ą
, zale
ż
ne od siły wymuszaj
ą
cej, niezale
ż
ne
od warunków pocz
ą
tkowych,
(
c) - drgania wymuszone o cz
ę
sto
ś
ci siły wymuszaj
ą
cej, niezale
ż
ne
od warunków pocz
ą
tkowych.
)
13
.
5
.
1
.
2
(
+
Ω
−
+
Ω
+
Ω
−
+
]
)
sin(
)
cos
sin
(
)
cos(
sin
[
4
)
(
2
2
2
2
t
h
t
h
ω
ε
ε
ω
ω
ε
ω
)
sin(
4
)
(
2
2
2
2
0
ε
ω
+
Ω
Ω
+
Ω
−
+
t
h
f
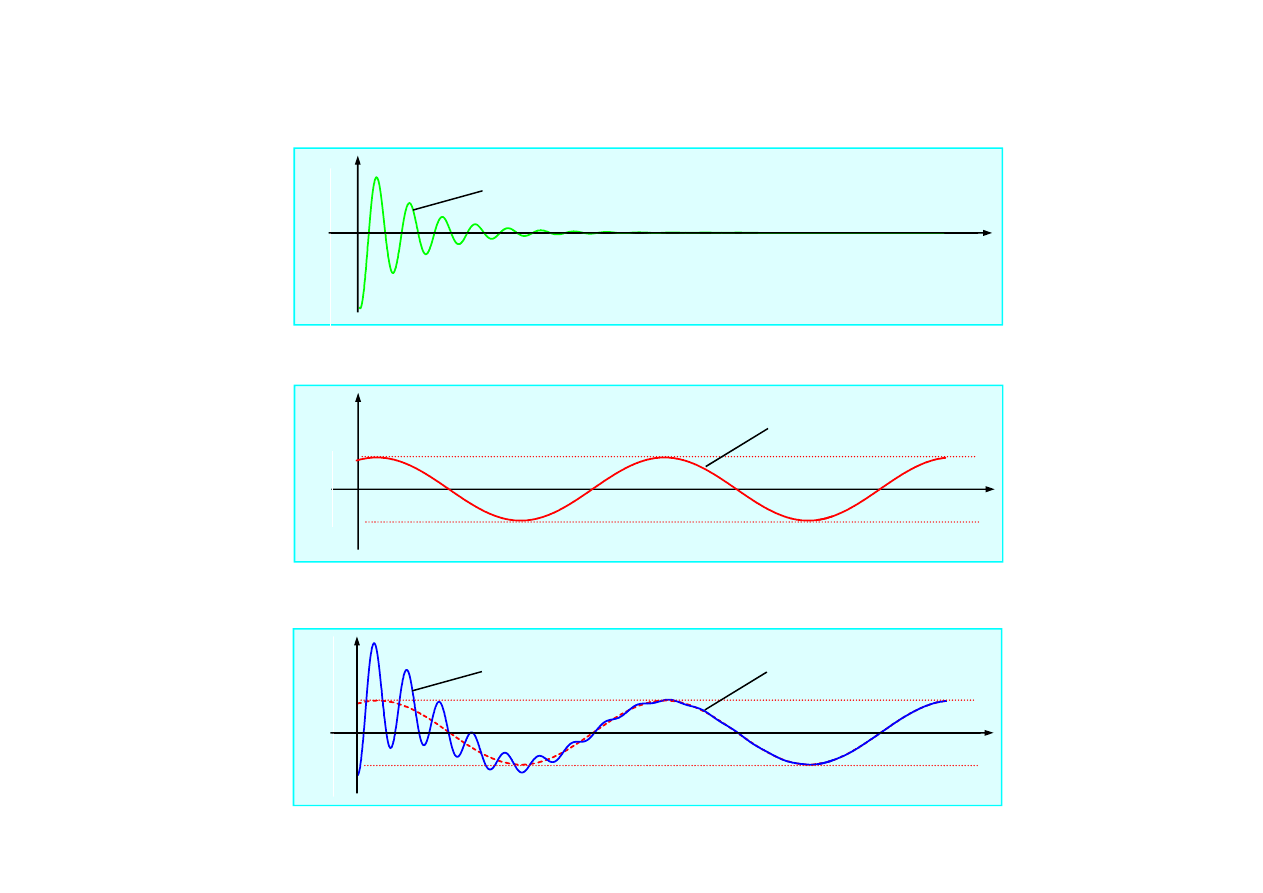
Superpozycja drga
ń
swobodnych tłumionych i wymuszonych
x(t)
zanikaj
ą
ce drgania
swobodne
t
+
x(t)
ustalone drgania
wymuszone
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
x(t)
zanikaj
ą
ce drgania
swobodne
t
ustalone drgania
wymuszone
| |
t
wymuszone
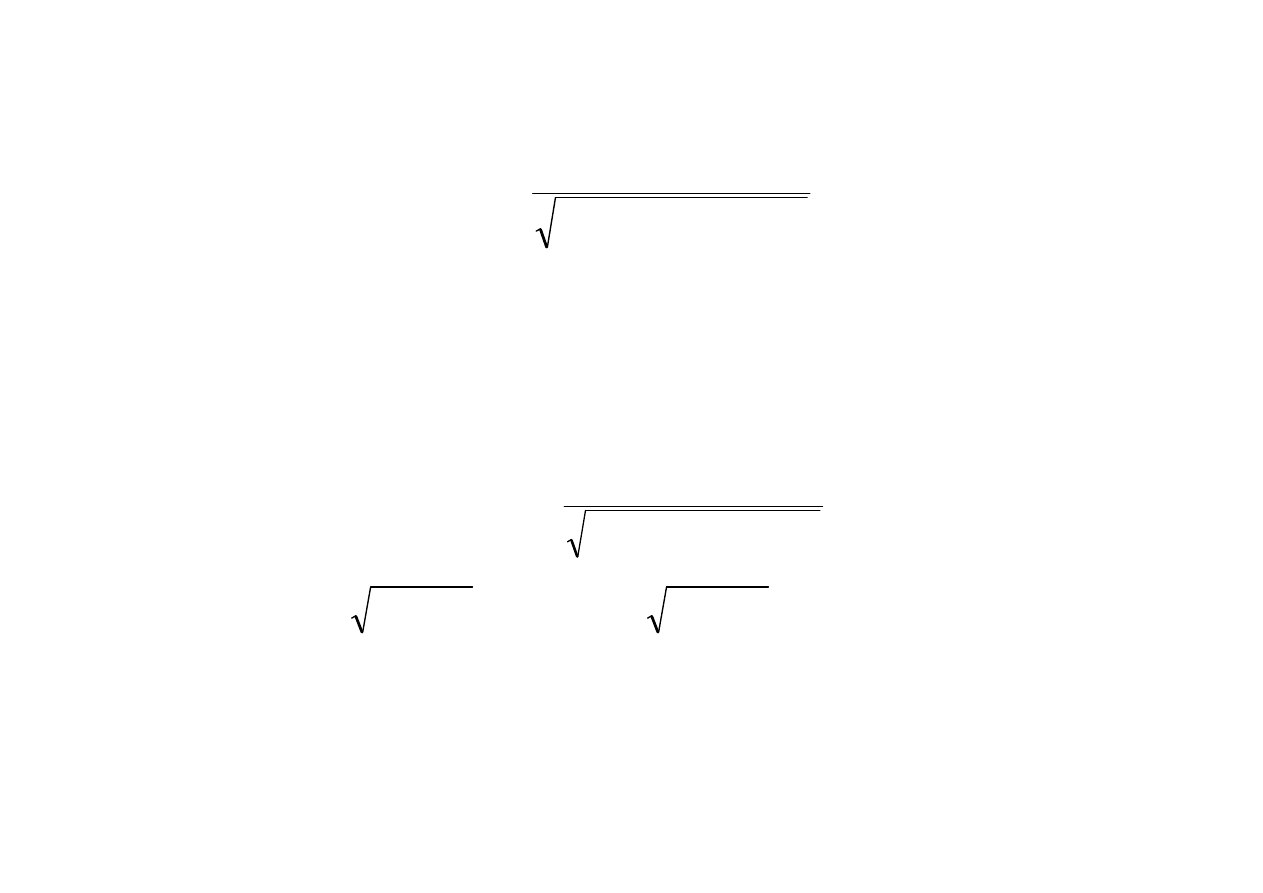
ht
e
t
C
C
t
x
−
+
=
)
(
)
(
2
1
2. Tłumienie krytyczne
0
ω
=
h
)
sin(
4
)
(
2
2
2
2
0
ε
ω
+
Ω
Ω
+
Ω
−
+
t
h
f
3. Tłumienie nadkrytyczne
0
ω
>
h
)
14
.
5
.
1
.
2
(
Stałe C
1
oraz C
2
zale
żą
zarówno od warunków pocz
ą
tkowych
jak i od siły wymuszaj
ą
cej.
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
t
r
t
r
e
C
e
C
t
x
2
1
2
1
)
(
−
−
+
=
)
sin(
4
)
(
2
2
2
2
0
ε
ω
+
Ω
Ω
+
Ω
−
+
t
h
f
)
15
.
5
.
1
.
2
(
Stałe C
1
oraz C
2
zale
żą
zarówno od warunków pocz
ą
tkowych
jak i od siły wymuszaj
ą
cej.
2
0
2
2
2
0
2
1
,
ω
ω
−
−
−
=
−
+
−
=
h
h
r
h
h
r
)
16
.
5
.
1
.
2
(
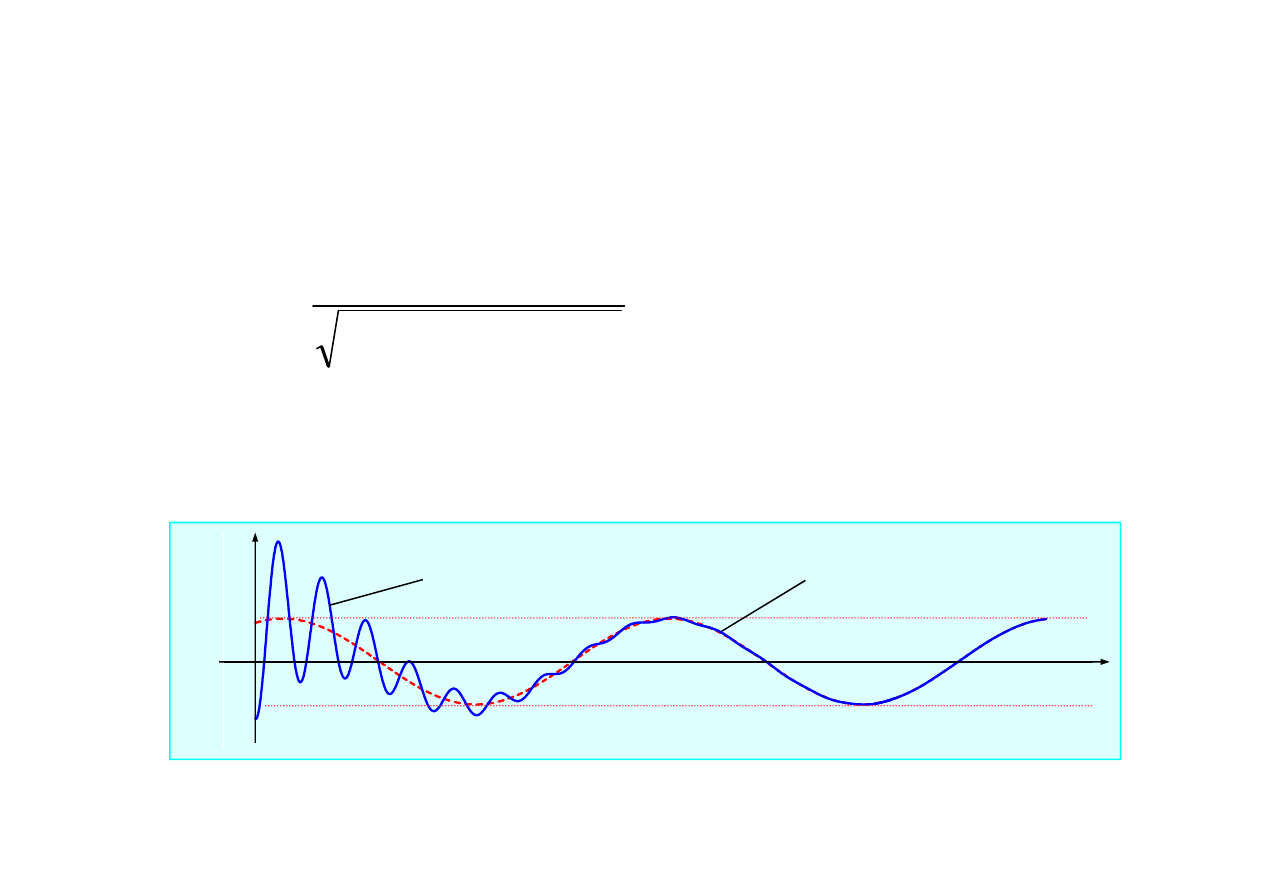
0
2
2
2
2
0
,
)
sin(
4
)
(
)
(
t
t
t
h
f
t
x
>>
+
Ω
Ω
+
Ω
−
≅
ε
ω
)
17
.
5
.
1
.
2
(
Niezale
ż
nie od poziomu tłumienia rozwi
ą
zania równania jednorodnego
zanikaj
ą
, wi
ę
c po pewnym czasie dominuj
ą
c
ą
cz
ęś
ci
ą
rozwi
ą
zania b
ę
d
ą
drgania wymuszone o stałej amplitudzie
Zanikanie drga
ń
swobodnych tłumionych, zale
ż
nych od warunków
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
pocz
ą
tkowych, nazywa si
ę
czasami
„zanikaniem stanów przej
ś
ciowych”.
x(t)
zanikaj
ą
ce drgania
swobodne
t
ustalone drgania
wymuszone
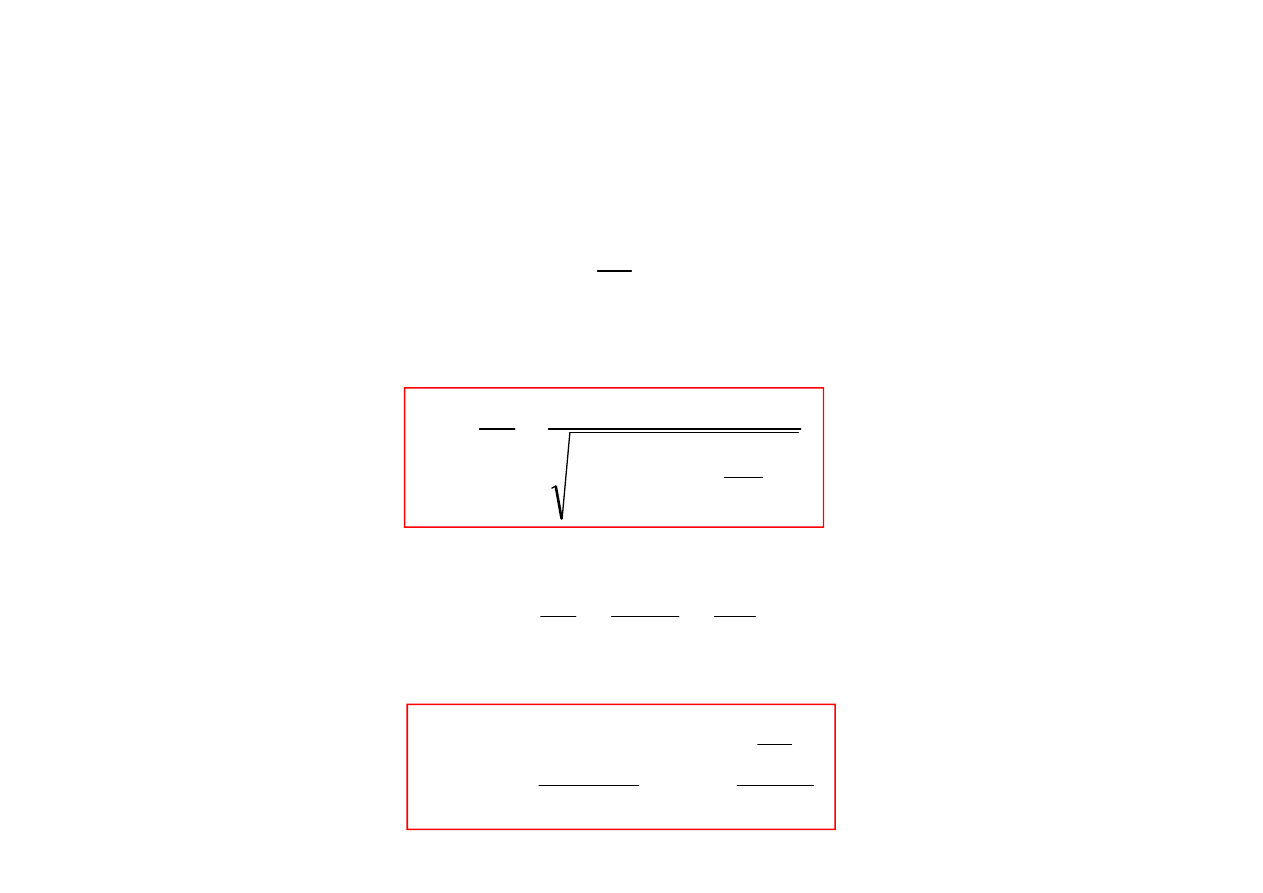
Współczynnik wzmocnienia amplitudy (zwany te
ż
współczynnikiem
dynamiczno
ś
ci obci
ąż
enia)
2
1
µ
h
x
A
=
=
Charakterystyki rezonansowe drga
ń
tłumionych wymuszonych
Charakterystyki drga
ń
wymuszonych podaje si
ę
w formie dwóch wykresów,
przedstawiaj
ą
cych amplitud
ę
i faz
ę
drga
ń
w funkcji stosunku cz
ę
sto
ś
ci siły
wymuszaj
ą
cej do cz
ę
sto
ś
ci drga
ń
swobodnych układu
0
ω
ν
Ω
=
)
18
.
5
.
1
.
2
(
)
19
.
5
.
1
.
2
(
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
2
2
0
2
2
2
4
)
1
(
ν
ω
ν
h
x
st
+
−
gdzie x
st
jest ugi
ę
ciem statycznym układu pod działaniem stałej siły F
0
2
0
0
2
0
0
0
ω
ω
f
m
F
k
F
x
st
=
=
=
Przesuni
ę
cie fazowe pomi
ę
dzy wymuszeniem a przemieszczeniem
1
2
tg
arc
2
tg
arc
2
0
2
2
0
−
=
Ω
−
Ω
−
=
ν
ν
ω
ω
ε
h
h
)
19
.
5
.
1
.
2
(
)
20
.
5
.
1
.
2
(
)
21
.
5
.
1
.
2
(
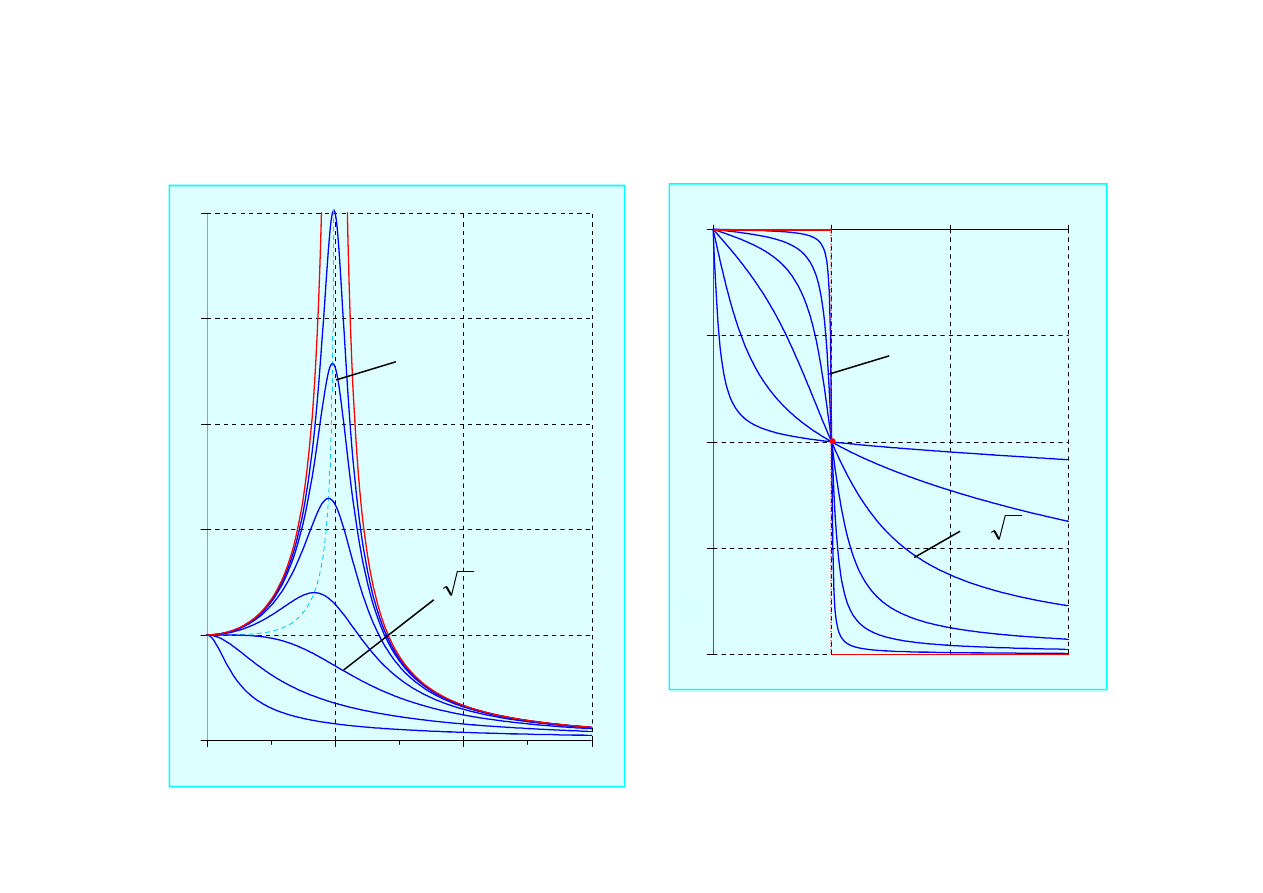
3
4
5
µ
Charakterystyki rezonansowe drga
ń
tłumionych wymuszonych
0
1
2
3
Ω / ω
-90
-45
0
h/
ω
ω
ω
ω
= 0
h/
ω
ω
ω
ω
= 0
0.01
0.01
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
0
1
2
3
Ω / ω
0
1
2
-180
-135
-90
ϕ
εεεε
2
1/
2
1/
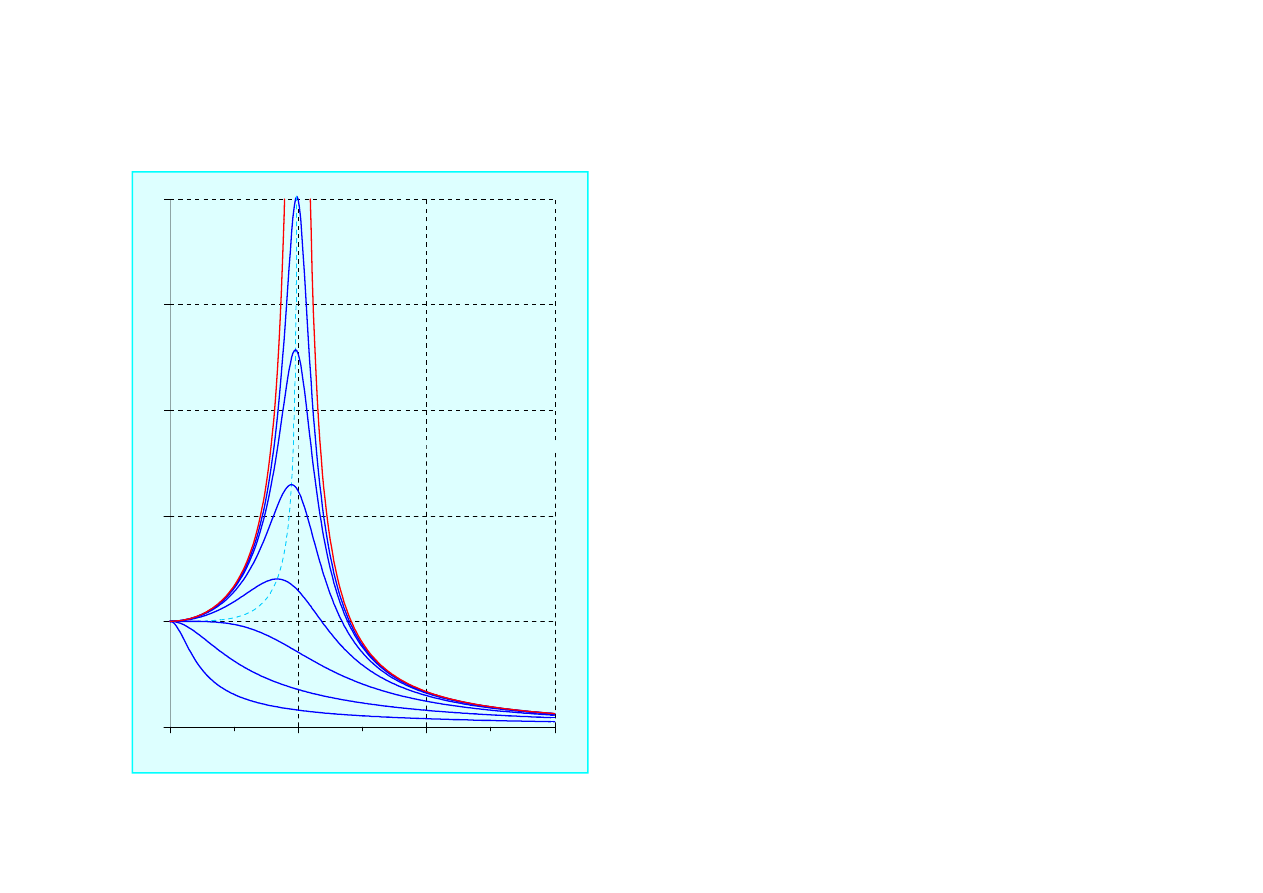
• Przy podkrytycznych warto
ś
ciach tłumienia
wyst
ę
puje wzmocnienie amplitudy; jest ono
tym silniejsze, im mniejsze jest tłumienie.
• W układzie bez tłumienia wzmocnienie
amplitudy jest niesko
ń
czone,
• Drgania tłumione maj
ą
w rezonansie
amplitud
ę
ograniczon
ą
.
• Cz
ę
sto
ść
siły wymuszaj
ą
cej odpowiadaj
ą
ca
najwi
ę
kszej warto
ś
ci wzmocnienia
Własno
ś
ci drga
ń
tłumionych wymuszonych sił
ą
harmoniczn
ą
3
4
5
µ
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
najwi
ę
kszej warto
ś
ci wzmocnienia
amplitudy maleje ze wzrostem tłumienia.
• Gdy tłumienie jest nadkrytyczne, to
wzmocnienie amplitudy nie wyst
ę
puje.
• Tłumienie nie wpływa znacz
ą
co na
amplitud
ę
drga
ń
przy bardzo małych
(
Ω
<<
ω
0
) i bardzo du
ż
ych (
Ω
>>
ω
0
)
warto
ś
ciach cz
ę
sto
ś
ci siły wymuszaj
ą
cej.
• Przy du
ż
ym tłumieniu amplituda drga
ń
jest
bardzo mała przy du
ż
ych cz
ę
sto
ś
ciach siły
wymuszaj
ą
cej (
Ω
>>
ω
0
).
0
1
2
3
Ω / ω
0
1
2
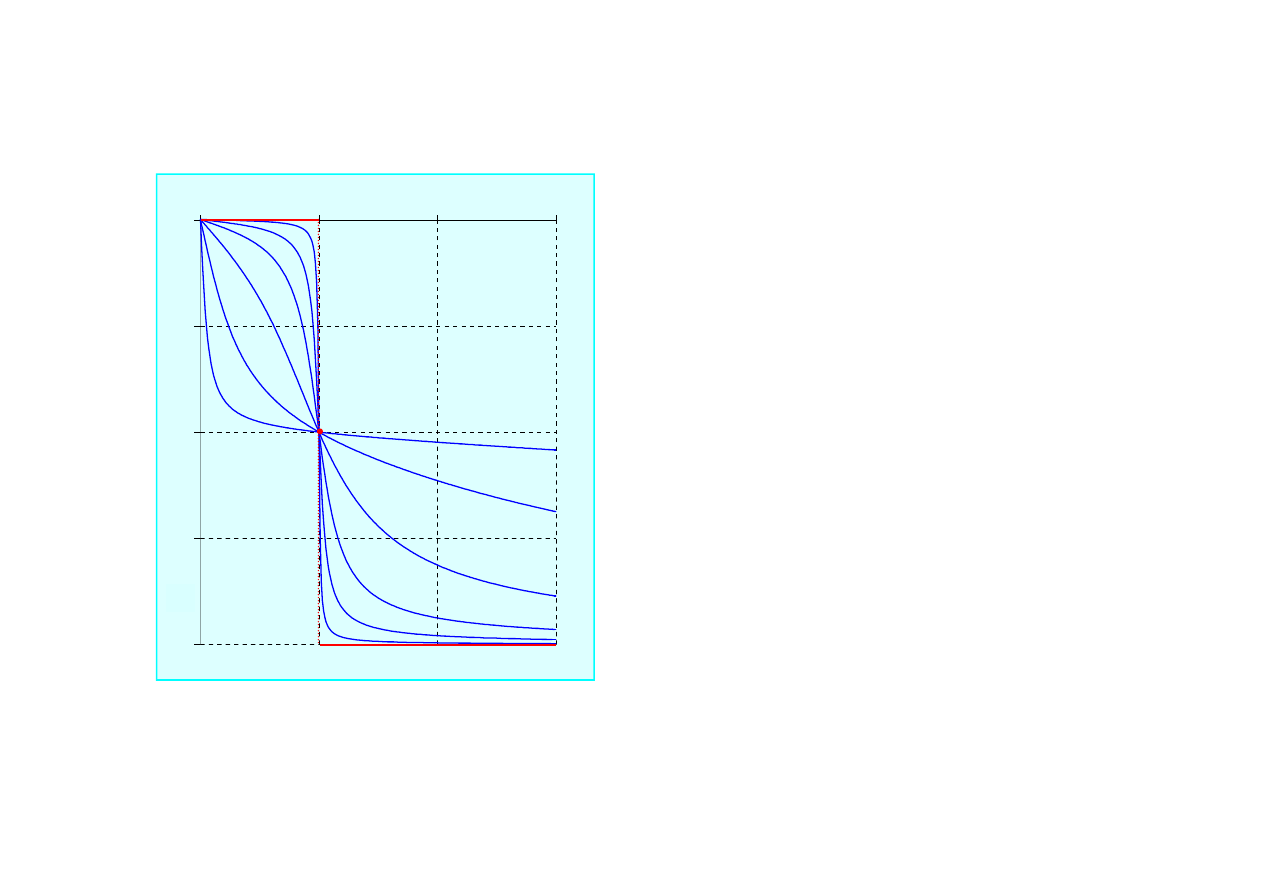
• W układzie bez tłumienia
przesuni
ę
cie fazowe jest równe zeru
gdy
Ω
<
ω
0
, za
ś
-
π
gdy
Ω
>
ω
0
; w
rezonansie jest ono równe -
π
/2.
• Przy bardzo du
ż
ym tłumieniu
przesuni
ę
cie fazowe jest bliskie -
π
/2
• Przesuni
ę
cie fazowe dla
Ω
=
ω
0
jest
zawsze równe -
π
/2, niezale
ż
nie od
0
1
2
3
Ω / ω
-90
-45
0
Własno
ś
ci drga
ń
tłumionych wymuszonych sił
ą
harmoniczn
ą
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
zawsze równe -
π
/2, niezale
ż
nie od
poziomu tłumienia.
-180
-135
ϕ
εεεε

•
Przy podkrytycznych warto
ś
ciach tłumienia wyst
ę
puje wzmocnienie
amplitudy; jest ono tym silniejsze, im mniejsze jest tłumienie.
•
W układzie bez tłumienia wzmocnienie amplitudy jest niesko
ń
czone,
•
Drgania tłumione maj
ą
w rezonansie amplitud
ę
ograniczon
ą
.
•
Cz
ę
sto
ść
siły wymuszaj
ą
cej odpowiadaj
ą
ca najwi
ę
kszej warto
ś
ci
wzmocnienia amplitudy maleje ze wzrostem tłumienia.
•
Gdy tłumienie jest nadkrytyczne, to wzmocnienie amplitudy nie
wyst
ę
puje.
Własno
ś
ci drga
ń
w rezonansie:
2.1.5. Drgania wymuszone tłumione
© F.A. Dul 2009
•
Tłumienie nie wpływa znacz
ą
co na amplitud
ę
drga
ń
przy bardzo małych
(
Ω
Ω
Ω
Ω
<<
ω
ωω
ω
0
) i bardzo du
ż
ych (
Ω
Ω
Ω
Ω
>>
ω
ωω
ω
0
) warto
ś
ciach cz
ę
sto
ś
ci siły
wymuszaj
ą
cej.
•
Przy bardzo du
ż
ym tłumieniu amplituda drga
ń
jest bardzo mała przy
du
ż
ych warto
ś
ciach cz
ę
sto
ś
ci siły wymuszaj
ą
cej,
Ω
Ω
Ω
Ω
>>
ω
ωω
ω
0
.
•
W układzie bez tłumienia przesuni
ę
cie fazowe jest równe zeru gdy
Ω
Ω
Ω
Ω
<
ω
ωω
ω
0,
za
ś
-
ππππ
gdy
Ω
Ω
Ω
Ω
>
ω
ωω
ω
0
; w rezonansie jest ono równe -
ππππ
/2.
•
Przy bardzo du
ż
ym tłumieniu przesuni
ę
cie fazowe jest bliskie -
ππππ
/2.
•
Przesuni
ę
cie fazowe dla
Ω
Ω
Ω
Ω
=
ω
ωω
ω
0
jest zawsze równe -
ππππ
/2, niezale
ż
nie od
poziomu tłumienia.
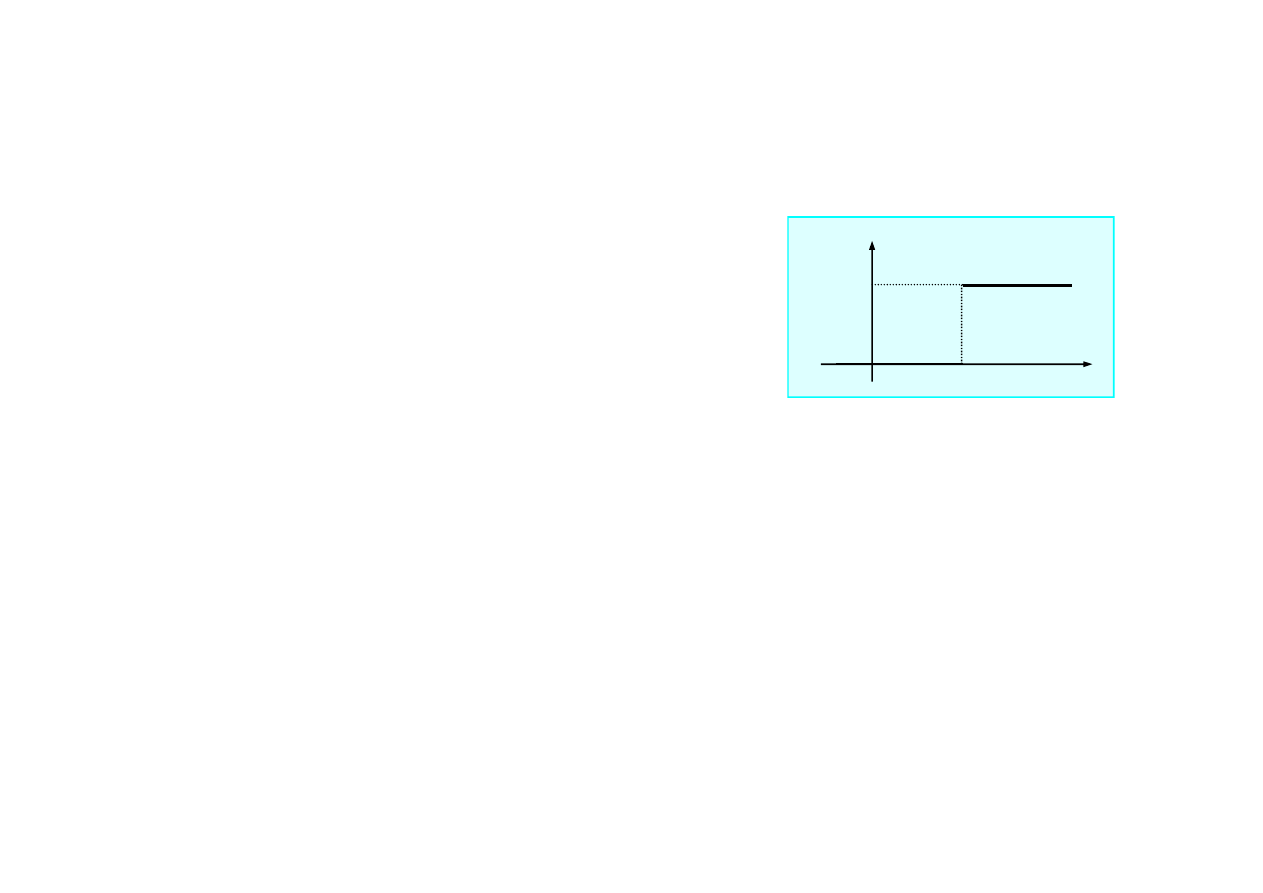
Skok jednostkowy - funkcja Heaviside’a
)
(
2
2
0
t
x
x
h
x
1
=
+
+
ω
&
&
&
≥
<
=
0
1
0
,
0
)
(
t
t
t
1
t
ττττ
1
1(t -
τ
)
)
1
.
7
.
1
.
2
(
2.1.7. Drgania wymuszone skokiem jednostkowym
)
2
.
7
.
1
.
2
(
© F.A. Dul 2009
Je
ż
eli przed przyło
ż
eniem (t<0) siły układ był nieruchomy
,
0
)
(
=
t
x
0
)
(
=
t
x
&
to rozwi
ą
zanie h(t) równania drga
ń
(2.1.7.1) jest
odpowiedzi
ą
na skok
jednostkowy.
Posta
ć
odpowiedzi na skok jednostkowy zale
ż
y od relacji pomi
ę
dzy
cz
ę
sto
ś
ci
ą
drga
ń
swobodnych
ω
ωω
ω
0
a tłumieniem h
)
3
.
7
.
1
.
2
(
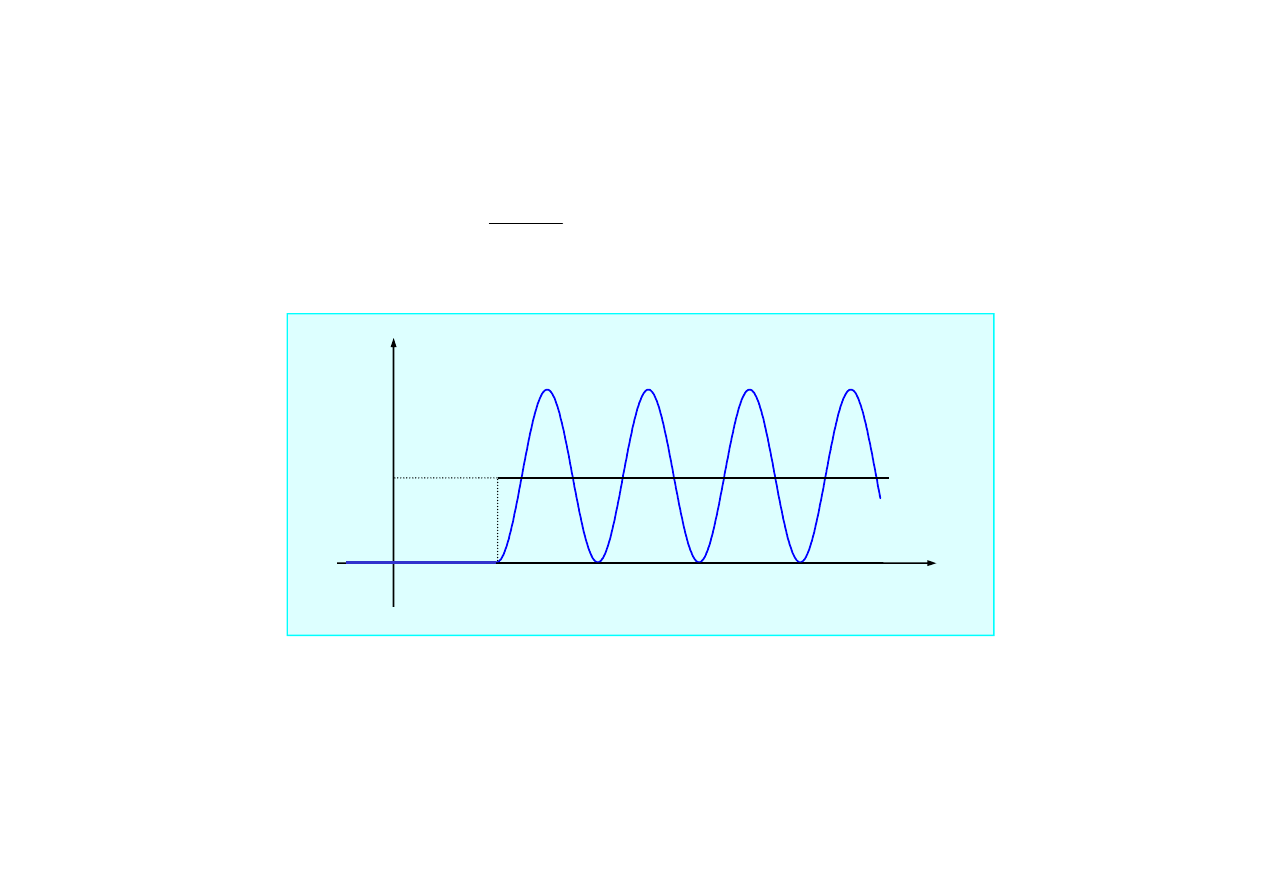
0
),
)
cos(
1
(
1
)
(
0
2
0
>
−
=
t
t
m
t
h
ω
ω
h(t -
ττττ
)
• dla układu nietłumionego
0
=
h
)
4
.
7
.
1
.
2
(
2.1.7. Drgania wymuszone skokiem jednostkowym
© F.A. Dul 2009
t
ττττ
1
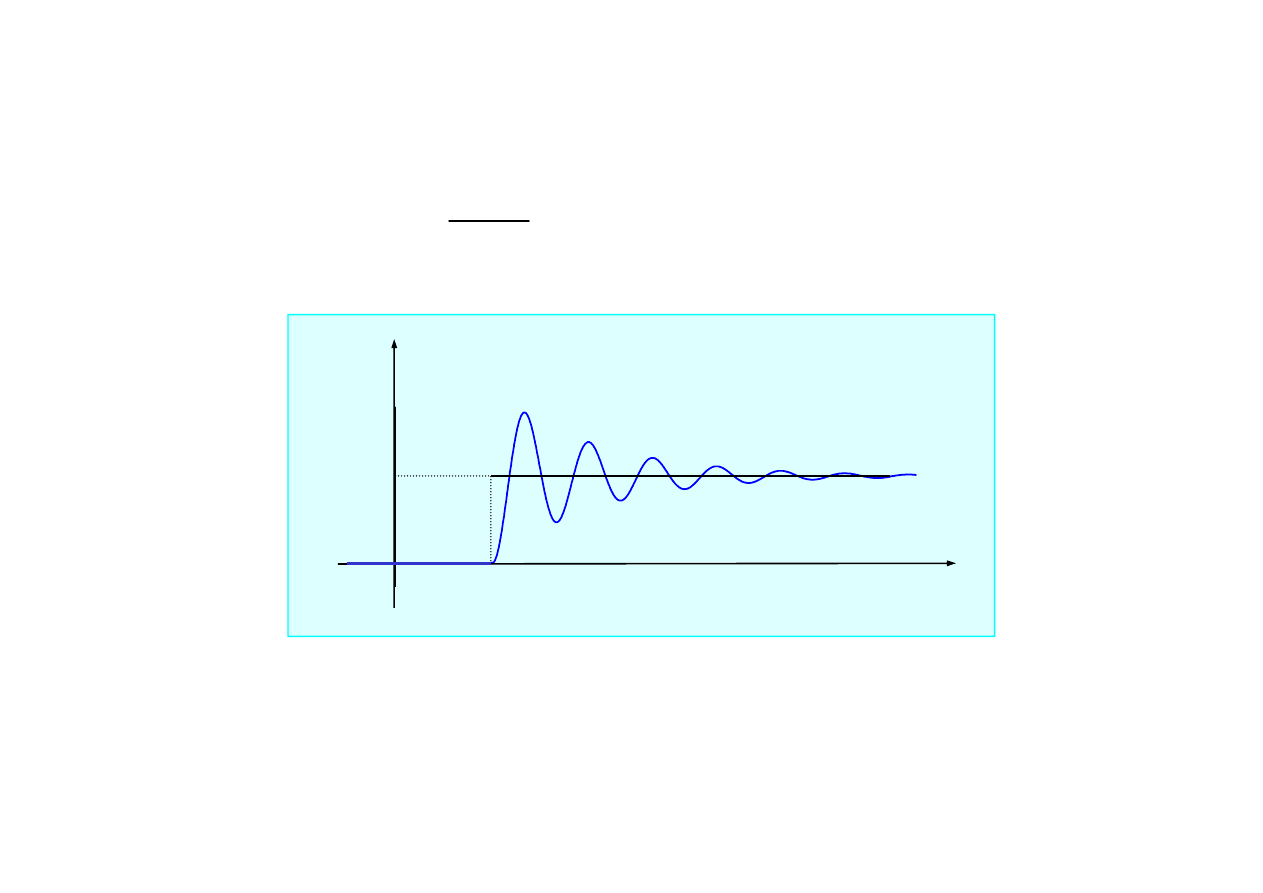
0
),
)
cos(
1
(
1
)
(
2
>
−
=
−
t
t
e
m
t
h
ht
ω
ω
h(t -
ττττ
)
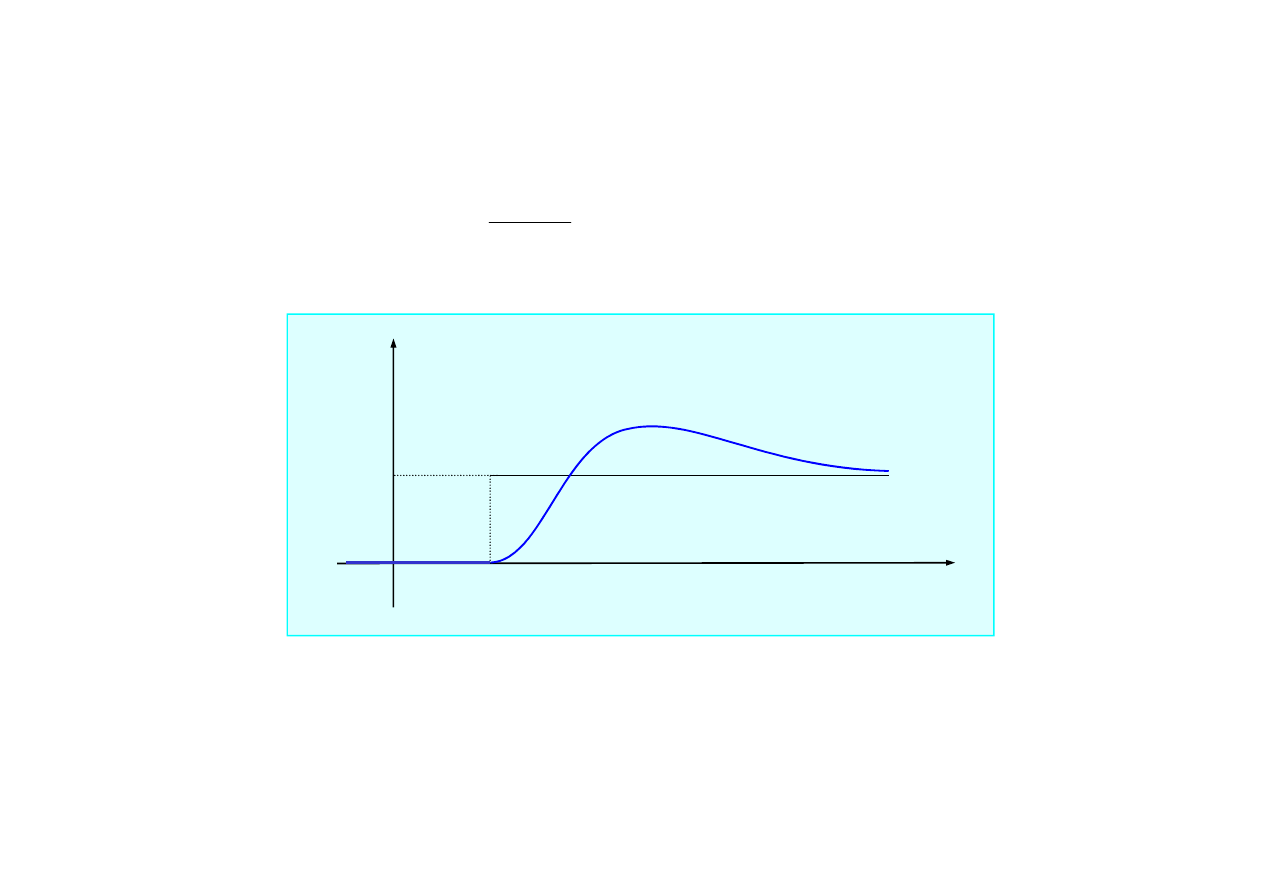
• dla układu z tłumieniem podkrytycznym
0
ω
<
h
)
5
.
7
.
1
.
2
(
2.1.7. Drgania wymuszone skokiem jednostkowym
© F.A. Dul 2009
t
ττττ
1
0
),
1
(
1
)
(
2
>
−
=
−
t
te
m
t
h
ht
ω
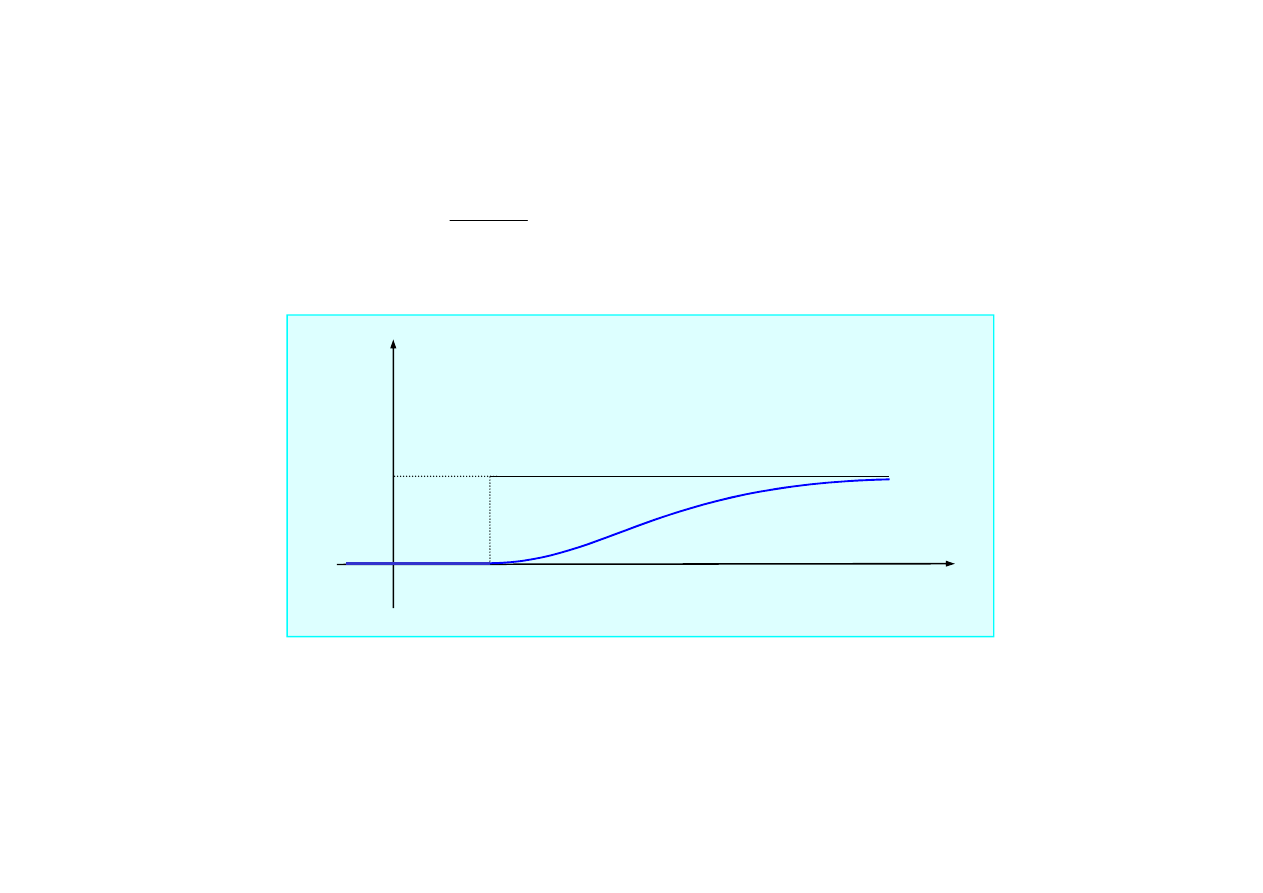
• dla układu z tłumieniem krytycznym
0
ω
=
h
)
6
.
7
.
1
.
2
(
h(t -
ττττ
)
2.1.7. Drgania wymuszone skokiem jednostkowym
© F.A. Dul 2009
t
ττττ
1
0
)
)
cosh(
1
(
1
)
(
2
>
−
=
−
t
t
e
m
t
h
ht
ω
ω
• dla układu z tłumieniem nadkrytycznym
0
ω
>
h
)
7
.
7
.
1
.
2
(
h(t -
ττττ
)
2.1.7. Drgania wymuszone skokiem jednostkowym
© F.A. Dul 2009
t
ττττ
1

1
)
(
,
0
0
,
0
)
(
=
=
∞
≠
=
∫
∞
∞
−
dt
t
t
t
t
δ
δ
t
ττττ
∞
∞
∞
∞
δδδδ
(t -
ττττ
)
Je
ż
eli przed przyło
ż
eniem (t<0) siły układ był nieruchomy
Impuls - dystrybucja
δ
-Diraca (pochodna 1(t) )
)
(
2
2
0
t
x
x
h
x
δ
ω
=
+
+
&
&
&
)
1
.
8
.
1
.
2
(
2.1.8. Drgania wymuszone impulsem jednostkowym
)
2
.
8
.
1
.
2
(
© F.A. Dul 2009
Je
ż
eli przed przyło
ż
eniem (t<0) siły układ był nieruchomy
,
0
)
(
=
t
x
0
)
(
=
t
x
&
Oznacza to,
ż
e w chwili t = 0 pr
ę
dko
ść
wzro
ś
nie skokowo do warto
ś
ci
m
1
v
0
=
to impuls f(t) =
δ
(t)/m spowoduje przyrost p
ę
du równy
1
)
(
)
0
(
v
)
0
(
v
=
=
−
−
+
=
∆
∫
dt
t
m
m
p
δ
)
3
.
8
.
1
.
2
(
)
4
.
8
.
1
.
2
(
,
0
)
0
(
=
x
m
x
/
1
)
0
(
=
&
Wynika st
ą
d,
ż
e przyło
ż
enie impulsu w chwili t = 0 odpowiada ruchowi
swobodnemu układu z warunkami pocz
ą
tkowymi
0
),
sin(
1
)
(
>
=
t
t
t
g
ω
Rozwi
ą
zanie g(t) równania ruchu (2.1.8.1) spełniaj
ą
ce takie warunki
pocz
ą
tkowe jest tzw.
impulsow
ą
funkcj
ą
przej
ś
cia
.
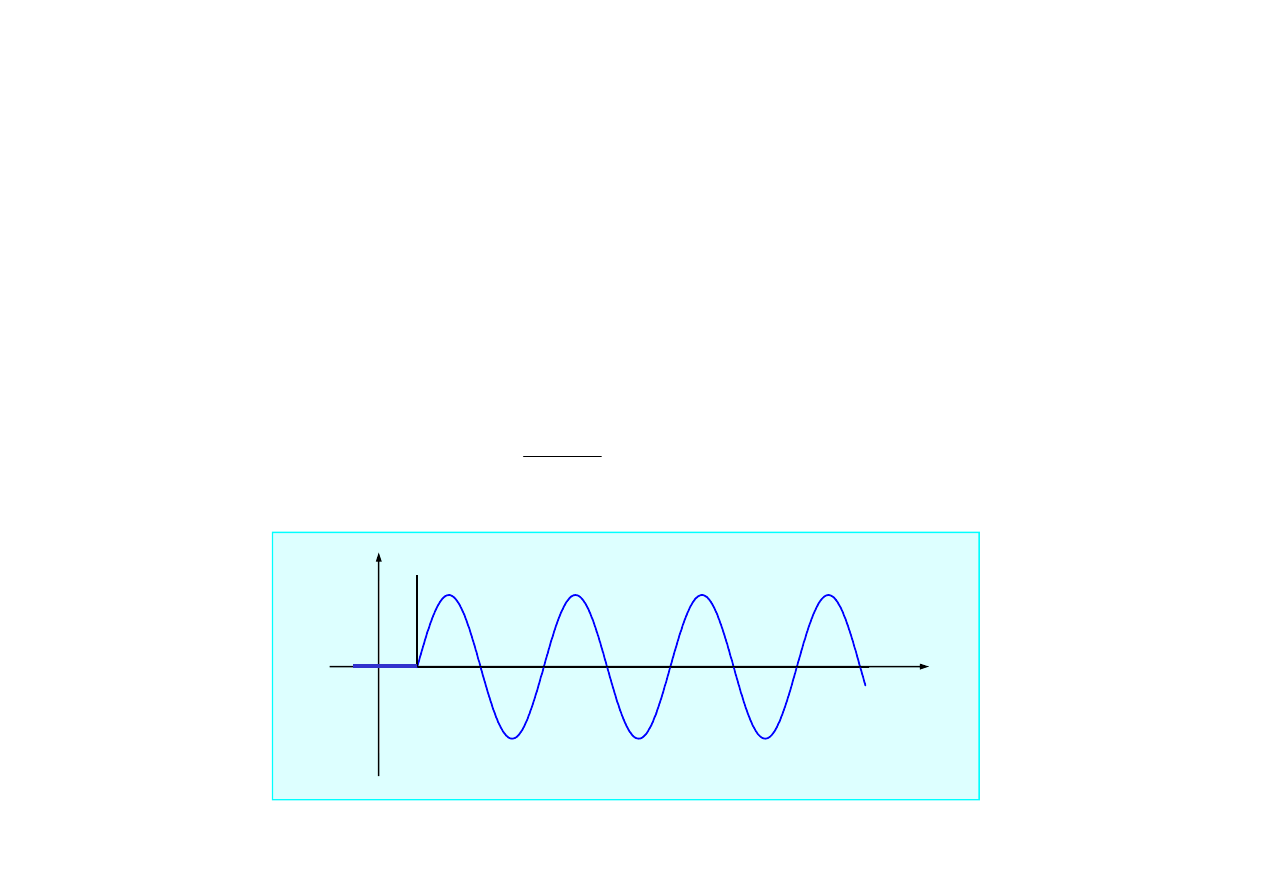
Impulsowa funkcja przej
ś
cia dla układu nietłumionego ma posta
ć
)
6
.
8
.
1
.
2
(
2.1.8. Drgania wymuszone impulsem jednostkowym
)
5
.
8
.
1
.
2
(
© F.A. Dul 2009
0
),
sin(
1
)
(
0
0
>
=
t
t
m
t
g
ω
ω
g(t -
ττττ
)
t
ττττ
∞
∞
∞
∞
)
6
.
8
.
1
.
2
(
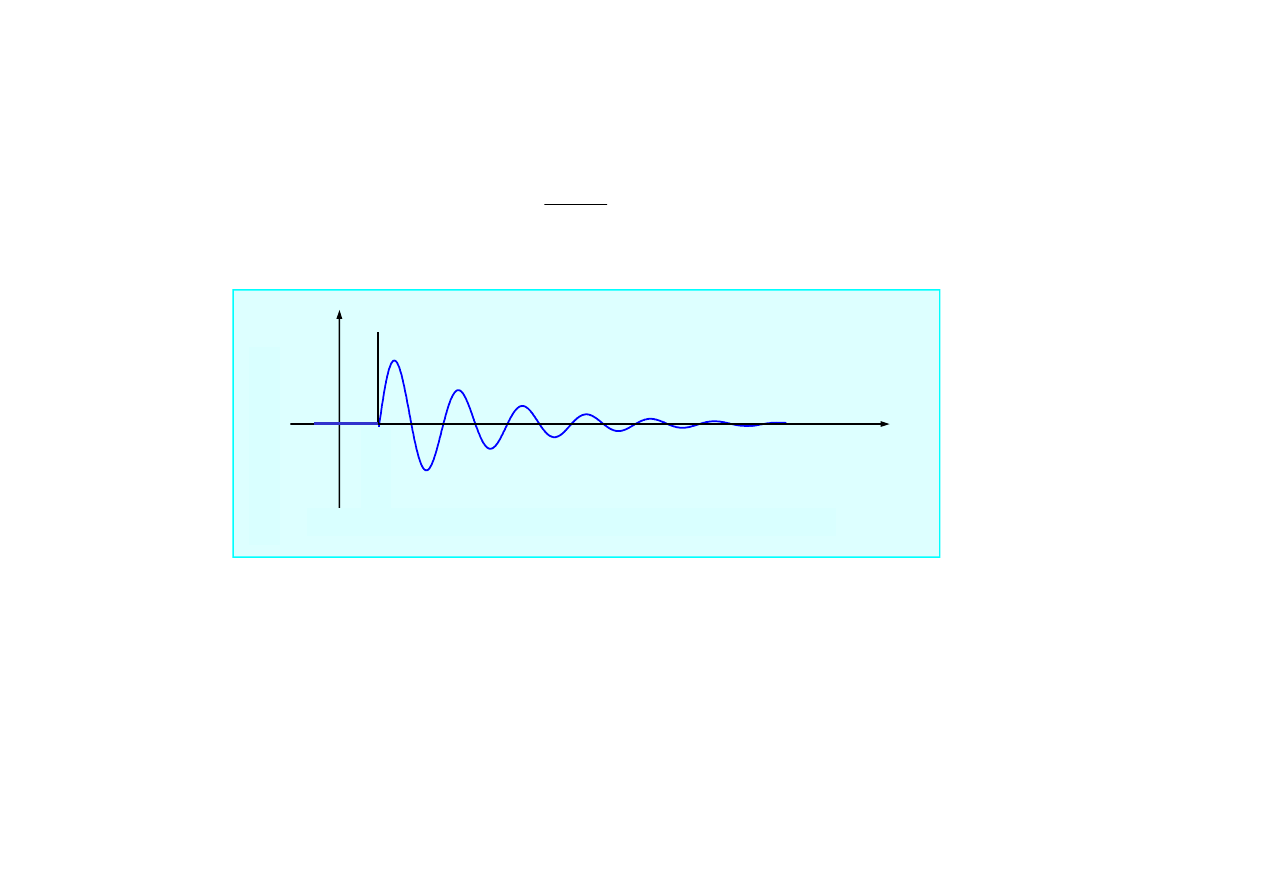
• dla układu z tłumieniem podkrytycznym
)
sin(
1
)
(
t
e
m
t
g
ht
ω
ω
−
=
)
7
.
8
.
1
.
2
(
g(t -
ττττ
)
t
∞
∞
∞
∞
ττττ
2.1.8. Drgania wymuszone impulsem jednostkowym
0
ω
<
h
© F.A. Dul 2009
t
ττττ
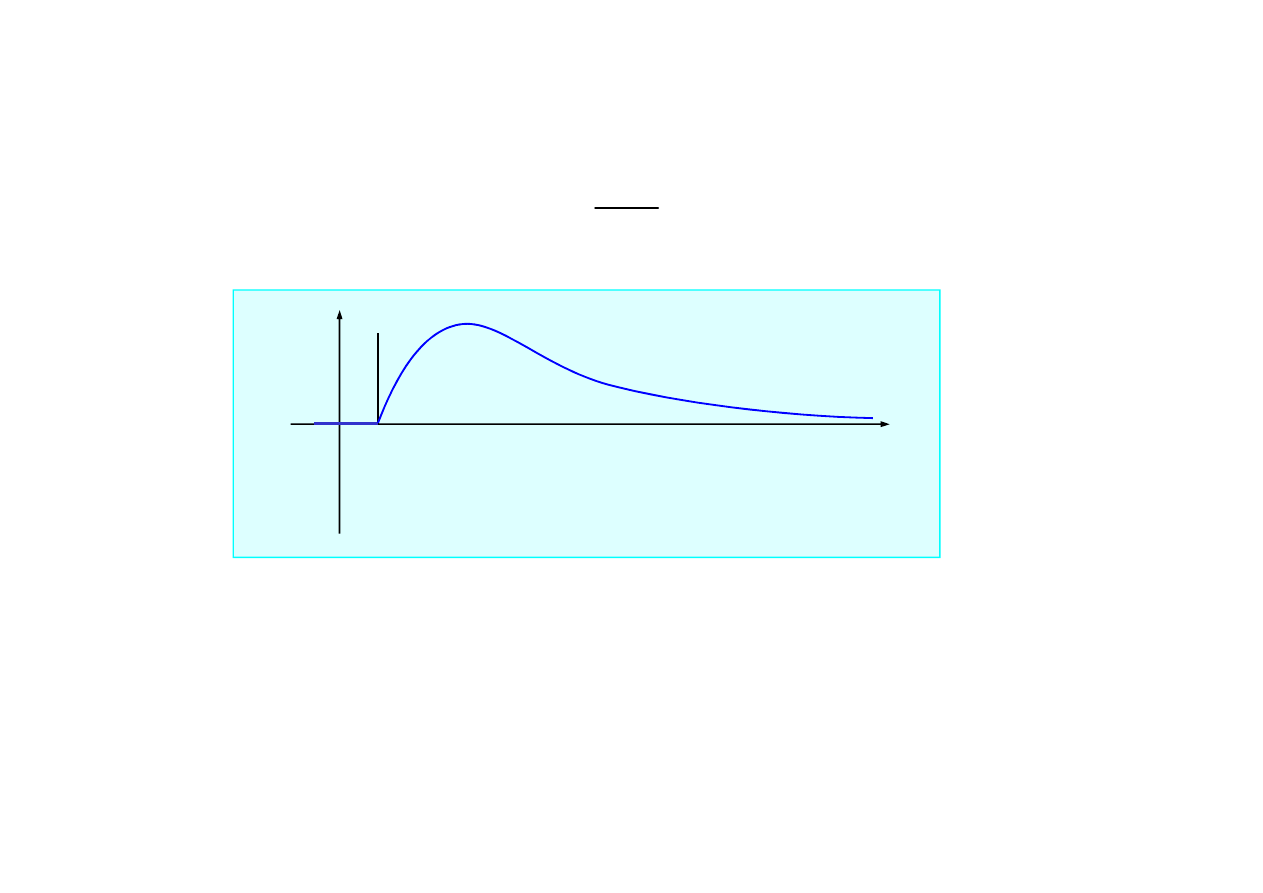
• dla układu z tłumieniem krytycznym
ht
te
m
t
g
−
=
ω
1
)
(
)
28
.
6
.
1
.
2
(
g(t -
ττττ
)
t
ττττ
∞
∞
∞
∞
2.1.8. Drgania wymuszone impulsem jednostkowym
0
ω
=
h
© F.A. Dul 2009
t
ττττ
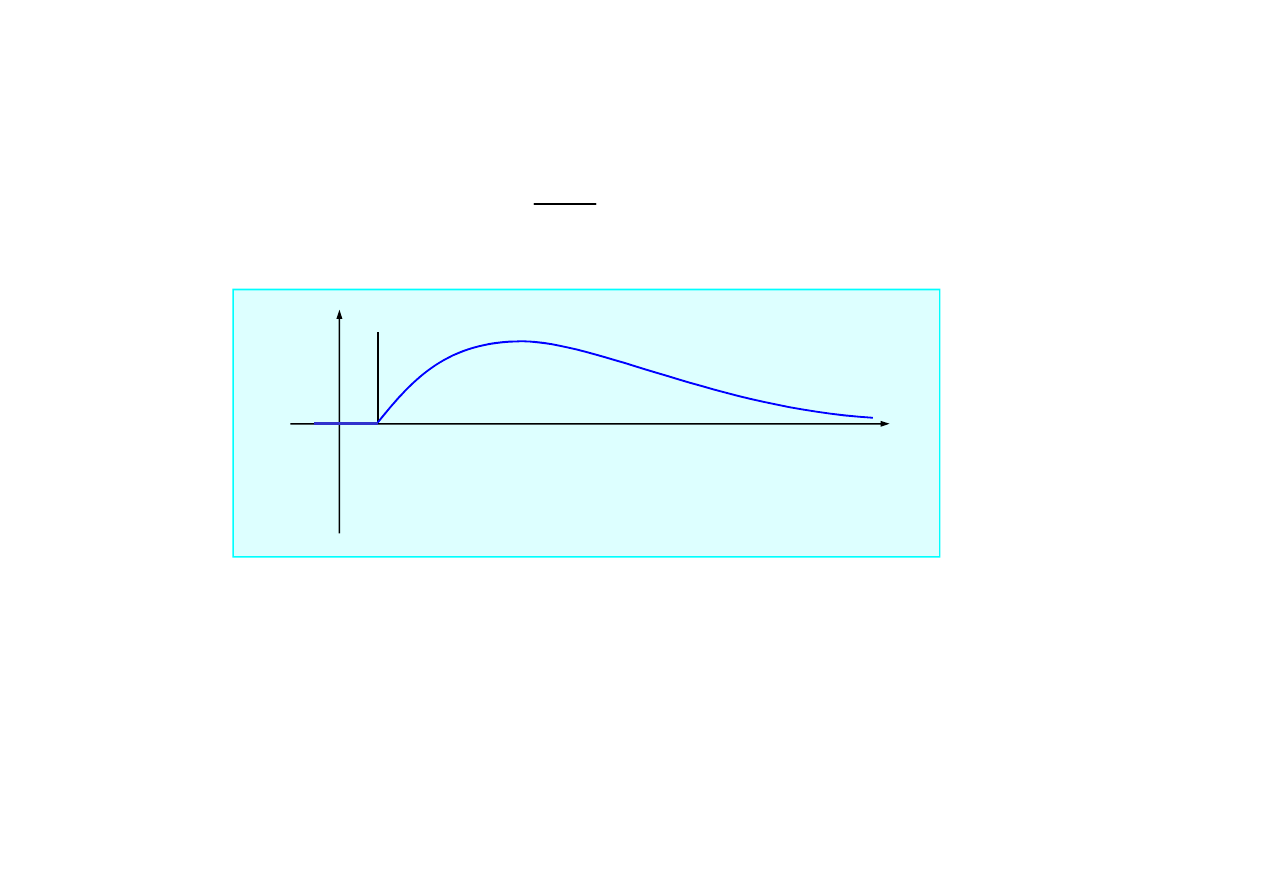
• dla układu z tłumieniem nadkrytycznym
)
sinh(
1
)
(
t
e
m
t
g
ht
ω
ω
−
=
)
29
.
6
.
1
.
2
(
g(t -
ττττ
)
t
ττττ
∞
∞
∞
∞
2.1.8. Drgania wymuszone impulsem jednostkowym
0
ω
>
h
© F.A. Dul 2009
t
ττττ

)
(
2
2
0
t
f
x
x
h
x
=
+
+
ω
&
&
&
Impuls dI(
τ
) siły f(
τ
) na przedziale czasu d
τ
jest równy
τ
τ
τ
d
f
dI
)
(
)
(
=
Odpowied
ź
układu na wymuszenie impulsem dI mo
ż
na wyrazi
ć
za
pomoc
ą
impulsowej funkcji przej
ś
cia
Sił
ę
f(t) przedstawia si
ę
za pomoc
ą
impulsów.
)
1
.
9
.
1
.
2
(
)
2
.
8
.
1
.
2
(
2.1.9. Drgania wymuszone sił
ą
dowoln
ą
© F.A. Dul 2009
Zasada superpozycji dla układów liniowych
)
(
),
(
2
1
t
x
t
x
)
(
)
(
2
1
t
bx
t
ax
+
s
ą
dowolnymi rozwi
ą
zaniami równania liniowego
jest równie
ż
rozwi
ą
zaniem równania liniowego.
Je
ż
eli
to kombinacja liniowa
(a, b - stałe dowolne)
)
(
)
(
)
(
)
(
)
(
τ
τ
τ
τ
τ
−
=
−
=
t
g
d
f
t
g
dI
t
dx
Rozwi
ą
zanie x(t) otrzyma si
ę
za pomoc
ą
zasady superpozycji
)
3
.
9
.
1
.
2
(
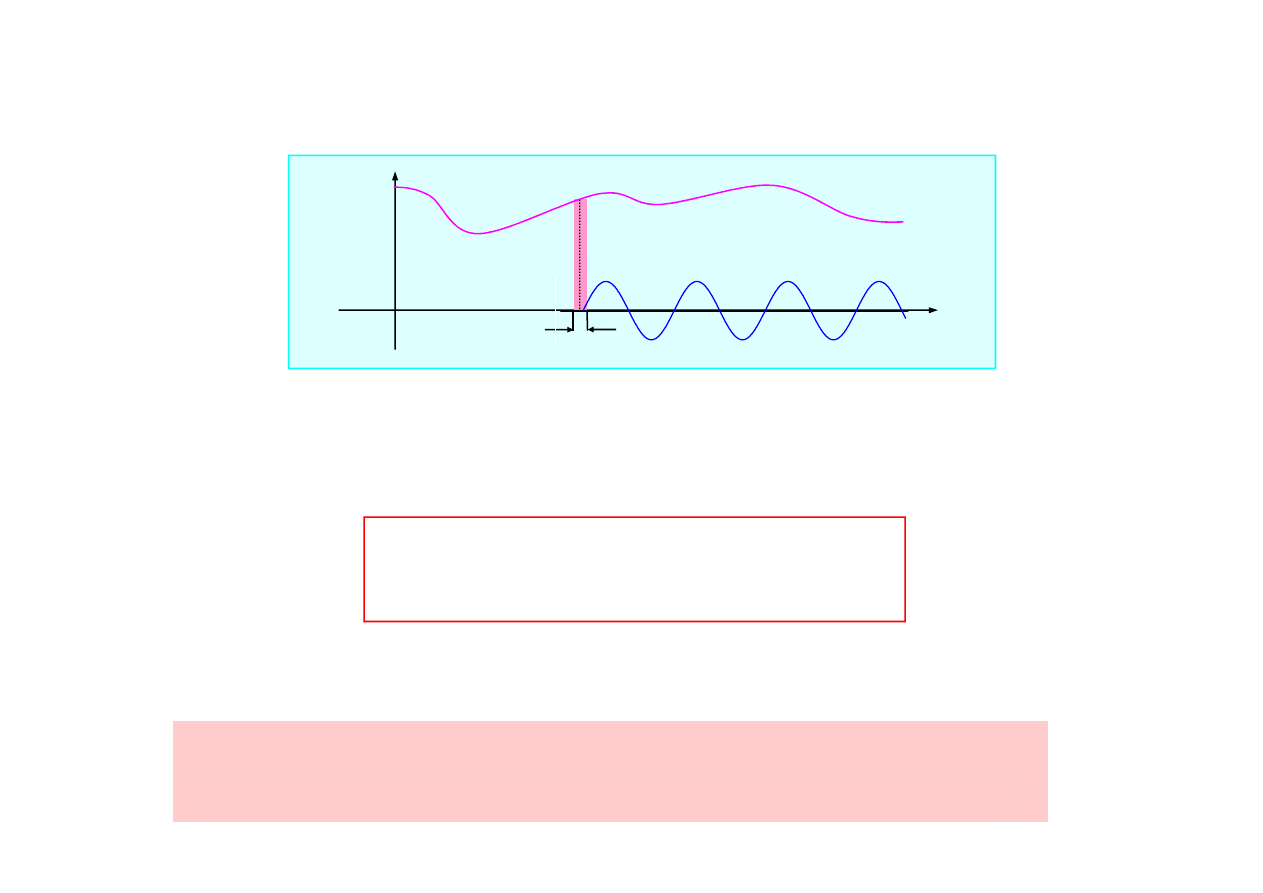
Odpowied
ź
układu na wymuszenie funkcj
ą
f(t) w przedziale czasu [0,t]
przy zerowych warunkach pocz
ą
tkowych w chwili t = 0 wyra
ż
a si
ę
za
)
(
)
(
)
(
)
(
)
(
τ
τ
τ
τ
τ
−
=
−
=
t
g
d
f
t
g
dI
t
dx
f(
τ
)
τ
d
τ
f(
τ
)
f(
τ
)d
τ
g(t-
τ
)
)
4
.
9
.
1
.
2
(
2.1.9. Drgania wymuszone sił
ą
dowoln
ą
© F.A. Dul 2009
∫
∫
−
=
−
=
t
t
d
t
g
f
t
g
dI
t
x
0
0
)
(
)
(
)
(
)
(
τ
τ
τ
τ
przy zerowych warunkach pocz
ą
tkowych w chwili t = 0 wyra
ż
a si
ę
za
pomoc
ą
całki Duhamela
)
5
.
9
.
1
.
2
(
Rozwi
ą
zanie x(t) wyra
ż
one poprzez całk
ę
Duhamela jest zgodne z
zasad
ą
przyczynowo
ś
ci
:
Ruch w chwili t > 0 zale
ż
y tylko od sił działaj
ą
cych w przedziale
[0,t], nie zale
ż
y za
ś
od sił pó
ź
niejszych,
τ
> t.
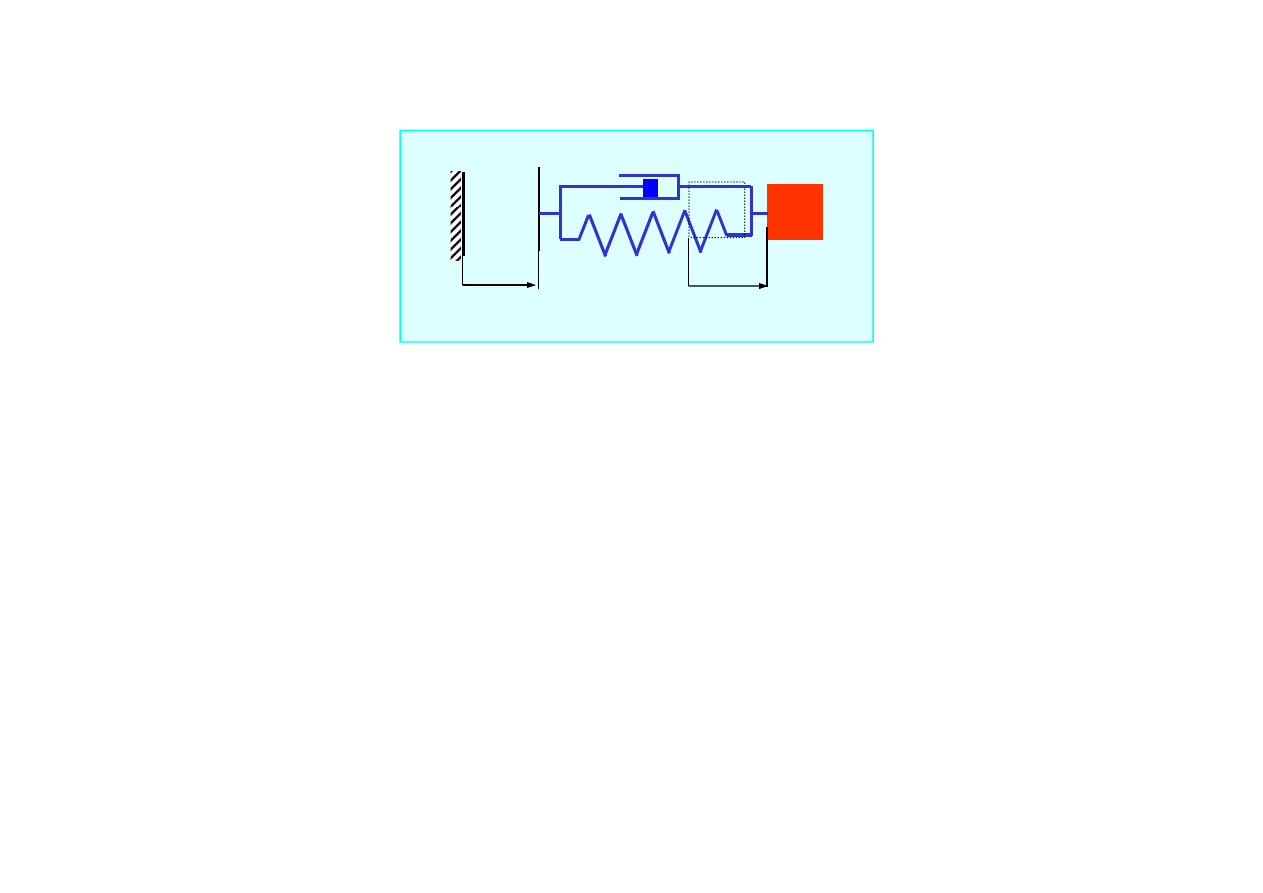
m
k
x(t)
c
ξξξξ
(t)
)
(
ξ
−
−
=
x
k
F
S
Siła spr
ęż
ysta
Siła oporu (tłumienie)
)
(
ξ
&
&
−
−
=
x
c
F
2.1.10. Drgania wymuszone kinematycznie
© F.A. Dul 2009
)
(
)
(
ξ
ξ
&
&
&
&
−
−
−
−
=
x
c
x
k
x
m
Siła oporu (tłumienie)
)
(
ξ
&
&
−
−
=
x
c
F
D
)
(
)
(
t
c
t
k
kx
x
c
x
m
ξ
ξ
&
&
&
&
+
=
+
+
Równanie ruchu
Posta
ć
równania ruchu drga
ń
wymuszonych kinematycznie jest
równowa
ż
na postaci równania drga
ń
wymuszonych sił
ą
)
(
)
(
)
(
t
c
t
k
t
F
ξ
ξ
&
+
=
)
1
.
10
.
1
.
2
(
)
2
.
10
.
1
.
2
(

Je
ż
eli wymuszenie
ξξξξ
(t) jest harmoniczne,
)
sin(
)
(
ϕ
ξ
+
Ω
=
t
H
t
)
cos(
)
sin(
)
(
ϕ
ϕ
+
Ω
Ω
+
+
Ω
=
t
H
c
t
kH
t
F
to siła wymuszaj
ą
ca ma posta
ć
2.1.10. Drgania wymuszone kinematycznie
Sił
ę
t
ę
mo
ż
na sprowadzi
ć
do siły harmonicznej
)
sin(
)
(
β
+
Ω
=
t
A
t
F
)
3
.
10
.
1
.
2
(
)
4
.
10
.
1
.
2
(
)
5
.
10
.
1
.
2
(
© F.A. Dul 2009
)
sin(
)
(
β
+
Ω
=
t
A
t
F
)
sin(
β
+
Ω
=
+
+
t
A
kx
x
c
x
m
&
&
&
)
5
.
10
.
1
.
2
(
)
6
.
10
.
1
.
2
(
Równanie drga
ń
wymuszonych kinematycznie przebiegiem
harmonicznym ma wi
ę
c posta
ć
Drgania opisane równaniem (2.1.7.6) bada si
ę
wi
ę
c tak samo jak
drgania wymuszone sił
ą
harmoniczn
ą
.

•
Cz
ę
sto
ść
drga
ń
układu wymuszonego sił
ą
harmoniczn
ą
jest równa
cz
ę
sto
ś
ci siły wymuszaj
ą
cej.
•
Po stłumieniu stanów przej
ś
ciowych układ drga z cz
ę
sto
ś
ci
ą
siły
wymuszaj
ą
cej.
•
Je
ż
eli cz
ę
sto
ść
siły wymuszaj
ą
cej jest równa cz
ę
sto
ś
ci własnej układu,
to wyst
ę
puje rezonans.
•
Amplituda drga
ń
w rezonansie mo
ż
e by
ć
wielokrotnie wi
ę
ksza ni
ż
poza nim.
Wnioski
2.1. Drgania wymuszone
© F.A. Dul 2009
poza nim.
•
W układzie bez tłumienia amplituda drga
ń
w rezonansie ro
ś
nie
nieograniczenie.
•
Przemieszczenie układu jest opó
ź
nione w fazie wzgl
ę
dem siły
wymuszaj
ą
cej o k
ą
t zale
ż
ny od stosunku cz
ę
sto
ś
ci wymuszenia i
cz
ę
sto
ś
ci drga
ń
własnych układu.
•
W rezonansie przemieszczenie układu jest opó
ź
nione w fazie
wzgl
ę
dem siły wymuszaj
ą
cej o k
ą
t
π
/2.
•
Ruch układu pod działaniem siły dowolnej mo
ż
e by
ć
uwa
ż
any za
zło
ż
enie ruchów wymuszonych impulsami lub skokami jednostkowymi.
Wyszukiwarka
Podobne podstrony:
P 10 id 343561 Nieznany
dodawanie do 10 4 id 138940 Nieznany
ldm rozmaite 10 id 264068 Nieznany
Dubiel LP01 MRS 10 id 144167 Nieznany
I CSK 305 10 1 id 208211 Nieznany
IMG 10 id 211085 Nieznany
na5 pieszak 03 02 10 1 id 43624 Nieznany
img 10 id 211004 Nieznany
cwicz 10 F id 124010 Nieznany
IMG 10 id 210949 Nieznany
Chemia 10 3 id 111757 Nieznany
IMG 10 id 210983 Nieznany
BiolMol 10 id 87436 Nieznany
egzamin09 10 id 153651 Nieznany
ETI Semestr 5 inz 10 10 id 1644 Nieznany
dodawanie do 10 3 id 138939 Nieznany
czynniki biologiczne 10 id 6672 Nieznany
więcej podobnych podstron