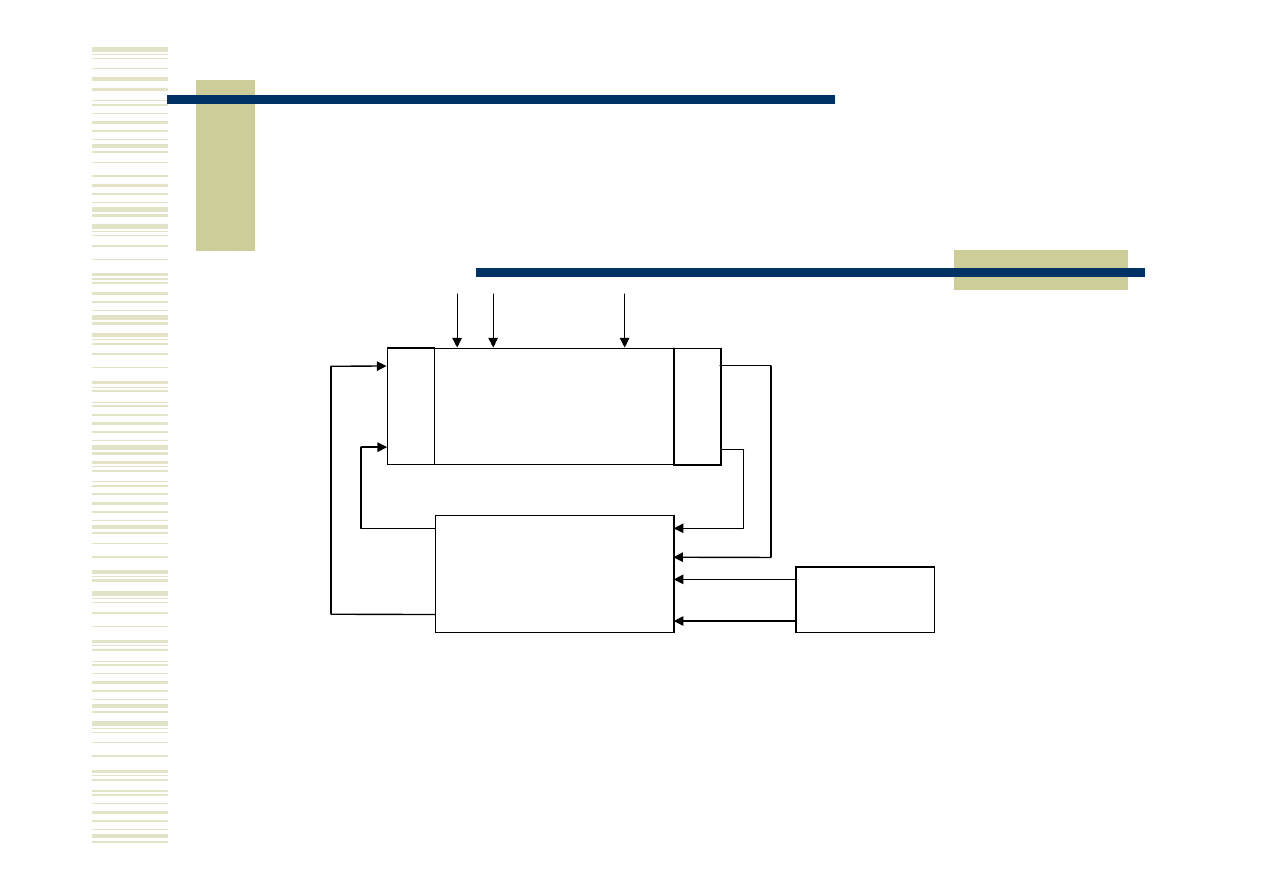
Układ logiczny
z
1
z
2
z
k
U
rz
ą
dze
n
ia
w
yk
ona
w
c
ze
OBIEKT
U
rz
ą
dz
en
ia
p
omiaro
w
e
#
#
U
w
U
p
x
1
x
m
y
1
UKŁAD LOGICZNY
x
m
y
2
w
l
w
1
#
#
OPERATOR
Z obiektem sterowania związane są:
Z obiektem sterowania związane są:
− urządzenia służące do pomiaru i przetwarzania danych o stanie obiektu
(x1, x2, …, xm) – sensory,
− urządzenia służące do przetwarzania i wzmacniania sygnałów
urządzenia służące do przetwarzania i wzmacniania sygnałów
wykonawczych (y1, y2, …, yn) – aktory,
− wielkości zakłócające proces (z1, z2, …, zk ).
Prawa algebry logiki
Dwuelementowa algebra Boole’a jest aksjomatyczną teorią funkcji
j d
t
j
ji i
t
j k i k ji
lt
t
i d ó h
jednoargumentowej negacji i n-argumentowej koniunkcji oraz alternatywy i dwóch
wartości 0; 1. Definicję negacji funkcji jednoargumentowej oraz koniunkcji
(iloczynu logicznego) i alternatywy (sumy logicznej) funkcji dwuargumentowej
przedstawiono w tabeli 1 a b c
a)
b)
c)
x
y
=
2
1
x
x
y
=
2
1
x
x
y
+
=
przedstawiono w tabeli 1.a, b, c.
1
x
y
1
x
2
x
y
1
x
2
x
y
0 1
0
0
0 0
0
0
1
0
0
1
0
0
1
1
1
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
1
1
1
Kolejność wykonywania działań, gdy wyrażenie nie zawiera nawiasów, jest
następująca: negacja, koniunkcja, alternatywa. Z definicji wyżej wymienionych
działań wynikają następujące zależności:
Prawa algebry logiki
0
Podstawowe prawa algebry Boole’a są następujące:
− prawa przemienności
0
0
1
1
1
0
=
⋅
=
⋅
=
+
=
+
=
+
=
+
x
x
x
x
x
x
x
x
x
x
x
x
1
2
2
1
1
2
2
1
x
x
x
x
x
x
x
x
⋅
=
⋅
+
=
+
− prawa łączności
0
1
=
⋅
=
⋅
x
x
x
x
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
)
(
)
(
)
(
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
=
=
+
+
=
+
+
=
+
+
− prawa de Morgana
p
g
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
+
+
=
=
+
+
− prawo podwójnego zaprzeczenia
x
x
=
− reguły sklejania
(
)(
)
,
,
1
2
1
2
1
1
2
1
2
1
x
x
x
x
x
x
x
x
x
x
=
+
=
+
+
,
,
2
1
2
1
1
2
1
2
1
1
x
x
x
x
x
x
x
x
x
x
+
=
+
+
=
+
Tworzenie funkcji logicznej
Postać normalna sumy tworzona jest na podstawie wszystkich wierszy tabeli zależności,
w których funkcja logiczna przyjmuje wartość 1. Poszczególne składniki tej sumy są
iloczynami wszystkich zmiennych wejściowych, przy czym zmienne posiadające w danym
oc y
ws ys
c
e
yc wejśc owyc , p y c y
e
e pos d jące w d y
wierszu wartość 0 pisane są ze znakiem negacji, natomiast posiadające wartość 1 – bez
znaku negacji.
Postać normalna iloczynu tworzona jest na podstawie wszystkich wierszy tabeli zależności,
w których funkcja logiczna przyjmuje wartość 0. Poszczególne czynniki tego iloczynu są
sumą wszystkich zmiennych wejściowych, przy czym zmienne posiadające w danym
wierszu wartość 0 pisane są bez znaku negacji, natomiast posiadające wartość 1 – ze
znakiem negacji.
Postać normalna iloczynu i postać normalna sumy są równoważne.
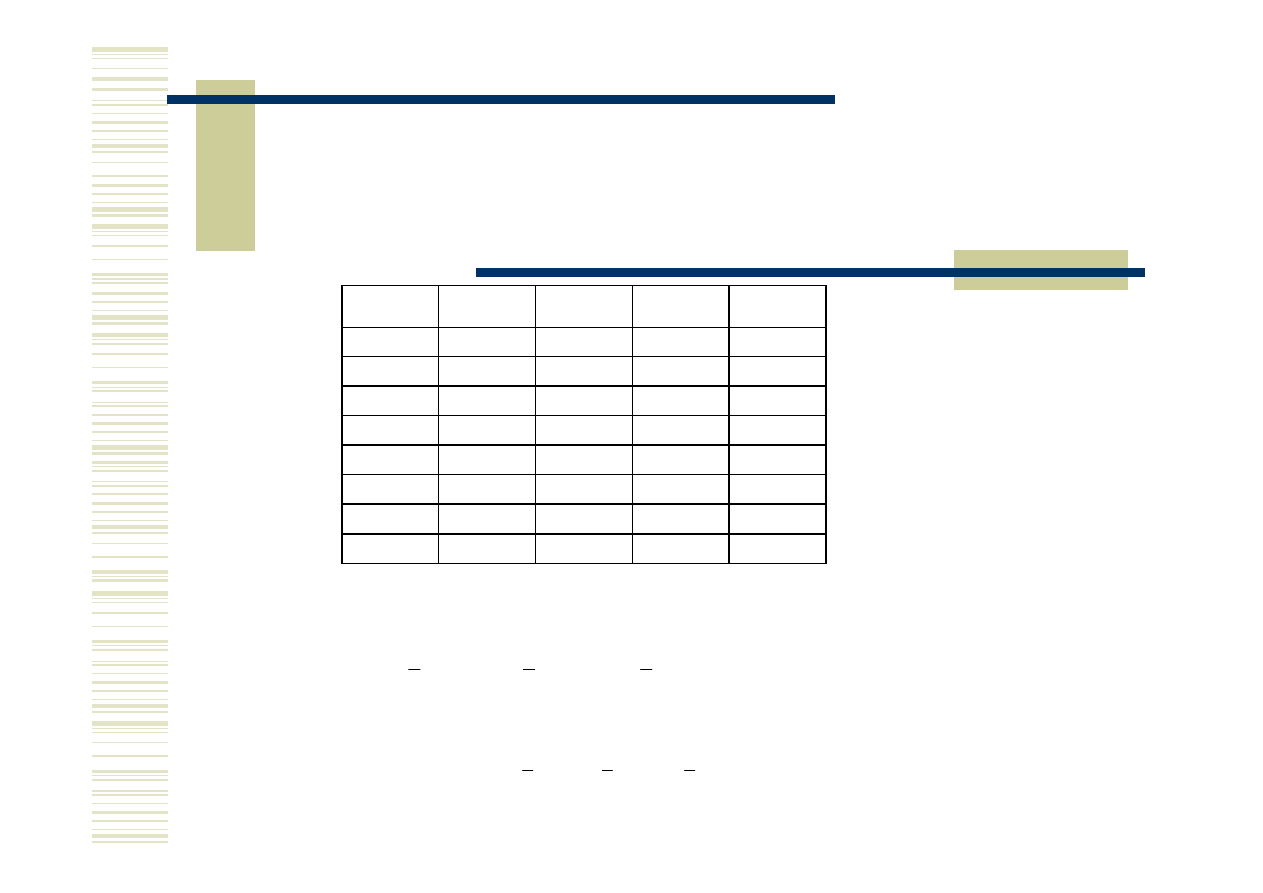
Przykład rozwiązania
Lp.
1
x
2
x
3
x
y
0
0
0
0
0
0
0
0
0
0
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4
1
0
0
0
5 1 0 1 1
6 1 1 0 1
7
1
1
1
1
7
1
1
1
1
Zgodnie z wyżej podanymi zasadami:
−
normalna zupełna postać alternatywna (sumy)
normalna zupełna postać alternatywna (sumy)
(a)
−
normalna zupełna postać koniunkcyjna (iloczynu)
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
y
+
+
+
=
normalna zupełna postać koniunkcyjna (iloczynu)
(b)
)
)(
)(
)(
(
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
y
+
+
+
+
+
+
+
+
=
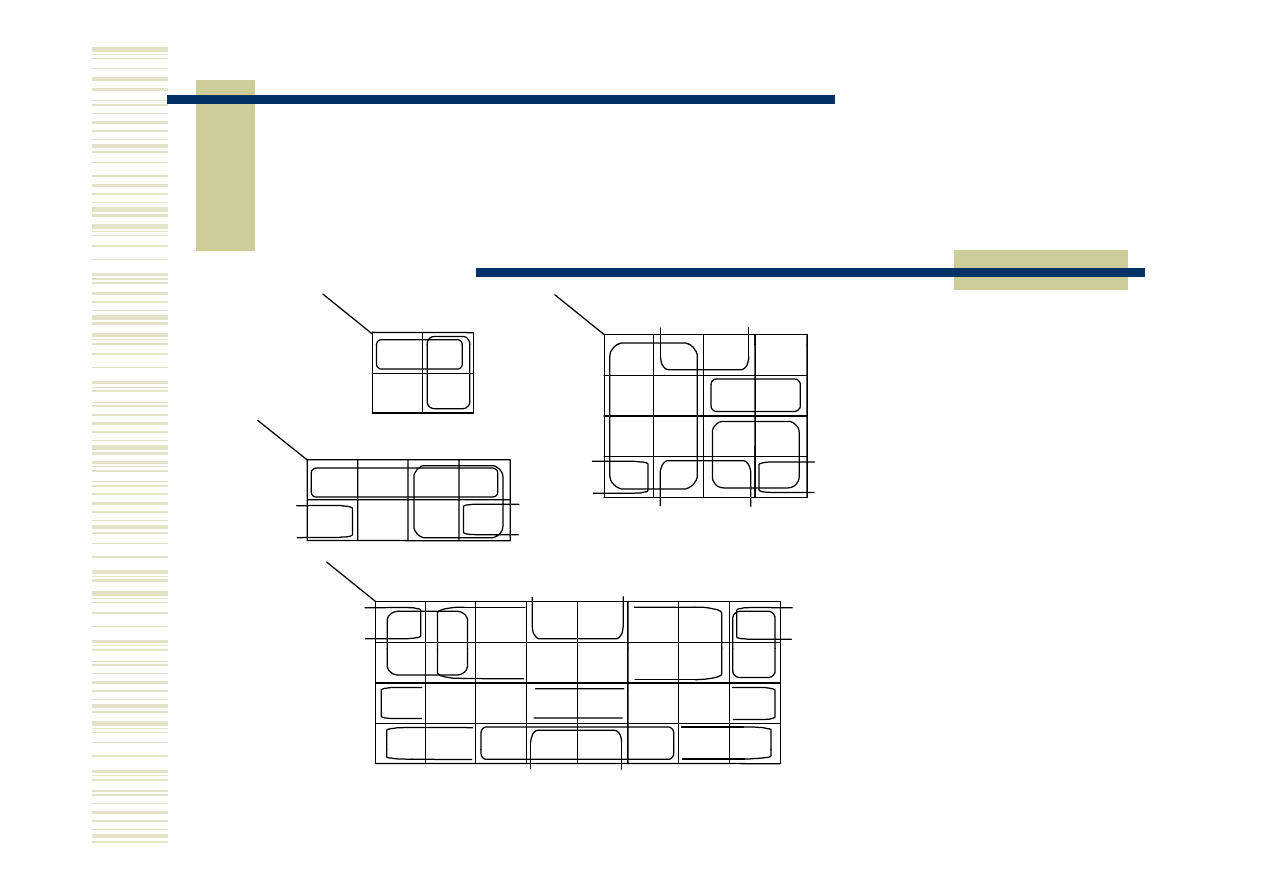
Minimalizacja funkcji logicznych
Minimalizacja funkcji logicznych
metodą Karnaugha
ą
g
c)
a)
x
2
x
1
0
1
x
3
x
4
x
1
x
2
00
01
11
10
b)
0
1
x
2
x
3
00
01
11
01
00
01
11
x
1
00
01
11
01
0
1
10
-
d)
x
3
x
4
x
5
x
1
x
2
000
001
011
010
110
111
100
101
00
01
11
10
10
Tabele Karnaugha dla dla funkcji 2-, 3-, 4- i 5-cio argumentowych
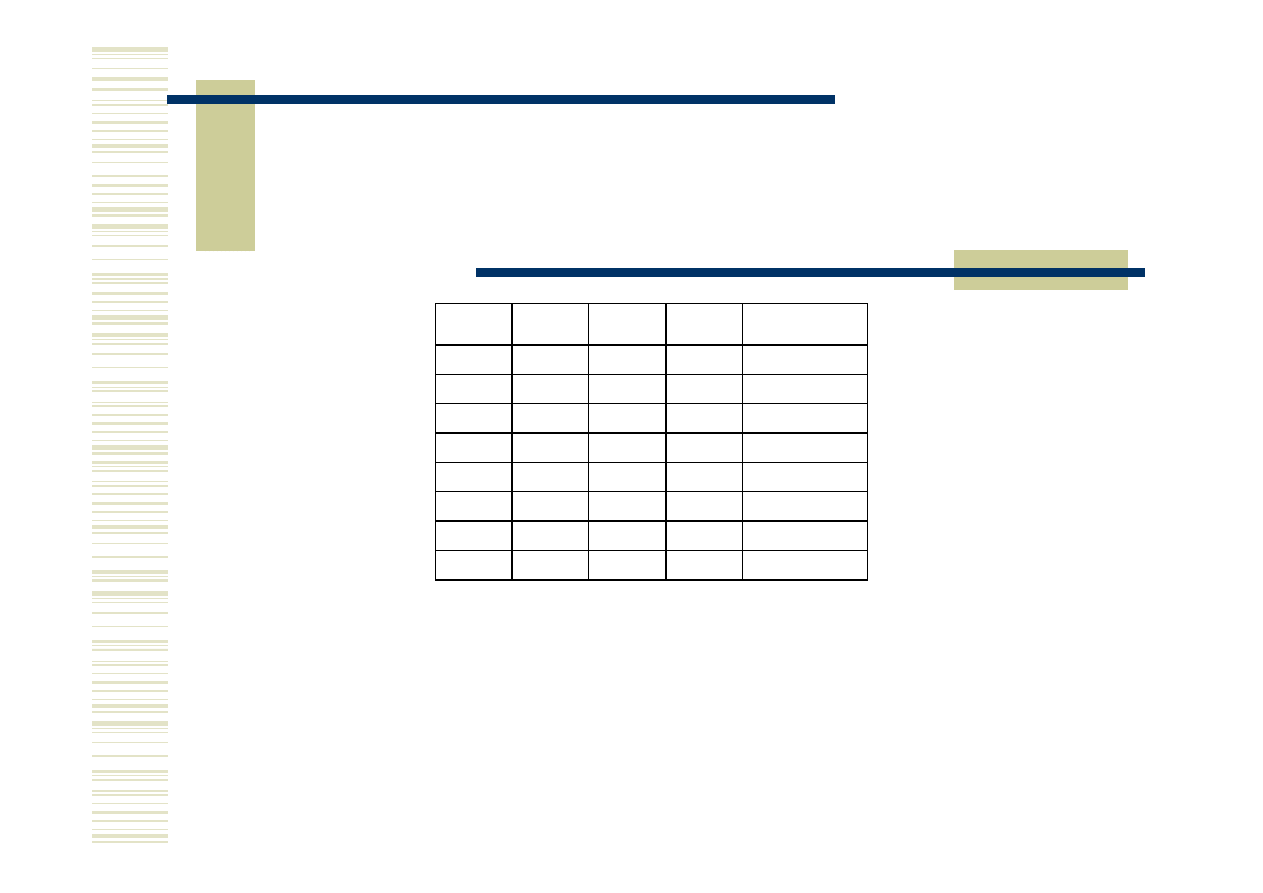
Zadanie do rozwiązania
lp.
1
x
2
x
3
x
y
0 0 0 0 0
1 0 0 1 1
2 0 1 0 1
3
0
1
1
1
3
0
1
1
1
4 1 0 0 0
5 1 0 1 0
6
1
1
0
1
7 1 1 1 1
Wyznaczyć postacie minimalne (alternatywną i koniunkcyjną) funkcji logicznej określonej
Wyznaczyć postacie minimalne (alternatywną i koniunkcyjną) funkcji logicznej określonej
za pomocą powyższej tabeli metodą tabel Karnaugha.
Metoda Quine’a McCluskeya
Metoda ta stosowana jest dla układów, które posiadają więcej niż
5 sygnałów wejściowych.
Metoda Quine’a Mc Cluskeya jest zazwyczaj wykorzystywana
y j
y
j y
y y
podczas komputerowo wspomaganej minimalizacji, ponieważ
oparta jest na dużej ilości stosunkowo prostych i powtarzalnych
kroków, polegających na porównywaniu ciągu znaków, które
można zapisać w postaci pętli.
Sygnał jest kształtowany zgodnie z określonym wcześniej przez
projektanta algorytmem.
O i
t d Q i ’ M Cl k
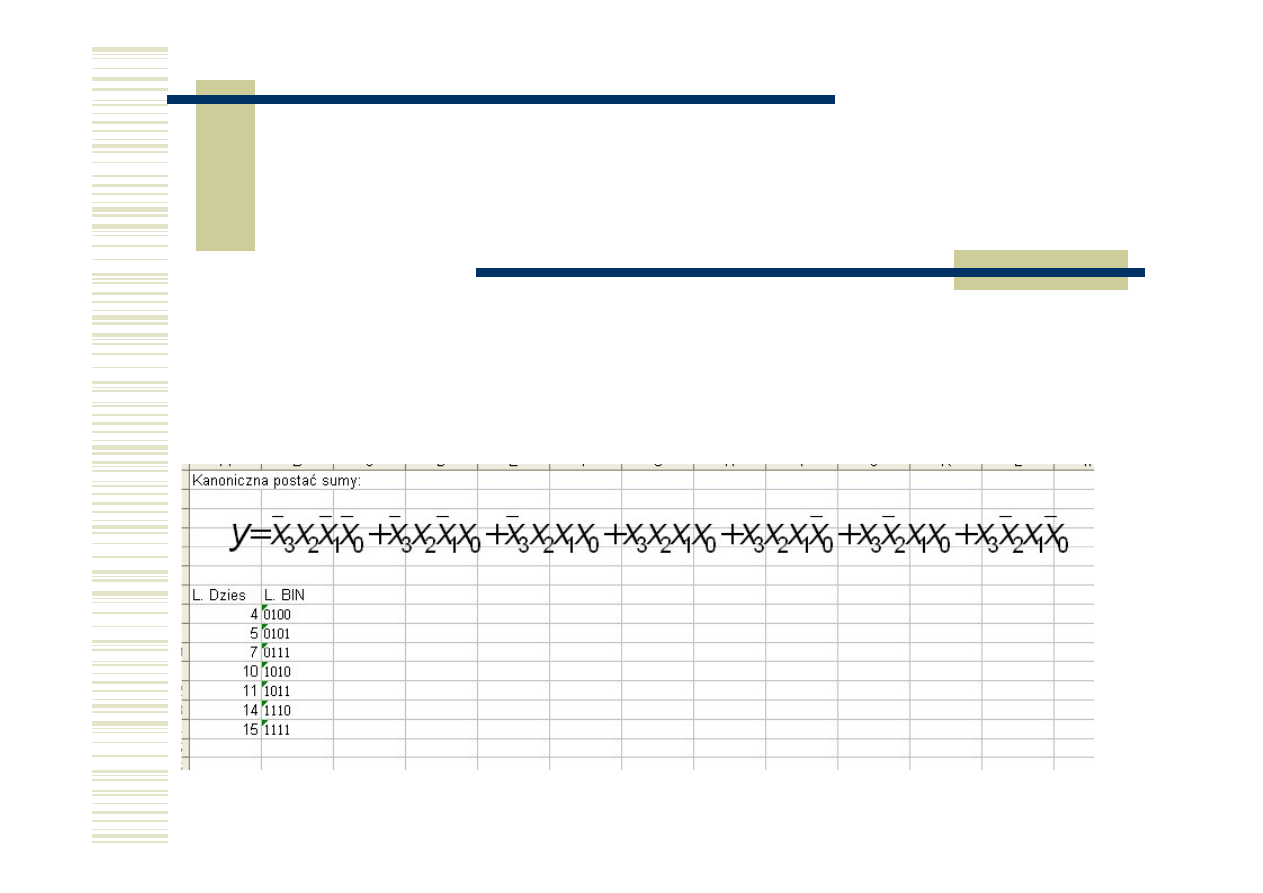
Opis metody Quine’a Mc Cluskeya
Pierwszy krok podstawowej jej wersji polega na wypisaniu (w postaci kolumnowej
ciągów zero-jedynkowych) wszystkich wartości składników postaci kanonicznej
sumy. Następnie porządkuje się tę kolumnę, dzieląc ją na grupy o jednakowej
liczbie jedynek w wierszu.
M t d Q i ’ M Cl k
d
Metoda Quine’a Mc Cluskeya - cd
01009
01019
01009
-----
010-
----
1- 1 -
01019
01119
11119
11109
-----
01019
10109
-----
----
01-1
1-109
101-9
10119
10109
01119
11109
10119
-----
----
-111
111-9
1-119
-----
11119
1-119
Wiersze różniące się w jednym tylko miejscu skleja się, tworząc następną kolumnę, przy
czym sklejenie np. 010 z 011 daje 01-. Kreska (lub znak x) oznacza, że argument
y
j
p
j
(
)
,
g
odpowiadający tej pozycji nie wchodzi do zapisu. Wynik ten zapisywany jest w kolejnej
kolumnie. Uprzedni podział na grupy upraszcza wyszukiwanie wyrażeń sąsiednich, gdyż
wiadomo, że muszą one należeć do dwóch różnych kolejnych grup. Sklejone wyrażenia
i
b
dk ślić f kt ż
t
t
j k l
i
oznacza się, aby podkreślić fakt, że są one reprezentowane w następnej kolumnie.
M t d Q i ’ M Cl k
d
Metoda Quine’a Mc Cluskeya - cd
Tabela implikantów do wyznaczenia postaci minimalnej
0100
0101
0111
1111
1110
1011
101
p
y
p
j
funkcji logicznej
0
010-
×
×
01-1
×
×
111
×
×
-111
×
×
1-1-
×
×
×
×
1 1
R li
j f k ji l i
j
Realizacja funkcji logicznej
x
y
Tabela zależności
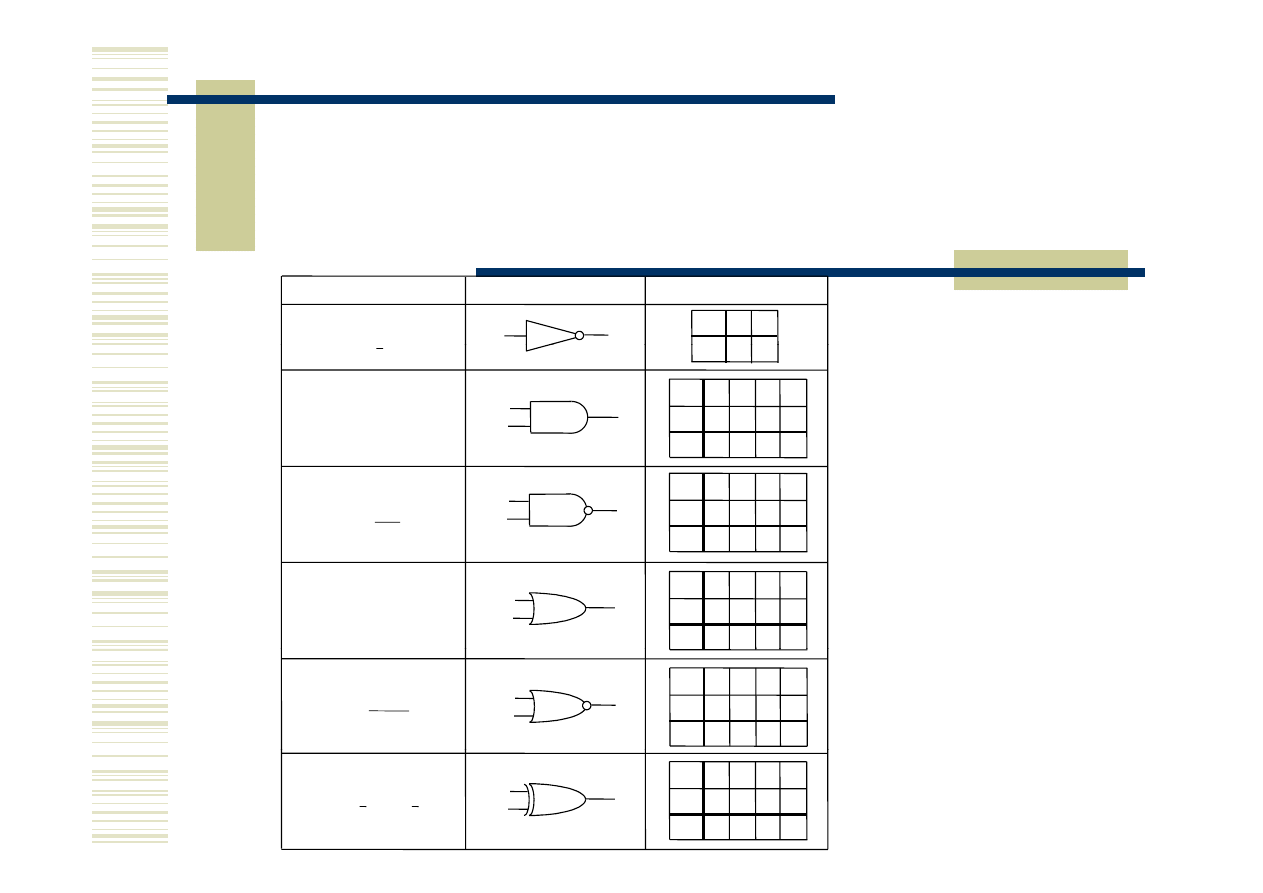
Nazwa funkcji
Symbol graficzny
Negacja
NOT
1
0
y
0
1
x
x
2
x
1
y
x
y =
Koniunkcja
AND
2
1
x
x
y =
1
0
y
0
0
0
1
1
x
1
0
0
0
1
y
0
1
0
1
x
2
Negacja koniunkcji
NAND
2
1
x
x
y =
x
2
x
1
y
0
0
0
1
1
x
1
1
1
1
0
y
0
1
0
1
x
2
0
0
0
1
y
x
2
x
1
y
Alternatywa
OR
2
1
x
x
y
+
=
0
0
0
1
1
x
1
0
1
1
1
y
0
1
0
1
x
2
Negacja alternatywy
NOR
2
1
x
x
y
+
=
x
2
x
1
y
0
0
0
1
1
x
1
1
0
0
0
y
0
1
0
1
x
2
Nierównoważność
EXOR
2
1
2
1
x
x
x
x
y
+
=
x
2
x
1
y
0
0
0
1
1
x
1
0
1
1
0
y
0
1
0
1
x
2
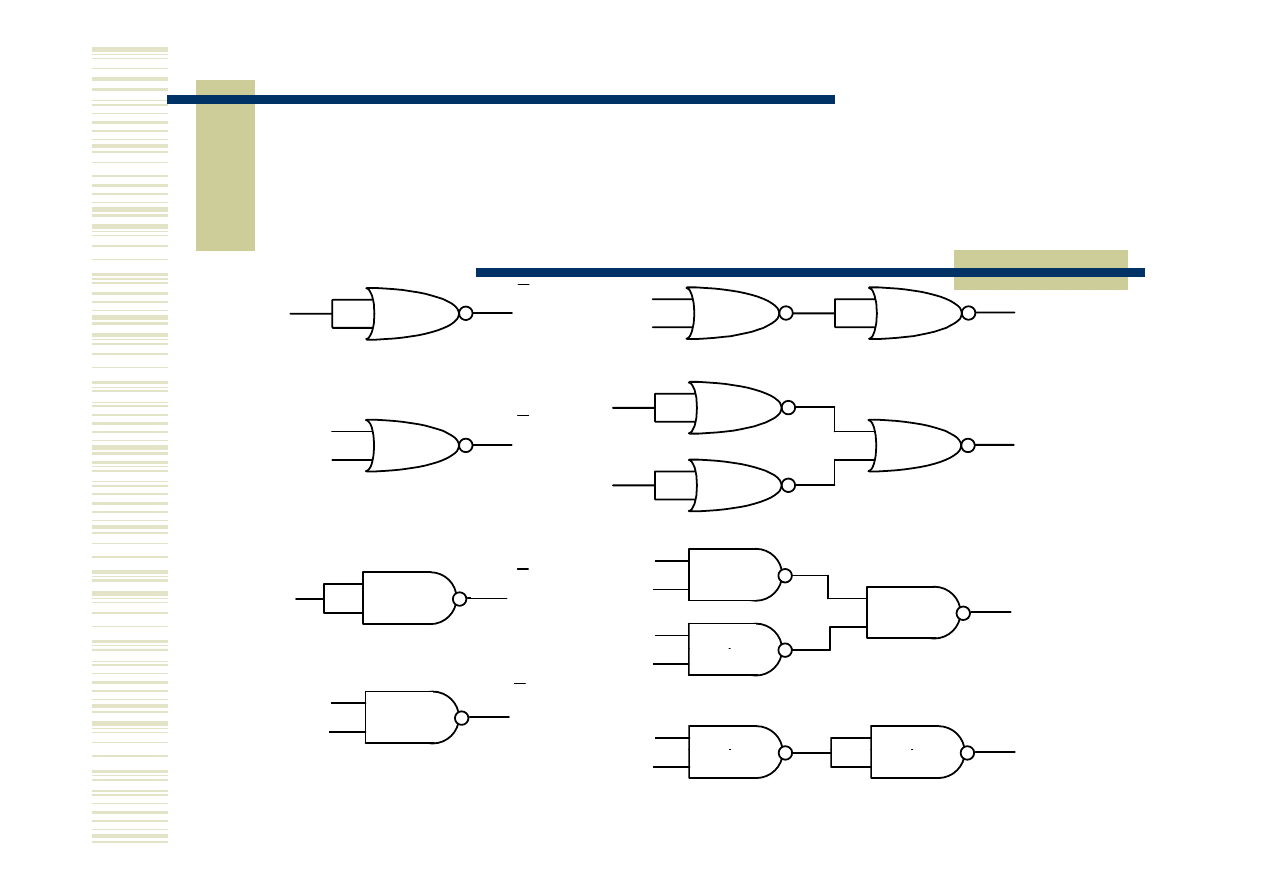
Realizacja funkcji logicznej - cd
a)
x
x
y
=
x
2
x
1
2
1
x
x
y
+
=
x
x
y
=
x
1
2
1
x
x
y
=
b)
0
x
2
b)
x
x
y
=
x
2
x
1
x
1
2
1
x
x
y
+
=
1
x
x
y
=
x
2
2
1
x
x
y
=
x
1
x
2
Realizacja funkcji logicznych negacji, alternatywy i koniunkcji za pomocą elementów
a) NOR, b) NAND
Realizacja funkcji logicznej - cd
Do realizacji funkcji logicznych (schematów tych funkcji) stosowane są elementy:
Do realizacji funkcji logicznych (schematów tych funkcji) stosowane są elementy:
elektroniczne (tranzystory), elektryczne (przekaźniki), pneumatyczne (zawory
rozdzielające) i inne. W przeszłości (przed pojawieniem się sterowników) wiele
firm na świecie projektowało systemy funkcjonalnie pełne elementów logicznych
firm na świecie projektowało systemy funkcjonalnie pełne elementów logicznych,
a układy sterowania realizowano przy użyciu tych elementów. Obecnie układy
sterujące realizowane są w sterownikach dzięki opracowywanym programom.
Tym niemniej w przemyśle maszynowym układy sterowania, realizujące
y
j
p
y
y
y
y
,
ją
określone funkcje logiczne, budowane są z elementów pneumatycznych
rozdzielających (zawory rozdzielające), sterujących kierunkiem przepływu
powietrza.
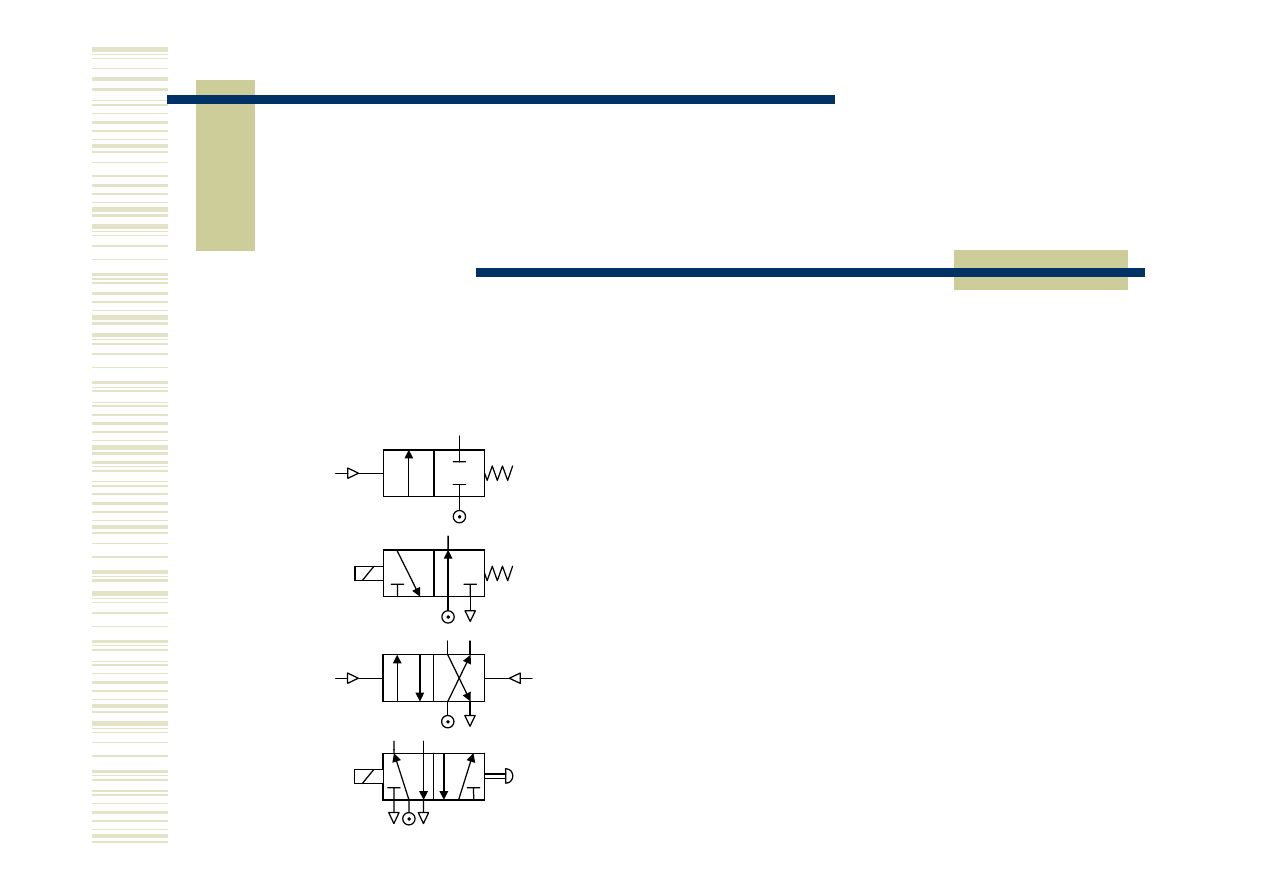
Realizacja funkcji logicznej - cd
Znaczenie symboli na elementach pneumatycznych:
A, B, C, ... – przyłącza robocze (wyjściowe) ,
P
il i
i t
t ść
ł
ó
1
P
– zasilanie powietrzem – wartość sygnału równa 1,
R, S, T, ... – odpowietrzenie – wartość sygnału równa 0,
X, Y, Z, ... – przyłącza sterujące (wejściowe).
A
Zawór rozdzielający dwupołożeniowy
P
ją y
p
y
(dwa pola) dwudrogowy normalnie zamknięty
sterowany z jednej strony sprężyną
z drugiej strony sygnałem ciśnieniowym
(wzrost ciśnienia)
B
Zawór rozdzielający dwupołożeniowy
X
Z
P
R
ją y
p
y
trzydrogowy normalnie otwarty sterowany
z jednej strony sprężyną z drugiej strony
sygnałem elektrycznym
A
B
Zawór rozdzielający dwupołożeniowy
Z
A
P
Y
R
B
X
Zawór rozdzielający dwupołożeniowy
czterodrogowy normalnie zamknięty
sterowany obustronnie sygnałem
ciśnieniowym (wzrost ciśnienia)
Zawór rozdzielający dwupołożeniowy
A
B
Zawór rozdzielający dwupołożeniowy
pięciodrogowy sterowany z jednej strony
przyciskiem z drugiej strony sygnałem
elektrycznym
R P S
A
B
Z
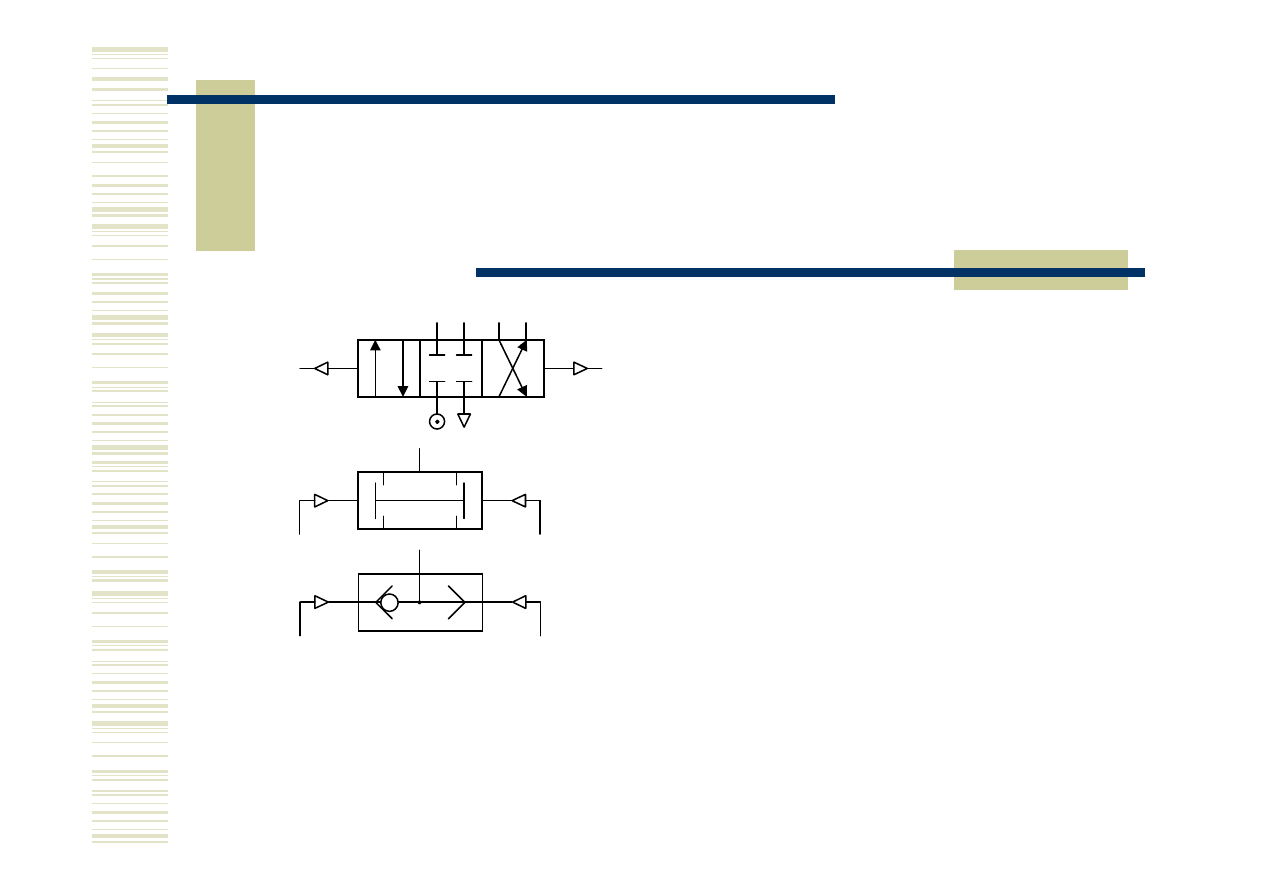
Realizacja funkcji logicznej - cd
A
B
Zawór rozdzielający trzypołożeniowy
t
d
ł ż i ś dk
P
T
X
czterodrogowy w położeniu środkowym
zamknięty, obustronnie sterowany sygnałem
ciśnieniowym (spadek ciśnienia)
Y
Zawór podwójnego sygnału
(koniunkcji A = X Y)
A
Y
X
Zawór przełącznik biegu
(alternatywy A = X + Y
A
Y
X
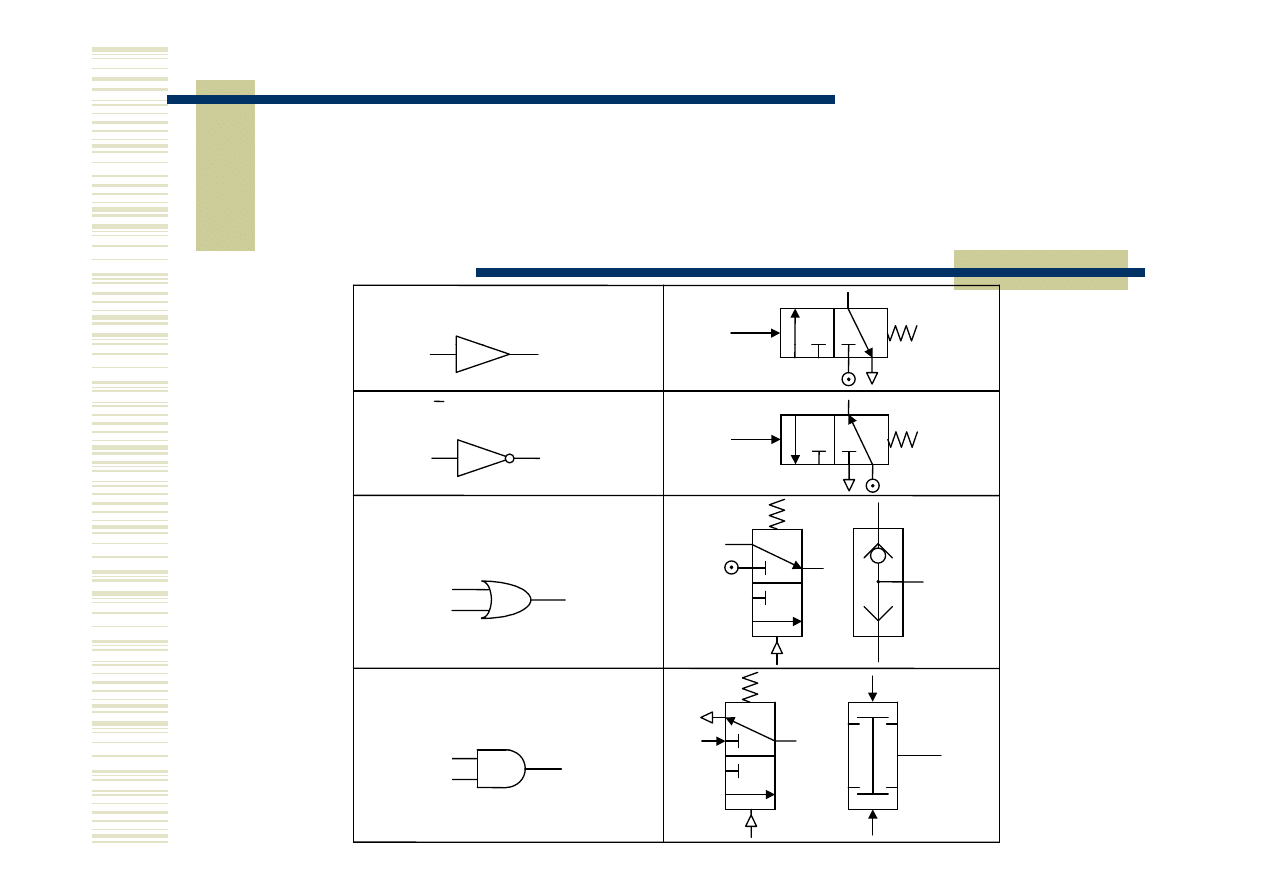
Realizacja funkcji logicznej
Realizacja funkcji logicznej -
przykłady
x
y
y
x
a) y = x
x
y
x
y
y
x
b) y = x
x
y
c) y = x
1
+ x
2
x
1
x
2
y
x
2
x
1
y
y
d) y = x
1
x
2
x
2
x
1
x
2
y
y
x
2
x
1
y
x
1
x
2
x
1
y
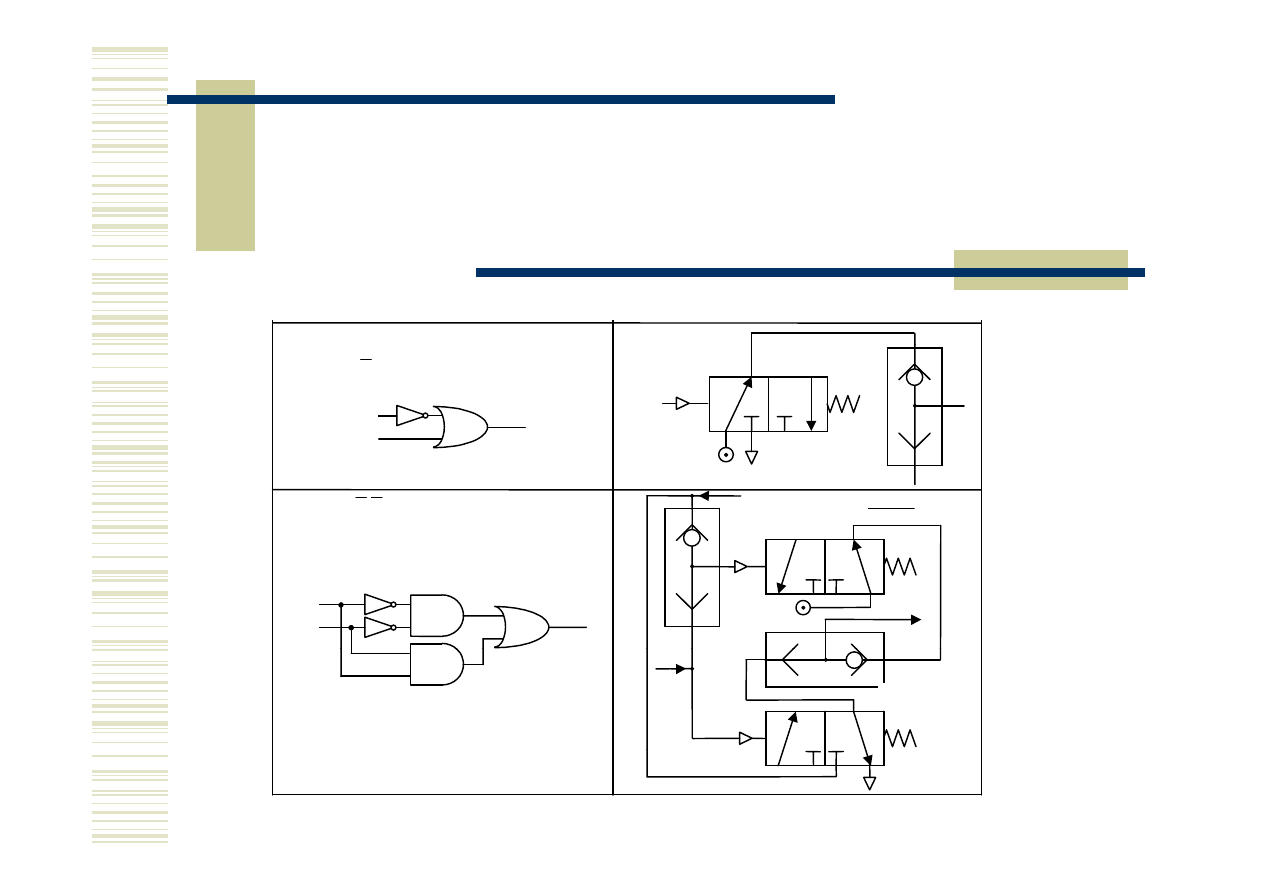
Realizacja funkcji logicznej
Realizacja funkcji logicznej -
przykłady
p y
y
e) y = x
1
+ x
2
x
2
x
1
y
x
1
y
f) y = x
1
x
2
+ x
1
x
2
x
2
x
1
x
1
+ x
2
y
x
2
x
1
y
x
2
x
1
+ x
2
.
Dziękuję za uwagę
Dziękuję za uwagę