Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

Rozwiązania

1.

( ( p ↔ q ) ˄ ( ~ q ˄ r ) ) → ( ( r ˄ ~ q ) → ( q ↔ p ) )

2.

( ( ( q ↔ r ) → p ) v ~ s ) ) → ( ( p ↓ r ) / ( t ˄ s ) )

3.

( ( ( p ˄ q ˄ r ) → ~ s ) ˄ ( ~ r ˄ t ) ) → ( ( q ↓ t ) → ( ~ p / ~ s ) )

4.

( ( ~ p ↔ q ) v ( r → ~ s ) ) → ( ( s / q ) → ~ r )

5.

( ( ( p ˄ q ) → ( r ┴ s ) ) ˄ ( t → ~ s) ) → ( ( ( r ↓ q ) ↔ t ) / ( ~ s ˄ p ) )

6.

( ( p → ( q ˄ r ) ) ↓ ( ~ s / q ) ) → ( ( ~ r v q ) → s )

7.

( ~ p ˄ ( q ┴ r ) ) → ( ( ( s ↓ q ) → r ) v ( ~ p ↔ r ) )

8.

( ( ( p v q ) → ( r / s ) ) ↓ p ) → ( ( q / r ) ↔ ( ~ s ˄ p ) )

9.

( ( r → ( p → q ) ) ˄ ( s / ( q ↓ p ) ) ) → ( s ┴ q )

10.

( ( ( p ↓ q ) ↔ ( r ┴ ~ s ) ) ˄ ( s ˄ q ) ) → ( ( ~ r ˄ p ) / t )

11.

( ( ( q ˄ r ) → p ) ˄ ( ~ ( p ↓ q ) ˄ s ) ) → ( ~ s / ( ~ q → r ) )

12.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

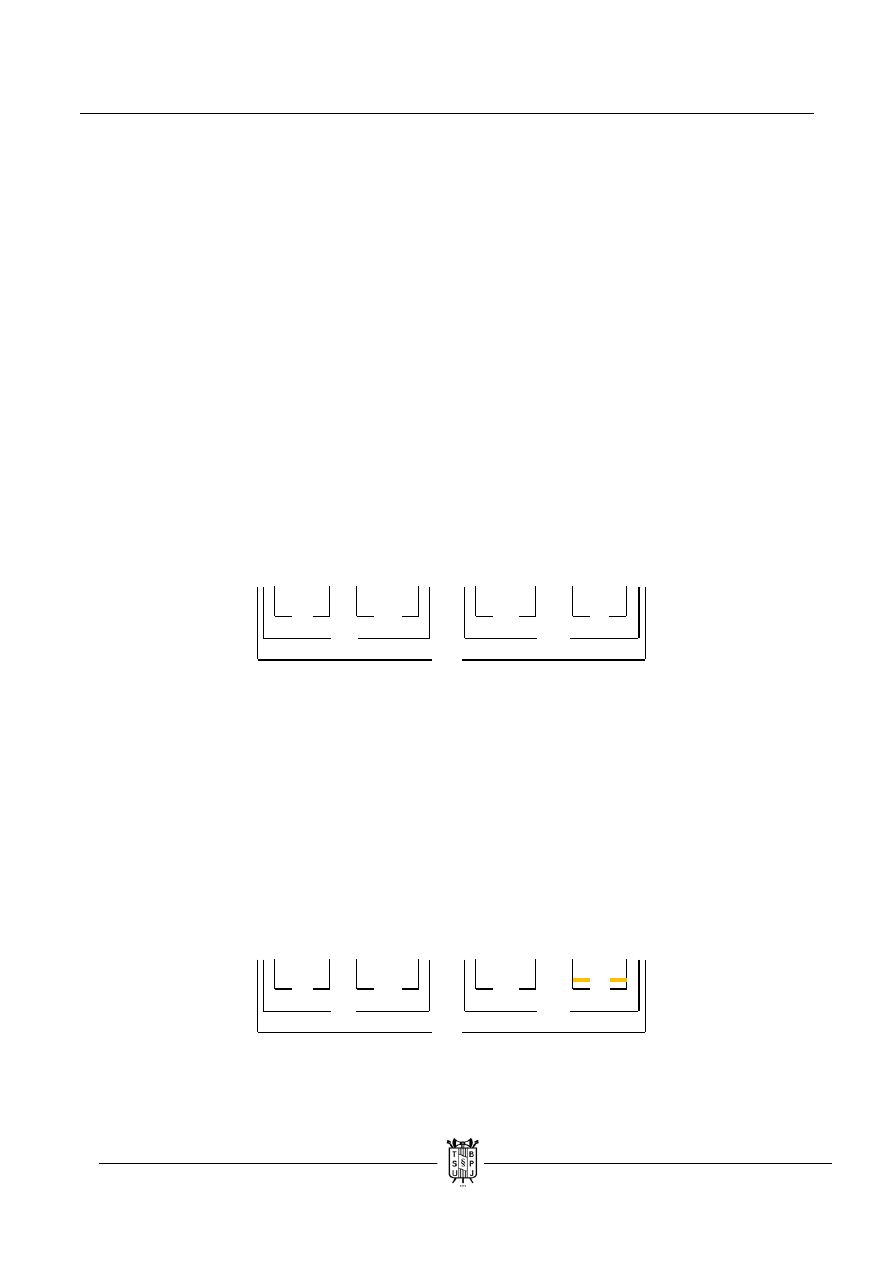
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

1.

( ( p ↔ q ) ˄ ( ~ q ˄ r ) ) → ( ( r ˄ ~ q ) → ( q ↔ p ) )

a. Zaczynamy od założenia, że całe wyrażenie ma wartość fałszu. Ponieważ implikacja jest

fałszywa tylko w jednym przypadku (1,0), to jej poprzednikowi nadajemy wartość
prawdy, a następnikowi wartość fałszu. Mamy teraz prawdziwą koniunkcję i fałszywą
implikację. Sytuacja jest o tyle prosta, że w obu wypadkach dzieje się tak tylko w jednym
przypadku. Zaczynając od lewej strony mamy prawdziwą równoważność, która przybiera
taką wartość w dwóch przypadkach (1,1 i 0,0). Na razie ją zostawiamy. Przechodzimy
do prawdziwej koniunkcji, której oba elementy musza być prawdziwe. To samo dzieje się
z drugą prawdziwą koniunkcją. Możemy przepisać wartości „r” i „~q” z jednej koniunkcji
do drugiej lub nadać wartości „r” i „~q” w obu koniunkcjach niezależnie. Tak czy inaczej
już w tym momencie koniecznie trzeba sprawdzić czy nie sprzeczności. Zostaje jeszcze
druga równoważność, ale na tym etapie jej nie ruszamy.

( ( p ↔ q ) ˄ ( ~ q ˄ r ) ) → ( ( r ˄ ~ q ) → ( q ↔ p ) )

1

1

1

1

1

1

1

0

1

0

0

b. Na tym etapie należy zwrócić uwagę na to, które wartości można przepisać. Możemy

z prawdziwości „~ q” wywnioskować, że samo „q” ma wartość fałszu oraz przepisać wartość
„r”. Jednak to nie wszystko. Warto pamiętać, że wszystkie funktory, poza implikacją,
są przemienne (tj. dla ich wartości logicznej bez znaczenia jest kolejność zdań stojących
przed i po funktorze). Oznacza to tyle, że „p ↔ q” i „q ↔ p” to dokładnie to samo. Dotyczy
to również „r ˄ ~ q” i „~ q ˄ r”. Już po przepisaniu wartości „p ↔ q” pod „q ↔ p”
pojawia się sprzeczność. Nie ma potrzeby ustalania wartości p. Zaznaczamy miejsce,
w którym zachodzi sprzeczność – badana formuła jest tautologią.

( ( p ↔ q ) ˄ ( ~ q ˄ r ) ) → ( ( r ˄ ~ q ) → ( q ↔ p ) )

0

0

1

1

1

1

0

1

0

1

1

1

0

1

0

0

Tautologia

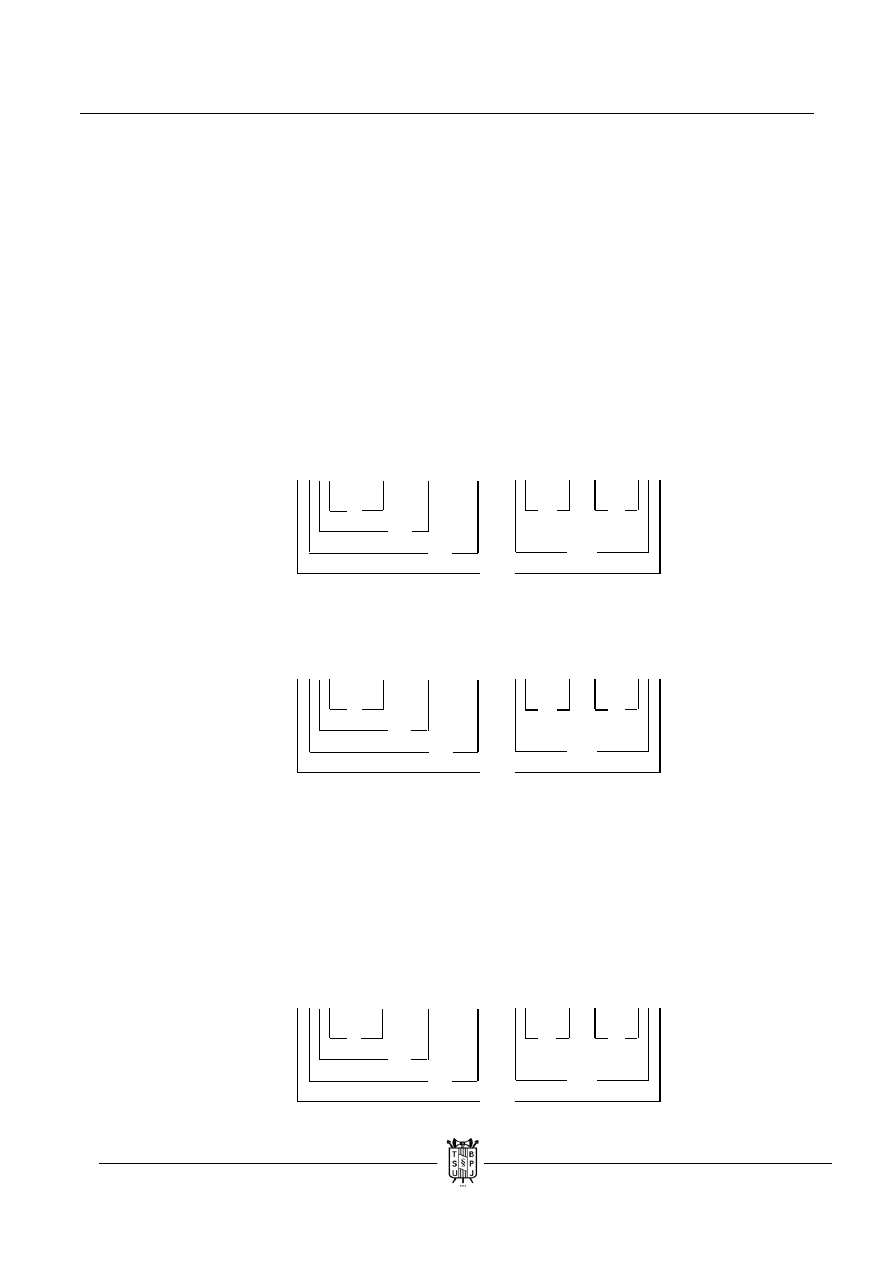
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

2.

( ( ( q ↔ r ) → p ) v ~ s ) ) → ( ( p ↓ r ) / ( t ˄ s ) )

a. Oczywiście zaczynamy od założenia, że całe wyrażenie ma wartość fałszu. Po przypisaniu

wartości jej poprzednikowi i następnikowi otrzymujemy prawdziwą alternatywę zwykłą,
która jest prawdziwa w trzech przypadkach (1,1 i 1,0 i 0,0) czyli kiedy chociaż jeden jej
element jest prawdziwy, a także fałszywą dysjunkcję, która przybiera taką wartość dla
(1,1). Z prawdziwą alternatywą zwykłą na razie nic nie zrobimy. Gdyby była prawdziwa,
to wtedy byłaby to inna bajka. Póki co musi wziąć się za dysjunkcję. Nadajemy jej
poprzednikowi i następnikowi wartości prawdy. Binegacja jest prawdziwa tylko wtedy,
kiedy oba jej elementy są fałszywe. Następnikiem fałszywej dysjunkcji jest koniunkcja,
która musi być prawdziwa, a dzieje się tak kiedy oba jej elementy są prawdziwe.

( ( ( q ↔ r ) → p ) v ~ s ) → ( ( p ↓ r ) / ( t ˄ s ) )

0 0

1 1

1

1

1

0

0

b. Przepisujemy wartości.

( ( ( q ↔ r ) → p ) v ~ s ) → ( ( p ↓ r ) / ( t ˄ s ) )

0

0

0 0

1 1

0

1

1

0

1

0

0

c. Wnioskujemy z wartości „~ s” i założenia o prawdziwości alternatywy zwykłej, że implikacja

ma wartość prawdy. Jeżeli następnik implikacji ma wartość fałszu, to żeby cała implikacja
była prawdziwa, wnioskujemy, że równoważność w jej poprzedniku ma wartość fałszu.
A skoro cała ona jest fałszywa i „r” fałszywe, to stąd wnioskujemy o prawdziwości „q”.
Nie pojawiła się sprzeczność, czyli badana formuła nie jest tautologią, bo istnieje taki zbiór
wartości występujących w niej zdań, dla którego formuła jest fałszywa. Znalezienie braku
sprzeczności kończy rozwiązywanie zadania.

( ( ( q ↔ r ) → p ) v ~ s ) → ( ( p ↓ r ) / ( t ˄ s ) )

1

0

0 0

1 1

0

0

1

1

1

0

1

0

0

nT, bo dla p=0, q=1, r=0, s=1 FF

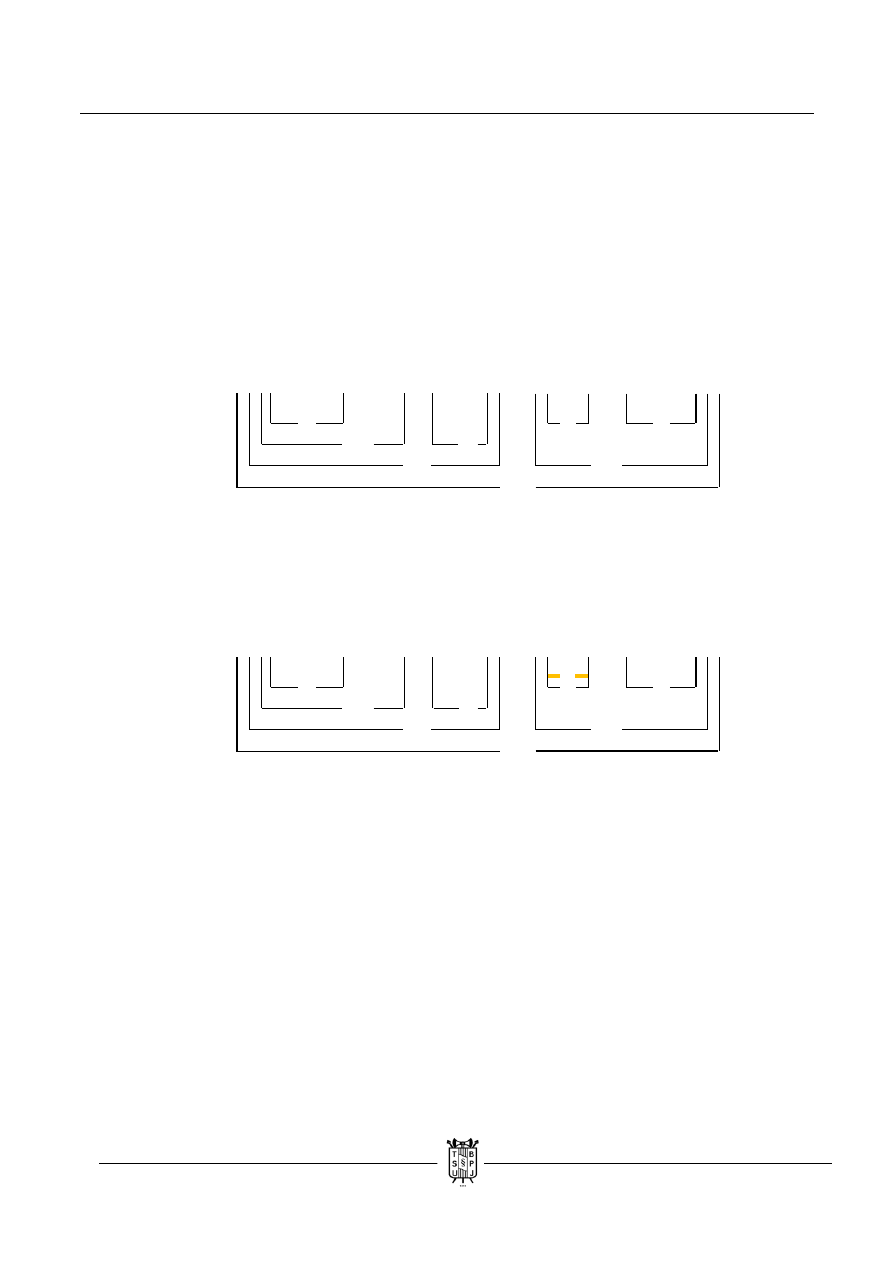
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

3.

( ( ( p ˄ q ˄ r ) → ~ s ) ˄ ( ~ r ˄ t ) ) → ( ( q ↓ t ) → ( ~ p / ~ s ) )

a. Koniunkcja jest jedynym prawem, które może być złożone z trzech lub więcej

elementów. Prawdziwa jest tylko wtedy, gdy każdy jej element jest prawdziwy.

( ( ( p ˄ q ˄ r ) → ~ s ) ˄ ( ~ r ˄ t ) ) → ( ( q ↓ t ) → ( ~ p / ~ s ) )

1

1

1

0

1

1

1

0

0

b. Przepisujemy wartość „t” i już na początku zadania mamy sprzeczność, gdyż binegacja jest

prawdziwa tylko wtedy, kiedy oba jej elementy są fałszywe.

( ( ( p ˄ q ˄ r ) → ~ s ) ˄ ( ~ r ˄ t ) ) → ( ( q ↓ t ) → ( ~ p / ~ s ) )

1

1

?

0

1

1

0

1

1

1

0

0

Tautologia

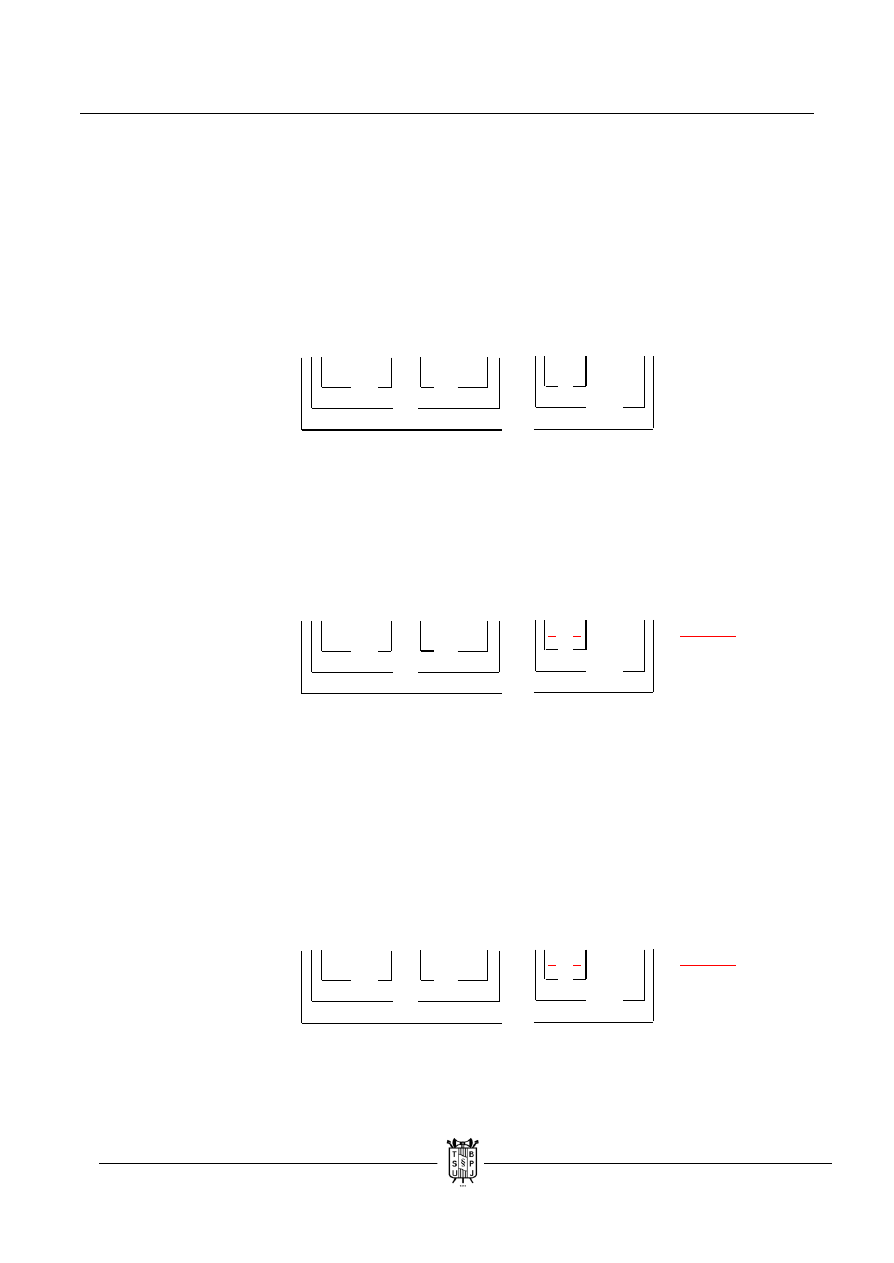
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

4.

( ( ~ p ↔ q ) v ( r → ~ s ) ) → ( ( s / q ) → ~ r )

a. Uzupełniamy wartości do momentu, kiedy jesteśmy zmuszeni zrobić warianty.

( ( ~ p ↔ q ) v ( r → ~ s ) ) → ( ( s / q ) → ~ r )

1

0

1

0

0

b. Możemy je przyjąć na prawdziwej alternatywie zwykłej lub na prawdziwej dysjunkcji.

W obu przypadkach mamy trzy możliwości, ale przy dysjunkcji od razu otrzymujemy
wartości elementów „s” i „q”. Dlatego warianty przyjmiemy na niej. Od razu uzupełniamy
też wartość „r”.

( ( ~ p ↔ q ) v ( r → ~ s ) ) → ( ( s / q ) → ~ r )

1

0 0

w1: (0,0)

1

0

w2: (0,1)

1

0

w3: (1,0)

0

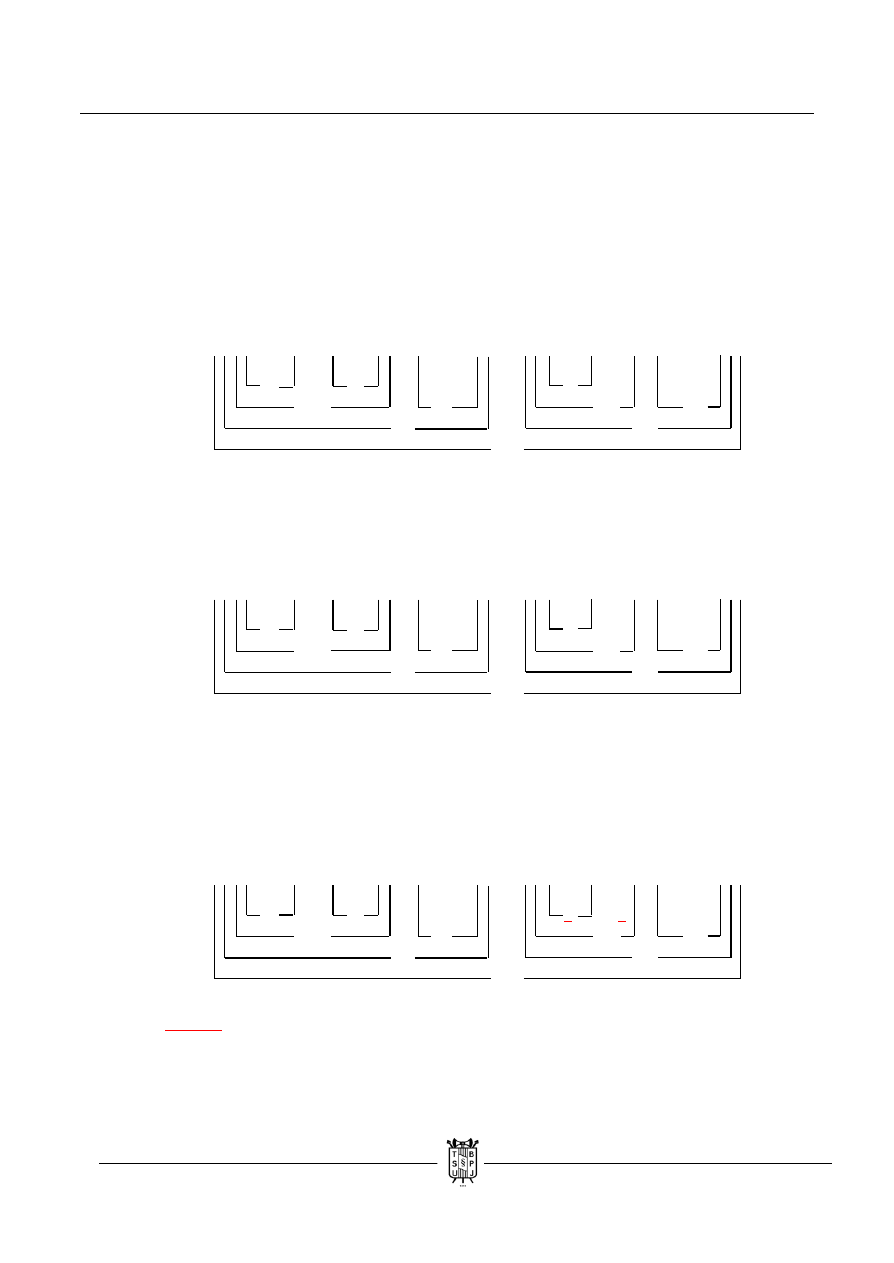
c. Skoro „s” jest fałszywe, to „~s” jest prawdziwe, przepisujemy wartość „q”(chociaż nie

ma ona większego znaczenia).. Jeżeli następnik implikacji jest prawdziwy, to bez
względu na wartość poprzednika jest ona zawsze prawdziwa. Chociaż tutaj znamy jego
wartość. A jeżeli choć jeden element alternatywy zwykłej jest prawdziwy, to jest ona
prawdziwa. W tym wariancie nie ma sprzeczności, więc kończymy zadanie określając
dla jakich wartości zdanie nie jest tautologią. Drugi wariant prowadzi do takiego samego
wniosku, a w trzecim wpadamy w podwarianty.

( ( ~ p ↔ q ) v ( r → ~ s ) ) → ( ( s / q ) → ~ r )

1

1

0 0

w1: (0,0)

1

1

0

w2: (0,1)

1

0

w3: (1,0)

0

nT, dla: p = ?, q = 0, r = 1, s = 0 FF

Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

5.

( ( ( p ˄ q ) → ( r ┴ s ) ) ˄ ( t → ~ s) ) → ( ( ( r ↓ q ) ↔ t ) / ( ~ s ˄ p ) )

a. Rozpoczynamy tak jak zawsze.

( ( ( p ˄ q ) → ( r ┴ s ) ) ˄ ( t → ~ s) ) → ( ( ( r ↓ q ) ↔ t ) / ( ~ s ˄ p ) )

1

1

1

1

1

1

1

0

0

b. Przepisujemy wartości.

( ( ( p ˄ q ) → ( r ┴ s ) ) ˄ ( t → ~ s) ) → ( ( ( r ↓ q ) ↔ t ) / ( ~ s ˄ p ) )

1

0

1

1

1

1

1

1

1

1

0

0

c. Przyjmujemy warianty na równoważności, gdyż są wtedy tylko dwa, a nie trzy, tak jakby

miało to miejsce w przypadku wyboru implikacji. Nie ma sprzeczności, więc zdanie jest
nietautologią. W drugim wariancie wpadamy w podwarianty.

( ( ( p ˄ q ) → ( r ┴ s ) ) ˄ ( t → ~ s) ) → ( ( ( r ↓ q ) ↔ t ) / ( ~ s ˄ p ) )

1

0

0

0

1

1

0 0

1

1

0

0

1

1

1

1

1

1

1

0

0

w1: (1,1)

w2: (0,0)

nT, dla: p = 1, q = 0, r = 0, s = 0, t = 1 FF

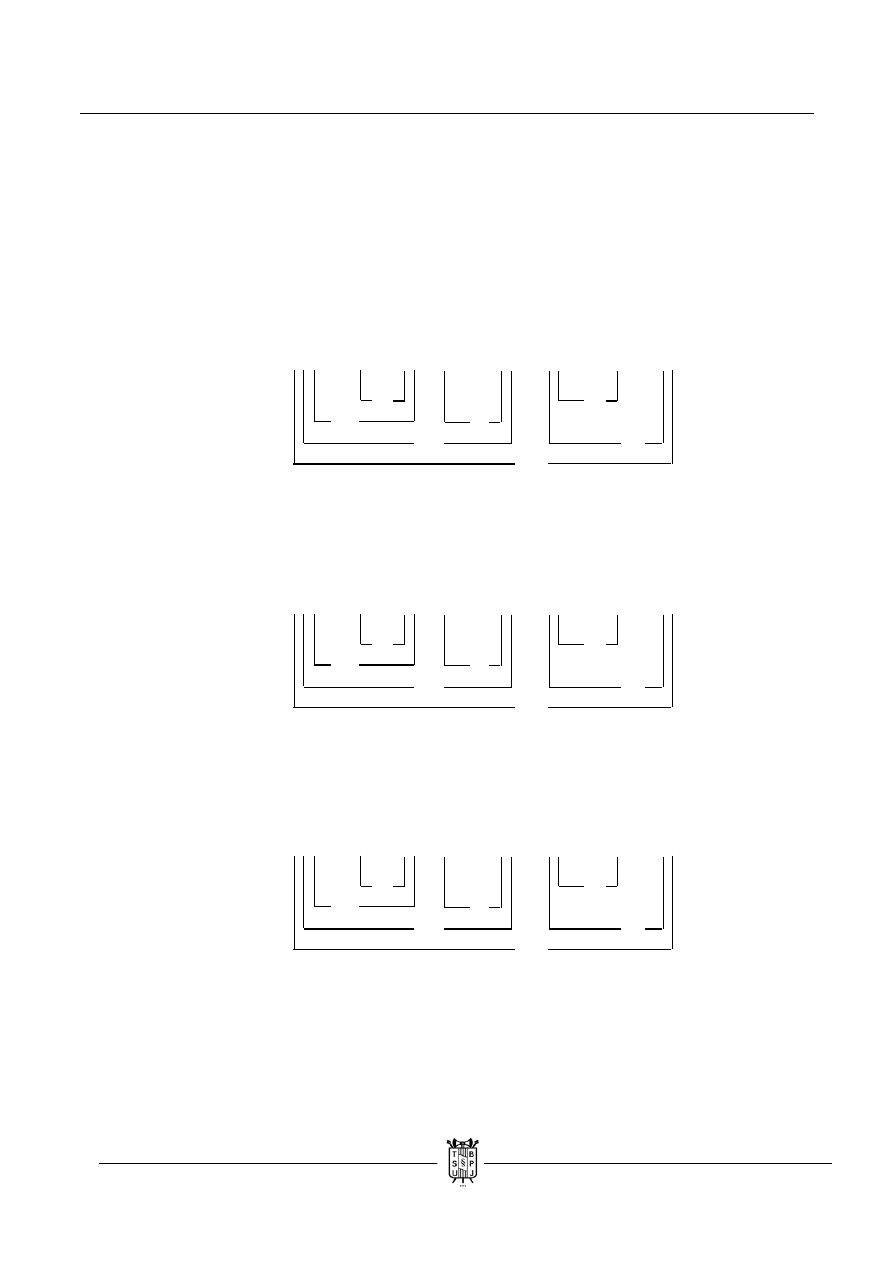
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

6.

( ( p → ( q ˄ r ) ) ↓ ( ~ s / q ) ) → ( ( ~ r v q ) → s )

a. Zaczynamy od założenia, że badane zdanie nie jest tautologią.

( ( p → ( q ˄ r ) ) ↓ ( ~ s / q ) ) → ( ( ~ r v q ) → s )

1

1

1

0

1

0

0

0

1

0

0

b. Przepisujemy wartości.

( ( p → ( q ˄ r ) ) ↓ ( ~ s / q ) ) → ( ( ~ r v q ) → s )

1

1

1

1

1

0

1

0

0

0

1

0

0

c. Wyciągamy wartość „r” z fałszywej koniunkcji. Zdanie jest nietautologią.

( ( p → ( q ˄ r ) ) ↓ ( ~ s / q ) ) → ( ( ~ r v q ) → s )

1 0

1

1

1

1

1

0

1

0

0

0

1

0

0

nT, dla: p = 1, q = 1, r = 0, s = 0 FF

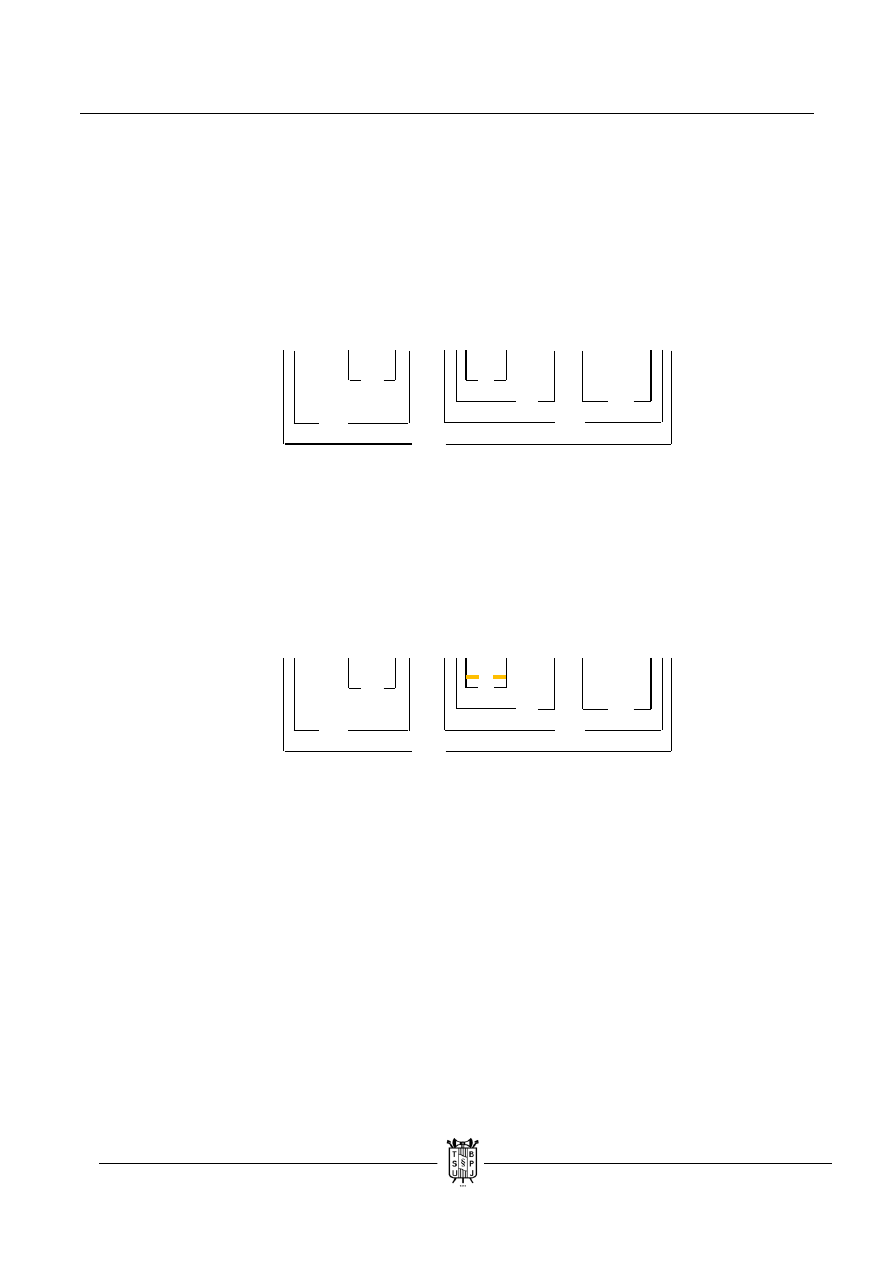
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

7.

( ~ p ˄ ( q ┴ r ) ) → ( ( ( s ↓ q ) → r ) v ( ~ p ↔ r ) )

a. Zaczynamy od zanegowania implikacji.

( ~ p ˄ ( q ┴ r ) ) → ( ( ( s ↓ q ) → r ) v ( ~ p ↔ r ) )

1

1

1

0

0

1

0

0

b. Wyciągamy wartość „r” z fałszywej równoważności, następnie „q” z prawdziwej

alternatywy rozłącznej. Ponieważ implikacja jest fałszywa, to jej następnik musi być
fałszywy, a poprzednik prawdziwy. Binegacja jest prawdziwa tylko jeżeli oba elementy
są fałszywe. Jednak „q” jest prawdziwe, dlatego mamy sprzeczność.

( ~ p ˄ ( q ┴ r ) ) → ( ( ( s ↓ q ) → r ) v ( ~ p ↔ r ) )

1

0

?

0

1

0

1

0

1

1

1

0

0

1

0

0

Tautologia

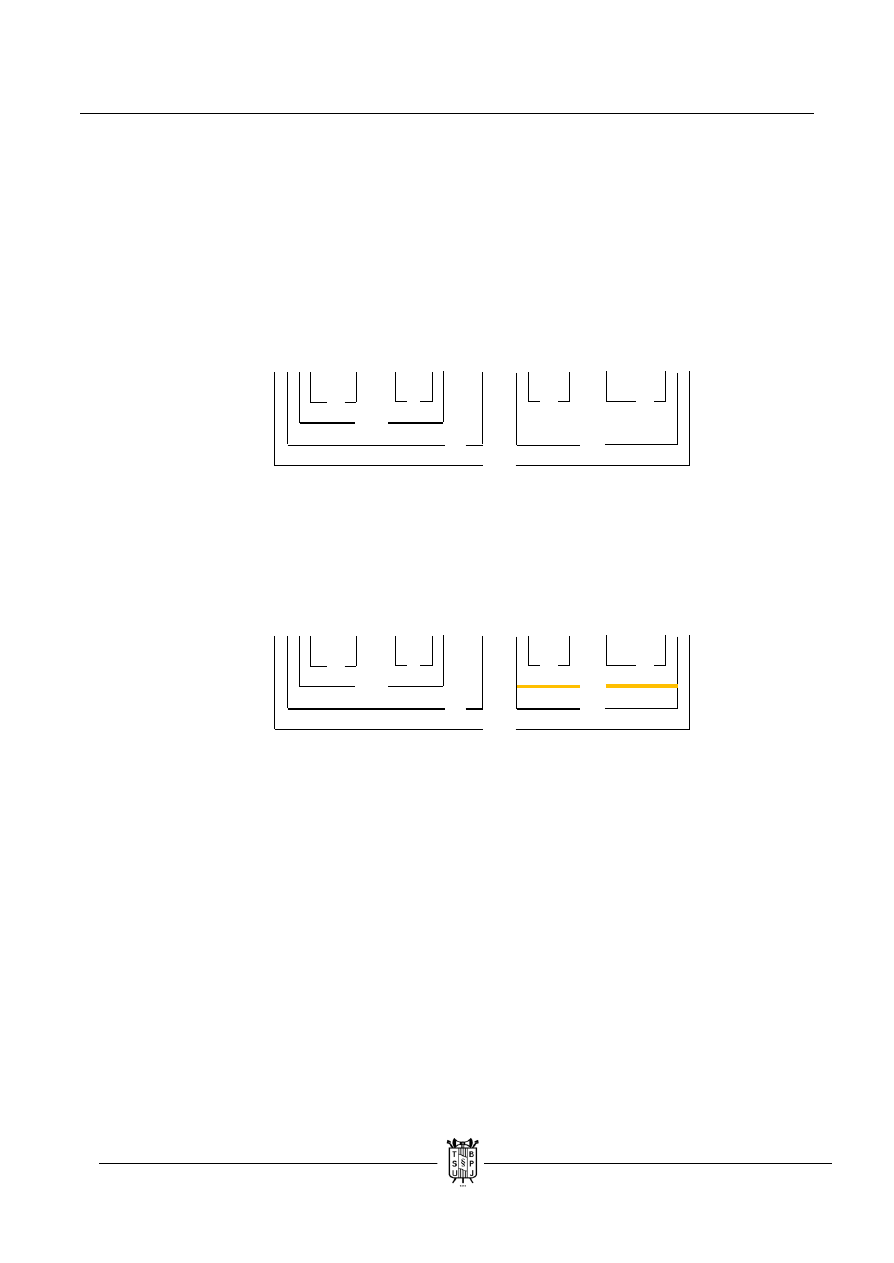
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

8.

( ( ( p v q ) → ( r / s ) ) ↓ p ) → ( ( q / r ) ↔ ( ~ s ˄ p ) )

a. Zaczynamy tak jak zawsze.

( ( ( p v q ) → ( r / s ) ) ↓ p ) → ( ( q / r ) ↔ ( ~ s ˄ p ) )

0

1 1

1

0

0

0

1

0

0

b. Wyciągamy wartość „q” z prawdziwej alternatywy zwykłej , przepisujemy pozostałe

wartości. Sprzeczność wychodzi na równoważności.

( ( ( p v q ) → ( r / s ) ) ↓ p ) → ( ( q / r ) ↔ ( ~ s ˄ p ) )

0

1

1 1

1 1

0

0

1

0

0

0

0

0

1

1

0

0

Tautologia

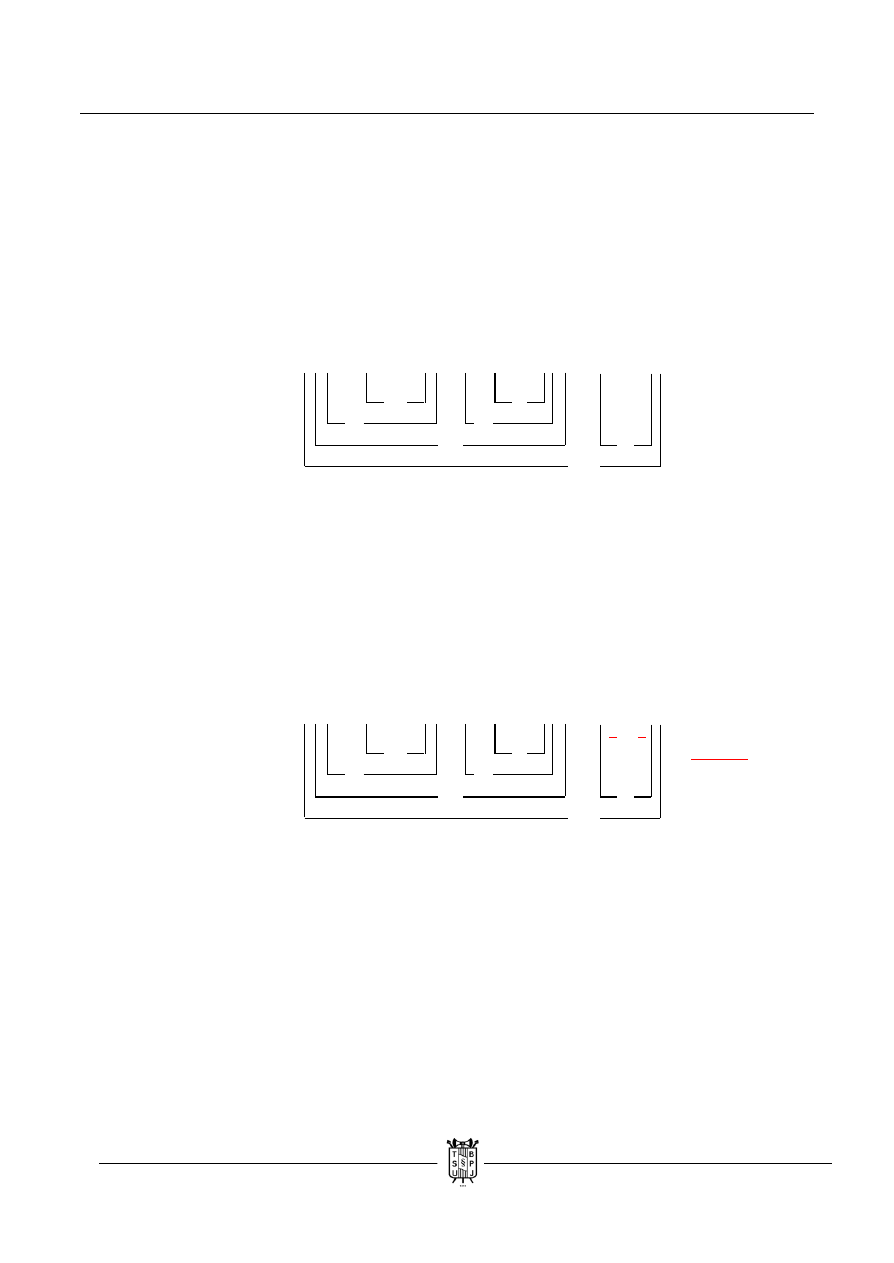
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

9.

( ( r → ( p → q ) ) ˄ ( s / ( q ↓ p ) ) ) → ( s ┴ q )

a. Implikacji nadajemy wartość fałszu.

( ( r → ( p → q ) ) ˄ ( s / ( q ↓ p ) ) ) → ( s ┴ q )

1

1

1

0

0

b. Warianty przyjmujemy na alternatywie rozłącznej, bo wtedy mamy dwa, a nie trzy, jakby

to było w przypadku wyboru implikacji lub dysjunkcji. Przepisujemy wartości i okazuje się,
że nie ma sprzeczności. Jeżeli następnik implikacji jest prawdziwy to jest on zawsze
prawdziwa. Jeżeli jeden z elementów binegacji jest prawdziwy to jest ona zawsze
fałszywa. Wobec czego kończymy zadanie. W drugim wariancie wpadamy w podwarianty,
z których żaden nie prowadzi do sprzeczności.

( ( r → ( p → q ) ) ˄ ( s / ( q ↓ p ) ) ) → ( s ┴ q )

?

1

1 ?

1

1

?

1

1

0

w1: (1,1)

1

1

w2: (0,0)

1

0

0

nT, dla: p = ?, q = 1, r = ?, s = 1 FF

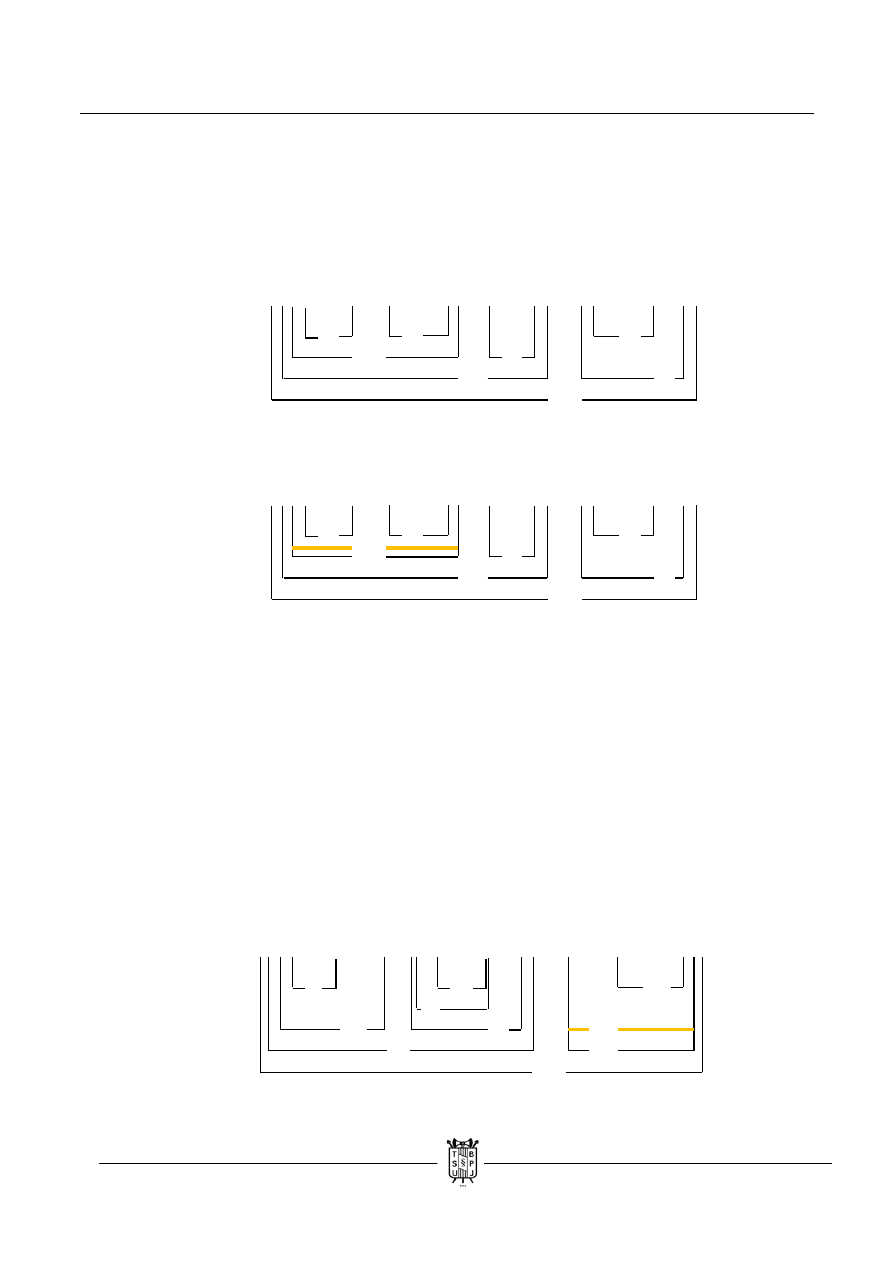
Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

10.

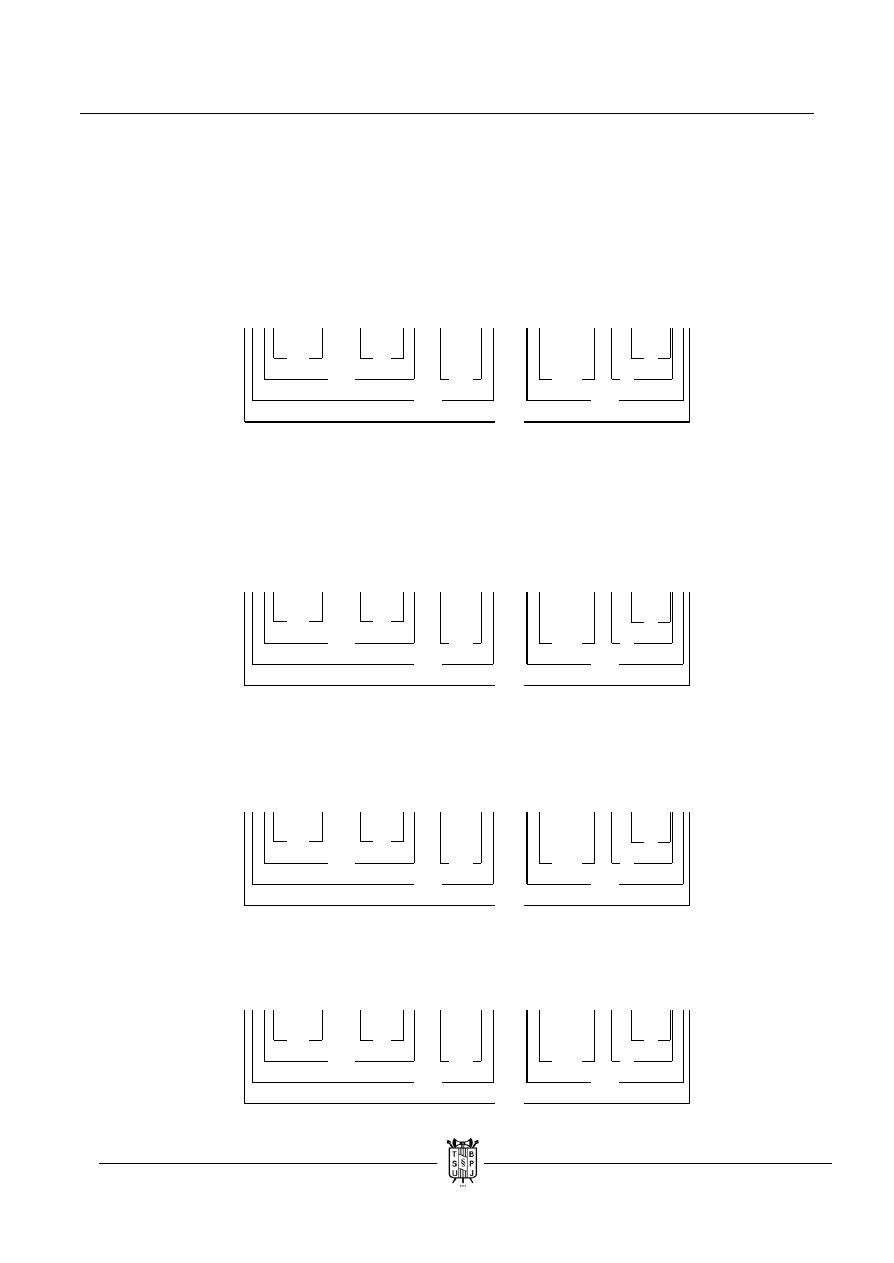
( ( ( p ↓ q ) ↔ ( r ┴ ~ s ) ) ˄ ( s ˄ q ) ) → ( ( ~ r ˄ p ) / t )

a. Zakładamy, że cała implikacja jest fałszywa.

( ( ( p ↓ q ) ↔ ( r ┴ ~ s ) ) ˄ ( s ˄ q ) ) → ( ( ~ r ˄ p ) / t )

1 1

1

1

1

1

1

1

1

0

0

b. Przepisujemy wartości. Wychodzi sprzeczność.

( ( ( p ↓ q ) ↔ ( r ┴ ~ s ) ) ˄ ( s ˄ q ) ) → ( ( ~ r ˄ p ) / t )

1

1

0

0

1 1

1

1

0

0

1

1

1

1

1

1

0

0

Tautologia.

11.

( ( ( q ˄ r ) → p ) ˄ ( ~ ( p ↓ q ) ˄ s ) ) → ( ~ s / ( ~ q → r ) )

a. Warto zauważyć, że zanegowana binegacja będąca poprzednikiem prawdziwej koniunkcji

przybiera wartość prawdy. Dopiero binegacja bez negacji jest fałszywa. Następnikiem tej
samej koniunkcji jest „s”, które musi być prawdziwe. Wobec tego „~s” jest fałszywe.
Z fałszywości dysjunkcji wynika, że oba jej elementy muszą być prawdziwe. Tym czasem,
jej poprzednik „~s” jest fałszywy, co prowadzi do wniosku, że mamy sprzeczność.

( ( ( q ˄ r ) → p ) ˄ ( ~ ( p ↓ q ) ˄ s ) ) → ( ~ s / ( ~ q → r ) )

0

0

1

1

1

1

1

1

0

0

Tautologia.

Zajęcia TBSP z Logiki dla Prawników 2013

Agnieszka Guzik, Filip Leszczyński

TOWARZYSTWO BIBLIOTEKI

SŁUCHACZÓW PRAWA UJ

ul. Bracka 12 /302, 31-005 Krak

ów

www.tbsp.pl

12.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

a. W pierwszej kolejności dochodzimy do momentu, w którym wyciągamy wartości „q” i „r”,

które możemy przepisać.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

1

1

1

1 1

0

1

1

1

0

0

b. Skoro „r” przybiera wartość prawdy, to alternatywa zwykła musi być prawdziwa, tak samo jak

binegacja musi być fałszywa. A jeżeli binegacja będąca następnikiem prawdziwej alternatywy
zwykłej jest fałszywa, to poprzednik prawdziwej alternatywy zwykłej musi przybierać wartość
prawdy.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

1

1

1

1 1

1

0

1

0

1

1

1

0

0

c. Jeżeli następnik prawdziwej równoważności jest prawdziwy, to jej poprzednik (koniunkcja)

musi przybierać taką samą wartość. Dzięki temu poznajemy wartość „p”, którą przepisujemy.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

1

1

1

1

1

1 1

1

1

0

1

0

1

1

1

0

0

d. Wyciągamy wartość „t” z prawdziwej implikacja. Brak sprzeczności. Zdanie jest nietautologią.

( ( ( p ˄ q ) ↔ ( r v s ) ) v ( t ↓ r ) ) → ( ( p → t ) / ~ ( q / r ) )

1

1

1

1 1

1

1

1 1

1

1

0

1

0

1

1

1

0

0

nT, dla: p = 1, q = 1, r = 1, s = ?, t = 1 FF