Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 59 – mjasina@pg.gda.pl 

13. Metoda 

sił – belki ciągłe, równanie trzech momentów

1

 

13.1. Belki ciągłe, równanie trzech momentów – podstawy teoretyczne 
Metoda sił jest metodą ogólną pozwalającą rozwiązywać różnego typu układy 
statycznie niewyznaczalne. 

łe. 

ne. 

owo. 

odpartych.  

 
Można ją zmodyfikować tak by w prosty (schematyczny) sposób, oparty na 

pewnych cechach metody, rozwiązywać statycznie niewyznaczalne belki ciąg

 
Belką ciągłą nazywamy belkę wspartą więcej niż dwu podporach, przy czym 

zakłada się, że jedna z podpór jest nieprzesuwna a pozostałe przesuw

 
Belka taka jest zwykle pozioma a siły zewnętrzne i związane z nimi reakcje 

skierowane są pion

 
Układ podstawowy metody sił  (UPMS) belki ciągłej tworzymy usuwając więzy 

wewnętrzne – zakładając przeguby nad podporami wewnętrznymi oraz w utwierdzeniu, 
jeżeli występuje taki warunek brzegowy.  

 
W powyższy sposób otrzymujemy bardzo korzystny z ekonomicznego punktu 

widzenia (prostota schematycznego podejścia oraz mały nakładu pracy przy 
całkowaniu) układ złożony z belek swobodnie p

 
W wyniku tego zabiegu otrzymuje się niewiadome – nadliczbowe metody sił 

i

X

, 

które są momentami zginającymi w przekrojach podporowych (nad podporami), są to 
tzw. momenty podporowe. 

 
Adaptacja metody sił do analizy belek ciągłych prowadzi do bardzo prostego układu 

równań kanonicznych. Równanie odniesionej d   k -tej podpory można zapisać w 
następującej post

o

aci  

 

1

1

1

1

1

1

1

0

6

3

6

k

k

k

k

k

k

k

k

k

k

k

k

l

l

l

l

X

X

X

EI

EI

EI

EI

δ

+

+

−

+

+

+

⎛

⎞

+

+

+

+

⎜

⎟

⎝

⎠

0

=

                                                          

 (13.1) 

 

1

 Rysunki zaczerpnięto z książki: Cywiński Z.:  Mechanika budowli w zadaniach 

Tom II, PWN, 1984. 

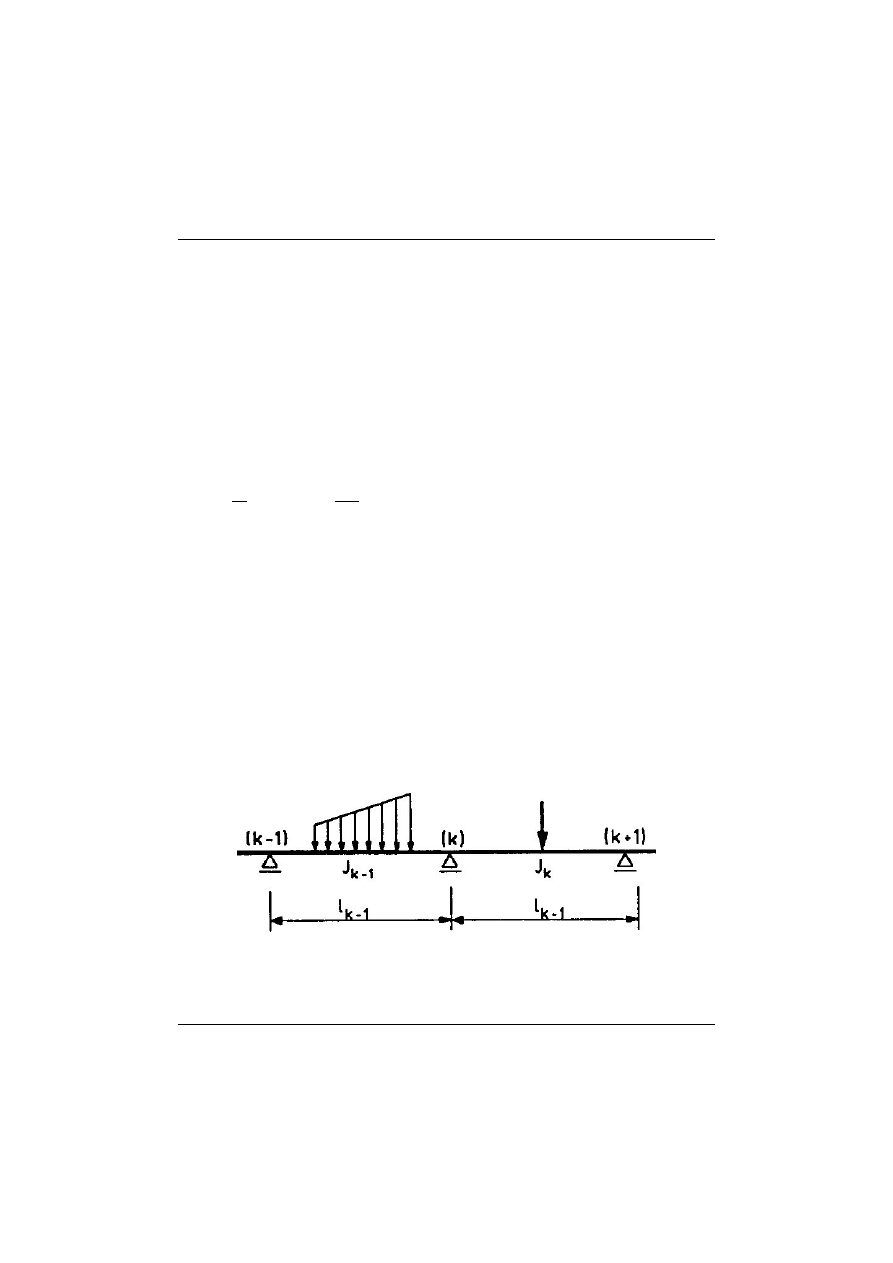
Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 60 – mjasina@pg.gda.pl 

gdzie:  

1

k

X

−

, 

k

X

, 

1

k

X

+

  –   nadliczbowe (momenty zginające w przekrojach) odpowiednio nad 

kolejnymi podporami 

1

k

− ,  , 

k

1

k

+ ;  

k

l

, 

  

–   rozpiętości przęseł;  

1

k

l

+

k

I

, 

1

k

I

+

  

–   momenty  bezwładności przekroju prętów położonych z lewej i 

prawej strony podpory  ; 

k

E

  

–   moduł sprężystości materiału; 

0

k

δ   

–   przemieszczenie,  zmianę  kąta obrotu osi pręta, w przekroju nad 

podporą  , od przyczyny zewnętrznej. 

k

 

Przyjmując oznaczenia: 

 

c

k

k

k

I

l

l

I

′ =

   i   

1

1

1

c

k

k

k

I

l

l

I

+

+

+

′ =

, (13.2) 

gdzie 

c

I

 jest porównawczym momentem bezwładności przekroju  

oraz 

 

0

k

c

0

6

k

N

EI

δ

= −

, (13.3) 

wzór (13.1) można wyrazić w formie równania trzech momentów. 

 
Wielkość 

 daną wzorem (13.3) określa się szczegółowo w zależności od rodzaju 

obciążenia (oddziaływania) zewnętrznego na poszczególne pręty (przęsła belki ciągłej – 
belki swobodnie podparte). 

0

k

N

 

 

Rys. 13.1   Belka ciągła - układ wyjściowy 

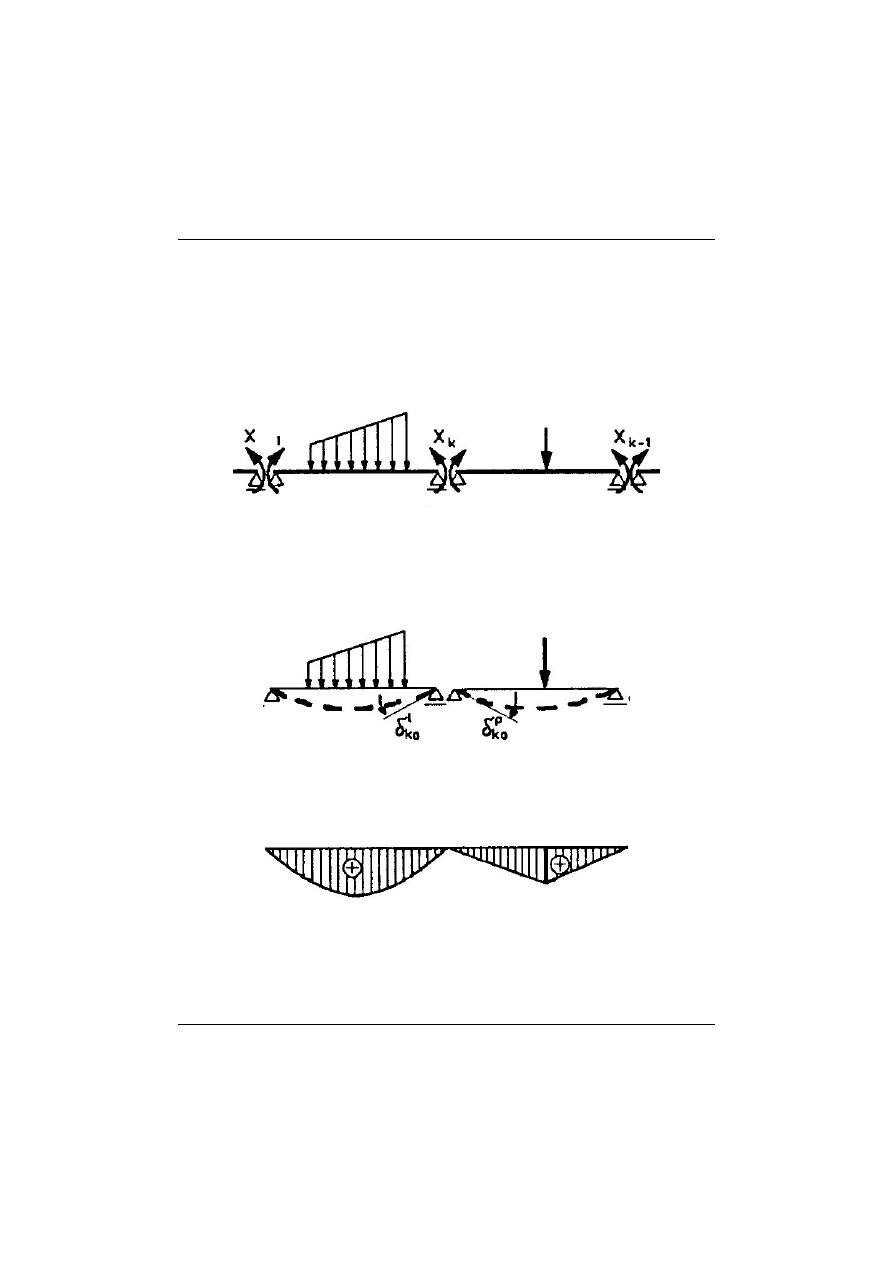
Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 61 – mjasina@pg.gda.pl 

Równanie trzech momentów (równanie (13.1) po podstawieniu (13.2) i (13.3) przybiera 
poniższą postać) 

 

(

)

1

1

1

2

k

k

k

k

k

k

k

k

1

0

X

l

X

l

l

X

l

N

−

+

+

′

′

′

′

⋅ + ⋅

⋅

+

+

⋅

=

+

. (13.4) 

 

1

k

X

−

, 

k

X

, 

1

k

X

+

 – nadliczbowe nad kolejnymi podporami 

1

k

−

,  , 

k

1

k

+

.  

 

Rys. 13.2   Belka ciągła - układ podstawowy metody sił 

 

0

0

l

k

k

0

p

k

δ

δ

δ

=

+

 – sumaryczna (z lewej i prawej strony podpory), zmiana kąta obrotu osi 

belki w przekroju nad podporą   od przyczyny zewnętrznej. 

k

 

Rys. 13.3   Belka ciągła – UPMS – zmiana kąta obrotu osi belki w przekroju nad podporą   

k

 

 

Rys. 13.4   Belka ciągła – UPMS – wykresy momentów od obciążenia zewnętrznego 

k

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 62 – mjasina@pg.gda.pl 

 

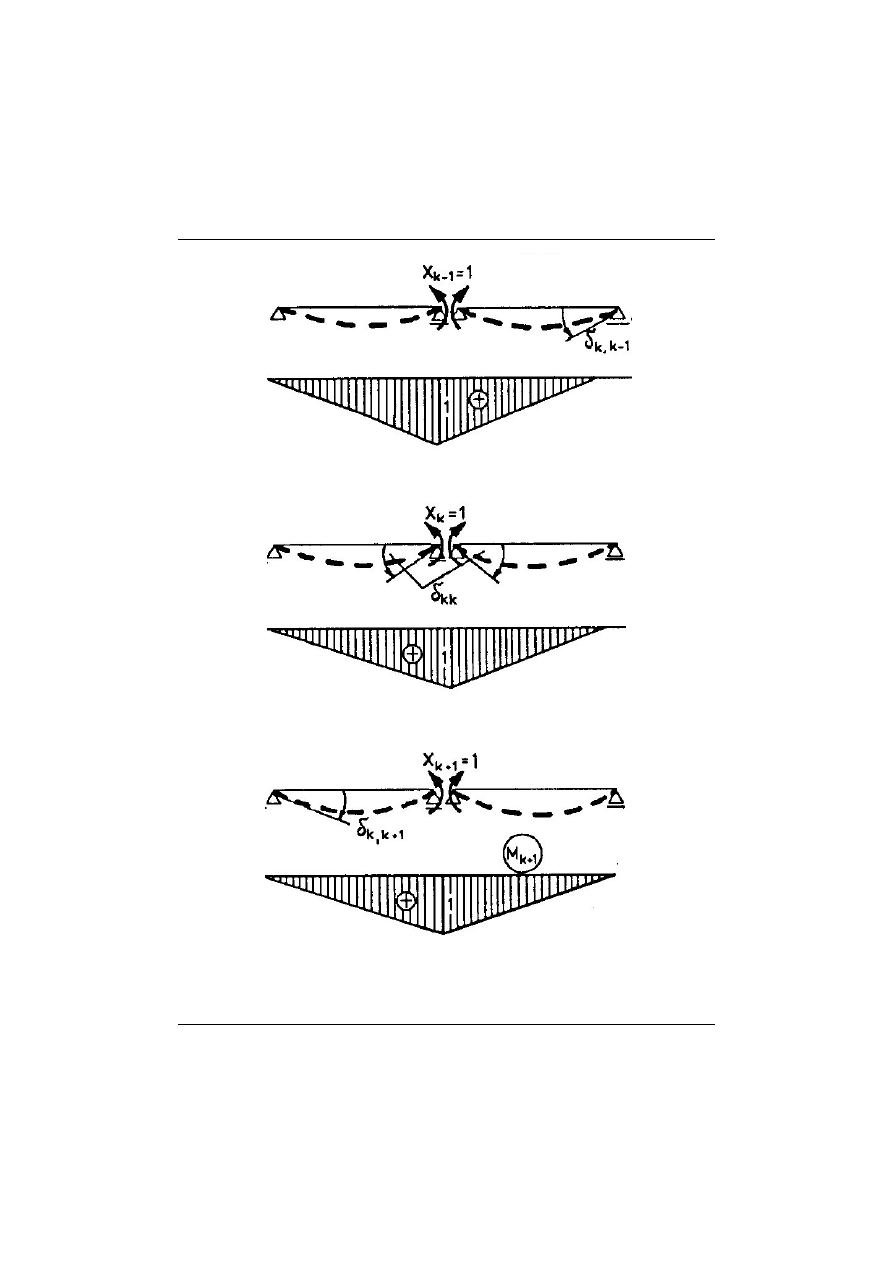
Rys. 13.5   Belka ciągła – UPMS – wykresy momentów od obciążenia 

 

1

1

k

X

−

=

 

Rys. 13.6   Belka ciągła – UPMS – wykresy momentów od obciążenia 

 

1

k

X

=

 

Rys. 13.7   Belka ciągła – UPMS – wykresy momentów od obciążenia 

 

1

1

k

X

+

=

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 63 – mjasina@pg.gda.pl 

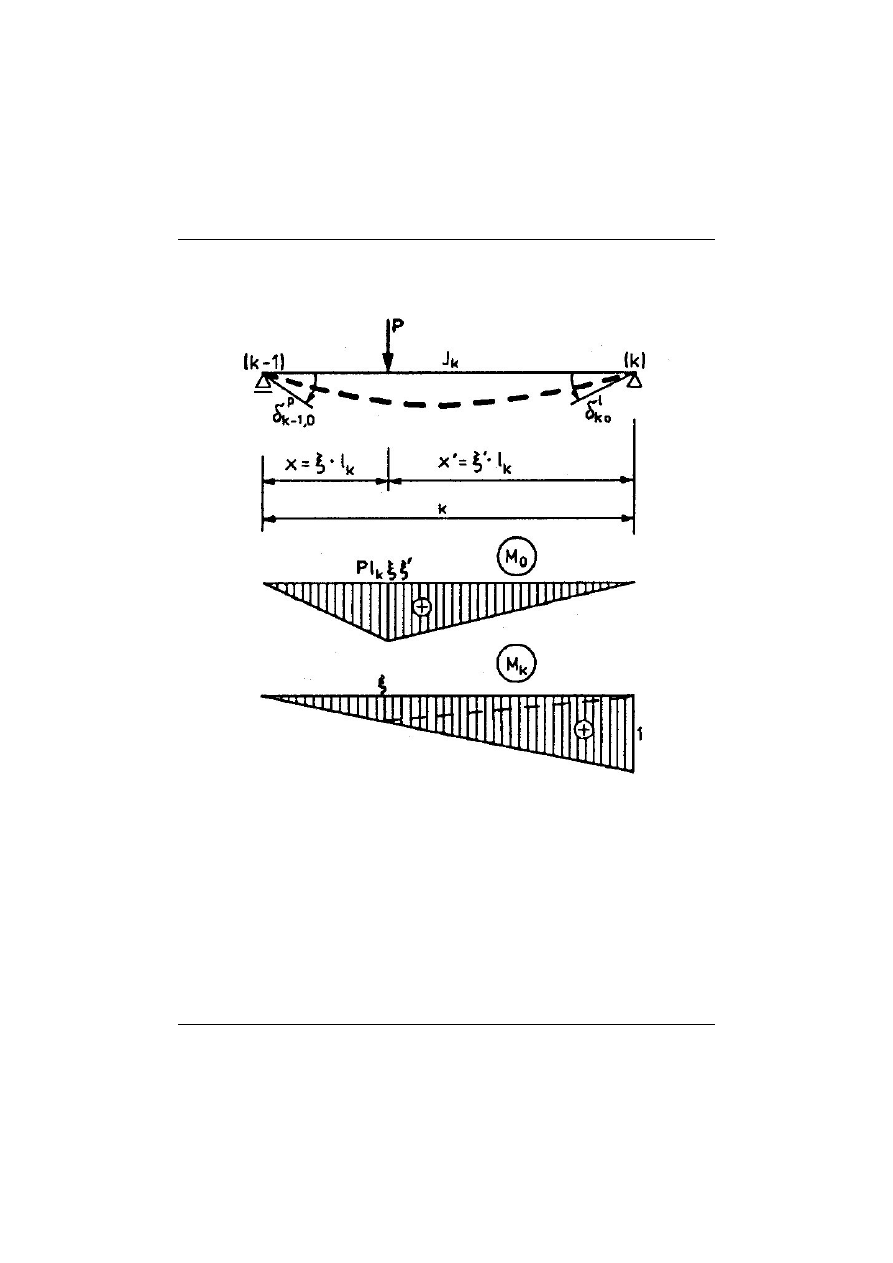
Przykładowe wyznaczenie wielkości współczynnika prawej strony 

0

k

N

 p

 obcią-

żeniu siłą skupioną. 

rzy

 

Rys. 13.8   UPMS – wyznaczenie 

0

k

N

N

kP

=

 – stan obciążenia zewnętrznego 

 

p

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 64 – mjasina@pg.gda.pl 

13.2. Belka ciągła, rozwiązanie z zastosowaniem równania trzech momen-

tów 

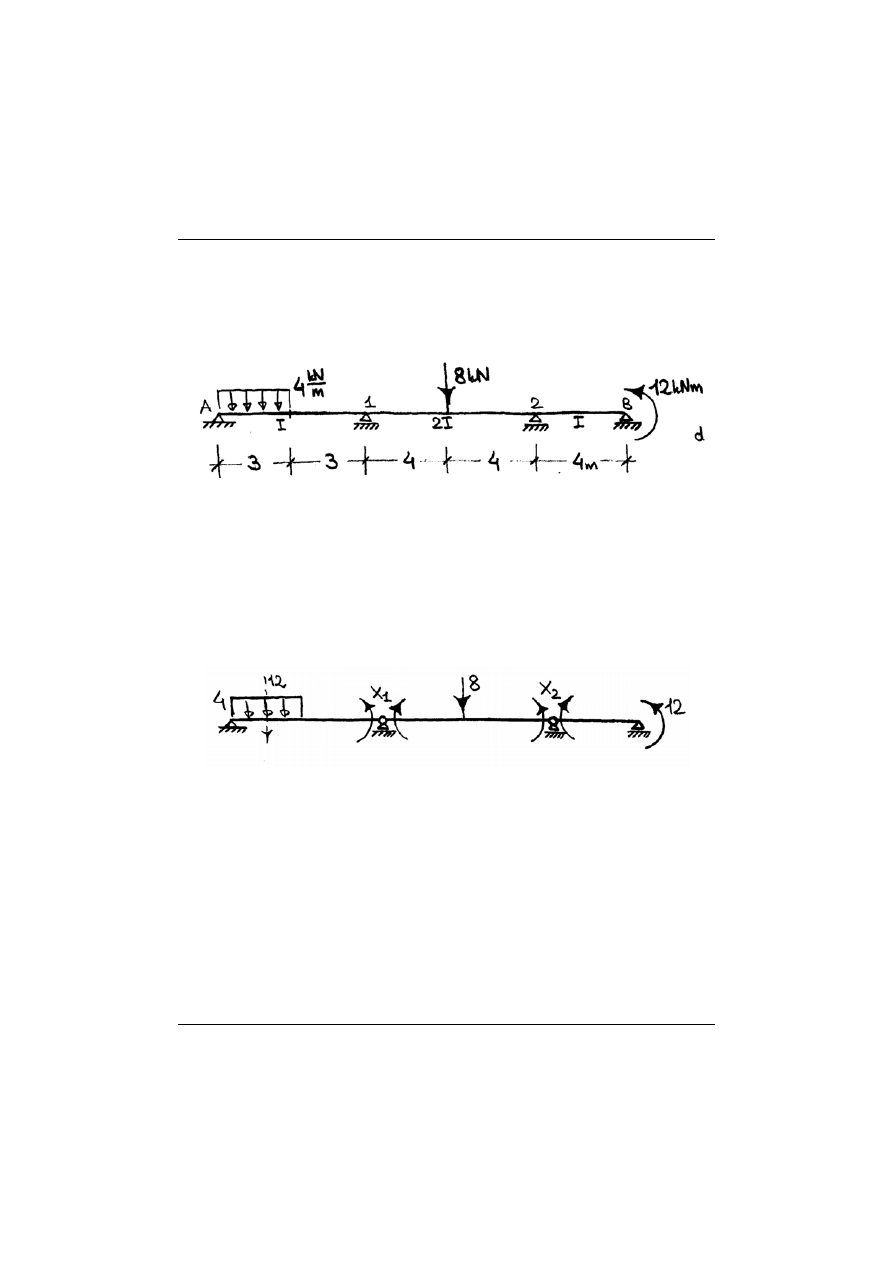
Dana jest belka ciągła przedstawiona na poniższym rysunku, sporządzić wykresy sił 
wewnętrznych.  Należy przyjąć, że we wszystkich prętach 

const

E

=

. 

 

Rys. 13.9   Belka ciągła 

 

Stosując równanie trzech momentów w zasadzie nie ma konieczności przyjmowania 
układu podstawowego metody sił, zbędne jest także rysowanie i całkowanie wykresów 
momentów zginających w UPMS od obciążenia zewnętrznego i od jednostkowych 
stanów nadliczbowych.  

 
W niniejszym rozwiązaniu, jedynie w celu poglądowym, przyjmiemy układ 

podstawowy metody sił pokazany na rys. 13.10. 

 

Rys. 13.10   Belka ciągła - układ podstawowy metody sił 

 
 

Równanie trzech momentów zapisujemy poniżej w poznanej wcześniej postaci (13.4). 
 

 

(

)

1

1

1

2

k

k

k

k

k

k

k

k

1

0

X

l

X

l

l

X

l

N

−

+

+

′

′

′

′

⋅ + ⋅

⋅

+

+

⋅

=

+

.  

 

W analizowanym zadaniu (stopień statycznej niewyznaczalności 

2

n

= ) mamy dwie 

niewiadome nadliczbowe 

1

X

 i 

2

X

 (lub zapisane w po

1, 2

k

staci 

,

k

X

=

), są to 

momenty zginające w przekrojach nad kolejnymi podpora i 

m

1

 i 

2

. 

 

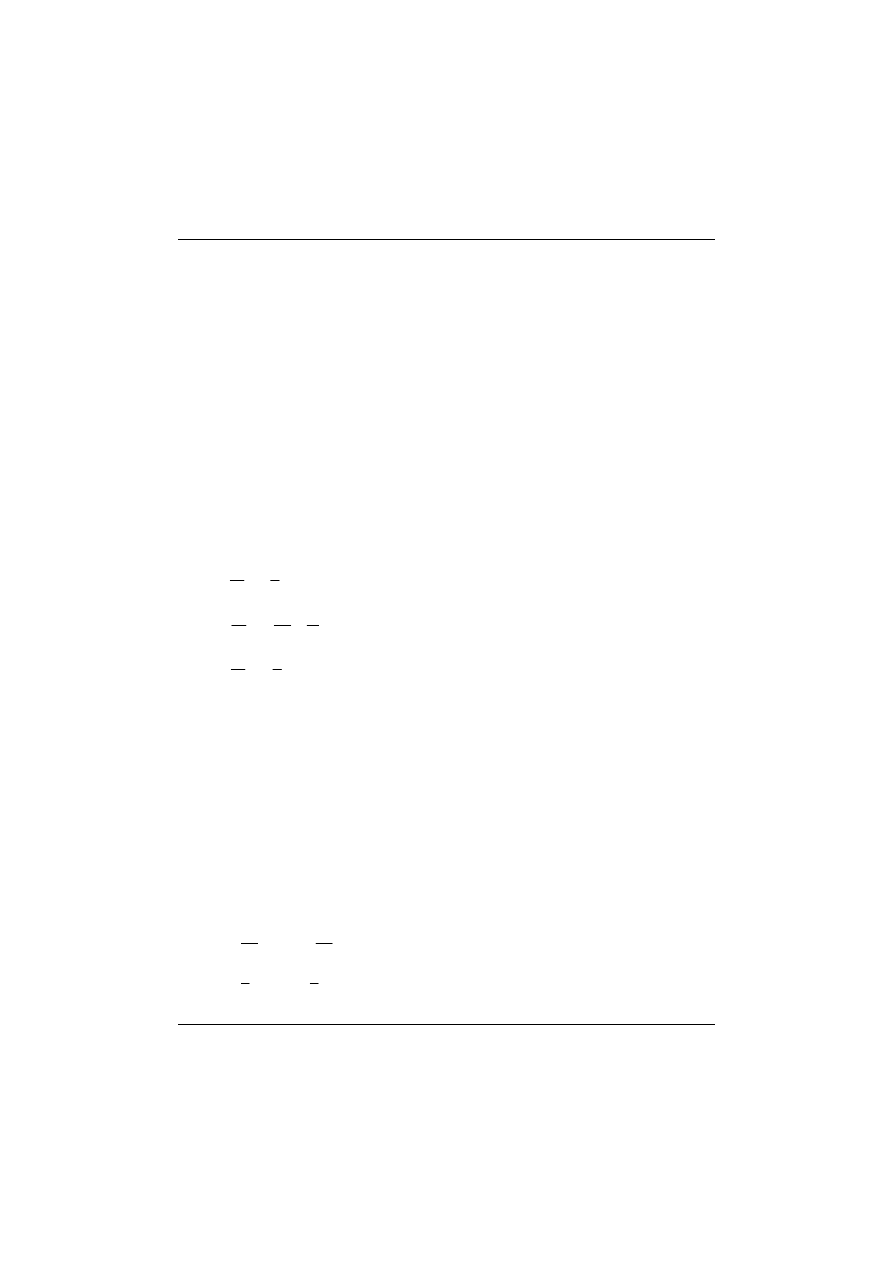
Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 65 – mjasina@pg.gda.pl 

Zatem w niniejszym rozwiązaniu równanie trzech momentów (13.4) zapiszemy 

dwukrotnie, przyjmując kolejno 

1

k

=  i 

2

k

= . 

 

Ze wzglądu na to, że moment bezwładności przekrojów poszczególnych prętów (w 
poszczególnych przęsłach) jest różny, przyjmujemy porównawczy moment bezwładno-
ści 

 

c

I

I

= . (13.5) 

Stosując oznaczenia (13.2) zgodne z zasadami obowiązującymi przy tej metodzie 

rozwiązania przyjmujemy: 

 

(

1)

1

A

c

I

I

I

I

−

=

= = , 

(1 2)

2

2

2

c

I

I

I

I

−

=

=

=

(2

)

3

, 

B

c

I

I

I

I

−

=

= =  (13.6) 

Na podstawie zależności (13.6) wyznaczymy zgodnie z (13.2) długości 

i

l ′

: 

 

1

1

1

1

1

2

2

2

2

2

3

3

3

3

3

6 [m]

4 [m]

2

2

4 [m]

c

c

c

I

I

l

l

l

l

I

I

I

l

I

l

l

l

I

I

I

I

l

l

l

l

I

I

′ =

=

= =

′ =

=

=

=

′ =

=

= =

 (13.7) 

Celem zapisania równania (13.4) dla 

1

k

=  i 

2

k

=  należy wyznaczyć współczynniki 

prawej strony równania, czyli wielkości 

0

,

1,

k

N

k

2

=

.  

10

N

 i 

 określa się kolejno (sumując) zgodnie z poniższą zależnością: 

20

N

 

 (13.8) 

10

10

10

20

20

20

l

p

l

N

N

N

N

N

N

=

+

=

+

p

Przyjmując zależności dane w tabelach współczynników 

 można zapisać:  

0

k

N

- przyjmując 

1

k

=   

 

2

2

10

1 1

2

10

2 2

7

7

4 6 6

94,5 [kNm ]

64

64

3

3

8 8 4

96 [kNm ]

8

8

l

p

N

ql l

N

Pl l

′

= −

= −

⋅ ⋅ = −

′

= −

= −

⋅ ⋅ = −

2

 (13.9) 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

 

http://www.okno.pg.gda.pl 

– 66 – mjasina@pg.gda.pl 

otrzymujemy 

 

; (13.10) 

2

10

10

10

( 94,5) ( 96)

190,5 [kNm ]

l

p

N

N

N

=

+

= −

+ −

= −

- przyjmując 

2

k

=  

 

2

20

2 2

2

20

3

3

8 8 4

96 [kNm ]

8

8

0 [kNm ]

l

p

N

Pl l

N

′

= −

= −

⋅ ⋅ = −

=

 (13.11) 

otrzymujemy 

 

. (13.12) 

2

20

20

20

96 [kNm ]

l

p

N

N

N

=

+

= −

Po podstawieniu (13.7) (13.10) i (13.12) do (13.4) otrzymujemy poniższy układ rów-
nań: 

 

(

)

(

)

1

1

2

2

2

10

1

2

2

2

3

3

3

20

0 2

2

X

l

l

X l

N

X l

X

l

l

X l

N

′ ′

′

+ ⋅

⋅

+

+

⋅ =

′

′

′

′

⋅ + ⋅

⋅

+

+

⋅ =

 (13.13) 

Wstawienie do (13.13) wartości liczbowych (przy uwzględnieniu momentu skupionego 

) prowadzi do postaci: 

2

3

12 [kNm ]

B

X

M

= −

=

 

(

)

(

)

1

2

1

2

1

2

1

2

2

6 4

4 20

4

190,

4 2

4 4

12 4 4

16

144

X

X

X

X

X

X

X

X

⋅

+

+

⋅ =

⋅

+ ⋅

= −

⋅ + ⋅

+

+ ⋅ = ⋅

+ ⋅

= −

5

 (13.14) 

Po rozwiązaniu układu równań (13.14) otrzymujemy nadliczbowe metody sił, które są 
poszukiwanymi momentami zginającymi w przekrojach podporowych:  

1

8,13 [kNm]

X

= −

,  

2

6,96 [kNm]

X

= −

, 

co pozwala narysować ostateczne wykresy sił wewnętrznych. 
 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 67 – mjasina@pg.gda.pl 

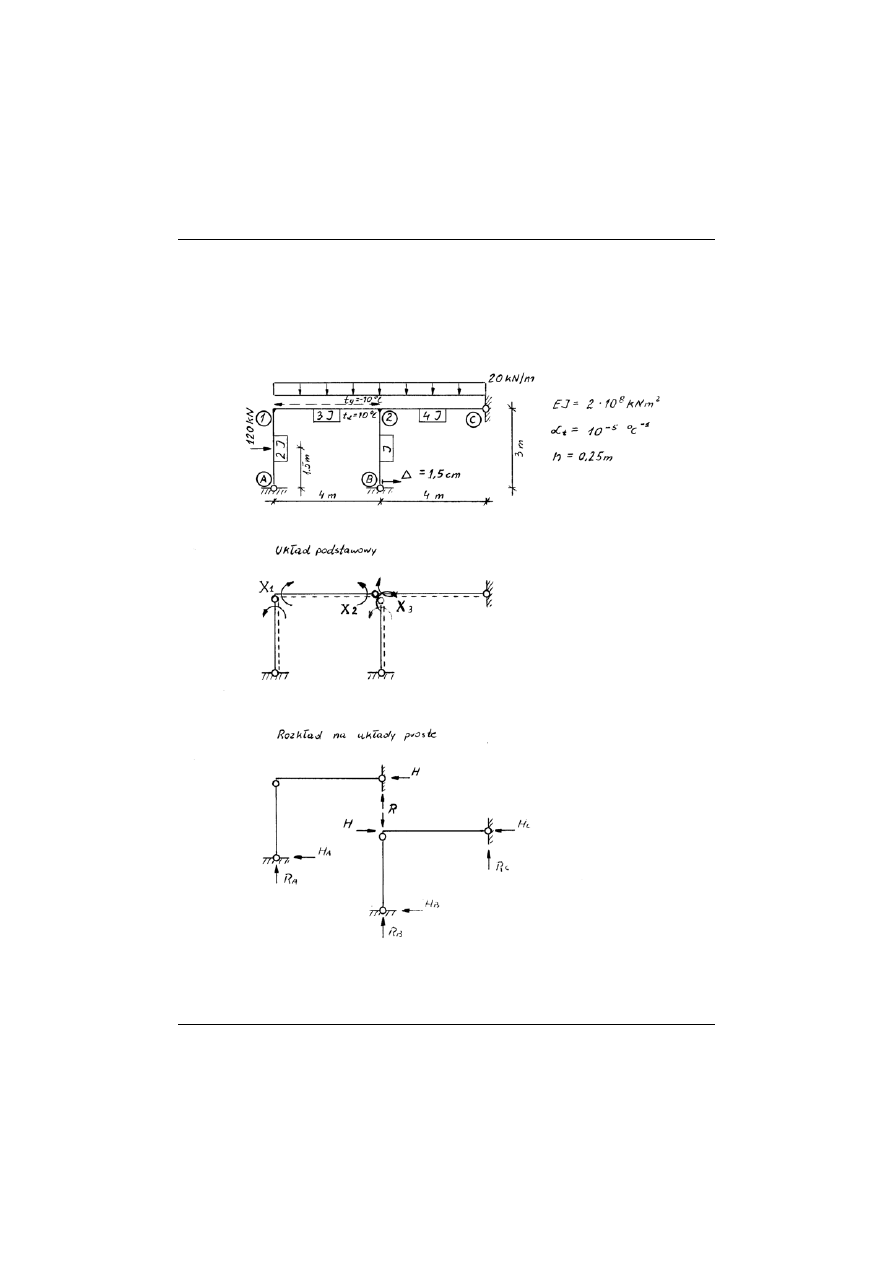
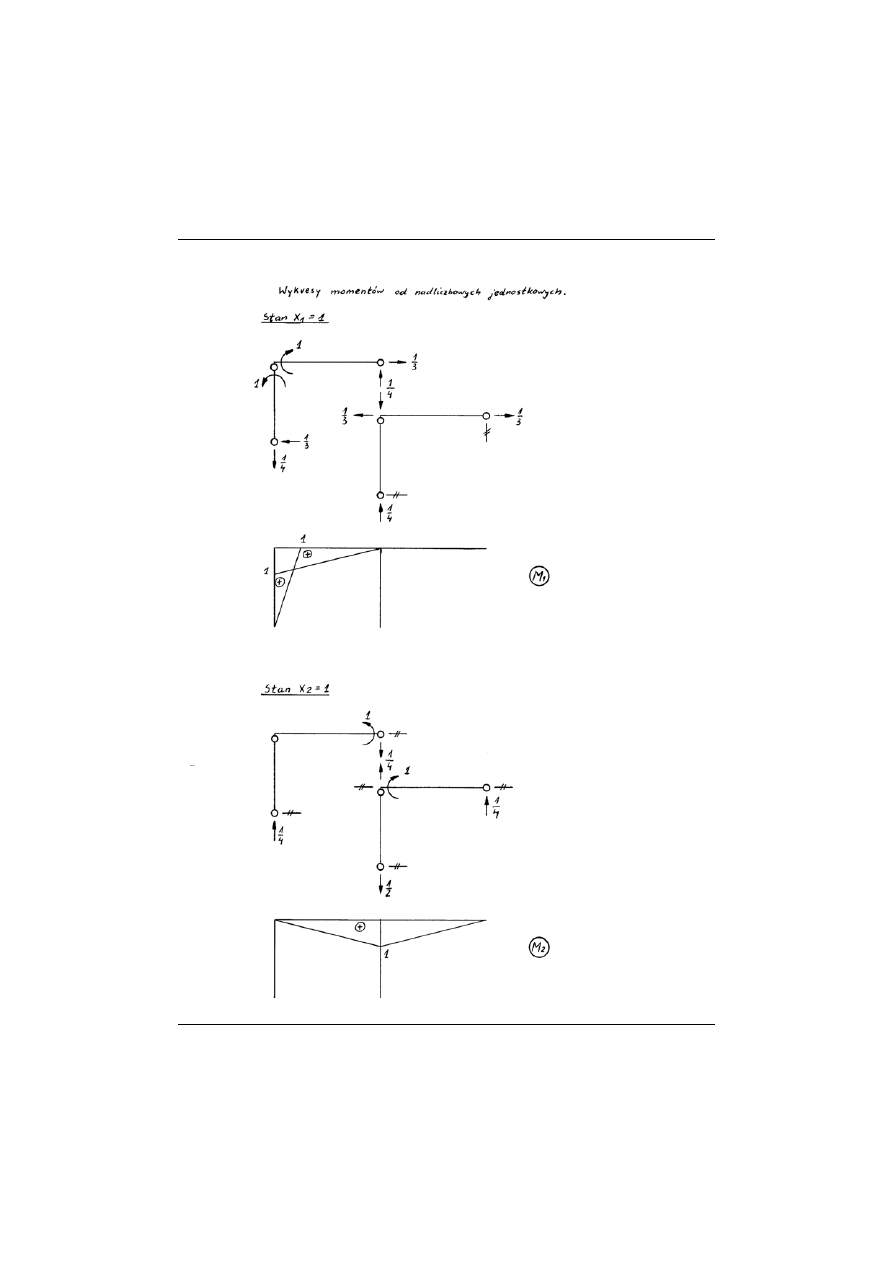
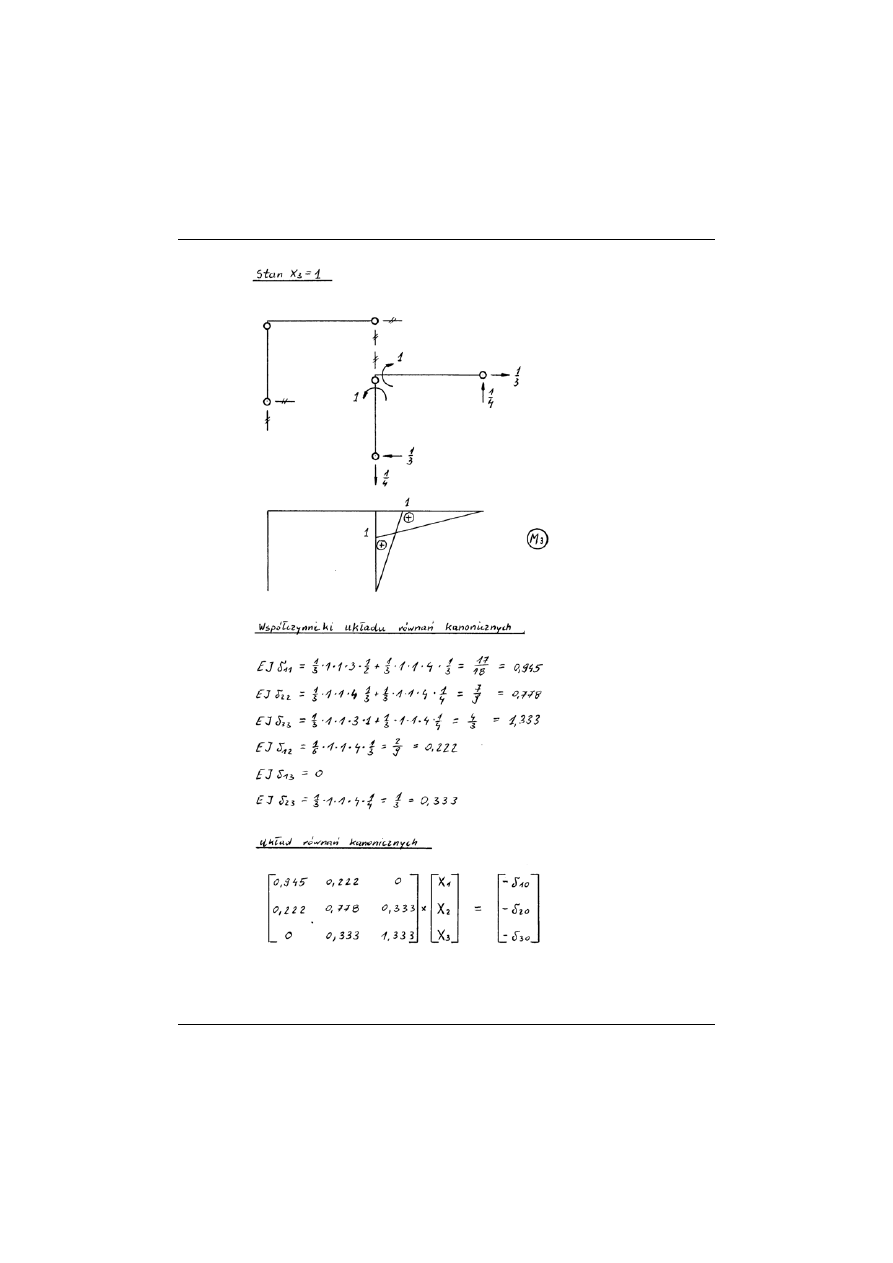
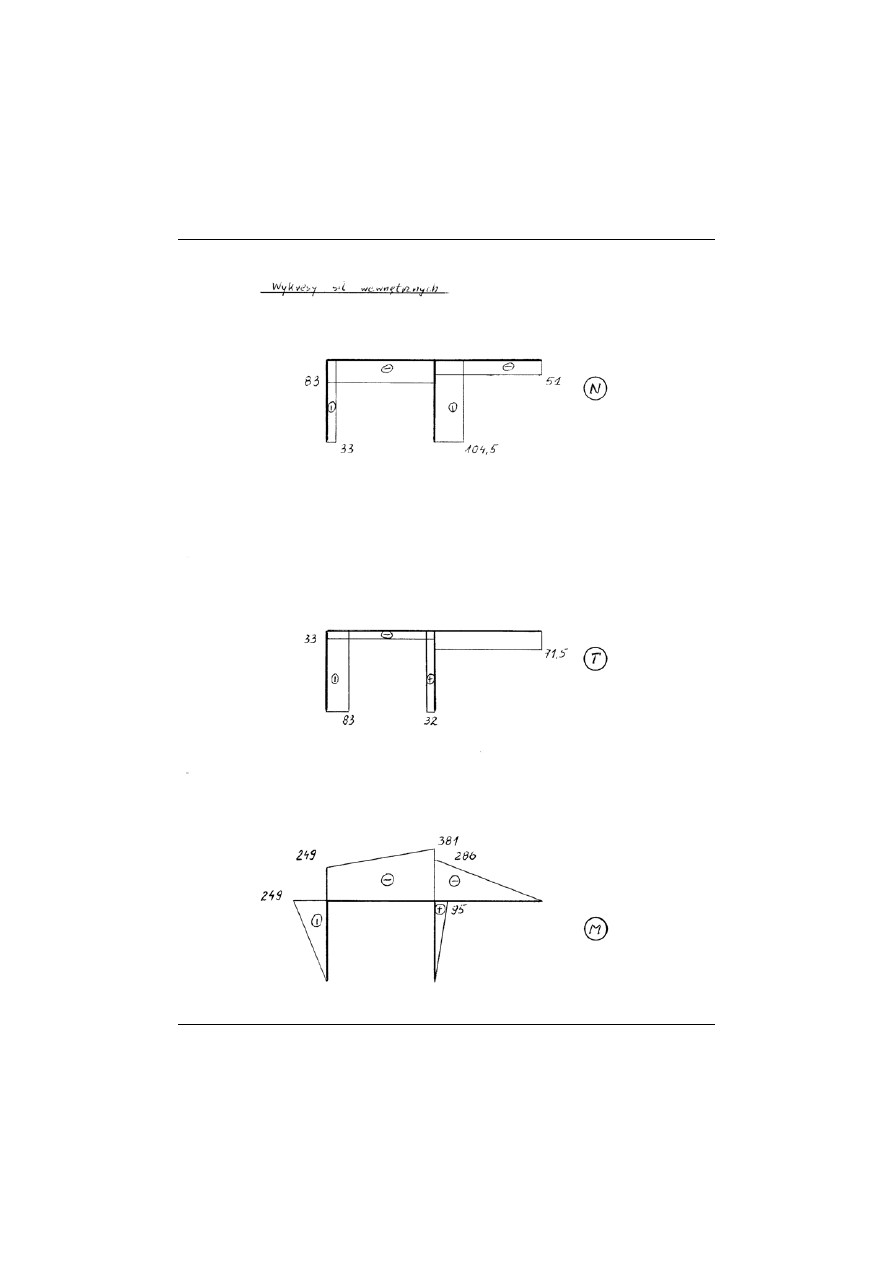
Stosując metodę sił wyznaczyć wykresy sił wewnętrznych 

M

,  , 

, przy zada-

nym obciążeniu zewnętrznym: 

T

N

I) obciążenie statyczne, 
II) obciążenie temperaturą (nierównomierne ogrzanie), 
III) obciążenie przemieszczeniem (osiadaniem) podpór. 

 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 68 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 69 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 70 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 71 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 72 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 73 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 74 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 75 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 76 – mjasina@pg.gda.pl 

 

Mechanika Budowli (C16) 

Wykład 

Marek Krzysztof Jasina 

14. Metoda sił – obciążenie: statyczne, temperaturą, przemieszczeniem podpór 

 

http://www.okno.pg.gda.pl 

– 77 – mjasina@pg.gda.pl