
Ć w i c z e n i e 6
WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W POWIE-
TRZU METODĄ FALI STOJĄCEJ
6.1 Opis teoretyczny
W ośrodkach sprężystych wytrącenie pewnego obszaru z położenia równowagi powoduje drgania
wokół tego położenia. W najprostszym przypadku – drgania harmonicznego, wychylenie z położe-
nia równowagi zmienia się w czasie cosinusoidalnie z częstotliwością kątową
ω
:
ωt
cos
A
A(t)
0
=
gdzie: A
0
– amplituda drgań, czyli największe wychylenie
T
π
2
ω
=
, T – okres drgań (niezależny
od stopnia złożoności drgania).
Wskutek sprężystości ośrodka zaburzenie to przenosi się do coraz dalszych obszarów z prędko-
ścią V zależną od właściwości danego ośrodka. Zjawisko to nazywamy falą mechaniczną.
W punkcie oddalonym od źródła zaburzenia o x
0
drgania pojawiają się z opóźnieniem
V
x
t
0
0
=
(np.
na jeziorze w chwili t = 0 rzuciliśmy kamień na odległość x
0
od brzegu. Fala pojawi się przy brzegu
dopiero po czasie t
0
tzn. w chwili t = t
0
). Drganie w tym punkcie opisuje więc równanie:
=
=
V
x
-
t
ω
cos
A
)
t
-
(t
ω
cos
A
t)
,
A(x
0
0
0
0
0
(6.1)
Zapisujemy t)
,
A(x
0
aby zaznaczyć, że wychylenie A dotyczy konkretnego punktu x
0
.Ogólnie
możemy zapisać dla wszystkich punktów x drgającego ośrodka:
=
V
x
-
t
ω
cos
A
t)
,
A(x
0
(6.2)
Równanie to opisuje falę rozchodzącą się w kierunku dodatniej osi x. W przypadku rozchodzenia
się fali w kierunku przeciwnym, należy x zastąpić przez –x i wówczas:
+
=
V
x
t
ω
cos
A
t)
,
A(x
0
(6.3)
Długością fali
λ
nazywamy najmniejszą odległość między punktami drgającymi w jednakowych
fazach. Jest ona równa drodze jaką określona faza przebędzie z prędkością V w czasie T:
T
V
λ
=
stąd
f
λ
V
=
(6.4)
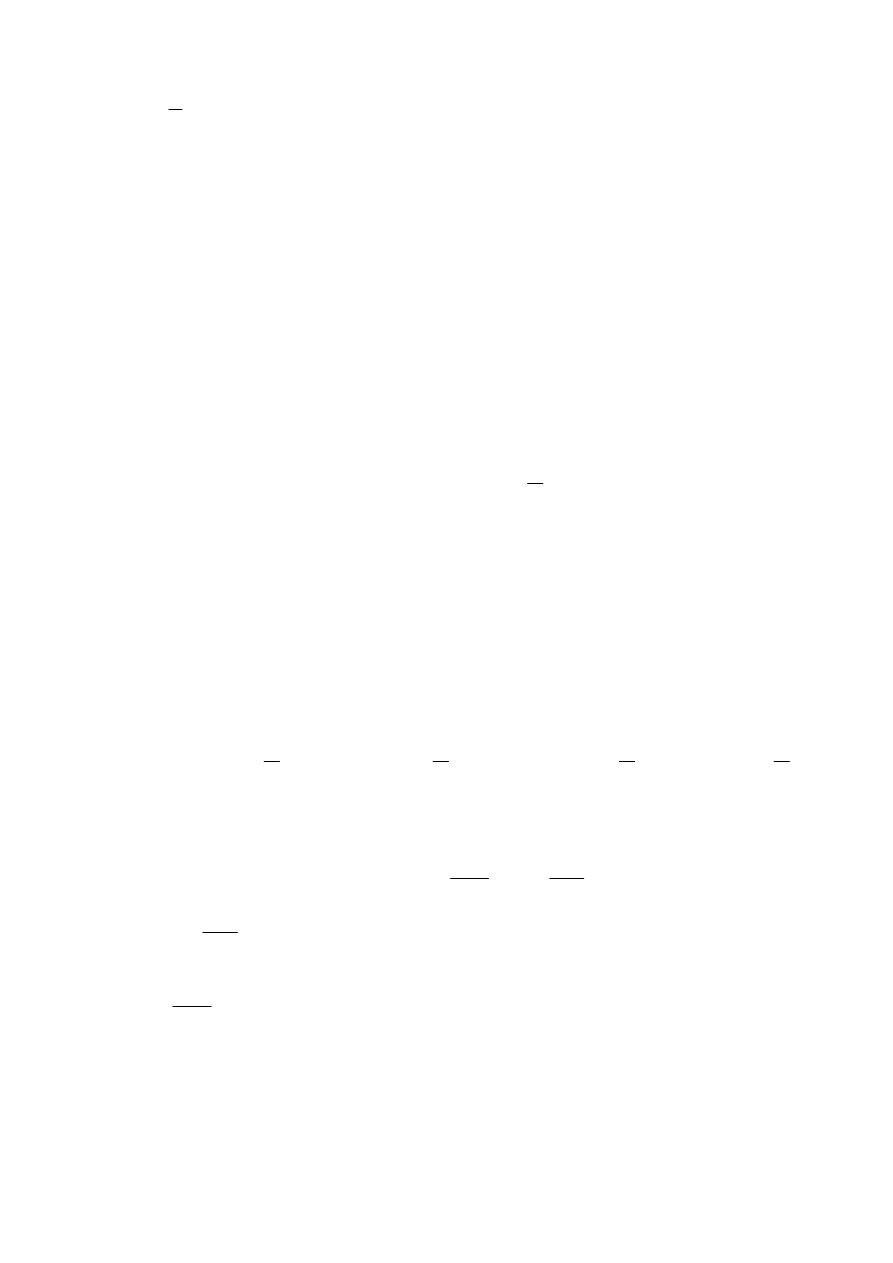
gdzie
T
1
f
=
- częstotliwość propagujących się drgań.
Jest to wzór słuszny dla każdego typu fali.
Powierzchnię utworzoną przez punkty, do których doszło w danej chwili zaburzenie nazywamy
czołem fali. Fale mogą więc być płaskie (w przypadku gdy fala rozchodzi się w jednym kierunku),
kuliste
(gdy źródło wysyła energię drgania tak samo we wszystkich kierunkach) oraz inne w przy-
padkach pośrednich.
W zależności od kierunku drgań cząsteczek ośrodka względem kierunku rozchodzenia się fali, fale
mogą być podłużne – cząstki drgają równolegle, lub poprzeczne - cząstki drgają prostopadle do
kierunku propagacji (czyli rozchodzenia się) fali. Fale poprzeczne powstają w ośrodkach charakte-
ryzujących się sprężystością postaci (sztywnością). Dla występowania fal podłużnych wystarczają-
cy jest warunek sprężystości objętości. W cieczach i gazach mogą rozchodzić się tylko fale podłuż-
ne. W ciałach stałych mogą występować również fale poprzeczne. Dźwięk (fala akustyczna) to fala
podłużna, czyli rozchodzące się rozrzedzenia i zagęszczenia powietrza. Zmiana ciśnienia p
∆ ma
również charakter harmoniczny. Falę akustyczną można więc traktować jak falę przemieszczeń (o
amplitudzie A
0
) lub jak falę zmian ciśnień o amplitudzie
0
0
A
V
ω
ρ
p
=
(gdzie ρ gęstość gazu) :
=
∆
V
x
-
t
ω
sin
p
t)
,
p(x
0
(6.5)
Ponieważ przemieszczenia przesunięte są w stosunku do ciśnień o 90
o
, maksymalnemu ciśnieniu
odpowiada zerowe przemieszczenie i odwrotnie maksymalnemu przemieszczeniu – zerowe ciśnie-
nie. Dlatego we wzorze tym występuje sinus zamiast cosinusa.
Metoda pomiaru prędkości dźwięku w niniejszym ćwiczeniu polega na wytworzeniu w słupie po-
wietrza (rurze) fali stojącej. Powstaje ona w wyniku interferencji (nałożenia się) dwóch identycz-
nych fal, ale rozchodzących się w przeciwnych kierunkach i o przesuniętych względem siebie fa-
zach o kąt
π
. W określonym punkcie x rury wychylenie cząsteczek gazu od położenia równowagi
można określić z równania:
+
−
=
+
+
+
=
V
x
t
ω
cos
A
V
x
-
t
ω
cos
A
π
V
x
t
ω
ω
cos
A
V
x
-
t
ω
cos
A
t)
,
A(x
0
0
0
0
(6.6)
Po jego przekształceniu otrzymujemy:
=
T
t
π
2
sin
λ
x
π
2
sin
A
2
t)
,
A(x
0
(6.7)
Czynnik
T
t
π
2
sin
wskazuje na to, że cząsteczka gazu w punkcie x drga z częstotliwością spo-
tykających się fal. Ich amplituda zależy od punktu x i określona jest przez czynnik
λ
x
π
2
sin
A
2
0
. Taki stan gazu w rurze nazywamy falą stojącą. W stanie tym można wyróżnić
takie płaszczyzny prostopadłe do osi rury, w których cząsteczki mają zerową amplitudę drgań (są to
tzw. węzły fali stojącej) oraz płaszczyzny, w których amplituda drgań jest równa 2 A
0
(są to tzw.
strzałki). Mierząc ciśnienie w tych płaszczyznach otrzymalibyśmy odpowiednio maksymalne i mi-
nimalne ciśnienie. Falę stojącą jest łatwo otrzymać poprzez nałożenie danej fali na jej odbicie, gdyż
fala odbijając się (np. od gładkiej ścianki) oprócz kierunku zmienia fazę drgań na przeciwną (tzn. o
kąt
π
). W tak wytworzonej sytuacji cały ośrodek (powietrze w rurze) jest pobudzany do drgania

przez dwie specyficzne fale. Udział w drganiu bierze cały ośrodek. Nie ma tu jednak zjawiska roz-
chodzenia się zaburzenia. Nie jest to więc fala w sensie opisanym wyżej, lecz szczególny stan drga-
nia ośrodka.
Położenie strzałek można wyznaczyć z warunku
1
λ
x
π
2
sin
S
=
:
4
λ
1)
(2n
x
n
S
+
=
n
=
0,1,2,..
(6.8)
Odległość między kolejnymi strzałkami oblicza się z różnicy sąsiednich położeń:
2
λ
x
x
n
1
n
S
S
=
−
+
i równa ona jest połowie długości interferujących ze sobą fal.
Podobnie można wyznaczyć odległość między kolejnymi węzłami, badając warunek
0
λ
x
π
2
sin
W
=
:
4
λ
2n
x
n
W
=
n
=
0,1,2,..
(6.9)
2
λ
x
x
n
1
n
W
W
=
−
+
Z zależności (6.8) i (6.9) łatwo pokazać, że odległość pomiędzy sąsiednimi węzłami i strzałkami
równa jest jednej czwartej długości fali.
6.2 Opis układu pomiarowego
Zestaw do wytwarzania i rejestracji fali stojącej w słupie powietrza przedstawiony jest na rys. 6.1.
Podstawowym jego elementem jest rozsuwana rura (tzw. rura Kunta), zakończona z dwóch stron
denkami. Poprzez małe otworki w denkach z jednej strony na słup powietrza w rurze oddziałuje
membrana głośnika, pobudzana do drgań z generatora akustycznego. Z drugiej strony słup powie-
trza działa na mikrofon, połączony poprzez wzmacniacz z oscyloskopem. Mała ilość otworków jak
i ich rozmiary pozwala przyjąć, że oba końce rury zakończone są nieruchomymi ściankami. Od-
działywania: słup powietrza – mikrofon oraz membrana głośnika - słup powietrza odbywa się po-
przez zmianę ciśnienia, które jak pokazano w poprzednim punkcie jest przesunięte w stosunku do
przemieszczeń cząsteczek o 90
0
. Ponieważ końce rury to nieruchome ścianki, fazy fali padającej i
odbitej muszą być takie, aby na nieruchomej ściance zawsze był węzeł (brak przemieszczeń. Za-
chodzi to tylko wtedy, gdy fala padająca i odbita są przesunięte w stosunku do siebie o kąt 180
0
. W
przypadku gdy długość rury jest całkowitą wielokrotnością połowy długości fali, zachodzi dodat-
kowo zjawisko rezonansu, w efekcie którego następuje zwiększenie amplitud w miejscu strzałek i
ciśnienia w miejscu węzłów. Zjawisko to łatwo daje się zaobserwować: na mikrofon umieszczony
w węźle fali stojącej działa maksymalne ciśnienie (strzałka ciśnienia) i drgania obserwowane na
oscyloskopie są wówczas największe. Zmieniając długość rury, przy ustalonej częstotliwości drgań
membrany, otrzymujemy kolejne maksyma amplitud drgań obserwowanych na oscyloskopie.
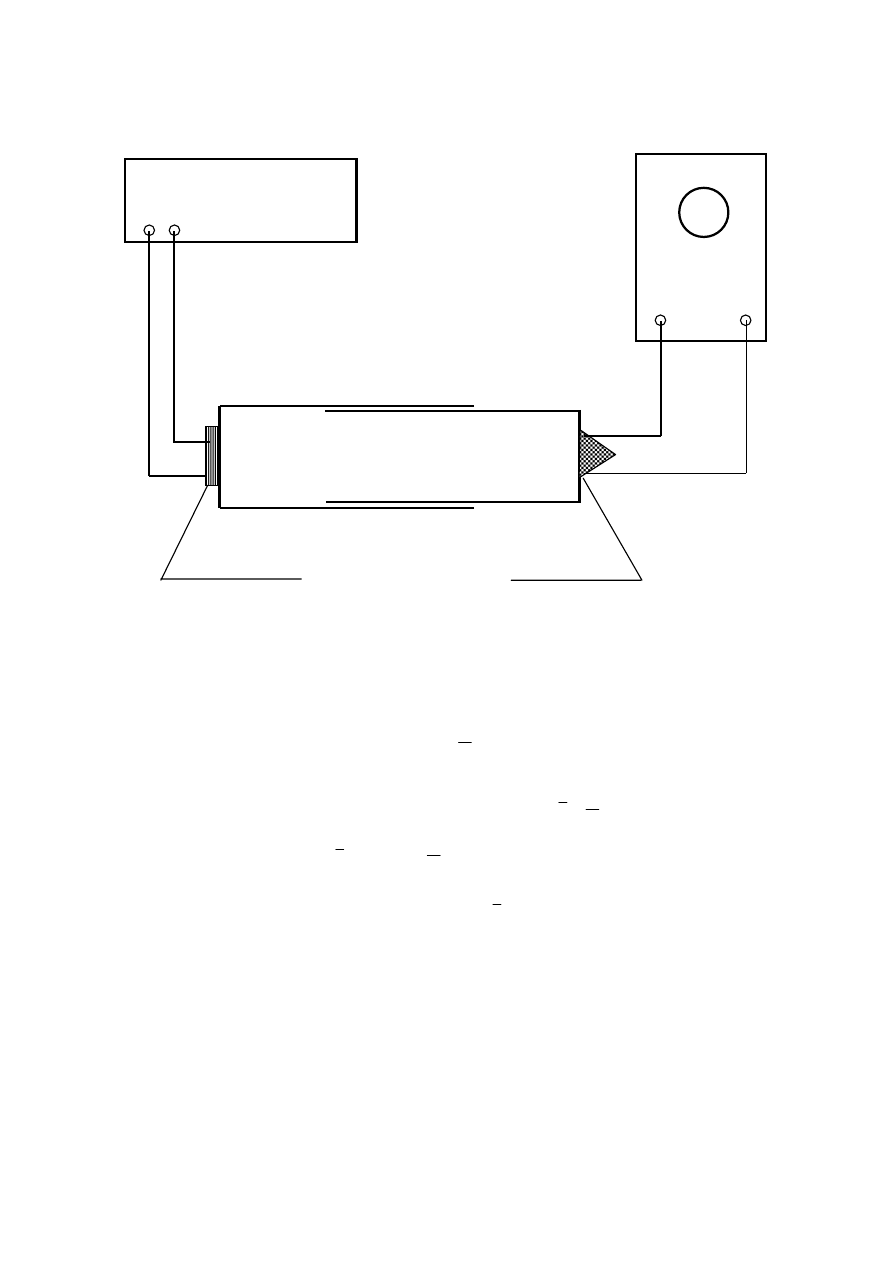
Generator
akustyczny
OSCYLOSKOP
R U R A
Głośnik
Mikrofon
Rys.6.1 Schemat układu do pomiaru prędkości dźwięku w powietrzu.
Oznaczając przez l(0) położenie rury dla którego otrzymujemy pierwsze maksimum amplitudy
drgań, a przez l(n) n = 1,2,3,..kolejne następne położenia. Z omówionej teorii powstawania fali sto-
jącej wynika związek:
2
)
0
(
)
(
λ
n
l
n
l
+
=
n
=
1,2,3,..
Funkcja l(n) jest funkcją liniową o współczynniku kierunkowym
2
a
λ
= i wyrazie wolnym b = l(0).
Znając współczynnik nachylenia a , a więc
2
λ
i korzystając ze wzory (6.4) łatwo wyznaczamy
prędkość dźwięku:
f
a
2
V
=
(6.10)
Wielkość l(n) odczytujemy na skali centymetrowej umieszczonej na bocznej powierzchni rury.
Częstotliwość f ustala się na generatorze drgań akustycznych.
6.3. Przebieg pomiarów
1. Włączyć generator drgań akustycznych i oscyloskop. Obraz na ekranie oscyloskopu powinien
być ostry.
2. Ustawić częstotliwość drgań generowanych przez generator na wartość z zakresu 1500 – 2500
Hz.

3. Wysuwając rurę znaleźć kolejno po sobie następujące położenia l(n) , dla których amplituda
drgań obserwowanych na oscyloskopie osiąga maksimum.
4. Pomiary powtórzyć dla 3 – 4 różnych wartości częstotliwości.
6.4. Opracowanie wyników pomiarów.
1. Rezultaty pomiarów przedstawić na wykresie, odkładając na osi odciętych kolejne numery re-
zonansów n (0,1,2,3,...), a na osi rzędnych odpowiadające im położenia rury l(n)
2. Po naniesionych punktach poprowadzić optymalną prostą. Wyznaczyć współczynnik nachylenia
prostej a oraz błąd jego wyznaczenia
a
σ
.
3. Obliczyć prędkość dźwięku w powietrzu (wzór 6.10)
4. Punkty 1-3 powtórzyć dla pozostałych częstotliwości.
5. Błąd pomiaru częstotliwości
f
σ
związany jest ze stabilizacją pracy generatora.
6. Korzystając z prawa przenoszenia błędów, możemy obliczyć średni błąd kwadratowy wyzna-
czonych prędkości:
(
)
(
)
2
2
V
2
2
σ
a
f
f
a
σ
σ
+
=
6.5. Pytania kontrolne
1. Wyprowadzić równanie fali stojącej.
2. Podać warunek fali stojącej w rurze zamkniętej z jednego końca.
3. Opisać falę akustyczną w powietrzu.
4. Opisać falę akustyczną w ciele stałym.
5. Czy można mówić o spolaryzowanej fali akustycznej w powietrzu oraz w ciele stałym?
6. Wymienić inne metody wyznaczenia prędkości dźwięku.
L i t e r a t u r a
[1] Crawford F.C.: Fale. PWN, Warszawa 1973.
[2] Massalski J.M.: Fizyka dla inżynierów, cz.2, WNT, Warszawa 1975.
[3] Resnik R., Halliday D.: Fizyka, t.1. PWN, Warszawa 1975.
Wyszukiwarka
Podobne podstrony:
LF E CW13(1)
LF E CW43(1)
LF E CW38(1)
LF 100 (2)
Cw06 S
Cw06
MC DUR LF 480
C16 2005 cw06
Fizyka Laboratorium (rok I), LF 17, TABELA POMIAR˙W
Fizyka Laboratorium (rok I), LF 17, TABELA POMIAR˙W
LF E CW09 id 267600 Nieznany
robot lf 01 opis
więcej podobnych podstron