LABORATORIUM

PODSTAWY

ELEKTRONIKI

LICZNIKI

Liczniki scalone serii 749x

2

Cel ćwiczenia

Zapoznanie się z budową i zasadą działania liczników synchronicznych i

asynchronicznych. Poznanie liczników dodających tj. zliczających w przód, jak również

liczników odejmujących tj. zliczających w tył. Program tego ćwiczenia jest zrealizowany na

praktycznych układach liczników stosowanych powszechnie.

Przebieg ćwiczenia.

1.

Zapoznanie się z zasadą działania liczników występujących na danym stanowisku

laboratoryjnym, korzystając z instrukcji

2.

Ustalić odpowiedni poziom napięcia wejściowego oraz jego częstotliwość do prawidłowej

obserwacji sygnału wyjściowego

3.

Przeprowadzić analizę stanów wyjściowych dla każdego licznika

4.

Zaprojektować i wykonać licznik modulo 2, oraz modulo 4. Przeprowadzić analizę

stanów wyjściowych dla każdego licznika

5.

Wyniki ćwiczenia zamieścić w sprawozdaniu

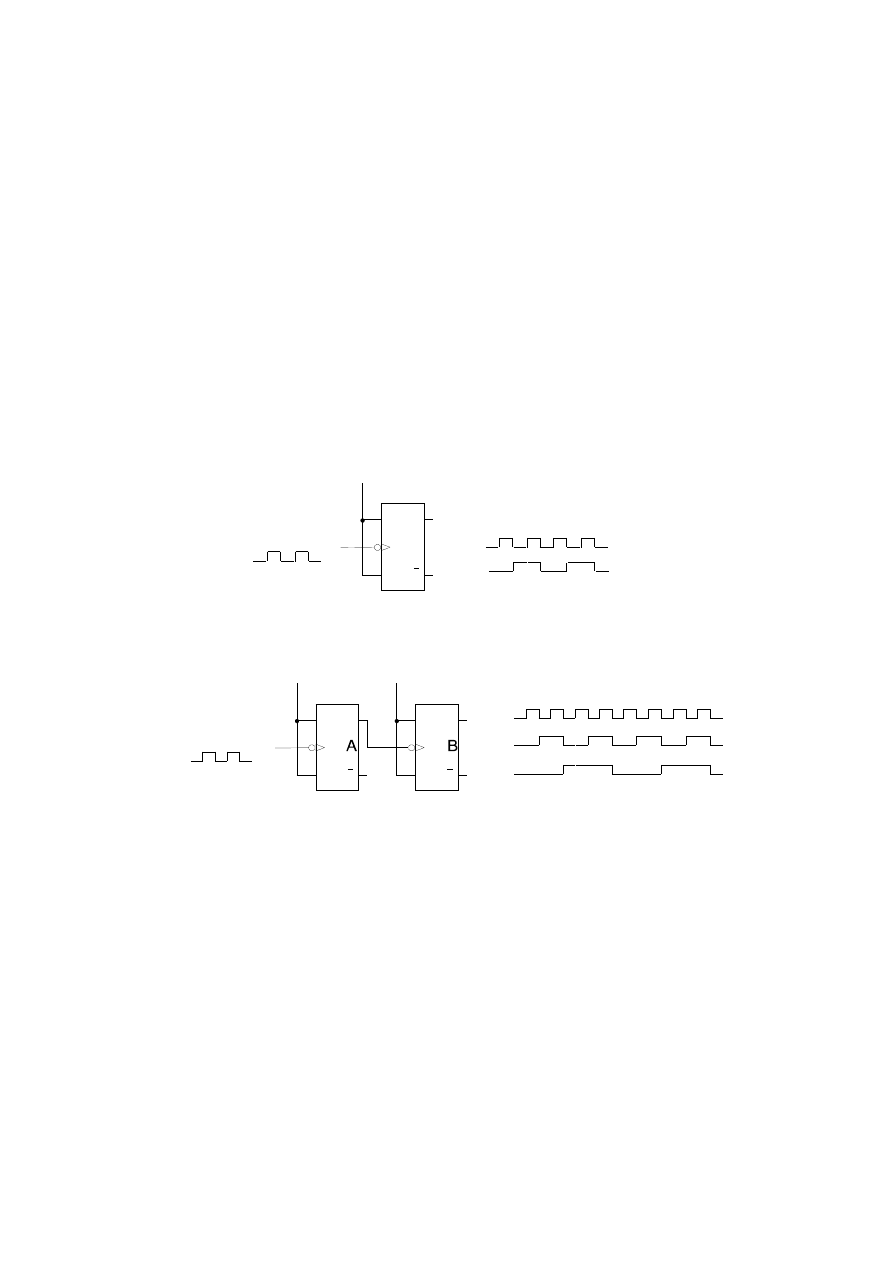
3

1.1

Wstęp teoretyczny.

Wiadomości podstawowe

.

Licznik jest to układ cyfrowy sekwencyjny, służący do zliczania i pamiętania liczby

impulsów podawanych na jego wejście zliczające.
Liczniki dodające (zliczające w przód, zliczające w górę) po każdym impulsie wejściowym
zwiększają liczbę pamiętaną w liczniku o jeden. Natomiast liczniki odejmujące (zliczające w
tył, zliczające w dół) zmniejszają o jeden zawartość licznika. W przypadku konieczności
dodawania i odejmowania impulsów w jednym liczniku, są używane tzw. liczniki rewersyjne
(dwukierunkowe).

Podstawowym elementem liczników jest przerzutnik synchroniczny. Przykład użycia

przerzutnika w funkcji licznika modulo 2 (dwójki liczącej) ilustruje poniższa aplikacja.

Łatwo zauważyć, że układ z dwóch dwójek liczących zlicza impulsy wejściowe w trybie
mod4.

Liczniki są budowane w ten sposób, że wyjście przerzutnika Q jest jednocześnie wyjściem
licznika. Liczba wyjść licznika jest równa liczbie przerzutników i określona mianem długości
licznika.

Określona kombinacja stanów przerzutników, z których zbudowano licznik jest nazywana

stanem licznika. Jeżeli licznik zbudowano z n przerzutników, to maksymalna liczba stanów
licznika wynosi . Rzeczywista liczba stanów licznika musi spełniać nierówność .
Liczba N nazywana jest pojemnością licznika.

J

K

C

Q

Q

1

C

Q

0 1 0 1

J

K

C

Q

Q

1

J

K

C

Q

Q

1

0 1 0 1 0 1 0 1 0
0 0 1 1 0 0 1 1 0

0 1 2 3 0 1 2 3 0

C

Qa

Qb

Dziesi

ę

tnie

n

N

2

max

=

n

N

2

≤

4

Jeżeli licznik przechodzi cyklicznie przez wszystkie stany (tzn. po przejściu N stanów

cykl jest powtarzany) to licznik taki nazywamy licznikiem modulo N.
Po podaniu na jego wejście zliczające K impulsów, licznik taki wskaże zliczenie L impulsów,
gdzie L = K mod N jest resztą z dzielenia całkowitego liczby K przez N.

Jeżeli licznik przechodzi przez wszystkie stany jednokrotnie ( i po osiągnięciu ostatniego

pozostaje w nim), to taki licznik nazywany jest licznikiem „do N”.

Liczniki są szczególnym rodzajem układów sekwencyjnych synchronicznych. Przebieg

zegarowy jest tutaj sygnałem wejściowym licznika, a zliczane impulsy są impulsami przebiegu
synchronizującego prace przerzutników.
Liczniki budowane w taki sposób, że wyjście przerzutnika jest źródłem sygnału zegarowego
(wejściowego) dla kolejnego przerzutnika nazywane są licznikami szeregowymi lub
asynchronicznymi. Przy takim połączeniu, zmianę stanów przerzutnika następnego powoduje
przerzutnik poprzedni. Zliczane impulsy są podawane tylko do jednego przerzutnika.

Liczniki scalone są budowane zarówno jako szeregowe lub równoległe (synchroniczne).

W liczniku równoległym sygnał zegarowy (będący dla licznika zawsze przebiegiem impulsów
zliczanych ) jest doprowadzony jednocześnie do wejść synchronizujących wszystkich
przerzutników. Pojawienie się kolejnego impulsu zliczanego sprawia, że wszystkie przerzutniki
jednocześnie przetwarzają informację wejściową i czas ustalania się kolejnego stanu licznika
wyznacza przerzutnik o najdłuższym czasie propagacji.

W wielu licznikach scalonych część przerzutników pracuje synchronicznie a część

asynchronicznie. Nazywane są one licznikami licznikami asynchroniczno - synchronicznymi.

Najczęściej stosowane są liczniki zliczające mod 10 (dekady) i mod 16 (licznik

dwójkowy- binarny).
Aby rozszerzyć pojemność licznika możemy połączyć go z innymi licznikami bądź
przerzutnikami. Łączenie to możemy przeprowadzić równolegle lub szeregowo.
Przy połączeniu szeregowym sygnał zliczany jest doprowadzany do pierwszego licznika, a
wyjście pierwszego licznika ( o najwyższej wadze) łączymy z wejściem zliczającym drugiego
licznika. Połączenie szeregowe ogranicza szybkość działania licznika (szeregowe połączenie
elementów będących źródłem opóźnienia). Pozbawione tej wady są liczniki połączone
równolegle. Obydwa przykłady przedstawiliśmy na rysunkach.

Połączenie szeregowe

mod10

mod10

c

c

R

R

Qa Qb Qc Qd

Qa Qb Qc Qd

Jednostki

Dziesi

ą

tki

Zerowanie

5

Połączenie równoległe

Połączenie równoległe polega na tym, że sygnał zliczany podawany jest jednocześnie do

pierwszego licznika i bramki AND, której wyjście podłączamy do wejścia drugiego licznika.
Oprócz impulsów zliczanych należy do bramki podłączyć te wyjścia licznika pierwszego, które
po zliczeniu N-1 impulsów (gdzie N – pojemność licznika pierwszego) mają stan wysoki. Dla
licznika mod 10 będzie to 9 impulsów. Po ich zliczeniu stan licznika wynosi wiec 1001 i oba
sygnały doprowadzone do wejść bramki AND mają poziom wysoki. Kolejny impuls przebiegu
zliczanego (dziesiąty) zostanie zatem przepuszczony przez bramkę AND. Licznik następny zliczy
więc jeden impuls. Ponieważ pierwszy licznik zostaje tym samym impulsem (zboczem
opadającym) wyzerowany, przeto bramka ponownie zablokuje przepuszczanie impulsów do
drugiego licznika. Zliczenie kolejnego impulsu przez drugi licznik nastąpi dopiero po kolejnych
dziesięciu impulsach wejściowych.

Połączenie liczników o pojemnościach N1, N2, itd. Daje w rezultacie licznik o

pojemności . Wykorzystując liczniki scalone o określonej

pojemności oraz funktory

takie jak np. bramki NAND czy NOR jesteśmy w stanie budować liczniki typu modN lub „do N”
praktycznie o dowolnej pojemności wykorzystując wejścia ustawiające licznika scalonego.

Jak łatwo zauważyć analizując przebiegi wyjściowe liczników, licznik modN jest

dzielnikiem częstotliwości przez N. Częstotliwość przebiegu wyjściowego jest N – krotnie
mniejsza niż częstotliwość wejściowa.

1.2

Scalone liczniki asynchroniczne.

Licznik 7490

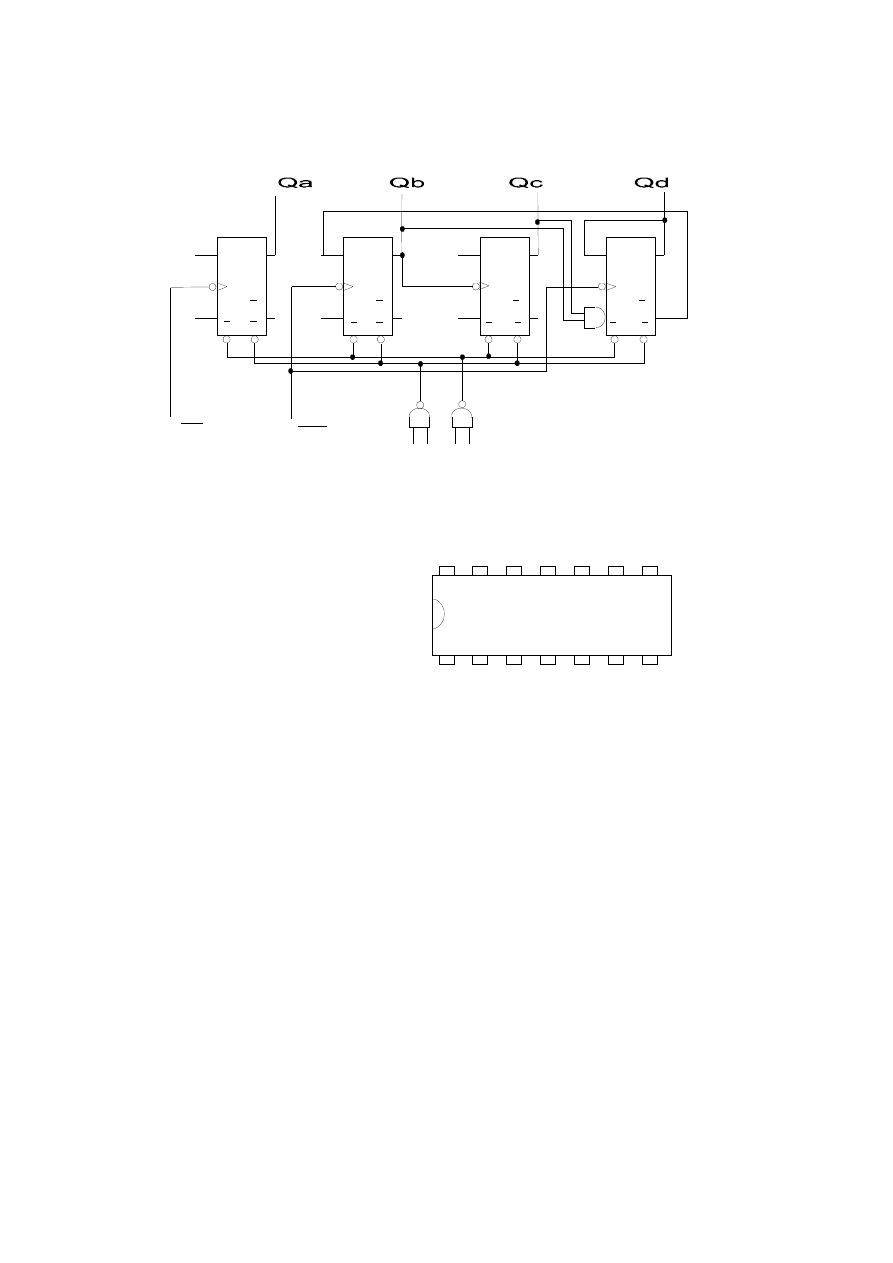
Układ ten zawiera cztery przerzutniki synchroniczne typu MS (Master - Slave). Pierwszy

z nich (A) jest jednobitowym licznikiem mod2, a trzy pozostałe (B,C,D) tworzą licznik mod5.
Trzy przerzutniki (A,B,C) są przerzutnikami typu JK, a czwarty przerzutnik jestprzerzutnikiem
RS.

Układ scalony ’90 ma dwa wejścia zliczające CPa i CPb , cztery wejścia sterujące R0(1),

R0(2), R9(1), R9(2), oraz cztery wyjścia Qa, Qb, Qc, Qd.

Może być wykorzystany jako licznik mod2. Wówczas wejściem zliczającym będzie

wejście CPa, a wyjściem tego licznika wyjście Qa. Wykorzystanie licznika zliczającego mod5
wymaga doprowadzenia przebiegu impulsów zliczanych do wejścia CPb, a wyjściami takiego
licznika są wyjścia Qb, Qc, Qd o wagach odpowiednio

mod10

mod10

c

c

R

R

Qa Qb Qc Qd

Qa Qb Qc Qd

Jednostki

Dziesi

ą

tki

Zerowanie

2

1 N

N

N

⋅

=

.

2

,

2

,

2

2

1

0

6

Opis wyprowadzeń:

1 CPb

8 Qc

2 R01

9 Qb

3 R02

10 GND

4 N.C.

11 Qd

5 Ucc

12 Qa

6 R91

13 N.C.

7 R92

14 CPa

Aby otrzymać licznik dziesiętny, należy wykonać zewnętrzne połączenie wyjścia

Qa z wejściem CPb. Wejściem licznika jest wówczas CPa, a wyjściem wyprowadzenia
Qa, Qb, Qc, Qd o wagach odpowiednio .
Połączenie takie jest szeregowym połączeniem licznika mod2 z licznikiem mod5. Licznik
ten zlicza w kodzie BCD 8421 i jest zarazem w tej konfiguracji dzielnikiem przez 10 o
wypełnieniu przebiegu wyjściowego (wyjście Qd) różnym od 0,5.

Połączenie szeregowe odwrotne (najpierw mod5, a potem mod2) daje nam

również licznik mod10 lecz nie będzie on zliczał w standardowym kodzie BCD, cechuje
się jednak (jako dzielnik częstotliwości przez 10) wypełnieniem przebiegu wyjściowego z
wyprowadzenia Qa równym 0,5.

1

14

7490

J

J

J

K

K

K

R

R

R

R

S

S

R

R

S

R

C

C

C

C

Q

Q

Q

Q

Q

Q

Q

Q

Cpa

Cpb

R01 R02

R91 R92

1

1

1

1

1

A

B

C

D

3

2

1

0

2

,

2

,

2

,

2

7

Licznik 7492

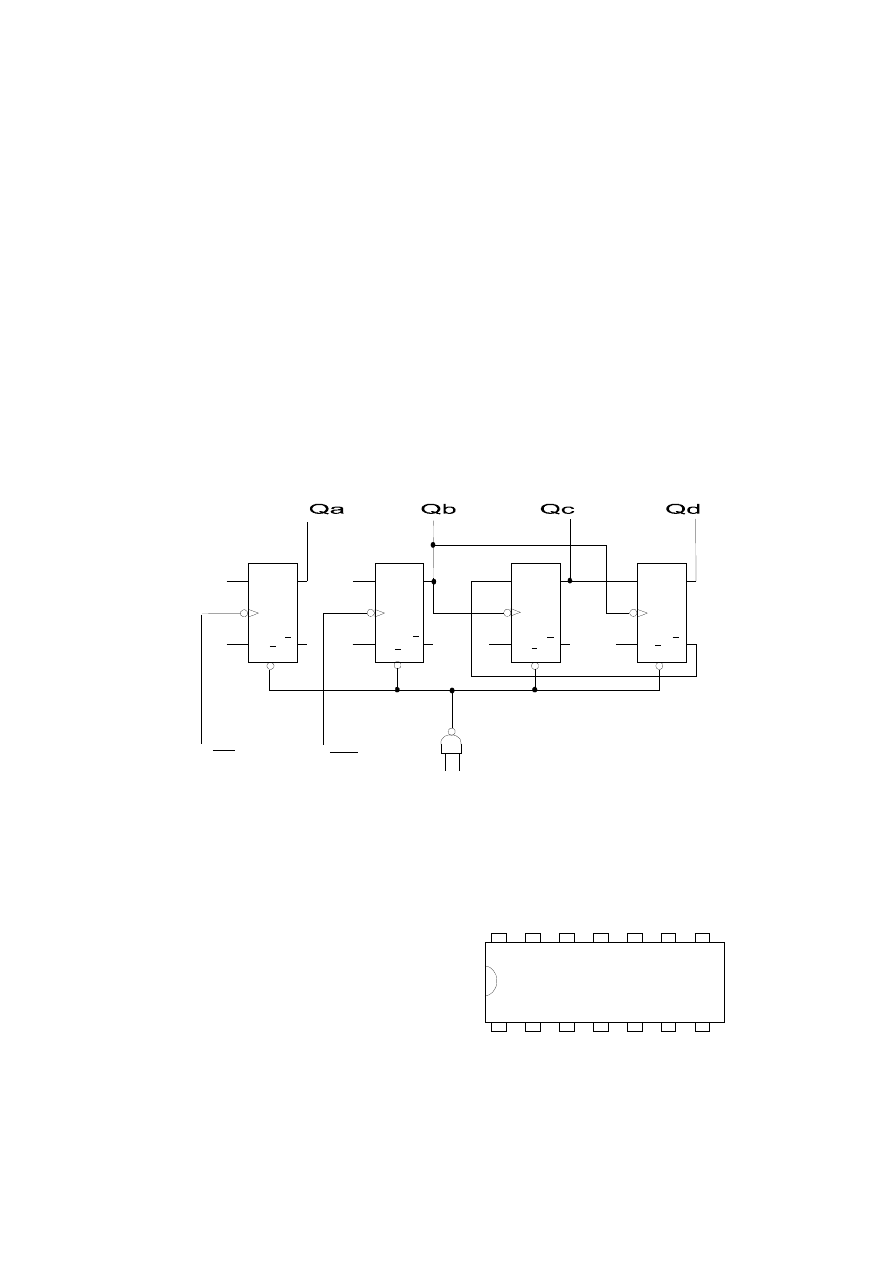
Scalony licznik ’92 jest licznikiem asynchronicznym zbudowanym z czterech

przerzutników typy JK-MS. Jeden przerzutnik (A) jest licznikiem mod2, a trzy pozostałe
(B,C,D) stanowią licznik mod6. Oba liczniki mogą być wykorzystywane niezależnie.
Wszystkie cztery przerzutniki są zerowane tym samym sygnałem, pochodzącym z wyjścia
bramki NAND. Doprowadzenie do obu wyjść tej bramki (R01, R02) sygnałów o
poziomie „H” zeruje licznik. Zliczanie jest możliwe, jeśli co najmniej na jednym z tych
wejść jest poziom niski „L”. Połączenie szeregowe licznika mod2 z licznikiem mod6
(wyjście Qa z wejściem CPb) stanowi licznik mod12, zliczający w kodzie naturalnym.
Połączenie w odwrotnej kolejności (wyjście Qd z wejściem CPa) jest także licznikiem
mod12, ale przeznaczeniem takiej konfiguracji połączeń jest praca układu jako dzielnika
częstotliwości przez 12. Przebieg wyjściowy (wyjście Qa) ma wówczas współczynnik
wypełnienia równy 0,5.

Opis wyprowadzeń:

1 CPb

8 Qc

2 R01

9 Qb

3 R02

10 GND

4 N.C.

11 Qd

5 Ucc

12 Qa

6 N.C.

13 N.C.

7 N.C.

14 CPa

1

14

7492

J

J

J

K

K

K

R

R

R

R

C

C

C

C

Q

Q

Q

Q

Q

Q

Q

Q

Cpa

Cpb

R01 R02

1

1

1

1

A

B

C

D

1

1

J

K

8

Licznik 7493

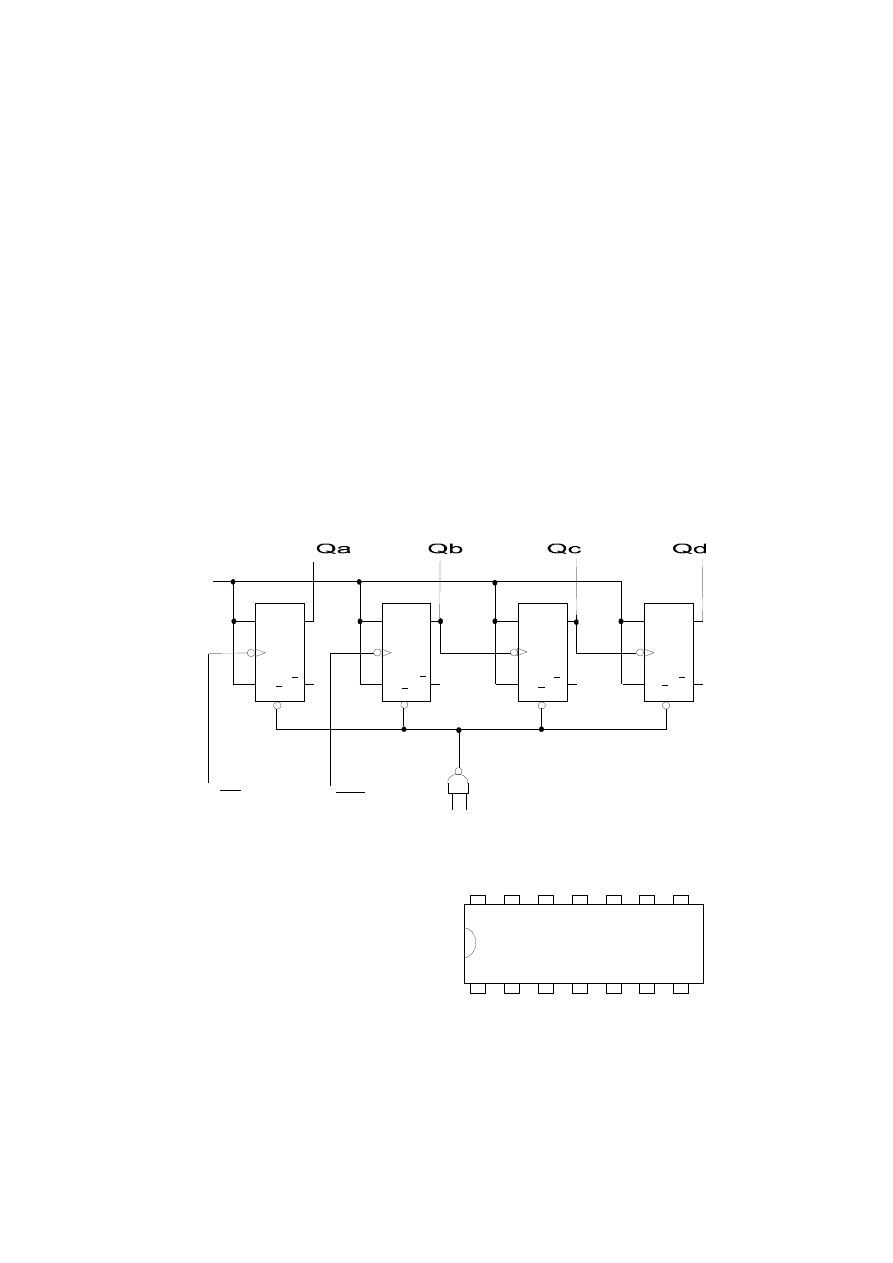
Układ scalony ’93 zawiera cztery przerzutniki JK-MS. Trzy przerzutniki (D,C,B)

są połączone szeregowo, tworząc licznik mod8, a czwarty przerzutnik (A) jest dwójką liczącą,
która może być wykorzystana dwojako: wspólnie z licznikiem mod8 tworząc licznik mod16, albo
oddzielnie jako licznik mod2. Łącząc wyjście Qa pierwszego przerzutnika z wejściem licznika 3
– bitowego (CPb), uzyskujemy licznik mod16 zliczający w kodzie naturalnym dwójkowym, przy
czym wyjściami licznika są wyprowadzenia Qa, Qb, Qc, Qd, gdzie Qa – LSB i Qd – MSB.
Łącząc wyjście czwartego przerzutnika (Qd) z wejściem pierwszego przerzutnika (CPa)
uzyskujemy także licznik mod16 zliczający w naturalnym kodzie dwójkowym, przy czym
wyjściami licznika są wyprowadzenia Qb, Qc, Qd, Qa, gdzie Qb – LSB i Qa – MSB. W obu tych
przypadkach przebieg czasowy na wyjściu MSB ma częstotliwość 16 – krotnie mniejszą niż
przebieg zliczany oraz współczynnik wypełnienia równy 0,5. Dzieje się tak dlatego, że wszystkie
przerzutniki w tym liczniku pracują w układzie dwójek liczących i kolejność ich połączeń nie ma
znaczenia. Zerowanie licznika ’93 odbywa się identycznie, jak opisanego wyżej licznika ’92.

Opis wyprowadzeń:

1 CPb

8 Qc

2 R01

9 Qb

3 R02

10 GND

4 N.C.

11 Qd

5 Ucc

12 Qa

6 N.C.

13 N.C.

7 N.C.

14 CPa

J

J

J

K

K

K

R

R

R

R

C

C

C

C

Q

Q

Q

Q

Q

Q

Q

Q

Cpa

Cpb

R01 R02

1

A

B

C

D

J

K

1

14

7493

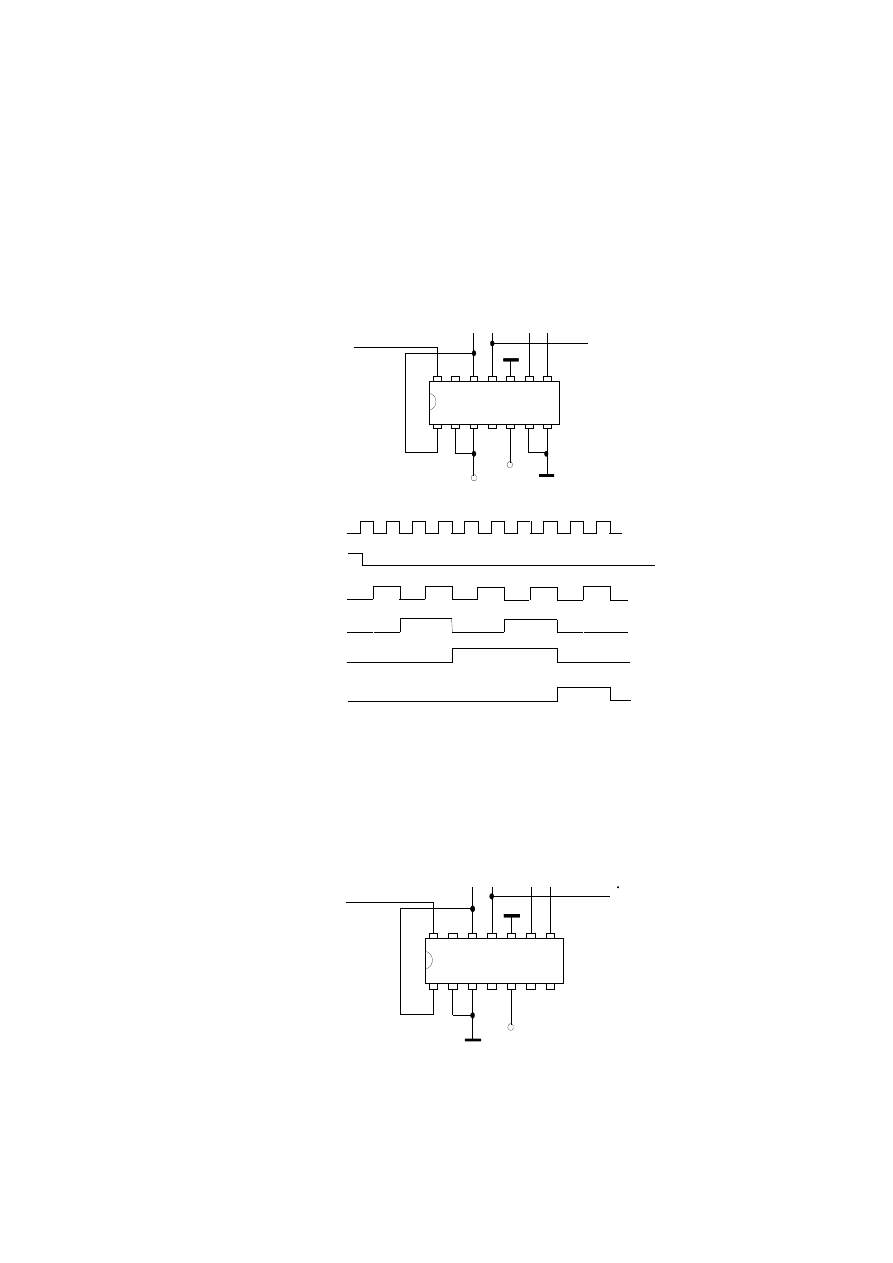
9

1. 3. Układy badane.

Licznik dziesiętny pracujący w kodzie BCD 8421 na układzie 7490.

4 – bitowy licznik dwójkowy na układzie 7493.

1

14

7490

+5 V

Zerowanie poziomem H

Qa Qd Qb Qc

Cpa

R01 R02

Qa

Qb

Qc

Qd

0 1 2 3 4 5 6 7 8 9 0

Cpa

1kHz

100 Hz

1

14

7493

+5 V

Qa Qd Qb Qc

Cpa 1,5 kHz

1/16

F

CPa

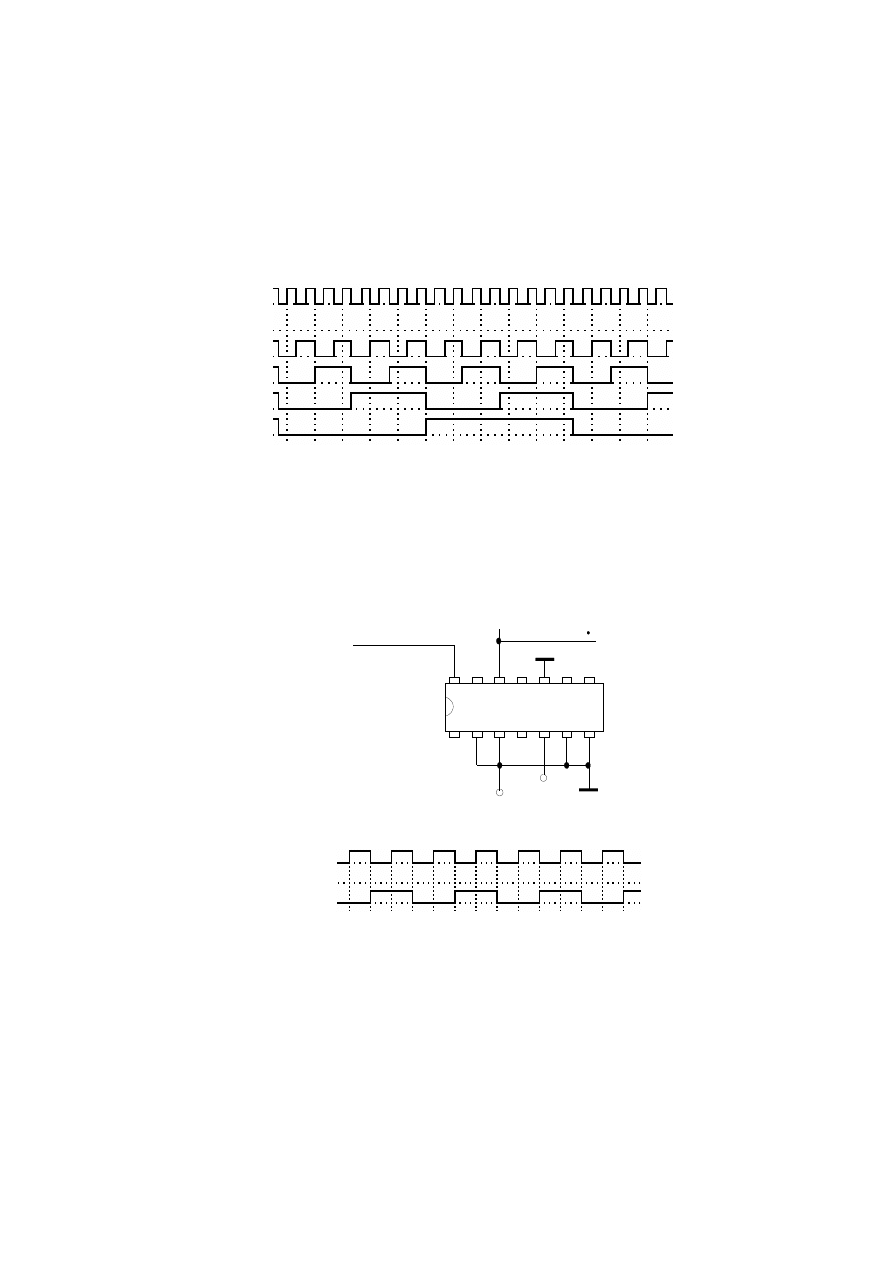
10

Cpa

Qa
Qb

Qc
Qd

1ms/dz

Dzielnik częstotliwości ½ na układzie 7490

Cpa

Qa

0,25 ms/dz

1

14

7490

+5 V

Zerowanie poziomem H

Qa

Cpa 2kHz

1/2 F

CPa

11

Dzielnik częstotliwości 1/9 na układzie 7493

Cpa

Qd

1ms/dz

1

14

7493

+5 V

Qa Qd Qb Qc

Cpa 899Hz

1/9 F

CPa