Politechnika Białostocka

Wydział Mechaniczny

Instrukcja do zajęć laboratoryjnych

Temat ćwiczenia: Analiza częstotliwościowa z wykorzystaniem
transformaty Fouriera

Numer ćwiczenia: 4

Laboratorium z przedmiotu:

Teoria sygnałów i systemów

Kod:

Białystok 2005

1. Wprowadzenie

2

3

Gęstość widmowa mocy

Na podstawie widma sygnału X(f) możemy wyznaczyć gęstość widmową mocy P

xx

(f)

określoną następująco:

− gęstość widmowa mocy własnej:

T

)

f

(

X

lim

T

)

f

(

X

)

f

(

X

lim

)

f

(

P

2

T

*

T

xx

∞

→

∞

→

=

=

(5)

lub inaczej przy N fragmentach sygnału o czasie trwania T

o

:

∑

=

∞

→

=

=

N

1

i

o

2

i

o

2

N

xx

T

)

f

(

X

N

1

T

)

f

(

X

N

1

lim

)

f

(

P

(6)

− gęstość widmowa mocy wzajemnej:

∑

=

∞

→

=

=

N

1

i

o

i

i

o

*

N

xy

T

)

f

(

Y

)

f

(

X

N

1

T

)

f

(

Y

)

f

(

X

N

1

lim

)

f

(

P

(7)

W praktyce często korzysta się z realizacji gęstości widmowej mocy obserwując pro-

ces N-krotnie w czasie jego trwania T

o

. Ilość fragmentów i ich transformat X

i

(f),

i = 1, ..., N należy dobrać tak, aby ocena widma była stacjonarna ze względu na N.

Stosowanie okna pomiarowego

Pomiar

każdego sygnału odbywa się w skończonym czasie a zatem ma początek i ko-

niec (również sygnał wygenerowany programowo przez system komputerowy). Zadane tak
warunki nie zapewniają pełnej reprezentacji sygnału w czasie (sygnał istnieje również poza
wyznaczonymi momentem jego początku i końca). Zatem mówi się o wycinku sygnału a nie
o jego całkowitej reprezentacji a co z tego wynika o istnieniu okna pomiarowego. Podczas

4

analizy takiego sygnału okno pomiarowe wprowadza zniekształcenia, ujawniające się głównie
przy analizie częstotliwościowej a przyczyną takiego stanu rzeczy jest fakt, że niezależnie od
woli osoby analizującej sygnał, transformacji do przestrzeni częstotliwości podlega iloczyn
sygnału i okna, w którym dokonano pomiaru.

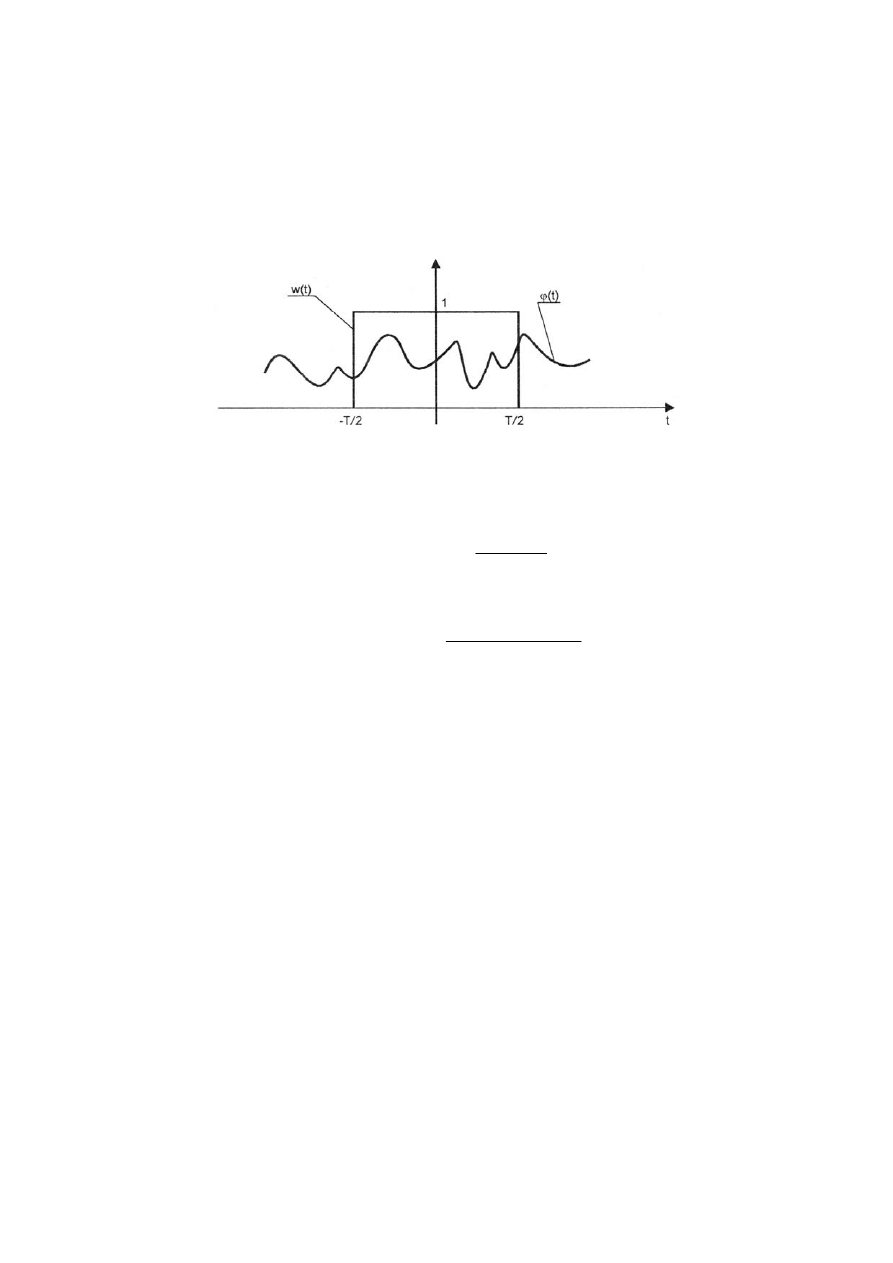
Na rys. 1 pokazano sygnał rzeczywisty φ(t) oraz funkcję okna prostokątnego w(t)

(w(t) = 1 dla –T/2

≤ t ≤ T/2 , w(t) = 0 dla t < –T/2 i t > T/2).

Rys. 1. Reprezentacja graficzna sygnału rzeczywistego w prostokątnym oknie pomiarowym

Transformata Fouriera okna prostokątnego opisuje postać (8):

fT

fT

T

f

W

π

π

)

sin(

)

(

=

(8)

lub też

T

f

f

T

f

f

T

f

W

i

i

)

(

)

)

(

sin(

)

(

−

−

=

π

π

(9)

gdzie:

T – długość okna,
f – częstotliwość bieżąca,
f

i

– dyskretna wartość częstotliwości środkowej transformaty okna (dowolne wartości

położenia prążków w badanym widmie).

Różnica (f – f

i

) wyraża odstęp częstotliwości bieżącej od środkowej. Wpływ okna po-

miarowego ujawnia się głównie w miejscach występowania prążków częstotliwościowych
w widmie badanego sygnału. Reprezentację graficzną funkcji W(f) pokazano na rys. 2.

5

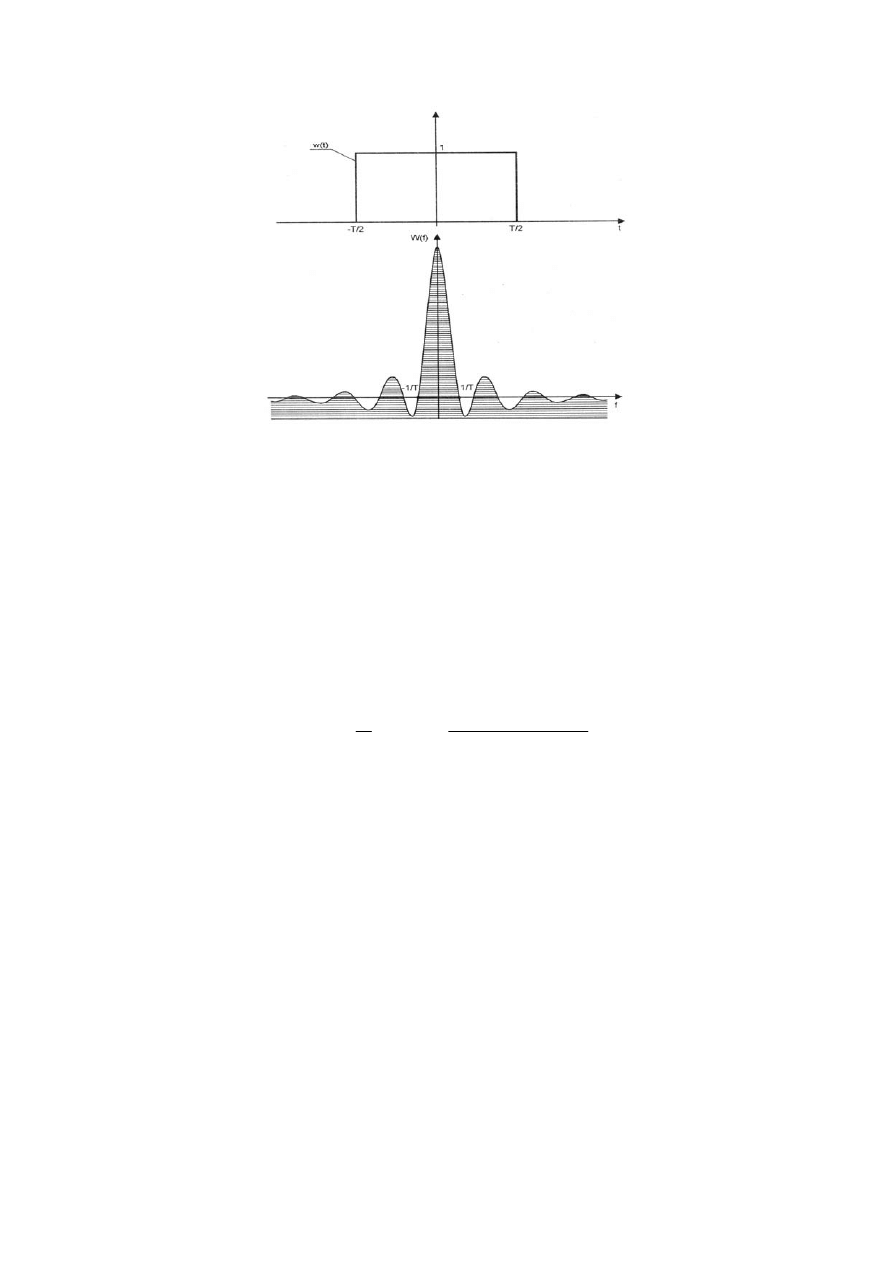
Rys. 2. Reprezentacja graficzna transformaty Fouriera prostokątnego okna pomiarowego

W wyniku uwzględnienia okna pomiarowego w(t), na podstawie pierwotnego sygnału

φ(t), otrzymuje się sygnał f(t):

)

(

)

(

)

(

t

w

t

t

f

⋅

=

ϕ

. (10)

Wówczas transformata F(f) określona jest zależnością:

dt

e

t

w

t

t

F

ft

∫

∞

∞

−

−

⋅

⋅

=

π

ϕ

2

)

(

)

(

)

(

. (11)

Zapisując mnożenie splotowe w postaci analitycznej i podstawiając (9) otrzymuje się:

df

T

f

f

T

f

f

f

T

f

F

i

i

∫

∞

∞

−

−

−

=

)

(

)

)

(

sin(

)

(

)

(

π

Φ

π

(12)

a zatem:

)

(

)

(

f

f

F

Φ

≠

(13)

Przykładem powstania zniekształcenia widma wywołanym istnieniem okna jest fakt,
że przy zmniejszaniu się odległości pomiędzy częstotliwościami analizowanego sygnału f

1

i f

2

wykresy funkcji W(f) „rozpięte” na tych częstotliwościach zaczną się sumować. Występują
wówczas zniekształcenia jakościowe (jedna składowa zamiast dwóch) i ilościowe (większa
amplituda). Oba błędy wynikają z utraty rozróżnialności składowych widmowych.

W celu polepszenia rozróżnialności i zmniejszenia zakłóceń widma wynikających z

obcięcia sygnału przez okno pomiarowe stosuje się różnego rodzaju okna korekcyjne. Nieza-
leżnie od typu zastosowanego okna korekcyjnego, osiągnięta w ten sposób modyfikacja pole-
ga na złagodzeniu pionowych obcięć sygnału na początku i na końcu pomiaru. Wyróżnia się
trygonometryczne, potęgowe i wykładnicze okna korekcyjne. Najczęściej wykorzystywane są
okna trygonometryczne a wśród nich najbardziej znane są okna, które przyjęły nazwy od na-
zwisk ich twórców:
- okno von Hanna (okno Hanninga):

6

2

0

)

(

2

)

2

cos(

5

,

0

5

,

0

)

(

T

t

dla

t

w

i

T

t

dla

T

t

t

w

Hn

Hn

>

=

≤

⋅

+

=

π

- okno Hamminga:

T

t

dla

t

w

i

T

t

dla

T

t

a

a

t

w

Hm

Hm

>

=

≤

⋅

−

+

=

0

)

(

)

2

cos(

)

1

(

)

(

π

, gdzie:

>

∈<

1

;

5

,

0

a

Okno Hanninga jest najbardziej rozpowszechnionym oknem korekcyjnym i w syste-

mach obróbki sygnałów bywa obligatoryjnie umieszczane w oprogramowaniu oraz często
w części sprzętowej.

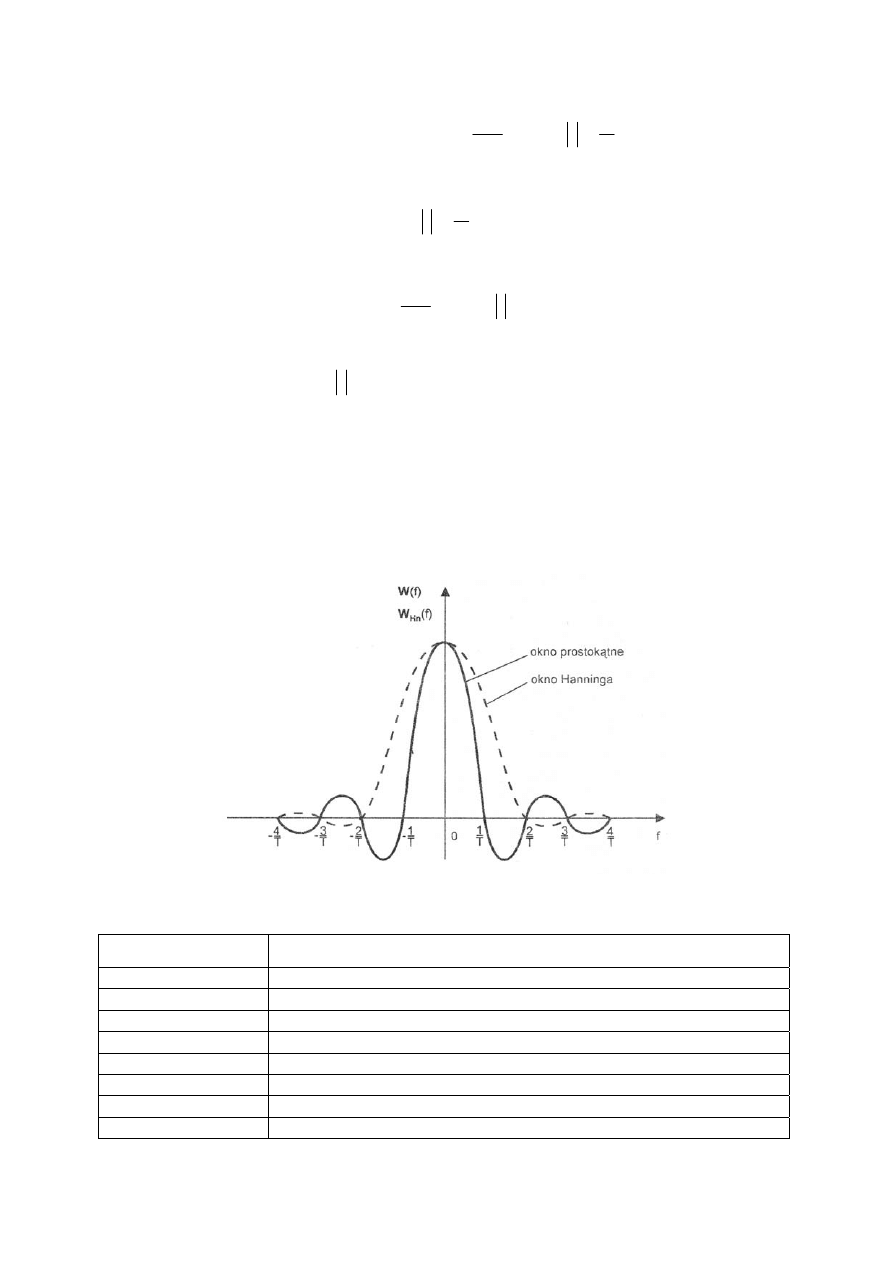
Na rys. 3 przedstawiono porównanie transformaty prostokątnego okna pomiarowego

W(f) i transformaty korekcyjnego okna Hanninga W

Hn

(f). Oczekuje się tutaj, że przy zastoso-

waniu okna korekcyjnego nastąpi znaczne zmniejszenie zniekształcenia widma, wynikające z
istnienia listków bocznych.

Rys. 3. Porównanie transformaty okna prostokątnego i okna Hanninga

Funkcje programu MATLAB do wykorzystania w ćwiczeniu:

Funkcja Przeznaczenie

fft

Dyskretna transformata Fouriera

abs Obliczenie

modułu (wartości bezwzględnej)

psd Estymacja

gęstości widmowej mocy metodą Welcha

hann

Okno Hanna (Hanning)

hamming

Okno Hamminga (Hamming)

rectwin Okno

prostokątne

triang Okno

trójkątne

blackman

Okno typu Blackman

7

2. Wykonanie ćwiczenia

a) wygenerować sygnały x

1

(t), x

2

(t) i x

3

(t) opisane następująco:

)

t

f

2

cos(

A

)

t

(

x

11

11

1

⋅

⋅

⋅

⋅

=

π

,

)

t

f

2

cos(

A

)

t

f

2

cos(

A

)

t

(

x

22

22

21

21

2

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

=

π

π

,

)

t

f

2

cos(

A

)

t

f

2

cos(

A

)

t

f

2

cos(

A

)

t

(

x

33

33

32

32

31

31

3

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

=

π

π

π

;

gdzie:

f

11

, f

21,

f

22,

f

31,

f

32,

f

33

– częstotliwości kolejnych składowych,

A

11

, A

21,

A

22,

A

31,

A

32,

A

33

– amplitudy kolejnych składowych,

b) wyznaczyć widma X

1

(f), X

2

(f) i X

3

(f) (funkcja fft(..)),

c) wykreślić widma amplitudowe | X

1

(f)|, | X

2

)| i X

3

f)|,

d) dokonać skalowania osi częstotliwości zgodnie z zależnością:

p

i

f

N

i

f

⋅

=

,

gdzie: i = 0 .. N-1 (N – ilość danych wektora sygnału),

f

p

– częstotliwość próbkowania.

e) dokonać skalowania osi amplitudy zgodnie z zależnością (4),

e) wykreślić widma amplitudowe wyskalowane w wartościach amplitudy i częstotliwości,

f) wyznaczyć estymację gęstości widmowej mocy sygnału x

1

(t), x

2

(t) i x

3

(t) metodą Welcha

(funkcja psd(..)),

g) wyznaczyć gęstość widmową mocy sygnału x

1

(t), x

2

(t) i x

3

(t) przy wykorzystaniu widma

X

1

(f), X

2

(f) i X

3

(f),

h) wyznaczyć widma sygnału x

1

(t), x

2

(t) i x

3

(t) z zastosowaniem okna Hanninga, Hamminga,

okna typu Blackman, okna prostokątnego i trójkątnego,

i) wykreślić widma amplitudowe sygnałów z zastosowaniem okien,

j) porównać widmo amplitudowe sygnału x

1

(t) z oknem prostokątnym o czasie trwania będą-

cym całkowitą wielokrotnością okresu T

1

=1/f

11

z widmem amplitudowym tego samego

sygnału z oknem prostokątnym o czasie trwania nie będącym całkowitą wielokrotnością

okresu T

1

,

k) porównać widmo amplitudowe sygnału x

1

(t) z oknem prostokątnym o czasie trwania nie

będącym całkowitą wielokrotnością okresu T

1

z widmem amplitudowym z zastosowaniem

okna Hanninga i Hamminga o takiej samej długości jak przy oknie prostokątnym.

8

Literatura

1. Szabatin J.: Podstawy teorii sygnałów. WKŁ, Warszawa 2003.
2. Pasko M., Walczak J.: Teoria sygnałów. Wydaw. Politechniki Śląskiej, Gliwice 1999.
3. Izydorczyk J., Płonka G.: teoria sygnałów. Wydaw. HELION, Gliwice 1999.
4. Kurowski W.: Podstawy teoretyczne komputerowego miernictwa systemów mecha-

nicznych. Wydaw. Politechniki Białostockiej, Białystok 1994.

5. Smyczek J.: Teoria sygnałów i informacji. Cz. I., Wydaw. Politechniki Łódzkiej,

Łódź 1991.

6. Wojnar A.: Teoria sygnałów. WNT, Warszawa 1988.

9