1. DANE OGÓLNE

1.1 Opis projektowanego mostu

Zaprojektowano most jednoprzęsłowyowy, wolnopodparty. Ustrój niosący stanowi 6 belek stalowych

IPN500 o rozstawie 0.9 m i pomost drewniany o konstrukcji: podkład górny (ułożony w jodełkę) 5 cm, pokład

dolny 10 cm, poprzecznice z bali o szerokości 24 cm, wysokości 24 cm i o rozstawie 0.6 m.

1.2. Parametry techniczno-użytkowe:

-długość całkowita ustroju niosącego

- rozpiętość teoretyczna mostu

- szerokość użytkowa obiektu

w tym

- jezdnia

- chodnik po stronie lewej

- chodnik po stronie prawej

- obciążenie mostu

10 m



1 m



+

11m

=

10.0m
6.0m
4m
1m
1m

- LM1, LM2 wg PN-EN 1991-2:2003 Oddziaływanie na konstrukcje. Część 2: Obciążenia ruchome mostów

1.3. Podstawy opracowania:
[1] Rozp MTiGM z dnia 2-03-1999r w sprawie warunków technicznych, jakim powinny odpowiadać drogi

publiczne i ich usytuowanie (Dz. U. Nr 43 z 1999 r.)

[2] Rozp MTiGM z dnia 30-05-2000r w sprawie warunków technicznych, jakim powinny odpowiadać drogowe

obiekty inżynierskie i ich usytuowanie (Dz. U. Nr 63 z 2000 r.)

[3] PN-EN 1990:2004 Podstawy projektowania konstrukcji

[4] PN-EN 1991-1-1:2004 Oddziaływania na konstrukcje - Część 1-1: Oddziaływania ogólne -

ciężar objętościowy, ciężar własny, obciążenia użytkowe w

budynkach

[5] PN-EN 1991-2:2003 Oddziaływanie na konstrukcje. Część 2: Obciążenia ruchome mostów

[6] PN-EN 1995-2:2007 Projektowanie konstrukcji drewnianych Część 2 Mosty

[7] PN-EN 338:2004 Drewno konstrukcyjne. Klasy wytrzymałości.

2. OBLICZENIA STATYCZO - WYTRZYMAŁOŚCIOWE

2.1. Pomost drewniany

Zaprojektowano pomost z drewna sosnowego klasy C30 (dylina górna i dolna) oraz klasy C40 (poprzecznice).
Cechy materiałowe i geometryczne:
- grubość pokładu górnego:

gg 5 cm



:=

- grubość pokładu dolnego:

gd 10 cm



:=

- szerokość poprzecznic:

bp 24 cm



:=

- wysokość poprzecznic:

hp 24 cm



:=

- rozstaw poprzecznic:

sp 60 cm



:=

- rozstaw belek:

sb 85 cm



:=

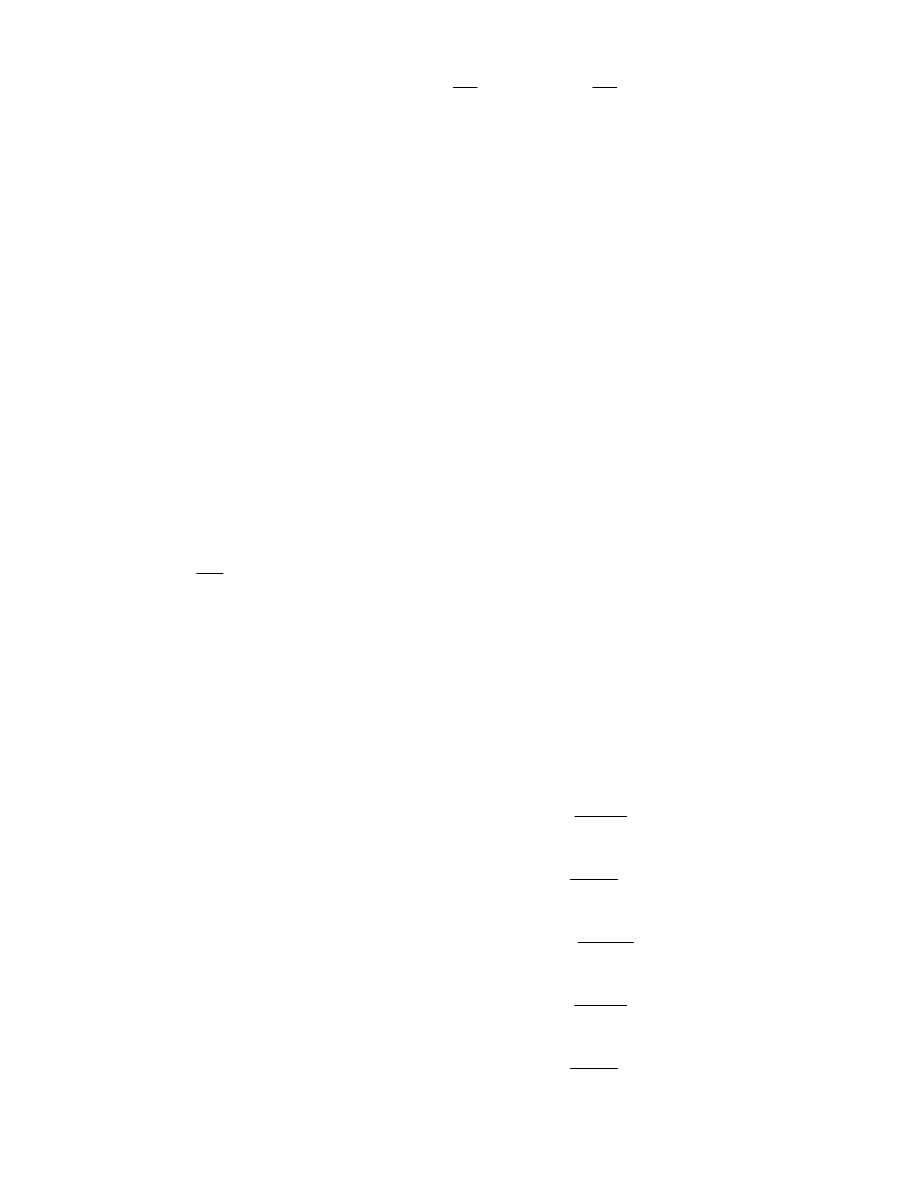
- ciężar objętościowy drewna:

ρd27 4.5

kN
m

3



:=

ρd40 5

kN
m

3



:=

Wytrzymałość drewna wg PN-EN 338:2004 Drewno konstrukcyjne. Klasy wytrzymałości:

Wytrzymałości charakterystyczne:

Pokład górny i dolny:

fm.k27 27 MPa



:=

- na zginanie (klasa C27):

fv.k27 2.8 MPa



:=

- na ścinanie (klasa C27):

fc0.k27 22 MPa



:=

- na ściskanie wzdłuż włókien (klasa C27):

Poprzecznice:

fm.k40 40 MPa



:=

- na zginanie (klasa C40):

fv.k40 3.8 MPa



:=

- na ścinanie (klasa C40):

fc90.k40 2.9 MPa



:=

- na ścinanie w poprzek włókien (klasa C40):
Wytrzymałości obliczeniowe:

fd kmod

fk

γm



:=

kmod

gdzie:

- częściowy współczynnik bezpieczeństwa (materiałowy):

- współczynnik modyfikacyjny, uwzględniający czas trwania obciążenia i

zawartość wilgoci w konstrukcji, zależny od klasy użytkowalności

konstrukcji i od klasy trwania obciążenia:

γm 1.3

:=

kmod 1

:=

- na zginanie (klasa C27):

fm.d27 kmod

fm.k27

γm



20.769 MPa



=

:=

- na ścinanie (klasa C27):

fv.d27 kmod

fv.k27

γm



2.154 MPa



=

:=

- na rozciąganie wzdłuż włókien (klasa C27):

fc0.d27 kmod

fc0.k27

γm



16.923 MPa



=

:=

- na zginanie (klasa C40):

fm.d40 kmod

fm.k40

γm



30.769 MPa



=

:=

- na ścinanie (klasa C40):

fv.d40 kmod

fv.k40

γm



2.923 MPa



=

:=

- na rozciąganie wzdłuż włókien (klasa C40):

fc90.d40 kmod

fc90.k40

γm



2.231 MPa



=

:=

2.2. Pokład dolny
2.2.1.

Obciążenie

Obciążenie ruchome stanowi jedno koło pojedyńczej osi β.QQa.k z Qa.k=400kN o nacisku P=200kN*β

Q

Obciążenie stałe stanowi pokład górny i dolny sosnowy.

Rys. 1. Schemat rozmieszczenia i rozkładania się obciążenia na pokład dolny

- szerokość oddziaływania obciążenia ruchomego:

b1 0.6 m



2 gg



+

gd

+

:=

b1 0.8m

=

- długość oddziaływania obciążenia ruchomego:

b2 0.35 m



2 gg



+

gd

+

:=

b2 0.55m

=

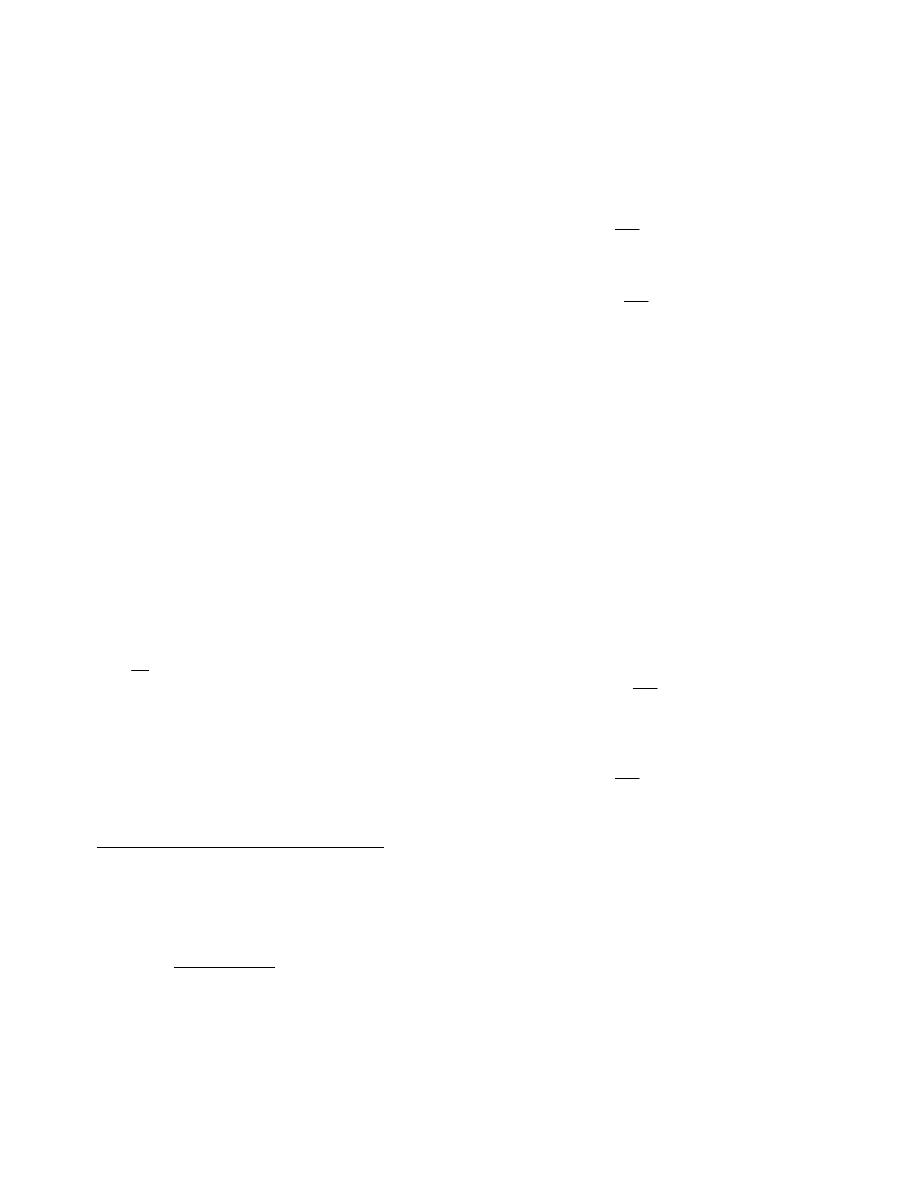
Obciążenie stałe:

- współczynnik obciążenia stałęgo:

- ciężar własny pokładu górnego i dolnego:

γG.j 1.35

:=

wartość charakterystyczna

Gk b1 gg gd

+

(

)



ρd27



:=

Gk 0.54

kN

m



=

wartość obliczeniowa

Gd Gk γG.j



:=

Gd 0.729

kN

m



=

Obciążenie ruchome
- obciążenie ruchome (jedno koło osi):

P

200kN βQ



:=

βQ

βQ αQ.1

=

1

=

- współczynnik dostosowawczy (korekcyjny)

βQ 1

:=

P

200kN βQ



:=

P 200 kN



=

- współczynnik zmiennego obciążenia wiodącego:

γQ.1 1.35

:=

- współczynnik redukcyjny przy częstych oddziaływaniach: ψ1 0.75

:=

wartość charakterystyczna:

Qk

P

sp

:=

Qk 333.333

kN

m



=

wartość obliczeniowa:

Qd Qk γQ.1



ψ1



:=

Qd 337.5

kN

m



=

2.2.2. Maksymalny moment zginający
- rozpiętość teoretyczna pokładu dolnego:

I

sp

:=

I 0.6m

=

Mmax

Gd Qd

+

(

)

I

2



8

:=

Mmax 15.22 kN m





=

2.2.3 Naprężenia od momentu zginającego

σmax

Mmax

Wx

fm.d27



=

- przekrój obciążony maksymalny momentem zginającym:

h

gd

:=

h 0.1m

=

x - liczba odstępów między belkami pokładu dolnego na dł. b

1

x

4

:=

b

b1 x 0.02



m

-

:=

b 0.72m

=

- wskaźnik wytrzymałości przekroju:

Wx

b h

2



6

:=

Wx 0.0012 m

3



=

σmax

Mmax

Wx

:=

σmax 12.684 MPa



=

σmax fm.d27



1

=

WARUNEK SPEŁNIONY

fm.d27 20.769 MPa



=

2.2.4 Maksymalna siła poprzeczna

Vmax

Gd Qd

+

(

)

I

2

:=

Vmax 101.469 kN



=

2.2.5 Naprężenia siły poprzecznej

τmax

Vmax Sx



Ix b

fv.d27



=

- przekrój obciążony maksymalną siłą poprzeczną:

h

gd

:=

h 0.1m

=

x - liczba odstępów między belkami pokładu dolnego na dł. b

1

x 4

=

b

b1 x 0.02



m

-

:=

b 0.72m

=

- statyczny moment bezwładności przekroju:

Sx

b h

2



8

:=

Sx 0.0009 m

3



=

- moment bezwładności przekroju:

Ix

b h

3



12

:=

Ix 0.00006m

4

=

τmax

Vmax Sx



Ix b

:=

τmax 2.114 MPa



=

τmax fv.d27



1

=

WARUNEK SPEŁNIONY

2.3. Poprzecznice
2.3.1. Obciążenie

Obciążenie ruchome stanowi jedno koło pojedyńczej osi β.QQa.k z Qa.k=400kN o nacisku P=200kN*β

Q

Obciążenie stałe stanowi pokład górny i dolny sosnowy oraz poprzecznice sosnowe.

Rys. 2. Schemat rozmieszczenia i rozkładania się obciążenia na poprzecznice

sb.o 66.5 cm



0.665m

=

:=

- rozstaw belek w świetle:

- rozpiętość teoretyczna poprzecznicy:

Obciążenia stałe

- współczynnik obciążenia stałego

Ipt 1.05 sb.o



:=

Ipt 0.698m

=

γG.j.1 1.35

:=

γG.j.2 1.00

:=

- ciężar własny pokładu górnego i dolnego:
wartość charakterystyczna:

Gk.1 0.6 m



gg gd

+

(

)



ρd27



:=

Gk.1 0.405

kN

m



=

wartości obliczeniowe:

G1.1.d Gk.1 γG.j.1



:=

G1.1.d 0.547

kN

m



=

G1.2.d Gk.1 γG.j.2



:=

G1.2.d 0.405

kN

m



=

- ciężar własny poprzecznicy:

wartość charakterystyczna:

Gk.2 bp hp

 ρd40



:=

Gk.2 0.288

kN

m



=

wartości obliczeniowe:

G2.1.d Gk.2 γG.j.1



:=

G2.1.d 0.389

kN

m



=

G2.2.d Gk.2 γG.j.2



:=

G2.2.d 0.288

kN

m



=

całkowite wartości obliczeniowe:

G1.d G1.1.d G2.1.d

+

:=

G1.d 0.936

kN

m



=

G2.d G1.2.d G2.2.d

+

:=

G2.d 0.693

kN

m



=

Obciążenie ruchome
- obciążenie ruchome (jedno koło osi):

P

200kN βQ



:=

βQ 1

:=

βQ αQ.1

=

1

=

- współczynnik dostosowawczy (korekcyjny)

P

200kN βQ



:=

P 200 kN



=

γQ.1 1.35

:=

- współczynnik zmiennego obciążenia wiodącego:

ψ1 0.75

:=

- współczynnik redukcyjny przy częstych oddziaływaniach:

- szerokość oddziaływania obciążenia ruchomego

b1 0.60 m



2 gg gd

+

hp

2

+















+

:=

b1 1.14m

=

Ze względu na bezpieczeństwo przyjęto:

wartość charakterystyczna:

b1 Ipt 0.698m

=

:=

Qk

P

Ipt

:=

Qk 286.43

kN

m



=

wartość obliczeniowa:

Qd Qk γQ.1



ψ1



:=

Qd 290.011

kN

m



=

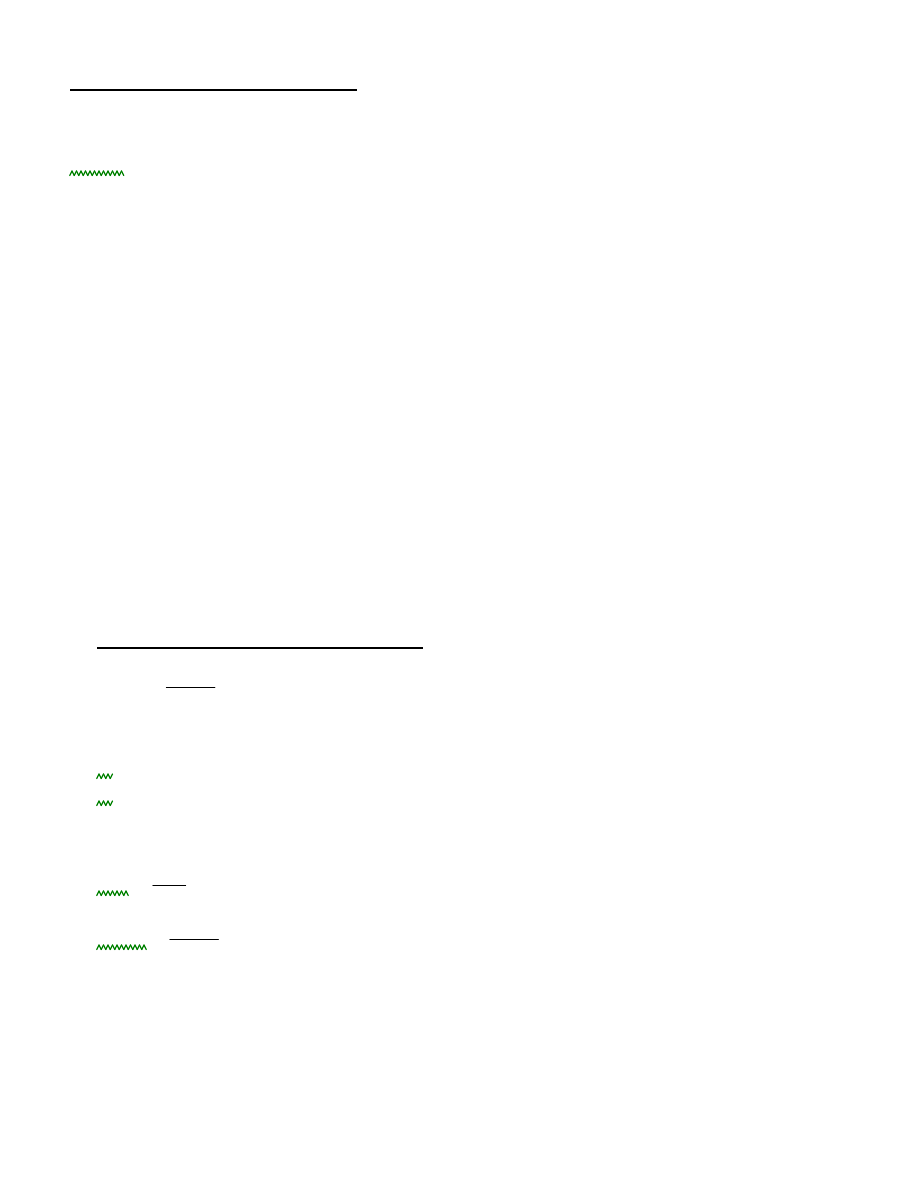
2.3.2. Maksymalny moment zginający
Odczytano z programu Soldis Projektant

Mmax 10.614 kN



m



:=

2.3.3. Naprężenia od momentu zginającego

σmax

Mmax

Wx

fm.d40



=

- przekrój obciążony maksymalnym momentem zginającym:

h

hp

:=

h 24 cm



=

b

bp

:=

b 24 cm



=

- wskaźnik wytrzymałości przekroju:

Wx

b h

2



6

:=

Wx 0.0023 m

3



=

σmax

Mmax

Wx

:=

σmax 4.607 MPa



=

σmax fm.d40



1

=

WARUNEK

SPEŁNIONY

fm.d40 30.769 MPa



=

2.3.4. Maksymalna siła poprzeczna:
Odczytano z programu Soldis Projektant

Vmax 101.540 kN



:=

2.3.5. Naprężenia od siły

poprzecznej

τmax

Vmax Sx



Ix b

fv.d40



=

- przekrój obciążony maksymalną siłą poprzeczną

h

hp

:=

h 0.24m

=

b

bp

:=

b 0.24m

=

- statyczny moment bezwładności przekroju:

Sx

b h

2



8

:=

Sx 0.001728 m

3



=

- moment bezwładności przekroju:

Ix

b h

3



12

:=

Ix 0.000276m

4

=

τmax

Vmax Sx



Ix b

:=

τmax 2.644 MPa



=

τmax fv.d40



1

=

WARUNEK

SPEŁNIONY

fv.d40 2.923 MPa



=

2.4. Docisk w miejscu styku z dźwigarem

σd

N

Fd

1.25fc90.d40



=

2.4.1. Obciążenie:

Obciążeniem jest maksymalna reakcja w układzie statycznym (patrz rysunek z wykresami sił

wewnętrznych).

bs 20 cm



:=

2.4.2 Powierzchnia docisku:

Fd bp bs



:=

gdzie:

szerokość stopki (belki):

Fd bp bs



:=

Fd 0.048m

2

=

2.4.3 Docisk:
N - maksymalna reakcja odczytana z programu Soldis Projektant

N Rmax

=

N

111.961 kN



:=

σd

N

Fd

:=

σd 2.333 MPa



=

σd 1.25fc90.d40



1

=

WARUNEK

SPEŁNIONY

1.25fc90.d40 2.788 MPa



=

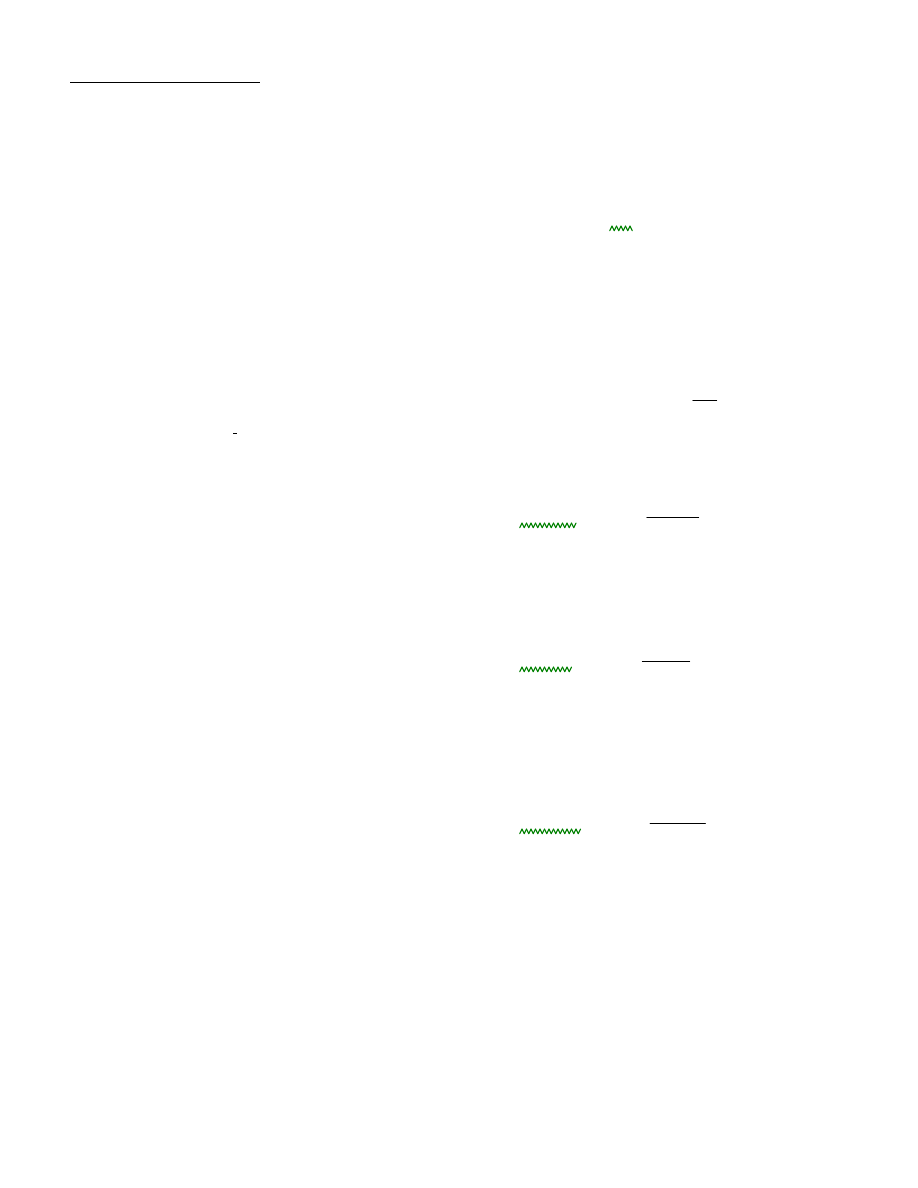
2.5. Elementy balustrady

Zaprojektowano balustrady (słupki, pochwyty i przeciągi) z drewna klasy C27

Cechy materiałowe i geometryczne:

- szerokość pochwytu:

- wysokość pochwytu:

- szerokość słupka:

-grubość słupka:

- wysokość słupka:

- rozstaw słupków:

-ciężar objętościowy drewna sosnowego C27:

bpo 14 cm



:=

hpo 14 cm



:=

bs 14 cm



:=

gs 14 cm



:=

hs 1 m



:=

ss 180 cm



:=

ρd27 4.5

kN
m

3



=

Wytrzymałości drewna :

- na zginanie (klasa C27):

- na ścinanie (klasa C27):

- na ściskanie wzdłuż włókien (klasa

C27):

fm.k27 27 MPa



=

fm.d27 kmod

fm.k27

γm



20.769 MPa



=

:=

fv.k27 2.8 MPa



=

fv.d27 kmod

fv.k27

γm



2.154 MPa



=

:=

fc0.k27 22 MPa



=

fc0.d27 kmod

fc0.k27

γm



16.923 MPa



=

:=

2.6. Obciążenie
Obciążenie stanowi siła rozłożona równomiernie 1.0 kN/m, działająca jako obciążenie zmienne poziomo lub

pionowo.Obciążenie stałe stanowi pochwyt balustrady.

Rys. 3. Schemat rozmieszczenia obciążenia na elementy balustrady

2.7. Pochwyt

Obciążenie stałe

-współczynnik obciążenia stałego:

-ciężar własny pochwytu:

wartość charakterystyczna:

γG.j 1.35

=

Gk bpo hpo



ρd27



:=

Gk 0.088

kN

m



=

wartość obliczeniowe:

Gd Gk γG.j



:=

Gd 0.119

kN

m



=

Obciążenie zmienne poziome i pionowe

-obciążenie równomiernie rozłożone:

P

1 kN

m



:=

-współczynnik zmiennego obciążenia wiodącego:

wartość charakterystyczna:

γQ.1 1.35

=

Qk P

:=

Qk 1

kN

m



=

wartość obliczeniowa:

Qd Qk γQ.1



:=

Qd 1.35

kN

m



=

2.7.1. Maksymalny moment zginający
- rozpiętość teoretyczna pochwytu:

Ipot ss 1.8m

=

:=

Mmax.poz

Qd

( )

Ipot

2



8

:=

Mmax.poz 0.547 kN m





=

Mmax.pio

Gd Qd

+

(

)

Ipot

2



8

:=

Mmax.pio 0.595 kN m





=

2.7.2. Naprężenia od momentu zginającego

σmax

Mmax

Wx

fm.d27



=

- przekrój obciążony maksymalnym momentem zginającym od siły poziomej:

h

bpo

:=

h 0.14m

=

b

hpo

:=

b 0.14m

=

- wskaźnik wytrzymałości przekroju:

Wx

b h

2



6

:=

Wx 0.000457 m

3



=

σmax

Mmax.poz

Wx

:=

σmax 1.196 MPa



=

σmax fm.d27



1

=

WARUNEK

SPEŁNIONY

fm.d27 20.769 MPa



=

- przekrój obciążony maksymalnym momentem zginającym od siły poziomej:

h

hpo

:=

b

bpo

:=

h 0.14m

=

b 0.14m

=

- wskaźnik wytrzymałości przekroju:

Wx

b h

2



6

:=

Wx 0.000457 m

3



=

σmax

Mmax.pio

Wx

:=

σmax 1.301 MPa



=

σmax fm.d27



1

=

WARUNEK

SPEŁNIONY

fm.d27 20.769 MPa



=

2.7.3. Maksymalna siła poprzeczna

Vmax.poz

Qd

( )

Ipot



2

:=

Vmax.poz 1.215 kN



=

Vmax.pio

Gd Qd

+

(

)

Ipot



2

:=

Vmax.pio 1.322 kN



=

2.7.4. Naprężenia od siły poprzecznej

τmax

Vmax Sx



Ix b

fv.d14



=

- przekrój obciążony maksymalną siłą poprzeczną od siły poziomej:

h

bpo

:=

h 0.14m

=

b

hpo

:=

b 0.14m

=

- statyczny moment bezwładności przekroju:

Sx

b h

2



8

:=

Sx 0.000343 m

3



=

- moment bezwładności przekroju:

Ix

b h

3



12

:=

Ix 0.000032m

4

=

τmax

Vmax.poz Sx



Ix b

:=

τmax 0.093 MPa



=

τmax fv.d27



1

=

WARUNEK

SPEŁNIONY

fv.d27 2.154 MPa



=

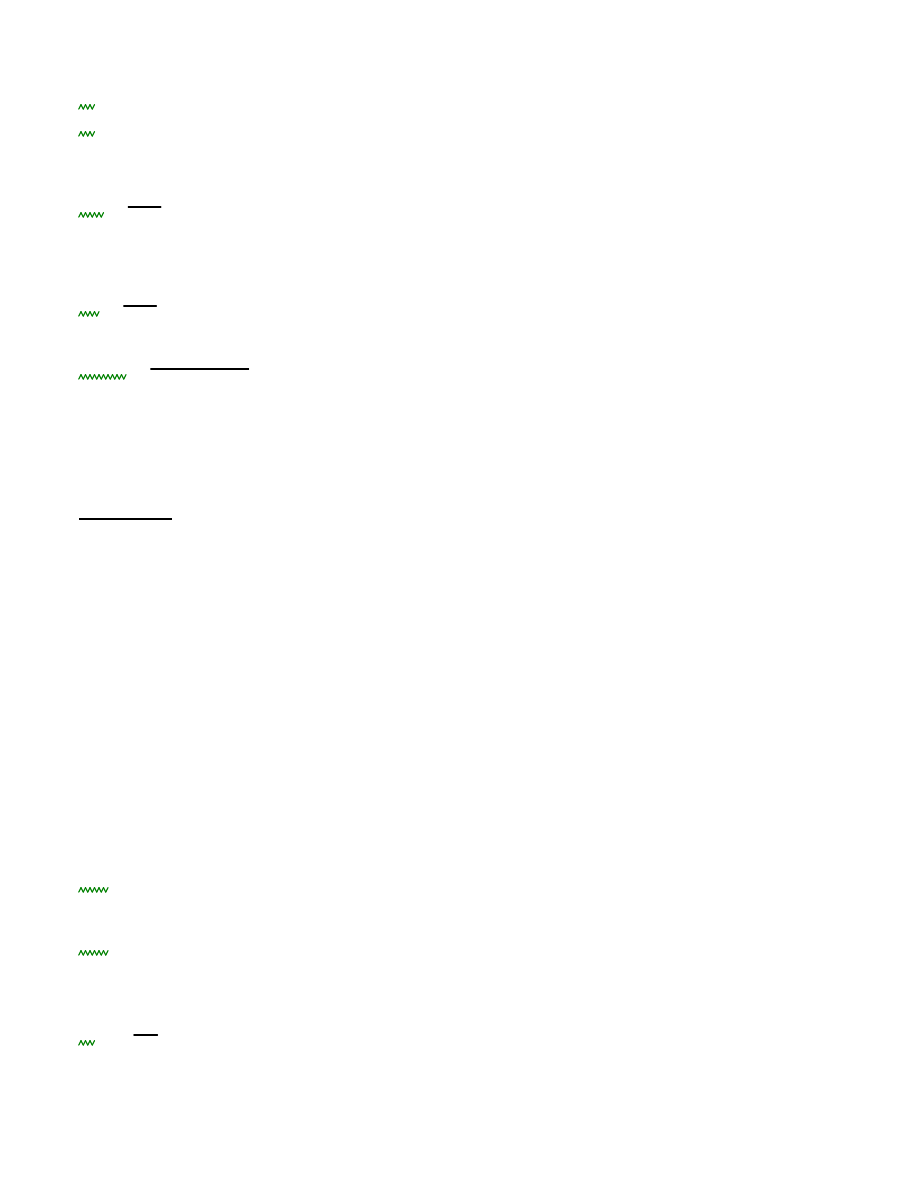
- przekrój obciążony maksymalną siłą poprzeczną od siły pionowej i obciążenia stałego:

h

hpo

:=

b

bpo

:=

h 0.14m

=

- statyczny moment bezwładności przekroju:

b 0.14m

=

Sx

b h

2



8

:=

Sx 0.000343 m

3



=

- moment bezwładności przekroju:

Ix

b h

3



12

:=

Ix 0.000032m

4

=

τmax

Vmax.pio Sx



Ix b

:=

τmax 0.101 MPa



=

τmax fv.d27



1

=

WARUNEK

SPEŁNIONY

fv.d27 2.154 MPa



=

2.8. Słupek

Rys. 4.

Schemat obciążenia do wyznaczenia M.max

Obciążenia stałe:

- rozstaw słupków:

- współczynnik obciążenai stałego:

- ciężar własny pochwytu:

wartość charakterystyczna:

ss 1.8m

=

γG.j 1.35

=

Gk bpo hpo



ρd27



ss



:=

Gk 0.159 kN



=

wartość obliczeniowa:

Gd Gk γG.j



:=

Gd 0.214 kN



=

Obciążenie zmienne poziome i pionowe

-obciążenie równomiernie rozłożone:

P

1 kN

m



:=

γQ.1 1.35

=

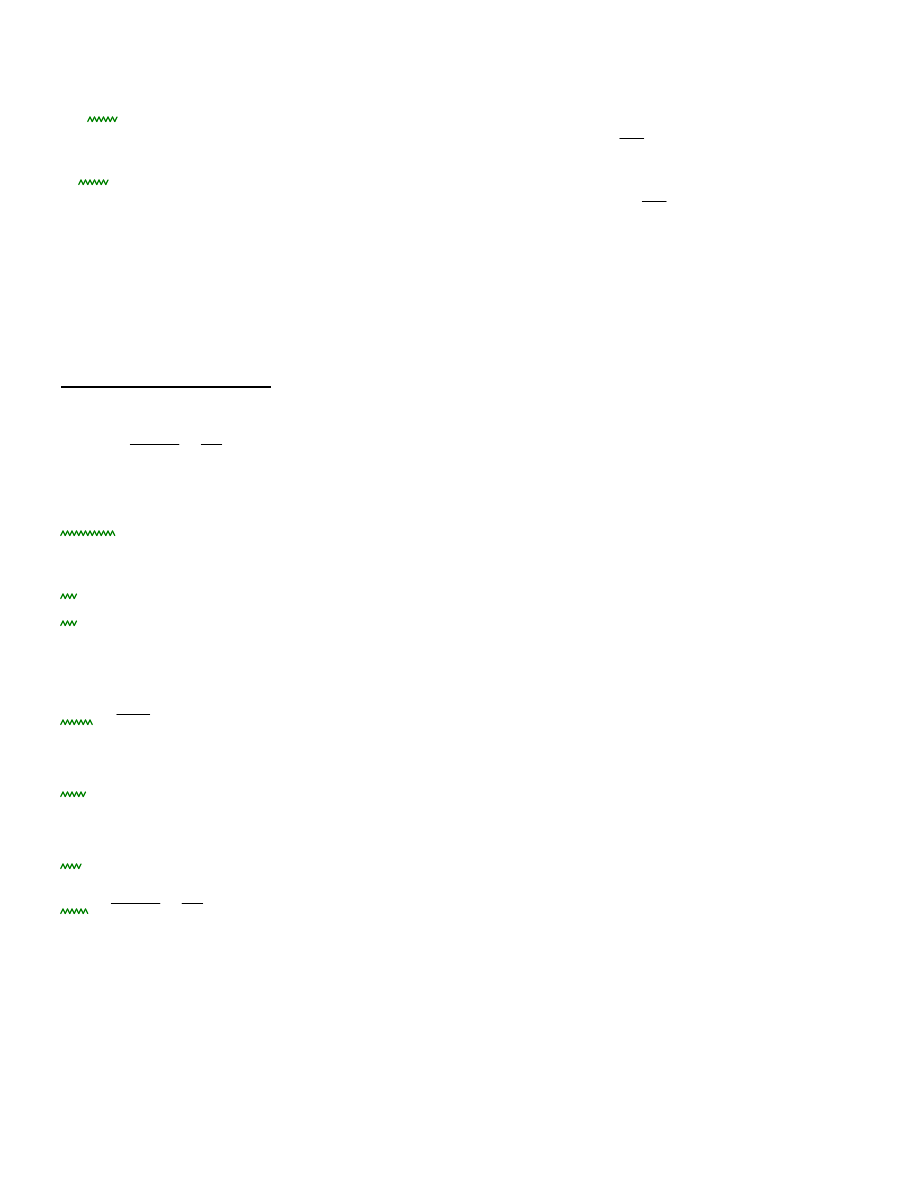
-współczynnik zmiennego obciążenia wiodącego:

wartość charakterystyczna:

Qk P

:=

wartośćobliczeniowa:

Qk 1

kN

m



=

Qd Qk γQ.1



:=

Qd 1.35

kN

m



=

- wypadkowa obciążenia równomiernie rozłożonego:

Qd.poz Qd ss



:=

Qd.poz 2.43 kN



=

Qd.pio Qd ss



:=

Qd.pio 2.43 kN



=

2.7.1. Naprężenia normalne

σmax

Mmax

Wx

N

Fd

+

fc0.d14



=

- moment maksymalny:

Mmax Qd.poz hs



:=

Mmax 2.43 kN m





=

- przekrój obciążony maksymalnym momentem zginającym od siły poziomej:

h

bs

:=

b

gs

:=

h 0.14m

=

b 0.14m

=

- wskaźnik wytrzymałości przekroju:

Wx

b h

2



6

:=

Wx 0.000457 m

3



=

- powierzchnia docisku:

Fd bs gs



:=

Fd 0.02m

2

=

- siła docisku:

N

Gd Qd.pio

+

:=

N 2.644 kN



=

σd

Mmax

Wx

N

Fd

+

:=

σd 5.448 MPa



=

σd fc0.d27



1

=

WARUNEK

SPEŁNIONY

fc0.d27 16.923 MPa



=