1

Katedra Geodezji Szczegółowej

UWM w Olsztynie

Ćwiczenie nr 7-8

" Obliczenie ciągu poligonowego: wiszącego, wyrównanie

metodą przybliżoną ciągu poligonowego zamkniętego”

Nazwisko i imię

Grupa: Data:

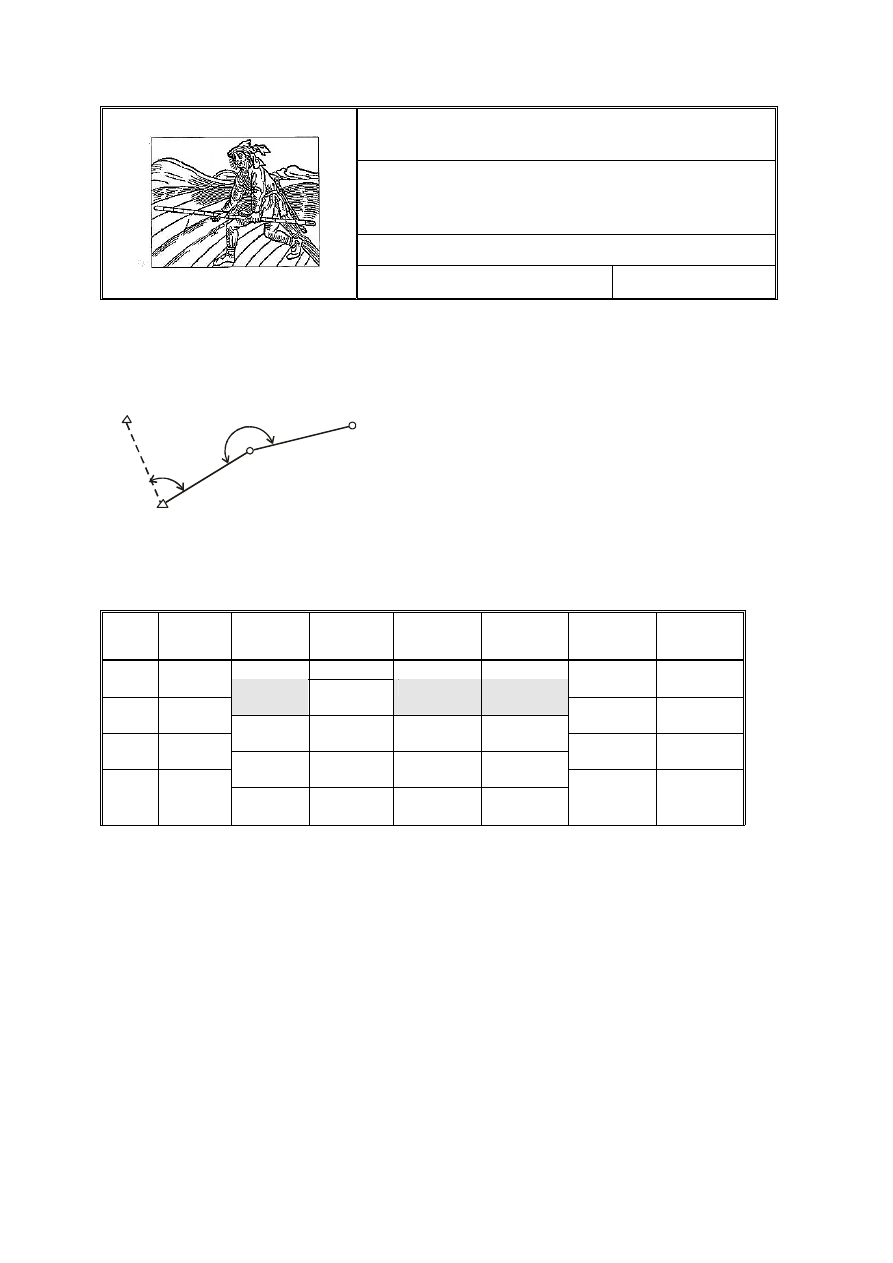
1. Oblicz współrzędne punktu nr. 2 (rys.1) w ciągu wiszącym. Obliczenia przeprowadź w tabeli nr. 1,

gdzie umieszczono wszystkie niezbędne do obliczeń dane. W ciągu tym pomierzono kąty lewe.

A

B

1

2

d

1

d

2

β

1

β

2

Rysunek 1. Ciąg wiszący

Tabela nr.1

Nr.

.

Kąt

Odległość

Azymut

ΔX

ΔY

X

Y

A

101.61+

N *0.1m

18.73

B 283.5643

1020.13 1017.99

233.88

1 135.8525

139.73

2

2

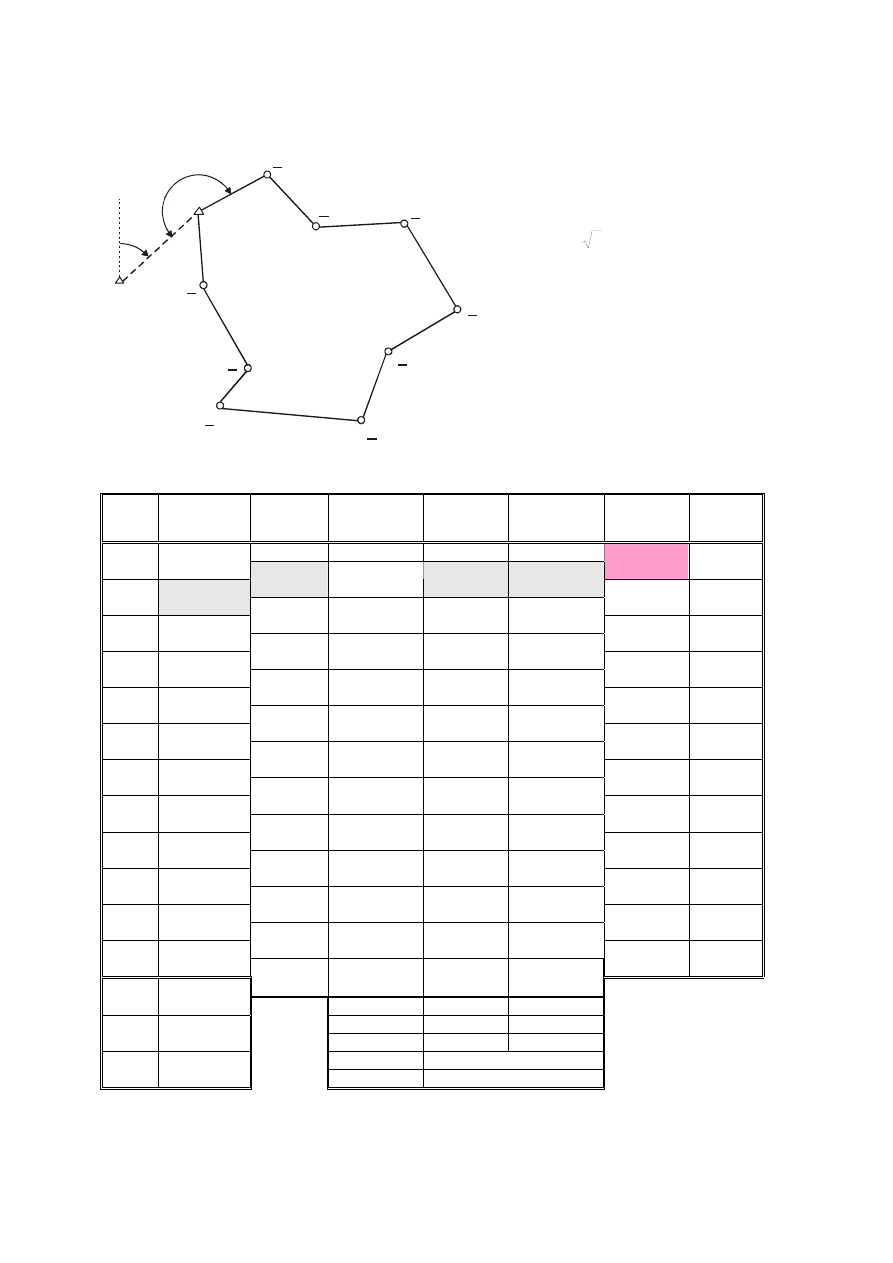
2. Oblicz współrzędne punktów 1 - 9 (rys.2) w ciągu zamkniętym. Obliczenia przeprowadź w tabeli

nr. 2, gdzie umieszczono wszystkie
niezbędne do obliczeń dane. W ciągu
pomierzono kąty wewnętrzne. Kąt
nawiązania w punkcie B jest kątem
lewym. Maksymalna odchyłka kątowa
wynosi

n

t

, gdzie t =2

c

. Maksymalna

odchyłka liniowa wynosi L/2000 gdzie L
jest długością ciągu.

Rysunek 2. Ciąg zamknięty
Tabela nr. 2

Nr.

.

Kąt

Odległość

Azymut

ΔX

ΔY

X

Y

A

101.61+

N*.02m

18.73

B

ψ=287.4524

1020.13 1017.99

97.87

1 102.1237

125.23

2 278.3692

93.98

3 122.2491

236.92

4 92.1973

404.31

5 102.7842

255.98

6 223.9754

185.94

7 122.0873

201.01

8 56.8482

218.95

9 311.6563

98.41

B 187.7482

1020.13

1017.99

S

=

suma
teor.

Sum

teor

Sum

prakt

suma
prakt.

Odch

pr

Odch

liniowa

odch.p

Odch

max

3. Korzystając z programu WinKalk Powtórz obliczenia ciągu zamkniętego. Wyniki obliczeń w

postaci wydruku załącz do ćwiczenia.

A

B

1

2

3

4

5

6

7

8

9

H

$ %

kąt nawiązania

`