Porównać reaktancje X’ i X

3.1.

Reaktancje stanu nieustalonego w osi podłu

Prądy zwarciowe generatora w poszczególnych stanach zwarcia

reaktancje w osi podłużnej

d

Χ ′′

,

d

X

′

i

d

X

(wzór 3.23). Stwierdzenie to jest oczywi

narusza synchronizmu maszyny tzn. n

gen

= n

s

= const.

Reaktancje te mogą być określone na podstawie analizy przebiegu linii sił pola magnetycznego w poszczególnych chwilach zwarcia
udarowego.

Rys.3.1. Rozkład linii sił pola magnetycznego od strumienia twornika w stanie podprzej

Rozpatrzmy

przebieg

strumienia

podłu

(rys. 3.12). Strumień wywołany przez prąd twornika wytwarza strumie

w osi podłużnej.

Φ

Strumień rozproszenia w warunkach zwarcia przechodzi takimi samymi drogami jak w warunkach normalnej pracy maszyny.
Natomiast strumień oddziaływania twornika na skutek ekranuj

powietrznej. Reluktancję (oporność magnetyczną

ad

R

µ

′′

gdzie

ad

R

µ

- reluktancja drogi strumienia w jarzmie i w z

przybliżeniu równa reluktancji oddziaływania twornika w warunkach pracy ustalonej dla osi podłu
żelaza magneśnicy jest niewielka.

f

R

µ

- reluktancja strumienia rozproszenia uzwojenia wzbudzaj

t

R

µ

- reluktancja strumienia rozproszenia uzwojenia tłumi

Przechodząc do permeancji (przewodności magnetycznej) zale

Λ

=

Λ ′′

Λ

=

Λ ′′

ad

ad

1

Stąd przewodność magnetyczna dla całego strumienia oddziaływania twornika

s

d

Λ

+

Λ

=

Λ ′′

σ

Reaktancje stanu nieustalonego w osi podłużnej

dy zwarciowe generatora w poszczególnych stanach zwarcia

I

′′

,

I

′

i

k

I

są określone przez sił

(wzór 3.23). Stwierdzenie to jest oczywiście oparte na zało

= const.

lone na podstawie analizy przebiegu linii sił pola magnetycznego w poszczególnych chwilach zwarcia

. Rozkład linii sił pola magnetycznego od strumienia twornika w stanie podprzejściowym

Rozpatrzmy

przebieg

strumienia

podłużnego

twornika

w

stanie

podprzej

d twornika wytwarza strumień rozproszenia

s

σ

Φ

i strumie

ad

s

d

Φ ′′

+

Φ

=

Φ ′′

σ

rozproszenia w warunkach zwarcia przechodzi takimi samymi drogami jak w warunkach normalnej pracy maszyny.

oddziaływania twornika na skutek ekranującego działania uzwojeń magne

magnetyczną) na drodze strumienia

ad

Φ ′′

można przedstawić jako sum

t

f

ad

R

R

R

µ

µ

µ

+

+

=

reluktancja drogi strumienia w jarzmie i w zębach stojana oraz w szczelinach przetwornikowych; jest ona w

eniu równa reluktancji oddziaływania twornika w warunkach pracy ustalonej dla osi podłu

zproszenia uzwojenia wzbudzającego

reluktancja strumienia rozproszenia uzwojenia tłumiącego

ci magnetycznej) zależność (2.25) można zapisać w postaci



















Λ

+

Λ

+

Λ

Λ

+

Λ

+

Λ

t

f

ad

t

f

ad

1

1

1

1

1

1

1

magnetyczna dla całego strumienia oddziaływania twornika

d

Φ ′′

t

f

ad

s

ad

Λ

+

Λ

+

Λ

+

Λ

=

Λ ′′

1

1

1

1

σ

lone przez siłę elektromotoryczną E

0

oraz

cie oparte na założeniu, że stan zwarcia nie

lone na podstawie analizy przebiegu linii sił pola magnetycznego w poszczególnych chwilach zwarcia

nego

twornika

w

stanie

podprzejściowym

i strumień oddziaływania twornika

ad

Φ ′′

(3.1)

rozproszenia w warunkach zwarcia przechodzi takimi samymi drogami jak w warunkach normalnej pracy maszyny.

magneśnicy jest zepchnięty do szczeliny

na przedstawić jako sumę trzech składników

(3.2)

stojana oraz w szczelinach przetwornikowych; jest ona w

eniu równa reluktancji oddziaływania twornika w warunkach pracy ustalonej dla osi podłużnej gdyż reluktancja

w postaci

(3.3)

(3.4)

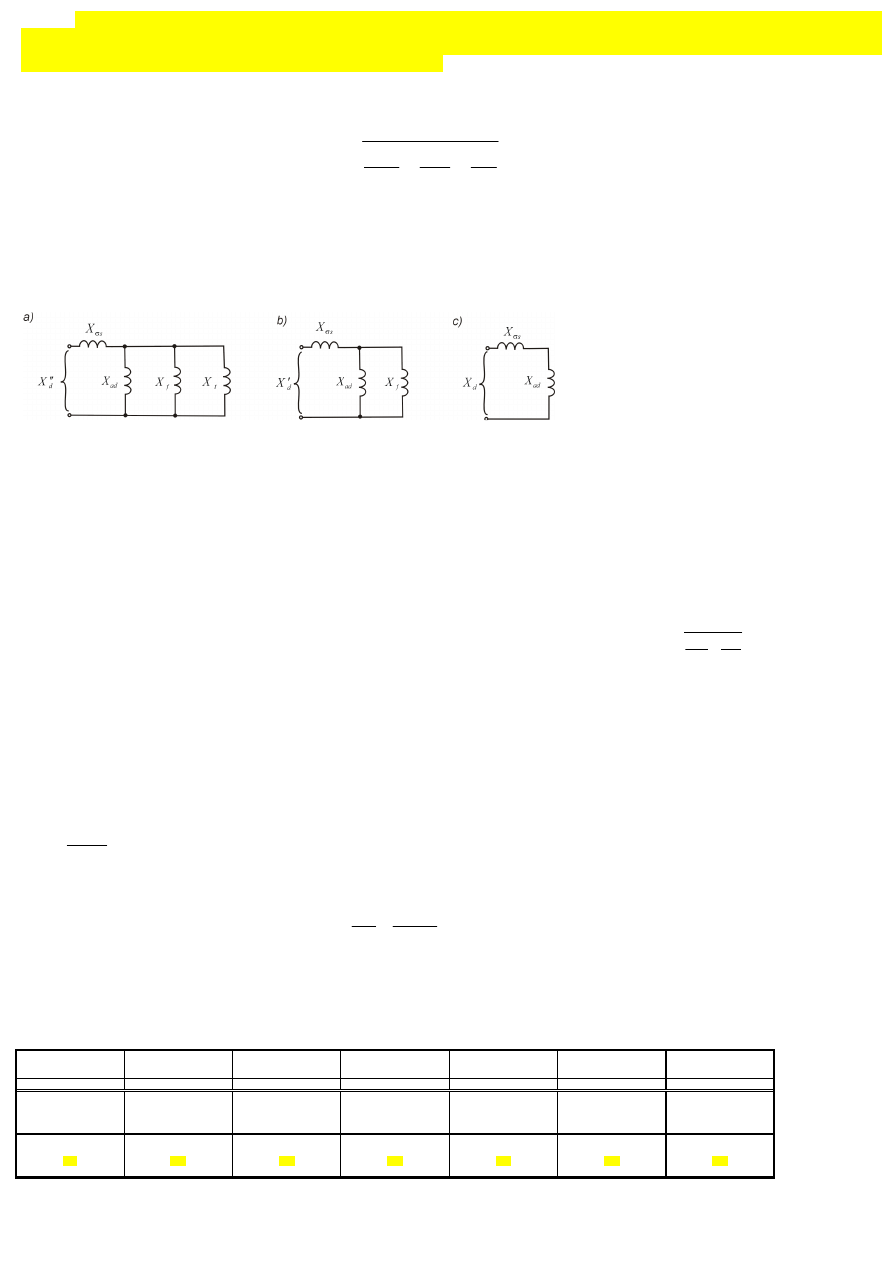
Pomiędzy przewodnością magnetyczną na drodze linii pola magnetycznego danego strumienia a reaktancją związaną z tym

strumieniem zachodzi znana zależność proporcjonalności, tzn. (

Λ

=

Λ

=

=

2

2

1

c

z

c

L

X

ω

ω

, gdzie c

1

, c

2

– stałe konstrukcyjne,

ω

ω

ω

ω

-

pulsacja, z – liczba zwojów uzwojenia wytwarzającego strumień).
Wszystkie przewodności magnetyczne występujące w wyrażeniu (3.27) są sprowadzone do liczby zwojów uzwojenia stojana stąd
współczynnik proporcjonalności c

2

dla każdej przewodności jest taki sam. A zatem wyrażenie (3.27) możemy zapisać w postaci

t

f

ad

s

d

X

X

X

X

X

1

1

1

1

+

+

+

=

′′

σ

(3.5)

gdzie:

X

σσσσ

s

– reaktancja rozproszenia uzwojenia stojana

X

ad

– reaktancja oddziaływania twornika w warunkach pracy ustalonej

X

f

– reaktancja rozproszenia uzwojenia wzbudzającego

X

t

– reaktancja rozproszenia uzwojenia tłumiącego

Wszystkie reaktancje są sprowadzone do uzwojenia stojana. Zależności (3.28) odpowiada schemat zastępczy jak na rys. 3.13a

Rys. 3.2. Schemat zastępczy dla reaktancji w osi podłużnej generatora w stanach nieustalonych z wyodrębnioną reaktancją

rozproszenia

a) reaktancja

d

Χ ′′

w stanie podprzejściowym, b) reaktancja

d

X

′

w stanie przejściowym,

c) reaktancja

d

X

dla stanu ustalonego

Ze względu na równoległe połączenie reaktancji X

ad

, X

f

i X

t

drugi składnik w wyrażeniu (3.28) ma małą wartość i

d

Χ ′′

jest tylko

nieznacznie większa od

s

X

σ

. W maszynach z cylindrycznym wirnikiem

(

)

s

d

X

σ

2

,

1

1

,

1

÷

=

Χ ′′

W stanie przejściowym nie występują prądy w obwodach tłumiących. Oznacza to, że

∞

→

t

X

i wyrażenie na reaktancję

przejściową ma postać

f

ad

s

d

X

X

X

X

1

1

1

+

+

=

′

σ

(3.6)

Temu wyrażeniu odpowiada schemat zastępczy reaktancji na rys. 3.13b.

W stanie ustalonym nie występują prądy ekranujące także w uzwojeniu wzbudzającym, co oznacza że

∞

→

f

X

i wyrażenie na reaktancję stanu

ustalonego ma postać

ad

s

d

X

X

X

+

=

σ

(3.7)

Jest to znane wyrażenie na podłużną reaktancję synchroniczną charakteryzującą stan magnetyczny maszyny w warunkach pracy ustalonej. Schemat zastępczy
generatora dla warunków ustalonych podano na rys. 3.13c. Reaktancje maszyny synchronicznej są określane zarówno na drodze obliczeniowej jak i pomiarów, i zwykle

są podawane w wartościach względnych. Jako wartość

odniesienia dla ich określenia przyjmuje się impedancję znamionową maszyny

phN

phN

N

I

U

Z

=

Reaktancja w wartościach względnych

phN

phN

N

U

X

I

Z

X

x

=

=

(3.8)

Na podstawie analizy danych literaturowych [K1], [K10], [K23], dla normalnie spotykanych konstrukcji turbogeneratorów
przykładowe wartości reaktancji oraz stałych czasowych zestawiono w tablicy 3.1.

Tablica 3.1. Wybrane parametry turbogeneratorów cylindrycznych

P

N

d

x

′′

d

x

′

d

x

d

T

′′

d

T

′

a

T

MW

-

-

-

s

s

s

2

0,15

0,26

1,62

0,06

0,05

0,08

6

0,13

0,19

1,72

0,09

0,07

0,16

30

0,15

0,24

2,34

0,13

1,05

0,20

50

0,15

0,22

2,02

0,16

1,30

0,26

120

0,15

0,21

1,84

0,20

1,80

0,20

200

0,19

0,27

1,88

0,12

0,92

0,31

360

0,22

0,23

2,43

0,11

0,89

0,37

500

0,26

0,35

2,55

0,17

1,36

0,36

Zagadnienia do zaliczenia:
1. wypisać równnania stanu generatora dla układu u, v, w i
gr a. g,d,0
gr b. a,b,0

2.narysować i omówić przebieg prądów generatora podczas zwarcia

gr a. w stojanie (dwa przypadki)
gr b. w wirniku

3. porównać reaktancje
gr a. x` i x
gr b. x" i x2