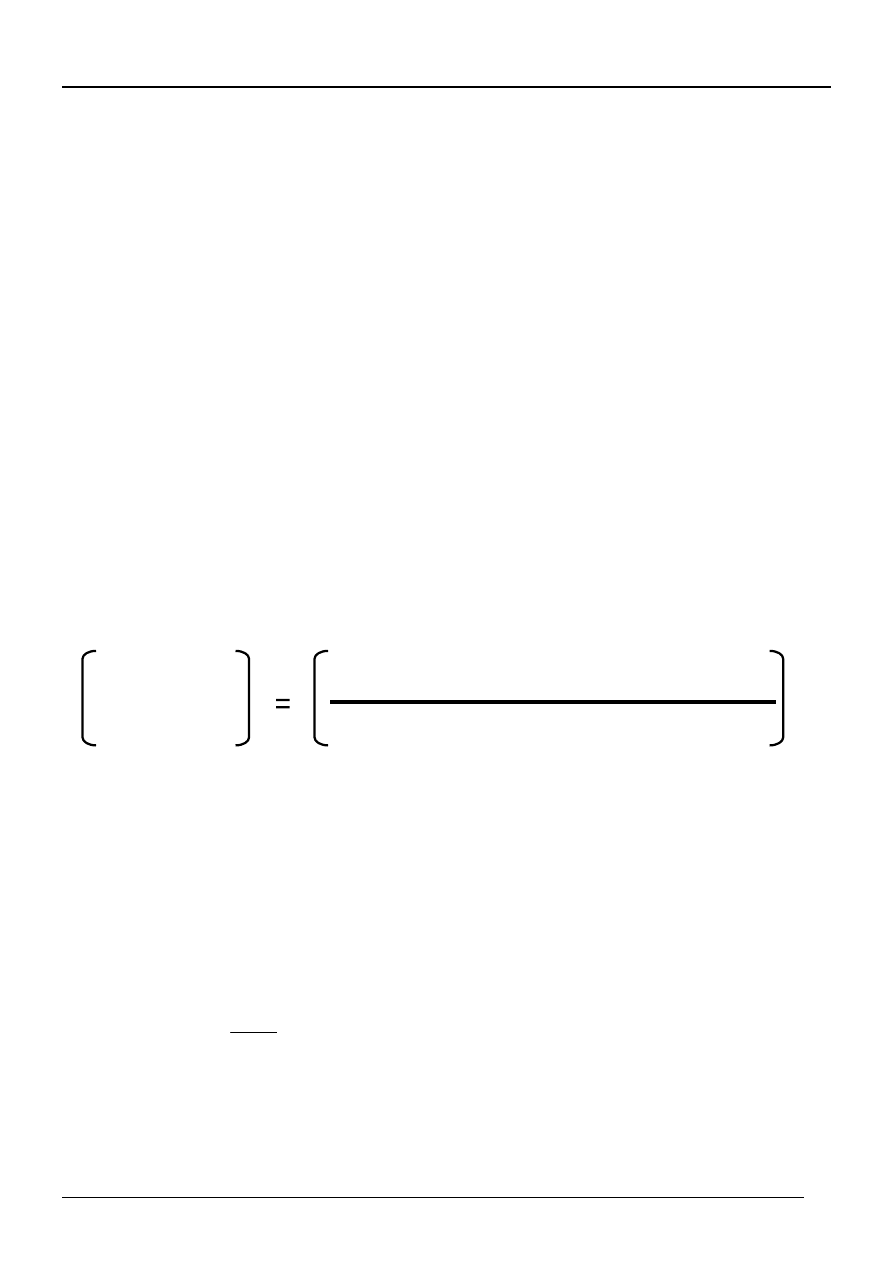
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
2. STOPA ZWROTU Z OBLIGACJI
Klasyczne miary stopy zwrotu:
1. Bieżąca stopa zwrotu
2. Stopa zwrotu w terminie do wykupu
3. Stopa zwrotu w terminie do wcześniejszego wykupu
Bieżąca stopa zwrotu
Bieżąca
Wartość rocznej płatności kuponowej
stopa zwrotu
aktualna cena rynkowa obligacji
Przykład 6.4
Obliczyć bieżącą stopę zwrotu obligacji o nominale N=1000zł,
kuponie r=23% oraz aktualnej cenie rynkowej 972 zł.:
%)
66
,
23
(
2366
,
0
972
230
g
≅
=
☺☺☺☺☺☺☺☺
Analiza obligacji – Stopa zwrotu z obligacji
1
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
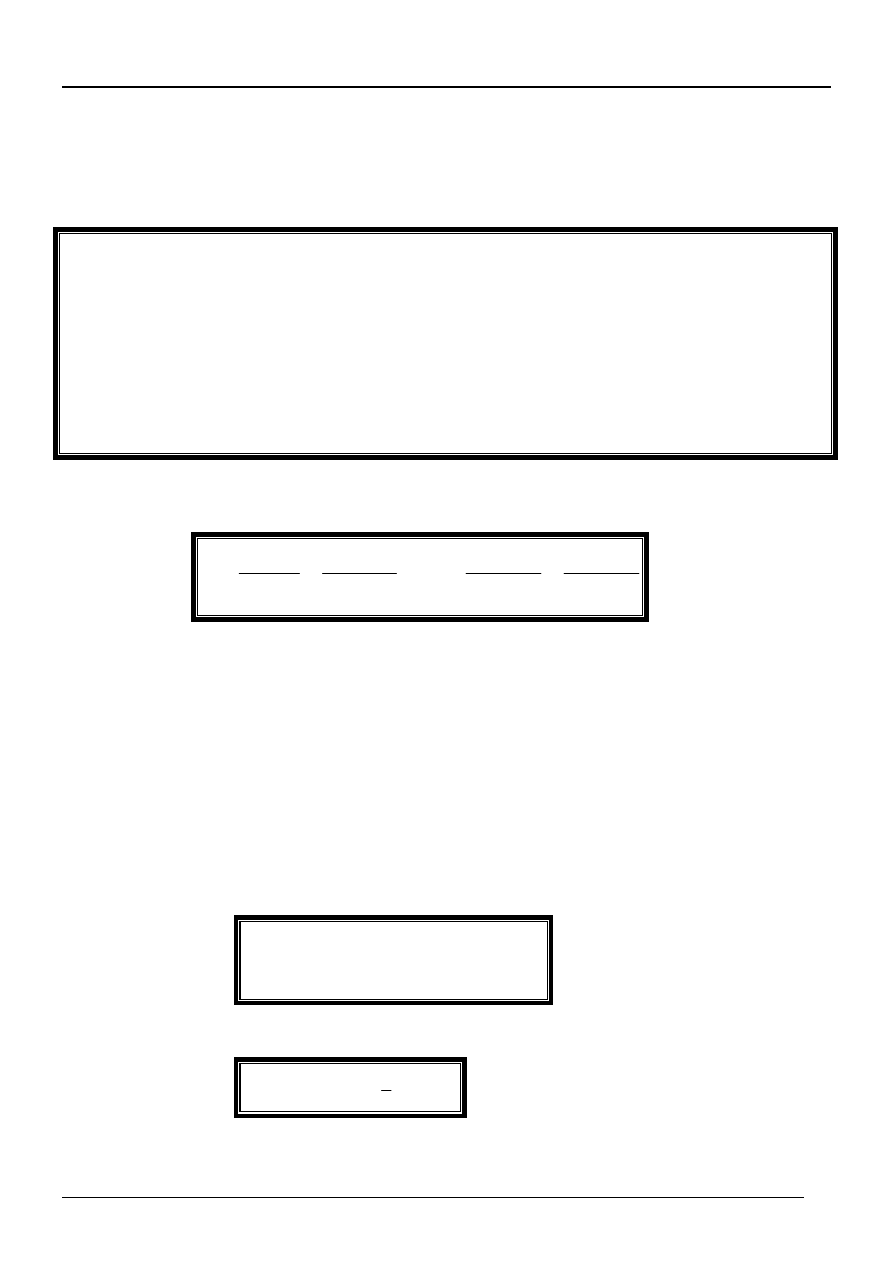
Stopa zwrotu w terminie do wykupu
Stopa zwrotu w terminie do wykupu
jest równa stopie pro-
centowej, dla której wartość teraźniejsza przepływów gotów-
kowych generowanych przez obligację jest równa aktualnej
cenie rynkowej
n
n
2
)
i
1
(
N
)
i
1
(
R
)
i
1
(
R
)
i
1
(
R
P
+
+
+
+
+
+
+
+
=
L
(6.13)
gdzie:
P – aktualna cena rynkowa obligacji
R – kupon (odsetki)
i – stopa zwrotu w terminie do wykupu (rozwiąza-
nie równania 6.13)
n
n
1
k
k
)
i
1
(
N
)
i
1
(
R
P
−
=
−
+
+
+
=
∑
(6.14)
N
a
)
i
r
(
N
P
i|
n
+
−
=
(6.15)
Analiza obligacji – Stopa zwrotu z obligacji
2
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Przykład 6.5
Wyznaczyć stopę zwrotu do wykupu obligacji:
Nominał (cena wykupu) N = 1000 zł
kupon r = 23%
n = 5 – 5 lat do wykupu
P = 1268,18 aktualna cena rynkowa.
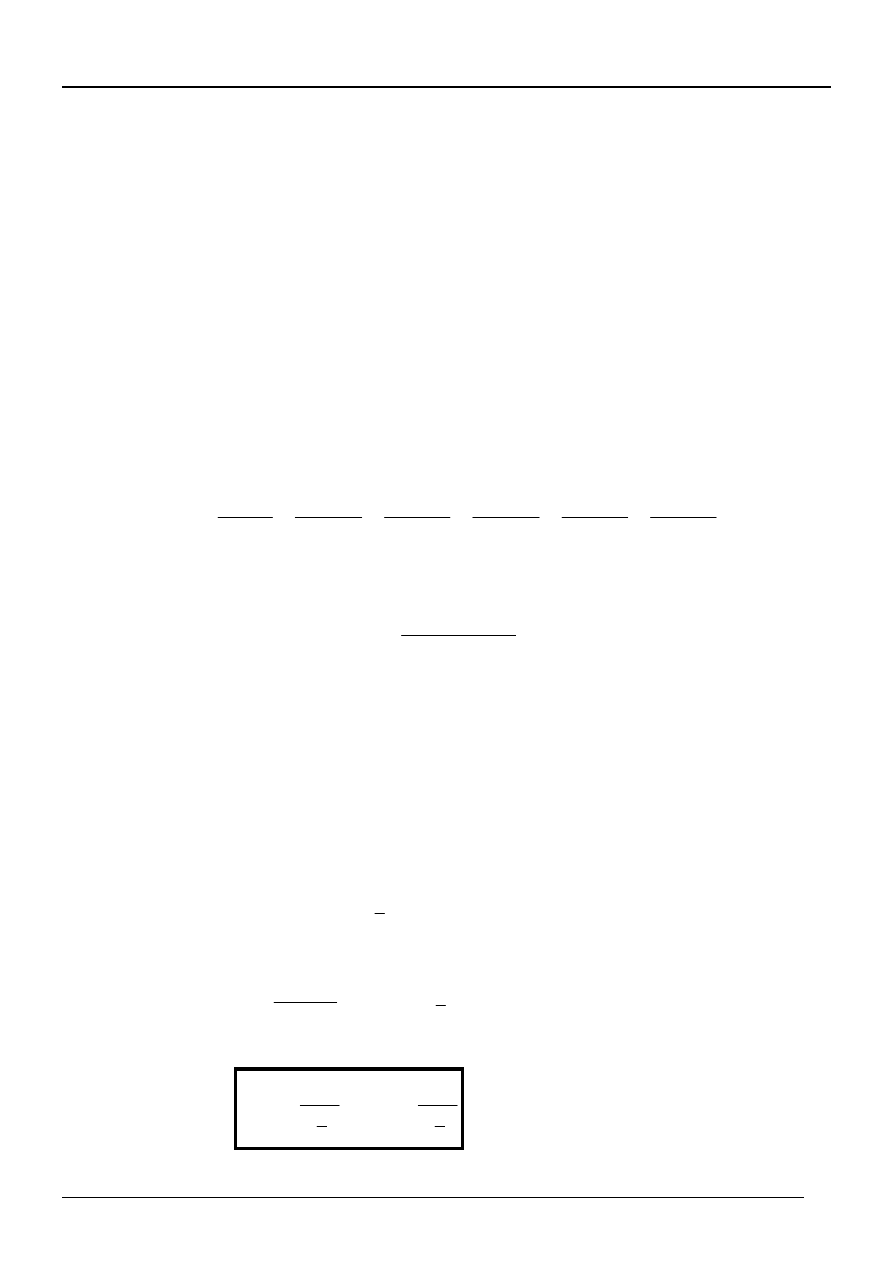
Należy rozwiązać równanie
5
5
4
3
2
)
i
1
(
1000
)
i
1
(
230
)
i
1
(
230
)
i
1
(
230
)
i
1
(
230
)
i
1
(
230
18
,
1268
+
+
+
+
+
+
+
+
+
+
+
=
1000
i
)
i
1
(
1
)
i
23
,
0
(
1000
18
,
1268
5
+
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
=
−
Rozwiązanie tego równania i = 0,15 (15%)
☺☺☺☺☺☺☺☺
Przybliżone rozwiązanie równania (6.15)
N
a
)
i
r
(
N
P
i|
n
+
−
=
i|
n
a
)
i
r
(
N
N
P
k
−
=
−
=
stąd
i|
n
i|
n
a
1
k
r
a
k
r
i
⋅
−
=
−
=
(6.16)
Analiza obligacji – Stopa zwrotu z obligacji
3
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
i
2
1
n
1
n
1
i
n
2
1
n
n
1
a
1
i|
n
⎥⎦
⎤
⎢⎣
⎡
+
+
=
+
+
≈
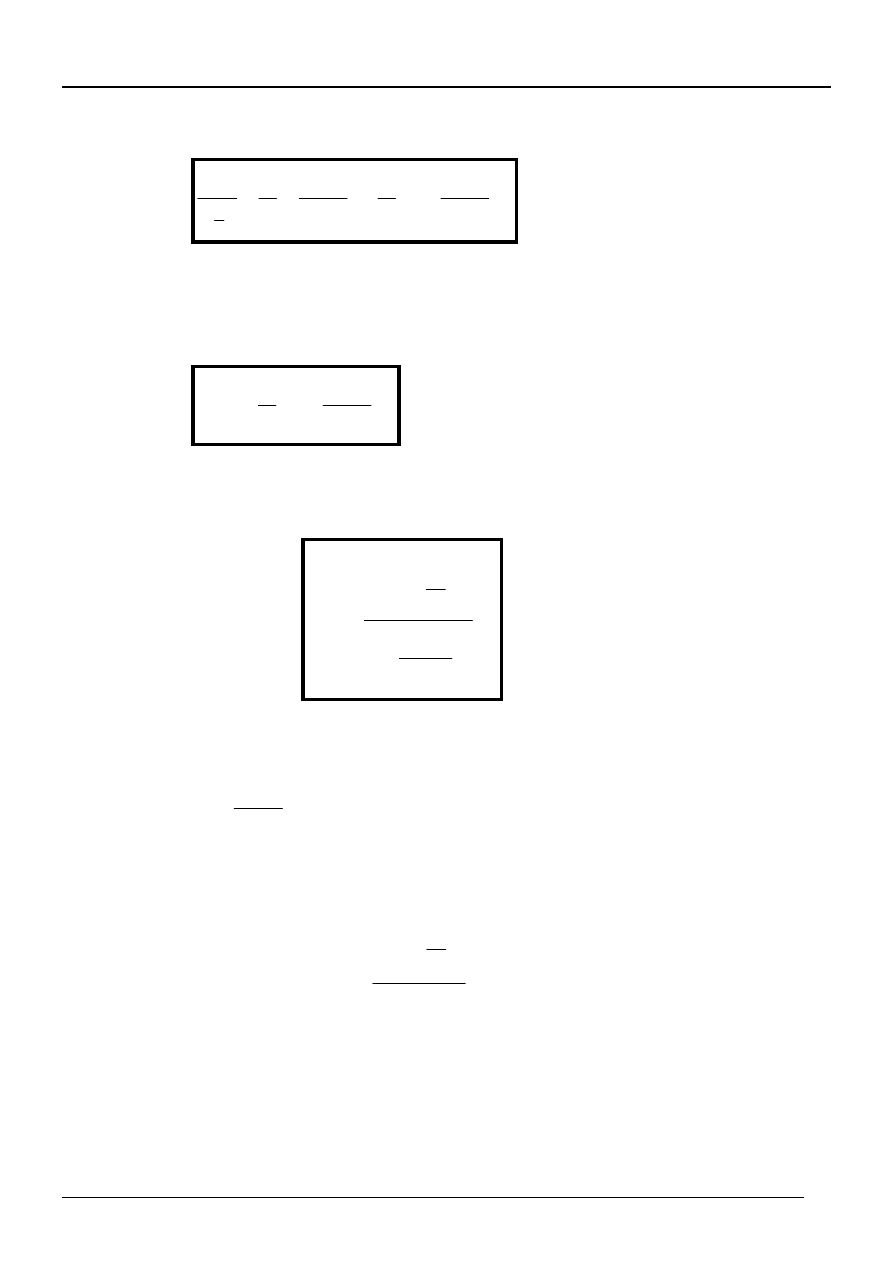
(6.17)
Podstawiając (6.17) do (6.16) mamy:
⎥⎦
⎤
⎢⎣
⎡
+
+
−
≈
i
2
1
n
1
n
k
r
i
(6.18)
rozwiązując względem „i” otrzymujemy:
Analiza obligacji – Stopa zwrotu z obligacji
4
(6.19)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
−
≈
k
n
2
1
n
1
n
k
r
i
+
Upraszczając
5
,
0
n
2
1
n
≈
+
otrzymujemy (metoda sprzedawcy –
bond salesman’s method)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
−
≈
k
5
,
0
1
n
k
r
i
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Przykład 6.6.
Obliczyć przybliżoną stopę zwrotu w terminie do wykupu ob-
ligacji z przykładu 6.
26818
,
0
1000
18
,
268
1000
1000
18
,
1268
k
=
=
−
=
zł
1519
,
0
160908
,
1
176364
,
0
26818
,
0
5
2
1
5
1
5
26818
,
0
23
,
0
i
≈
=
⋅
+
+
−
≈
i
≈ 15,19%
Metoda sprzedawcy
(bond salesman’s method)
1555
,
0
13409
,
1
176364
,
0
26818
,
0
5
,
0
1
5
26818
,
0
23
,
0
i
=
=
⋅
+
−
≈
i
≈ 15,55%
☺☺☺☺☺☺☺☺
Stopa zwrotu w terminie do wykupu obligacji zerokuponowej
P = Nv
n
P = (1+i)
n
1
P
N
i
n
1
−
⎟
⎠
⎞
⎜
⎝
⎛
=
(6.20)
Analiza obligacji – Stopa zwrotu z obligacji
5
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Analiza obligacji – Stopa zwrotu z obligacji
6
Podstawowe formuły matematyczne wyceny obligacji
Oznaczenia
:
C
n
– cena bieżąca obligacji na n-okresów (lat) do wykupu)
n – liczba okresów (lat) pozostałych do terminu wykupu
r – stopa kuponu obligacji
N – nominał obligacji
R= rN – kwota kuponu obligacji
i – stopa zwrotu w terminie do wykupu
v = (1+i)
-1
– czynnik dyskontujący
Oznaczenia dodatkowe:
W – cena wykupu obligacji W
≠ N
q – zmodyfikowana stopa kuponu obligacji
R = rN = qW;
q=rN /W
(6.21)
G – kwota bazowa obligacji
iG = rN;
G = rN/i
(6.22)
G – kwota, którą należy zainwestować ze stopą zwrotu „i” tak,
aby otrzymać okresowe płatności równe kwocie kuponu
obligacji
K – Wartość początkowa (PV) ceny wykupu obligacji
K
=
Wv
n
= W(1+i)
-n
(6.23)
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
1. Formuła bazowa
n
i|
n
n
Wv
Ra
C
+
=
K
Ra
C
i|
n
n
+
=
(6.24)
K
rNa
C
i|
n
n
+
=
2. Formuła premia /dyskonto
i|
n
n
a
)
iW
rN
(
W
C
−
+
=
(6.25)
(Podstawiając
i|
n
n
ia
1
v
−
=
do 6.24)
i|
n
n
a
)
i
q
(
W
W
C
−
+
=
(Podstawiając rN = qW )
3. Formuła kwoty bazowej
(6.26)
n
n
v
)
G
W
(
G
C
−
+
=
(Podstawiając rN = iG oraz
i|
n
n
ia
v
1
=
−
do 6.24)
4. Formuła Makehama
(6.27)
)
K
W
)(
i
/
q
(
K
C
n
−
+
=
(Podstawiając rN = gW oraz
i
/
)
v
1
(
a
n
i|
n
−
=
do 6.24)
Porównując (6.24) i (6.27) otrzymujemy:
)
K
W
)(
i
/
q
(
Ra
i|
n
−
=
(6.28)
Analiza obligacji – Stopa zwrotu z obligacji
7
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Przykład 6.7.
Wyznaczyć cenę bieżącą obligacji o nominale 1000zł, oprocen-
towanej rocznie na 20%, z ceną wykupu 1050zł na 5 lat przed
wykupem. Do obliczeń przyjąć stopę zwrotu w terminie do
wykupu 22%.
Dane:
N = 1000zł; r = 0,2; n = 5; W= 1050 zł; i = 0,22
R = rN = 0,2
⋅1000 = 200zł
Dane dodatkowe:
q – zmodyfikowana stopa kuponu
q = rN/W = 0,2
⋅1000/1050 = 0,190476
G – kwota bazowa obligacji
G = rN/i = 0,2
⋅1000/0,22 = 909,09 zł
v
n
– czynnik dyskontujący (tablice)
v
n
= (1+0,22)
-5
≈ 0,37000
i|
n
a
–
wartość początkowa renty jednostkowej
86364
,
2
a
a
22
,
0
|
5
i|
n
≈
=
K – wartość początkowa ceny wykupu W
K
=
Wv
n
= 1050
⋅(1+0,22)
-5
=
1050
⋅0,37≈ 388,50zł
Analiza obligacji – Stopa zwrotu z obligacji
8
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Obliczenia
1. Formuła bazowa
50
,
388
86364
,
2
200
K
Ra
C
i|
n
n
+
⋅
=
+
=
C
5
= 572,73 + 388,5 = 961.23 zł
2. Formuła premia /dyskonto
i|
n
n
a
)
iW
rN
(
W
C
−
+
=
= 1050 +(200 –0,2
⋅1050)⋅2,86364
C
5
= 1050 –88,77 = 961,23 zł
3. Formuła kwoty bazowej
= 909,09 + (1050 – 909,09)
⋅0,37
n
n
v
)
G
W
(
G
C
−
+
=
C
5
= 909,09 +52,14 = 961,23 zł
4. Formuła Makehama
=388,50 + (0,190476/0,22)(1050–388,5)
)
K
W
)(
i
/
q
(
K
C
n
−
+
=
C
5
= 388,5 + 572,73 = 961,23 zł
☺☺☺☺☺☺☺☺
Analiza obligacji – Stopa zwrotu z obligacji
9
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Analiza obligacji – Czas trwania obligacji
10
3. CZAS TRWANIA OBLIGACJI (Duration)
Pomiar zmienności ceny obligacji:
Przykład 6.8.
Zmiana ceny obligacji 2 i 10 letnich.
Wniosek 1.
Ceny obligacji zmieniają się w przeciwnym kierun-
ku niż wymagana stopa zwrotu
Wniosek2.
Przy niewielkich zmianach stopy zwrotu, procento-
wa zmiana ceny danej obligacji jest w przybliżeniu
taka sama przy wzroście jak i przy spadku tej stopy.
Wniosek3.
Przy dużych zmianach stopy zwrotu, procentowa
zmiana ceny danej obligacji jest różna w zależno-
ści od kierunku zmiany tej stopy.
Wniosek4.
Przy zmianie stopy zwrotu o tą samą liczbę punk-
tów bazowych, procentowy wzrost ceny jest więk-
szy niż jej spadek.
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
y = f(x);
∆y ≈ f ′(x
0
)
∆
n
i|
n
n
Wv
Ra
C
+
=
(Formuła bazowa)
n
n
2
1
n
)
i
1
(
W
)
i
1
(
R
)
i
1
(
R
)
i
1
(
R
)
i
(
C
−
−
−
−
+
+
+
+
+
+
+
+
=
L
(6.29)
)
1
n
(
)
1
n
(
3
2
n
)
i
1
(
nW
)
i
1
(
nR
)
i
1
(
R
2
)
i
1
(
R
)
i
(
C
+
−
+
−
−
−
+
−
+
−
−
+
−
+
−
=
′
L
(6.30)
M
)
i
1
(
)
i
(
C
1
n
−
+
−
=
′
(6.31)
n
n
1
j
j
)
i
1
(
nW
)
i
1
(
j
R
M
−
=
−
+
+
+
=
∑
(6.32)
i
M
)
i
1
(
)
i
(
C
1
n
∆
+
−
≈
∆
−
i
C
M
)
i
1
(
C
)
i
(
C
n
1
n
n
∆
⎟
⎠
⎞
⎜
⎝
⎛
+
−
≈
∆
−
(6.33)
Czas trwania Macaulaya (Frederik Macaulay 1938)
n
n
1
j
n
j
n
c
C
nWv
)
j
1
(
j
R
C
M
M
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
=
=
∑
=
−
(6.34)
(
)
n
n
n
c
C
nWv
)
Ia
(
R
M
+
=
(6.35)
Zmodyfikowany czas trwania Macaulaya
M
z
= M
c
/(1+i) = M
c
v (6.36)
i
M
C
)
i
(
C
z
n
n
∆
−
≈
∆
(6.37)
Analiza obligacji – Czas trwania obligacji
11
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Zmodyfikowany czas trwania określa przybliżoną procentową
zmianę ceny obligacji odpowiadającą danej zmianie stopy pro-
centowej
Czas trwania Macaulaya – Średnio ważony czas
n
n
n
2
n
c
C
v
)
W
R
(
n
C
Rv
2
C
Rv
1
M
+
+
+
+
=
L
(6.38)
Wagi
n
j
j
C
Rv
w
=
dla j=1,2, . . . n-1
(6.39)
n
n
n
C
v
)
W
R
(
w
+
=
Suma wag
1
C
v
)
W
R
(
C
Rv
C
Rv
n
n
n
2
n
=
+
+
+
+
L
(6.40)
(6.41)
∑
=
−
=
n
1
j
j
w
j
M
Przykład 6.9.
Wyznaczyć czas trwania Macaulaya obligacji 25%, o nominale
1000zł, z 5-cio letnim okresem wykupu przy założeniu 20%
stopy zwrotu w okresie do wykupu.
Analiza obligacji – Czas trwania obligacji
12
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Rok Przepływy
pieniężne
Czynnik
dyskontujący
Zdyskontowane
przepływy
Wagi
Wartości
złożone
j R
j
v
j
R
j
v
j
w
j
jw
j
1 250 0,8333 208,33 0,1812 0,1812
2 250 0,6944 173,61 0,1510 0,3020
3 250 0,5787 144,67 0,1258 0,3774
3 250 0,4823 102,56 0,1048 0,4192
5 1250 0,4019 502,34 0,4370 2,185
∑
C
n
=1149,53
1,000
3,4648
Czas trwania obligacji
M
c
= 3,4648
Zmodyfikowany czas trwania obligacji
M
z
=
3,4648 /1,2 = 2,8873
Przykład 6.10.
Wyznaczyć czas trwania obligacji z przykładu 6.9 posługując
się wzorem (6.35)
(
)
n
n
n
c
C
nWv
)
Ia
(
R
M
+
=
n
i|
n
n
Wv
Ra
C
+
=
(W = N =1000)
i
nv
)
i
1
(
a
i
nv
a
)
Ia
(
n
i|
n
n
i|
n
n
−
+
=
−
=
&&
Analiza obligacji – Czas trwania obligacji
13
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Tablice finansowe
=
2
,
0
|
5
a
2,99061
v
5
=
0,40188
C
5
=
250
⋅2,99061+1000⋅0,40188=1149,5325
(Ia)
5
=
(2,99061
⋅- 5⋅0,40188) /0,2=7,8967
M
c
=
(250
⋅7,8967 + 5⋅1000⋅0,40188) / 1149,5325
M
c
= 3,4653
☺☺☺☺☺☺☺☺
Obliczenie przybliżonej procentowej zmiany ceny obligacji
i
M
C
)
i
(
C
z
n
n
∆
−
≈
∆
(
∆i = 0,01)
Stopa zwrotu zmieni się o 1% = 100 punktów bazowych
%
M
01
,
0
M
C
)
i
(
C
z
z
n
n
−
=
⋅
−
≈
∆
(6.42)
Zmodyfikowany czas trwania obligacji wyrażony w procentach
wyznacza przybliżoną procentową zmianę ceny obligacji spo-
wodowaną zmianą stopy procentowej o 100 punktów bazo-
wych
Czas trwania nie może być traktowany jako średni ważony
termin do wykupu obligacji. (Nie jest miarą czasu)
Analiza obligacji – Czas trwania obligacji
14
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Przykład 6.11.
Obliczyć procentową zmianę ceny obligacji wywołaną zmianą
stopy zwrotu w terminie do wykupu o 100 punktów bazowych.
M
z
= 2,8873
M
z
% = M
z
0,01 = 0,028873
Obliczanie przybliżonej zmiany ceny obligacji
(6.43)
i
C
M
)
i
(
C
n
z
n
∆
⋅
⋅
−
≈
∆
– Nominalny czas trwania
n
z
N
C
M
M
⋅
=
Wartość cenowa punktu bazowego – nominalna wartość punk-
tu bazowego
(price value of a basis point – dollar value of a basis point
(
∆
i = 0,0001))
∆C
n
(i)
≈ M
N
⋅0,0001 (6.44)
P
b
= M
N
⋅0,0001
(6.45)
Wartość cenowa punktu bazowego informuje o ile zmieni się
cena obligacji przy zmianie stopy zwrotu w terminie do wyku-
pu o jeden punkt bazowy.
Analiza obligacji – Czas trwania obligacji
15
Prof. Piotr Chrzan
MATEMATYKA FINANSOWA
Przykład 6.12.
Obliczyć nominalny czas trwania oraz wartość cenową punktu
bazowego obligacji z zadania 6.9
Nominalny czas trwania obligacji
M
N
= M
Z
⋅C
n
= 2,8873
⋅1149,5325 = 3319,045187
Wartość cenowa punktu bazowego
P
b
=M
N
⋅0,0001 = 0,3319
☺☺☺☺☺☺☺☺
UOGÓLNIENIA
(6.46)
∑
=
−
+
=
n
1
j
j
j
)
j
1
(
R
)
i
(
PV
i
)
i
1
(
D
)
i
(
PV
)
i
(
PV
1
∆
+
−
≈
∆
−
(6.47)
Czas trwania ciągu płatności {R
k
} (Duration)
PV
v
jR
D
n
1
j
j
j
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑
=
(6.48)
Zmodyfikowany czas trwania ciągu płatności {R
k
}
)
i
1
(
D
D
z
+
=
= Dv
(6.49)
i
D
)
i
(
PV
)
i
(
PV
z
∆
−
≈
∆
(6.50)
i
PV
D
)
i
(
PV
z
∆
⋅
−
≈
∆
(6.51)
Analiza obligacji – Czas trwania obligacji
16