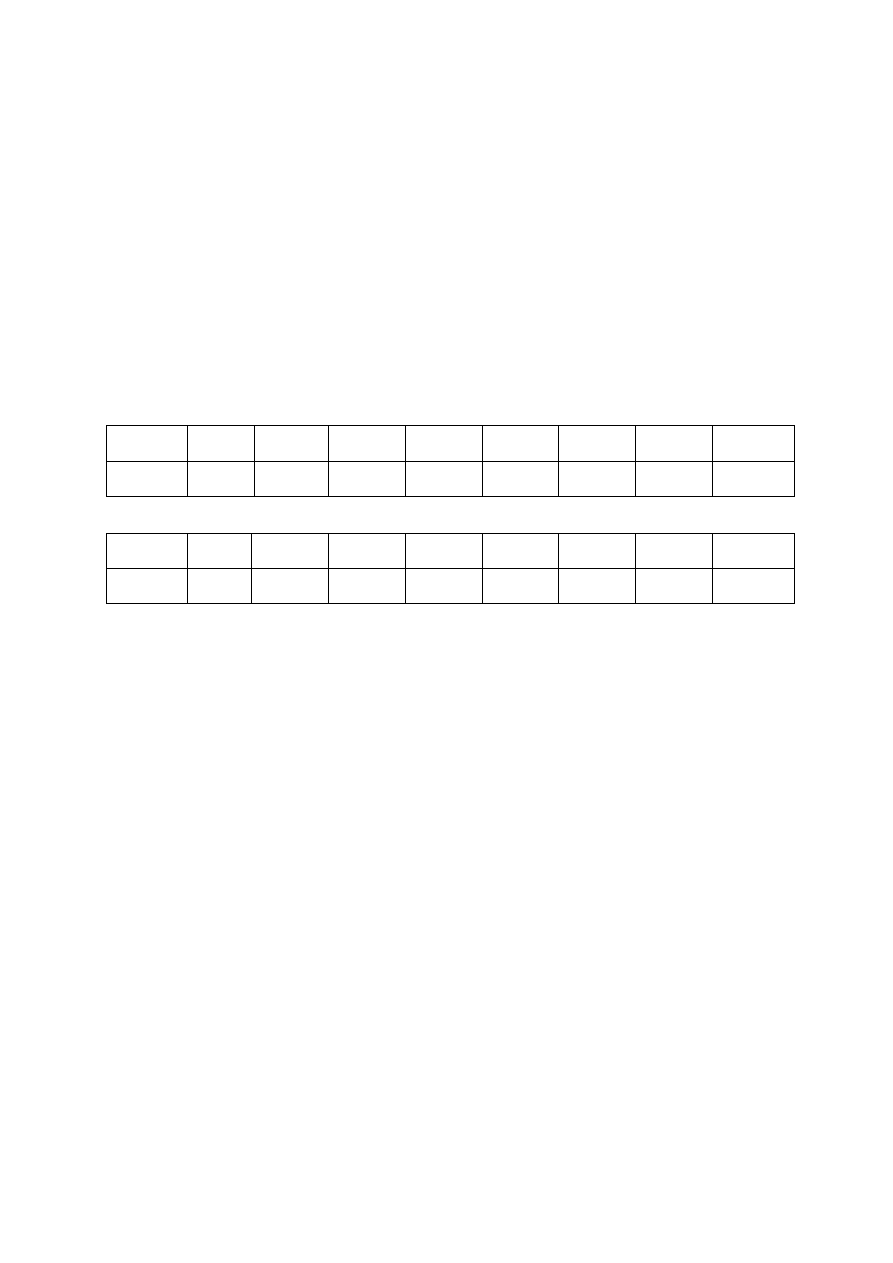
1

Egzamin ze statystyki, Studia Licencjackie Stacjonarne wrzesień 2008

ZESTAW I

(imię, nazwisko, numer albumu) .........................................................................................................

Przy rozwiązywaniu zadań, jeżeli nie zostało zaznaczone inaczej, należy przyjąć poziom
istotności 0,05. Wariancja z próby podawana jest w postaci nieobciążonego estymatora.

Zadanie 1.
Obiektem badania są rozkłady dochodów miesięcznych na głowę mieszkańców miasta Ź w latach
2007 i 1999. Wylosowano dwie próby liczące po 1000 osób, a wyniki zostały przedstawione w
poniższych tabelach:

2007 r.

dochód w
zł/mies.

600-800 800-1000 1000-1200 1200-1400 1400-1600 1600-1800 1800-2000 ponad

2000

udział
osób

0,1 0,15 0,25 0,12 0,07 0,06 0,05 0,2

1999 r.

dochód w
zł/mies.

400-500 500-600 600-700 700-800 800-900 900-1000

1000-1100

ponad

1100

liczba
osób

80 170 250 110 80 60 50 200

1.1. Posługując się miarami pozycyjnymi należy porównać zróżnicowanie dochodów w obu latach. (2
pkt.)
Wskazówka: rozwiązanie tego zadania nie wymaga pracochłonnych obliczeń.















1.2. Średni dochód w 2007 r. obliczony na podstawie danych indywidualnych wyniósł 1412 zł. Czy
gdyby znana była górna granica ostatniego przedziału dochodowego w tabeli, to średnia obliczona
jedynie na podstawie tej tabeli również wynosiłaby 1412 zł? (odpowiedź proszę uzasadnić) (1pkt.)

2

1.3. Proszę ocenić kierunek i siłę asymetrii rozkładu z 1999 r. Można w tym celu posłużyć się miarami
pozycyjnymi lub wykresem. (2 pkt.)






















Zadanie 2.
Jan Lognormalny twierdzi, że w 2007 r. logarytm naturalny dochodów w mieście Ź miał rozkład
normalny. Aby sprawdzić tę hipotezę podzielił próbę na 10 przedziałów i obliczył wartość statystyki
testowej χ

2

= 16,5 (parametry rozkładu oszacował na podstawie próby).

2.1. Czy wynik testu pozwala przyznać rację Janowi L., jeżeli przyjąć poziom istotności 0,05? (2 pkt.)











2.2. Proszę podać poziom istotności, przy którym nie można zaprzeczyć tezie o normalności rozkładu?
(2 pkt.)

3

Zadanie 3
Przedstawiciel Ligi Mężczyzn Polskich twierdzi, że w mieście Ź. przeciętne dochody mężczyzn w
2007 r. były wyższe od przeciętnych dochodów kobiet. W celu sprawdzenia tego przypuszczenia
wykorzystał przedstawioną W Zadaniu 1 próbę losową. Średnie wartości dochodu dla kobiet i
mężczyzn wyniosły, odpowiednio, 1370 i 1440 zł przy odchyleniach standardowych 880 zł i 990 zł. W
próbie znalazło się 400 kobiet i 600 mężczyzn.

Czy powyższy wynik można uznać za sprzeczny z opinią Ligi? (4 pkt.)






















Zadanie 4
W próbie z 2007 r. opisanej w Zadaniu 1 odsetek osób z dochodami poniżej 900 zł wyniósł 20%.

Należy wyznaczyć przedział, w którym najprawdopodobniej znajdzie się odsetek osób z dochodami
poniżej 900 charakteryzujący populację generalną. Metoda powinna zapewniać, iż ów odsetek zmieści
się w przedziale z prawdopodobieństwem 0,95. (3 pkt.)

4

Zadanie 5
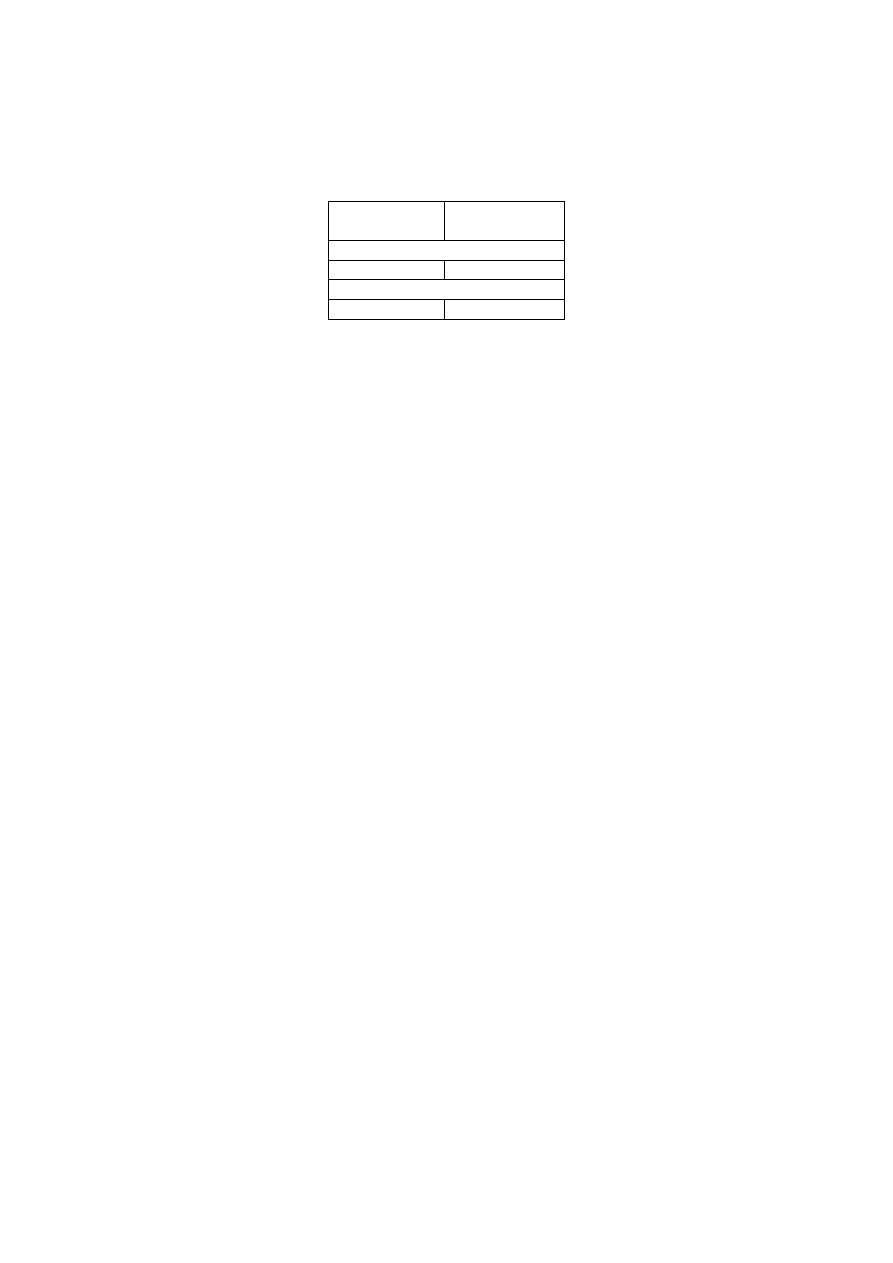
Wśród kobiet i mężczyzn wylosowanych do próby zostały obliczone odsetki osób otrzymujących
świadczenia społeczne. Poniższa tabela przedstawia procentowe rozkłady liczby osób otrzymujących
świadczenia dla obu grup.

Otrzymują

świadczenia

Nie otrzymują

świadczeń

mężczyźni

18% 82%

kobiety

22% 78%

Łącznie zbadano 400 kobiet i 600 mężczyzn

5.1. Proszę ocenić czy w badanej próbie istnieje zależność między płcią i otrzymywaniem świadczeń
społecznych. Na pytanie można odpowiedzieć bez wykonywania żadnych obliczeń. (2 pkt.)








5.2. Czy na podstawie tej próby można też stwierdzić istnienie zależności w populacji generalnej? (3
pkt.)


















Zadanie 6
Dla próby z roku 2007 oszacowano model liniowy, w którym zmienną objaśnianą był dochód osoby
(Y), zaś objaśniającą liczba ukończonych lat edukacji (X). Wyniki oszacowania parametrów
strukturalnych modelu były następujące:

i

i

i

e

x

y

+

+

⋅

=

99

,

892

29

,

55

Ponadto znane są odchylenia standardowe: S(X)=2,26 S(Y)=325,8 S(e)=301,01

6.1. Czy zależność liniowa między dochodem i wykształceniem jest statystycznie istotna? (3 pkt.)

5

6.2. Proszę ocenić dopasowanie powyższego modelu do danych. (3 pkt.)











Zadanie 7
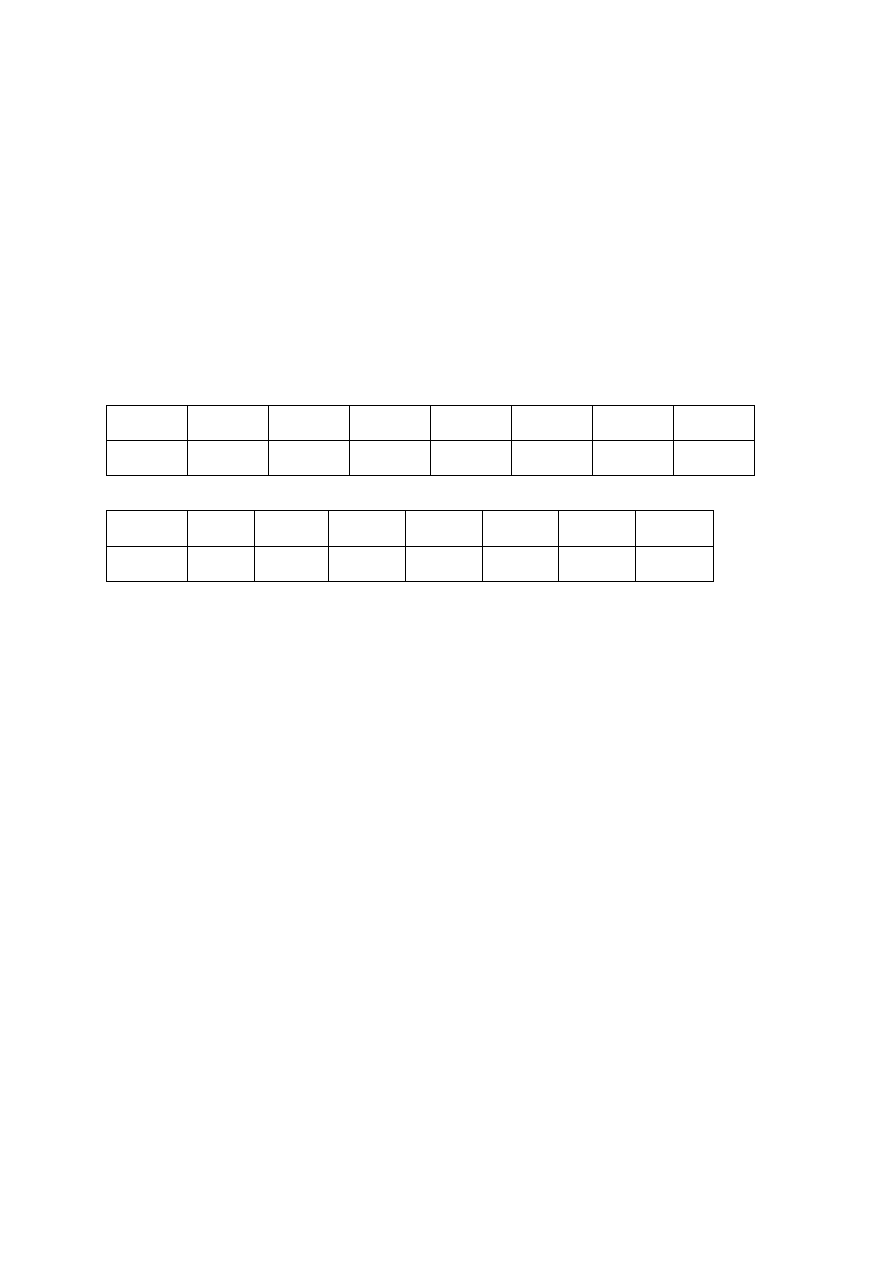
W badanych próbach średnie wydatki na konsumpcję w 1999 r. w cenach bieżących wynosiły 760 zł,
w 2007 r. 1390 zł. Ponadto, znana była struktura konsumpcji badanej próby w 1999 r. oraz zmiany cen
czterech grup towarów w latach 2007/1999:

Grupa
towarów

Indeks

cen

2007/1999

Udział

wydatków

Żywność 1,55 35%
Mieszkanie 1,64

20%

Ubranie 1,50 8%
Pozostałe 1,52 37%

7.1. O ile procent zmienił się wolumen (fizyczne rozmiary) konsumpcji w badanym okresie? (3 pkt.)
Wskazówka: grupy towarów można potraktować jak pojedyncze towary.

6

7.2. Ile wynosiła średnia roczna zmiana nominalnych wydatków konsumpcyjnych (w cenach
bieżących) w tym okresie? (1 pkt.)

CZĘŚĆ TESTOWA (9 punktów)

Przy wszystkich pytaniach należy otoczyć kółkiem prawidłową odpowiedź T-tak lub N-nie.

Punktacja

: odpowiedź poprawna 1 pkt; brak odpowiedzi 0 pkt; odpowiedź błędna -1 pkt.

Jeżeli całkowita suma punktów z tej części będzie ujemna, jako wynik zostanie przyjęte 0
pkt.

1. Jeżeli wariancja zmiennej o rozkładzie normalnym w próbie nr 1 jest wyższa niż wariancja w
próbie nr 2 zaś średnie i liczebności prób są jednakowe, to:
a/ przedział ufności wyznaczony za pomocą próby nr 1 będzie dłuższy, T N

b/ możliwa jest sytuacja, że identyczną hipotezę o wartości średniej w populacji generalnej przy
identycznym poziomie istotności odrzuci się dla próby nr 2, nie odrzuci zaś dla próby nr 1, T N

c/ oznacza to, że próby zostały wylosowane z różnych populacji generalnych. T N

2. Oszacowanie parametrów modelu regresji liniowej:
a/ pozwala wyznaczyć oszacowanie warunkowej wartości oczekiwanej zmiennej objaśnianej (Y) dla
dowolnej danej wartości zmiennej objaśniającej (X), T N

b/ wymaga danych jedynie w postaci wartości zmiennej objaśniającej i objaśnianej, T N

c/ powinno być wykorzystywane do prognozowania wartości Y na podstawie X, jedynie wtedy gdy
statystyka t (Studenta) dla zmiennej X przekroczy wartość krytyczną. T N

3. Linie lotnicze sprzedają codziennie 2000 biletów na samoloty mające w sumie 1960 miejsc a
prawdopodobieństwo rezygnacji z lotu przez pasażera z wykupionym biletem wynosi 0,02. Czy
jest prawdą, że:
a/ Nigdy nie zdarza się aby do odlotu zgłosiło się więcej pasażerów niż wynosi liczba miejsc w
samolocie, T N

b/ Do obliczenia przybliżonego prawdopodobieństwa, że w losowo wybranym dniu zgłosi się mniej
pasażerów niż 1950 można wykorzystać twierdzenie graniczne, T N

c/ Prawdopodobieństwo, że liczba zgłaszających się do odlotu pasażerów będzie niższa od 1950
wynosi w przybliżeniu tyle samo ile prawdopodobieństwo, że liczba pasażerów przekroczy 1970.
T N

7

Egzamin ze statystyki, Studia Licencjackie Stacjonarne wrzesień 2008

ZESTAW II

(imię, nazwisko, numer albumu) .........................................................................................................

Przy rozwiązywaniu zadań, jeżeli nie zostało zaznaczone inaczej, należy przyjąć poziom
istotności 0,05. Wariancja z próby podawana jest w postaci nieobciążonego estymatora.

Zadanie 1.
W poniższych tabelach zostały przedstawione rozkłady dochodów miesięcznych na głowę w mieście
Ó. Pierwsza tabela przedstawia dochody w gospodarstwach o dochodach mniejszych niż 800 zł
miesięcznie, w drugiej w pozostałych. Obydwie próby liczyły po 1000 osób.

dochód w
zł/mies.

100-200 200-300 300-400 400-500 500-600 600-700 700-800

liczba
osób

50 60 140 250 250 170 80

dochód w
zł/mies.

800-

1000

1000-

1200

1200-

1400

1400-

1600

1600-

1800

1800-

2000

ponad

2000

udział
osób

0,25 0,14 0,11 0,15 0,1 0,1 0,15

1.1. Wśród osób z dochodami co najmniej 800 zł miesięcznie średni dochód obliczony na podstawie
danych indywidualnych wyniósł 1365 zł. Czy gdyby znana była górna granica ostatniego przedziału
dochodowego w tabeli, to średnia obliczona jedynie na podstawie tej tabeli również wynosiłaby 1365
zł? (odpowiedź proszę uzasadnić) (1 pkt.)






1.2. Proszę zilustrować graficznie pierwszy z rozkładów i na podstawie rysunku ocenić, która z
poniższych wartości klasycznego współczynnika asymetrii może być dla niego prawdziwa:

-3,4 -0,34 0,34 3,4 (2 pkt.)

8

1.3. Posługując się miarami pozycyjnymi należy ocenić, w której grupie zróżnicowanie dochodów
było większe. (2 pkt.)
Wskazówka: rozwiązanie tego zadania nie wymaga pracochłonnych obliczeń.















Zadanie 2.
Odchylenie standardowe dochodów w próbie opisanej w punkcie 1.1. wynosi 440 zł.

Należy wyznaczyć przedział, w którym najprawdopodobniej znajdzie się średnia w populacji
generalnej. Metoda powinna zapewniać, iż ów odsetek zmieści się w przedziale z
prawdopodobieństwem 0,95. (3 pkt.)













Zadanie 3.
Rzecznik Praw Mężczyzn twierdzi, że w mieście Ó odsetek osób z dochodami poniżej 800 zł jest
wyższy wśród mężczyzn niż wśród kobiet. W celu weryfikacji tego przypuszczenia wylosowano 800
kobiet i 800 mężczyzn, wśród których stwierdzono wartości tych odsetków równe, odpowiednio: 0,26
i 0,3.

Czy wyniki te potwierdzają przypuszczenie Rzecznika? (4 pkt.)

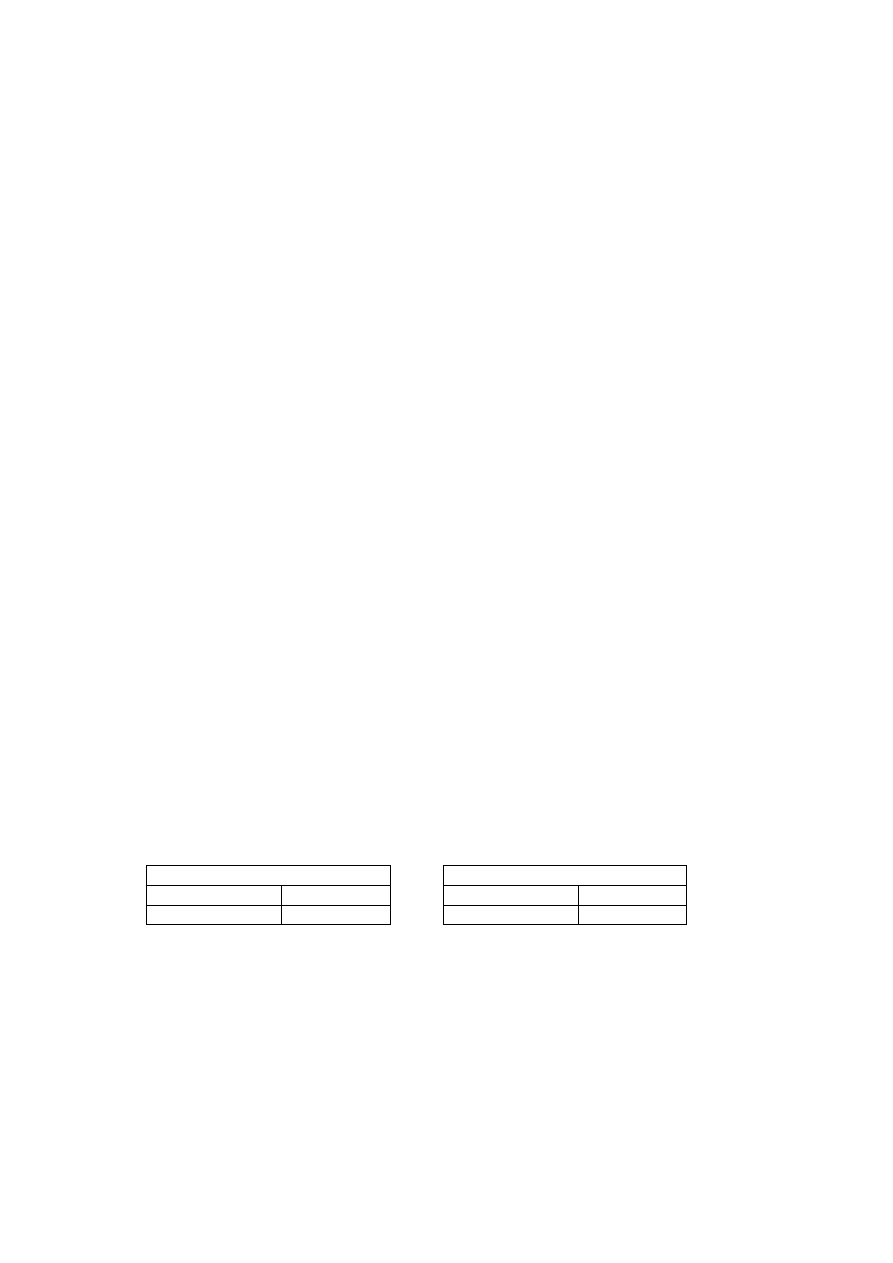
9

Zadanie 4
Stowarzyszenie Na Rzecz Normalności postanowiło sprawdzić, czy logarytm naturalny dochodów w
mieście Ó miał rozkład normalny. Aby sprawdzić tę hipotezę ekspert Stowarzyszenia podzielił badaną
próbę na 8 przedziałów i obliczył wartość statystyki testowej χ

2

= 11,2 (parametry rozkładu oszacował

na podstawie próby).

4.1. Czy wynik testu zaprzecza tezie o normalności rozkładu, jeżeli przyjąć poziom istotności 0,1? (2
pkt.)








4.2. Proszę podać poziom istotności, przy którym nie można zaprzeczyć tezie o normalności rozkładu?
(2 pkt.)








Zadanie 5
Wylosowano 1000 osób posiadających dzieci w celu zbadania zależności między wykształceniem
głowy gospodarstwa domowego i liczbą dzieci. W próbie znalazło się 700 osób z wykształceniem
średnim i 300 z wykształceniem wyższym. Poniższe tabele przedstawiają procentowe rozkłady liczby
dzieci dla obu grup.

Wykształcenie średnie

Wykształcenie wyższe

Liczba dzieci

Liczba dzieci

1 lub 2

3 lub więcej

1 lub 2

3 lub więcej

70% 30%

75% 25%

5.1. Proszę ocenić czy w badanej próbie istnieje zależność między wykształceniem i liczbą dzieci. Na
pytanie można odpowiedzieć bez wykonywania żadnych obliczeń. (2 pkt.)

10

5.2. Czy na podstawie tej próby można też stwierdzić istnienie zależności w populacji generalnej? (3
pkt.)




















Zadanie 6
Posługując się próbą liczącą 1000 elementów oszacowano model liniowy, w którym zmienną
objaśnianą był dochód na głowę (DOCH), zaś objaśniającą liczba dzieci w gospodarstwie (LD).
Wyniki oszacowania parametrów strukturalnych modelu były następujące:

i

i

i

e

LD

DOCH

+

+

⋅

−

=

1225

180

Ponadto znane są odchylenia standardowe: S(DOCH)=615 S(LD)=1,04 S(e)=586

6.1. Proszę ocenić dopasowanie powyższego modelu do danych. (3 pkt.)
















6.2. Czy zależność liniowa między zmienna objaśnianą i objaśniającą jest statystycznie istotna? (3
pkt.)

11

Zadanie 7
W roku 2007 r. wśród wszystkich zbadanych gospodarstw wydatki konsumpcyjne w cenach bieżących
wynosiły 1375 zł, zaś w 2003 r. 1010 zł (również w cenach bieżących). Ponadto, znana była struktura
konsumpcji badanej próby w 2003 r. oraz indeksy ilości dla czterech grup towarów w latach
2007/2003:

Mieszkanie

i

energia

Żywność i

używki

Transport i

łączność

Pozostałe

Indeks ilości

2007/2003

1,02 1,08 1,3 1,4

Udział

wydatków

0,25 0,4 0,1 0,25

7.1. Ile wynosiła średnia roczna zmiana nominalnych wydatków konsumpcyjnych (w cenach
bieżących) w okresie 2003 - 2007? (1 pkt.)








7.2. O ile procent wzrosły w tym okresie ceny konsumpcji? (3 pkt.)
Wskazówka: grupy towarów można potraktować jak pojedyncze towary.

12

CZĘŚĆ TESTOWA (9 punktów)

Przy wszystkich pytaniach należy otoczyć kółkiem prawidłową odpowiedź T-tak lub N-nie.

Punktacja

: odpowiedź poprawna 1 pkt; brak odpowiedzi 0 pkt; odpowiedź błędna -1 pkt.

Jeżeli całkowita suma punktów z tej części będzie ujemna, jako wynik zostanie przyjęte 0
pkt.

1. Oszacowany został model regresji liniowej

β

α

+

⋅

=

X

Yˆ

:

a/ Jeżeli oszacowanie parametru α jest statystycznie istotne, to współczynnik korelacji
(zależności) liniowej między X i Y w tej samej próbie jest statystycznie różny od zera,

T N

b/ Jeżeli dopasowanie modelu do danych jest słabe, to współczynnik korelacji liniowej
r(X,Y) jest niski,

T N

c/ Jeżeli oszacowanie parametru α jest większe od błędu standardowego tego oszacowania, to
zmienna X wywiera istotny wpływ na zmienną Y.

T N

2. Linie lotnicze dysponują dziennie samolotami mającymi w sumie 1455 miejsc.
Prawdopodobieństwo zgłoszenia się do odlotu pasażera z wykupionym biletem wynosi
0,97 a linie sprzedają codziennie 1500 biletów. Czy jest prawdą, że:

a/ Prawdopodobieństwo, że liczba zgłaszających się do odlotu pasażerów przekroczy 1460
osób wynosi w przybliżeniu tyle samo ile prawdopodobieństwo, że liczba pasażerów będzie
niższa od 1450.

T N

b/ Nigdy nie zdarza się aby do odlotu zgłosiło się więcej pasażerów niż wynosi liczba miejsc
w samolocie?

T N

c/ Do obliczenia przybliżonego prawdopodobieństwa, że w losowo wybranym dniu zgłosi się
więcej pasażerów niż 1460 można posłużyć się granicznym rozkładem normalnym.

T N

3. Wariancja estymatora parametru Θ:

a/ jest miernikiem jego precyzji,

T N

b/ nie może być oszacowana na podstawie próby,

T N

c/ powinna być znana aby można było wykonać test dla wartości parametru Θ w populacji
generalnej.

T N