Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

1

15.



15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI

KOŁOWYCH DRGAŃ WŁASNYCH

15.1. Wprowadzenie

Rozwiązywanie zadań z zakresu dynamiki budowli sprowadza się aż do dwóch zagadnień. Należy

określić częstość drgań własnych układu w przypadku drgań swobodnych oraz wartość amplitudy
przemieszczenia w przypadku drgań wymuszonych obciążeniem zewnętrznym.

Znajomość częstości drgań własnych konstrukcji pozwala uniknąć zjawiska rezonansu. Nie wolno

obciążać konstrukcji urządzeniami, których częstość kołowa pokrywa się z częstością drgań własnych, gdyż
wtedy amplitudy przemieszczeń układu wzrastają w sposób niekontrolowany. W drugim typie zadań układ
obciążony jest urządzeniem o znanej sile wymuszania i częstości drgań. Trzeba wtedy wyliczyć amplitudy
przemieszczeń i porównać je z dopuszczalnymi.

Analizę układu należy rozpocząć od ustalenia stopnia swobody dynamicznej (niezależne, możliwe

kierunki ruchu masy). Dalej należy zapisać równania ruchu po kierunkach swobody dynamicznej, określić
wartości przemieszczeń powstałych od sił dynamicznych.

W układach statycznie wyznaczalnych przemieszczenia liczymy w prosty sposób korzystając z

równania pracy wirtualnej. W układach statycznie niewyznaczalnych obliczenia komplikują się, gdyż
potrzebne są wykresy momentów od sił jednostkowych w układach niewyznaczalnych.

Przemieszczenia od sił jednostkowych (wyznaczony w ten sam sposób jak w metodzie sił) dają układ

zwany macierzą podatności [

D]. Ten sposób rozwiązywania zadania nazywa się często rozwiązaniem “przez

podatność”.

Istnieją jednak układy, które prościej rozwiązuje się metodą przemieszczeń aniżeli metodą sił (nakład

pracy jest mniejszy). Tego typu ramy łatwiej rozwiązać “przez sztywność”, klasyczną metodą przemieszczeń
przyjmując układ podstawowy (muszą być zablokowane kierunki swobody dynamicznej) obciążony siłami
dynamicznymi. W tym przypadku trzeba stworzyć macierz sztywności układu [

K], czyli określić reakcje od

jednostkowych przemieszczeń.

Ramy statycznie wyznaczalne rozwiązujemy zazwyczaj korzystając z koncepcji metody sił

(wyznaczamy macierz podatności), natomiast układy statycznie niewyznaczalne rozwiązujemy korzystając z
metody przemieszczeń (wyznaczając macierz sztywności) lub metody sił. Podział ten wynika z nakładu pracy,
jaką trzeba wykonać przy rozwiązywaniu układu poszczególnymi metodami.

W układach statycznie wyznaczalnych obliczenie współczynników

δ

ik

nie jest skomplikowane. Ten sam

układ, rozwiązywany metodą przemieszczeń wymagałby zapewne blokowania obrotów i przesuwów, co
zwiększyłoby liczbę współczynników

r

ik

.

Obie macierze charakterystyczne: podatności

[ D]=[

ik

] i sztywności [ K ]=[r

ik

] są symetryczne:



ik

=

ki

r

ik

=r

ki

oraz zachodzi między nimi zależność:

[ D]

−1

=[ K ]

[ D]⋅[ K ]=[ K ]⋅[ D]=[ I ]

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

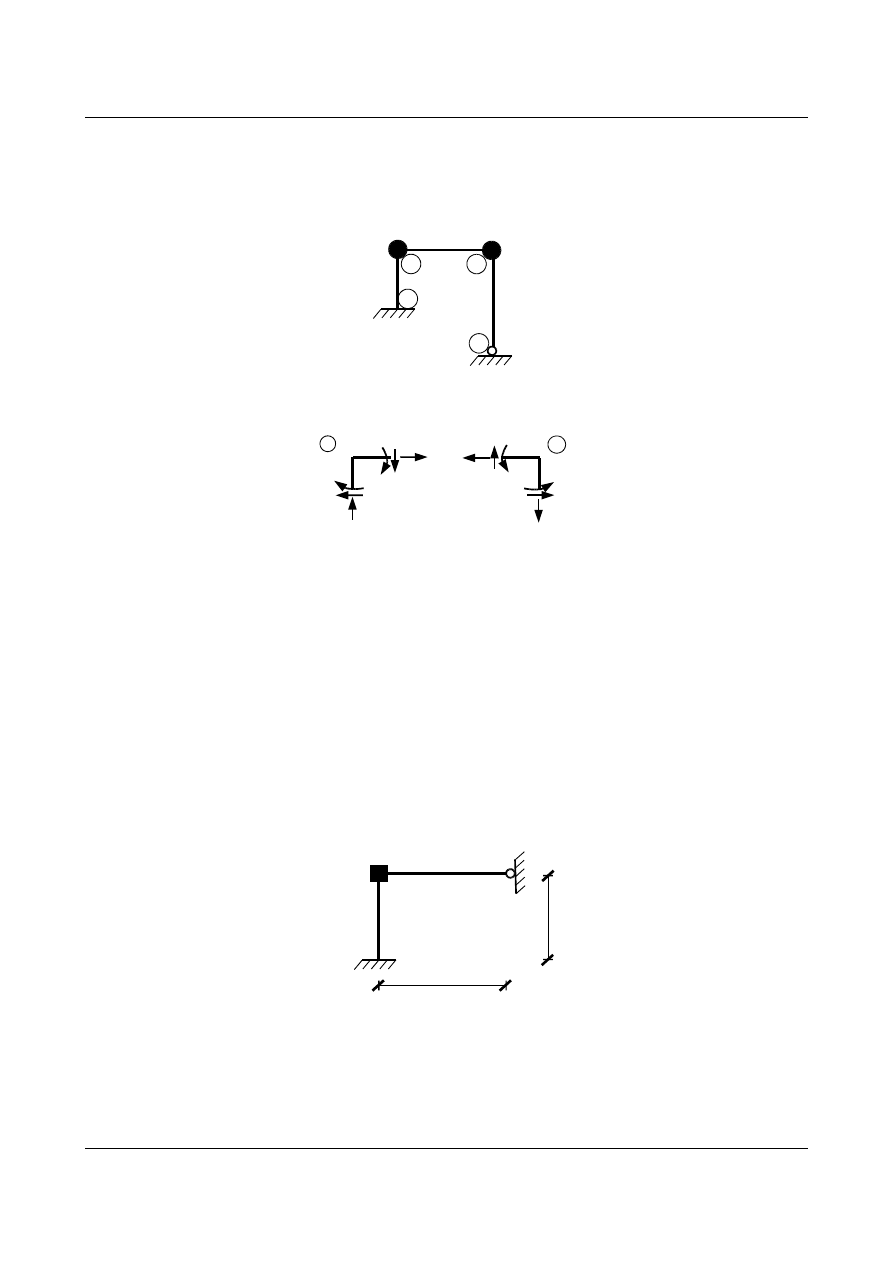
Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

2

15.2. Rozwiązywanie przez sztywność (metoda przemieszczeń)

Dla dowolnego układu o zadanej geometrii, sposobie podparcia i rozkładzie masy

3

1

2

0

J

1

, A

1

J

2

, A

2

J

3

, A

3

ρ, μ

znamy wzory transformacyjne na przywęzłowe momenty przęsłowe, siły tnące i normalne.

N

10

N

23

T

10

T

23

T

21

T

12

N

12

N

21

M

21

M

12

M

10

M

23

1

2

Niewiadome przemieszczenia z węzła

1 (φ

1

,

u

1

,

v

1

) i

2 (φ

2

,

u

2

,

v

2

) wyznaczymy zapisując dla każdego z tych

węzłów równania równowagi:

∑

X

=0

∑

Y

=0

∑

M

=0

Otrzymany w ten sposób układ równań jednorodnych, ma rozwiązanie nieosobliwe wówczas, gdy wyznacznik
tego układu będzie równy zero. Otrzymywane w ten sposób równanie charakterystyczne umożliwia wyliczenie
częstości drgań własnych. Metodę tę przybliżymy rozwiązując zadanie.

Zadanie 1

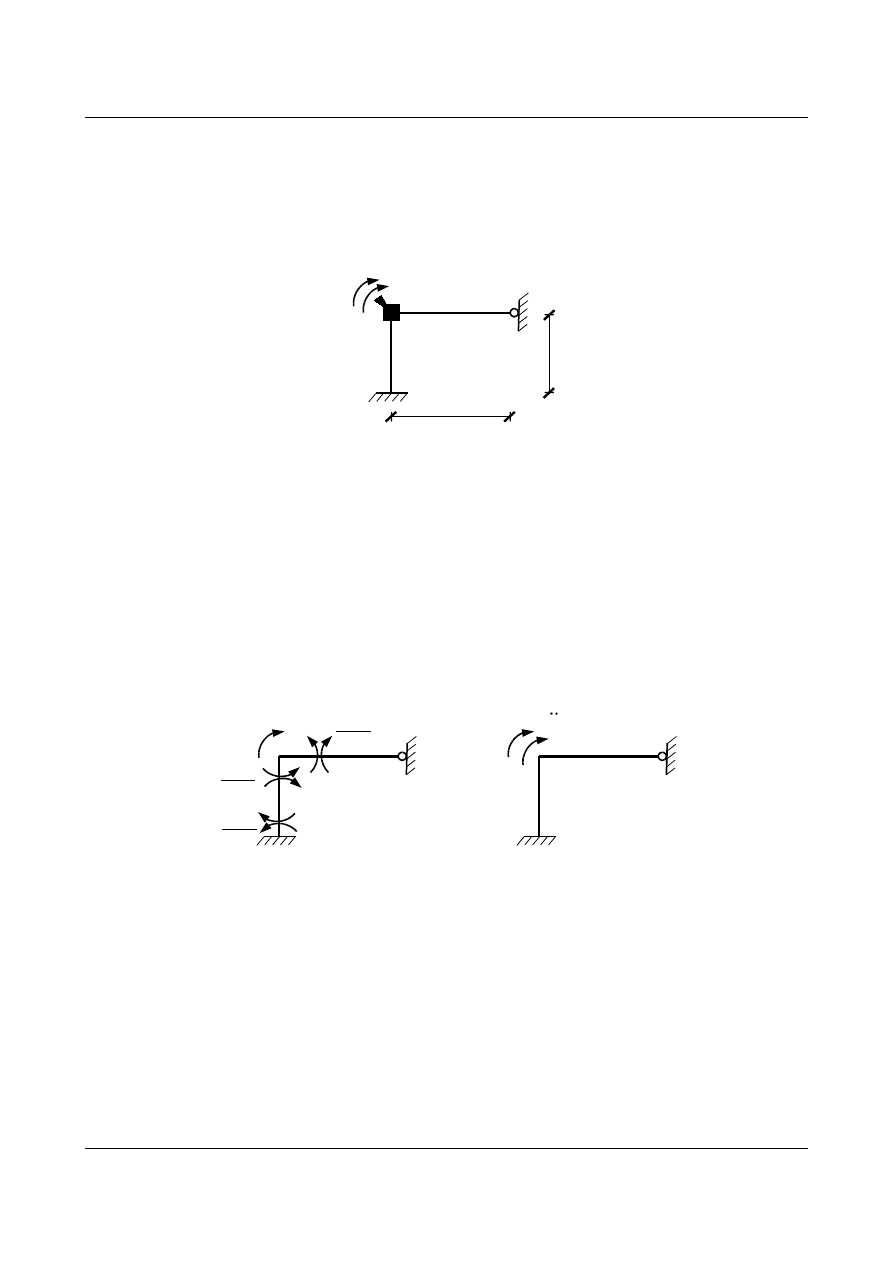
Obliczyć częstości kołowe i postacie drgań własnych dla układu z rysunku 15.1.

1

2

0

m, I

m

6

4

[m]

Rys. 15.1. Rama obciążona masą skupioną

Parametry geometryczne i fizyczne układu są następujące:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

3

EJ

=6000 kN m

2

m

=300 kg

I

m

=25 kgm

2

Masa ma możliwość ruchu tylko w jednym kierunku (

SSD = 1). Kierunek ten (w

1

= φ) i siłę dynamiczną B

1

będącą wynikiem działania bezwładności masy opisuje rys. 15.2.

1

2

0

w

1

, B

1

6

4

[m]

R

1

, φ

Rys. 15.2. Kierunki stopni swobody dynamicznej i układ podstawowy metody przemieszczeń

Funkcja rozwiązująca różniczkowe równanie ruchu dla drgań harmonicznych ma postać:

w

1

t =a

1

sin

t

¨w

1

t =−a

1



2

sin

 t

(15.1)

Zapiszmy zatem równanie kanoniczne metody przemieszczeń:

R

1

=r

11

w

1

t r

1 P

=0

(15.2)

Aby wyznaczyć wartości współczynników

r

11

i

r

1P

musimy zapisać sumy momentów w węźle

1, kolejno w

stanie

φ = 1 oraz P:

2 EJ

r

11

a)

4

b)

r

1P

B

1

= -I

m

w

1

(t)

4 EJ

4

3 EJ

6

Rys. 15.3. Wartości momentów: a) w stanie φ = 1, b) w stanie P

Z sumy momentów w węźle

1 otrzymamy:

r

11

=0,5 EJ EJ =1,5 EJ

r

1 P

=I

m

¨w

1

t

Podstawiając te wartości do równania kanonicznego (15.2) dostajemy różniczkowe równanie ruchu:

1,5 EJ

⋅w

1

t I

m

¨w

1

t =0

(15.3)

Wykorzystując funkcję (15.1) otrzymujemy rozwiązanie:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

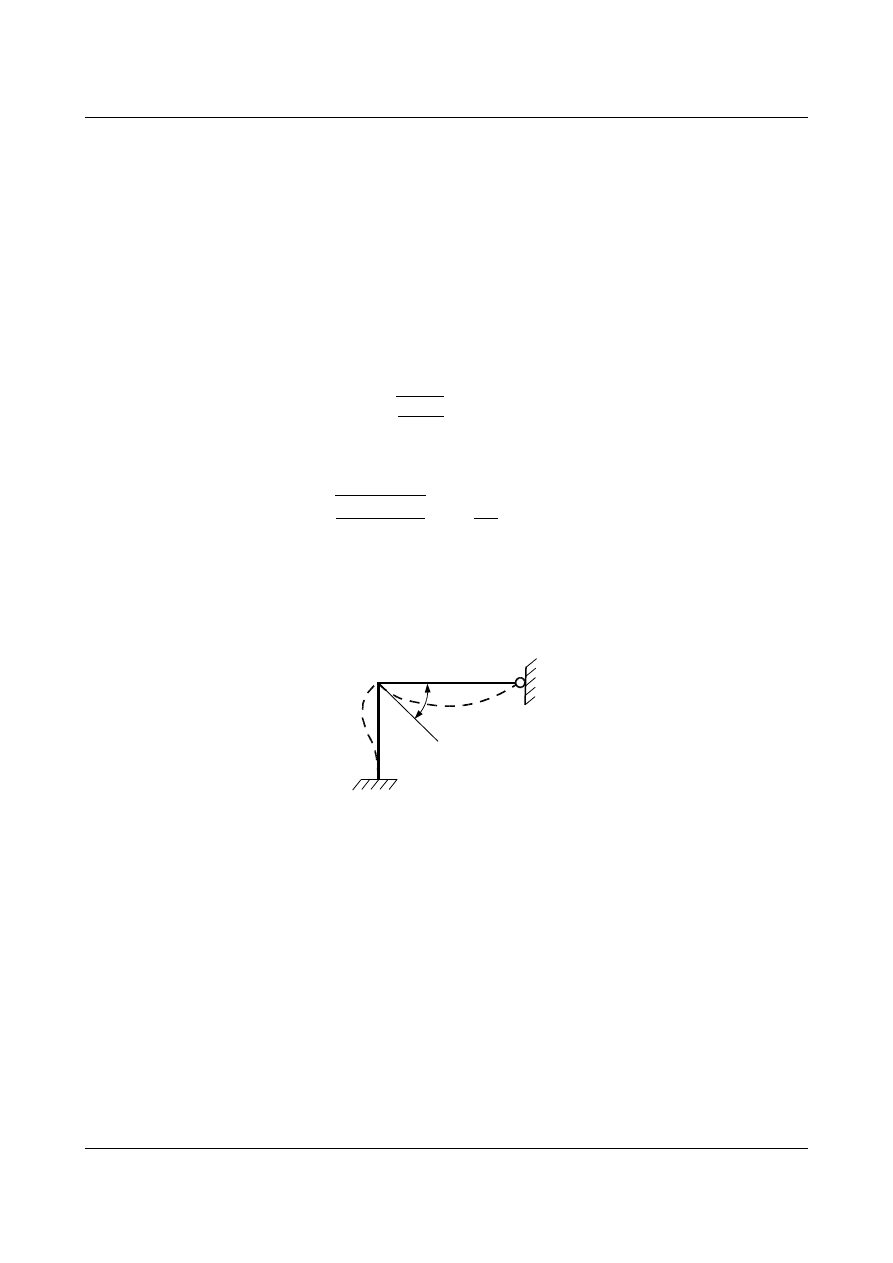
Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

4

1,5 EJ a

1

sin

t−I

m

a

1



2

sin

 t=0

(15.4)

Wyeliminowanie zmiennej czasu

t prowadzi do równania jednorodnego:



1,5 EJ

−I

m



2



a

1

=0

(15.5)

Równanie to ma nietrywialne rozwiązanie (

a

1

≠ 0), gdy:

1,5 EJ

−I

m



2

=0

(15.6)

zatem:

=



1,5 EJ

I

m

(15.7)

Po podstawieniu danych liczbowych do rozwiązania (15.7) otrzymujemy:

=



1,5

⋅6000 ⋅10

3

25

=600

[

rad

s

]

Postać drgań własnych w przypadku

SSD = 1 ogranicza się do jednej amplitudy przemieszczenia a

1

, która

może przyjmować dowolną, różną od zera wartość.

Przemieszczeniem (kierunkiem swobody dynamicznej) w tym zadaniu jest kąt obrotu (rys. 15.4).

a

1

Rys. 15.4. Postać drgań własnych

15.3. Rozwiązanie przez podatność (metoda sił)

Zastosowanie koncepcji metody sił w obliczeniach częstości kołowych drgań własnych pokażemy na
przykładach układów statycznie wyznaczalnych.

Zadanie 2

Znaleźć częstości kołowe drgań własnych i narysować ich postacie, dla układu z rys. 15.5.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

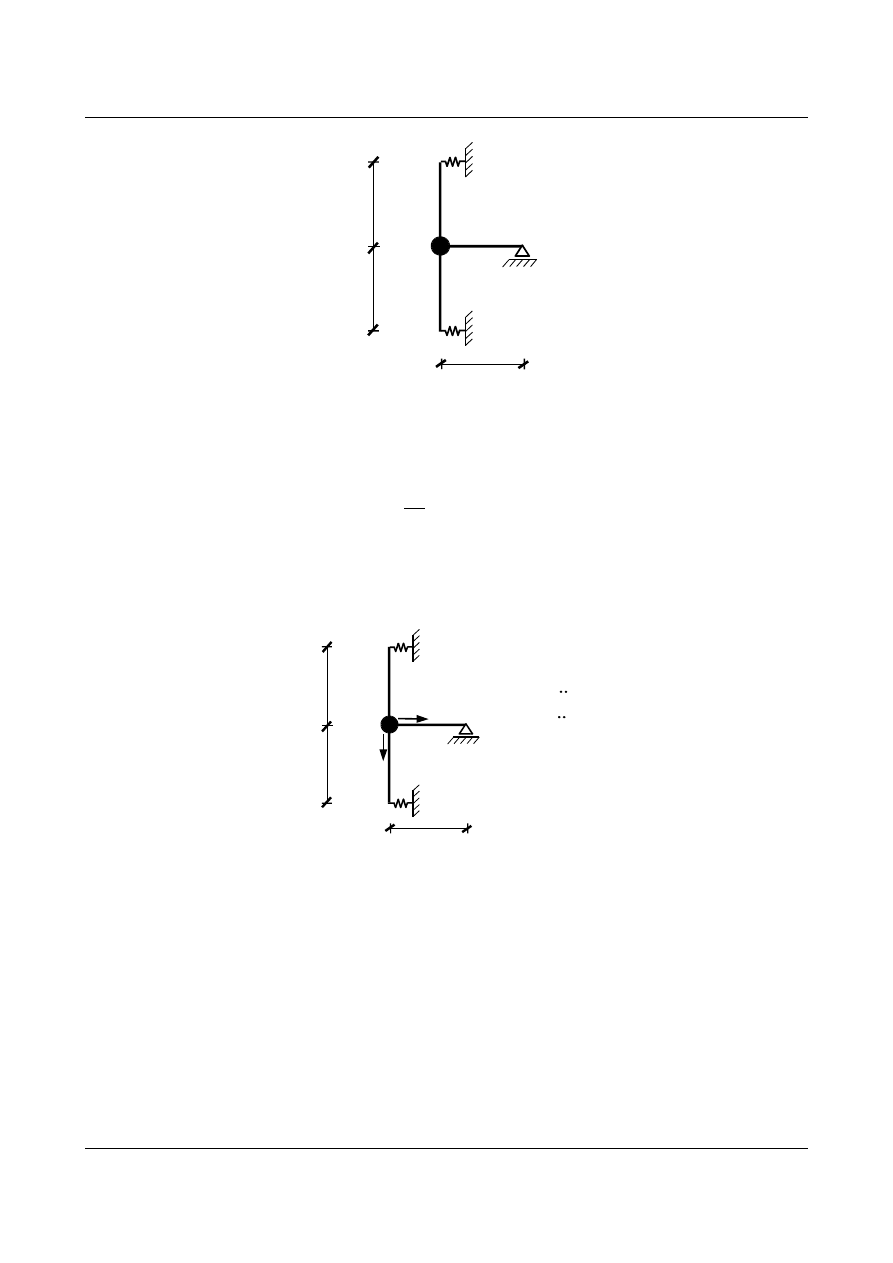
Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

5

k

k

m

3

3

3

[m]

Rys. 15.5. Rama obciążona masą skupioną

Parametry geometryczne i fizyczne układu są następujące:

EJ

=31000 kN m

2

k

=

EJ

4

m

=200 kg

Masa ma możliwość ruchu w dwóch kierunkach (

SSD = 2), ich kierunki i siły dynamiczne będące wynikiem

działania bezwładności masy przedstawiono na rys. 15.6.

k

k

m

3

3

3

B

2

= -mw

2

(t)

B

1

= -mw

1

(t)

w

1

, B

1

w

2

, B

2

[m]

Rys. 15.6. Układ obciążony dynamicznie

Funkcja rozwiązująca różniczkowe równanie ruchu dla drgań harmonicznych ma postać:

w

i

t=a

i

sin

t

¨w

i

t=−a

i



2

sin

 t

(15.8)

Wiemy, że na przemieszczenie w danym kierunku wpływ mają obie siły:

{

w

1

t =

11

B

1



12

B

2

w

2

t =

21

B

1



22

B

2

(15.9)

Po podstawieniu wyrażeń na siły bezwładności otrzymujemy układ równań różniczkowych:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

6

w

1

t =−m⋅¨w

1

t ⋅

11

−m⋅¨w

2

t ⋅

12

w

2

t =−m⋅¨w

1

t ⋅

21

−m⋅¨w

2

t ⋅

22

Wykorzystując funkcję (15.8) otrzymujemy:

{

a

1

sin

 t=

11

⋅m⋅a

1



2

sin

 t 

12

⋅m⋅a

2



2

sin

t 

a

2

sin

t=

21

⋅m⋅a

1



2

sin

 t

22

⋅m⋅a

2



2

sin

t 

(15.10)

Wyeliminowanie zmiennej czasu

t prowadzi do układu równań jednorodnych:

{



11

m



2

−1a

1



12

m



2

a

2

=0



21

m



2

a

1



22

m



2

−1a

2

=0

(15.11)

Dla ułatwienia obliczeń zastosujemy podstawienie:

=

EJ



2

m



ij

'

=

ij

EJ

(15.12)

Wówczas po przekształceniach mamy:

{



11

'

−a

1



12

'

a

2

=0



21

'

a

1



22

'

−a

2

=0

(15.13)

Jest to układ równań jednorodnych, który posiada rozwiązanie, gdy:

det

∣



11

'

−



12

'



21

'



22

'

−

∣

=0

(15.14)

Z warunku (15.14) otrzymujemy równanie charakterystyczne:



11

'

−

22

'

−−

12

'



21

'

=0

(15.15)

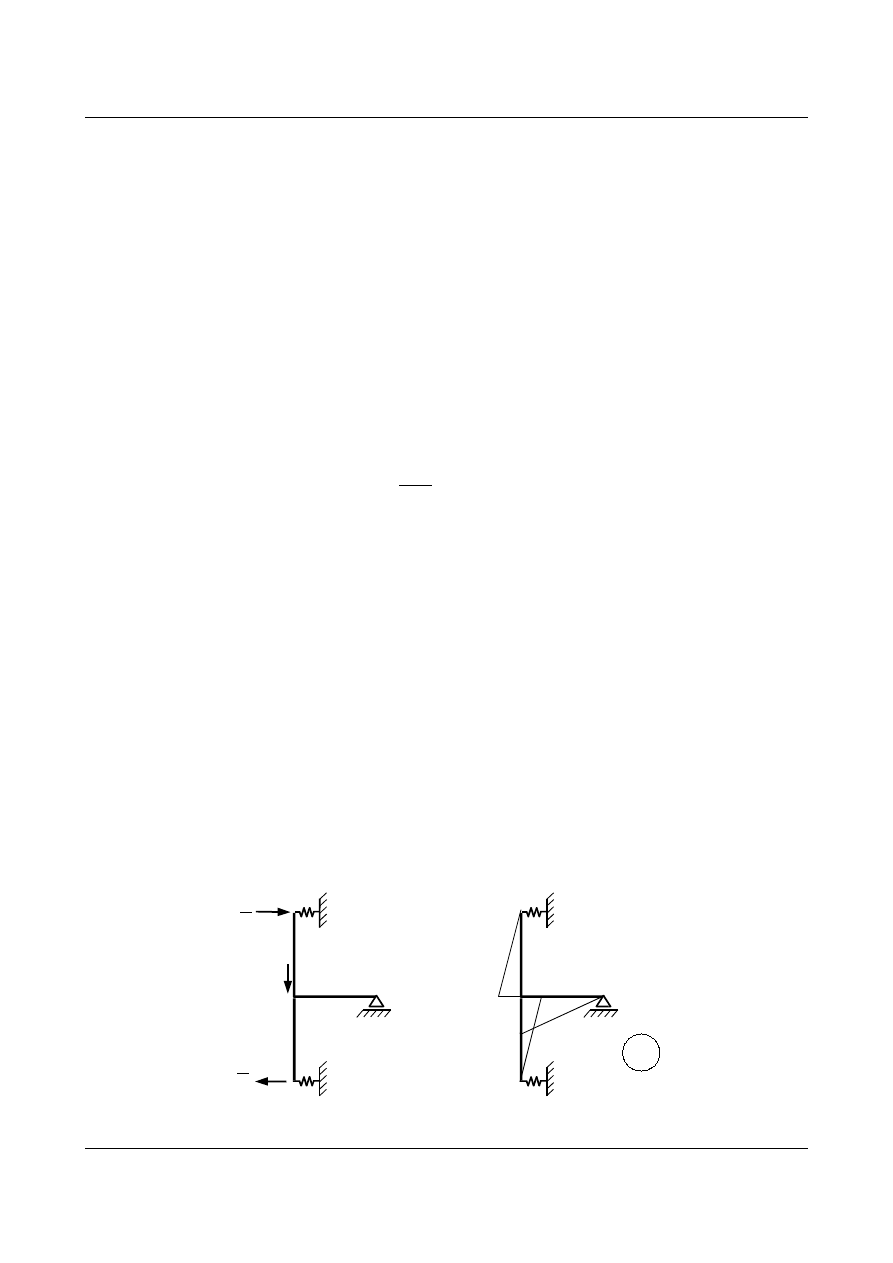
Teraz obliczymy współczynniki równania

δ

ik

, narysujmy więc wykresy od stanów jedynkowych:

B

1

= 1

1

2

1

2

1,5

1,5

3,0

M

1

Rys. 15.7. Obciążenie po kierunku pierwszym

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

7

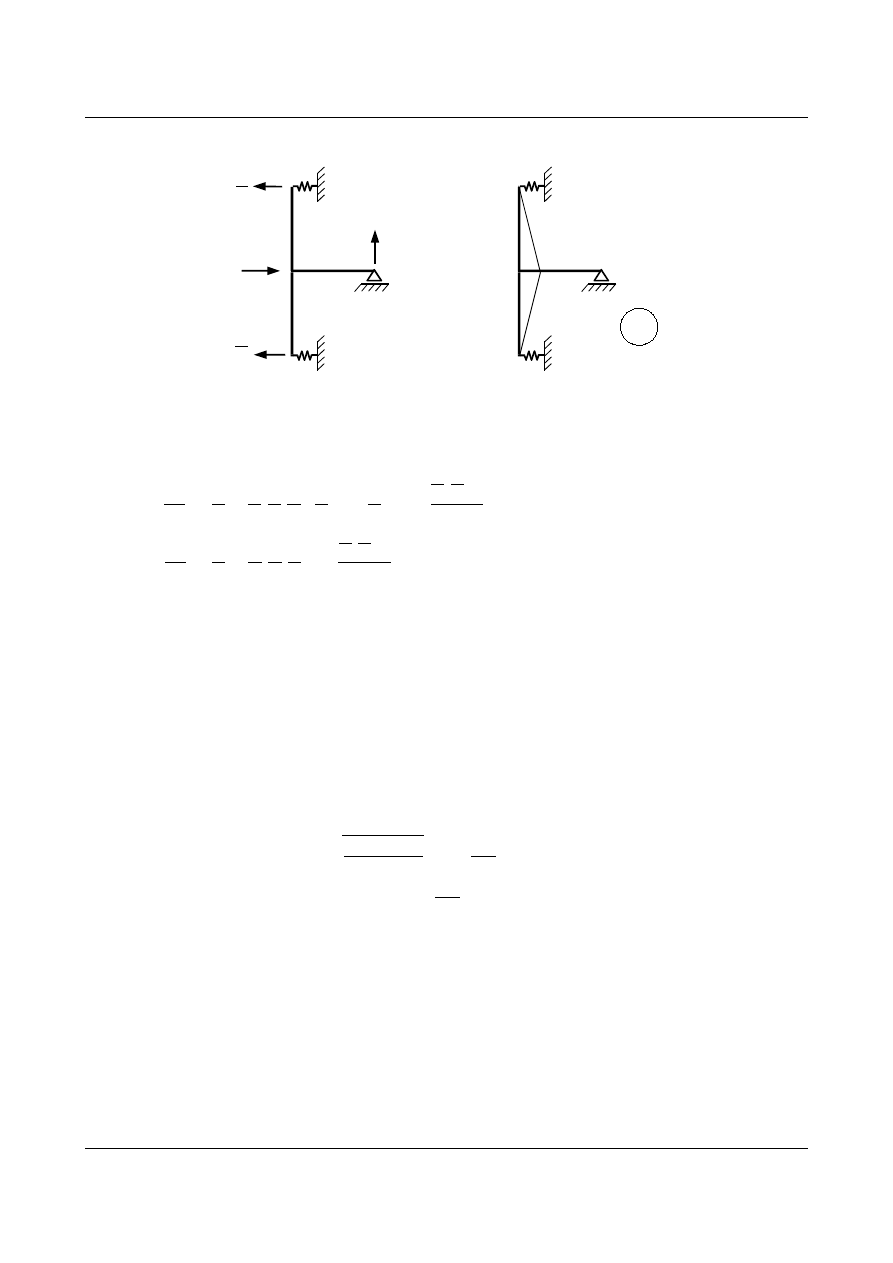
B

2

= 1

0

1
2

1
2

1,5

M

2

Rys. 15.8. Obciążenie po kierunku drugim

Na podstawie rys. 15.7 i 15.8 obliczamy współczynniki

δ

ik

:



11

=

1

EJ



2

⋅

1

2

⋅3 ⋅

3
2

⋅

2

3

⋅

3
2



1

2

⋅3 ⋅3 ⋅

2
3

⋅3



2 ⋅

1

2

⋅

1

2

⋅4

EJ





11

'

=EJ 

11

=15,5



22

=

1

EJ



2

⋅

1

2

⋅3 ⋅

3

2

⋅

2
3

⋅

3
2



2 ⋅

1

2

⋅

1

2

⋅4

EJ





22

'

=EJ 

22

=6,5



12

=0

Po podstawieniu do równania (15.15):

15,5 −6,5 −=0

(15.16)

Otrzymujemy dwa pierwiastki rzeczywiste:



1

=6,5



2

=15,5

(15.17)

z których wyliczmy częstości drgań własnych:



I

=



31000

⋅1000

15,5

⋅200

=100

[

rad

s

]



II

=154,422

[

rad

s

]

(15.18)

Ponieważ



12

=0 z układu (15.13) otrzymujemy dwa niezależne równania. Zmienne a

i

są rozprzężone dlatego

mając nawet wartości własne

 nie możemy stworzyć wektora własnego. Amplituda przemieszczenia a

1

może zmieniać się niezależnie od amplitudy

a

2

.

Przyjmując

a

1

= 1 otrzymujemy:

6,5 −15,5⋅a

2

=0

a

2

=0

i na odwrót dla

a

2

= 1 dostaniemy:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

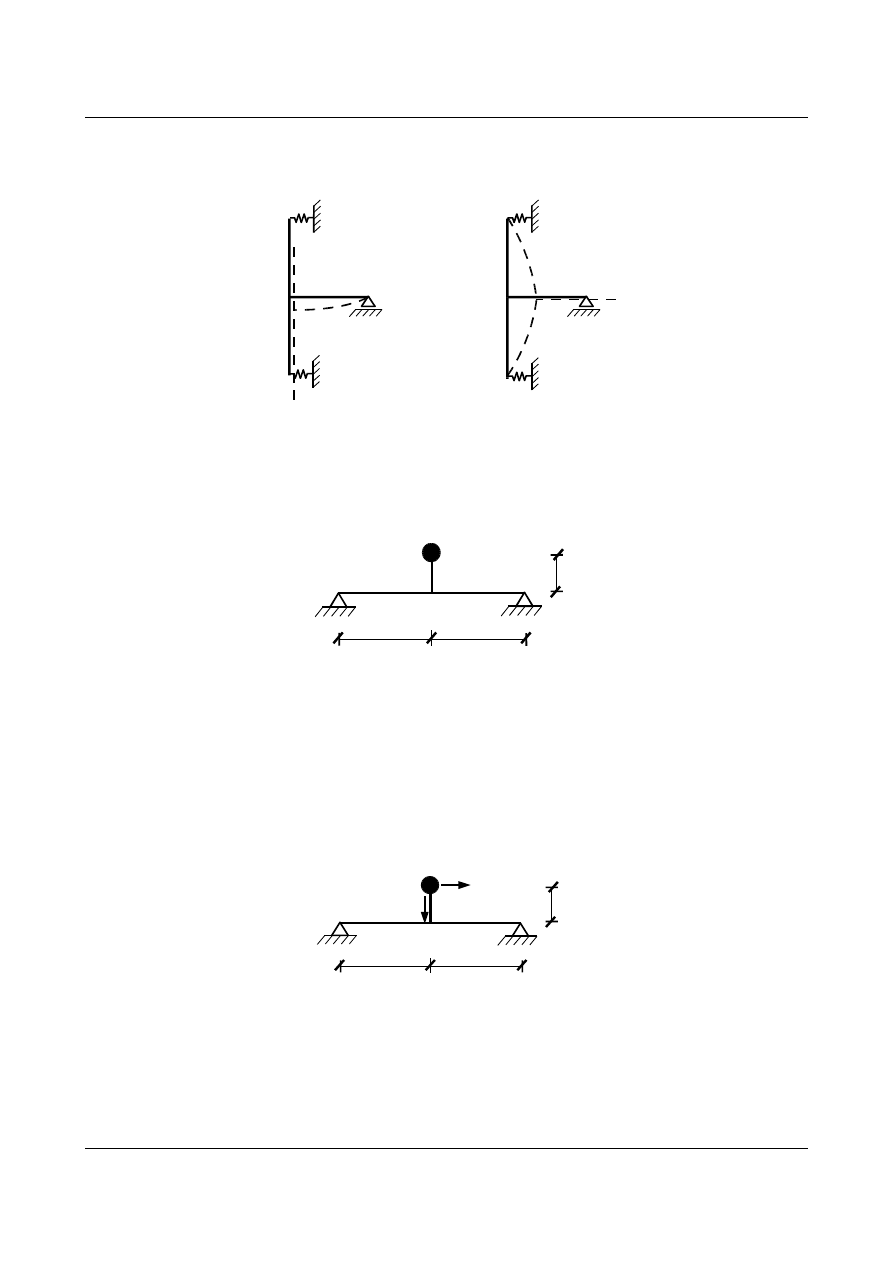
8

a

1

=0

Rys. 15.9. Postacie drgań

Zadanie 3

Znaleźć częstości kołowe drgań własnych i narysować ich postacie dla układu z jedną masą (rys. 15.10).

3

3

1

m

[m]

Rys. 15.10. Układ z jedną masą

W zadaniu przyjęto następujące wartości liczbowe:

EJ

=9000 kN m

2

m

=400 kg

W układzie o dwóch stopniach swobody dynamicznej przyjęto dwa prostopadłe do siebie kierunki
przemieszczeń (rys. 15.11).

w

1

, B

1

3

3

1

w

2

, B

2

[m]

Rys. 15.11. Kierunki stopni swobody dynamicznej

Podobnie jak poprzednio przyjęto funkcję opisującą przemieszczenia:

w

i

t =a

i

sin

 t

¨w

i

t =−a

i



2

sin

 t

(15.19)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

9

Do równań ruchu:

{

w

1

t =

11

B

1



12

B

2

w

2

t =

21

B

1



22

B

2

(15.20)

podstawiamy wyrażenia na siły bezwładności:

w

1

t =−m⋅¨w

1

t ⋅

11

−m⋅¨w

2

t⋅

12

w

2

t =−m⋅¨w

1

t ⋅

21

−m⋅¨w

2

t ⋅

22

Równania różniczkowe rozwiązujemy przyjmując postać funkcji rozwiązującej (15.19):

{

a

1

sin

 t=

11

⋅m⋅a

1



2

sin

 t 

12

⋅m⋅a

2



2

sin

t 

a

2

sin

t=

21

⋅m⋅a

1



2

sin

 t 

22

⋅m⋅a

2



2

sin

t 

(15.21)

{



11

m



2

−1a

1



12

m



2

a

2

=0



21

m



2

a

1



22

m



2

−1a

2

=0

(15.22)

Po wprowadzeniu symboli zastępczych:

=

EJ



2

m



ij

'

=

ij

EJ

(15.23)

mamy:

{



11

'

−a

1



12

'

a

2

=0



21

'

a

1



22

'

−a

2

=0

(15.24)

Układ równań jednorodnych posiada rozwiązanie, gdy:

det

∣



11

'

−



12

'



21

'



22

'

−

∣

=0

(15.25)

To prowadzi do równania charakterystycznego:



11

'

−

22

'

−−

12

'



21

'

=0

(15.26)

Aby obliczyć współczynniki podatności

δ

ik

, narysujmy wykresy od stanów jedynkowych:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

10

1

1

M

2

M

1

3
2

1

2

1

1

2

Rys.15.12. Wykresy momentów od obciążeń jednostkowych

Na podstawie rys. 15.12 obliczamy współczynniki

δ

ik

:



11

=

1

EJ



2

⋅

1

2

⋅3 ⋅

3

2

⋅

2
3

⋅

3
2







11

'

=EJ 

11

=4,5



22

=

1

EJ



2

⋅

1

2

⋅3 ⋅

1

2

⋅

2
3

⋅

1

2



1

2

⋅1 ⋅1 ⋅

2
3

⋅1







22

'

=EJ 

22

=0,83



12

=0

I podstawiamy do równania (15.26):

4,5−0,83−=0

(15.27)

otrzymujemy:



1

=4,5



2

=0,83

Stąd częstość drgań własnych:



I

=



9000

⋅1000

4,5

⋅400

=70,7107

[

rad

s

]



II

=



9000

⋅1000

0,83

⋅400

=164,3167

[

rad

s

]

(15.28)

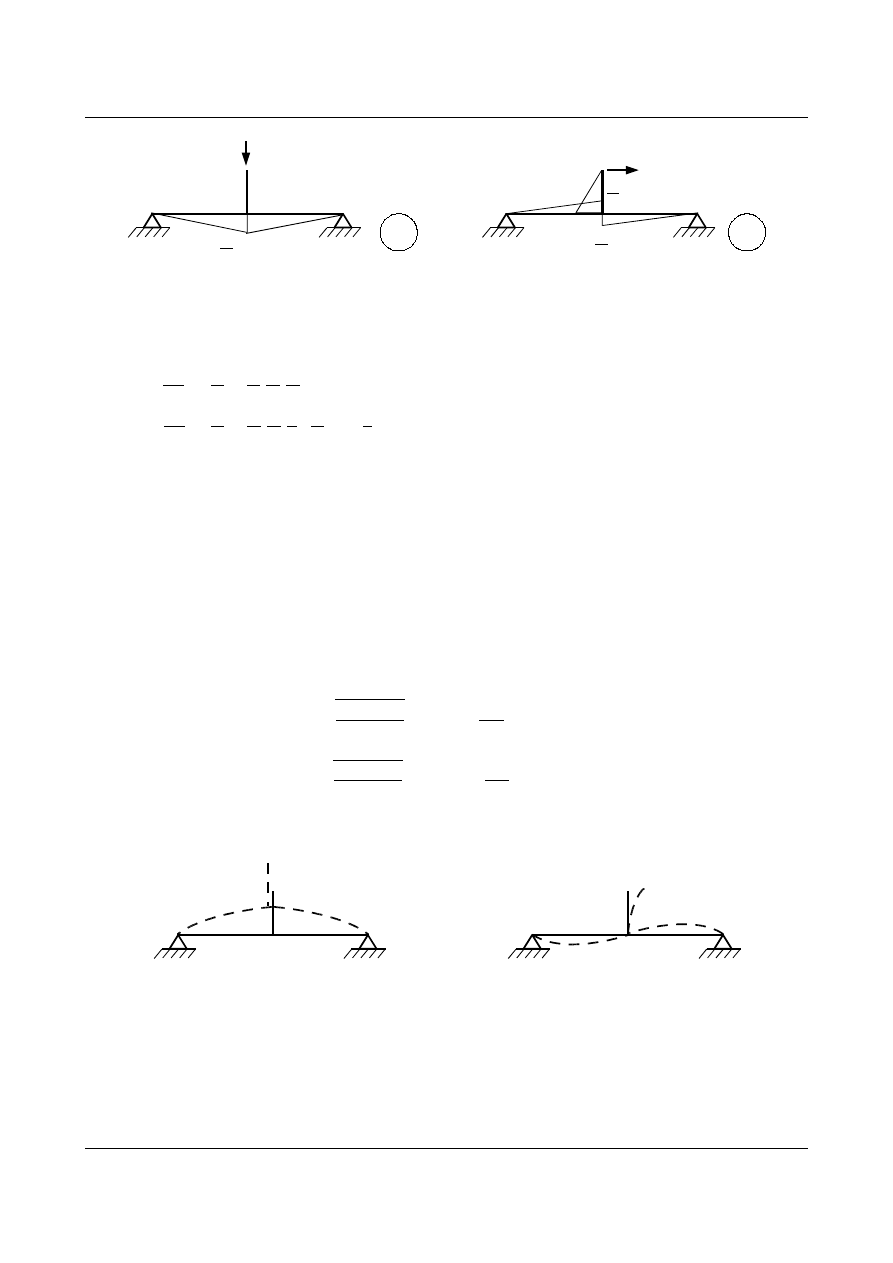
Postacie drgań własnych dla rozprzężonych amplitud przemieszczeń przedstawiono na rys. 15.13.

a

1

≠0

a

2

=0

a

1

=0

a

2

≠0

Rys. 15.13. Postacie drgań

Zadanie 4

Sprawdzić czy dla układu z rys. 15.14 możliwe jest dobranie takiej wartości współczynnika

k, aby drgania

uległy rozprzężeniu. Jeżeli tak, to określić wartość sztywności

k podpory podatnej.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

11

k

m

6

3

[m]

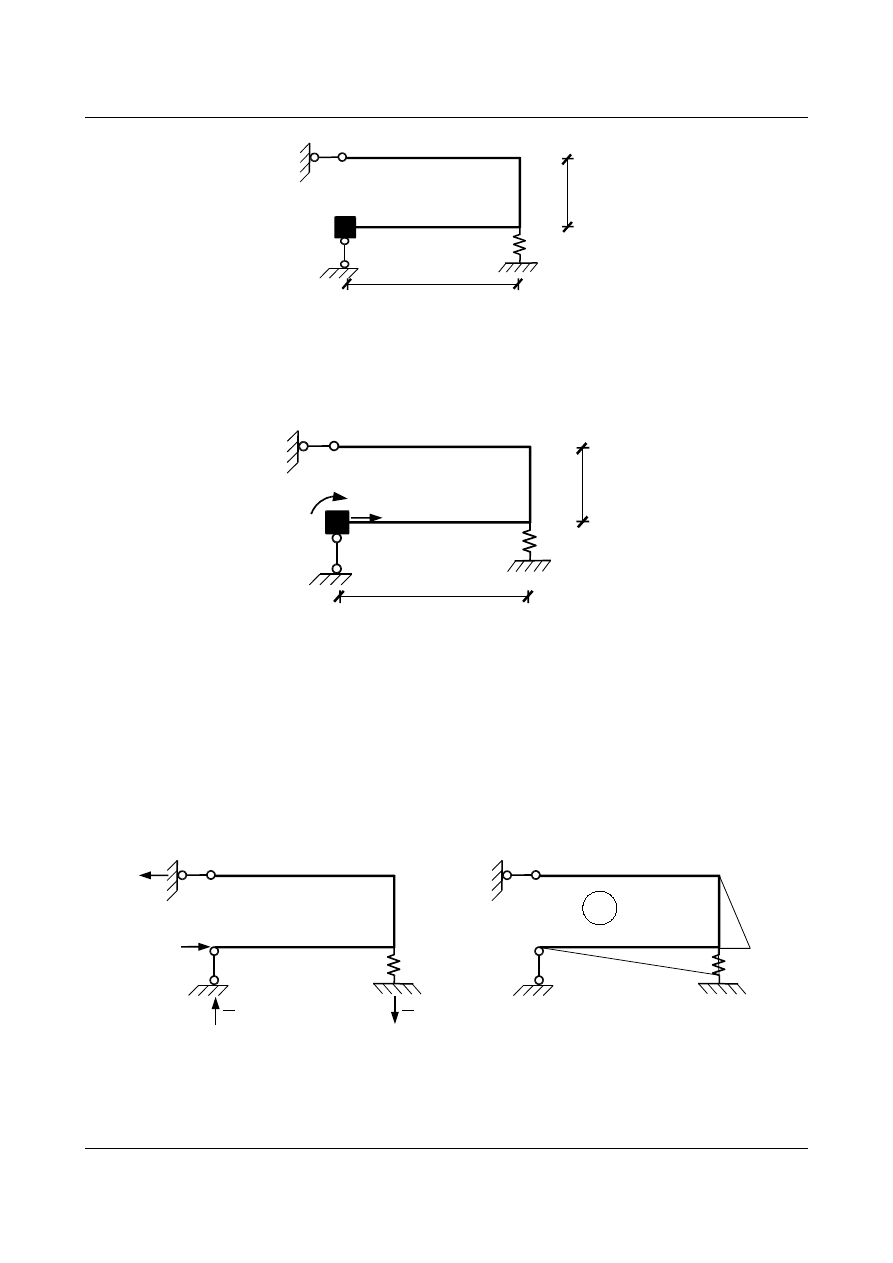
Rys. 15.14. Rama obciążona masą

Układ ma dwa stopnie swobody dynamicznej przemieszczenie liniowe i kątowe.

Masa może przemieszczać się tylko w poziomie, ale z uwagi na gabaryty może też się obracać. Mamy do
czynienia z bezładnością liniową i kątową.

k

m

6

3

w

1

, B

1

w

2

, B

2

[m]

Rys. 15.15. Kierunki swobody dynamicznej

B

1

=−m ¨w

1

B

2

=− J

0

¨w

2

(15.29)

gdzie:

[kg /m

2

]

to rozkład masy,

J

0

[m

4

]

to moment bezwładności obrotowej.

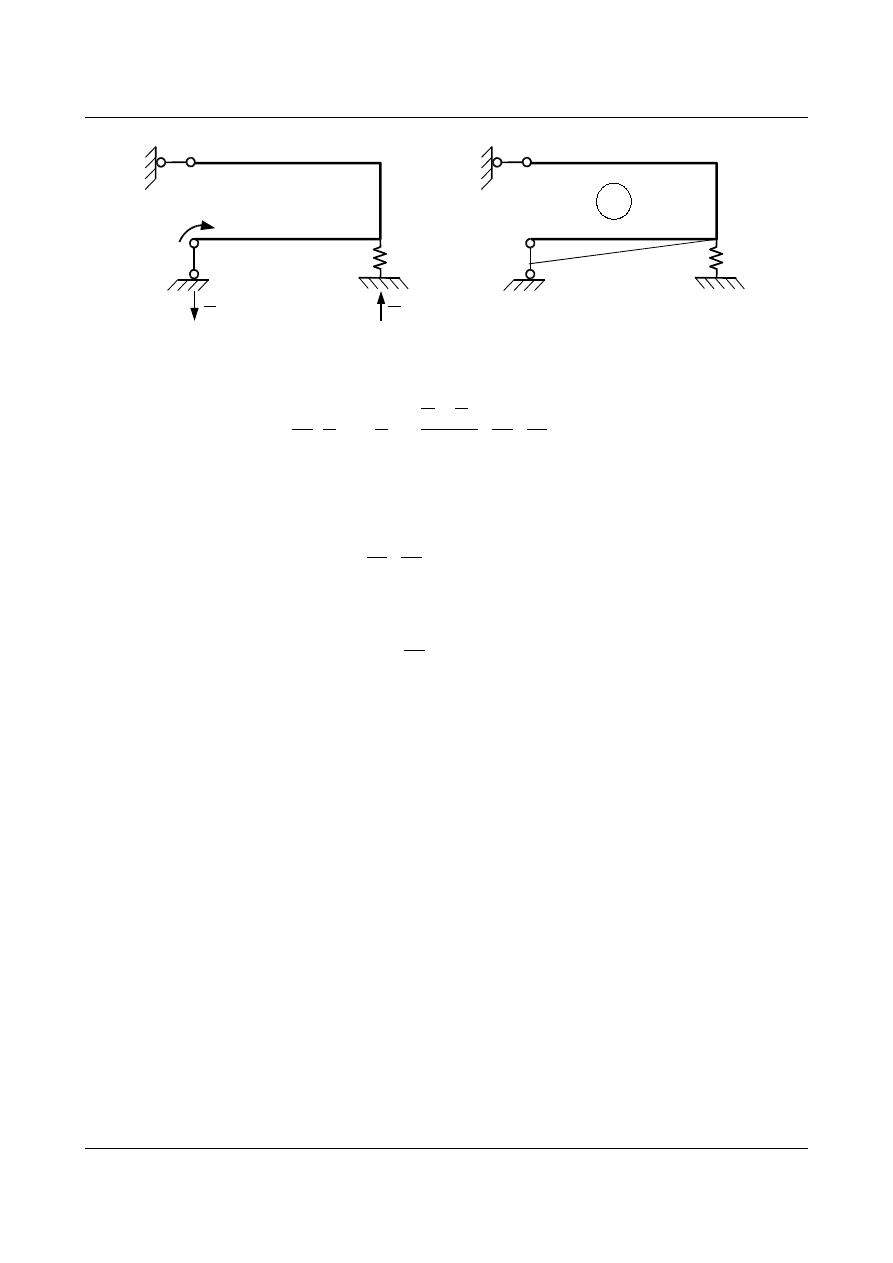
Do wyznaczenia współczynników podatności potrzebne są wykresy momentów (rys. 15.16, rys. 15.17)

B

1

=1

1

1

2

1
2

3

M

1

Rys. 15.16. Obciążenie jednostkowe po kierunku pierwszym

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

15. DRGANIA WŁASNE RAM – OBLICZANIE CZĘSTOŚCI KOŁOWYCH...

12

B

2

=1

1

2

1

2

1

M

2

Rys. 15.17. Obciążenie jednostkowe po kierunku drugim



12

=

1

EJ



1

2

⋅6 ⋅3 ⋅

2

3

⋅1





1

2



−

1

2



k

=

6

EJ

−

1
4 k

Aby drgania uległy rozprzężeniu w układzie równań ruchu (15.13) współczynnik



12

'

powinien być równy

zero. Stąd otrzymujemy zależność:

6

EJ

−

1

4 k

=0

z której wynika poszukiwana wartość parametru

k :

k

=

EJ

24

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater