Wykład I

1. Pojęcie algorytmu

Definicja nieformalna

Algorytmem jest pewna ściśle określona procedura obliczeniowa, która dla właściwych

danych wejściowych „produkuje” żądane dane wyjściowe zwane wynikiem działania
algorytmu.

Inne definicje:
Algorytm to

−

ciąg kroków obliczeniowych prowadzących do przekształcania danych wejściowych w
dane wyjściowe;

−

skończony ciąg reguł, które aplikuje się na skończonej liczbie danych, pozwalający
rozwiązywać zbliżone do siebie klasy problemów;

−

zespół reguł charakterystyczny dla pewnych obliczeń lub czynności.

Źródłosłów:

Perski pisarz – matematyk Abu Jafar Mohammed ibn Musa al-Khowarizmi

( IXw n.e.)

−

podał regułę wyjaśniającą krok po kroku zasady operacji arytmetycznych na liczbach
dziesiętnych;

−

po łacinie jego nazwisko brzmi: Algorismus.

Słowo algorytm często jest również kojarzone z greckim matematykiem Euklidesem (365-

300 p.n.e.), który przedstawił m.in. sformalizowane algorytmy:

•

dzielenia kąta na połowy;

•

badania identyczności dwóch kątów;

•

obliczania Największego Wspólnego Podzielnika tzw. NWP dwóch liczb
naturalnych.

Algorytmy stworzone przez Euklidesa wykorzystywały w swoich działaniach elementarne

operacje, które mogły być wykonane w sposób jednoznaczny, tzn.

−

dla algorytmów geometrycznych były to operacje typu prosta – okrąg, wykonywane
przy pomocy cyrkla i linijki;

−

dla algorytmów obliczeniowych (numerycznych) były to operacje arytmetyczne: +, -, *, /
oraz porównywania.

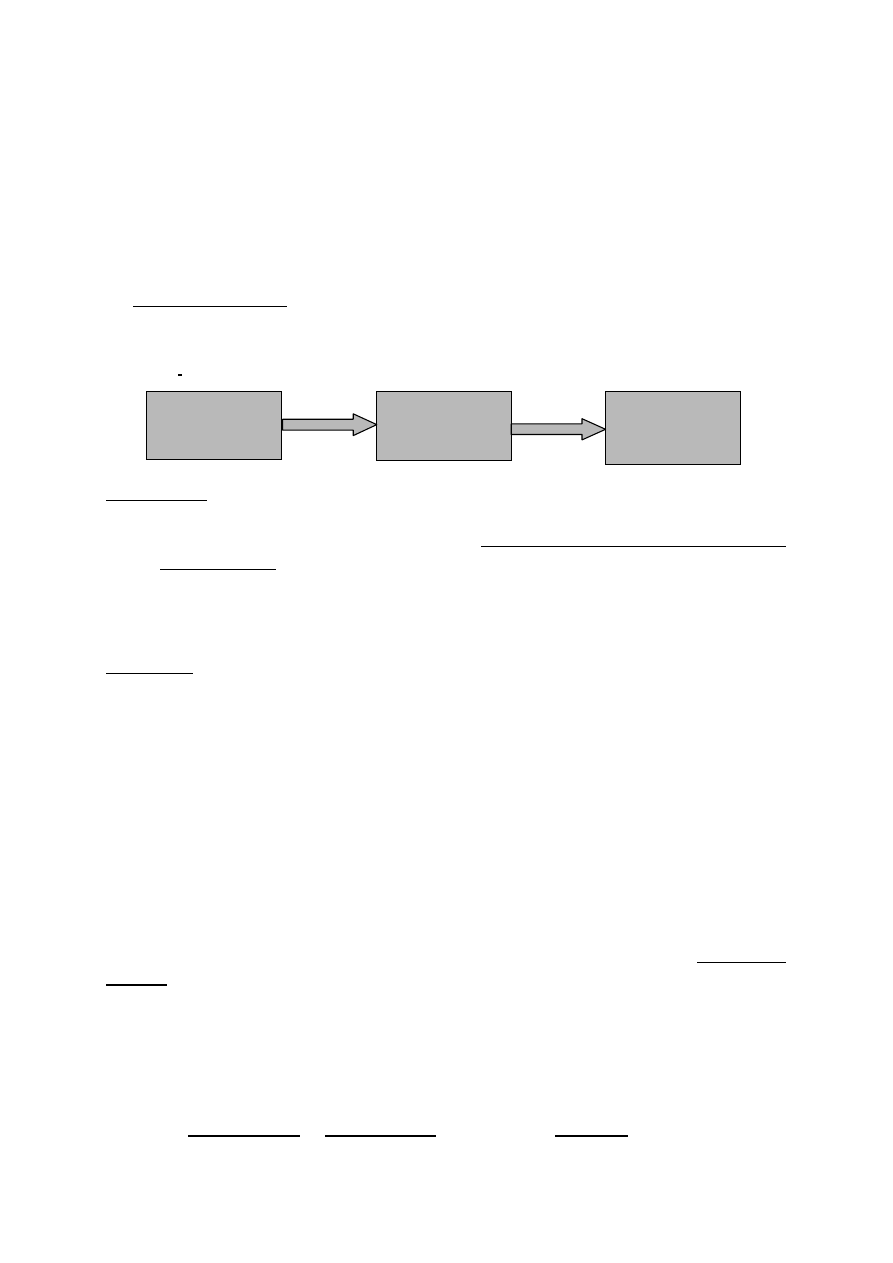
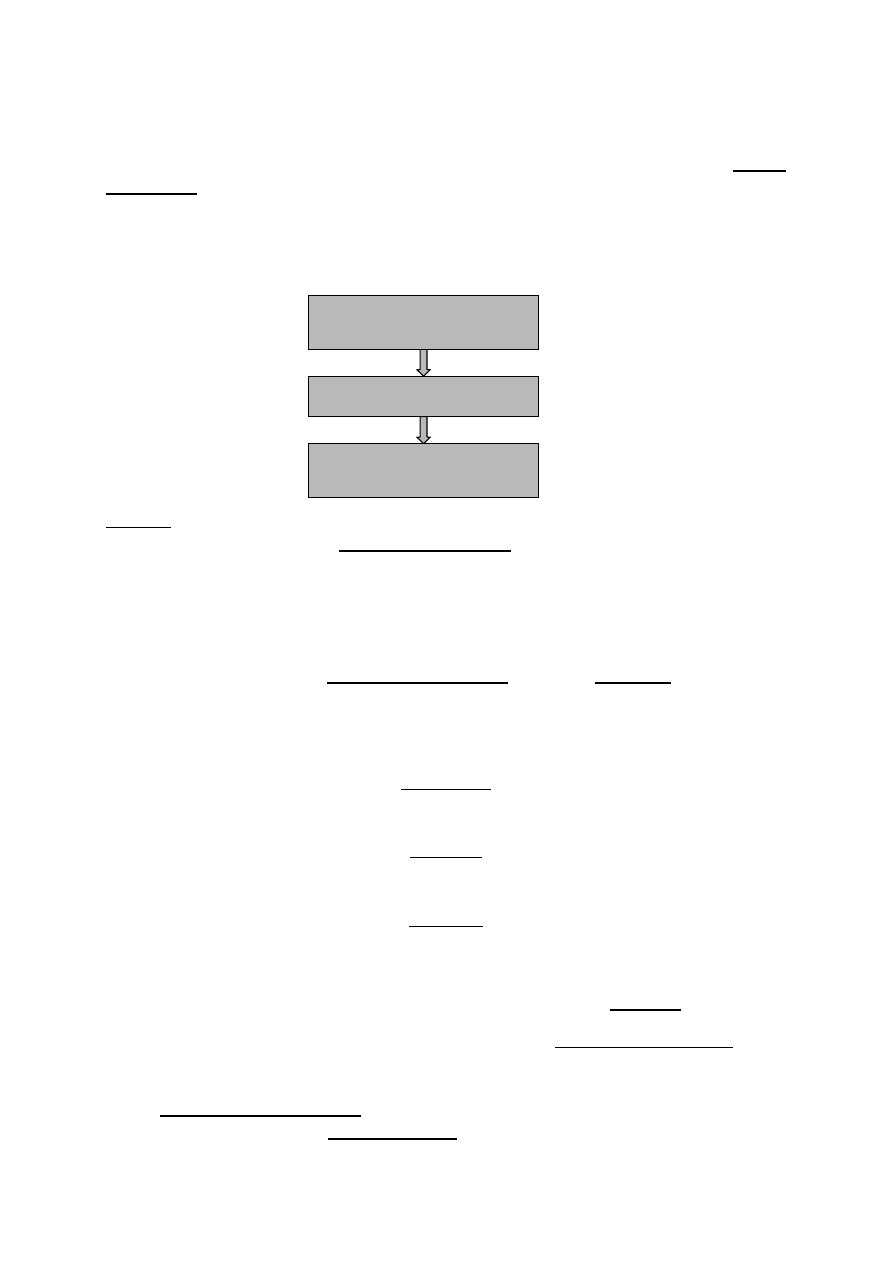
Nas interesować będą algorytmy w kontekście informatycznym, tzn. przekształcające

efektywnie dane wejściowe na dane wyjściowe zwane również wynikiem.

Dane

wejściowe

Algorytm

Dane

wyjściowe

Cechy algorytmu informatycznego:

!

posiada dane wejściowe, które pochodzą z dokładnie określonego zbioru, np. ze
zbioru liczb naturalnych N, ze zbioru liczb rzeczywistych R;

!

produkuje pewien wynik (niekoniecznie numeryczny);

!

jest precyzyjnie zdefiniowany, tzn. każdy jego krok jest jednoznacznie określony i
obejmuje wyłącznie operacje elementarne;

!

jest skończony, tzn. w skończonym czasie wyprodukuje wynik, a czas jego działania
powinien być możliwie precyzyjnie określony;

!

jest jednoznaczny ( inaczej powtarzalny), tzn. jego wielokrotne wykonywanie dla
identycznych danych wejściowych daje zawsze taki sam wynik;

!

jest kompletny, tzn. uwzględnia wszystkie możliwe przy-padki, jakie mogą wystąpić
podczas jego wykonywania;

!

jest uniwersalny, tzn. umożliwia rozwiązanie całej klasy zadań, a nie tylko
pojedynczego, ustalonego zadania.

Formy przedstawiania algorytmu informatycznego

!

opis słowny, zazwyczaj z formułami matematycznymi

!

schemat graficzny

•

schematy blokowe czyli ciągi znormalizowanych symboli graficznych
połączonych skierowanymi liniami

•

strukturogramy czyli graficzne schematy zwarte

!

specjalne języki matematyczne zwane pseudokodami

!

języki programowania wyższego poziomu np. PASCAL, Fortran, C, BASIC, ADA,
Simula, itp.

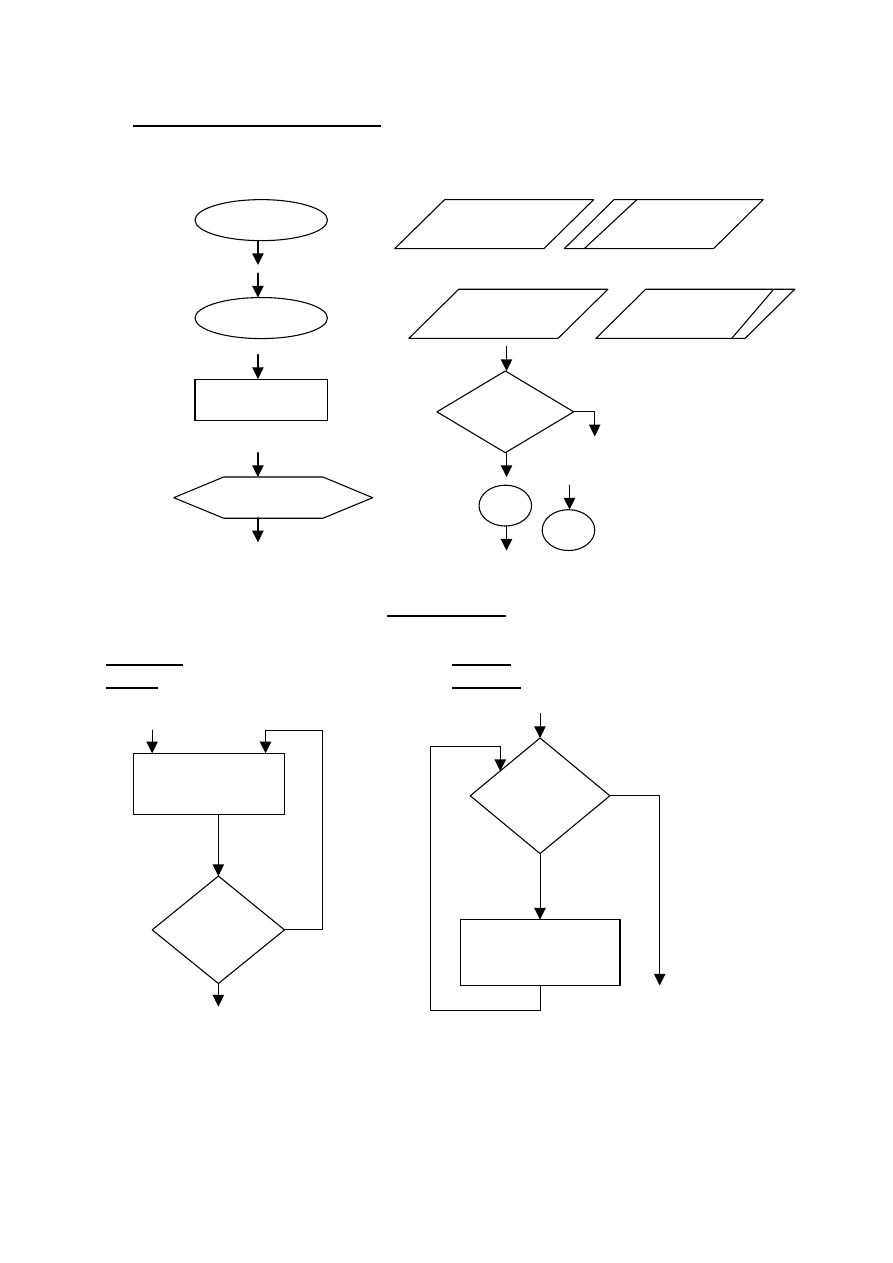
Schematy blokowy – lista bloków

Tzw. schematy Bohma – Jacopiniego.

Bloki iteracyjne

Powtarzaj <ciąg czynności>
dopóki <warunek>

Dopóki <warunek>
wykonuj <ciąg czynności>

początek

koniec

x=x

⋅

y

dla i=1 do n

wprowadzić

a,b,c

pisz
„Brak danych”

WE

W4

warunek

Blok decyzyjny

1

2

Bloki

łącznikowe

Blok

iteracyj

Blok

operacy

Blok

końca

Blok
począ

tk

Tak

Nie

Ciąg czynności

warunek

Tak

Nie

Ciąg czynności

warunek

Tak

Nie

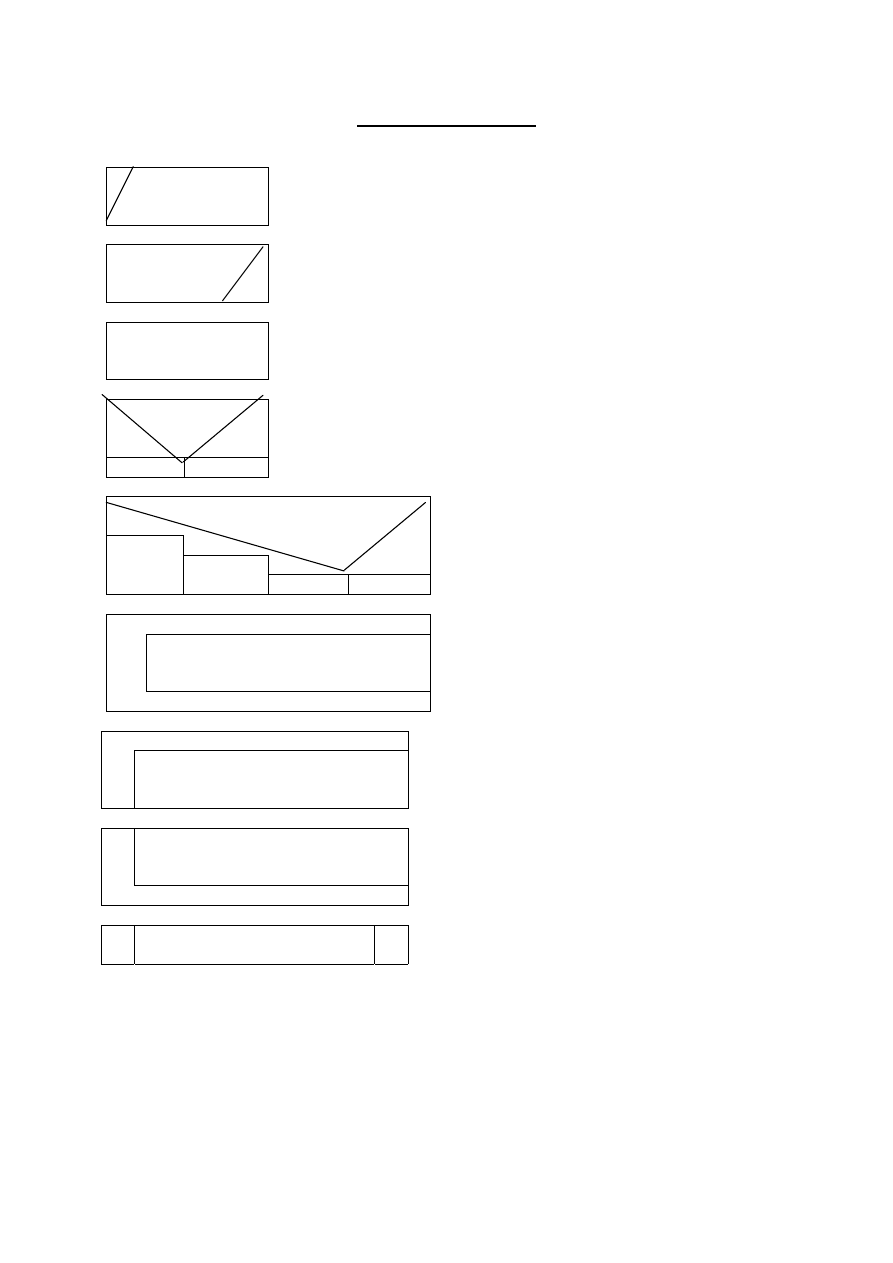
Strukturogramy zwarte

(Diagramy Nassi - Shnaeidermana)

A

Blok wejścia (klawiatura, plik)

A

Blok wyjścia (monitor, drukarka, plik)

Operacja

Blok operacyjny

Warunek

tak

nie

Blok 1

Blok 2

Blok decyzyjny

wyrażenie

W1

W2

W3

Inaczej

Blok 1

Blok 2

Blok 3

Blok

Blok wyboru z szeregu możliwości

i=1,m

Blok - treść pętli

Pętla - cykliczne wykonanie bloku dla 1,...,m

warunek

blok

pętla typu
dopóki <warunek> wykonuj <blok>

blok

warunek

pętla typu
powtarzaj <blok> aż do <warunek>

nazwa algorytmu

blok procedury
(odrębnego, nazwanego fragmentu algorytmu)

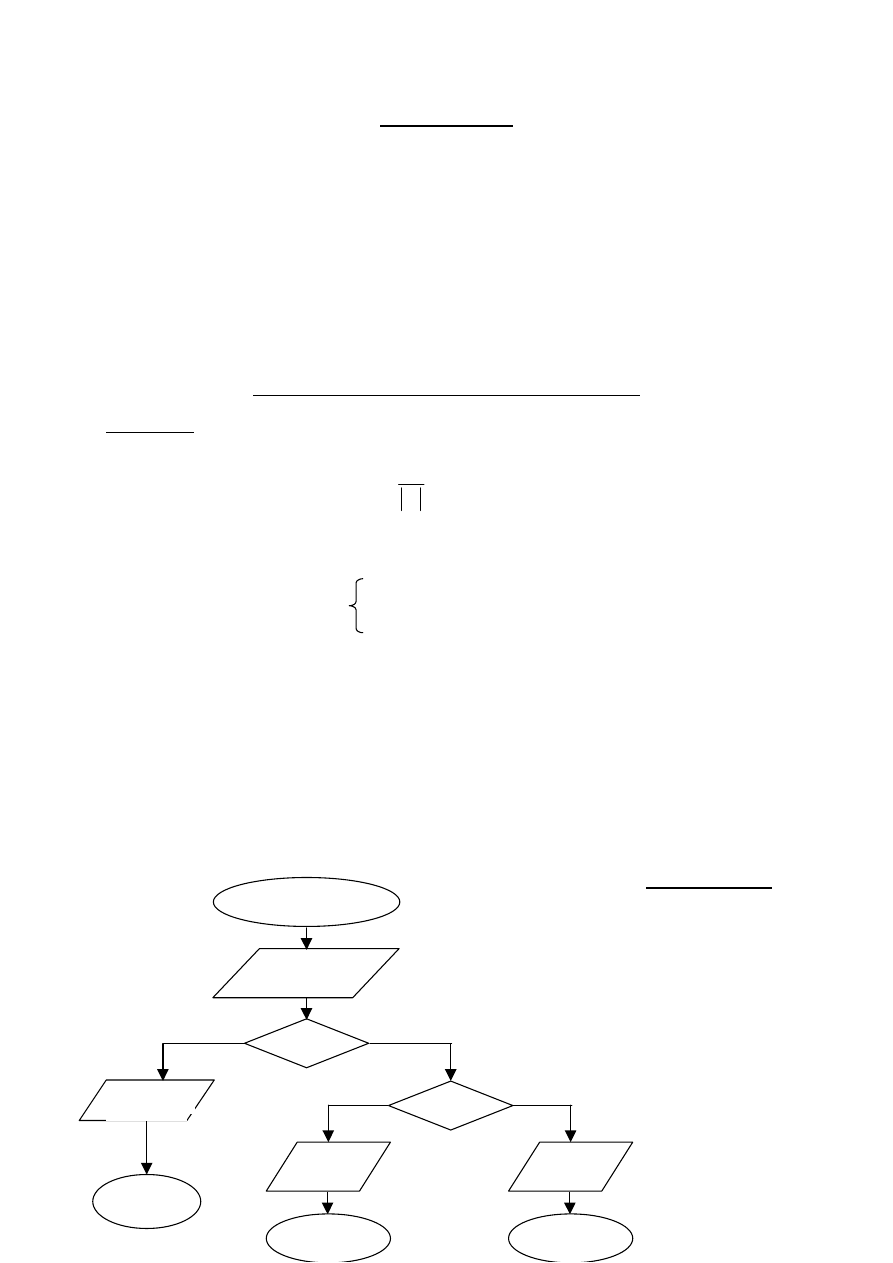
Typy algorytmów

Z punktu widzenia organizacji wykonywanych czynności (obliczenia, rysowanie,

porównywanie) rozróżniamy trzy podstawowe typy algorytmów:

!

liniowy (sekwencyjny): wszystkie czynności są wykonywane w ściśle określonej
kolejności, jedna za drugą;

!

z rozgałęzieniami (selekcja): kolejność i zakres wykonywanych czynności zależy od
warunków, których spełnienie (lub niespełnienie) zależy od danych wejściowych oraz
pewnych wyników pośrednich;

!

iteracyjny (pętla): pewien ciąg identycznych czynności (tzw. cykl lub pętla) jest
powtarzalny wielokrotnie dla różnych danych.

Przykłady różnych form przedstawienia algorytmu.

Opis słowny
Problem: Oblicz wartość funkcji:

x

x

f(x)

=

Dane : dowolna liczba rzeczywista x

∈

R

Wynik: wartość funkcji f(x) określona jest wzorem:

Algorytm:

krok 0:

Podaj wartość danej x

krok 1: Jeśli x>0, to f(x)=1.

Zakończ algorytm

krok2:

Jeśli x=0, to f(x)=0

{

}

0

x

Dla

<=

Zakończ algorytm

krok 3:

Mamy f(x)=-1.

{

}

0

x

Dla

<

Zakończ algorytm

Schemat blokowy

-1 dla x<0

f(x)=

0 dla x=0
1 dla x>0

początek

x=0

TAK

NIE

NIE

TAK

x<0

podaj x

wynik =

koniec

koniec

koniec

wynik = 1

wynik = 0

wynik=-

1

Koniec

Zapis w pseudokodzie :

Funkcja f(x)
początek

wczytanie x
jeżeli x>0 to pisz f(x)=1
w przeciwnym razie

jeżeli x=0 to pisz f(x)=0
w przeciwnym razie pisz f(x)= -1

koniec

Program w języku Turbo Pascal

PROGRAM funkcja;
VAR x: Real;
BEGIN

READ (x);
IF x>0 THEN WRITE(1)

ELSE IF x=0 THEN WRITE(0)

ELSE WRITE(-1);

END.

Kilka faktów z historii algorytmiki

W rozwoju algorytmiki można wskazać kilka istotnych dat oraz osób, które są ważnymi

punktami zwrotnymi:

1801 -

Francuz Joseph Marie Jacquard
- konstrukcja krosna tkackiego „programowanego” przez kartę perforowaną

1833 -

Anglik Charles Babbage
- konstrukcja maszyny do wyliczania pewnych formuł matematycznych

1890 -

Amerykanin Herman Hollerith
- maszyna do opracowywania danych statystycznych (spisy ludności)
1911 – powstała IBM

1930 -

badania teoretyczne
Allan Turing, Carl Gődel, Markov

1940 -

pierwsze maszyny liczące: MARK1, ENIAC
EDVAC: pierwszyy prawdziwy komputer
- koncepcja Johannesa von Neumanna
program jako dane w pamięci komputera

lata 60-te - pierwsze duże systemy informatyczne (COBOL, ALGOL)

- początki metodologii: intuicja, wyczucie prowadziły do wielu błędów, małej
wiarygodności; potrzebne były duże nakłady na wdrożenie i dalszy rozwój

- brak metod na sprawdzanie poprawności oprogramowania (jedynie testowanie do
pełnego wyeliminowania błędów).

Impulsem w kierunku przejścia od sprawdzania poprawności programów komputerowych

metodą prób i błędów do udowadniania, że posiada on pożądane własności (czyli jest poprawny)
był artykuł Johna McCarthyego „A basis for a mathematical theory of computation”. Innymi
teoretykami byli: Dijkstra, Hoare, Floyd, Writh.

2. Podstawowe zasady analizy algorytmów

Układając algorytmy (programy) staramy się poznać ich własności. Chcemy wiedzieć

między innymi:

!

czy ułożony algorytm jest rzeczywiście rozwiązaniem postawionego problemu;

!

czy przeznaczony czas pracy komputera jest wystarczający

!

czy ilość miejsca w pamięci jest wystarczająca

!

jakie będą skutki po dokonaniu pewnych zmian w algorytmie, czy zmiany te nie
zmienią wyników

!

czy będzie działał dla każdej możliwej konfiguracji danych wejściowych.

Te i inne problemy spowodowały powstanie działu informatyki o nazwie Analiza

algorytmów, którego podstawowym zadaniem jest szukanie najlepszych algorytmów. Szukanie
to sprowadza się do znalezienia odpowiedzi na następujące trzy pytania:

Pytanie 1

Czy dany problem MOŻE BYĆ rozwiązany na komputerze w dostępnym czasie i dostępnej
pamięci?

Pytanie 2

Który ze znanych algorytmów jest najlepszy (ogólnie i dla konkretnego zestawu danych
wejściowych); czy jest on algorytmem optymalnym?

Pytanie 3

Jak udowodnić, że wybrany algorytm rozwiąże dany problem?

Analizując więc algorytmy należy zwrócić uwagę na jego :

!

poprawność semantyczną, czyli czy wykonuje on postawione zadania;

!

prostotę;

!

czas działania;

!

ilość zajmowanej pamięci;

!

optymalność.

Przedstawione teraz będą metody analizy algorytmów, które są pomocne przy znajdowaniu

odpowiedzi na postawione wyżej pytania 1, 2 i 3.

A. Poprawność semantyczna,czyli algorytm rozwiąże postawione zadanie

Powiedzieliśmy wcześniej, że działanie algorytmu (oznaczmy go literą K ), zależy od

wartości początkowych otrzymanych z zewnątrz, czyli od tzw. danych wejściowych (α).

Np. - dla algorytmu obliczającego NWP(m,n) będą to dwie liczby naturalne m oraz n .

- dla algorytmu znajdującego największy element w ciągu liczbowym (a

1

, ..., a

n

),

będą to elementy tego ciągu oraz liczba n oznaczająca długość ciągu.

Natomiast wartości, które algorytm przekazuje na zewnątrz nazywane są danymi

wyjściowymi (β) lub wynikiem algorytmu.

Np. - algorytm NWP(m,n) powinien podać jako wynik wartość największego wspólnego

podzielnika liczb m i n.

Mamy więc następujący układ:

Definicja

Mówimy, że algorytm K jest semantycznie poprawny względem warunków początkowego α
i końcowego β, jeżeli:

−

dla każdych danych wejściowych spełniających warunek α obliczenia algorytmu K
dochodzą do punktu końcowego;

−

końcowe wartościowanie zmiennych spełnia warunek β.

Przyjmujemy, ze: algorytm semantycznie poprawny

≡

algorytm

poprawny.

Odwracając zagadnienie, postawmy pytanie:

Kiedy algorytm jest niepoprawny ?.

Odpowiedzi mogą być również trzy:

Po pierwsze:

albo dochodzi do końca, ale wyniki nie spełniają warunku końcowego β
(źle liczy)

Po drugie:

albo zatrzymuje się w punkcie niekońcowym algorytmu
(zawiesza się)

Po trzecie:

albo obliczenia algorytmu są nieskończone
(zapętla się).

Co więc trzeba wykazać, żeby stwierdzić, że analizowany algorytm jest poprawny?

Wystarczy pokazać, że dla każdych danych wejściowych spełniających warunek α ma on

trzy następujące własności:

1) jeżeli obliczenie algorytmu K dochodzi do punktu końcowego, to otrzymane wyniki

spełniają warunek końcowy β;

2) obliczenie algorytmu K nie jest przerwane;

warunek początkowy

α

(dane wejściowe)

Algorytm K

warunek końcowy

β

(dane wyjściowe

)

3) obliczenie algorytmu K nie jest nieskończone.

Czy zawsze te wszystkie trzy warunki są jednocześnie spełnione?

Jeżeli dla algorytmu K spełniony jest tylko warunek:

Pierwszy " to algorytm K jest

częściowo poprawny względem warunku początkowego α i warunku końcowego β;

Drugi " to algorytm K ma

własność określoności obliczeń względem warunku początkowego α;

Trzeci " to algorytm K ma

własność stopu względem warunku początkowego α..

B. Metoda niezmienników

Metoda niezmienników:

!

służy do dowodzenia poprawności algorytmów

!

polega na opisywaniu własności wartościowań zmiennych otrzymywanych, gdy
obliczenie algorytmu przechodzi przez jego wyróżnione punkty ;własności te
nazywane są właśnie niezmiennikami algorytmu.

Przykład

Rozwazmy algorytm dzielenia całkowitego liczb naturalnych. Jego sformułowanie jest

następujace:

Dla dwóch liczb naturalnych x, y znaleźć dwie liczby naturalne q oraz r takie, że:

r

y

+

∗

=

q

x

gdzie

q - iloraz całkowity dzielenia x przez y
r - reszta z tego dzielenia.

Np. dla x=11, y=4 mamy 11 = 2 * 4 + 3

czyli q=2 oraz r=3

Zapis algorytmu w pseudokodzie:

początek

{

}

y

0

x

0

:

≤

∧

≤

α

1: q:=0 ; r:=x ;
2: dopóki y<=r wykonuj

początek

q:=q+1 ; r:=r-y

koniec;

3:

{

}

y

<

≤

∧

+

∗

=

r

0

r

y

q

x

:

β

koniec;

Mamy więc:

Warunek początkowy α : 0<=x

∧

0<=y

Warunek końcowy β : x=q*y+r

∧

0

≤

r<y

Algorytm składa się z dwóch części:

1. incjalizacji wartości zmiennych: q oraz r (etykieta 1)

2. iteracji dopóki , która oblicza iloraz q oraz resztę r z dzielenia całkowitego x przez y.

( etykieta 2)

Przeprowadzimy dowód na częściową poprawność tego algorytmu względem warunków α i

β. Polegać on będzie a pokazaniu, że:

dla danych wejściowych spełniających warunek początkowy α, jeżeli obliczenia dochodzą
do końca , to wartości zmiennych x, y, q oraz r spełniają warunek końcowy β.

Postawmy w tym celu następujące pytanie:

Jaki warunek spełniają zmienne x, y, q oraz r w punkcie pośrednim algorytmu, tzn. w
etykiecie 2, a dokładniej,
jaki warunek spełniają te zmienne w chwili sprawdzania warunku „y<=r” sterującego
iteracją dopóki?

Określmy w tym celu następujący nowy warunek
γ:

y

r

r

y

≤

∧

≤

∧

+

∗

=

0

0

q

x

jako niezmiennik naszej instrukcji warunkowej dopóki.

Pokażemy, że za każdym razem,

gdy obliczenie algorytmu rozpoczyna się ze stanem spełniającym warunek

początkowy

α

orazdochodzi z wartościami x, y, q oraz r do sprawdzania

warunku iteracji „y<=r”,

wówczas

dla tych wartości zmiennych jest spełniony warunek γ.

Zauważmy, że istnieją tylko dwa przypadki dojścia obliczeń do etykiety 2 :

1) bezpośrednio od etykiety 1 i wtedy mamy

q=0, r=x,

a ponieważ z definicji warunku α mamy, że 0

≤

x

∧

0

≤

y,

to warunek

γ: x=0*y+x=x

∧

0

≤

r

∧

0

≤

y

jest oczywiście spełniony

2) przy wyjściu od samej etykiety 2, gdy warunek zachodzi i powtarza się wykonanie

instrukcji iteracyjnej.

Załóżmy więc, że

−

rozpoczynamy działanie od etykiety 2

−

spełnione są warunki

γ:

y

r

r

y

≤

∧

≤

∧

+

∗

=

0

0

q

x

oraz

warunek iteracji: „y<=r”

Wykonuje się wtedy instrukcja złożona, która

−

zmiennej q nadaje nową wartość q’=q+1

−

zmiennej r nadaje nową wartość r’=r-y

A wtedy mamy dla warunku γ:

γ(x, y, q’, r’)

≡

x=q’*y+r’

0

≤

r’

∧

0

≤

y

≡

x=(q+1)*y+r-y i 0

≤

r-y

∧

0

≤

y

Ponieważ:

1) (q+1)*y+r-y=q*y-r=x

więc 1-szy czynnik warunku γ jest spełniony;

2) 0

≤

r-y jest też prawdziwy, bo wiemy, że y

≤

r z założenia warunku iteracyjnego, czyli

0

≤

r-y

3) czynnik 0

≤

y jest też spełniony, ponieważ założono, że warunek „0

≤

y” zachodzi w

α

,a

wartość zmiennej y nie ulega zmianie.

Stosując indukcję względem liczby wykonywanych sprawdzeń warunku iteracji „y

≤

r” (tj.

liczby przejść obliczeń przez etykietę 2), wnioskujemy, że przy każdym sprawdzeniu warunku
iteracji zachodzi warunek γ.

Mogą teraz zajść dwa przypadki:

1) Warunek iteracyjny „y

≤

r” pozostaje ciągle spełniony i wtedy obliczenie NIGDY nie

dochodzi do etykiety 3;

2) W pewnej chwili przy sprawdzaniu warunku iteracji mamy y>r i obliczenie

przechodzi do etykiety 3.
Ponieważ wtedy spełniony jest również warunek γ, co przy fakcie, że y>r daje nam
prawdziwość warunku końcowego

β:

r

y

+

∗

=

q

x

∧∧∧∧

0

≤≤≤≤

r<y

Udowodniliśmy więc następujący fakt:

jeżeli obliczenie algorytmu startuje z danymi wejściowymi spełniającymi warunek

αααα

i

dochodzi do punktu końcowego, to otrzymane wyniki spełniają warunek końcowy

ββββ

.

Oznacza to, że algorytm jest częściowo poprawny względem warunków

α

i

β

.

Nie jest on jednak poprawny, bo np. dla danych: x=0, y=0 jego obliczenia są nieskończone
(brak własności stopu!)

Uogólniając, metoda niezmienników polega na:

1) wyróżnieniu w programie pewnych szczególnych miejsc
2) przypisaniu do nich warunków na wartościowanie zmiennych algorytmu
3) udowodnieniu, że

jeżeli początkowy stan obliczenia spełnia warunek początkowy

α

, to ilekroć obliczenie

algorytmu dochodzi do wyróżnionego miejsca, zawsze przyporządkowany temu miejscu
warunek jest spełniony przez aktualne wartościowanie zmiennych.
W szczególności, gdy dochodzi do punktu końcowego, to wartościowanie zmiennych
spełnia warunek końcowy

β

Należy zwrócić uwagę na to, że bardzo istotny jest wybór wyróżnionych miejsc (czyli

niezmienników) w analizowanej instrukcji.
Na przykład:

!

dla instrukcji typu dopóki jest to miejsce sprawdzania warunku sterującego iteracją

!

dla instrukcji typu powtarzaj są to dwa miejsca:

- początek instrukcji
- -miejsce sprawdzania warunku sterującego iteracją

C. Dowodzenie własności stopu

Stosuje się dwie metody dowodzenia:

1) Metoda liczników iteracji

−

wprowadzenie dodatkowej zmiennej całkowitej służącej do obliczania liczby wykonań
instrukcji iteracyjnej (licznik wykonań iteracji)
# szuka się wyrażenia, którego wartość w trakcie realizacji algorytmu ograniczyłaby z

góry wartość tej zmiennej (licznika)

#

W przypadku rozpatrywanego algorytmu dzielenia:

poczatek

{

}

0

y

i

0

x

:

1

>

≥

α

1: q:=0; r:=x
2: dopóki r

≥

y wykonuj

początek

q:=q+1; r:=r-y

koniec

3:

{

}

<

≤

+

∗

=

r

0

i

r

y

q

x

:

β

zmienna q pełni rolę licznika iteracji dopóki; mamy zatem, że górna ilość wykonań iteracji
wynoai q

≤

x/y



2) Metoda malejących wielkości

−

rozpatruje się takie wielkości (wyrażenia arytmetyczne), które zwiększają (lub
zmniejszają) swoją wartość w sposób nieregularny i dla których istnieje wartość
ograniczająca je z góry (lub z dołu).

−

Przykład

Numeryczny algorytmy przybliżonego rozwiązywania równania nieliniowego metodą

bisekcji wykonuje iteracje tak długo, aż przedział zawierający pierwiastek tego równania
osiągnie zamierzoną szerokość

ε

>0 .

3

. ZŁOŻONOŚĆ OBLICZENIOWA

Każde wykonanie algorytmu na komputerze wymaga pewnej pracy oraz pewnej ilości

miejsca w jego pamięci. Dlatego też przed kodowaniem algorytmu do postaci akceptowanej
przez komputer, jego testowaniem a następnie użytkowaniem, powinniśmy odpowiedzieć sobie
na pytanie:

Czy nasz sprzęt umożliwia stosowanie rozważanego algorytmu dla przewidywanych
danych?

Okazuje się bowiem, że dla wielu znanych algorytmów czas ich działania zwiększa się zbyt

szybko w miarę, jak wzrasta wielkość danych wejściowych. Dokonując oceny różnych
algorytmów rozwiązujących dane zagadnienia chcemy wiedzieć, jaka jest ich złożoność
obliczeniowa, czyli inaczej, jaka ilość zasobów komputerowych potrzebna jest do ich
wykonania.

Za podstawowe zasoby komputerowe uważa się:

−

czas działania algorytmu

−

ilość zajmowanej pamięci.

Chcemy jednak, żeby te dwie wartości (czas i pamięć) były na tyle reprezentatywne, by np.

użytkownik małego komputera osobistego oraz użytkownik potężnego superkomputera,
używający tego samego algorytmu - mogli się porozumieć do do jego sprawności obliczeniowej.
Czy bowiem stwierdzenie:

Mój program (algorytm) jest szybki, bo rozwiązał zadanie w 55 sekund !

może posłużyć za obiektywną ocenę jego sprawności ?

Dodatkowo powinniśmy bowiem wiedzieć:

−

na jakim komputerze program był wykonywany

−

jaki miał procesor (częstotliwość zegara)

−

co działo się w pamięci komputera podczas jego wykonywania

−

jakiego kompilatora użyto do napisania programu, itp.

Stąd wynika oczywisty wniosek:

Ocena sprawności algorytmu przy pomocy kryteriów sprzętowych nie jest oceną

obiektywną!

Należy więc znaleźć miarę uniwersalną, która ma decydujący wpływ na czas

wykonywania określonego algorytmu. Parametrem tym jest rozmiar danych wejściowych
algorytmu.

Pojęcie to ma różne znaczenie dla różnych zagadnień, np.:

−

w sortowaniu ciągu n-elementowego jest to ilość elementów tego ciągu, czyli n.

−

dla zadań grafowych jest to liczba krawędzi rozpatrywanego grafu

−

przy wyznaczaniu wartości wielomianu - stopień tego wielomianu

−

dla operacji na macierzach - wymiary macierzy

−

dla wyliczenia wartości funkcji n! -wartość danej n.

Przed przystąpieniem do wyznaczania złożoności obliczeniowej algorytmów należy jeszcze

określić jednostki, w jakich będzie ona liczona.

Dla złożoności pamięciowej jednostką taką będzie słowo pamięci i jest to sprawa oczywista.

Dla złożoności czasowej problem jest bardziej złożony, ponieważ jednostka ta powinna

być własnością samego tylko algorytmu jako metody rozwiązania problemu, a nie powinna
zależeć od komputera, języka programowania, kodowania , itp.

W tym celu wyróżnia się w klasie algorytmów charakterystyczne dla niego operacje -

nazywane są one operacjami dominującymi.

Przykłady operacji dominujących:
# w algorytmach sortowania

−

porównanie dwóch elementów w ciągu wejściowym

−

przestawienie dwóch elementów w ciągu

# w algorytmach numerycznych, np. obliczania wartości wielomianu

−

operacje arytmetyczne: +, -, /, *

# w algorytmach przeglądanie drzewa binarnego

−

przejście dowiązania pomiędzy dwoma węzłami w drzewie.

Za jednostkę złożoności czasowej przyjmuje się wykonanie jednej operacji dominującej.

Zanim przejdziemy do szczegółowego omówienia własności funkcji złożoności czasowej,

postawmy następujące pytanie:

Czy postęp w szybkości obliczeń komputerów zmniejsza znaczenie efektywności

algorytmów?

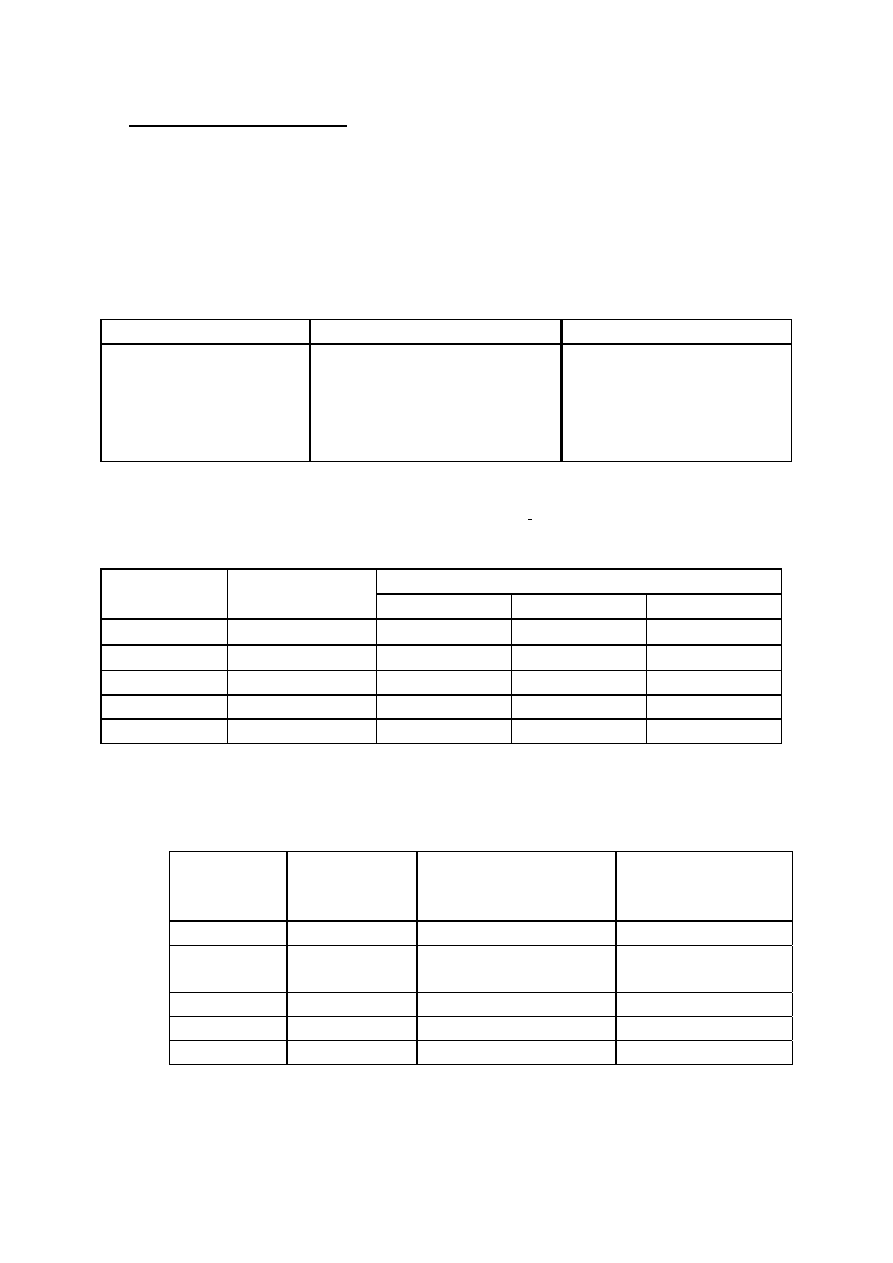
W celu ilustracji odpowiedzi na to pytanie rozważmy pięć algorytmów A

1

, A

2

,..., A

5

,

rozwiązujących ten sam problem i mających następujące złożoności czasowe:

Algorytm

Złożoność czasowa f(n)

f(n=10)

A

1

n

10

A

2

n*logn

≈

33

A

3

n

2

100

A

4

n

3

1000

A

5

2

n

1024.

gdzie n - rozmiar danych wejściowych.

Zakładając, że jednostką czasu jest jedna milisekunda, pokażemy, jakiego maksymalnego

rzędu zadania mogą rozwiązać te algorytmy odpowiednio w: 1 sekundzie, 1 minucie, 1 godzinie.

Maksymalny rozmiar zadania

Algorytm

Złożoność czasowa

1sek

1min

1godzina

A

1

n

1000

6x10

4

3,6

⋅

10

6

A

2

nlogn

140

4893

2,0

⋅

10

5

A

3

n

2

31

244

1897

A

4

n

3

10

39

153

A

5

2

n

9

15

21

Przypuśćmy teraz, że nowa generacja komputerów jest 10-krotnie szybsza. Pokażemy, jaki

jest wzrost rozmiaru zadań, które mogą być rozwiązane dzięki wzrostowi szybkości
komputerów:

Algorytm

Złożoność

czasowa

Maksymalny rozmiar

zadania przed

przyśpieszeniem

Maksymalny rozmiar

zadania po

przyśpieszeniu

A

1

n

S

1

10S

1

A

2

n*logn

S

2

około 10S

2

dla dużych

n

A

3

n

2

S

3

3.16 S

3

A

4

n

3

S

4

2.15 S

4

A

5

2

n

S

5

S

5

+ 3.3

Zauważamy, że np.:

−

dla A

5

10-krotny wzrost szybkości pozwolił zwiększyć zadania tylko o 3;

−

dla A

3

rozmiar ten wzrósł więcej niż 3-krotnie

−

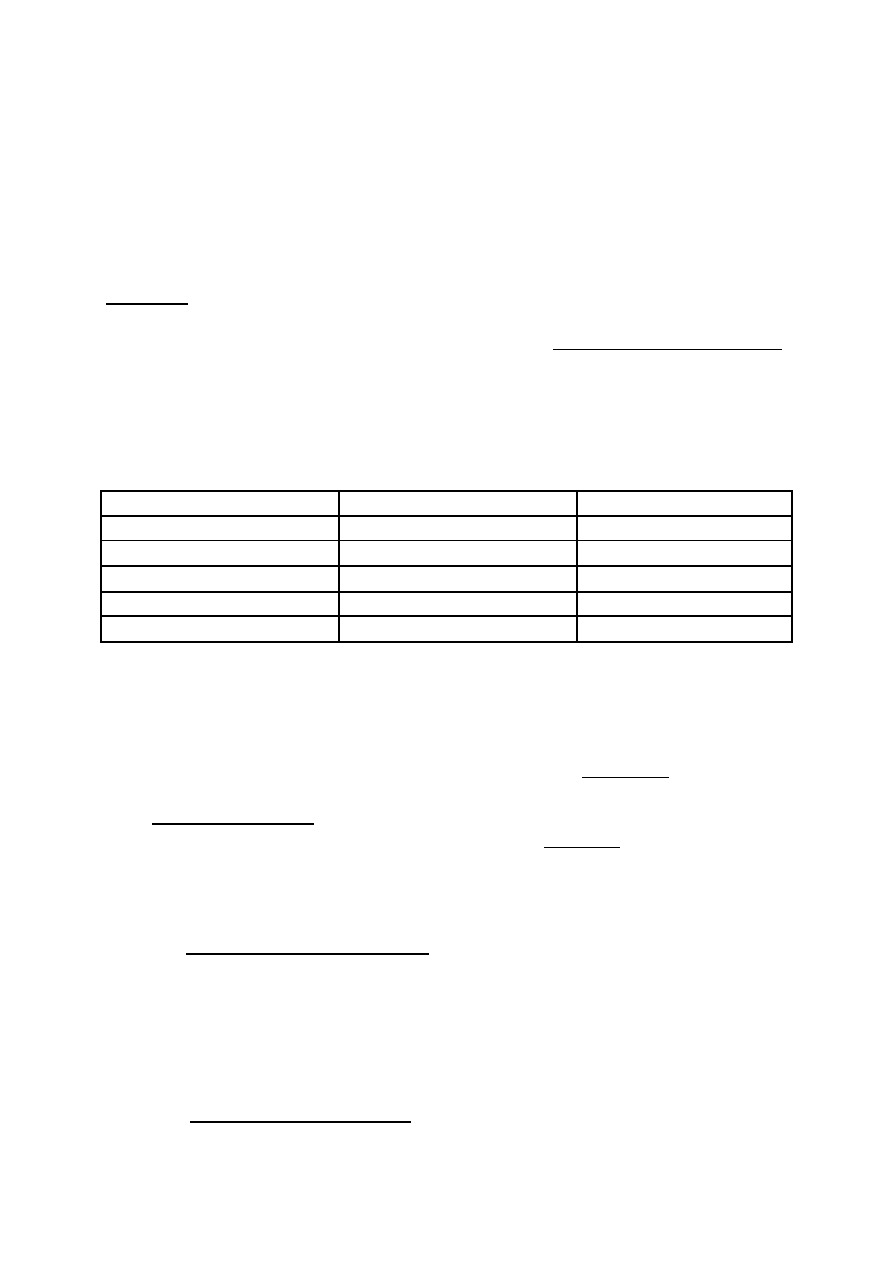
dla A

1

rozmiar wzrósł 10-krotnie, czyli tyle, ile wzrosła prędkość komputera

Traktując 1 minutę jako podstawę porównania można łatwo stwierdzić, że:

−

zastępując A

4

przez A

3

możemy rozwiązać zadanie 6 razy większe

−

zastępując A

4

przez A

2

możemy rozwiązać zadanie 125 razy większe

# jest to lepsze niż 2-krotne zwiększenie zadania uzyskane przez 10-krotny

wzrost szybkości komputera.

WNIOSEK: Bardziej opłacalne jest konstruowanie szybszych algorytmów.

Rozpatrywane wyżej funkcje złożoności czasowej są tzw. złożonościami asymptotycznymi,

tzn. nie uwzględniają stałej proporcjonalności. Może się, więc zdarzyć, że analizując faktyczne
funkcje złożoności czasowej, (dokładnie wyznaczone), algorytm asymptotycznie gorszy jest
szybszy dla małych zadań niż algorytm asymptotycznie lepszy.

Dla ilustracji przypuśćmy, że rozważane algorytmy A

1

, ..., A

5

mają następujące faktyczne

funkcje złożoności czasowej:

Algorytm

Funkcje złożoności czasowej

Kiedy najszybsze

A

1

1000 n

n>1024

A

2

100 n*logn

59

≤≤≤≤

n

≤≤≤≤

1024

A

3

10 n

2

10

≤≤≤≤

n

≤≤≤≤

58

A

4

n

3

A

5

2

n

2

≤≤≤≤

n

≤≤≤≤

9

Wyznaczając złożoność czasową algorytmu (jest to funkcja rozmiaru danych n) rozróżniamy

jej dwie postacie:

1) złożoność pesymistyczna

−

ilość operacji dominujących potrzebnych przy trafieniu na „najgorsze” dane wejściowe
rozmiaru n

2) złożoność oczekiwana

−

ilość operacji dominujących potrzebnych przy „typowych” danych wejściowych
rozmiaru n.

Formalne definicje tych pojęć są następujące:

Przez pesymistyczną złożoność czasową algorytmu rozumie się funkcję:

{

}

n

D

d

:

t(d)

sup

W(n)

∈

=

gdzie: sup

- kres górny zbioru

D

n

- zbiór wszystkich możliwych zestawów danych wejściowych rozmiaru n

t(d)

- liczba operacji dominujących dla zestawu danych wejściowych d

Przez oczekiwaną złożoność czasową algorytmu rozumie się funkcję:

∑

≥

∗

=

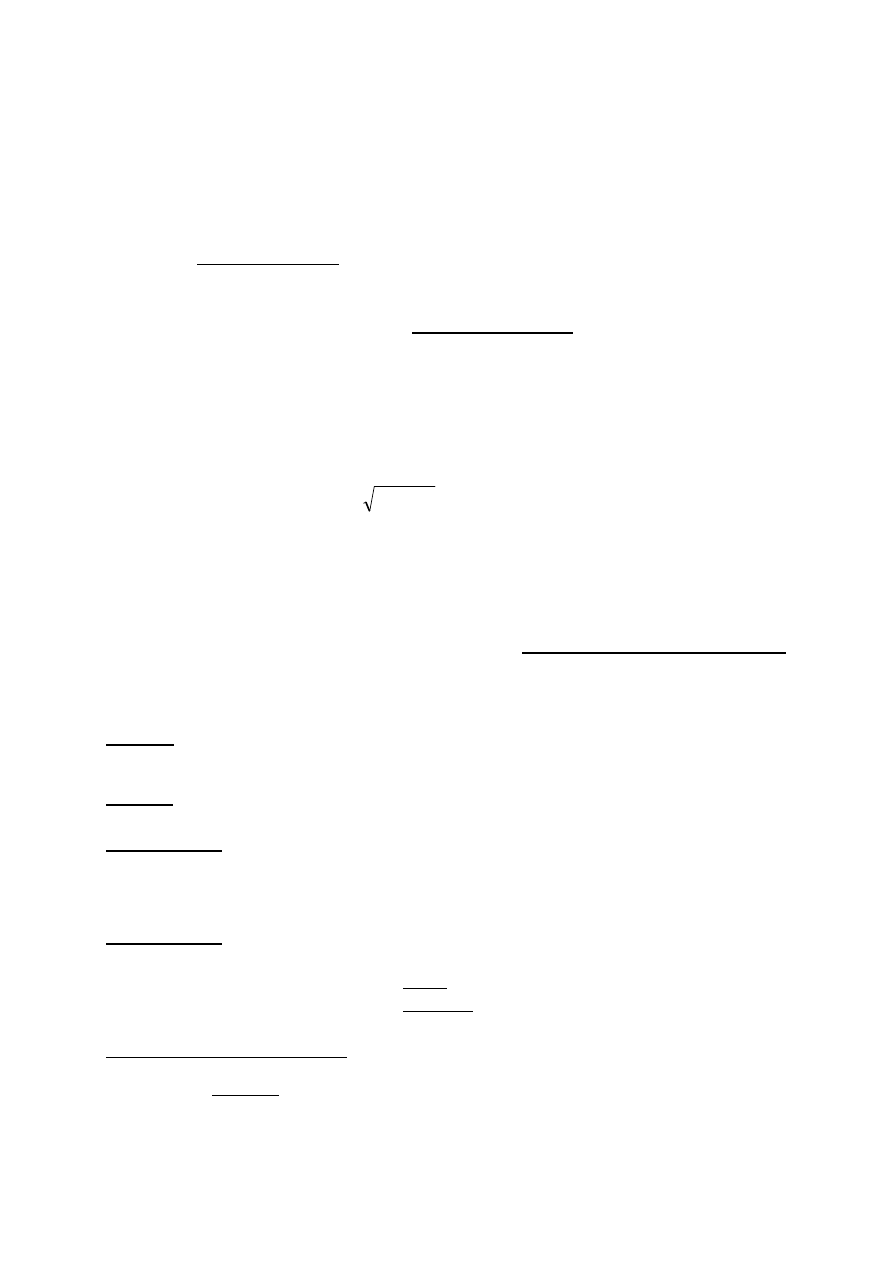
0

k

nk

p

k

A(n)

gdzie: p

nk

- rozkład prawdopodobieństwa zmiennej losowej X

n

, tzn. prawdopodobieństwo, że

dla danych rozmiaru n algorytm wykona k operacji dominujących (k

≥

0),

X

n

jest zmienną losową, której wartością jest t(d), dla d

∈

D

n

czyli jest to wartość oczekiwaną ave(X

n

) zmiennej losowej X

n

.

W celu stwierdzenia, na ile funkcje W(n) i A(n) są reprezentatywne dla wszystkich danych

wejściowych rozmiaru n, rozważa się dwie wrażliwości algorytmu:

miarę wrażliwości pesymistycznej:

( ) ( )

{

}

n

2

1

2

1

D

d

,

d

:

d

t

d

t

sup

(n)

∈

−

=

∆

miarę wrażliwości oczekiwane:

)

dev(X

(n)

n

=

δ

gdzie dev(X

n

) jest standardowym odchyleniem zmiennej losowej X

n

, tzn.

∑

≥

⋅

=

=

0

k

nk

2

n

n

n

n

p

))

ave(X

-

(k

)

var(X

i

)

var(X

)

dev(X

,

var(X

n

) oznacza wariancję zmiennej losowej X

n

.

Jak należy interpretować wartości wrażliwości

∆∆∆∆

(n) i

δδδδ

(n):

Im większe wartości

∆∆∆∆

(n) i

δδδδ

(n), tym algorytm jest bardziej wrażliwy na dane wejściowe

i tym bardziej jego zachowanie w wypadku rzeczywistych danych może odbiegać od
zachowania opisanego funkcjami W(n) i A(n).

Przykład:

Algorytm przeszukiwanae sekwencyjnego ciągu.

Problem: Dla podanego n-elementowego ciągu liczb naturalnych oraz liczby x sprawdzić, czy

liczba x jest elementem tego ciągu.

Dane wejściowe:

n, (n

≥≥≥≥

0) liczba naturalna

L[1..n+1] tablica z elementami ciągu (a

1

, ..., a

n

) na miejscach od 1do n ,

x poszukiwany element.

Dane wyjściowe (wynik):
zmienna

logiczna

p taka, że

p= prawda gdy element x należy do ciągu
p= fałsz,

gdy element x nie należy do ciągu

Zapis algorytmu w pseudokodzie:

początek

j := 1;
L[n+1] := x;

dopóki L[j]

#

x wykonuj j:= j+1;

p := j

≤

n

koniec;

Realizacja algorytmu (zestaw danych 1)

Dla: n=4; ciągu (1,4,2,8), x=4 mamy:

L[1]=1, L[2]=4, L[3]=2, L[4]=8

j=1 , L[5]=4

1 # 4, TAK j=1+1=2 ( L[1]#4 )
4 # 4, NIE ( L[2)#4 )
p=2

≤

4 (prawda)

Realizacja algorytmu (zestaw danych 2)

Ddla: n=4; ciągu (1,4,2,8), x=5 mamy

L[1]=1, L[2]=4, L[3]=2, L[4]=8

j=1 L[5]=5

1#5, TAK j=1+1=2 (L[1]#5 )
4#5, TAK j=2+1=3 (L[2]#5 )
2#5, TAK j=3+1=4 (L[3]#5 )
8#5, TAK j=4+1=5 (L[4]#5 )
5#5, NIE (L[5]#5 )
p=5

≤

4 (falsz)

Analiza złożoności algorytmu:

Rozmiar danych wejściowych

: n

Operacje dominujące

: porównania L[j])#a

Pesymistyczna złożoność czasowa :

W(n)=n+1

Pesymistyczna wrażliwość czasowa:

∆∆∆∆

(n)=n

bo najwięcej porównań n+1
bo najmniej porównań 1
stąd

∆

(n)=(n+1)-1=n

Jaka jest

więc oczekiwana złożoność czasowa ?

Niech prawdopodobieństwo znalezienia elementu x na każdym z n możliwych miejsc

jest takie samo, oraz element x należy do ciągu (a

1

,.... a

n),

tzn.

1,2,...n

k

dla

n

1

p

nk

=

=

Wówczas

2

1

n

2

)

1

n

(

n

n

1

n

1

k

n

1

n

1

k

n

1

n

1

k

nk

k

k

p

k

A(n)

+

+

=

=

=

=

=

=

⋅

=

⋅

=

∑

∑

∑

Do obliczenia oczekiwanej wrażliwości czasowej należy znaleźć wcześniejsze wariancje

zmiennej losowej X

n

( )

(

)

(

)

( )

(

)

(

)

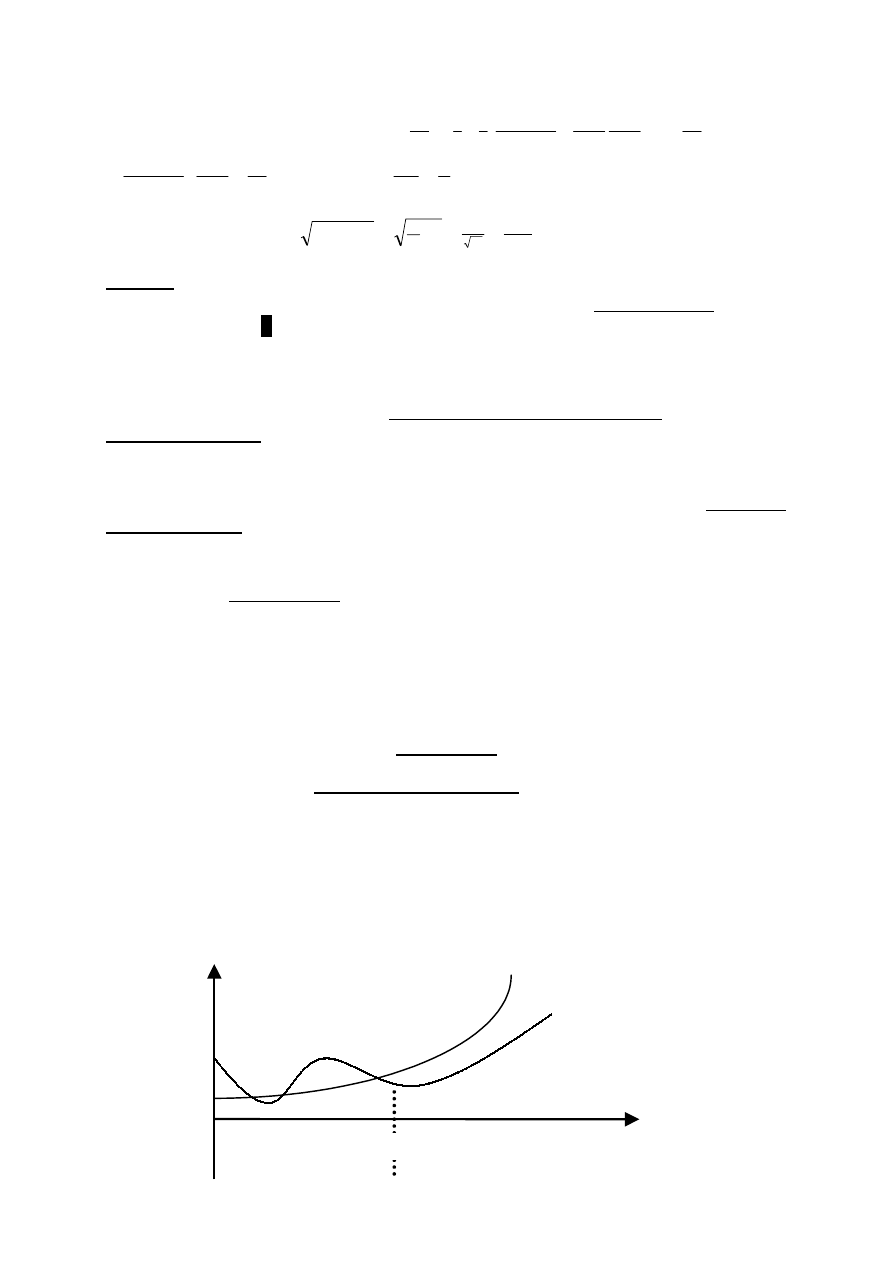
2

12

1

12

n

12

1

n

4

1)

(n

6

1)

1)(2n

n(n

2

2

1

n

2

1)

n(n

2

1)

2(n

6

1)

1)(2n

n(n

n

1

n

1

k

n

1

2

2

1

n

n

1

k

nk

2

n

n

n

1

-

3

-

3n

-

2

4n

-

n

k

p

X

ave

k

)

var(X

2

2

≈

=

+

=

=

=

⋅

+

−

=

⋅

−

=

⋅

−

=

+

+

+

+

+

+

+

+

+

=

+

=

∑

∑

i teraz

( )

0,25n

n

X

var

)

dev(X

δ(n)

3,464

n

12

n

2

12

1

n

n

≈

≈

=

=

=

=

Wniosek:

Funkcja wrażliwości i funkcja złożoności są liniowe, a więc mocno wrażliwe na układ

danych wejściowych.

Jest oczywiste, że faktyczna złożoność czasowa algorytmu w chwili jego użycia różni się od

wyliczonej teoretycznie, pewnym współczynnikiem proporcjonalności lub pewnymi
elementami stałymi. Ponieważ analiza złożoności interesuje się głównie zależnością
efektywności algorytmu (czasu działania) od rozmiaru problemu w sytuacji, gdy ten ostatni
wzrasta nieograniczenie, nie jest istotna dokładna formuła tej zależności, lecz jej zachowanie
asymptotyczne. Pomijamy w niej stałe elementy i inne, pozostawiając jedynie najbardziej
znaczące składniki formuły, czyli te, które decydują o zachowaniu się formuły, gdy rozmiar n
dąży do nieskończoności.

Reasumując, istotną częścią informacji, która jest zawarta w funkcji złożoności czasowej

W(n) jest jej rząd wielkości, czyli jej zachowania asymptotyczne, gdy n dąży do
nieskończoności. Poniżej omówione będą pewne pojęcia związane z tym zagadnieniem.

Niech f, g, h : N→R

+

∪

{0}, gdzie N - zbiór liczb naturalnych

R

+

- zbiór liczb rzeczywistych dodatnich

będą trzema dowolnymi funkcjami.

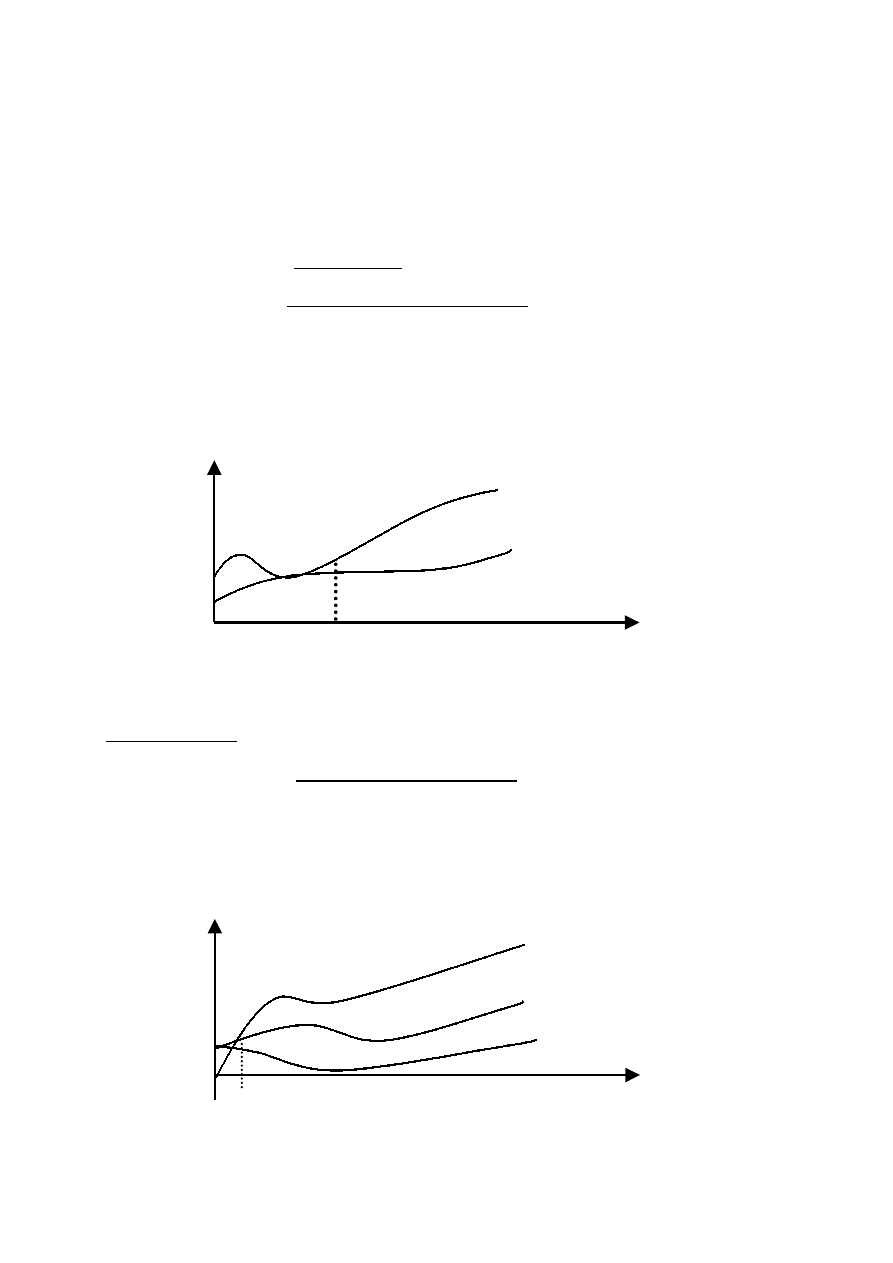
NOTACJA O

Mówimy, że funkcja f jest co najwyżej rzędu funkcji g, co zapisujemy jako

f(n)= O (g (n))

jeżeli istnieje stała rzeczywista c>0 i stała naturalna n

0

takie, że

f(n)

≤≤≤≤

c

⋅⋅⋅⋅

g(n), dla każdego n

≥

n

0

c

⋅⋅⋅⋅

g(n)

f(n)

n

o

n

f(n) = O(g(n))

Np.

Dla (n) = n

2

+2n mamy, że n

2

+2n=O(n

2

), bo istnieje stała c=3>0 i stała

naturalna n

o

=1 takie, że

n

2

+2n

≤≤≤≤

3

⋅⋅⋅⋅

n

2

= 3g(n) dla każdego n

≥

1

⋅

i g(n)= n

2

Czyli f(n) = n

2

+2n jest co najwyżej rzędu O(n

2

)

NOTACJA

Ω

Ω

Ω

Ω

Mówimy, że funkcja f jest co najmniej rzędu funkcji g, co zapisujemy jako

f(n) =

Ω

Ω

Ω

Ω

(g(n))

jeżeli istnieje stała c>0 i stała naturalna n

o

, takie, że

c

⋅⋅⋅⋅

g(n)

≤≤≤≤

f(n) dla każdego n

≥≥≥≥

n

o .

Inaczej mówiąc: g(n) = O(f(n))

f(n) =

Ω

Ω

Ω

Ω

(g(n))

NOTACJA

Θ

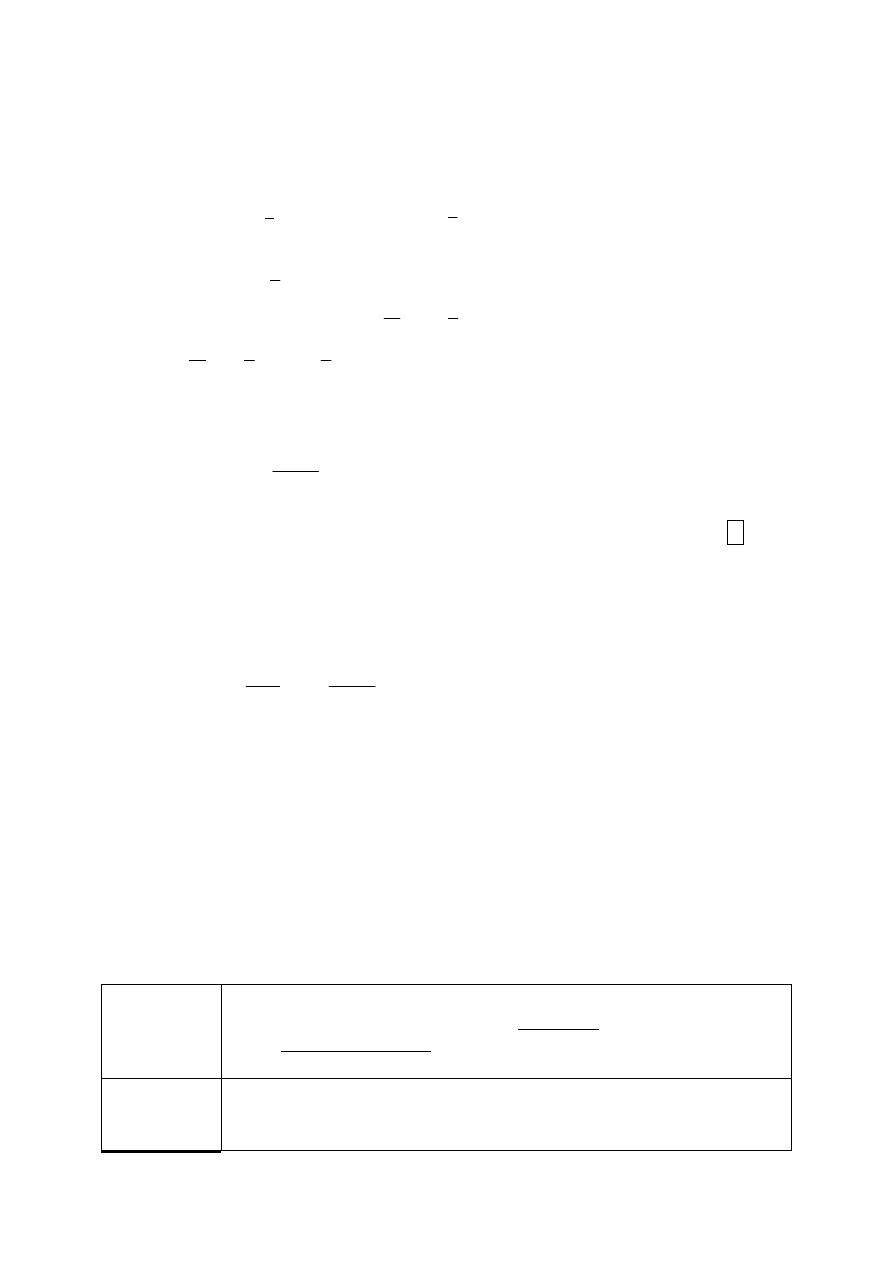
Mówimy, że funkcja f jest dokładnie rzędu funkcji g, co zapisujemy jako

f(n) =

Θ

Θ

Θ

Θ

(g(n))

jeżeli istnieja stałe c

1

>0, c

2

>0 oraz stała naturalna n

o,

takie, że

c

1

⋅⋅⋅⋅

g(n)

≤≤≤≤

f(n)

≤≤≤≤

c

2

⋅⋅⋅⋅

g(n)dla każdego n

≥

n

o

Czyli inaczej f(n) = O(g(n)) i f(n) =

Ω

Ω

Ω

Ω

(g(n)).

f(n) =

Θ

Θ

Θ

Θ

(g(n))

c

⋅⋅⋅⋅

g(n)

f(n)

n

o

n

c

2

⋅⋅⋅⋅

g(n)

f(n)

n

o

n

c

1

⋅⋅⋅⋅

g(n

)

Np. Dla funkcji

3n

2

n

2

1

f(n)

−

=

mamy, że

( )

2

n

3n

2

n

2

1

f(n)

Θ

=

−

=

ponieważ istnieją stałe c

1

⋅

>0,

c

2

⋅

>0 i n

o

, dla których

2

n

2

c

3n

-

2

n

2

1

2

n

1

c

≤

≤

dla każdego n

≥

n

o

Można bowiem sprawdzić, że dla

7

o

n

,

2

1

2

c

,

14

1

1

c

=

=

=

zachodzi nierówność

7.

n

dla

≥

≤

≤

2

n

2

1

3n

-

2

n

2

1

2

n

14

1

Do porównania rzędów wielkości dwóch danych funkcji f(n) i g(n) można wykorzystać

obliczenia następującej granicy:

g(n)

f(n)

lim

E

n

∞

→

=

Jeżeli

E=+∞, to g(n) = O(f(n)) ale NIE f(n)=O(g(n))
E=c>0, to f(n) =

Θ

Θ

Θ

Θ

(g(n))

E=0, to f(n) = O(g(n))

ale NIE g(n)=O(f(n)).

Np. Dla f(n)=nlogn, g(n)=n

2

0

2

n

nlogn

lim

g(n)

f(n)

lim

n

n

=

=

∞

→

∞

→

czyli n·logn=O(n

2

) ale nie n

2

=O(n logn)

Większość ze znanych algorytmów ma złożoność czasową należącą do podanego niżej

wykazu. To, że funkcji tych jest raczej mało, wynika z własności „pochłaniania” przez „duże
O” stałych współczynników i wyrazów niższego rzędu.

Np. Funkcje:

n

3

,

5 n

3

+2 n

2

-100n+5, 6 n

3

+4·n·log(n)+2

są rzędu O(n

3

)

Wykaz podstawowych złożoności czasowych

logn

−

złożoność logarytmiczna

−

np. algorytmy, w których zadanie rozmiaru n sprowadzane jest do
zadania rozmiaru n/2, plus pewna stała liczba działań

# np. przeszukiwanie binarne

n

−

złożoność liniowa

−

np. algorytmy, w których dla każdych n-elmentowych danych
wejściowych wykonywana jest stała liczba działań

# np. algorytm Hornera obliczania wartości wielomianu

n

⋅⋅⋅⋅

logn

−

złożoność nlogn (liniowo-logarytmiczna)

−

np. algorytmy, w których zadanie rozmiaru n zostaje sprowadzone do
dwóch podzadań rozmiaru n/2, plus pewna liczba działań liniowa
względem rozmiaru n, potrzebnych do wykonania najpierw rozbicia a
następnie scalenia rozwiązań podzadań rozmiaru n/2 w rozwiązanie
rozmiaru n

# np. sortowanie przez scalanie

n

2

−

złożoność kwadratowa

−

np. algorytmy, w których jest wykonywana pewna stała liczba działań
dla każdej pary danych wejściowych (mają podwójną iterację

# np. wyzerowanie elementów tablicy 2-wymiarowej

n

3

, n

4

−

dalsze złożoność wielomianowe

logn

n

−

złożoność podwykładnicza

2

n

−

złożoność wykładnicza

−

np. algorytmy, w których jest wykonywana stała liczba działań, dla
każdego podzbioru danych wejściowych

n!

−

złożoność wykładnicza n!

−

np. algorytmy, w których jest wykonywana stała liczba działań, dla
każdej permutacji danych wejściowych.

W celu uświadomienia sobie jak różne rodzaje złożoności czasowej wpływają na sens

stosowania ich do rozwiązywani problemów o dużym rozmiarze przeanalizujmy następujące
zestawienia.

Przyjmijmy, że komputer, na którym wykonujemy te algorytmy może wykonać 1 milion

operacji na 1 sek.

n=10

n=20

n=30

n=40

n=50

n

3

0,001s

0,008s

0,027s

0,064s

0,125s

2

n

0,001s

1,05s

17,9m

1,27d

35,7r

3

n

0,059s

58,1m

6,53r

3,86·10

5

r

2,28·10

10

r

n!

3,63s

7,71·10

4

r

8,41·10

18

r

2,59·10

34

r

9,64·10

50

r

dla n!=24! czas jest większy niż obecny wiek wszechświata.

3.Rekurencja (rekursja)

Wiele ważnych algorytmów ma strukturę rekurencyjną, którą można opisać

następująco:

W celu rozwiązania danego problemu algorytm wywołuje sam siebie w sposób

bezpośredni lub pośredni.

Zastosowanie rekursji często prowadzi do bardziej zrozumiałych i zwięzłych opisów

algorytmów, niż było to możliwe bez rekursji. Do obliczenia złożoności czasowej algorytmów
rekurencyjnych stosujemy równania rekurencyjne. Przykład takiego równania wraz z
rozwiązaniem będzie podany w dalszej części.

Często zdarza się, że w celu rozwiązania pewnego problemu dzielimy go na podproblemy.

Następnie znajdujemy rozwiązania podproblemów – są one prostsze niż rozwiązania problemu
złozonego- i za ich pomocą znajdujemy rozwiązanie problemu wyjściowego.

Metoda ta, zwłaszcza stosowana rekurencyjnie, prowadzi często do efektywnych

algorytmów rozwiązujących takie problemy, których podproblemy mają identyczną postać, ale
są za to mniejszego rozmiaru.

Taka metoda konstrukcji algorytmów nazywana jest metodą „dziel i zwyciężaj” (ang. divide

and conquer).

Składa się ona z trzech etapów:

1) DZIEL : dzielimy problem na podproblemy
2) ZWYCIĘŻAJ : rozwiązujemy podproblemy rekurencyjnie
3) POŁĄCZ : łączymy rozwiązania podproblemów, aby otrzymać rozwiązanie

wyjściowego problemu.

Technikę „dziel i zwyciężaj” zilustrujemy dwoma przykładami:

Przykład 1

Problem: Dana jest tablica n liczb całkowitych a[1], ..., a[n].

Czy w tablicy występuje element x ?

Rozwiązanie:

Dziel:

Podzielimy tablice na dwie części:
CZĘŚĆ I:

pierwszy element tablicy, tzn. a[1]

CZĘŚĆ II:

pozostałe (n-1) elementów, tzn. a[2], ..., a[n]

Zwyciężaj: Jeżeli pierwszy element jest równy x, to wynikiem jest napis „TAK

WYSTĘPUJE”

i kończymy obliczenia,

w przeciwnym razie

sprawdzamy, czy x występuje w pozostałych n-1 elementach (czyli w

części II)

Podane zostały warunki tylko pozytywnego zakończenia problemu. W przypadku, gdy

przebadaliśmy całą tablicę i element x nie został znaleziony, to działanie algorytmu powinno się
zakończyć wraz z podaniem napisu „NIE ZNALEZIONO”.

Realizacja rozwiązania problemu w postać programu może być następująca.

SZUKAJ ([a

1

, ..., a

n

], lewy, prawy, x)

{lewy- oznacza lewą, prawy- oznacza prawą granicę przeszukiwanego obszaru

tablicy;

na poczatku lewy=1, prawy=n}

początek

jeżeli lewy > prawy to „BRAK W CIĄGU”
w przeciwnym razie

jeżeli a[lewy]=x to „JEST W CIĄGU”
w przeciwnym razie SZUKAJ([a

1

, ..., a

n

], lewy+1, prawy, x)

koniec

Warunkiem zakończenia algorytmu jest:

albo znalezienie szukanego elementu :( a[lewy]=x )
albo wyjście poza obszar poszukiwany :(lewy>prawy).

Przykładowe realizacjealgorytmów dla dwóch zestawów danych:
1) dla ciągu: 0, 7, 8, 5 i szukanego elementu: x=8 dostajemy

SZUKAJ ([0,7,8,5],1,4,8) {ciąg,lewy=1, prawy=4, x=8}

⇓

1>4

Nie ( czy lewy>prawy ? )
0=8

Nie ( czy a[1]=x ? )
SZUKAJ ([0,7,8,5],2,4,8)

⇓

2>4

Nie ( czy lewy>prawy ?)
7=8

Nie ( czy a[2]=x ? )
SZUKAJ ([0,7,8,5],3,4,8)

⇓

3>4

Nie ( czy lewy>prawy ? )
8=8

Tak ( czy a[3]=x ? )

↓↓↓↓

” JEST W CIĄGU”

2) dla ciągu : 0, 7, 8, i szukanego elementu: x=5 dostajemy:

SZUKAJ ([0,7,8],1,3,5) {ciąg,lewy=1, prawy=3, x=5}

⇓

1>3

Nie ( czy lewy>prawy ? )
0=5

Nie ( czy a[1]=x ? )
SZUKAJ ([0,7,8],2,3,5)

⇓

2>3

Nie ( czy lewy>prawy ?)

7=5

Nie ( czy a[2]=x ? )
SZUKAJ ([0,7,8],3,3,5)

⇓

3>3

Nie ( czy lewy>prawy ? )
8=5

Nie ( czy a[3]=x ? )

SZUKAJ ([0,7,8],4,3,5)

⇓

4>3

Tak

( czy lewy>prawy ? )

↓↓↓↓

” BRAK W CIĄGU”

Algorytm ten posiada dwie ważne cechy algorytmów rekurencyjnych:

1) zakończenie rekurencji jest jasno określone:

- znaleziono element ( a[lewy]=x )

lub

- przekroczono zakres tablicy ( lewy>prawy )

2) duży problem został rozbity na dwa mniejsze

1-szy - elementarny
2-gi - na analogiczny problem, tylko o mniejszym rozmiarze

Przykład 2

Problem:

Znaleźć największy i najmniejszy element w zbiorze n-elementowym S. Załóżmy
dodatkowo, że n jest potęgą liczby 2.

Rozwiązanie:

DZIEL:

Podziel zbiór S na dwa podzbiory S

1

i S

2

, z których każdy zawiera n/2

elementów.

ZWYCIĘŻAJ:

Znajdź minimalne i maksymalne elementy w zbiorach S

1

i S

2

a następnie

wybierz element mniejszy z dwóch znalezionych minimów i element
większy z dwóch znalezionych maksimów.

Procedura realizująca ten algorytm może mieć następującą formę:

MAXMIN(S);
{ S- dany zbiór elementów }
początek

1. jeżeli |S|=2 wtedy { |S| oznacza moc zbioru S }

początek

2.

{ niech S={a, b} }

3.

powrót (MAX(a,b), MIN(a,b))

koniec

w przeciwnym razie
początek

4.

podziel S na dwa rozłączne równoliczne podzbiory S

1

i S

2

,

5.

(max1, min1):= MAXMIN(S

1

);

6.

(max2, min2):= MAXMIN(S

2

);

7.

powrót (MAX(max1, max2), MIN(min1, min2)

koniec

koniec

Zauważmy, że wywoływanie rekurencji zostaje zastopowane, gdy zbiór, który mamy

podzielić, zawiera dokładnie 2 elementy!

Obliczymy teraz funkcję złożoności czasowej. Jako operację dominującą przyjmijmy

porównanie dwóch elementów zbioru S. Porównania te wykonują się w instrukcji 3 i 7.

Oznaczmy przez T(n) liczbę porównań między elementami zbioru S, które wykonuje

procedura MAXMIN w celu znalezienia maksymalnego i minimalnego elementu w zbiorze n-
elementowym.

Mamy

T(2)=1 dla n=2. (instrukcja 3)
natomiast dla n>2, T(n) jest równe całkowitej liczbie porównań wykonanych w
dwu wywołaniach MAXMIN (linie 5 i 6) dla zbiorów rozmiaru n/2, plus dwa
porównania z linii 7.;l

Dostajemy, więc







>

+

=

=

2

n

dla

2

2T(n/2)

2

n

dla

1

T(n)

Można pokazać, ze rozwiązaniem tego równania rekurencyjnego jest funkcja:

.

2

n

)

n

(

T

2

3

−

⋅

=

a więc T(n)=O(n).

Klasycznym przykładem algorytmu rekurencyjnego jest obliczanie funkcji SILNIA (

ozn. n! )

Definicja funkcji n! jest następująca:

0! = 1
n! = 1

⋅

2

⋅

.....

⋅

(n-1)

⋅

n

co można łatwo zapisać w postaci rekurencyjnej:







<

−

⋅

≤

=

0

n

dla

!

1)

(n

n

0

n

dla

1

n!

Przykładowy algorytm można przedstawić następująco:

Funkcja SILNIA(n);

początek

jeżeli n

≤

0 wtedy pisz (1)

w przeciwnym wypadku

pisz (n*SILNIA(n-1))

koniec

Schemat realizacji funkcji SILNIA(3) jest następujący.

SILNIA(3)

3

≤

0 NIE 3!=3

⋅

2!

⇓

2

≤

0 NIE 2!=2

⋅

1!

⇓

1

≤

0 NIE 1!=1

⋅

0!

⇓

0

≤

0 TAK

Dla n=0 nie następuje wywołanie rekurencyjne,
Dla n>0 kolejne wywołania odbywają się dla malejących systematycznie wartości argumentu
aż do wywołania z argumentem 0, który zatrzymuje całą rekursję.

OGÓLNIE:

zależność, której spełnienie przez algorytm wywołania gwarantuje uniknięcie dalszej
rekursji, nazywamy przypadkiem bazowym (ang. base case), lub warunkiem stopu rekursji
(ang. stopping case).

Jedną z konsekwencji każdego wywołania rekursywnego jest zajęcie pewnego obszaru
pamięci, który jest wykorzystywany przez stos, na którym zapamiętywane są wyniki kolejnych,
jeszcze nie zakończonych wywołań procedury. Stos podzielony jest na fragmenty stosu, będące
blokami kolejnych miejsc pamięci- każdy fragment zawiera dane o jednym trwającym
wywołaniu procedury. W przypadku bardzo dużej liczby wywołań rekurencyjnych szybko może
nastąpić przepełnienie stosu, a w konsekwencji przerwanie pracy procedury.

Przykładem takiej „kłopotliwej” procedury rekurencyjnej jest procedura generowania n-

tego wyrazu ciągu Fibonacciego

Ciąg Fibonacciego

Definicja ciągu Fibonacciego jest następująca:

f(0) = 1
f(1) = 1
f(n) = f(n-1) + f(n-2)

dla n

≥

2.

Przykładowe początkowe wyrazy:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Rekurencyjna funkcja obliczającą n-ty wyraz tego ciągu ma postać:

Funkcja Fibo(n);

początek

jeżeli n

≤

1 wtedy Fibo:=1

w przeciwnym razie Fibo:=Fibo(n-1) + Fibo(n-2)

koniec;

3!=3

⋅⋅⋅⋅

2=6

↑↑↑↑

2!=2

⋅⋅⋅⋅

1=2

↑↑↑↑

1!=1

⋅⋅⋅⋅

1=1

↑↑↑↑

0!=1

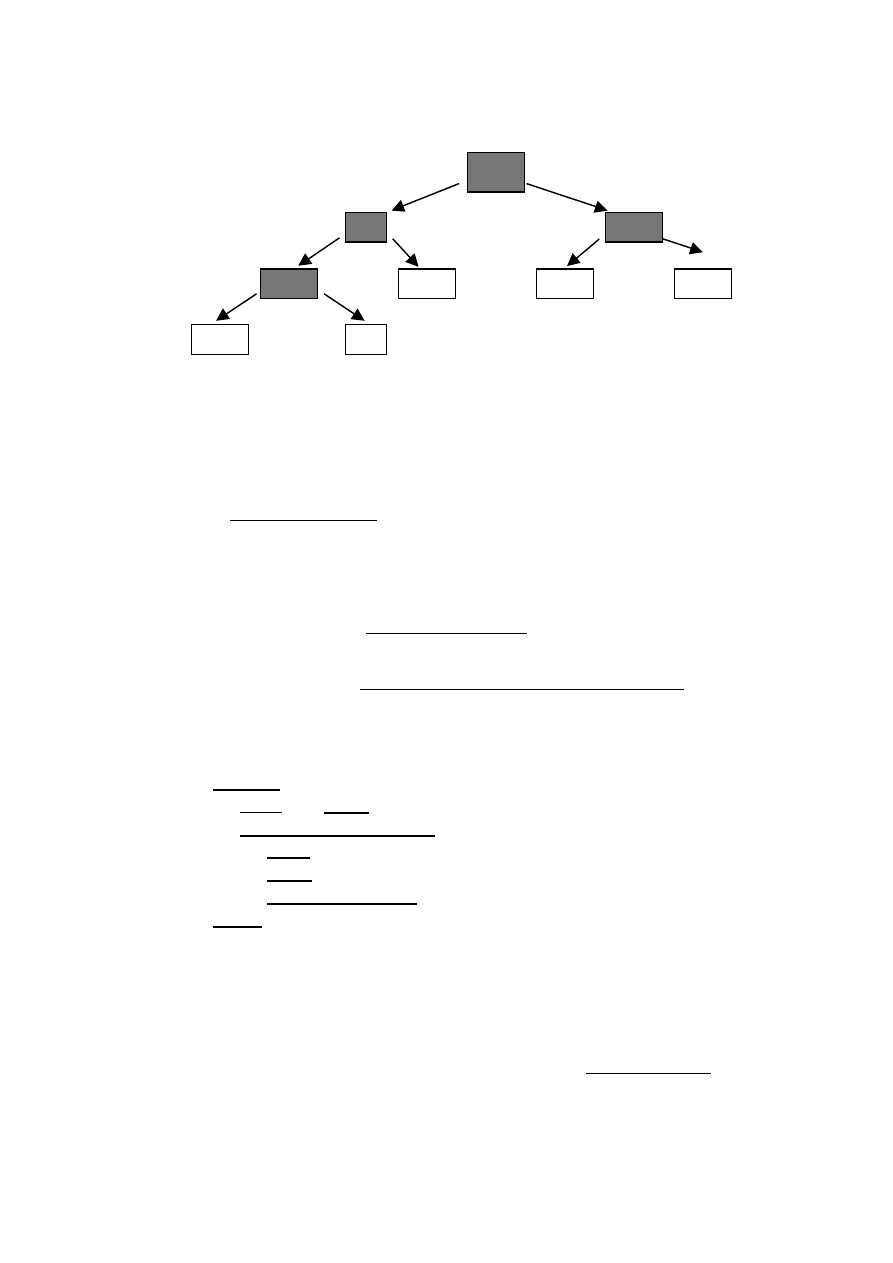
Prześledźmy schemat wywołań funkcji Fibo dla n=4

F(4)

F(3)

F(2)

F(2)

F(1)

F(1)

F(0)

F(1)

F(0)

F(4) = F(3) + F(2) = F(2) + F(1) + F(1) + F(0) = F(1) + F(0) + F(1) + F(1) + F(0) = 2F(0) +

3F(1) =
= (1+1) + (1+1+1) = 2 + 3 = 5

Widać tu wyraźnie, że pewna część obliczeń wywoływana jest wielokrotnie - 3-razy F(1) i 2-
razy F(0).
Algorytm ten ma złożoność czasową:

T(n)=(1,6)

n

. Przyczyną tak dużej złożoności

czasowej jest wielokrotne obliczanie tych samych wartości. Np.

dla n=30 wyraz F(30) ma 832040 wywołań funkcji F(0) i F(1),

natomiast odpowiadający mu algorytm iteracyjny ma tylko 30 dodawań !!!

Problem stopu rekursji

W wielu algorytmach rekurencyjnych, z pozoru poprawnie skonstruowanych, może być

ukryty poważy błąd polegający na nieskończonej ilości wywołań rekurencyjnych, czyli błędnie
sformułowanego warunku stopu.

Przeanalizujmy nastepujący przykład:

Funkcja Dokoncaswiata(n);

początek

jeżeli n=1 wtedy pisz(1)
w przeciwnym przypadku

jeżeli n mod 2=0

{ n jest parzysta }

wtedy pisz( Dokoncaswiata(n-2)*n )
w przeciwnym razie pisz(

Dokoncaswiata(n-1)*n )

koniec;

Z pozoru wszystko jest poprawne, bowiem:

1) jest przypadek bazowy (stop)
2) problem rzędu n jest upraszczany do problemu o rozmiarze niższym: n-1 lub n-2.

Dokładna analiza pokazuje jednak, że dla n

≥≥≥≥

2 wszystkie wywołania funkcji kończą się

parzystą wartością n, a to oznacza, że po dojściu do n=2 przejdziemy kolejno do n=0, potem n=-
2, itd. Nigdy, więc nie znajdzie się przypadek bazowy ( n=1 ), który zatrzyma rekursję.

Wniosek:

Należy zawsze sprawdzać, czy dla wartości parametrów wejściowych
należących do dziedziny wartości, które mogą być użyte, rekurencja kiedyś się
skończy.

NWP - rekurencyjny algorytm Euklidesa

Na zakończenie rozważań o rekurencji omówimy jeden z klasycznych algorytmów

rekurencyjnych, którym jest algorytm Euklidesa obliczający największy wspólny podzielnik
dwu liczb naturalnych.

Definicja

Największym wspólnym podzielnikiem ( ozn. NWP ) dwu liczb całkowitych nazywamy

największą liczbę będącą podzielnikiem ich obu.

Poniższa zależność rekurencyjnia podana przez Euklidesa w IV wieku p.n.e., jest podstawą

obliczenia NWP:







≠

=

=

0

n

mod

m

gdy

n)

mod

m

NWP(n,

0

n

mod

m

gdy

n

n)

NWP(m,

gdzie m, n >0.

Przykład:

Obliczyć NWP dla dwóch licz całkowitych: 243 i 114.

Mamy

NWP(243,114)= NWP(114,15)= NWP(15,9)= NWP(9,6)= NWP(6,3)= NWP(3,0)= 3

Postać pseudokodu funkcji EUKLID realizującej NWP :

Funkcja EUKLID(m,n);
{zakładamy, że m

≥

0, n

≥

0}

początek

jeżeli n=0 wtedy EUKLID:=m
w przeciwnym razie

EUKLID:= EUKLID (n, m mod n)

koniec;

Np. Dla m=30 i n=31 kolejne wywołania funkcji EUKLID sa następujaceL

EUKLID(30,21) " EUKLID(21,9) " EUKLID(9,3) " EUKLID(3,0) = 3

Mamy tu trzy rekurencyjne wywołania funkcji EUKLID. Ciąg wywołań nie może być

nieskończony, gdyż za każdym wywołaniem zmniejsza się wartość drugiego argumentu.

Zatem funkcja EUKLID zawsze się kończy i oblicza poprawny wynik.

Liczba wywołań rekurencyjnych funkcji EUKLID dla m>n>0 wynosi: O(log b).

4. Podstawowe struktury danych

Dane, z którymi pracują algorytmy, są zbiorami, na których dozwolone są pewne operacje.

Rodzaj tych operacji określa wewnętrzna organizacja danego zbioru. Ze względu na to, że
operacje te mogą powiększać, zmniejszać lub zmieniać ich zawartość, zbiory takie nazywamy
zbiorami dynamicznymi.

Operacje wykonywane na zbiorach dynamicznych można podzielić na dwie grupy:

Zapytania – czyli operacje, które pozwalają uzyskać wyłącznie pewne informacje na

temat zbioru

Operacje modyfikujące - czyli operacje, które mogą zmieniać zbiór

Lista typowych operacji na zbiorach dynamicznych:

Oznaczenia: S- zbiór, x - element zbioru S, k- wartość klucza dla elementu zbioru S

SZUKAJ(S,k)

Zapytanie, które dla zbioru S oraz wartości klucza k, daje w
wyniku albo element x ze zbioru S, o kluczu równym k, albo NIC,
gdy taki element nie należy do S

DOPISZ(S,x)

Operacja modyfikująca, która dodaje element x do zbioru S

USUŃ(S,x)

Operacja modyfikująca, która usuwa element x ze zbioru S

MINIMUM(S)

Zapytanie, które podaje element ze zbioru S o najmniejszej
wartości klucza

MAKSIUM(S)

Zapytanie, które podaje element ze zbioru S o największej
wartości klucza

NASTĘPNIK(S,x)

Zapytanie, które podaje następnik elementu x w zbiorze S lub
NIC, gdy x jest największym w S

POPRZEDNIK(S,x)

Zapytanie, które podaje element poprzedzający x w zbiorze S
lub NIC, gdy x jest najmniejszym w S

Uwaga: Dla operacji typu ZAPYTANIE zakładamy, że zbiór S jest liniowo uporządkowany.

Operacja SZUKAJ może być wykonywana również na zbiorze nieuporządkowanym.

A)

Listy

Lista jest to skończony ciąg elementów

q=[x

1

, x

2

, ... x

n

],

czyli elementy ułożone w porządku liniowym. Porządek ten określają wskaźniki związane z
każdym elementem listy.

Skrajne elementy listy x

1

i x

n

nazywane są końcami listy (x

n

-lewym, x

n

-prawym), natomiast

wielkość |q|=n - długością listy (lub rozmiarem listy).

Szczególnym przypadkiem jest lista pusta: q=[] o długości 0.

Niech dane będą dwie listy:

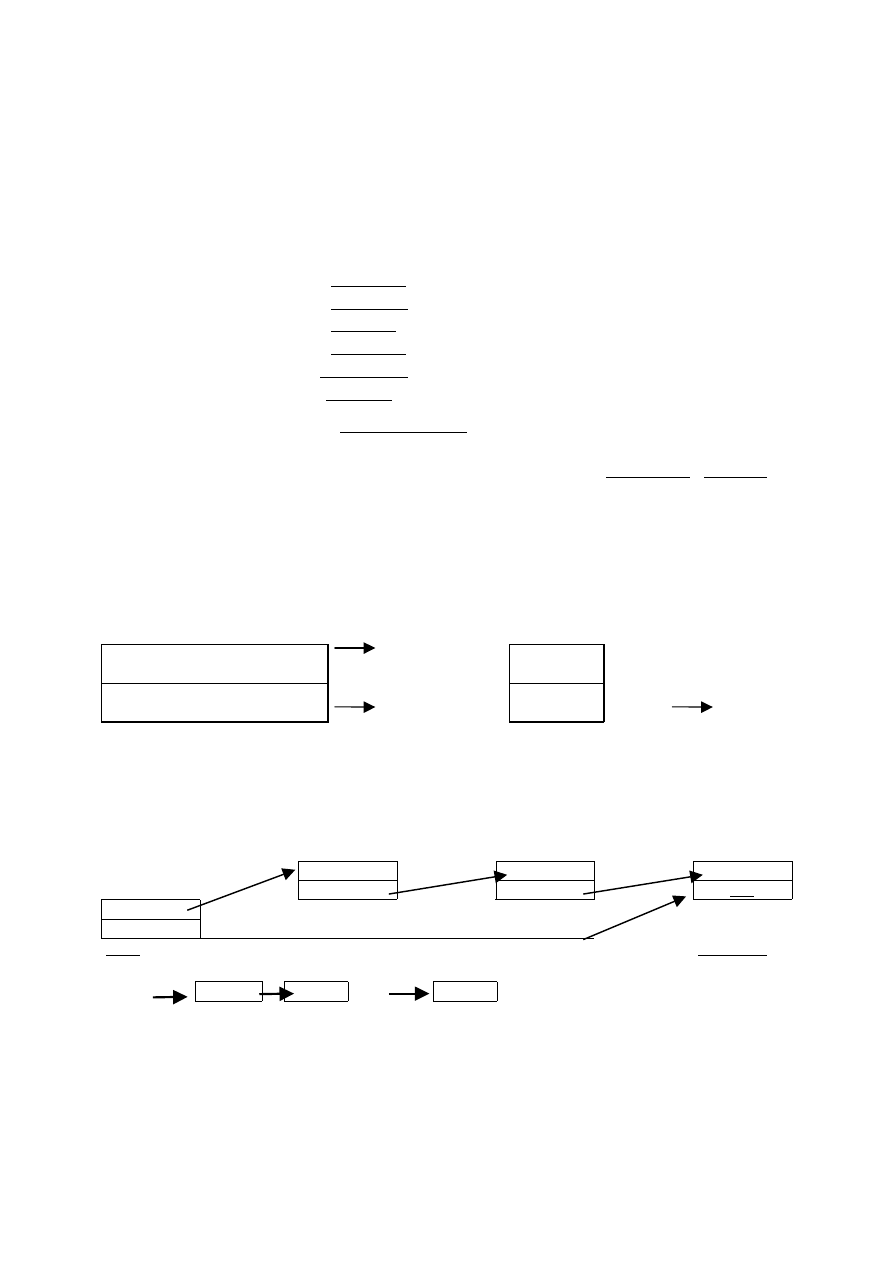
q=[x

1

, x

2

,... x

n

] , r=[y

1

, y

2

,... y

m

] oraz 0

≤

i

≤

j

≤

n

Podstawowymi operacjami na listach są:

−

dostęp do elementu listy:

q[i]=x

i

−

podlista

q[i..j]=[x

i,

x

i+1

,... x

j

]

−

złożenie (konkatenacja) list

qr=[x

1,

...x

n

, y

1

,..., y

m

]

Obsługa listy ogranicza się do operacji wykonywanych na jej końcach:

a) front(q)=q[1]

- pobieranie lewego końca listy

b) push(q,x)=[x]&q

- wstawienie elementu x na lewy koniec listy

c) pop(q)=q[2...|q|]

- usunięcie bieżącego lewego krańca listy

d) rear(q)=q(|q|)

- pobieranie prawego końca listy

e) inject(q,x)= q&[x]

- wstawienie elementu x n prawy koniec listy

f) eject(q)= q[1,...,|q|-1] -usunięcie bieżącego prawego końca listy

Do budowy listy używane są dwa typy komórek:

Typ INFO;

-

jest komórką informacyjną zawierającą dwa wskaźniki: do początku i do końca
listy.

Typ ELEMENT

-

jest

komórką roboczą i zawiera dwa pola:

−

wartość elementu

−

wskaźnik do następnego elementu listy

Lewy koniec
(głowa)

???

Wartość

Prawy koniec
(ogon)

???

Gdzie
następny

???

Typ

INFO

Typ ELEMENT

W zależności od wykazu dozwolonych operacji rozróżniamy różne rodzaje list:

1) lista jednokierunkowa

25

475

3

NIC

głowa

ogon

INFO

ELEMENT

x

1

x

2

....

x

n

operacje: front, push, pop

2) lista jednokierunkowa cykliczna

S

125

-42

operacje: front, push, pop, rear, inject

3) lista dwukierunkowa

18

8

125

45

NIC

NIC

3) lista dwukierunkowa cykliczna

5

8

40

50

x

1

x

2

....

x

n

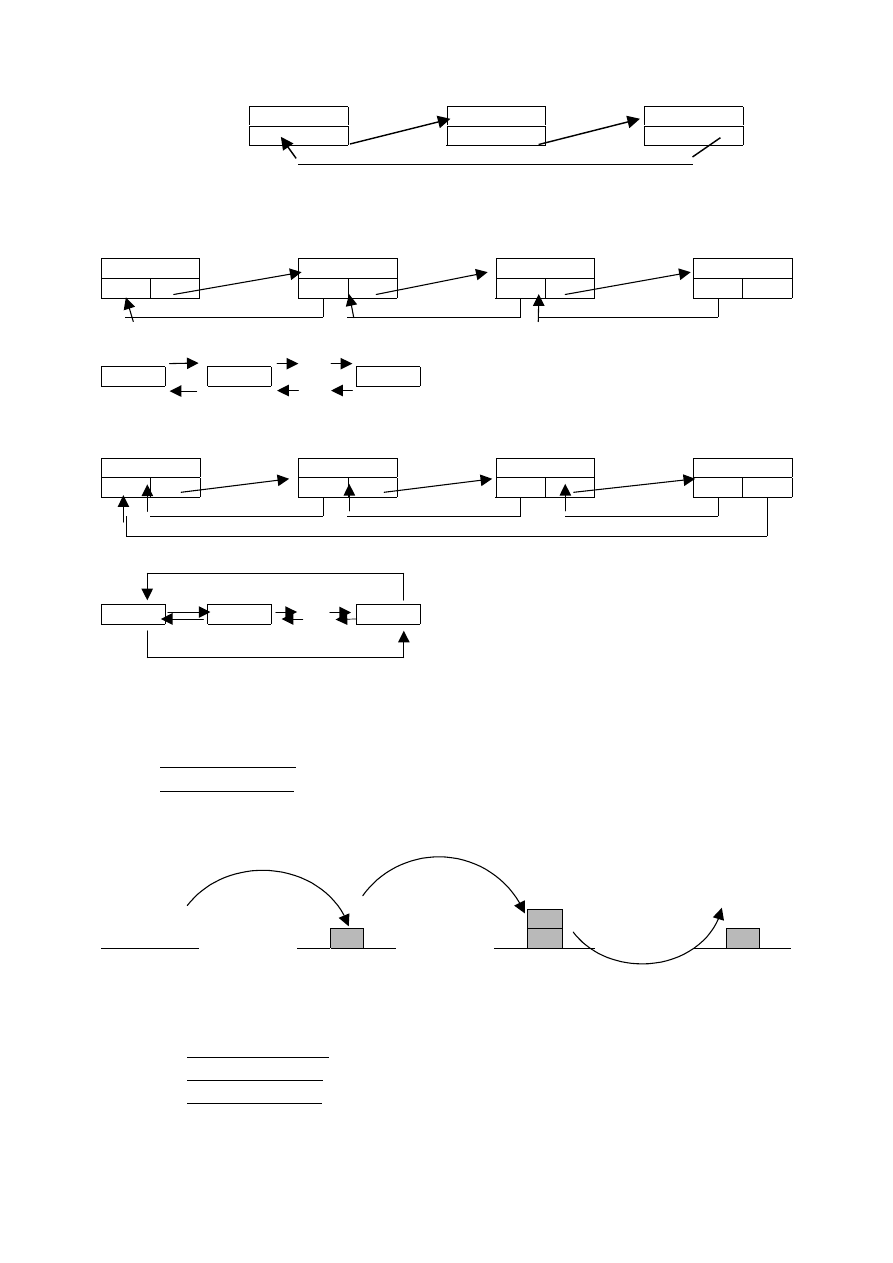
5) STOS (lista jednokierunkowa)

Dozwolone operacje

−

dopisanie elementu od strony wierzchołka stosu PUSH

−

usunięcie elementu z wierzchołka stosu POP

Zasada LIFO

→

→

→

→

Last-In-First-Out

→

→

→

→

Stos pusty

push(5)

push(15)

pop(15)

15

5

5

5

6) Kolejka (lista jednokierunkowa)

Dozwolone operacje
-

pobieranie elementu z dołu ( z czoła kolejki )

-

dopisanie elementu od strony wierzchołka PUSH

-

usunięcie elementu od strony czoła INJECT

Zasada FIFO

→

→

→

→

First -In-First-Out

→

→

→

→

x

1

x

2

....

x

n

kolejka pusta

push(5)

push(15)

15

5

5

15

Inject (5)

B) DRZEWA

Drzewo (ang. tree) jest strukturą podobną do listy jednokierunkowej, z tą różnicą, że każdy

element może mieć dowiązania do więcej niż jednego swojego następnika.
Na przykład:

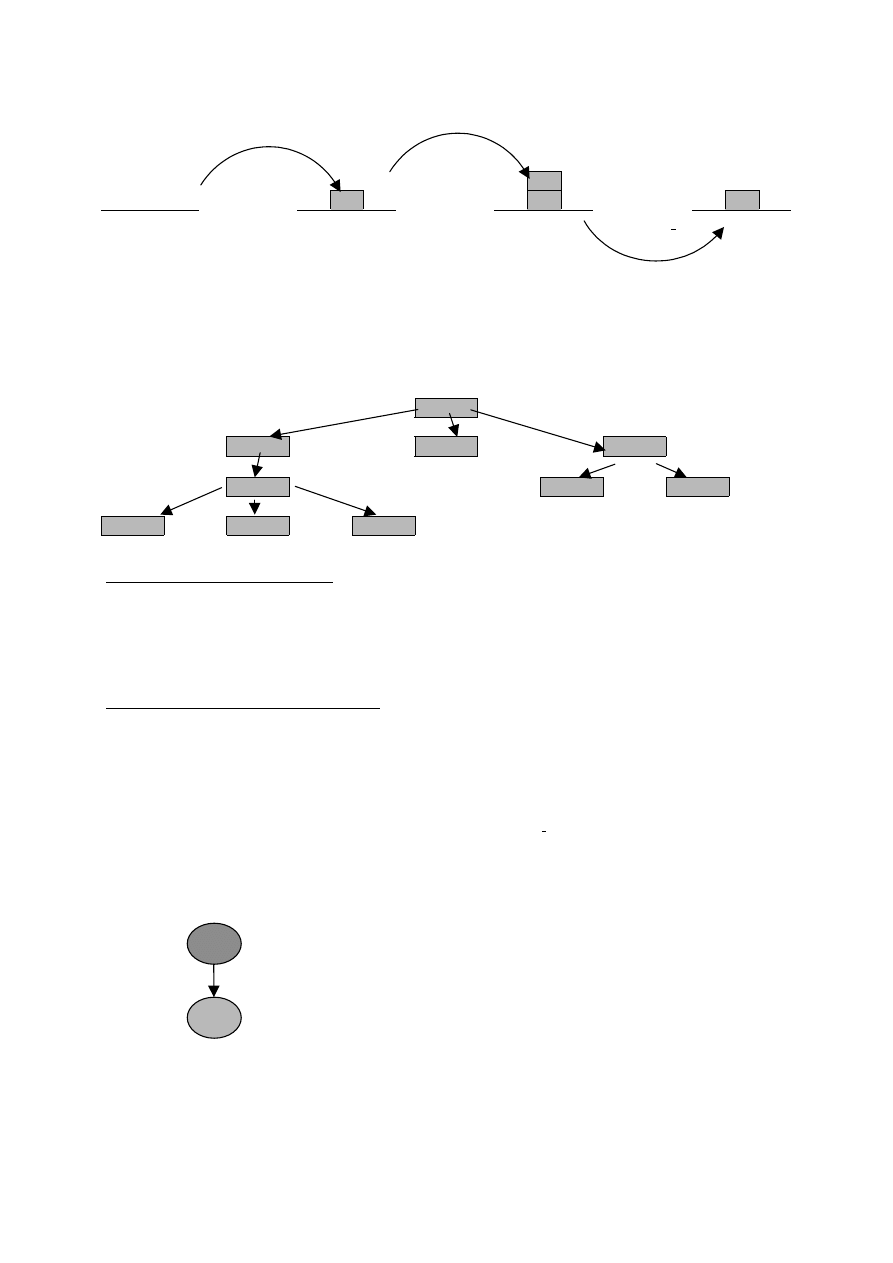
A

B

C

D

E

F

G

H

I

J

Definicja drzewa (rekurencyjna)

Drzewem nazywamy

−

strukturę pustą (drzewo puste)

lub

−

węzeł, zwany korzeniem drzewa (ang. root), połączony z zerem lub większą liczbą drzew
zwanych poddrzewami (ang. subtrees)

Podstawowe terminy dotyczące drzew:

Korzeń

- wyróżniony wierzchołek

Gałąź

- dowolne połączenie pomiędzy węzłami

Liść

- węzeł nie mający poddrzew

Węzeł wewnętrzny - węzeł nie będący liściem.

Dla dwóch węzłów połączonych gałęzią zachodzą powiązania:

Węzeł rodzicielski:

ten, z którego gałęzi wychodzi

Węzeł potomny:

ten, do którego gałęzi wchodzi

Korzeń jest jedynym węzłem, który NIE MA węzła rodzicielskiego.

Wszystkie węzły leżące na drodze od korzenia do danego węzła nazywane są przodkami

tego ostatniego.

A

B

Rodzic dla B (poprzednik B, ojciec B)

Potomek A (następnik A, syn A)

Węzły, dla których dany węzeł pełni rolę przodka nazywane są jego potomkami.
Bezpośredni potomkowie węzła nazywani są jego synami, on zaś nazywany jest ich ojcem.

Pomiędzy węzłami - synami tego samego węzła ojca - istnieje relacja rodzeństwa, a ich określa
się braćmi .

Stopniem węzła nazywamy liczbę jego następników, natomiast stopniem drzewa -

największą liczbę spośród stopni jego węzłów.

Głębokością węzła nazywamy liczbę większą o 1 od liczby jego przodków. Głębokość

drzewa (lub wysokość drzewa) to maksymalna spośród głębokości jego węzłów.

korzeń

Głębokość 1

A

B

C

D

Głębokość 2

gałęzie

E

F

Głębokość 3

H

I

J

liście

Głębokość 4

Synowie E

: H,I,J

Ojciec F

: D (zawsze TYLKO JEDEN)

Bracia

: H,I,J

Stopień E

: 3

Stopień drzewa

: 3

Głębokość F

: 3

Głębokość drzewa : : 4

Elementy składowe przykładowego drzewa

Drzewo stopnia 2 nazywane jest często drzewem binarnym. Struktura organizacji

dowolnego wierzchołka takiego drzewa jest następująca:

Adres ojca

Adres lewego syna

Adres prawego syna

Wartość węzła

Sposoby przeglądania (odwiedzania) wierzchołków drzewa

Metoda PREORDER

1. odwiedź korzeń drzewa
2. odwiedź lewe poddrzewo (jeżeli istnieje) metodą PREORDER
3. odwiedź prawe poddrzewo (jeżeli istnieje) metodą PREORDER

czyli Korzeń-Lewe-Prawe ( K-L-P)

Metoda INORDER

1. odwiedź lewe poddrzewo (jeżeli istnieje) metodą INORDER

2. odwiedź korzeń drzewa
3. odwiedź prawe poddrzewo (jeżeli istnieje) metodą INORDER

czyli Lewe-Korzeń-Prawe ( L-K-P )

Metoda POSTORDER

1. odwiedź lewe poddrzewo (jeżeli istnieje) metodą POSTORDER
2. odwiedź prawe poddrzewo (jeżeli istnieje) metodą POSTORDER
3. odwiedź korzeń drzewa

czyli Lewe-Prawe-Korzeń ( L-P-K )

Metoda LEVELORDER

1. odwiedź korzeń drzewa
2. odwiedź następniki korzenia od lewej do prawej
3. odwiedź wnuki korzenia od lewej do prawej
4. itd...

Przykład

A

B

C

D

E

F

G

PREORDER =

A-B-D-E-C-F-G

( K-L-P )

1

2

5

3

4

6

7

INORDER

=

D-B-E-A-F-C-G

( L-K-P )

4

2

6

1

3

5

7

POSTORDER

= D-E-B-F-G-C-A

( L-P-K )

7

3

6

1

2

4

5

LEVELORDER

= A-B-C-D-E-F-G

1

2

3

4

5

6

7