Algorytmy i struktury danych

1. Klasyczne algorytmy.

a) Badanie, czy liczba jest liczbą pierwszą

- Metoda naiwna:

Dla danej liczby n sprawdzamy czy dzieli się ona kolejno przez 2, 3 ... n-1. Jeżeli przez

żadną z nich się nie dzieli - to liczba n jest liczbą pierwszą.

Udoskonalenie 1: Zamiast testowania wszystkich liczb do n-1 możemy sprawdzać

podzielność n przez liczby ≤ pierwiastek[n].

Udoskonalenie 2: Za pomocą Sita Eratostenesa możemy wygenerować wszystkie liczby

pierwsze ≤ pierwiastek[n] i sprawdzić podzielność tylko przez nie.

Metoda ta wymaga wykonania bardzo dużej liczby dzieleń: pierwiastek[n]/logn.

- Test pierwszości Fermata:

Metoda należy do grupy "Testów probabilistycznych" (wymagających stosowania liczb

losowych). Test ten sprawdza czy liczba jest złożona, czy prawdopodobnie pierwsza.

Małe twierdzenie Fermata mówi, że jeśli p jest liczbą pierwszą i 1 ≤ a < p to a

p-1

≡

1(mod p).

Aby stwierdzić czy p jest liczbą pierwszą , możemy wybrać kilka losowych wartości a i

sprawdzić czy ta równość jest dla nich spełniona. Jeśli dla któregokolwiek nie jest to

wiemy na pewno, że liczba p jest liczbą złożoną. Jeśli wszystkie ją spełniają to p jest

prawdopodobnie liczbą pierwszą lub pseudopierwszą (liczba naturalna, która spełnia

niektóre własności charakteryzujące liczby pierwsze).

Dzięki użyciu algorytmu szybkiego potęgowania, test ten możemy wykonać w czasie O(k

log

3

n) (gdzie k jest liczbą losowo wybranych a).

- Metoda Millera-Rabina:

Metoda należy do grupy "Testów probabilistycznych" (wymagających stosowania liczb

losowych). Test ten sprawdza czy liczba jest złożona, czy prawdopodobnie pierwsza.

Niech p > 2 będzie nieparzystą liczbą naturalną, a k parametrem określającym

dokładność testu. Naszym zadaniem będzie sprawdzenie, czy liczba p jest liczbą

pierwszą. Zatem:

- wyliczamy maksymalną potęgę dwójki dzielącą p-1 i przedstawiamy p-1 jako 2

s

d,

- powtarzamy k-razy:

* wybieramy losowo liczbę a z przedziału [1,n-1],

* jeśli a

d

≠ 1(mod n) oraz a

2^r d

≠ -1(mod n) dla wszystkich r z przedziału [0,s-1] - to

liczba jest złożona,

- jeśli k-krotne wykonanie testu nie zwróciło informacji, iż liczba jest złożona - to liczba

jest prawdopodobnie liczbą pierwszą.

Dzięki użyciu algorytmu szybkiego potęgowania, test ten możemy wykonać w czasie O(k

log

3

n) (gdzie k jest liczbą losowo wybranych a).

b) Algorytmy Euklidesa (przez odejmowanie i przez dzielenie)

Algorytm Euklidesa - algorytm znajdowania największego wspólnego dzielnika (NWD)

dwóch liczb naturalnych.

- Algorytm Euklidesa przez odejmowanie (zwykły):

Zasada działania:

- wczytaj liczby a i b,

- jeśli a = b to koniec algorytmu - NWD(a,b) = a (lub NWD(a,b) = b),

- jeśli a > b to za a podstaw a-b i przejdź do kroku drugiego,

- jeśli a < b to za b podstaw b-a i przejdź do kroku drugiego.

Metoda ta nie jest efektywna.

- Algorytm Euklidesa przez dzielenie (szybki):

W algorytmie wykorzystywana jest zależność:

Zasada działania:

- oblicz c jako resztę dzielenia a przez b,

- zastąp pozycję a liczbą b, a liczbę b liczbą c,

- jeśli b = 0, to szukane NWD(a,b) = a, w przeciwnym wypadku przejdź na początek

algorytmu.

c) Liniowe przeszukiwanie ciągu w poszukiwaniu żądanego elementu z wykorzystaniem

wartownika

Wyszukiwanie liniowe z wartownikiem polega na wyszukiwaniu elementu w zbiorze

nieuporządkowanym.

W przeciwieństwie do zwykłego wyszukiwania liniowego (sekwencyjnego), algorytm ten

wykorzystuje istnienie tzw. wartownika (element na n+1 miejscu tablicy) - dzięki

któremu upraszcza się sprawdzanie założeń i zmniejsza liczba porównań.

Zasada działania:

- niech i = 1, a T[n+1] = K,

- jeśli T[i] != K to zwiększ wartość i oraz powtórz ten krok,

- jeśli T[i] = K to sprawdź, czy i ≤ n - jeśli tak to zakończ algorytm sukcesem, w

przeciwnym wypadku zakończ algorytm niepowodzeniem.

Złożoność obliczeniowa: O(n)

d) Wyszukiwanie elementu w zbiorze uporządkowanym (wyszukiwanie binarne)

Wyszukiwanie binarne polega na wyszukiwaniu elementu w zbiorze uporządkowanym

przez relację (T[1] ≤ T[2] ≤ ... ≤ T[n] - czyli klucze posortowane rosnąco).

Zasada działania:

- oznaczamy za l pierwszy element tablicy (T[1]), a za r ostatni element (T[n]),

- jeśli l > r to kończymy algorytm niepowodzeniem. W przeciwnym wypadku

przypisujemy: m = podłoga z [(l+r)/2],

- jeśli K (szukany element) jest większy od T[m] to przypisz: r = m - 1 i wróć do

drugiego kroku,

- jeśli K (szukany element) jest mniejszy od T[m] to przypisz: l = m + 1 i wróć do

drugiego kroku,

- jeśli K (szukany element) jest równy T[m] to zakończ algorytm sukcesem.

Złożoność obliczeniowa: O(lgn) - dla 1000000 elementów, w celu odnalezienia szukanej

wartości koniecznych jest tylko około 20 porównań!

e) Znajdowanie najmniejszego lub największego elementu w zbiorze

Znajdowanie Minimum/Maksimum w określonym zbiorze elementów polega na

zwróceniu indeksu elementu, którego wartość jest najmniejsza/największa.

Zasada działania (Maksimum):

- niech m = T[1], a j = 1 (po zakończeniu algorytmu m będzie przechowywało wartość

elementu maksymalnego, a j jego indeks),

- iterujemy po tablicy od elementu T[2] do T[n],

- jeśli T[i] ≥ m to oznacza, że znaleźliśmy większy element od tego, który aktualnie

uważamy za maksymalny. W związku z tym: m = T[i], a j = i,

- po zakończeniu pętli zwracamy m oraz j.

Do znalezienia Minimum/Maksimum koniecznych jest co najmniej n-1 porównań!

f) Znajdowanie jednocześnie najmniejszego i największego elementu w zbiorze

(algorytm optymalny)

Algorytm podstawowy (nieoptymalny) - najpierw wyszukaj Minimum, a potem wyszukaj

Maksimum (co najmniej 2(n-1) porównań).

Algorytm optymalny - zasada działania:

- bierz kolejne pary elementów i na miejsce nieparzyste wstawiaj element mniejszy, a na

parzyste element większy. W przypadku nieparzystej liczby elementów - ostatni z nich

oznacz jako c,

- znajdź minimum w zbiorze elementów o nieparzystych indeksach, a maksimum w

zbiorze elementów o parzystych indeksach,

- porównaj otrzymane minimum oraz maksimum z elementem c (o ile istnieje!).

Liczba porównań: sufit z [3n/2] - 2

g) Obliczanie wartości wielomianu - schemat Hornera

Schemat Hornera - sposób obliczania wartości wielomianu dla danej wartości

argumentu wykorzystujący minimalną liczbę mnożeń.

Zasada działania (na podstawie przykładu):

Wielomian postaci: W(x) = a

0

+ a

1

x + a

2

x

2

+ ... + a

n

x

n

przekształcamy do postaci: W(x) = a

0

+ x(a

1

+ x(a

2

+ ... + x(a

n-1

+ xa

n

)...))

Następnie definiujemy:

b

n

= a

n

,

b

n-1

= a

n-1

+ b

n

x,

...

b

0

= a

0

+ b

1

x.

Dzięki takiemu rozumowaniu - wynikiem W(x) będzie b

0

.

h) Szybkie podnoszenie do potęgi

Algorytm szybkiego potęgowania - metoda pozwalająca na szybkie obliczenie potęgi

o wykładniku naturalnym.

Chcąc wykonać działanie: a

b

wykonujemy tak naprawdę serię mnożeń (a

b

= a*a

b-1

=

a*a*a*...*a). Jednak w przypadku dużych liczb - metoda ta jest nieefektywna. W

związku z tym, w popularnych algorytmach (np. w algorytmie szyfrowania RSA) do

podnoszenia liczb do określonych potęg wykorzystywany jest algorytm szybkiego

potęgowania.

Zasada działania:

W celu obliczenia a

b

wystarczy znać wynik a

podłoga z [b/2]

.

Przykład:

Aby obliczyć 5

175

wystarczy znać wartość x = 5

87

, a następnie policzyć wartość y = x

2

=

5

174

i wynik ten pomnożyć przez 5. Dzięki takiemu rozumowaniu, przechodząc z 5

87

do

5

175

wystarczy wykonać 2 mnożenia - zamiast 88.

2. Złożoność obliczeniowa algorytmu (czasowa i pamięciowa).

a) Złożoność czasowa

Za miarę złożoności czasowej algorytmu możemy przyjąć:

- liczbę instrukcji,

- liczbę operacji arytmetycznych,

- liczbę wywołań rekurencyjnych funkcji,

- liczbę porównań.

Przed wykonaniem pomiaru złożoności czasowej algorytmu musimy określić, które z

wykonywanych operacji są w danym algorytmie najważniejsze, a więc jakie działania są

tzw. operacjami

dominującymi. Przykładowo, w algorytmie mnożenia macierzy za operacje dominujące

można przyjąć dodawanie oraz mnożenie, natomiast w algorytmie wyszukiwania

operacją dominującą będzie porównywanie kluczy.

t(A,d) - liczba operacji dominujących wykonywanych przez algorytm A dla konkretnego

zestawu danych d.

Rozmiar danych możemy określić następująco:

- fizyczny rozmiar danych (liczba bitów, liczba bajtów),

- mnogościowy rozmiar danych (liczba danych wejściowych),

- geometryczny rozmiar danych (wymiar przestrzeni danych).

Przykładowo, w algorytmach sortowania rozmiarem danych będzie ilość rekordów/kluczy

do posortowania, a w przypadku algorytmu wykonującego działania na macierzach - ich

wymiar.

Złożoność obliczeniowa (czasowa) algorytmu - związek pomiędzy rozmiarem

danych n, a czasem wykonania algorytmu A - T(A,n).

Złożoność obliczeniowa optymistyczna (konieczna) algorytmu - liczba operacji

dominujących koniecznych do wykonania algorytmu dla co najwyżej jednego

(najlepszego) zestawu danych - T

MIN

(A,n) = min{t(A,d):d D

n

} gdzie D

n

to zbiór danych

o rozmiarze n.

Złożoność obliczeniowa pesymistyczna (wystarczająca) algorytmu - liczba

operacji dominujących wystarczających do wykonania algorytmu dla dowolnego

(najgorszego) zestawu danych - T

MAX

(A,n) = max{t(A,d):d D

n

} gdzie D

n

to zbiór danych

o rozmiarze n.

Złożoność obliczeniowa średnia (oczekiwana) algorytmu - średnia liczba operacji

dominujących potrzebnych do wykonania algorytmu dla określonego zestawu danych.

Ten typ złożoności zależy od przyjętego modelu probabilistycznego.

b) Złożoność pamięciowa

Za miarę złożoności pamięciowej algorytmu możemy przyjąć:

- liczbę użytych w programie zmiennych,

- liczbę słów maszynowych potrzebnych do zapamiętania zmiennych.

s(A,d) - liczba słów pamięci potrzebnych do wykonania algorytmu A dla konkretnego

zestawu danych d.

Złożoność pamięciowa algorytmu - związek pomiędzy rozmiarem danych n, a

zapotrzebowaniem algorytmu A na pamięć - S(A,n).

Tak samo jak w przypadku złożoności czasowej, rozważa się również S

MIN

(A,n),

S

MAX

(A,n) oraz S

AVE

(A,n).

3. Notacja asymptotyczna.

a) Notacja asymptotyczna

Notacja asymptotyczna wprowadzona została z powodu trudności w dokładnym

obliczaniu złożoności czasowej lub pamięciowej algorytmów. Można to utożsamiać z

pewnego rodzaju "oszacowaniem" złożoności.

b) Rzędy wielkości funkcji

Niech f i g będą funkcjami, a c, c

1

i c

2

stałymi.

Podstawowe:

- f(n) = O(g(n))

* funkcja f jest co najwyżej rzędu g,

* f(n) ≤ cg(n),

* utożsamiać ze złożonością pesymistyczną.

- f(n) = Ω(g(n))
* funkcja f jest co najmniej rzędu g,

* f(n) ≥ cg(n),

* utożsamiać ze złożonością optymistyczną.

- f(n) = Θ(g(n))
* funkcja f jest dokładnie rzędu g,

* c

1

g(n) ≤ f(n) ≤ c

2

g(n),

* funkcje f i g są asymptotycznie równoważne.

Dodatkowe:

- f(n) = o(g(n))

* funkcja f jest niższego rzędu niż g (o-małe),

* f(n) < cg(n).

- f(n) = ω(g(n))
* funkcja f jest wyższego rzędu niż g (ω-małe),
* f(n) > cg(n).

- f(n) ~ g(n)

* funkcje f i g są asymptotycznie równe.

Uwaga: Używany wyżej znak równości oznacza należenie funkcji do klasy funkcji, a

nie ich równość!

c) Własności zdefiniowanych symboli

- duże symbole są zwrotne - f(n) = O(f(n)),

- wszystkie symbole są przechodnie - f(n) = O(g(n)) ? g(n) = O(h(n))

→ f(n) = O(h(n)),

- wszystkie symbole zachowują mnożenie przez skalar różny od zera - c*O(f(n)) =

O(f(n)),

- symbol Θ jest symetryczny - f(n) = Θ(g(n))

↔ g(n) = Θ(f(n)),

- f(n) = Θ(g(n))

↔ f(n) = O(g(n)) ? f(n) = Ω(g(n)),

- jeśli f(n) = o(g(n)) to f(n) = O(g(n)) ale implikacja odwrotna nie musi zachodzić,

- jeśli f(n) = ω(g(n)) to f(n) = Ω(g(n)) ale implikacja odwrotna nie musi zachodzić.

d) Typy złożoności

- stała - Θ(1)
- podlogarytmiczna - Θ(lglgn)
- logarytmiczna - Θ(lgn)
- podliniowa - Θ(n

c

) dla 0 < c < 1

- liniowa - Θ(n)
- liniowo-logarytmiczna - Θ(nlgn)
- kwadratowa - Θ(n

2

)

- kubiczna - Θ(n

3

)

- wielomianowa - Θ(n

k

) dla k ≥ 1

- wykładnicza - Θ(2

n

)

- nadwykładnicza - Θ(n!) lub Θ(n

n

)

Algorytmy, które mają jedną z dwóch ostatnich typów złożoności są w praktyce

nieprzydatne.

e) Związek notacji asymptotycznej ze złożonością czasową

Definicja: Wybrane operacje mogą być uznane za operacje dominujące algorytmu A, gdy

czas wykonania algorytmu A, wyrażony jako funkcja rozmiaru danych i obliczona dla

tych właśnie operacji, jest asymptotycznie równoważny (Θ) czasowi wykonania
algorytmu A.

Prościej: Rozkładamy algorytm na pojedyncze instrukcje i sprawdzamy ile razy zostaną

one wykonane. Czas wykonania algorytmu będzie sumą wykonania ich wszystkich

razem.

W związku z tym, czas działania algorytmu zapisuje się najczęściej w postaci: T(A,n) =

O(f(n)).

4. Algorytmy sortowania.

a) Sortowanie

Sortowanie to wyznaczenie takiej permutacji indeksów, która określa niemalejący
porządek kluczy.
Sortowanie jest stabilne, gdy zachowuje wejściowy porządek rekordów o tych samych
kluczach (czyli jeśli mamy dwie takie same wartości w tablicy - to po posortowaniu będą
one występowały w odpowiedniej kolejności).

b) Sortowanie przez wybieranie (selekcję)

Sortowanie przez wybieranie (ang. Selection sort)

Zasada działania:
Znajdujemy najmniejszy klucz w tablicy T[1...n] i zamieniamy go z elementem
pierwszym. Następnie wyszukujemy najmniejszy klucz w tablicy T[2...n] i zamieniamy
go z elementem drugim. Powtarzamy to n-1 razy, gdyż nie ma potrzeby wyszukiwania
miejsca dla ostatniego elementu (będzie największy zatem będzie znajdował się na
dobrym miejscu).

Pseudokod:
SELECTION-SORT(T[1...n])
for i=1 to n-1
do

min=1
for j=i+1 to n
do

if T[j]<T[min]

then min=j

zamień(T[i],T[min])

return T

Złożoność obliczeniowa:
- optymistyczna: n

2

- pesymistyczna: n

2

- średnia: n

2

Właściwości:

- ilość porównań kluczy oraz ich zamian jest niezależna od danych wejściowych,

- algorytm jest stabilny.

c) Sortowanie przez wstawianie (ang. Insertion sort)

Zasada działania:

Można to sobie skojarzyć z układaniem talii kart: W danym momencie trzymamy w ręku

karty posortowane oraz karty pozostałe do posortowania. W celu kontynuowania procesu

sortowania bierzemy pierwszą z brzegu kartę ze sterty nieposortowanej i wstawiamy ją

na właściwe miejsce w pakiecie już wcześniej posortowanym.

Pseudokod:
INSERTION-SORT(T[1...n])

for i=2 to n
do

key=T[i]
T[0]=i-1
j=i-1
while key<T[j]
do

T[j+1]=T[j]
j=j-1

T[j+1]=key

return T

Złożoność obliczeniowa:
- optymistyczna: n
- pesymistyczna: n

2

- średnia: n

2

Właściwości:

- algorytm jest stabilny.

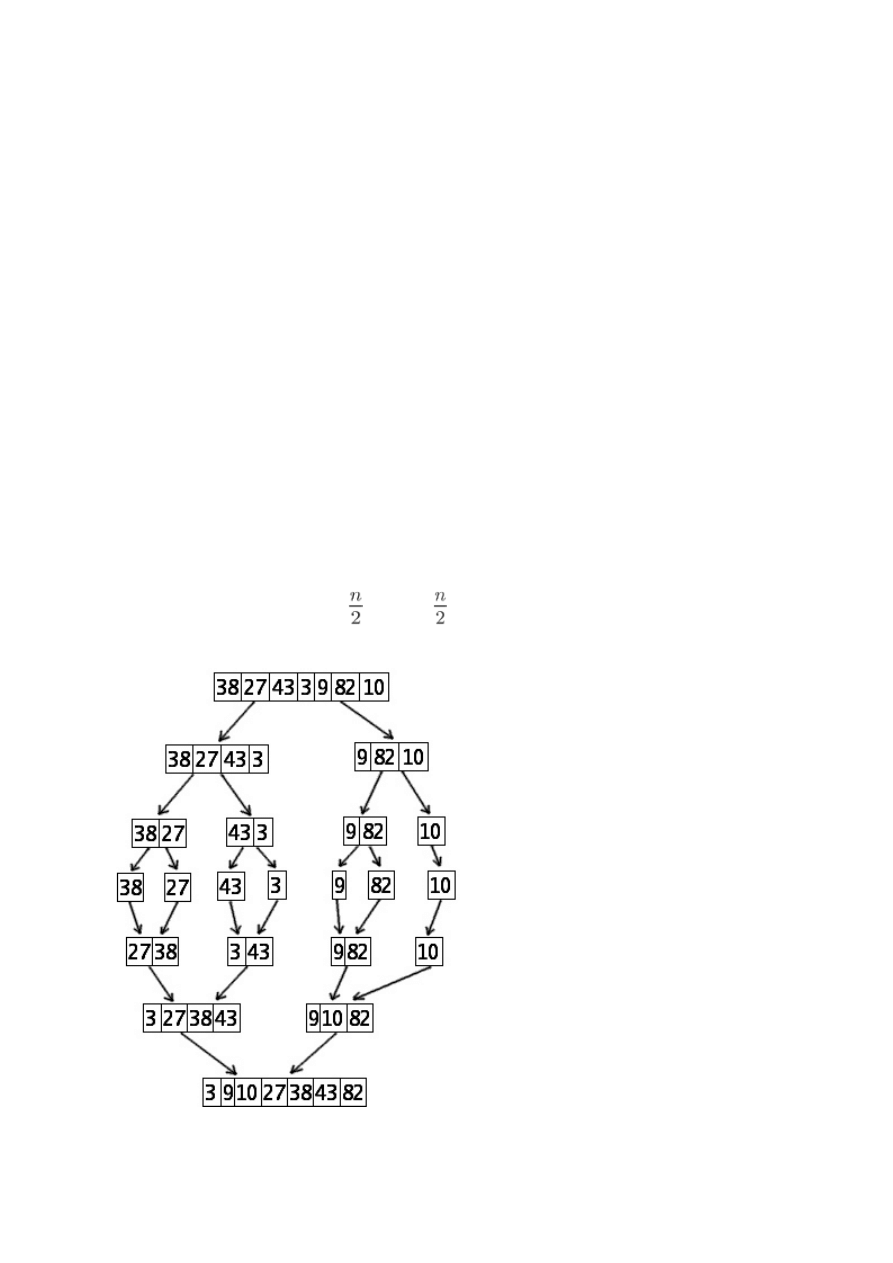
d) Sortowanie przez scalanie (ang. Merge sort)

Zasada działania:

- (Baza) Jeżeli n = 1, to ciąg jest już posortowany,

- (Dziel) Jeżeli n ≥ 2, to dzielimy ciąg odpowiednio na dwa podciągi o liczbie elementów
równej odpowiednio: podloga z

i sufit z

,

- (Zwyciężaj) Rekurencyjnie sortujemy otrzymane podciągi,

- (Połącz) Łączymy posortowane ciągi w jeden ciąg posortowany.

Złożoność obliczeniowa:

- optymistyczna: nlgn

- pesymistyczna: nlgn

- średnia: nlgn

Właściwości:

- algorytm jest stabilny.

e) Sortowanie szybkie (ang. Quick sort)

Zasada działania 1:

- (Baza) Jeżeli n = 1, to ciąg jest już posortowany,

- (Dziel) Jeżeli n ≥ 2, to w każdym kroku algorytmu klucze sortowanego ciągu

są rozdzielane względem (dowolnie) wybranego klucza x (elementu podziału) na

podzbiór elementów mniejszych lub równych

i podzbiór elementów większych

od x. W ten sposób znamy miejsce x,

- (Zwyciężaj) Sortowanie rekurencyjne otrzymanych podzbiorów zgodnie z powyższym

opisem.

Zasada działania 2:

Wybierany jest pewien element tablicy, tzw. element osiowy (zazwyczaj pierwszy

dostępny), po czym na początek tablicy przenoszone są wszystkie elementy mniejsze od

niego, na koniec wszystkie większe, a w powstałe między tymi obszarami puste miejsce

trafia wybrany element. Potem sortuje się osobno początkową i końcową część tablicy.

Rekursja kończy się, gdy kolejny fragment uzyskany z podziału zawiera pojedynczy

element, jako że jednoelementowa podtablica nie wymaga sortowania.

Złożoność obliczeniowa:
- optymistyczna: nlgn
- pesymistyczna: n

2

- średnia: nlgn

Właściwości:

- algorytm nie jest stabilny,
- pomimo gorszej złożoności w przypadku pesymistycznym (od Merge sort) to właśnie
ten algorytm uważany jest za szybki. Wszystko dzięki wartości stałej ukrytej w
złożoności średniej (Quick Sort -> 1,39, Merge Sort - 20).

f) Inne algorytmy sortujące:
- sortowanie przez kopcowanie (ang. Heap sort),
- sortowanie bąbelkowe (ang. Bubble sort),
- sortowanie pozycyjne (ang. Radix sort),
- sortowanie przez zliczanie (ang. Counting sort).

5. Algorytmy rekurencyjne.

Rekurencja - odwoływanie się definicji lub funkcji do samej siebie. Każda definicja/

funkcja rekurencyjna potrzebuje przynajmniej jednego przypadku bazowego (nie

rekurencyjnego), który określa, kiedy procedura rekurencyjna ma przestać wywoływać

samą siebie (spełnienie własności stopu).

Funkcja rekurencyjna jest poprawna, gdy w praktyce spełnia następujące warunki:

• wprost rozwiązuje podstawowy przypadek/przypadki

• każde wywołanie rekurencyjne ma argumenty mniejsze, niż argumenty z którymi

wywołaliśmy funkcję

Przykłady:

• Silnia

n! = 1,

dla n = 0

n*(n-1)!,

dla n

1

Pseudokod:
SILNIA (n: INTEGER)

1.

2. if n = 0
3.

then return 1

4.

else return n * SILNIA(n-1)

• Symbol Newtona

• Liczby Fibonacciego

Metoda "dziel i zwyciężaj"

Odmiana rekurencji. Często stosowana i bardzo wydajna. Składa się z następujących

etapów:

• Dziel - rozbicie problemu na dwa lub więcej podproblemów o mniejszych

rozmiarach

• Zwyciężaj - rekurencyjne rozwiązanie tych podproblemów (ale dla małych

podproblemów stosujemy metody bezpośrednie)

• Łącz - połączenie otrzymanych rozwiązań w rozwiązanie głównego problemu

Lista klasycznych algorytmów, dla których istnieją efektywne rozwiązania oparte na tej

metodzie:

• sortowanie

• znajdowanie otoczki wypukłej

• wyznaczanie pary najmniej odległych punktów

• mnożenie macierzy metodą Strassena

Czas działania algorytmu opartego na tej metodzie:

gdzie mamy k podproblemów,

jest czasem koniecznym do wyznaczenia

podproblemów, a

to czas konieczny do połączenia rozwiązań podproblemów w

główne rozwiązanie.

Przykłady:

1. Wyszukiwanie maksimum w ciągu

Idea:

• (baza) Jeśli n = 1, to jedyny element ciągu jest jego maksimum

• (dziel) Jeżeli n >= 2, to dzielimy ciąg odpowiednio na dwa podciągi o liczbie

elementów równej odpowiednio: podloga z

i sufit z

• (zwyciężaj) Rekurencyjnie rozwiązujemy problem dla otrzymanych podciągów

• (połącz) porównujemy otrzymane maksima

Złożoność czasowa (liczba porównań kluczy):

2. Sortowanie przez scalanie (Merge Sort).

3. Sortowanie szybkie (Quick Sort).

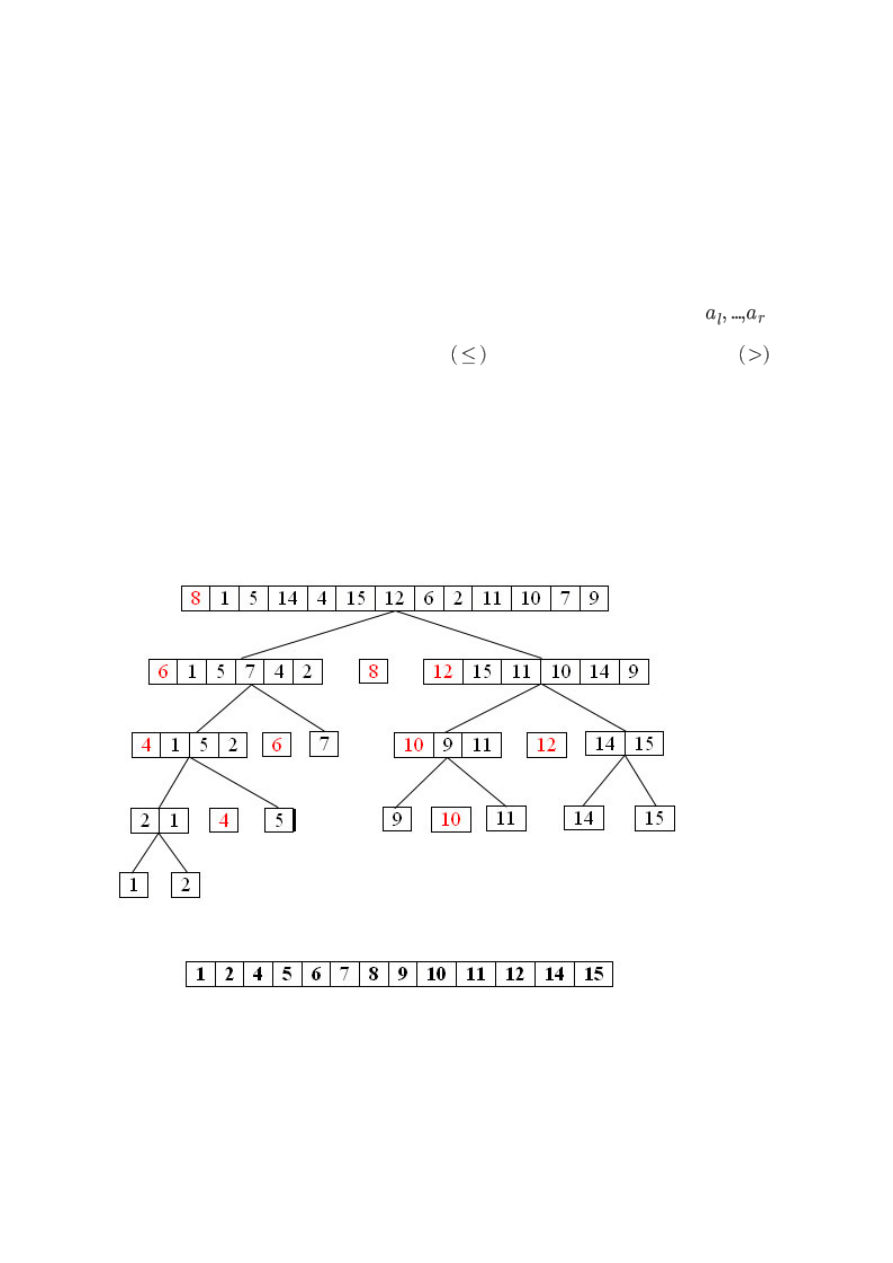
4. Problem selekcji (wyboru)

Specyfikacja problemu selekcji:

Dane:

- klucze związane z rekordami

, przy czym

K, dla

, gdzie K to zbiór liniowo uporządkowany przez relację

. Klucze są parami

różne. Liczba k taka, że

.

Wynik: Wyznaczyć k-ty co do wielkości klucz K spośród kluczy

, tzn. K jest

większy od dokładnie k-1 innych kluczy.

Jeżeli k = 1 to mamy problem minimum, jeżeli k = n to mamy problem maksimum.

Zakładamy, że klucze są dane w tablicy.

Problem można rozwiązać, sortując najpierw klucze, a potem odczytując k-ty element

w posortowanej tablicy. Złożoność takiego rozwiązania wynosi O(n lg n).

Inne rozwiązanie:

Najpierw znajdujemy element pierwszy, potem drugi, aż dojdziemy do k-tego. W tym

rozwiązaniu złożoność (dla wyszukiwania elementu środkowego w tablicy) wynosi

.

Rozwiązanie rekurencyjne oparte na metodzie "dziel i zwyciężaj":
SELEKCJA (T[l...r], k)

1. if l = r
2.

then return T[l]

3. j <- Podzial(T[l...r])
4. m <- j - l + 1;
5. if k = m
6.

then return T[j]

7.

else if k < m

8.

then return SELEKCJA(T[l...j-1], k)

9.

else return SELEKCJA(T[j+1...r],k-m)

W przypadku pesymistycznym nawet

porównań, ale można dowieść że w

przypadku średnim mamy O(n) porównań.

6. Abstrakcyjne struktury danych.

a) Abstrakcyjne struktury danych

Abstrakcyjną strukturą danych nazywamy system algebraiczny (relacyjny):

ADT = <A,(f

i

)

i

ε

I

,(r

j

)

j

εJ>, gdzie A to uniwersum tego systemu, f

i

to funkcje, a r

j

to relacje.

Funkcje i relacje są obliczalne.

Specyfikacją struktury danych (ADT) nazywamy taki zbiór formuł (własności) F

zapisanych w języku matematycznym lub algorytmicznym, że wszystkie wymienione w

zbiorze F własności są prawdziwe w strukturze ADT. Zbiór F charakteryzuje własności

funkcji, relacji i elementów ADT.

Podstawowymi problemami związanymi z konstruowaniem nowych Abstrakcyjnych

Struktur Danych są:

- wybór aksjomatów,

- wykazanie, że aksjomaty te są niesprzeczne i wystarczające (generują to co chcemy

osiągnąć),

- znalezienie minimalnego zbioru aksjomatów.

b) Stos (kolejka LIFO - Last In, First Out, ang. Stack)

Stos jest abstrakcyjną strukturą danych na której możemy wykonywać takie operacje

jak:

- wkładanie elementu na stos (PUSH),

- usunięcie ze stosu ostatnio włożonego elementu (POP),

- zwrócenie ostatnio wstawionego elementu ze stosu (PEEK).

Strukturą stosów nazywamy system algebraiczny S=(E

SUMA

S,PUSH,POP,PEEK,EMPTY,=

E

,=

S

), gdzie:

- E - dowolny niepusty zbiór,

- S - zbiór (skończonych) stosów o elementach z E,

- PUSH - E×S

→ S,

- POP - S

→ S,

- PEEK - S

→ E,

- EMPTY - S

→ B

0

,

- =

E

- E×E

→ Bool, równość elementów,

- =

S

- S×S

→ Bool, równość stosów.

oraz spełnione są następujące własności (specyfikacja struktury stosów):

- ~EMPTY(PUSH(e,s)) - jeśli coś jest na stosie, to stos nie może być pusty,

- PEEK(PUSH(e,s)) =

E

e - wkładając element na stos i zwracając ostatnio dodany -

otrzymamy ten sam element,

- POP(PUSH(e,s)) =

S

s - wkładając element na stos i usuwając go - otrzymujemy ten

sam stos,

- ~EMPTY(s)

→ PUSH(PEEK(s),POP(s)) =

S

s - dodając ściągnięty element ze stosu -

otrzymamy ten sam stos,

- while ~EMPTY(s) do s

← POP(s) ma własność stopu,

- s

1

=

S

s

2

↔ P(EMPTY(s

1

) ? EMPTY(s

2

) ? bool), gdzie P jest programem:

begin

bool ← TRUE
while ~EMPTY(s

1

) ? ~EMPTY(s

2

) ? bool do

bool = (PEEK(s

1

) =

E

PEEK(s

2

))

s

1

← POP(s

1

)

s

2

← POP(s

2

)

end;

Implementacje:

- tablica (podstawowe 3 operacje

→ O(1)),

- lista dowiązana (podstawowe 3 operacje

→ O(1)).

Zastosowanie:

- kompilatory (analiza syntaktyczna, rekurencje),

- systemy operacyjne,

- obliczanie wartości wyrażeń arytmetycznych,

- podstawowa struktura danych dla wielu algorytmów.

c) Kolejka FIFO (First In First Out, ang. queue)

Kolejka FIFO jest abstrakcyjną strukturą danych na której możemy wykonywać takie

operacje jak:

- dodawanie elementu na koniec kolejki (ENQUEUE),

- usuwanie elementu z początku kolejki (DEQUEUE),

- zwrócenie pierwszego elementu znajdującego się w kolejce (FIRST).

Strukturą kolejek FIFO nazywamy system algebraiczny Q=(E

SUMA

Q,ENQUEUE,DEQUEUE,FIRST,EMPTY,=

E

,=

Q

), gdzie:

- E - dowolny niepusty zbiór,

- Q - zbiór (skończonych) kolejek FIFO o elementach z E,

- ENQUEUE - E×Q

→ Q,

- DEQUEUE - Q

→ Q,

- FIRST - Q

→ E,

- EMPTY - Q

→ B

0

,

- =

E

- E×E

→ Bool,

- =

Q

- Q×Q

→ Bool.

oraz spełnione są następujące własności (specyfikacja struktury kolejek FIFO):

- ~EMPTY(ENQUEUE(e,q)) - jeśli coś jest w kolejce, to kolejka nie może być pusta,

- ~EMPTY(q)

→ FIRST(ENQUEUE(e,q)) =

E

FIRST(q) - kolejka nie jest pusta, gdy można

coś zwrócić po dodaniu,

- EMPTY(q)

→ FIRST(ENQUEUE(e,q)) =

E

e

- EMPTY(q)

→ EMPTY(DEQUEUE(ENQUEUE(e,q))) - kolejka będzie pusta gdy usuniemy

ostatnio dodany element,

- ~EMPTY(q)

→ ENQUEUE(e,DEQUEUE(q)) =

Q

DEQUEUE(ENQUEUE(e,q))

- while ~EMPTY(q) do q

← DEQUEUE(q) ma własność stopu,

- q

1

=

Q

q

2

↔ P(EMPTY(q

1

) ? EMPTY(q

2

) ? bool), gdzie P jest programem:

begin

bool ← TRUE
while ~EMPTY(q

1

) ? ~EMPTY(q

2

) ? bool do

bool = (FIRST(q

1

) =

E

FIRST(q

2

))

q

1

← DEQUEUE(q

1

)

q

2

← DEQUEUE(q

2

)

end;

Implementacje:

- tablica (podstawowe 3 operacje

→ O(1)),

- lista dowiązana (podstawowe 3 operacje

→ O(1)).

Zastosowanie:

- systemy operacyjne (kolejki procesów),

- sieci komputerowe.

c) Kolejka priorytetowa (ang. priority queue)

Strukturą kolejek priorytetowych nazywamy system algebraiczny PQ=(PQ

SUMA

E,INSERT,MAX,DELETE_MAX,MEMBER,EMPTY,≤

E

,=

EQ

), gdzie:

- E - dowolny niepusty zbiór liniowa uporządkowany przez relację ≤

E

,

- Q - zbiór (skończonych) kolejek priorytetowych o elementach z E,

- INSERT - E×PQ

→ PQ - wstawienie elementu do kolejki,

- MAX - PQ

→ E - zwrócenie elementu maksymalnego w kolejce,

- DELETE_MAX - PQ

→ PQ - usunięcie elementu maksymalnego z kolejki,

- MEMBER - E×PQ

→ Bool - sprawdzenie czy element jest w kolejce,

- EMPTY - PQ

→ Bool - sprawdzenie czy kolejka priorytetowa jest pusta.

Powyższa definicja dotyczy kolejek priorytetowych opartych na maksimum. Można

rozważać także kolejki oparte na minimum (zmiana MAX na MIN, DELETE_MAX na

DELETE_MIN oraz znaków nierówności).

Generalnie mówimy, że w danym momencie mamy dostęp do elementu o najwyższym

priorytecie (ale nie mamy dostępu jednocześnie do elementu maksymalnego i

minimalnego).

Dopuszczalne jest istnienie elementów o takim samym priorytecie - wtedy zamiast

pojęcia "zbioru" stosuje się pojęcie "multizbioru" - zbioru w którym elementy mogą się

powtarzać. Mogą w związku z tym wynikać pewne niejednoznaczności związane z funkcją

DELETE_MAX (stosuje się wtedy funkcję EXTRACT_MAX - która usuwa i zwraca element

maksymalny). Przy "multizbiorach" nie stosuje się funkcji MEMBER.

Dodatkowe operacje stosowane w kolejkach priorytetowych:

- konstruowanie kolejki z danych elementów (często okazuje się szybsze niż wstawianie

elementów po kolei),

- zmiana priorytetu,

- usunięcie wskazanego elementu,

- połączenie dwóch kolejek w jedną.

Zastosowanie:

- systemy operacyjne,

- sieci komputerowe,

- algorytmy (podstawowa struktura wielu z nich).

Uwaga: Stos i kolejka FIFO są szczególnymi kolejkami priorytetowymi.

Implementacje:

- kopiec (ang. heap)

Kopiec (typu max) to etykietowane drzewo binarne (V, Et, key), gdzie:

- V - zbiór węzłów,

- Et - zbiór liniowo uporządkowany,

- key : V

→ Et - funkcja etykietująca (porządkująca węzły) spełniająca własność kopca:

Dla wszystkich v należących do V, dla wszystkich l należących do LD(v), dla wszystkich p

należących do PD(v) : key(l) ≤ key(v) ≥ key(p)

gdzie:

- LD(v) - lewe poddrzewo węzła v,

- PD(v) - prawe poddrzewo węzła v.

Czyli za każdym razem, dzieci danego węzła muszą mieć mniejsze wartości od swojego

rodzica.

Dodatkowo zakładamy, że drzewo jest kompletne (za wyjątkiem ostatniego poziomu).

Pomimo, że kopiec definiujemy jako drzewo binarne, to implementujemy go jako tablice.

Wykorzystujemy fakt, że drzewo jest kompletne.

parent(k) = podłoga z [k/2]

left(k) = 2k

right(k) = 2k+1

gdzie k to numer węzła w tablicy.

Zapisując drzewo do tablicy - zapisujemy je poziomami od lewej do prawej (zaczynając

od korzenia).

Wysokość h kopca o n węzłach: h = podłoga z [lgn]

Klucze w kopcu nie są uporządkowane, ale wiemy gdzie znajduje się element

maksymalny - w korzeniu drzewa. Dlatego kopiec może posłużyć nam do

zaimplementowania struktury kolejek priorytetowych. Dla uproszczenia zapisu

utożsamiamy węzły z kluczami (ale w praktyce może być inaczej!). Operacją dominującą

dla algorytmów działających na kopcu będzie porównywanie kluczy.

Kopiec jako implementacja kolejki priorytetowej:

Operacja INSERT:

- wstaw klucz na koniec tablicy,

- napraw własność kopca do góry (procedura FIX-UP - zamieniaj nowy klucz z jego

rodzicem dopóki rodzic nie będzie większy od niego).

T(INSERT,n) = O(lgn)

W najlepszej sytuacji - 0 lub 1 porównanie.

W najgorszej sytuacji - podłoga z [lg(n+1)] porównań.

Koszt wstawienia n kluczy do pustego kopca jest rzędu O(nlgn).

Operacja EXTRACT_MAX:

- zwracamy klucz w korzeniu (pierwszy element w tablicy),

- zastępujemy klucz w korzeniu ostatnim kluczem w tablicy.

- napraw własność kopca w dół (procedura FIX-DOWN - sprawdź czy węzeł po lewej nie

jest większy od korzenia, sprawdź czy węzeł po prawej nie jest większy od korzenia -

jeśli taka sytuacja zaistnieje to zamień ze sobą korzeń oraz węzeł, a następnie naprawiaj

dalej).

T(EXTRACT_MAX,n) = O(lgn)

Liczba porównań kluczy w procedurze FIX-DOWN dla węzła o indeksie k z poziomu l

wynosi co najwyżej 2(h-l).

Czas algorytmu sortowania z wykorzystaniem kolejki priorytetowej zaimplementowanej

jako kopiec wynosi: Θ(nlgn).

e) Słownik

Strukturą słowników nazywamy system algebraiczny SL=(SL

SUMA

E,INSERT,SEARCH,DELETE,EMPTY,≤

E

,=

SL

), gdzie:

- E - dowolny niepusty zbiór,

- SL - zbiór (skończonych) słowników o elementach z E,

- INSERT - E×SL

→ SL - wstawienie elementu do słownika,

- SEARCH - E×SL

→ Bool - sprawdzenie czy element znajduje się w słowniku,

- DELETE - E×SL

→ SL - usunięcie elementu ze słownika,

- EMPTY - SL

→ Bool - sprawdzenie czy słownik jest pusty.

Podstawową różnicą pomiędzy kolejką priorytetową, a słownikiem jest to, iż w kolejce

priorytetowej żądaliśmy dostępu do elementu o największym priorytecie, a w przypadku

słownika żądamy dostępu do dowolnego elementu.

Dodatkowe operacje stosowane w słownikach:

- MINIMUM - wybór elementu o najmniejszym kluczu,

- MAXIMUM - wybór elementu o największym kluczu,

- SUCCESOR - wyszukanie następnego elementu względem wybranego (porządek

liniowy),

- PREDECESSOR - wyszukanie poprzedniego elementu względem wybranego (porządek

liniowy).

Tak jak w przypadku kolejek priorytetowych, istnieje możliwość dublowania się kluczy.

Można to rozwiązać na kilka sposobów:

- tworzenie listy elementów dla każdego klucza (kojarzyć ze skorowidzem nazw w

podręcznikach),

- zmiana operacji ze zbiorów na multizbiory (kojarzyć z książką telefoniczną),

- ignorowanie zdublowanych kluczy (zbiór zmiennych w programach komputerowych).

Zastosowanie:

- bazy danych,

- kompilatory (tablice symboli),

- algorytmy.

Implementacje:

- tablica indeksowana kluczem,

- tablica uporządkowana,

- lista dwukierunkowa uporządkowana,

- zrównoważone drzewa przeszukiwań binarnych (drzewa AVL),

- drzewa przeszukiwań binarnych (drzewa BST, ang. binary search tree)

Drzewo przeszukiwań binarnych to etykietowane drzewo binarne (V, Et, key), gdzie:

- V - zbiór węzłów,

- Et - zbiór liniowo uporządkowany,

- key : V

→ Et - funkcja etykietująca (porządkująca węzły) spełniająca własność drzewa

BST:

Dla wszystkich v należących do V, dla wszystkich l należących do LD(v), dla wszystkich p

należących do PD(v) : key(l) ≤ key(v) ≤ key(p)

gdzie:

- LD(v) - lewe poddrzewo węzła v,

- PD(v) - prawe poddrzewo węzła v.

Czyli w lewym węźle zawsze znajduje się wartość mniejsza od wartości korzenia, a w

prawym węźle wartość większa od wartości korzenia.

Przechodząc drzewo w porządku inorder otrzymamy posortowane klucze.

Drzewo BST jako implementacja słownika:

SEARCH:

- jeśli drzewo jest puste, to brak elementu o wskazanym kluczu,

- jeśli wskazany element jest poszukiwanym elementem, to element istnieje w drzewie i

algorytm zwraca korzeń lub true,

- jeśli poszukiwana wartość jest mniejsza od wskazanego elementu to przeszukaj

rekurencyjnie lewe poddrzewo,

- jeśli poszukiwana wartość jest większa od wskazanego elementu to przeszukaj

rekurencyjnie prawe poddrzewo.

Koszt wyszukiwania jest rzędu O(h), gdzie h to wysokość drzewa. W najgorszym

wypadku jest on liniowy.

INSERT: (wstawianie węzła v do drzewa T)

- jeśli drzewo jest puste to za T wstaw v,

- jeśli drzewo nie jest puste to:

* w przypadku gdy węzeł, który chcemy wstawić jest taki sam jak aktualnie rozważany -

to sposób postępowania zależy od tego co założyliśmy w kwestii dublowanych kluczy,

* w przypadku gdy węzeł, który chcemy wstawić jest mniejszy od aktualnie rozważanego

- to wywołaj rekurencyjnie wstawianie w lewym poddrzewie,

* w przypadku gdy węzeł, który chcemy wstawić jest większy od aktualnie rozważanego

- to wywołaj rekurencyjnie wstawianie w prawym poddrzewie.

Koszt wstawiania jest rzędu O(h), gdzie h to wysokość drzewa. W najgorszym wypadku

jest on liniowy.

MINIMUM:

- jeśli drzewo jest puste, to operacja jest nieokreślona,

- w przeciwnym wypadku schodzimy po drzewie zawsze w kierunku lewego poddrzewa -

ostatni węzeł to element minimalny.

Koszt wyszukania minimum jest rzędu O(h), gdzie h to wysokość drzewa. W najgorszym

wypadku jest on liniowy.

Operacja MAKSIMUM analogicznie do MINIMUM - tylko schodzi się w kierunku prawego

poddrzewa.

SUCCESOR:

- jeśli węzeł v jest węzłem o maksymalnym kluczu, to operacja jest nieokreślona,

- jeśli węzeł v zawiera niepuste prawe poddrzewo, to następnik jest elementem

minimalnym w tym poddrzewie,

- jeśli węzeł v nie zawiera prawego poddrzewa, to następnik jest najniższym przodkiem

węzła v, którego lewy syn jest również przodkiem tego węzła.

Koszt wstawiania jest rzędu O(h), gdzie h to wysokość drzewa. W najgorszym wypadku

jest on liniowy.

DELETE:

- znajdź węzeł o kluczu k w drzewie - jeśli nie istnieje to zakończ algorytm,

- jeśli węzeł zostanie odnaleziony to:

* jeżeli stopień(v) = 0, to usuwamy węzeł v,

* jeżeli stopień(v) = 1, to wycinamy węzeł v ustalając powiązanie między jedynym

synem węzła v, a jego ojcem (o ile istnieje),

* jeżeli stopień(v) = 2, to znajdujemy następnik (lub poprzednik) węzła v w drzewie T -

nazwijmy go w. Zamieniamy teraz dane węzłów v i w, a następnie usuwamy węzeł w.

Koszt usuwania jest rzędu O(h), gdzie h to wysokość drzewa. W najgorszym wypadku

jest on liniowy.

Drzewem AVL nazywamy wyważone drzewo BST.

Drzewo binarne jest wyważone, gdy dla każdego węzła wysokość jego lewego poddrzewa

rożni się co najwyżej +- 1 od wysokości jego prawego poddrzewa.

Maksymalna liczba n węzłów drzewa o wysokości h wynosi 2

h+1

- 1.

Wysokość dowolnego drzewa AVL jest rzędu Θ(lgn) i spełnia warunek:
lg(n+1) - 1 ≤ h ≤ 1,44lg(n+2) - 1,32

Dla przypadku najgorszego wysokość drzewa AVL jest o około 44% większa niż dla

przypadku najlepszego.

7. Algorytm Huffmana.

Algorytm Huffmana - jeden z najbardziej znanych algorytmów kodujących. Algorytm ten

oparty jest na metodzie zachłannej (w danym kroku wykonywana jest operacja, która

wydaje się być najkorzystniejsza) i wykorzystuje strukturę kolejek priorytetowych oraz

drzewa binarne. Algorytm ten wykorzystywany jest w algorytmie kompresji formatu

MP3.

Oznaczenia:

- S = {x

1

,...,x

n

} - alfabet, czyli skończony zbiór znaków, które będziemy kodować,

- P = {p

1

,...,p

n

} - prawdopodobieństwo wystąpienia znaku x

i

w skończonym,

kodowanym tekście,

- B = {b

1

,...,b

k

} - zbiór znaków używanych do kodowania (najczęściej 0 i 1),

- C = {c

1

,...,c

n

} - słowa kodów złożone ze znaków zbioru B, przy czym c

i

jest kodem

znaku x

i

.

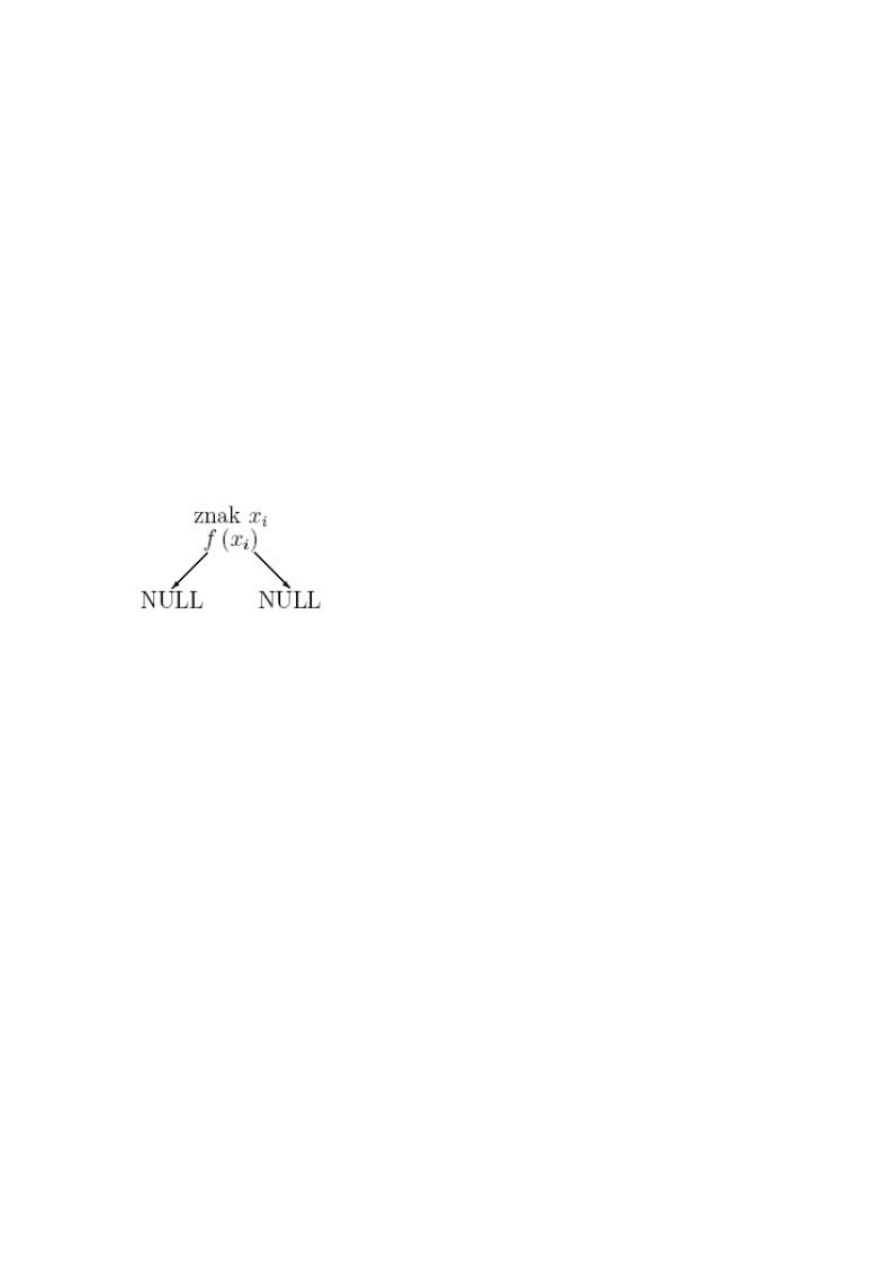
Obliczenie zbioru C nazywamy kodowaniem, a sam zbiór C kodem.

Średnia długość kodu: L

śr

(C) = suma od i = 1 do n [p

i

l(c

i

)], gdzie l(c

i

) oznacza długość

kodu symbolu c

i

.

Kod optymalny, to kod dla którego wartość L

śr

(C) jest najmniejsza przy ustalonych

zbiorach S, P i B.

Przykładowo:

S = {a,b,c}, P={1/2,1/4,1/4}, B={0,1}, C = {1,00,01}

to L

śr

(C) = 1/2*1 + 1/4*2 + 1/4*2 = 3/2.

Kod C nazywamy prefiksowym (przedrostkowym), jeśli żadne słowo ze zbioru C nie jest

prefiksem (przedrostkiem) innego słowa z C (czyli czy jakieś jedno słowo nie zawiera się

na początku innego słowa).

Każdy kod optymalny dla B = {0,1} można przedstawić w postaci lokalnie pełnego

drzewa binarnego. Jednak nie każde drzewo lokalnie pełne daje kod regularny.

Kodowanie Huffmana, to pierwszy algorytm, który konstruuje kod optymalny, prefiksowy

dla B = {0,1}. Algorytm buduje tzw. drzewo Huffmana.

Zasada działania:

Niech t oznacza tekst do kodowania, a S - zbiór znaków występujących w danym tekście.

- dla każdego znaku x

i

ze zbioru S oblicz ilość wystąpień tego znaku w pliku i niech jest to

f(x

i

). Dla każdego znaku x

i

utwórz węzeł drzewa binarnego postaci:

- w następnym kroku tworzymy kolejkę priorytetową drzew binarnych, gdzie kluczem

jest pole f korzenia. Kolejka oparta jest na minimum.

Pseudokod:
KODOWANIE_HUFFMANA(PQ)
FOR i = 1 TO n−1
DO utwórz nowy węzeł x

left(x) = extract_min(PQ)
right(x) = extract_min(PQ)
f(x) = f(left(x)) + f(right(x))
insert(x, PQ)

Po zakończeniu algorytmu kolejka priorytetowa PQ zawiera jedno drzewo binarne -

drzewo Huffmana, które pozwala nam odczytać utworzone kody zgodnie z regułą: na

lewo 0, na prawo 1 (lub na odwrót).

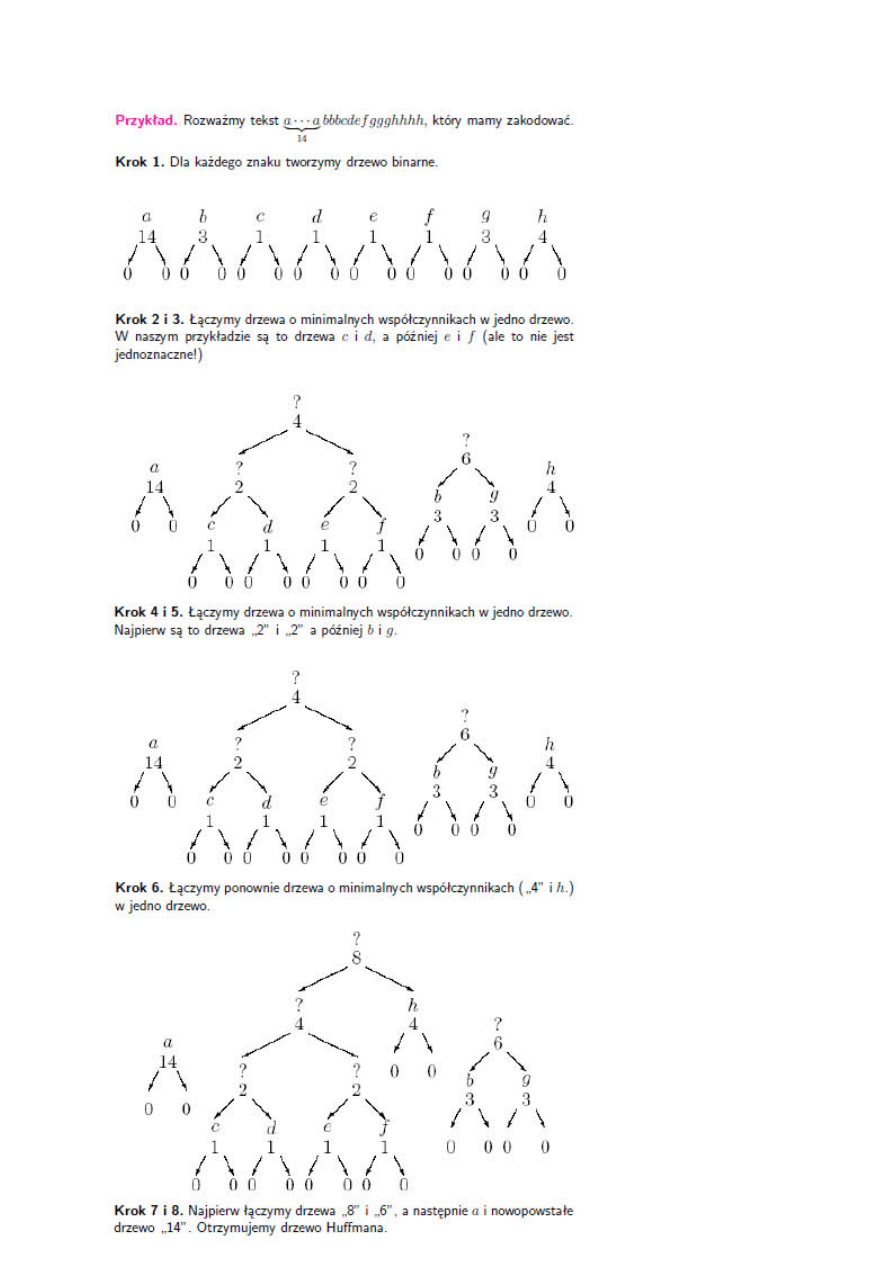
Koszt algorytmu jest zależny od implementacji struktury kolejki priorytetowej. Jeśli ta

oparta jest na kopcu to: O(nlgn) (gdzie n to liczba znaków potrzebnych do

zakodowania).