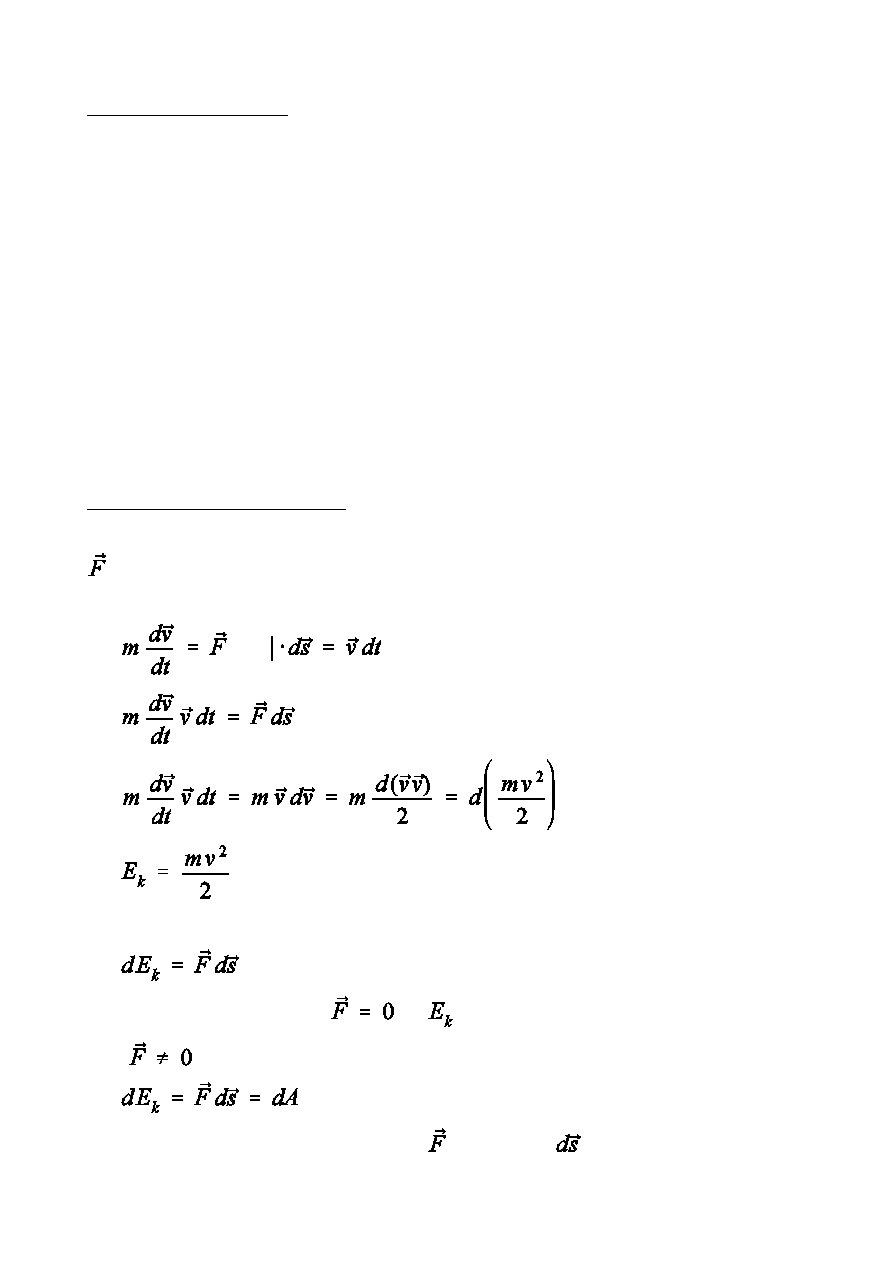
Praw a zach owania 1

PRAWA ZACHOWANIA

Podstawowe terminy

Cia»a tworzce uk»ad mechaniczny oddzia»ywuj mi“dzy sob i z cia»ami nie

naleócymi do uk»adu za pomoc

a) si» wewn“trznych -

si» dzia»ajcych na dane cia»o ze strony innych

cia» tego samego uk»adu,

b) si» zewn“trznych -

si» dzia»ajcych na dane cia»o ze strony cia» nie

naleócych do rozpatrywanego uk»adu.

Uk»ad zamkni“ty

- uk»ad w którym nie wyst“puj si»y zewn“trzne.

Energia kinetyczna czstki

- wypadkowa si» dzia»ajcych na czstk“

- energia kinetyczna czstki

Dla uk»adu zamkni“tego

, a

pozostaje sta»a.

Dla

dA - praca wykonana przez si»“ na drodze

Praw a zach owania 2

Energia kinetyczna czstki, cd

-

Praca si»y wypadkowej zamienia si“ na

przyrost energii kinetycznej czstki

Si»y zachowawcze

Jeóeli w kaódym punkcie przestrzeni czstka jest poddana dzia»aniu innych
cia», to mówimy, óe czstka znajduje si“ w polu si».

Pole stacjonarne - pole, które nie zmienia si“ w czasie.

Pole zachowawcze - pole stacjonarne, w którym praca wykonana nad

czstk przez si»y pola zaleóy tylko od pocztkowego
i ko½cowego po»oóenia czstki, nie zaleóy natomiast
od drogi, po której porusza si“ czstka.

Praca si» zachowawczych na drodze zamkni“tej jest równa zeru.

Praw a zach owania 3

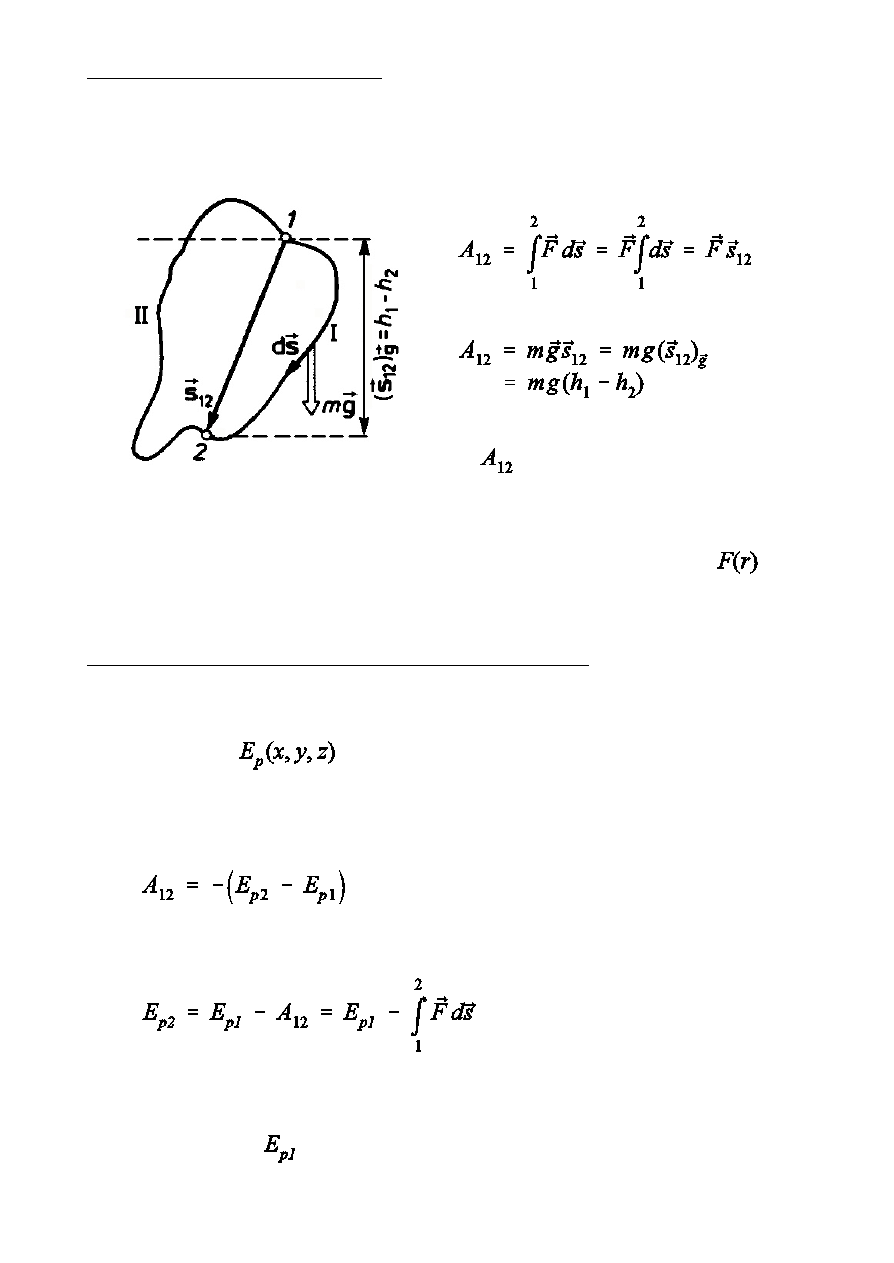
Zachowawczoу si»y ci“ókoÑci

Si»a ci“ókoÑci jest si» zachowawcz. Si»a ta ma w dowolnym punkcie t“
sam wartoу, ten sam kierunek i ten sam zwrot.

nie zaleóy od kszta»tu toru

»czcego punkt 1 i 2, a wi“c jest
si» zachowawcz.

Moóna pokazaƒ, óe si» zachowawcz jest równieó si»a centralna

.

Energia potencjalna czstki w zewn“trznym polu si»

W zachowawczym polu si» kaódemu punktowi pola moóna przypisaƒ wartoу
pewnej funkcji

, tak, óe praca si» pola przy przejÑciu od punktu

1 do punktu 2 równa jest ubytkowi tej funkcji (przyrostowi ze znakiem
minus):

Std

Energia potencjalna okreÑlona jest z dok»adnoÑci do pewnej sta»ej
addytywnej (tutaj

).

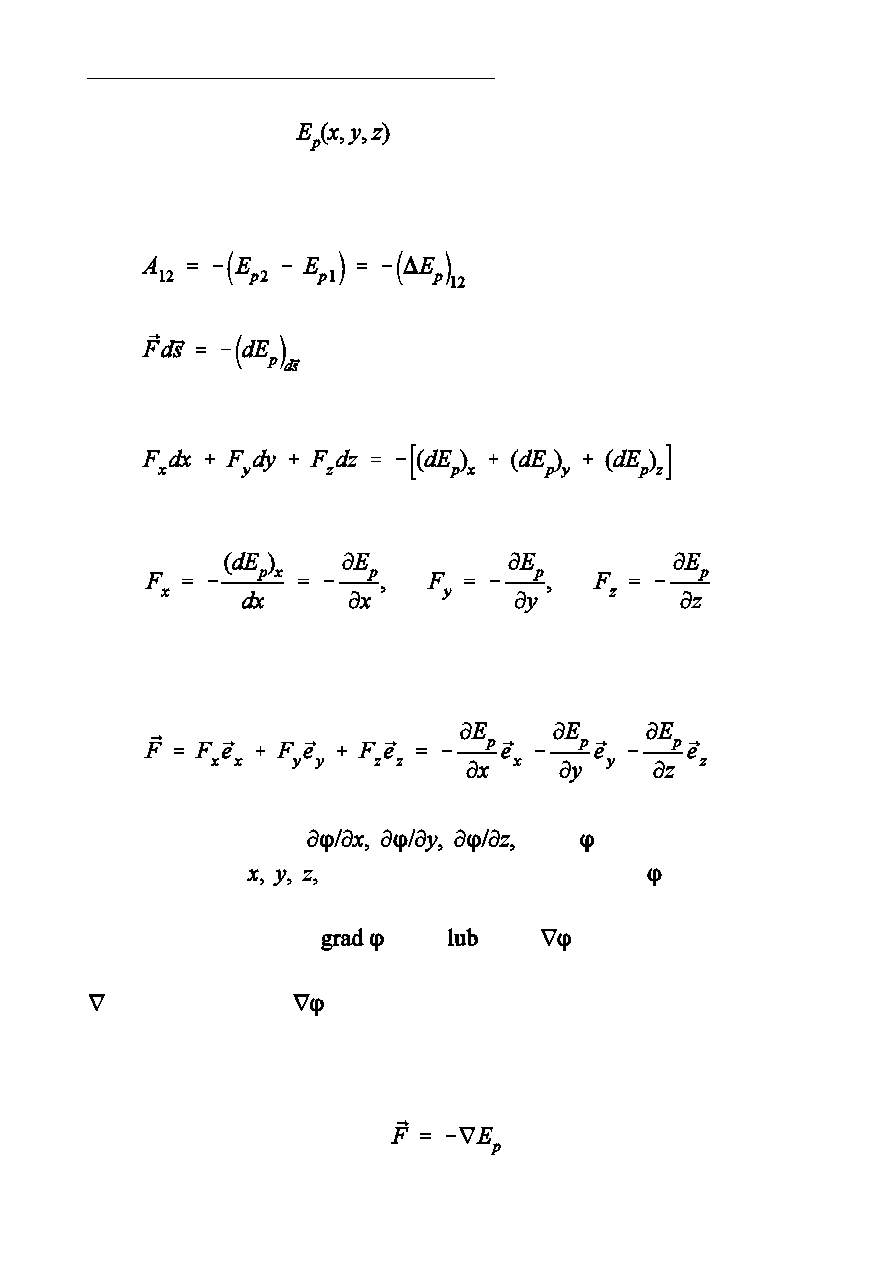
Praw a zach owania 4

Zwizek energii potencjalnej z si»ami pola

Znajc postaƒ funkcji

moóna okreÑliƒ si»“, która dzia»a na czstk“

w kaódym punkcie pola.

Poniewaó dla dowolnych dwóch punktów 1 i 2 mamy

wi“c zachodzi

lub inaczej

czyli

Znajc sk»adowe, moóna okreÑliƒ wektor si»y

Wektor o sk»adowych

gdzie jest skalarn funkcj

wspó»rz“dnych

nazywamy gradientem funkcji i oznaczamy

symbolem

- operator nabla,

czytamy „gradient fi”

Si»a zachowawcza jest równa gradientowi energii potencjalnej ze
znakiem minus.

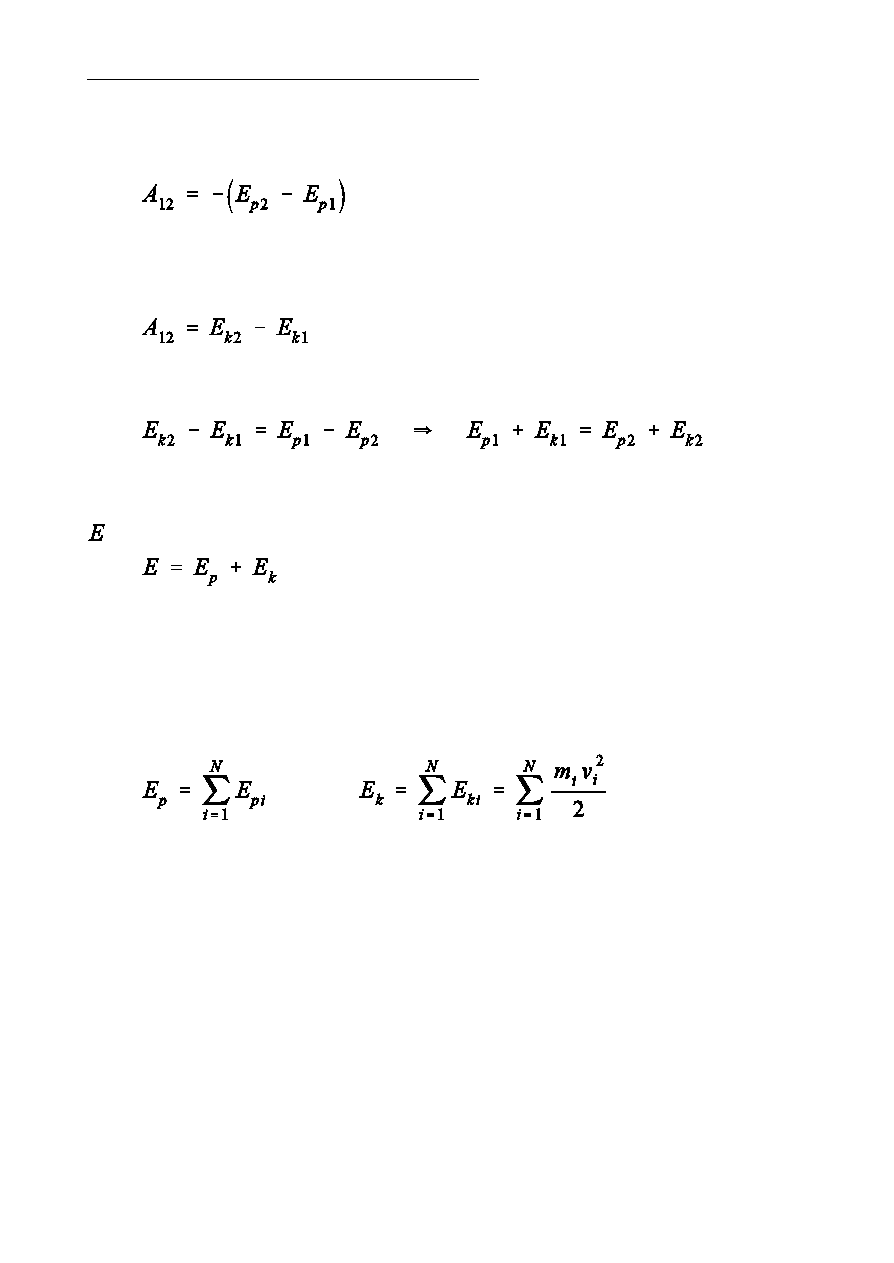
Praw a zach owania 5

Prawo zachowania energii mechanicznej

PokazaliÑmy, óe praca si»y zachowawczej wióe si“ ze zmian energii
potencjalnej cia»a

oraz, óe praca dowolnej si»y (zachowawczej lub niezachowawczej) powoduje
zmian“ energii kinetycznej cia»a

Porównujc te dwa wyraóenia otrzymujemy

Widzimy wi“c, óe w polu si» zachowawczych ca»kowita energia mechaniczna

cia»a zdefiniowana jako

jest taka sama w kaódym punkcie tego pola.

Podobny wniosek moóemy wysnuƒ dla uk»adu N cia», na które dzia»aj tylko
si»y zachowawcze.

Prawo zachowania energii mechanicznej
Ca»kowita energia mechaniczna uk»adu cia», na które dzia»aj tylko si»y
zachowawcze, jest sta»a.

Dla uk»adu zamkni“tego (w nieobecnoÑci si» zewn“trznych)
Ca»kowita energia mechaniczna uk»adu zamkni“tego, wewntrz którego
dzia»aj tylko si»y zachowawcze, jest wielkoÑci sta».

Praw a zach owania 6

Prawo zachowania p“du

Rozwaómy uk»ad N wzajemnie oddzia»ywujcych ze sob czstek

si»y wewn“trzne dzia»ajce na i-t czstk“

wypadkowa si» zewn“trznych dzia»ajcych na i-t czstk“

Równanie ruchu dla i-tej czstki ma postaƒ

Sumujc wszystkie powyósze N równa½ stronami otrzymujemy

Wprowadzajc p“d uk»adu

Otrzymujemy

Przy braku si» zewn“trznych

, czyli p“d uk»adu zamkni“tego jest

sta»y

Prawo zachowania p“du
P“d zamkni“tego uk»adu punktów materialnych jest sta»y

P“d jest sta»y równieó w przypadku uk»adu nie zamkni“tego, o ile
wypadkowa si» zewn“trznych jest równa zeru.

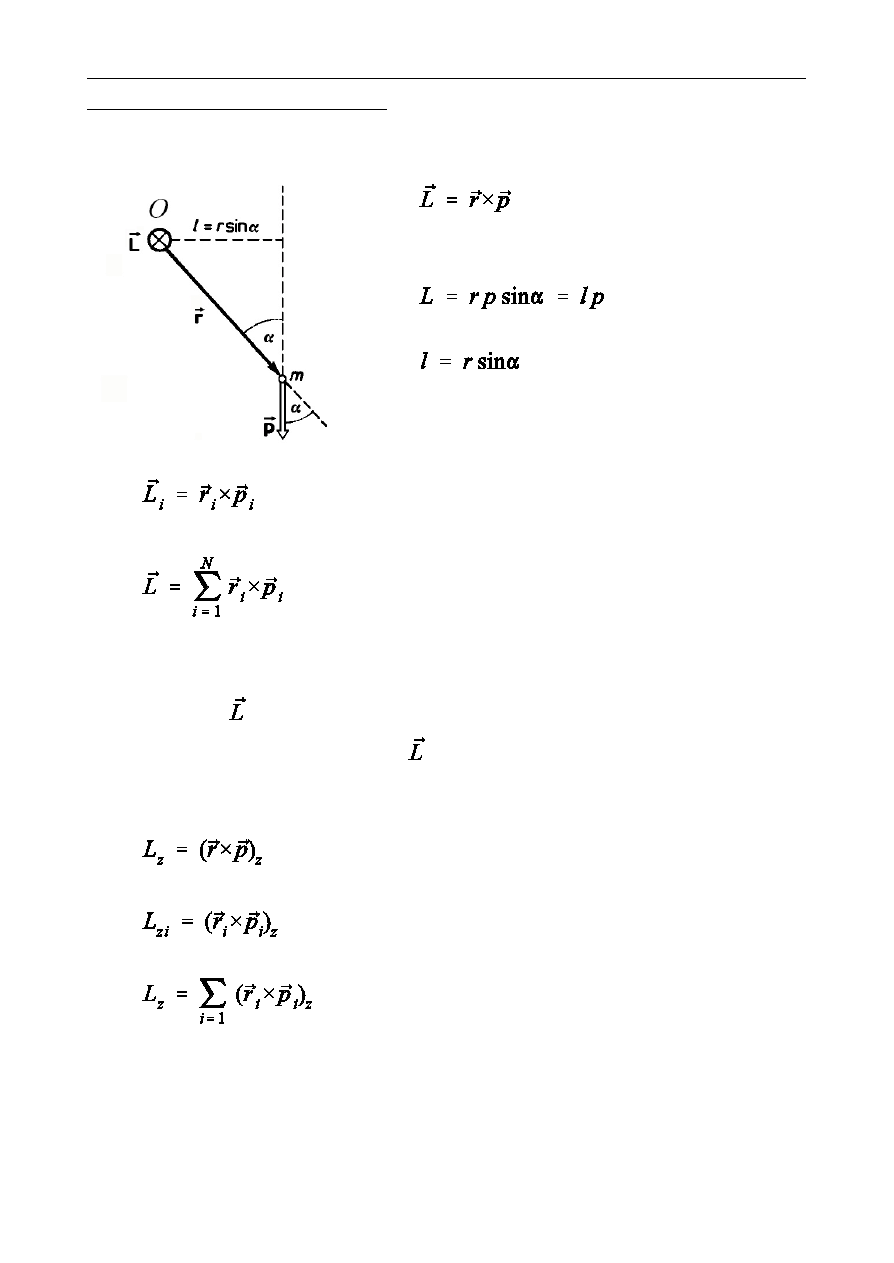
Praw a zach owania 7

Moment p“du wzgl“dem punktu O, rami“ wektora p“du wzgl“dem punktu
O, moment p“du wzgl“dem osi

-

moment p“du masy m.

wzgl“dem punktu O

-

r a m i“ w ek t ora p“du

wzgl“dem punktu O

moment p“du i-tej czstki wzgl“dem punktu O

moment p“du uk»adu N czstek wzgl“dem punktu O

Rzut wektora na pewn oÑ z przechodzc przez punkt O, wzgl“dem

którego jest okreÑlony wektor nazywamy momentem p“du czstki

wzgl“dem tej osi

- moment p“du i-tej czstki wzgl“dem osi z

- moment p“du uk»adu N punktów materialnych

wzgl“dem osi z

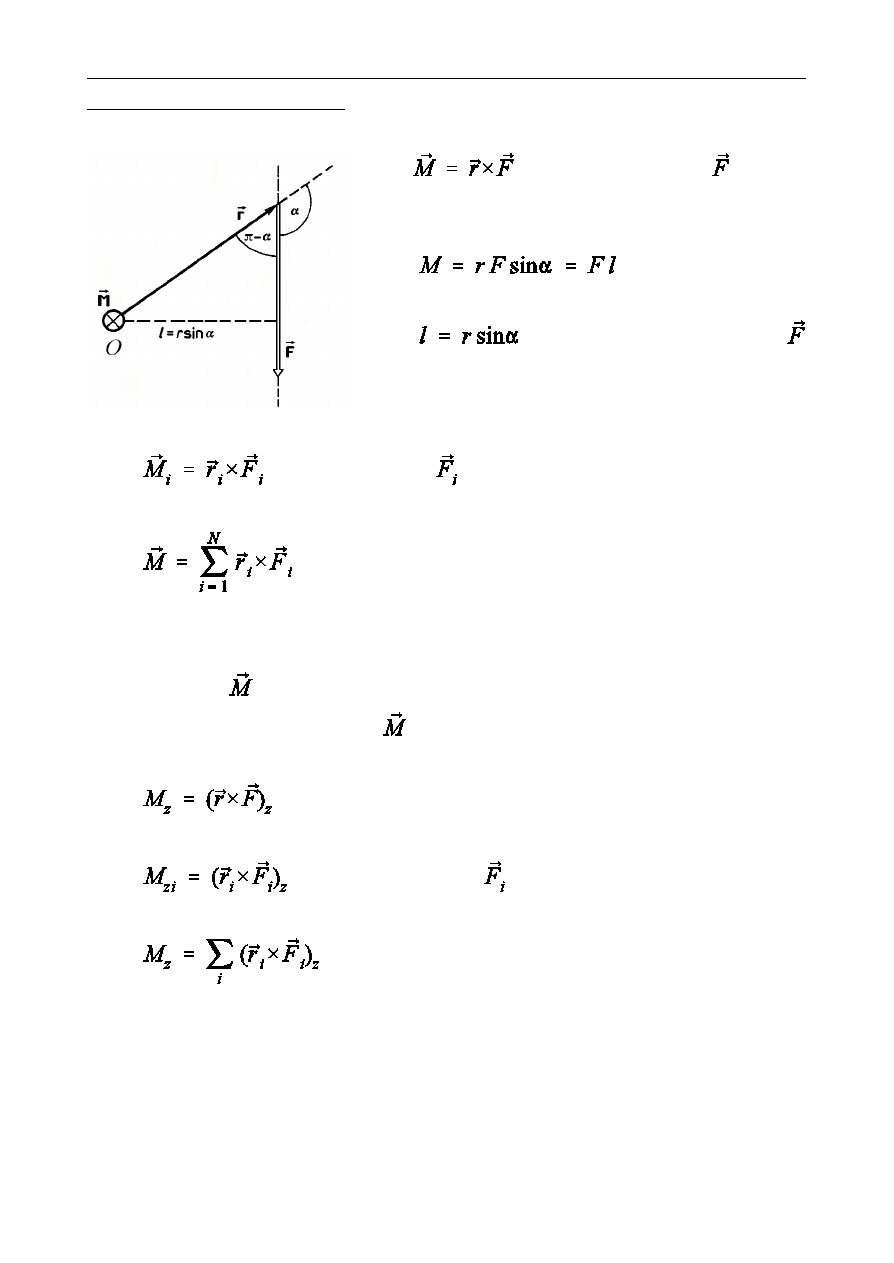
Praw a zach owania 8

Moment si»y wzgl“dem punktu O, rami“ wektora si»y wzgl“dem punktu O,
moment si»y wzgl“dem osi

- moment si»y

wzgl“-

dem punktu O

- rami“ wektora si»y

wzgl“dem punktu O

moment si»y

wzgl“dem punktu O

wypadkowy moment N si» wzgl“dem punktu O

Rzut wektora

na pewn oÑ z przechodzc przez punkt O, wzgl“dem

którego jest okreÑlony wektor

nazywamy momentem si»y wzgl“dem tej

osi

- moment si»y

wzgl“dem osi z

wypadkowy moment si» dzia»ajcych na uk»ad

wzgl“dem osi z

Moment si»y wzgl“dem osi charakteryzuje zdolnoу si»y do obracania cia»a
wzgl“dem tej osi.

Praw a zach owania 9

Prawo zachowania momentu p“du

Moóna pokazaƒ, óe

Pochodna po czasie momentu p“du jest równa sumie momentów si»
zewn“trznych.

Przy braku si» zewn“trznych

Zasada zachowania momentu p“du
Moment p“du zamkni“tego uk»adu czstek jest sta»y.

Moment p“du jest sta»y równieó dla uk»adu niezamkni“tego, o ile ca»kowity
moment si» zewn“trznych jest równy zeru.

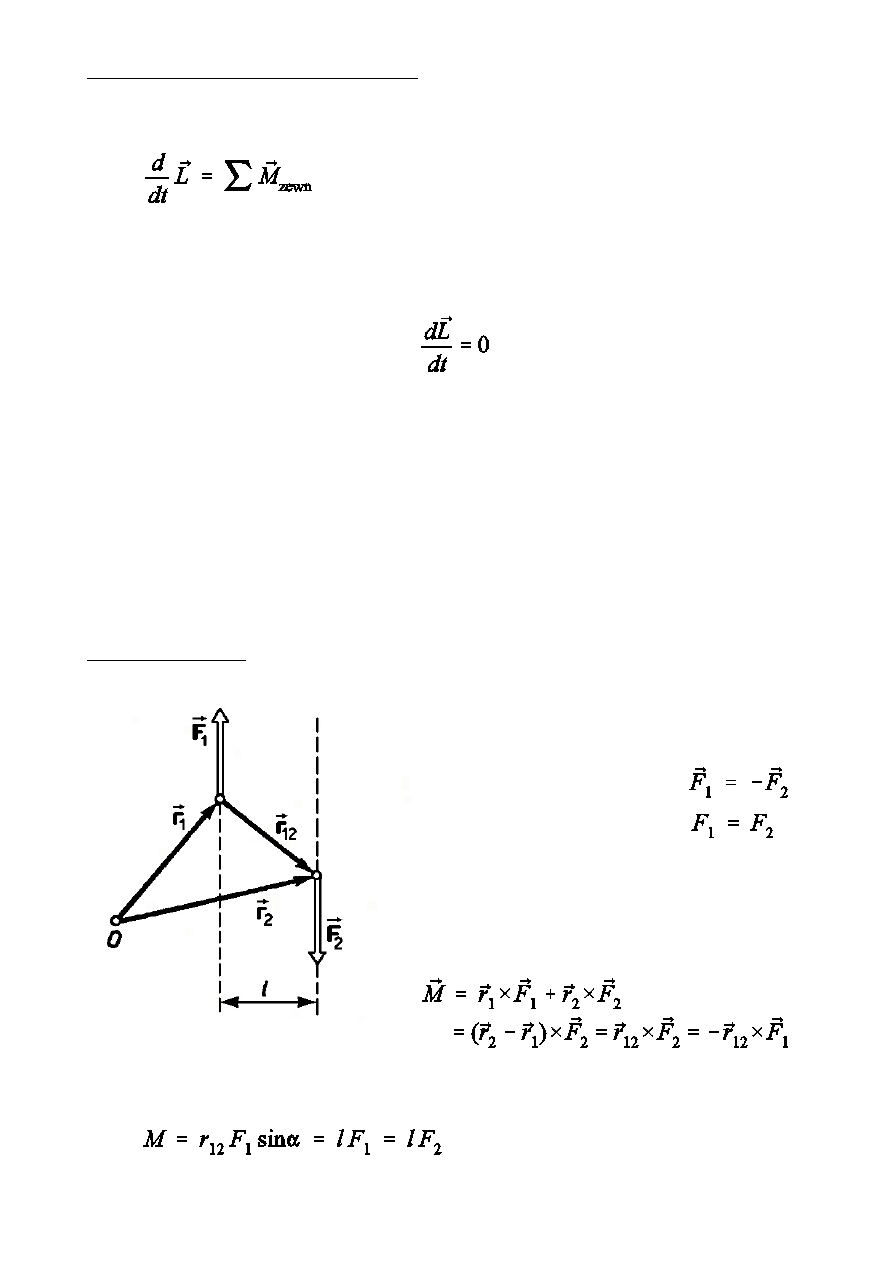
Moment pary si»

Para si» - dwie równe co do wartoÑci i o
ró wn oleg»ym

k i e r u n k u s i » y o

przeciwnych zwrotach, nie dzia»ajce

wzd»uó jednej prostej.

l - rami“ pary si»

Moment pary si» nie zaleóy od wyboru
punktu O

Moment pary si» jest liczbowo równy iloczynowi wartoÑci jednej z si» i
ramienia pary si»