1

WYDZIAŁ TRANSPORTU PW Zakład Sterowania Ruchem

LABORATORIUM PODSTAW AUTOMATYKI III

Rok akad.

2009/2010

Data wykonania ćwiczenia

2010r. Uzyskane

punkty

za:

Specjalizacja

Imiona i Nazwiska studentów

przygotowanie

i realizację

zaliczenie

poprawę

zaliczenia

. . . . . . . . . .

1.

Zespół

2.

3.

4.

5.

Ćwiczenie nr 1

Temat ćwiczenia: Badanie obiektów dynamicznych z zastosowaniem programu

MATLAB

1

Wprowadzenie

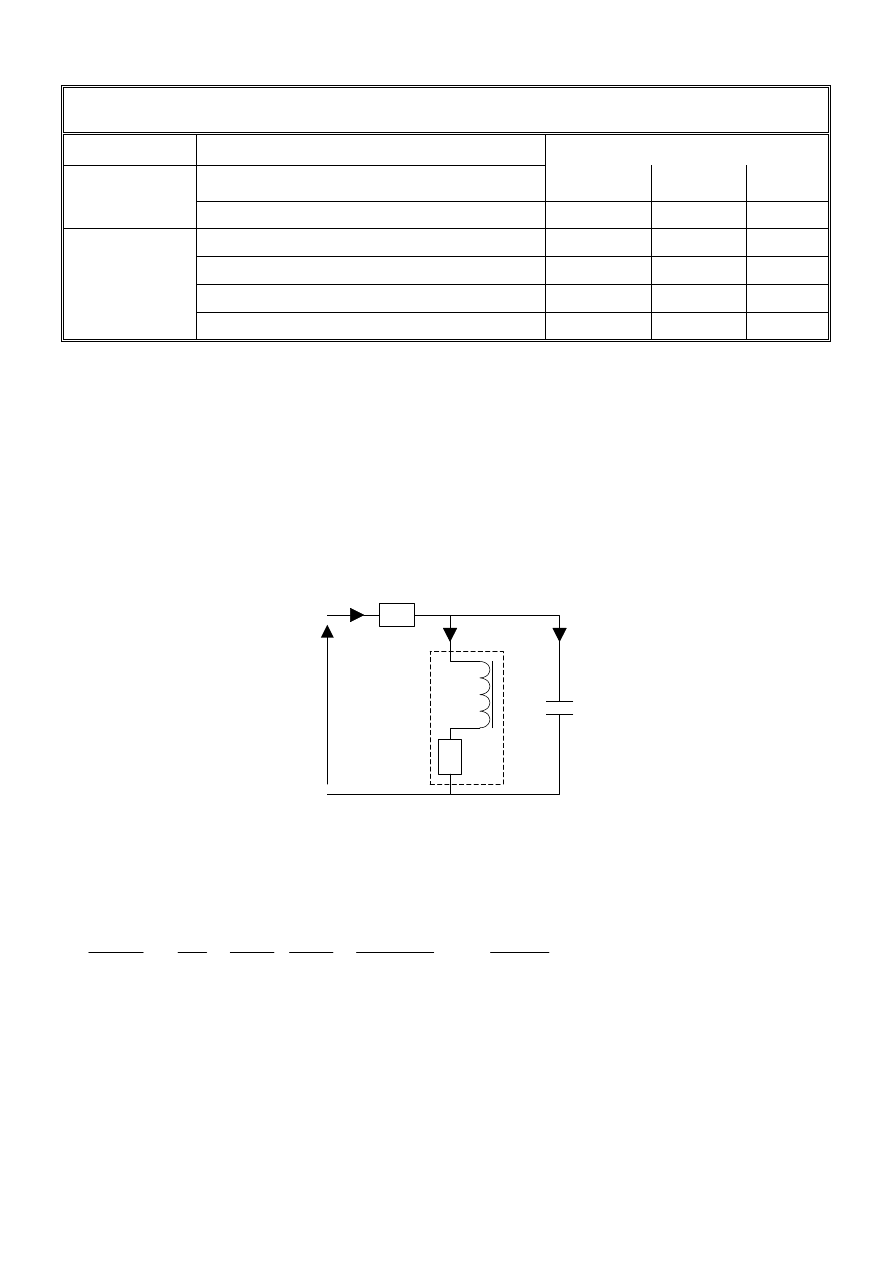
Dany jest schemat obwodu elektrycznego wzbudzenia przekaźnika o indukcyjności L i oporze

czynnym RP (rysunek 1). W szereg z przekaźnikiem dołączony jest kondensator o pojemności C.
Przewody łączące tak powstały dwójnik ze źródłem zasilania mają opór R

d

. Zakładamy, że

indukcyjność cewki i rdzenia pozostaje stała w czasie (normalnie ulega zmianie po rozpoczęciu
ruchu kotwicy).

L

R

d

R

L

i

1

(t)

C

u(t)

i(t)

i

2

(t)

Rysunek 1. Obwód przekaźnika.

Korzystając z równań różniczkowych opisujących poszczególne elementy obwodu, oraz praw

Ohm'a i Kirchoff'a, ułożyć można równanie różniczkowe zwyczajne drugiego rzędu (1) opisujące
zadany dwójnik i stanowiące podstawę do dalszych rozważań.

 

 

 

 

LC

R

t

u

t

i

LC

R

R

R

dt

t

di

C

R

L

R

dt

t

i

d

d

d

d

L

d

L

























1

2

2

(1)

Przyjmując za sygnał wejściowy napięcie u(t) przyłożone do wyprowadzeń dwójnika, a za

sygnał wyjściowy prąd płynący przez cewkę, uzyskujemy liniowy układ dynamiczny o jednym
wejściu u(t) i jednym wyjściu i(t). Traktując obie strony równania (1) odwrotnym przekształceniem
Laplace'a, oraz przyjmując zerowe warunki początkowe (kondensator w chwili t = 0

+

jest

rozładowany i w żadnej z gałęzi nie płynie prąd) uzyskujemy równanie transformat (2)
rozpatrywanego układu.

2

 

 

 

 

LC

R

s

u

s

i

LC

R

R

R

s

si

C

R

L

R

s

i

s

d

d

d

L

d

L

























1

2

(2)

Odpowiednie podzielenie stronami równania (2) sprowadza je do postaci (3) będącej zarazem

transmitancją operatorową układu.

 

 

 





































LC

R

R

R

s

C

R

L

R

s

LC

R

s

u

s

i

s

G

d

d

L

d

L

d

1

1

2

 





d

L

d

L

d

R

R

s

L

C

R

R

LCs

R

s

G











2

1

(3)

W zależności od wartości współczynników wielomianu mianownika wyrażenia (3), układ można

utożsamiać z członem inercyjnym drugiego rzędu, bądź ze stabilnym członem oscylacyjnym
(człon niestabilny posiada dwa ostatnie współczynniki o wartości ujemnej, co w rozpatrywanym
obwodzie nie zachodzi – wartości rezystancji, pojemności i indukcyjności są rzeczywistymi
liczbami dodatnimi).
W przypadku rzeczywistych pierwiastków równania charakterystycznego (4)





0

2











d

L

d

L

d

R

R

s

L

C

R

R

LCs

R

(4)

układ jest członem inercyjnym drugiego rzędu, w przypadku zespolonych bądź urojonych –
stabilnym członem oscylacyjnym.
Wykonanie ćwiczenia polega na wyznaczeniu określonych charakterystyk opisywanego układu
dla zadanych przez prowadzącego parametrów za pomocą narzędzi zaimplementowanych
w środowisku MATLAB.

2

Zasady współpracy z programem MATLAB (niezbędne do wykonania ćwiczenia)

Wykonanie ćwiczenia polega na uruchomieniu programu MATLAB (wersja 5.3., dydaktyczna)

przez kliknięcie na ikonę tego programu na pulpicie WINDOWS. Po zgłoszeniu się programu
następuje otwarcie okna poleceń MATLAB Command Window (gotowość sygnalizowana
kursorem: >> ). Należy wpisać następnie polecenie

clear;clc

i zatwierdzić je naciskając

klawisz Enter. Spowoduje to wyczyszczenie pola poleceń, zapamiętanych zmiennych i ustawienie
kursora w lewym górnym rogu pola. Z menu File wybiera się polecenie Open a następnie należy
wybrać katalog MATLABzad w którym wskazuje się na określony plik tekstowy typu skryptowego
(tzn. z rozszerzeniem *.m, znamiennym dla MATLAB’a). Zbiór tych plików umieszczonych
w katalogu MATLABzad zawiera następujące pliki typu skryptowego:

Każdy z tych plików zawiera ciągi poleceń wykonujących algorytm obliczeń i ew. kreślenia

charakterystyk lub funkcji napisanych w języku programowania wysokiego poziomu
akceptowanym przez środowisko MATLAB’a. Kliknięcie na określony plik i akceptacja otwarcia
tego pliku spowodują, że automatycznie zgłosi się program MATLAB Editor/Debugger, który

3

otworzy swoje własne okno i wyświetli zawartość wskazanego pliku. W trybie MATLAB
Editor/Debugger dokonuje się edycji, poprawek i modyfikacji programów standardu MATLAB.

Aby wykonać program zapisany w wybranym pliku należy (jeden z wielu sposobów):

1. Z menu wybrać opcje Edit a następnie Select all i skopiować do pamięci poleceniem Copy

(lub klikając w pasku poleceń na ikonę kopiowania),

2. Otworzyć okno MATLAB Command Window i poleceniem Paste z menu Edit wprowadzić

ciąg poleceń z wybranego pliku tekstowego do obszaru poleceń MATLAB Command
Window,

3. Uruchomić wpisany w obszar poleceń program - przez akceptację przycisku Enter ,
4. Jeśli wynikiem programu jest wykreślenie funkcji lub charakterystyk, następuje otwarcie okna

graficznego Figure No. 1 z wykreślonymi charakterystykami lub funkcjami, jeśli na tle rysunku
pojawią się dwie prostopadłe osie, oznacza to, że przeciągając mysz do wybranego miejsca
na rysunku (charakterystyce), należy kliknąć w tym miejscu aby wstawić opis odnoszący się
do rysunku (charakterystyki),

5. Jeśli wynikiem są obliczenia, następuje wyświetlenie wyników w formacie zadanym przez

program z pliku skryptowego na ekranie monitora bezpośrednio po sekwencji poleceń
odnoszących się do tego programu,

6. Po uzyskaniu wyników wybranego programu można uruchomić program następnego pliku

skryptowego otwierając (powrót do okna) okno MATLAB Editor/Debugger i zamykając otwarty
uprzednio w tym oknie plik poleceniem File/Close oraz okno rysunku Figure No 1, po
zamknięciu okna rysunku i zamknięciu pliku otworzyć żądany plik poleceniem File/Open
i powtórzyć czynności od p.1.,

7. Wyniki a w tym i rysunki należy wyprowadzić na drukarkę, wydruki opisać,
8. Aby zakończyć działanie MATLAB’a zamyka się kolejno okna Figure No. 1 (jeśli było otwarte),

MATLAB Editor/Debugger i na końcu MATLAB Command Window w wyniku czego następuje
powrót do systemu operacyjnego Windows.

3

Wykonanie ćwiczenia

Realizacja ćwiczenia wymaga kolejnego wykonania wszystkich programów zapisanych

w plikach od P3_1_char_skokowe.m do P3_6_wsp_wielom_char.m. Poniżej zamieszczono opis
realizowanych funkcji, poparty przykładami m-plików zrealizowanymi dla wybranych parametrów
elektrycznych obwodu. Zamieszczone wyniki powinny zostać wykorzystane podczas odpowiedzi
na postawione pytania.

3.1 Wyznaczenie charakterystyk skokowych.

Jedną z podstawowych charakterystyk opisujących układ dynamiczny jest jego odpowiedź na

skok jednostkowy 1(t) zadany na wejście u(t).

Skoro u(t) = U·1(t), toteż transformatą tego sygnału będzie wymuszenie u(s) = U·s

-1

.

Współczynnik U będzie wartością napięcia, jaką podano na dwójnik. Korzystając z transmitancji
operatorowej (3) wyznaczamy odpowiedź układu w dziedzinie zmiennej zespolonej s ze wzoru
(4).

 

   









s

R

R

s

L

C

R

R

LCs

R

U

s

u

s

G

s

i

d

L

d

L

d















2

3

(4)

Przekształcenie operatorowe Laplace’a powyższego wyrażenia stanowi wartość natężenia

prądu w funkcji czasu od chwili podania napięcia na zaciski wejściowe.

Do wyznaczenia charakterystyki skokowej wykorzystamy gotową funkcję step znajdującą się

w dodatkowym pakiecie control narzędzi programu MATLAB. Postać funkcji jest następująca:
[y, x, t]= step(L, M)
gdzie:
t – wektor kolejnych chwil czasu dla których obliczane są macierze wartości wektorów x i y,

4

y – macierz wartości sygnału wyjściowego w kolejnych chwilach symulacji,
x – macierz wartości wektora stanu dla kolejnych chwil czasu,
L – wektor współczynników wielomianu licznika transmitancji G(s),
M - wektor współczynników wielomianu mianownika transmitancji G(s).

Przykładowy m.plik powodujący wykreślenie charakterystyki skokowej przyjmie zatem postać
(przyjęto U

1

= L

1

= C

1

= R

d1

= 1, R

L1

= 4, U

2

= L

2

= 1, C

2

= 0.2, R

d2

= 5, R

L2

= 1):

%Przykład m-pliku;
%JCK;
%Charakterystyka skokowa obiektu o transmitancji;
% 1;
%G(s)=--------------;
% T2s^2+T1s+T0;
%=================================================;
U1=1;
L1=1;
C1=1;
Rd1=1;
Rl1=4;
T21=Rd1*L1*C1;
T11=Rl1*Rd1*C1+L1;
T01=Rl1+Rd1;
%wyznaczenie współczynników licznika transmitancji;
l1=[0,0,U1];
%wyznaczenie współczynników mianownika transmitancji;
m1=[T21,T11,T01];
% wyznaczenie wektora odpowiedzi;
[y1,x1,t1]=step(l1,m1);
%=================================================;
U2=1;
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
T22=Rd2*L2*C2;
T12=Rl2*Rd2*C2+L2;
T02=Rl2+Rd2;
%wyznaczenie współczynników licznika transmitancji;
l2=[0,0,U2];
%wyznaczenie współczynników mianownika transmitancji;
m2=[T22,T12,T02];
% wyznaczenie wektora odpowiedzi;
[y2,x2,t2]=step(l2,m2);
%=================================================;
% wykres obu odpowiedzi skokowych odpowiednio na jednym rysunku;
plot(t1,y1,'g',t2,y2,'m')
title('Charakterystyki czasowe (skokowe) obiektu');
ylabel('Amplituda odpowiedzi na wymuszenie jednostkowe 1(t)');
xlabel('czas [s]');
gtext('U1=1;L1=1;C1=1;Rd1=1;Rl1=4');
gtext('U2=1;L2=1;C2=0.2;Rd2=5;Rl2=1');
grid;pause;close;clear;clc;

Uruchomienie powyższego m-pliku pozwala uzyskać następującą charakterystykę

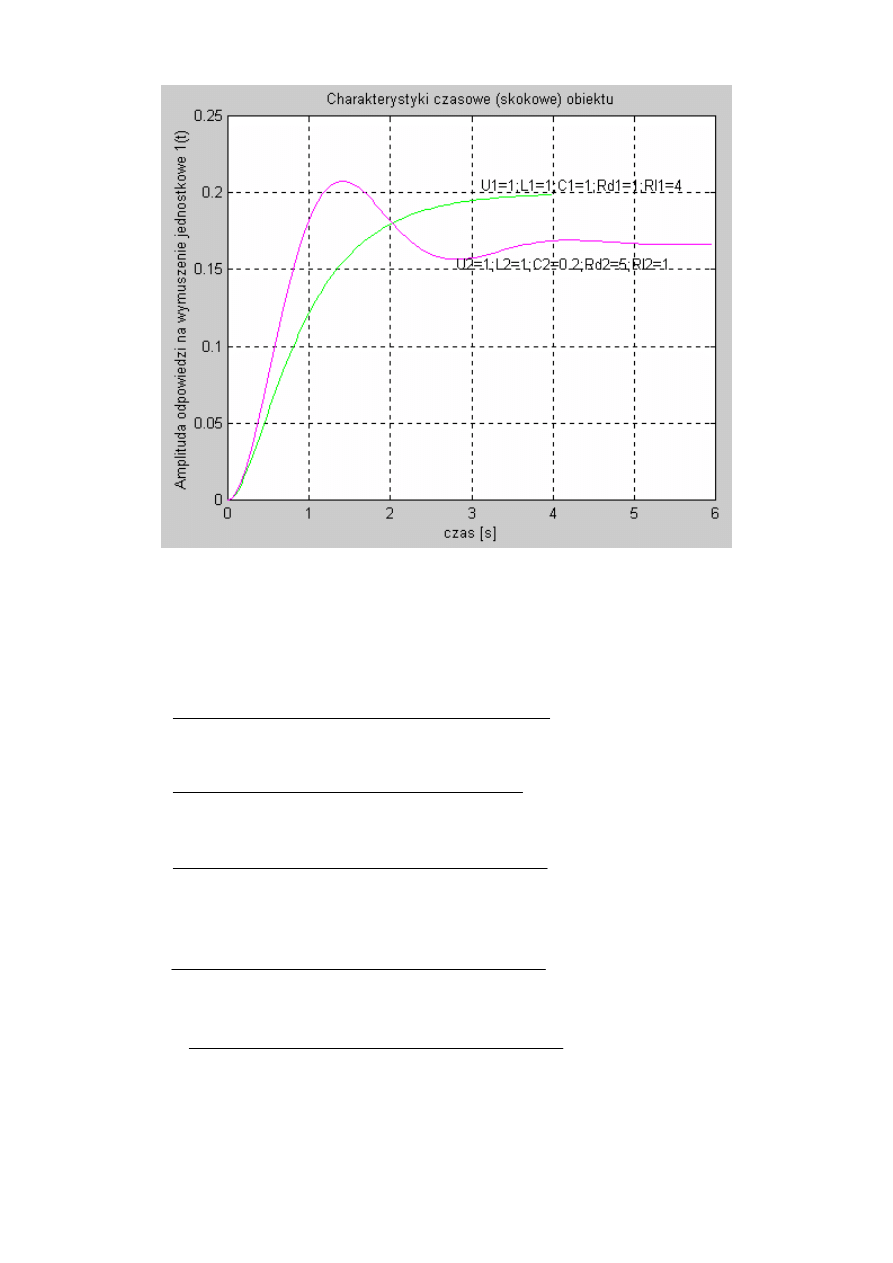
5

3.2 Wyznaczenie charakterystyk amplitudowo-fazowych.

Do wykreślenia charakterystyk częstotliwościowych układu konieczna jest znajomość

transmitancji G(s) liniowego układu ciągłego. Na podstawie transmitancji widmowej G(jω)
wyznacza się odpowiednio wartości (w postaci wektorów) części rzeczywistych P(ω) i urojonych
Q(ω). Podstawmy do wzoru (3) s = jω. W efekcie otrzymamy

 

 





d

L

d

L

d

R

R

j

L

C

R

R

j

LC

R

j

G

















2

1

 











L

C

R

R

j

LC

R

R

R

j

G

d

L

d

d

L











2

1

(5a)

 





















2

2

2

2

2

1

1











L

C

R

R

LC

R

R

L

C

R

R

j

LC

R

R

R

j

G

d

L

d

L

d

L

d

d

L



















(5)

Stąd część rzeczywista P(ω) i urojona Q(ω) przyjmują następujące postaci

 

















2

2

2

2

2

1

1









L

C

R

R

LC

R

R

LC

R

R

R

j

P

d

L

d

L

d

d

L















(6)

 

















2

2

2

2

1









L

C

R

R

LC

R

R

L

C

R

R

j

Q

d

L

d

L

d

L















(7)

Dla wartości pulsacji ω (w poniższym programie zmienna oznaczająca pulsację występuje jako

zmienna w) zmieniającej się od 0 do 100 rd/s co 0,01. Do wykreślenia charakterystyk
amplitudowo-fazowych zastosowano standardową funkcję plot. Funkcja ta ma następującą
postać:

6

plot(x, y, ‘typ linii’)
gdzie:
x – zbiór wartości na osi X (wartości zmiennej niezależnej) ,
y – zbiór wartości na osi Y (wartości funkcji),
typ linii – znaki oznaczające kolor i rodzaj linii.

%Przykład m-pliku;
%JCK;
%Charakterystyki częstotliwościowe - charakterystyki;
%amplitudowo-fazowe obwodu przekaźnika;
% 1;
%G(s)=--------------;
% T2s^2+T1s+T0;
%Wykreślenie ch-k polega na obliczeniu części wspólnej ws;
%a następnie części rzeczywistej P i urojonej Q odpowiednio dla;
%zadanych wartości parametrów elektrycznych obwodu a następnie;
%dokonaniu wykreślenia przy pomocy funkcji plot;
w=0:0.01:100;
roz=size(w);
%======================================================;
L1=1;
C1=1;
Rd1=1;
Rl1=4;
ws1=1./(((ones(roz)-
(w.^2)*L1*C1)*Rd1+Rl1).^2+((Rl1*Rd1*C1+L1)^2).*(w.^2));
P1=((ones(roz)-(w.^2)*L1*C1)*Rd1+Rl1).*ws1;
Q1=-((Rl1*Rd1*C1+L1)^2).*(w.^2).*ws1;
%======================================================;
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
ws2=1./(((ones(roz)-
(w.^2)*L2*C2)*Rd2+Rl2).^2+((Rl2*Rd2*C2+L2)^2).*(w.^2));
P2=((ones(roz)-(w.^2)*L2*C2)*Rd2+Rl2).*ws2;
Q2=-((Rl2*Rd2*C2+L2)^2).*(w.^2).*ws2;
%======================================================;
%wykreślenie ch-k amplitudowo-fazowych
plot(P1,Q1,'r',P2,Q2,'g');

%comet(P1,Q1,0.05);pause;

%comet(P2,Q2,0.05);pause;

title('Charakterystyki amplitudowo-fazowe obiektu dynamicznego');
xlabel('oś wartości rzeczywistych P1, P2');
ylabel('oś wartości urojonych Q1, Q2');
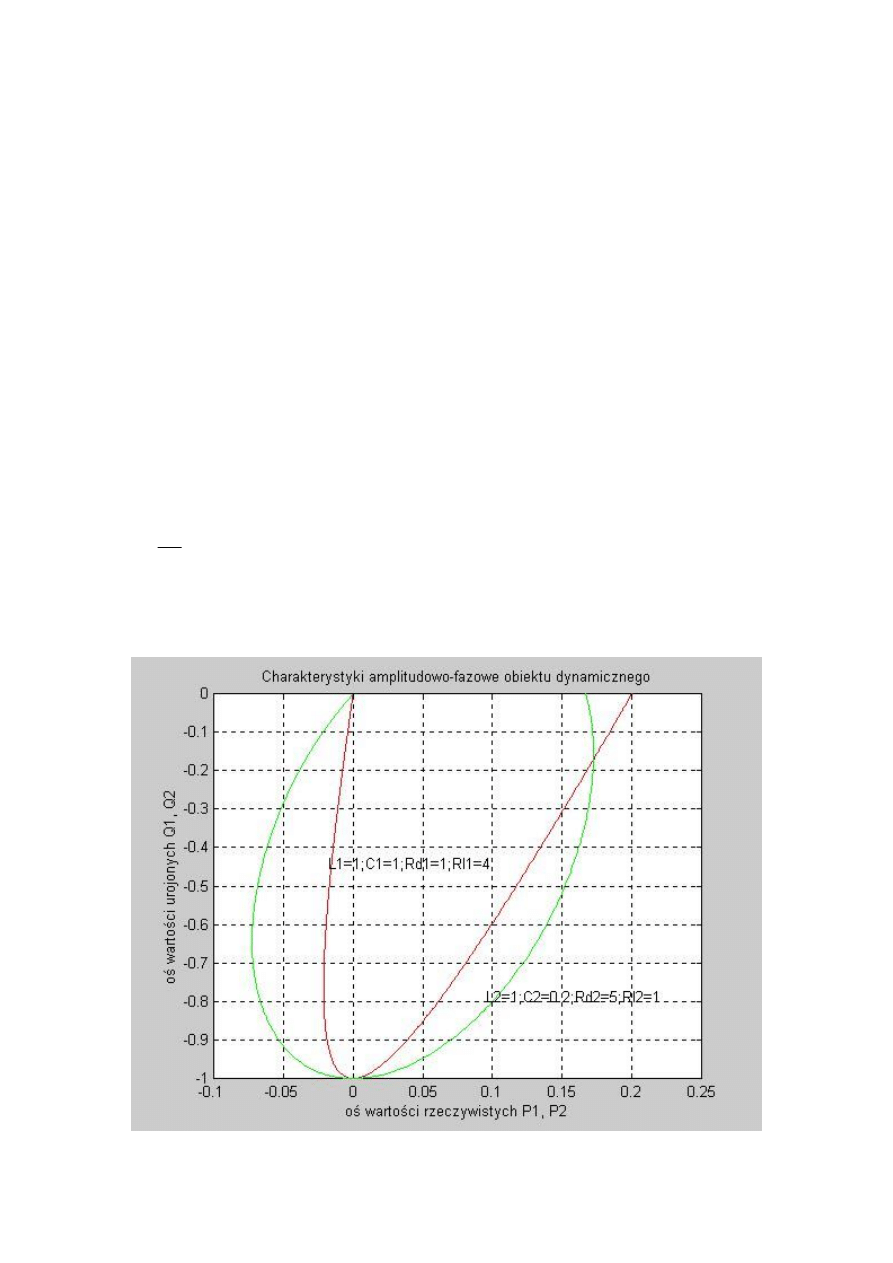
gtext('L1=1;C1=1;Rd1=1;Rl1=4');
gtext('L2=1;C2=0.2;Rd2=5;Rl2=1');grid;pause;
%wyznaczenie współczynników licznika transmitancji;
l1=[0,0,1];
l2=[0,0,1];
%wyznaczenie współczynników mianownika transmitancji;
T21=Rd1*L1*C1;
T11=Rl1*Rd1*C1+L1;
T01=Rl1+Rd1;
T22=Rd2*L2*C2;
T12=Rl2*Rd2*C2+L2;
T02=Rl2+Rd2;

7

m1=[T21,T11,T01];
m2=[T22,T12,T02];
nyquist(l1,m1,w);gtext('L1=1;C1=1;Rd1=1;Rl1=4');grid;hold on;
nyquist(l2,m2,w);gtext('L2=1;C2=0.2;Rd2=5;Rl2=1');grid;pause;
close;clear;clc;

Alternatywną metodą do zastosowania funkcji plot jest zastosowanie funkcji comet. Funkcja ta

pozwala zaobserwować animację rysowania wykresu charakterystyki amplitudowo-fazowej
w miarę wzrostu pulsacji, i ma następującą postać:
comet(x,y,dł)
gdzie:
x – odcięta trajektorii komety ruchomego wykresu imitującego jej lot,
y – rzędna trajektorii komety ruchomego wykresu imitującego jej lot,
dł – długość „ogona” komety w przedziale (0,1).

Aby uruchomić tę funkcję w m-pliku należy po wklejeniu usunąć znaczki

%

sprzed instrukcji

comet, a umieścić jeden przed instrukcją plot.

Wyznaczenie charakterystyk amplitudowo-fazowych (Nyquista) w zakresie pulsacji ω od 0 do

+∞ i od -∞ do 0 odbywa się za pomocą standardowej funkcji nyquist o postaci:
nyquist(L, M, w)
gdzie:
L i M to wektory współczynników wielomianów licznika – L i mianownika – M transmitancji G(s)
o postaci

G s

L

M

( ) 

(8)

w - zakres pulsacji dla którego będzie kreślona charakterystyka.

W wyniku uruchomienia opisywanego m-pliku uzyskuje się następujące charakterystyki

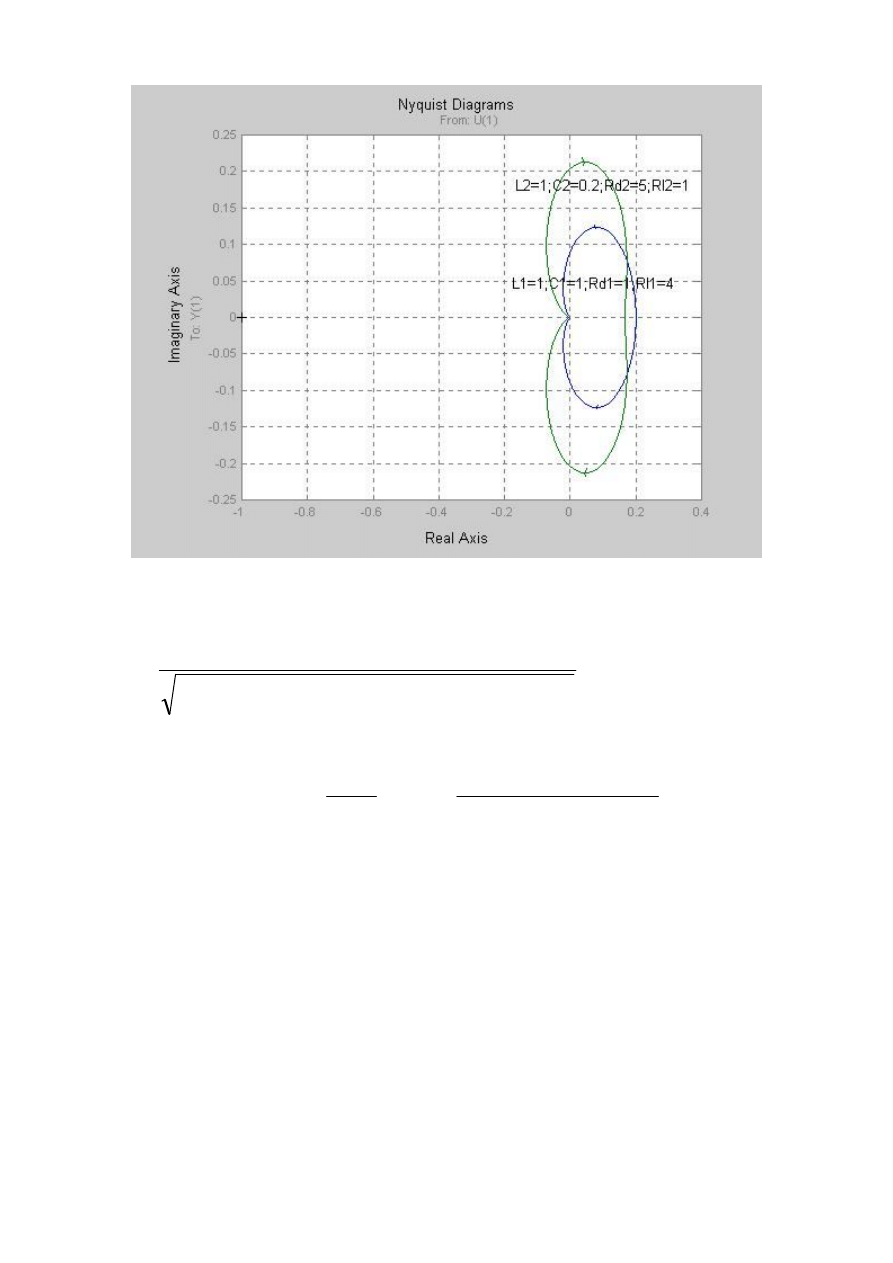
8

3.3 Charakterystyka amplitudowa i charakterystyka fazowa

Amplitudą A(ω) nazywamy moduł transmitancji widmowej (5) o następującej postaci

 













2

2

2

2

1

1







L

C

R

R

LC

R

R

R

A

d

L

d

d

L











(9)

Faza transmitancji widmowej stanowi argument tej funkcji. Wyliczamy ją na podstawie prostej
zależności (10).

 

 





 

 









2

1

arg















LC

R

R

R

L

C

R

R

arctg

P

Q

arctg

G

d

d

L

d

L













(10)

Do wykreślenia charakterystyk amplitudowo-fazowych w funkcji pulsacji zastosujemy poznaną

już funkcję plot.

Do wykreślenia charakterystyk logarytmicznych modułu i fazy zostanie zastosowana

standardowa funkcja bode o postaci:
[moduł,faza,pulsacja]=bode(L, M)
gdzie:
L i M to wektory współczynników wielomianów licznika – L i mianownika – M transmitancji G(s)
o postaci (8).

Pulsacja ω (w poniższym programie zmienna oznaczająca pulsację występuje także jako

zmienna w) i zmienia się od 0 do 100 [rd/s], co 0,01 [rd/s].

%Przykład m-pliku;
%JCK;
% Charakterystyki częstotliwościowe - amplitudowe i fazowe;
% 1;
%G(s)=--------------;
% T2s^2+T1s+T0;

9

%Wykreślenie ch-k polega na obliczeniu części wspólnej ws;
%a następnie części rzeczywistej P i urojonej Q odpowiednio;
%dla zadanych wartości parametrów elektrycznych obwodu;
%a następnie dokonaniu wykreślenia przy pomocy funkcji plot;
w=0:0.01:100;
roz=size(w);
%======================================================;
L1=1;
C1=1;
Rd1=1;
Rl1=4;
ws1=1./(((ones(roz)-
(w.^2)*L1*C1)*Rd1+Rl1).^2+((Rl1*Rd1*C1+L1)^2).*(w.^2));
P1=((ones(roz)-(w.^2)*L1*C1)*Rd1+Rl1).*ws1;
Q1=-((Rl1*Rd1*C1+L1)^2).*(w.^2).*ws1;
%======================================================;
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
ws2=1./(((ones(roz)-
(w.^2)*L2*C2)*Rd2+Rl2).^2+((Rl2*Rd2*C2+L2)^2).*(w.^2));
P2=((ones(roz)-(w.^2)*L2*C2)*Rd2+Rl2).*ws2;
Q2=-((Rl2*Rd2*C2+L2)^2).*(w.^2).*ws2;
%======================================================;
%wykreślenie ch-k amplitudowych i fazowych;
plot(w,P1,'r',w,Q1,'r',w,P2,'g',w,Q2,'g');
ylabel('Q1, Q2, P1, P2');
xlabel('pulsacja');
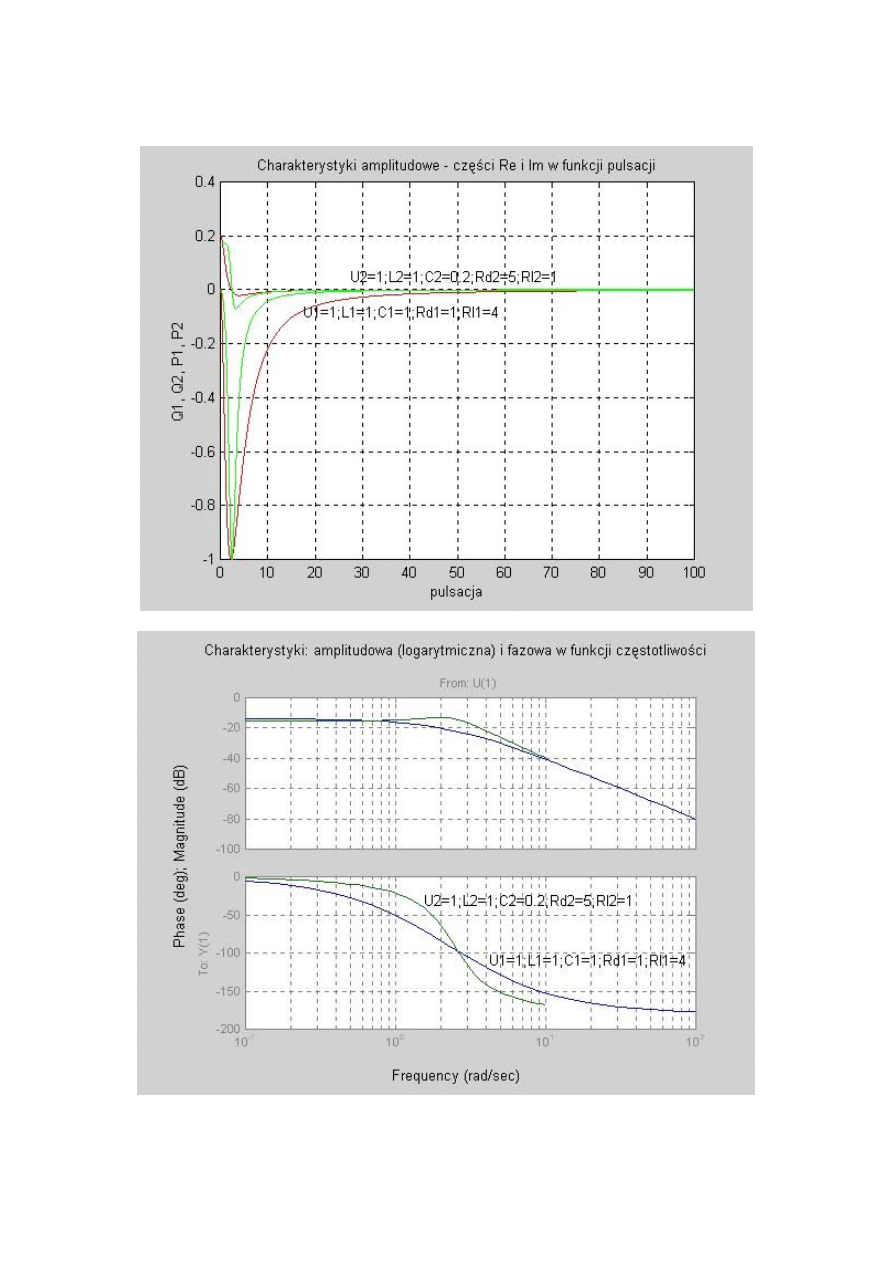
title('Charakterystyki amplitudowe - części Re i Im w funkcji
pulsacji');
gtext('U1=1;L1=1;C1=1;Rd1=1;Rl1=4');
gtext('U2=1;L2=1;C2=0.2;Rd2=5;Rl2=1');
grid;pause;
%======================================================;
T21=Rd1*L1*C1;
T11=Rl1*Rd1*C1+L1;
T01=Rl1+Rd1;
%wyznaczenie współczynników licznika transmitancji;
l1=[0,0,1];
%wyznaczenie współczynników mianownika transmitancji;
m1=[T21,T11,T01];
T22=Rd2*L2*C2;
T12=Rl2*Rd2*C2+L2;
T02=Rl2+Rd2;
%wyznaczenie współczynników licznika transmitancji;
l2=[0,0,1];
%wyznaczenie współczynników mianownika transmitancji;
m2=[T22,T12,T02];
bode(l1,m1);grid;hold on;
bode(l2,m2);grid;hold on;
title('Charakterystyki: amplitudowa (logarytmiczna) i fazowa w
funkcji częstotliwości');
gtext('U1=1;L1=1;C1=1;Rd1=1;Rl1=4');grid;
gtext('U2=1;L2=1;C2=0.2;Rd2=5;Rl2=1');
grid;pause;
close;clear;clc;

10

W wyniku uruchomienia opisywanego m-pliku uzyskuje się następujące charakterystyki

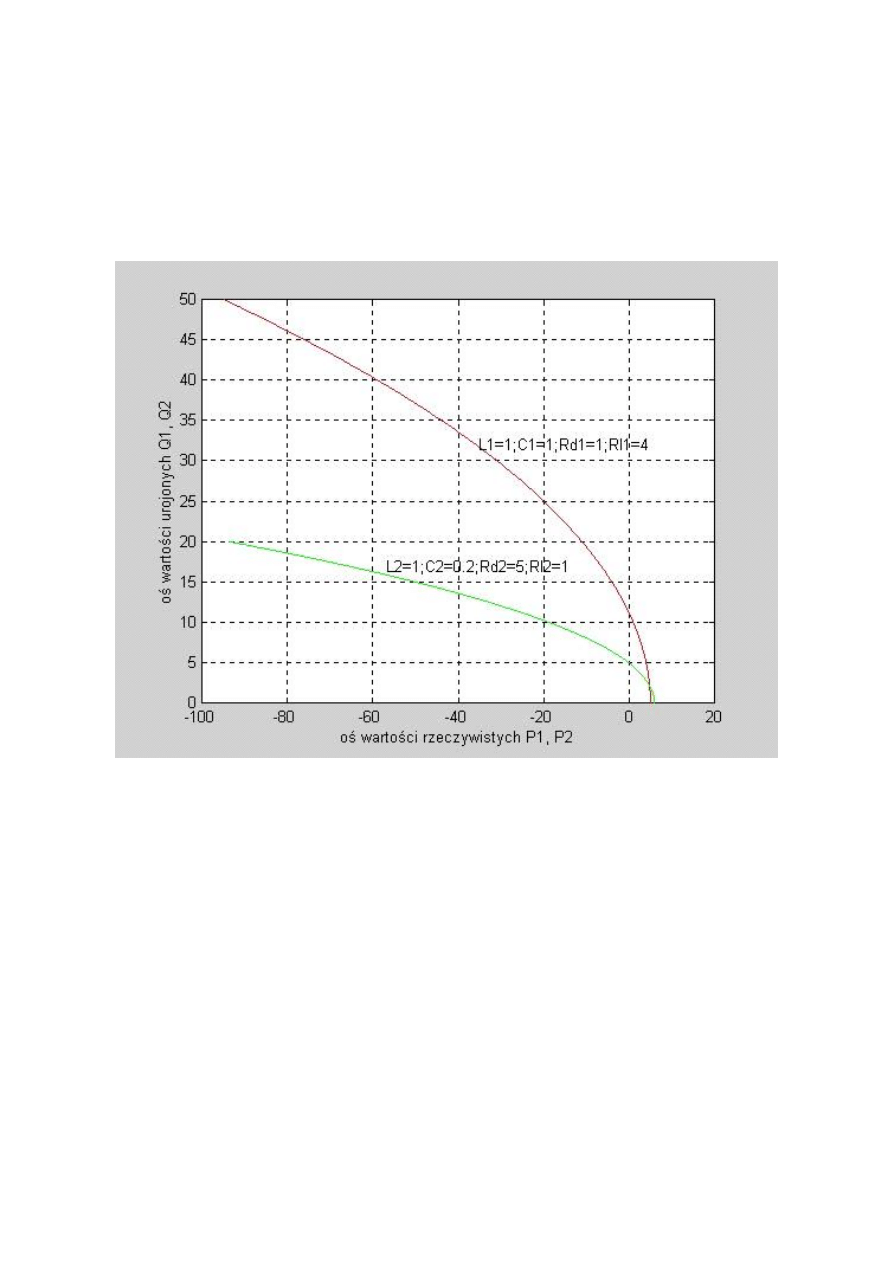
3.4 Graficzne kryterium stabilności Michajłowa na podstawie hodografu oraz przy użyciu

charakterystyk częstotliwościowych

11

Zgodnie z kryterium Michajłowa układ n-tego rzędu, określony równaniem charakterystycznym,

będącym mianownikiem M(s) transmitancji operatorowej G(s) jest stabilny wtedy i tylko wtedy, gdy
zmiana argumentu wektora M(jω) przy zmianie parametru ω od 0 do +∞ wyniesie n(/2), czyli
wykres (hodograf) M(jω) przejdzie przez n kwadrantów (ćwiartek układu współrzędnych). Do
wykreślenia hodografu zastosujemy funkcję plot i obliczywszy wcześniej część rzeczywistą P(ω)
i urojoną Q(ω) wektora M(jω).

Poszukiwany wektor M(jω) jest odwrotnością wyrażenia (5a).
Uruchomienie poniższego m-pliku pozwala uzyskać następującą charakterystykę

%Przykład m-pliku;
%JCK;
%Wyznaczenie stabilności układu dynamicznego za pomoca graficznego
kryterium Michajlowa;
% 1;
%G(s)=--------------;
% T2s^2+T1s+T0;
w=0:0.01:10;
roz=size(w);
%======================================================;
L1=1;
C1=1;
Rd1=1;
Rl1=4;
P1=Rl1+Rd1-(w.^2)*L1*C1*Rd1;
Q1=(Rl1*Rd1*C1+L1).*w;
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
P2=Rl2+Rd2-(w.^2)*L2*C2*Rd2;

12

Q2=(Rl2*Rd2*C2+L2).*w;
plot(P1,Q1,'r',P2,Q2,'g');
xlabel('oś wartości rzeczywistych P1, P2');
ylabel('oś wartości urojonych Q1, Q2');
gtext('L1=1;C1=1;Rd1=1;Rl1=4');
gtext('L2=1;C2=0.2;Rd2=5;Rl2=1');grid;pause;
close;clear;clc;

3.5 Określenie sterowalności i obserwowalności układu

Korzystając z równania różniczkowego (1) będącego podstawą obliczeń oraz dwie zmienne

stanu x

1

(t) i x

2

(t) = x

1

’(t) można ułożyć następujący układ równań obiektu dynamicznego (11).

 

 

 

 

 

 

 

 











































t

x

t

y

t

u

LC

R

t

x

C

R

L

R

t

x

LC

R

R

R

t

x

t

x

t

x

d

d

L

d

L

d

1

2

1

2

2

1

1

1

'

(11)

Wielowymiarowy liniowy układ dynamiczny można opisać równaniami stanu x’(t) = Ax(t) +

Bu(t) i równaniem wyjścia y(t) = Cx(t) + Du(t). W rozpatrywanym przykładzie mamy do czynienia
z układem o jednym sygnale wejściowym u(t) i jednym wyjściowym i(t), zatem wektory u(t) = [u(t)]
i y(t) = [y(t)]. Wektor zmiennych stanu przyjmuje postać

 

 















t

x

t

x

t

x

2

1

)

(

a macierze stanu A, wejścia B, wyjścia C i transmisyjna D postaci









































C

R

L

R

LC

R

R

R

A

d

L

d

L

d

1

1

0





















LC

R

B

d

1

0





0

1



C

 

0



D

Układ jest całkowicie sterowalny, gdy macierz S

S

b Ab A B .



2

.. = n

czyli jest rzędu n lub gdy wyznacznik macierzy S

det

det

S

b .





b Ab A

..

0

2

.

Układ jest całkowicie obserwowalny, gdy rząd macierzy O





O

c





 





c A c A

...

2

jest równy n. n jest liczbą kolumn macierzy S i O. W rozpatrywanym przykładzie n = 2.

Do wyznaczenia sterowalności w MATLAB, stosuje się funkcję rank(macierz), która oblicza

rząd macierzy, w naszym przypadku: S lub O. Parametry funkcji rank określa się na podstawie
macierzy typu A, B lub C.

%Przykład m-pliku;
%JCK;
disp('Sprawdzenie sterowalności i obserwowalności');
disp('============================================================
======')

13

disp('Sprawdzenie sterowalności i obserwowalności dla L1=1; C1=1;
Rd1=1; Rl1=4');
L1=1;
C1=1;
Rd1=1;
Rl1=4;
A1=[0 1;(-(Rd1+Rl1)/Rd1/L1/C1) (-Rl1/L1-1/Rd1/C1)];
B1=[0; (-1/Rd1/L1/C1)];
C1=[1 0];
disp('obliczenie rzędu macierzy S1 i wyznacznika S1');
disp('macierz stanu A1');disp(A1);
disp('macierz wejścia B1');disp(B1);
rzd=rank([B1 A1*B1]);
disp('rząd macierzy S1'); disp(rzd);
wyz=det([B1 A1*B1]);
disp('wyznacznik macierzy S1'); disp(wyz);
disp('obliczenie rzędu macierzy O1 i wyznacznika O1');
disp('macierz stanu A1');disp(A1);
disp('macierz wyjścia C1');disp(C1);
rzd=rank([C1' A1'*C1']);
wyz=det([C1' A1'*C1']);
disp('rząd macierzy O1'); disp (rzd);
disp('wyznacznik macierzy O1'); disp(wyz);
disp('============================================================
======')
disp('Sprawdzenie

sterowalnosci

i

obserwowalnosci

dla

L2=1;

C2=0.2; Rd2=5; Rl2=1');
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
A2=[0 1;(-(Rd2+Rl2)/Rd2/L2/C2) (-Rl2/L2-1/Rd2/C2)];
B2=[0; (-1/Rd2/L2/C2)];
C2=[1 0];
disp('obliczenie rzędu macierzy S1 i wyznacznika S1');
disp('macierz stanu A2');disp(A2);
disp('macierz wejścia B2');disp(B2);
rzd=rank([B2 A2*B2]);
disp('rząd macierzy S2'); disp(rzd);
wyz=det([B2 A2*B2]);
disp('wyznacznik macierzy S2'); disp(wyz);
disp('obliczenie rzędu macierzy O2 i wyznacznika O2');
disp('macierz stanu A2');disp(A2);
disp('macierz wyjścia C2');disp(C2);
rzd=rank([C2' A2'*C2']);
wyz=det([C2' A2'*C2']);
disp('rząd macierzy O2'); disp (rzd);
disp('wyznacznik macierzy O2'); disp(wyz);
disp('Nacisnij dowolny klawisz by zakonczyc.');
pause;clear;clc;

Po uruchomieniu powyższego m-pliku uzyskujemy następujące wyniki:

Sprawdzenie sterowalności i obserwowalności
==================================================================
Sprawdzenie sterowalności i obserwowalności dla L1=1; C1=1; Rd1=1;
Rl1=4

14

obliczenie rzędu macierzy S1 i wyznacznika S1
macierz stanu A1
0 1
-5 -5

macierz wejścia B1
0
-1

rząd macierzy S1
2

wyznacznik macierzy S1
-1

obliczenie rzędu macierzy O1 i wyznacznika O1
macierz stanu A1
0 1
-5 -5

macierz wyjścia C1
1 0

rząd macierzy O1
2

wyznacznik macierzy O1
1

==================================================================
Sprawdzenie sterowalnosci i obserwowalnosci dla L2=1; C2=0.2;
Rd2=5; Rl2=1
obliczenie rzędu macierzy S1 i wyznacznika S1
macierz stanu A2
0 1.0000
-6.0000 -2.0000

macierz wejścia B2
0
-1

rząd macierzy S2
2

wyznacznik macierzy S2
-1

obliczenie rzędu macierzy O2 i wyznacznika O2
macierz stanu A2
0 1.0000
-6.0000 -2.0000

macierz wyjścia C2
1 0

rząd macierzy O2
2

15

wyznacznik macierzy O2
1

Nacisnij dowolny klawisz by zakonczyc.

3.6 Wyznaczenie współczynników i pierwiastków wielomianu charakterystycznego układu.

Współczynniki i pierwiastki wielomianu charakterystycznego wyznacza się na podstawie

macierzy stanu A za pomocą standardowej funkcji poly.
poly(A) – dla macierzy kwadratowej A stopnia n tworzy n+1 elementowy wektor współczynników
wielomianu charakterystycznego det(sI-A). Współczynniki uporządkowane są w kierunku
malejących potęg.
Pierwiastki wielomianu charakterystycznego zostają wyznaczone przy pomocy funkcji roots (W).

%Przykład m-pliku;
%JCK;
%Wyznaczenie

współczynników

i

pierwiastków

wielomianu

%charakterystycznego;
disp('Wyznaczenie

współczynników

i

pierwiastków

wielomianu

charakterystycznego');
disp('************************************************************
************');
disp('dla A1[0 1;(-(Rd1+Rl1)/Rd1/L1/C1) (–Rl1/L-1/Rd1/C1)]');
L1=1;
C1=1;
Rd1=1;
Rl1=4;
L2=1;
C2=0.2;
Rd2=5;
Rl2=1;
a1=-(Rd1+Rl1)/(Rd1*L1*C1);
b1=-(Rl1/L1)-1/(Rd1*C1);
A1=[0 1;a1 b1];
disp('wspolczynniki=');disp(poly(A1));
W1=poly(A1)
disp('pierwiastki=');disp(roots(W1));
disp('dla A2[0 1;(-(Rd2+Rl2)/Rd2/L2/C2) (–Rl2/L2-1/Rd2/C2)]');
a2=-(Rd2+Rl2)/(Rd2*L2*C2);
b2=-(Rl2/L2)-1/(Rd2*C2);
A2=[0 1;a2 b2];
disp('wspolczynniki=');disp(poly(A2));
W2=poly(A2);
disp('pierwiastki=');disp(roots(W2));
disp('Nacisnij dowolny klawisz by zakonczyc.');
pause;clear;clc;

Po uruchomieniu powyższego m-pliku uzyskujemy następujące wyniki:

Wyznaczenie

współczynników

i

pierwiastków

wielomianu

charakterystycznego
******************************************************************
******
dla A1[0 1;(-(Rd1+Rl1)/Rd1/L1/C1) (–Rl1/L-1/Rd1/C1)]
wspolczynniki=

16

1 5 5

W1 =

1 5 5

pierwiastki=
-3.6180
-1.3820

dla A2[0 1;(-(Rd2+Rl2)/Rd2/L2/C2) (–Rl2/L2-1/Rd2/C2)]
wspolczynniki=
1.0000 2.0000 6.0000

pierwiastki=
-1.0000 + 2.2361i
-1.0000 - 2.2361i

Nacisnij dowolny klawisz by zakonczyc.

3.7 Polecenia i pytania do plików skryptowych.

Nazwa pliku

Punkt

instrukcji

Działanie

programu

Zadania do wykonania w czasie zajęć

1.

P3_1_char_skokow
e.m

3.1

Wyznaczenie
charakterystyk
skokowych
(czasowych)
członu inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Wydrukować ch-ki odpowiedzi skokowych.
 Uzasadnić na podstawie wykreślonych

charakterystyk, jaki wpływ na ch-kę skokową mają
wartości parametrów obiektu inercyjnego drugiego
rzędu: T

1

, T

2

- stałe czasowe i k - współczynnik

proporcjonalności (wzmocnienia). Jaki jest związek
pomiędzy tymi parametrami a parametrami
elektrycznymi charakteryzującymi rozpatrywany
obwód?

 Uzasadnić na podstawie wykreślonych

charakterystyk, jaki wpływ na ch-kę skokową mają
wartości parametrów obiektu oscylacyjnego: T

0

-

stała czasowa, ξ

0

- współczynnik tłumienia i k -

współczynnik proporcjonalności (wzmocnienia).
Jaki jest związek pomiędzy tymi parametrami a
parametrami elektrycznymi charakteryzującymi
rozpatrywany obwód?

 Podać interpretacje stałych czasowych obiektu

inercyjnego drugiego rzędu.

 Czy na podstawie uzyskanych ch-k skokowych

można ocenić liniowość względnie nieliniowość
układu dynamicznego?

2.

P3_2_char_ampfaz.
m

3.2

Wyznaczenie
charakterystyk
amplitudowo-
fazowych członu
inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Wydrukować ch-ki amplitudowo-fazowe.
 Od których parametrów i jak zależy

charakterystyka amplitudowo-fazowa? Zaznaczyć
strzałką na ch-kach kierunek wzrostu pulsacji.

 Dla wybranej ch-ki amplitudowo-fazowej dla

wartości pulsacji ω=0 i ω=10 wrysować wektory
modułu transmitancji i odczytać z wykresu dla tych
modułów wartości części rzeczywistych (P) i

17

Nazwa pliku

Punkt

instrukcji

Działanie

programu

Zadania do wykonania w czasie zajęć

urojonych (Q), wskazać kąt przesunięcia fazowego i
obliczyć wartość tgφ tego przesunięcia.

 Naszkicować lub wydrukować ch-ki amplitudowo-

fazowe Nyquista.

 Czym różnią się ch-ki Nyquista od zwykłych

charakterystyk amplitudowo-fazowych?

 Porównać ch-kę Nyquista obiektu inercyjnego

drugiego rzędu z ch-ką Nyquista stabilnego członu
oscylacyjnego.

 W jakim celu stosuje się ch-ki Nyquista?
 Co można powiedzieć o stabilności układu

regulacji na podstawie uzyskanych ch-k Nyquista?

3.

P3_3_char_amp_i_f
az.m

3.3

Wyznaczenie
charakterystyk
amplitudowych w
funkcji pulsacji i
logarytmicznych
charakterystyk
amplitudowo-
fazowych (tzw.
(Bode Diagrams)
członu inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Uzyskać odpowiednio 2 typy wykresów.
 Wydrukować ch-ki amplitudowe i charakterystyki

logarytmiczne amplitudowo-fazowe.

 Określić różnice między charakterystykami

amplitudowymi i logarytmicznymi amplitudowymi.

 Jaki wpływ na przebieg charakterystyk mają

wartości parametrów obiektu inercyjnego? Jaki
wpływ mają parametry elektryczne obwodu?

 Odczytać z wykresów ch-k amplitudowych

wartości ekstremów części urojonych i
odpowiadające im wartości pulsacji ω. W którym
kierunku przesuwają się wartości ekstremów
urojonych ze wzrostem pulsacji?

 Na wykresach ch-k logarytmicznych

zidentyfikować i opisać ch-ki fazowe.

 Odczytać w [dB] „podbicie” ch-k amplitudowych

a następnie wartości pulsacji dla których występują
te maksima, obliczyć jakie to częstotliwości w [Hz].

4.

P3_4_stab_Michajlo
w.m

3.4

Wyznaczenie
stabiln ości
graficznym
kryterium
Michajłowa członu
inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Czy człony, dla parametrów dla których zostały

wykreślone ch-ki, są obiekteami stabilnym?

 Jakie są inne kryteria stwierdzania stabilności

układów automatyki?

5.

P3_5_ster_obs.m

3.5

Określenie
sterowalności i

obserwowalności
członu inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Uzyskać obliczenia rzędu macierzy i wartości

wyznaczników, tak, jak w przykładzie.

 Dokonać interpretacji otrzymanych wyników

oceniając sterowalność i obserwowalność.

6.

P3_6_wsp_wielom_ch
ar.m

Przykład

6.3

Wyznaczenie
współczynników i
pierwiastków
wielomianu
charakterystyczneg

 Uzyskać obliczenia współczynników i

pierwiastków wielomianu charakterystycznego - jak
w przykładzie.

 Napisać wielomiany charakterystyczne i porównać

z wielomianem mianownika transmitancji układu.

18

Nazwa pliku

Punkt

instrukcji

Działanie

programu

Zadania do wykonania w czasie zajęć

o członu
inercyjnego
drugiego rzędu i
stabilnego członu
oscylacynego.

 Dokonać interpretacji otrzymanych wyników.

1.1 Wnioski.

W sprawozdaniu należy udzielić odpowiedzi na wszystkie pytania zawarte w instrukcji oraz
zalecone przez prowadzącego. Sprawozdanie powinno zawierać opisane oryginalne wydruki
wyników uzyskanych podczas realizacji ćwiczenia. We wnioskach należy uzupełnić
i uporządkować odpowiedzi na postawione pytania lub zagadnienia należące do zadań
wykonanych w czasie zajęć.

2

Niezbędny zakres tematyczny obowiązujący do przygotowania się do zajęć:

Pojęcia: obiekt dynamiczny ciągły i liniowy, równanie różniczkowe opisujące taki obiekt,
identyfikacja obiektu dynamicznego, transmitancja operatorowa i widmowa, moduł transmitancji,
kąt przesunięcia fazowego, podstawowe człony dynamiczne (układy – proporcjonalny, inercyjny,
różniczkujący rzeczywisty, całkujący, inercyjny drugiego rzędu i oscylacyjny), transmitancje tych
członów i podstawowe charakterystyki członów, obserwowalność, sterowalność, stabilność (oraz
kryteria i wyznaczanie obserwowalności, sterowalności i stabilności) układu dynamicznego i
układu regulacji, równanie charakterystyczne i wielomian charakterystyczny, stała czasowa
w podstawowych członach dynamicznych,
Charakterystyki układów dynamicznych – charakterystyki skokowe i częstotliwościowe,
interpretacja

charakterystyk,

sposoby

wyznaczania

charakterystyk,

obliczanie

modułu

transmitancji i przesunięcia fazowego,
Równania wektorowo-macierzowe układu dynamicznego. Macierze: stanu, wejścia i wyjścia.
Zastosowanie macierzy równań stanu.

3

Literatura pomocna do wykonania ćwiczenia, przygotowania sprawozdania i przygotowania
się do zaliczenia:

1. Brzózka J., Ćwiczenia z automatyki w MATLABIE i SIMULINKU, Mikom, Warszawa, 1997.
2. Dębowski A.: Automatyka. Podstawy teorii, WNT, Warszawa 2008.
3. Frelek B. i inni, Laboratorium podstaw automatyki, W PW, 1984.
4. Mrozek B+Z, Matlab 5.x i Simulink 2.x, Wydawnictwo PLJ, Warszawa 1998.
5. Nowacki P., Szklarski L., Górecki H.: Podstawy teorii układu regulacji autonomicznej. Tom I,

PWN, Warszawa 1970.

6. Pełczewski W., Teoria sterowania, WNT, Warszawa 1980.
7. Żelazny M., Podstawy automatyki, PWN, Warszawa 1976.
8. Badania obiektów dynamicznych (z zastosowaniem programu MATLAB) - Przykłady

programów do wykonania w czasie zajęć laboratoryjnych. Opracowanie WTPW, Warszawa
2002.