STANY NIEUSTALONE W OBWODACH ELEKTRYCZNYCH

I. Wprowadzenie do ćwiczenia

1. Rozwiązywanie równań różniczkowych zwyczajnych

Dowolne równanie różniczkowe zwyczajne rzędu n

(1)

z warunkami początkowymi:

,
, …,
(2)

można, za pomocą metody zmiennych stanu, przedstawić jako układ n równań różniczkowych rzędu pierwszego. Najczęściej dobiera się je tak, aby każda kolejna zmienna {y₁,y₂, …,y_n} była pochodną po czasie poprzedniej:

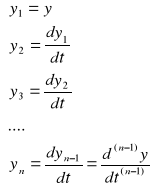
(3)

Równanie (3) można zapisać w postaci:

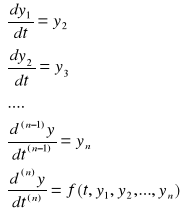
(4)

Równanie (4) można zapisać w postaci wektorowej:

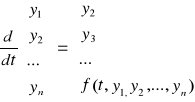
(5)

z wektorem warunków początkowych:

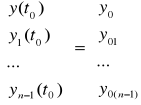
(6)

2. Rozwiązywanie układów równań różniczkowych zwyczajnych w MATLABie.

Rozwiązywanie układu równań różniczkowych zwyczajnych realizują w MATLABie funkcje ODE (ordinary differential equations). W zależności od zastosowanego algorytmu numerycznego rozróżnia się funkcje: ode45 i ode23 (metody Rungego-Kutty), ode113 (metoda Adamsa), ode15s (metoda Geara), itd.

Sposób wywołania każdej funkcji ODE jest jednakowy:

[t, y]=funkcja_ODE( plik_ODE, przedział czasu, warunek początkowy).

gdzie: plik_ODE nazwa m-pliku z definicją wybranego układu równań różniczkowych,

przedział czasu - wektor określający czas początkowy i końcowy [t_o t_k],

warunek początkowy - wektor określający warunki początkowe funkcji i jej (n-1) pochodnych.

Przykład 1

Równanie różniczkowe opisujące ruch masy m zawieszonej na idealnej sprężynie o współczynniku sprężystości k ma postać:

Wyznaczyć przebieg y(t) (czyli rozwiązać równanie różniczkowe) dla y₀=1,
w czasie od 0 do 10s. Do obliczeń przyjąć m=1; k=1.

Rozwiązanie:

Zgodnie z (1) równanie to można przedstawić w postaci:

.

Wprowadzając zmienne stanu y₁, y₂ zgodnie z (3) otrzymujemy:

,

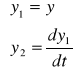
czyli zgodnie z (4)

,

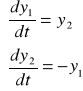
co w postaci wektorowej zgodnie z (5) można zapisać następująco:

.

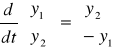
Wektor wartości początkowych zgodnie z 6:

.

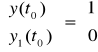
Uzyskany układ równań można zapisać w m-pliku wahadlo.m na trzy sposoby:

- pierwszy

function wah = wahadlo(t,y)

wah=[y(2); -y(1)];

- drugi

function wah=wahadlo(t,y);

wah=zeros(2,1);

wah(1)=y(2);

wah(2)=-y(1);

- trzeci

Korzystając z równania stanu
, dla u=0 otrzymujemy w naszym przykładzie:

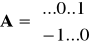
oraz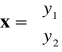
. Wobec tego m-plik funkcyjny ma postać:

function wah=wahadlo(t,y)

A=[0 1; -1 0];

wah=A*y;

Rozwiązanie równania różniczkowego uzyskujemy wywołując funkcję ODE w przestrzeni roboczej MATLABa:

<< [t,y]=ode45(`wahadlo',[0 10],[1;0]);

Aby narysować przebieg y(t) należy podać polecenie:

<< plot(t,y(:,1));

Wywołanie funkcji ode i wykres y(t) można zrealizować jednocześnie w m-pliku
np.: wyk_wah.m

[t,y]=ode45(`wahadlo',[0 10],[1;0]);

plot(t,y(:,1));

grid;

xlabel(`t [s]');

ylabel(`y');

Realizacja tego zagadnienia przedstawiona jest na rys. 1.

Rys. 1. Ruch masy zawieszonej na idealnej sprężynie (położenie początkowe y₀=1)

II. Opis zadania laboratoryjnego

W obwodzie przedstawionym na rys.2 w chwili t=0 zamknięto wyłącznik. Wyznaczyć przebieg prądu płynącego przez cewkę i napięcia na kondensatorze jeżeli e(t) = E_msin*t. Przeprowadzić analizę stanu nieustalonego.

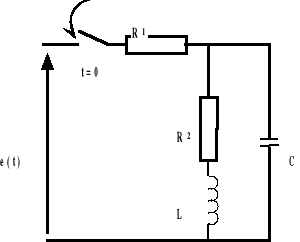
Rys. 2. Schemat układu RLC

Rozpatrywany układ opisany jest za pomocą następujących równań:

Po przekształceniach otrzymujemy:

- postać równań stanu

,

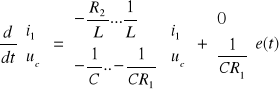
- drugiego stopnia równanie różniczkowe względem U_c

gdzie:
;
;
;
.

Przebieg ćwiczenia

Należy napisać m-plik funkcyjny pozwalający rozwiązać układ równań różniczkowych. Można wybrać dowolny sposób opisu funkcyjnego omawianego układu. Należy pamiętać, że nazwa m-pliku musi być taka sama jaka nazwa funkcji. W pliku wykonawczym należy zastosować procedurę ode45. Pliki należy zapisać w utworzonym, innym dla każdego studenta, katalogu.

Dla parametrów obwodu, podanych przez prowadzącego, należy przeprowadzić:

- analizę stanu nieustalonego układu,

- analizę układu przy różnych wartościach pulsacji * sygnału wymuszającego,

- analizę dla różnych parametrów: R, L, C.

W sprawozdaniu należy przedstawić między innymi:

- najważniejszą część skryptu m-pliku funkcyjnego, w której zamodelowano analizowany obwód elektryczny,

- wykresy przebiegów napięcia na kondensatorze i prądu płynącego przez cewkę (dla wybranych przypadków),

- wnioski końcowe z przeprowadzonego ćwiczenia.

---