Stany nieustalone (przejściowe)

Komutacja - zmiana parametrów (lub konfiguracji) w obwodzie elektrycznym

Energia nagromadzona w C (pole elektryczne E) lub w L nie może zmieniać się skokowo

gdyż wówczas moc chwilowa:

Energia w C związana jest z ładunkiem q Energia w L związana jest ze strumieniem

Dlaczego strumień musi być ciągły

Stąd (t^-)=(t⁺) -warunek ciągłości strumienia

Analogicznie dla q na kondensatorze

q(t^-)=q(t⁺)

Najczęściej rozpatrujemy liniową cewkę i liniowy kondensator, czyli

=Li oraz L=const

q=C U oraz C=const.

Wówczas

Stąd

i(t^-)=i(t⁺)

nazywamy warunkiem ciągłości prądu w cewce

Analogicznie dla pojemności C otrzymamy warunek ciągłości napięcia na kondensatorze:

U_c(t^-)=U_c(t⁺)

Najczęściej komutację rozpatrujemy w chwili t^- = t⁺ = 0 . Warunki ciągłości nazywamy wówczas warunkami początkowymi.

Stan nieustalony w obwodzie typu RL (lub RC)

Rozwiązanie stanu nieustalonego polega na rozwiązaniu równania opisującego obwód po komutacji z uwzględnieniem warunków początkowych wynikających z obwodu przed komutacją.

1. Wymuszenie stałe: niech e(t)= E

Przed komutacją i_L(0^-)=0 Zatem z warunku ciąglości i_L(0⁺)=0

Po komutacji z II prawa Kirchhoffa dla sygnałów w postaci czasowej mamy:

U_L+U_R=e(t)

Gdzie:

stąd otrzymujemy równanie różniczkoowe liniowe o współczynnikach stałych opisujące powyższy obwód zwane niejednorodnym:

(równanie niejednorodne)
(10.1)

Równanie jednorodne:
(10.2)

Po prostych przekształceniach:

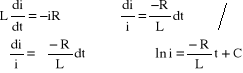
ootrzymamy:

jeżeli teraz przyjmiemy, że: e^c=A oraz
to otrzymamy wzór:

rozwiązanie ogólne równania jednorodnego

Do rozwiązania równania niejednorodnego (10.1) wykorzystamy twierdzenie na mocy którego, jeżeli znajdziemy dowolną funkcję i_W(t) , która spełni niejednorodne równanie różniczkowe to suma tej funkcji i rozwiązania równania jednorodnego będzie pełnym rozwiązaniem (całką ogólną) równania niejednorodnego, czyli:

Szukana funkcja i_W(t) jest zawsze rozwiązaniem stanu ustalonego (w przypadku wymuszeń stałych i sinusoidalnych) w rozpatrywanym obwodzie elektrycznym

R

Sprawdźmy czy funkcja
spełnia równanie różniczkowe niejednorodne (10.1)

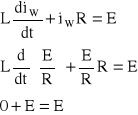
Zatem rozwiązanie równania niejednorodnego ma postać:

W celu wyznaczenia stałej A wykorzystuje się warunki początkowe i(0^-)=i(0⁺)=0

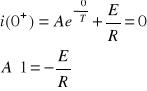
Ostatecznie rozwiązaniem staje się funkcja:

Napięcie U_L można obliczyć:

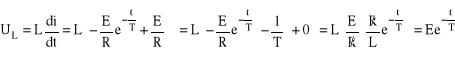
Interpretacja graficzna stałej czasowej

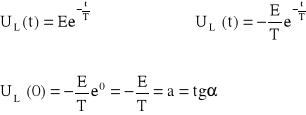
styczna ma równanie:

b - rzędna punktu przecięcia b=E stąd:

t₁ - miejsce zerowe

czyli

stąd t=T stała czasowa obwodu

Przypadek z wymuszeniem sinusoidalnym

t=0 U_R

Niech: e(t)=E_msin(t+)

Z II prawa Kirchhoffa U_C+U_R=e(t):

U_C(t)+i(t)R=e(t) równanie niejednorodne

Ponieważ

stąd
(10.3)

Rozważmy równanie jednorodne przy podstawieniu: T=RC

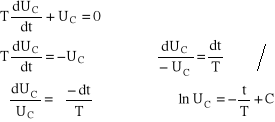
składowa swobodna (przejściowa)

Szukamy składowej wymuszonej - stan ustalony

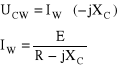
gdzie

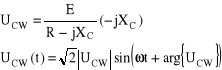
rozwiązanie równania niejednorodnego (10.3), zatem ma postać:

zgodnie z warunkiem ciągłości mamy warunek początkowy:

czyli

stąd:

Czyli:

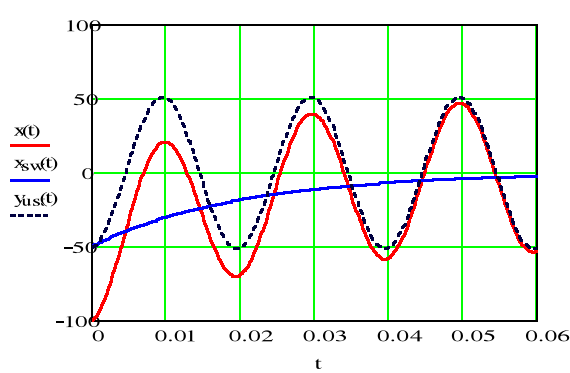
Zasilanie obwodu R,L napięciem sinusoidalnym.

Udar prądowy.

R L

E = Emsin(

I_u =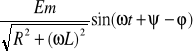

L
i_p = A
T =

i(t) = A
+

Załóżmy, że przed zwarciem obwód nie był obciążony tzn. i(0_-) = 0

i(0₊) = 0 = A +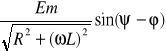

A =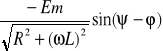

stąd prąd

i(t) =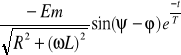
+

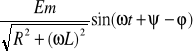
i(t) =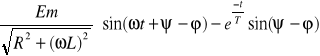

Określenie warunków występowania największej możliwej wartości prądu:

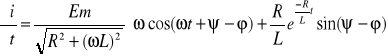
= 0

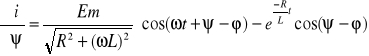
= 0

Po przeniesieniu składników na drugą stronę równań i po podzieleniu stronami otrzymamy:

ale tg
=
stąd: tg
=-tg(
)

Powyższy warunek spełniają dwie wartości kąta

Największa możliwa wartość chwilowa (bezwzględna) prądu przy zamknięciu obwodu RL ( załączenie e(t) = Emsin(
) nastąpi jeżeli zwarcie (zamknięcie) powstaje w chwili przechodzenia e(t) przez 0

Współczynnik udaru

gdzie I_m =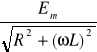
i_ud - największa możliwa wartość chwilowa

W celu znalezienia momentu, w którym nastąpi największa wartość prądu należy rozwiązać równanie:

czyli cos(

ponieważ cos
=
stąd cos(
rozwiązanie tego równania daje nam szukaną wartośc t (rozwiązania analityczne oczywiście nie istnieje, tylko metoda numeryczna bądź graficzna)

Jeżeli twierdzimy, że i_max wystąpi np. przy

to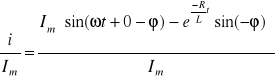

ponieważ sin
=

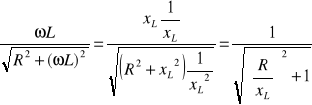
stąd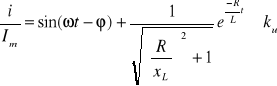

max = 1 max = 1

Stąd wniosek. 1
k_u
2 !!!

Obwód II rzędu RLC

t=0 R L C

II prawo Kirchhoffa

U_L(t) + U_R(t) + U_C(t) = e(t) (10.4)

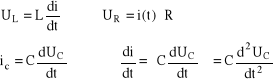
Wstawiamy do (10.4) i otrzymujemy liniowe równanie niejednorodne rzędu II:

r. Niejednorodne (10.5)

Szukane rozwiązanie będzie postaci

U_C = U_cu + U_cp

składowa ustalona składowa swobodna (przejściowa)

spełniająca równanie (10.4) spełniająca równanie jednorodne czyli:

(10.6)

W celu rozwiązania powyższego równania rozwiązujemy tzw. równanie charakterystyczne

tj. równanie przy podstawieniu

- pierwiastki równania charakterystycznego

Rozpatruje się 3 przypadki zależne od Δ równania charakterystycznego:

Przypadek aperiodyczny:

a) Δ>0

czyli rozwiązanie równania jednorodnego (10.6) ma postać:

Mówimy, że składowa przejściowa ma

charakter aperiodyczny:

Przypadek aperiodyczny graniczny:

b) Δ=0 czyli

Rozwiązanie równania jednorodnego:

rezystancja krytyczna

c) Przypadek oscylacyjny Δ<0 czyli

wówczas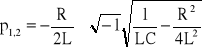

przyjmujemy nadal, że:
- tzw. współczynnik tłumienia
pulsacja drgań własnych

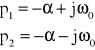
wówczas:

można przekształcić do:

(10.7)

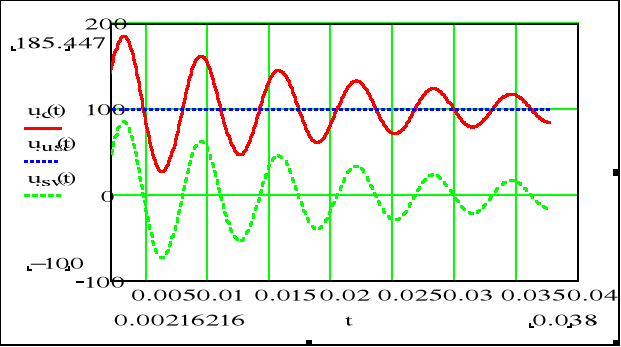
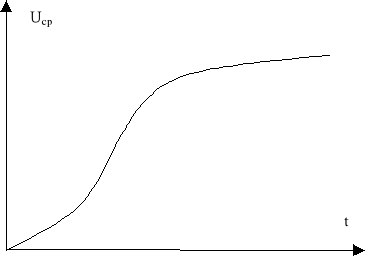
Charakter oscylacyjny składowej przejściowej (swobodnej) U_sw

Załóżmy, że e(t)=E, a przypadek jest oscylacyjny wówczas stan ustalony ma postać:

Stan nieustalony jest sumą składowej przejściowej i stanu ustalonego (w przypadku wymuszeń stałych lub okresowych)

Korzystając z drugiej postaci rozwiązania (10.7) mamy:

(10.8)

Warunek początkowy dla prądu:

Załóżmy niezerowy warunek początkowy dla napięcia na kondensatorze:

Wówczas wstawiając warunki początkowe do równania 10.8 i jego pochodnej:

Otrzymujemy układ równań z którego należy wyznaczyć stałe A oraz δ

Uogólnienie rozwiązania obwodu rzędu II

Ogólna postać równania różniczkowego niejednorodnego:

Najpierw rozwiązujemy równanie jednorodne:

Równanie jednorodne sprowadzamy do równania charakterystycznego przez podstawienie :

Równanie charakterystyczne:

Mamy 3 przypadki:

1. Przypadek aperiodyczny graniczny  p₁=p₂=
   

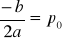
Wówczas rozwiązanie ogólne równania jednorodnego ma postać:

2) Przypadek aperiodyczny >

p₁=
, p₂=

Wówczas rozwiązanie ogólne równania jednorodnego ma postać:

3) Przypadek oscylacyjny:

p₁=
,

p₂=
czyli

Wówczas rozwiązanie ogólne równania jednorodnego ma postać:

lub po przekształceniu:

Rozwiązanie równania niejednorodnego ( po wyznaczeniu stanu ustalonego) ma zatem postać:

y(t)= y_p(t)+y_ust(t)

Dalej, w celu wyznaczenia stałych postępujemy analogicznie jak przedstawiono w przykładzie RLC

STANY NIEUSTALONE - ZADANIA

METODA KLASYCZNA

ZAD 1. Opornik o rezystancji R=10Ω i cewka o indukcyjności L=0,1H połączone są szeregowo. W chwili t = 0 przy warunkach początkowych zerowych do obwodu zostaje doprowadzone napięcie u(t). Wyznaczyć przebiegi prądu w obwodzie i napięcia na cewce oraz wykonać wykresy tych przebiegów, gdy napięcie doprowadzone ma wartość:

a) u(t)=U=110 V

b) u(t)=100 sin(314t+π/4) V

W obydwu przypadkach obliczyć energię pola magnetycznego nagromadzoną w cewce po upływie czasu t=0,01s.

Rozwiązanie:

Warunek początkowy w obwodzie jest zerowy, tzn. i(0-)= i(0+)=0

a)

Równanie różniczkowe (niejednorodne) dla obwodu po komutacji:

Rozwiązanie ogólne równania jednorodnego:

Stan ustalony po komutacji:

Zatem rozwiązanie ogólne równania niejednorodnego:

Wykorzystując warunek początkowy mamy:

Stąd

Zatem rozwiązanie szczególne równania niejednorodnego ma postać:

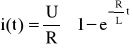
Po podstawieniu wartości:

Energia pola magnetycznego zgromadzona w cewce

po upływie czasu t=0.01s

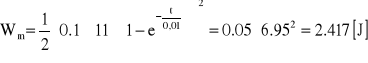
b) Rozwiązanie w przypadku b różni się tylko stanem ustalonym:

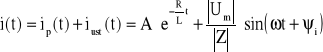
gdzie:

Wówczas: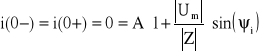

Stąd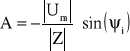

Otrzymane rozwiązanie ma postać:

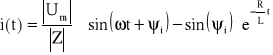
Po wstawieniu wartości liczbowych:

Po upływie czasu t = 0.01 s energia pola magnetycznego zgromadzona w cewce wynosi:

ZAD 2.

Opornik o rezystancji R=100Ω i kondensator o pojemności C = 100μF połączone są szeregowo. W chwili t = 0 do obwodu zostaje doprowadzone napięcie u(t). Wyznaczyć przebieg napięcia na kondensatorze oraz przebieg prądu w obwodzie, jeżeli napięcie doprowadzone do obwodu ma wartość:

a) u(t)=U=100 V

b) u(t)=141 sin(314t+π/6) V

W obydwu przypadkach obliczyć napięcie na kondensatorze po upływie czasu t=5τ, gdzie τ oznacza stałą czasową obwodu.

Rozwiązanie:

Niech dany będzie warunek początkowy zerowy, tzn. u_c(0-)=0. Przebieg napięcia na kondensatorze ma postać:

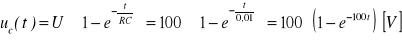
Prąd w obwodzie:

Stała czasowa obwodu równa się τ = RC = 0,01 s. Po upływie czasu wynoszącego 5τ napięcie na kondensatorze osiąga wartość:

a prąd w obwodzie

Po upływie czasu odpowiadającemu pięciu stałym czasowym obwodu szeregowego RC, napięcie na kondensatorze osiąga 99,33% wartości ustalonej, a prąd w obwodzie maleje o

99,33% względem swej wartości początkowej.

b) Przebieg napięcia na kondensatorze jest określony wyrażeniem:

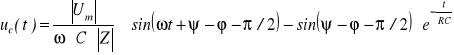
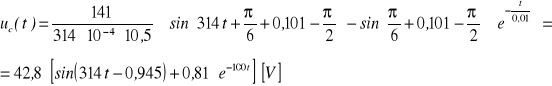
Stała czasowa τ = RC =0,01 s; stąd po upływie czasu odpowiadającemu 5τ napięcie na kondensatorze wynosi

Prąd w obwodzie obliczamy na podstawie zależności:

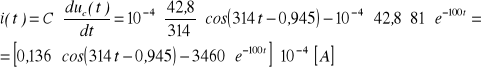
Po czasie równym 5τ prąd w obwodzie osiąga wartość:

ZAD 3.

W obwodzie przedstawionym na rysunku wyłącznik zostaje przestawiony w pozycję 2 w chwili t = 0. Przed przełączeniem panuje w obwodzie stan ustalony. Wyznaczyć przebieg prądu w obwodzie w dwóch przypadkach:

1. u(t) = U = 90 [V]

2. u(t) = 110 sin(1,57t - π/3) [V]

Dane: R₁ = 4 Ω, R₂ = 6 Ω, L = 5 H

Rozwiązanie:

Dla czasu t > 0 równanie napięć w obwodzie ma postać:

Stąd

1. Z warunku początkowego mamy

Zatem

Energia stracona w obwodzie określona jest wzorem:

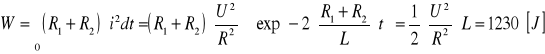
Energia zużyta w opornikach R₁ i R₂ pochodzi z energii pola magnetycznego cewki w chwili

t = 0, a mianowicie:

Bilans energii w obwodzie jest zachowany.

2. Z warunku początkowego mamy:

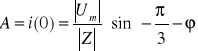
przy czym

Zatem

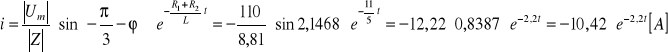
Energia zużyta w opornikach R₁ i R₂:

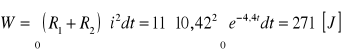
Energia pola magnetycznego cewki w chwili t = 0 wynosi:

Wynik uzyskany jest zgodny z zasadą zachowania energii.

ZAD 4.

W obwodzie przedstawionym na rysunku (a) przed zamknięciem wyłącznika napięcie na kondensatorze równało się zeru. W chwili t = 0 do obwodu doprowadzone zostaje napięcie stałe E = 21 [V]. Obliczyć wartości chwilowe prądów w gałęziach obwodu i napięcia na kondensatorze metodą superpozycji stanu ustalonego i przejściowego. Rezystancje oporników wynoszą: R₁ = 100 Ω, R₂ = 200 Ω, a pojemność kondensatora C = 500 μF.

rysunek (a)

rysunek (b) rysunek (c)

Rozwiązanie:

Zgodnie z metodą superpozycji stanu ustalonego i przejściowego prądy w stanie nieustalonym możemy wyrazić w postaci:

gdzie:

prąd w stanie nieustalonym w
gałęzi,

składowa ustalona prądu w
gałęzi,

składowa przejściowa prądu w
gałęzi,

Analogiczne równanie dla kondensatora:

W celu wyznaczenia składowych ustalonych prądów wpisujemy równania w stanie ustalonym obwodu (rys. b) zgodnie z prawem Kirchhoffa:

Składowe przejściowe prądów wyznaczamy z równań wypisanych dla wartości chwilowych przy wymuszeniu równym zeru (rys. c):

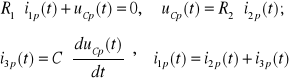
Skąd otrzymujemy:

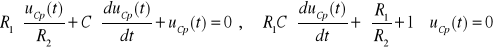
Po pomnożeniu ostatniego równania przez R₂ otrzymujemy:

Zatem:

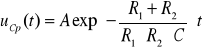
gdzie stałą całkowania A wyznaczamy z warunku początkowego (zgodnie z prawem komutacji dla kondensatora):

czyli

oraz

Stąd

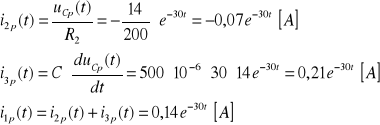
Zatem prądy w gałęziach obwodu w stanie nieustalonym wynoszą:

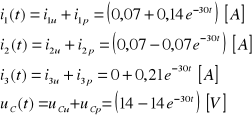
ZAD 5.

W obwodzie przedstawionym na rysunku przed zamknięciem wyłącznika panował stan ustalony. W chwili t = 0 zostaje zamknięty wyłącznik. Wyznaczyć warunki początkowe (wartość prądu w cewce i napięć na kondensatorach w chwili t = 0), jeśli:

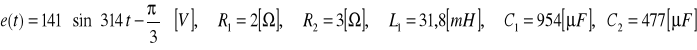
Rozwiązanie:

Dla t < 0 obwód przedstawia się jako obwód jednooczkowy o rezystancji
, indukcyjności L = 0,0318 H i pojemności

Prąd w obwodzie wynosi:

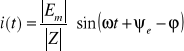
gdzie

Stąd

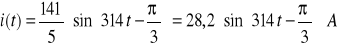
Warunki początkowe:

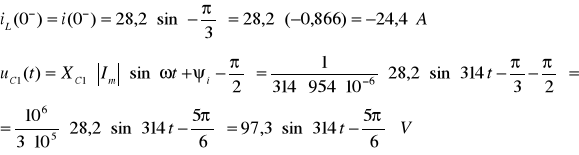
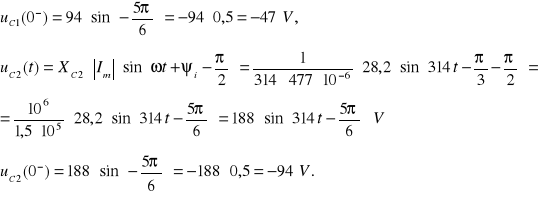
ZAD 6.

Obliczyć prąd i₁ przy wymuszeniu nie okresowym.

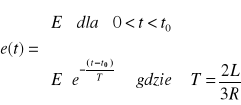
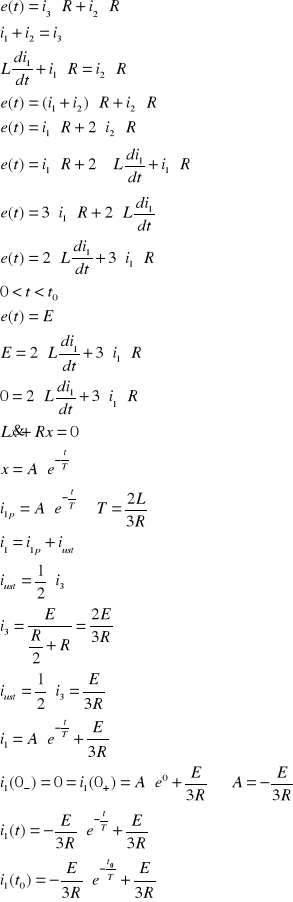
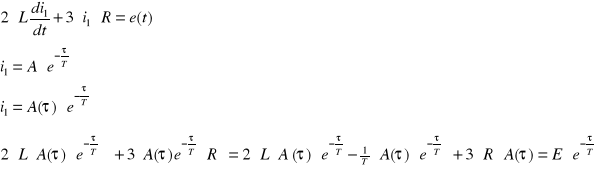
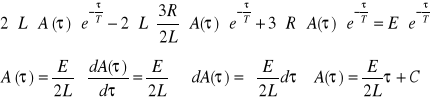
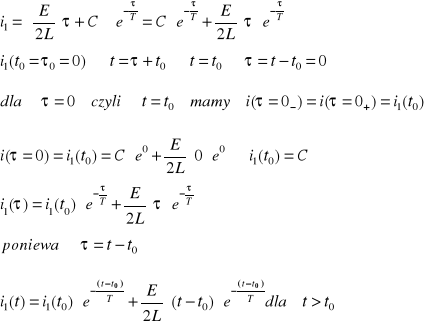
Odpowiedź:

ZAD 7.

Dane:

, R=10ၗ, L=0,1H , ၷ=1000

e(t)=U_L+2iR

Równanie jednorodne

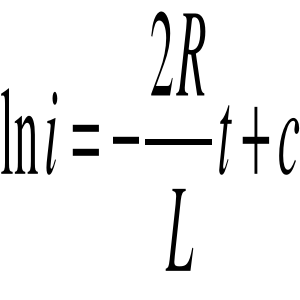
- rozwiązanie równania ogólnego jednorodnego

gdzie
, A=e^c

i=i_p+i_u

W stanie ustalonym

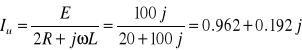
Warunki początkowe

105

131

Stany nieustalone

_______________________________________________________________________________________

i(t)

u(t)

t=0

L

i(t)

u(t)



e(t)

i(t)

R

U_R

L

U_L

t=0

i(t)

U_R(t) U_L(t) U_C(t)

e(t)



t=0

R



I

E

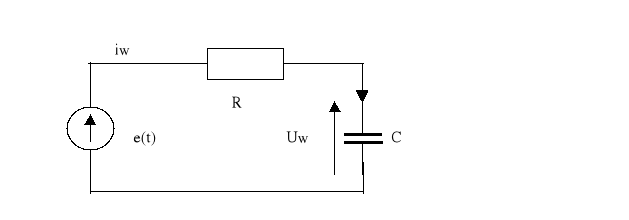
R i(t)

e(t) U_C U_C0(0-)

t

T

E



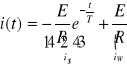
składowa swobodna składowa

(przejściowa) wymuszona

i_s(t)

t

i(t)

i_W(t)

i(t)

T

0

L
- w stanie ustalonym

E

składowa swobodna (przejściowa)

C

R

R₁

t = 0

u(t)

i(t)

L

R₂

R₁

t = 0

E

i₁(t)

C

R₂

i₂(t)

i₃(t)

u_C(t)

R₁

i_1u(t)

C

E

R₂

i_2u(t)

u_Cu

R₁

i_1p(t)

C

R₂

i_2p(t)

u_Cp

i_3p(t)

R₂

R₁

L₂

C₂

e(t)

t=0

R₃

C₁

L₁

R

R

R

L

E

t=0

i₁

i₂

i₃

t₀

t

E

0

t₀

t

τ

0

R

R

R

L

e(t)

R

R

L

e(t)

i_u(t)

i

R

R

R

L

e(t)

---