
Wykład 17
Izolatory i przewodniki
Wszystkie ciała możemy podzielić na przewodniki i izolatory albo dielektryki.
Przewodnikami są wszystkie metale, roztwory kwasów i zasad, roztopione soli, nagrzane gazy
itp. Charakterystyczną cechą przewodników, z punktu widzenia mikroskopowego jest
obecność w nich swobodnych ładunków elektrycznych, które pod wpływem nawet słabego
pola elektrycznego mogą przemieszczać się w ciele na duże odległości. W metalach ładunkami
swobodnymi są elektrony; w roztworach kwasów i zasad swobodnymi ładunkami są dodatnie i
ujemnie naładowane jony - kationy i aniony.
W dielektrykach nie ma ładunków swobodnych, a istniejące ładunki - elektrony i jądra
atomowe, są silnie związane między sobą tak, że działanie zewnętrznego pola elektrycznego
może powodować tylko małe przemieszczenia ładunków względem ich położeń
równowagowych. Izolatorami są bursztyn, szkło, kauczuk itp.
Podział ciał na izolatory i przewodniki jest umowny, ponieważ zdolności ciał do
przewodnictwa elektrycznego silne zależą od warunków zewnętrznych - temperatury, ciśnienia
itd. Ponadto istnieje liczna grupa ciał, zwanych półprzewodnikami, które wykazują zdolności
do przewodnictwa pośrednie między przewodnikami i izolatorami.
Przewodniki w polu elektrycznym
Umieścimy przewodnik w zewnętrznym polu elektrostatycznym. Wskutek działania
pola elektrycznego swobodne ładunki zaczną poruszać się w kierunku przeciwnym do
kierunku pola. Ten ruch uporządkowany ładunków nie może trwać w nieskończoność i po
upływie pewnego czasu nastąpi stan statyczny. W sytuacji statycznej, która powstaje gdy
ładunki po wszystkich przegrupowaniach przestały poruszać się, przewodnik musi mieć
następujące właściwości:
1. Pole elektryczne wewnątrz przewodnika jest równe zeru:
0
=
wewn
E
. (17.1)
Jeżeliby pole wewnątrz przewodnika nie było równe zeru, swobodne ładunki doznawałyby
działanie siły, wskutek czego zaczęłyby się poruszać się, a to byłoby sprzeczne z założeniem,
że mamy sytuację statyczną.
211
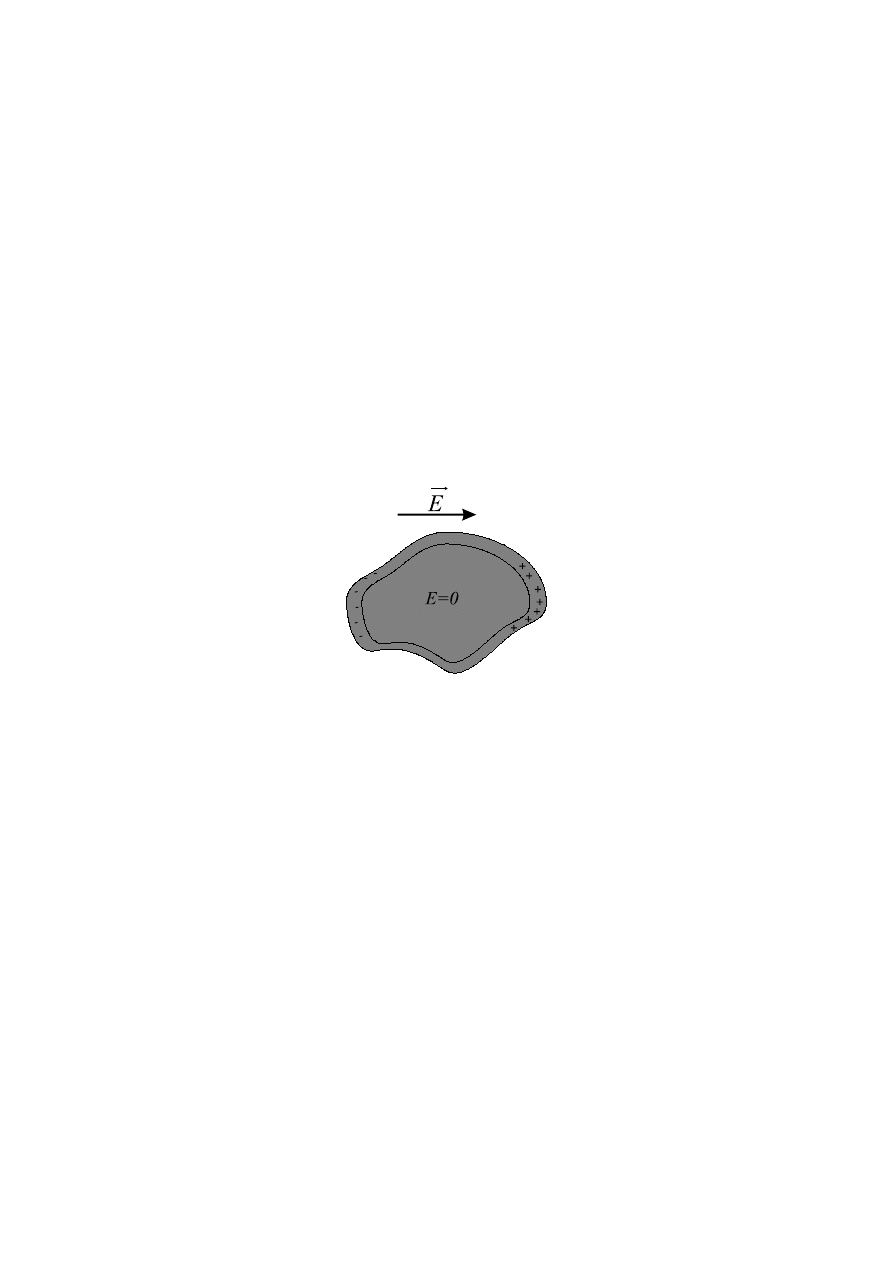
2. Na powierzchni przewodnika wektor natężenia pola elektrycznego jest prostopadły
do tej powierzchni:
n
E
E
=
,
0
=
τ
E
. (17.2)
Gdyby tak nie było, to pod działaniem składowej pola, stycznej do powierzchni przewodnika
τ
E
elektrony przemieszczałyby się i nie mielibyśmy sytuacji statycznej.
3. Każdy punkt objętości przewodnika ma ten sam potencjał. Istotnie, w dowolnym
punkcie wewnątrz przewodnika, zgodnie z (17.1)
0
=
⋅
−
=
l
d
E
d
wewn
ϕ
, skąd
const
=
ϕ
.
4. Powierzchnia przewodnika też jest powierzchnią ekwipotencjalną, ponieważ,
zgodnie (17.2) dla dowolnej linii na powierzchni przewodnika
0
=
⋅
−
=
⋅
−
=
l
d
E
l
d
E
d
τ
ϕ
, skąd
const
=
ϕ
.
5. Całkowity ładunek wewnątrz przewodnika jest równy zeru. Ta właściwość
przewodnika wynika z prawa Gaussa i wzoru (17.1)
0
0
=
⋅
⋅
=
∫
S
d
E
Q
wewn
ε
.
6. W naładowanym przewodniku w stanie statycznym wszystkie nie skompensowane
ładunki elektryczne rozkładają się wyłącznie na powierzchni przewodnika. Ta właściwość
przewodnika też wynika z prawa Gaussa i wzoru (17.1).
7. Pole elektryczne na powierzchni przewodnika wynosi
212
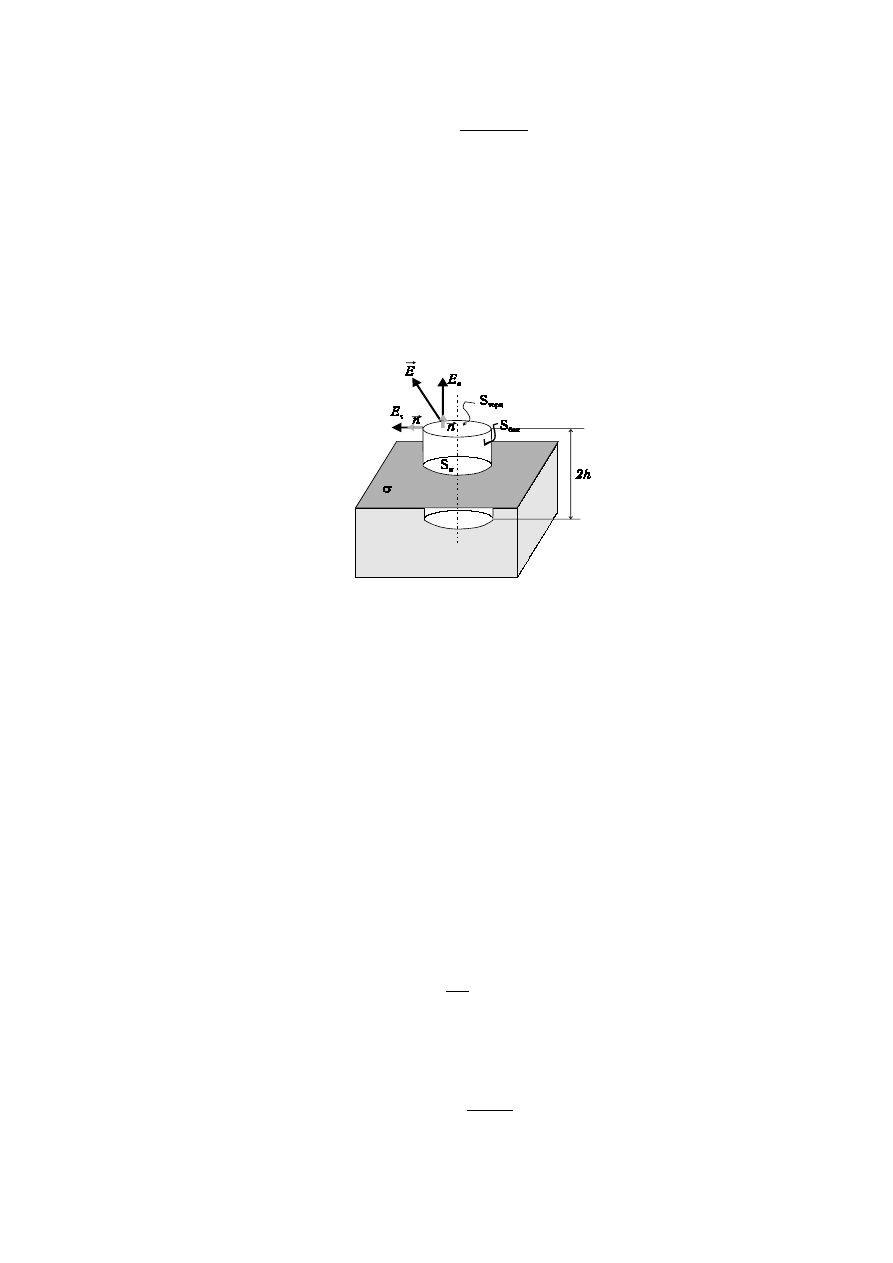
n
z
y
x
z
y
x
E
⋅
=
0
)
,
,
(
)
,
,
(
ε
σ
, (17.3)
gdzie
)
,
,
(
z
y
x
σ
- gęstość powierzchniowa ładunku w punkcie
)
,
,
(
z
y
x
powierzchni
przewodnika;
S
S
n
∆
∆
=
/
jest jednostkowy wektor skierowany na zewnątrz powierzchni
przewodnika.
Dla udowodnienia (17.3) znajdziemy strumień pola elektrycznego przez powierzchnie
małego walca prostopadłego do powierzchni przewodnika.
Wskutek (17.2) oraz małości walca strumień przez boczne powierzchni walca jest
równy zeru. Przez dolną podstawę walca strumień też jest równy zeru, ponieważ wewnątrz
przewodnika
0
=
E
. A zatem całkowity strumień pola przez powierzchnie małego walca jest
równy strumieniowi tylko przez górną podstawę
S
∆
:
S
E
∆
⋅
=
Φ
.
Zgodnie z prawem Gaussa ten strumień jest równy ładunkowi
q
objętemu przez powierzchnie
walca. Ponieważ ładunek ten jest zgromadzony tylko na powierzchni przewodnika,
wprowadzając gęstość powierzchniową ładunku na elemencie
S
∆
powierzchni przewodnika
S
q
∆
=
σ
,
otrzymujemy
0
ε
σ
S
S
E
∆
⋅
=
∆
⋅
=
Φ
.
213
Skąd wynika wzór (17.3):
0
)
(
ε
σ
=
⋅
=
=
n
E
E
E
n
.
8. Gęstość powierzchniowa ładunków elektrycznych
)
,
,
(
z
y
x
σ
zależy od kształtu
powierzchni przewodnika i jest największa na ostrzach i występach.
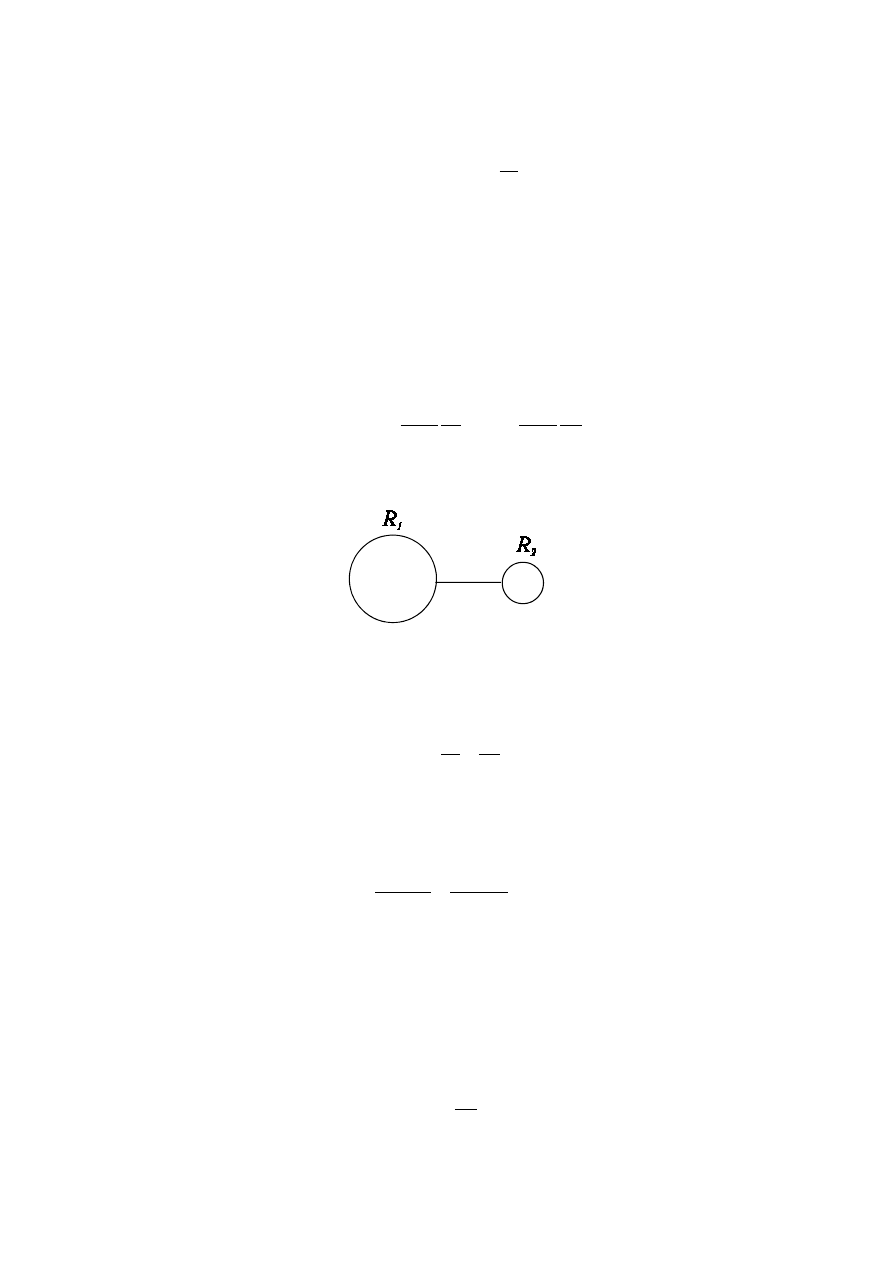
Rozważmy dwie naładowane kuli metaliczne o promieniach
1
R i
2
R (
1
R >
2
R ),
połączone przewodnikiem. W stanie statycznym potencjały dwóch kul muszą być równe, a
zatem:
2
2
0
2
1
1
0
1
4
1
4
1
R
q
R
q
πε
ϕ
πε
ϕ
=
=
=
Skąd
2
2
1
1
R
q
R
q
=
. (17.4)
Ponieważ
1
2
1
1
4
σ
π
R
q
=
i
2
2
2
2
4
σ
π
R
q
=
, ze wzoru (17.4) otrzymujemy
2
2
2
2
1
1
2
1
4
4
R
R
R
R
σ
π
σ
π
=
.
Stąd
2
2
1
1
σ
σ
R
R
=
. (17.5)
Ze wzoru (17.5) wynika, że
1
1
2
1
2
σ
σ
σ
>>
=
R
R
. (17.6)
214

A więc gęstość powierzchniowa ładunków elektrycznych
)
,
,
(
z
y
x
σ
jest największa tam gdy
powierzchnia przewodnika jest najbardziej zakrzywiona, czyli na ostrzach i występach.
Zgodnie z (17.3)
E
0
ε
σ =
, a zatem ze wzoru (17.6) otrzymujemy
1
1
2
1
2
E
E
R
R
E
>>
=
. (17.7)
Równanie (17.7) oznacza, że natężenie pola elektrycznego jest największe tam gdy największa
jest gęstość powierzchniowa ładunków, czyli na ostrzach i występach naładowanego
przewodnika.
9. W pozbawionym ładunku obszarze, który jest otoczony przewodnikiem tworzącym
zamkniętą powierzchnią, pole elektryczne znika.
Już wiemy, że w stanie statycznym wewnątrz przewodnika, znajdującym się w polu
elektrycznym, nie ma pola elektrycznego, oraz całkowity ładunek w dowolnej części wewnątrz
przewodnika jest równy zeru. A zatem jeżeli usuniemy jakąś wewnętrzną część przewodnika,
to w powstałym wydrążeniu pole elektryczne w stanie statycznym zawsze będzie równe zeru.
Ta właściwość zamkniętej przewodzącej powłoki ekranowania wewnętrznego obszaru od pola
elektrycznego zewnętrznego znajduje szerokie zastosowanie w praktyce, jako ekran
elektryczny.
10. Jeżeli ładunek elektryczny Q otoczymy uziemionym ekranem elektrycznym, to pole
elektryczne ładunku Q znika na zewnątrz ekranu.
Rozważmy wewnątrz przewodnika - ekranu elektrycznego, zamkniętą powierzchnię,
otaczającą ładunek Q . Ponieważ w stanie statycznym pole wewnątrz przewodnika jest równe
zeru, to strumień pola elektrycznego przez wybraną dowolną powierzchnię wewnątrz
przewodnika musi być równy zeru. Zgodnie z prawem Gaussa, to oznacza, że wewnątrz
objętości otoczoną powierzchnią Gaussa całkowity ładunek jest równy zeru. Wewnątrz
powierzchni Gaussa (w wydrążeniu) znajduje się ładunek Q , a zatem dla tego, żeby całkowity
ładunek wewnątrz powierzchni Gaussa był równy zeru, w przewodniku musi być indukowany
ładunek Q
−
. Ten indukowany ładunek może znajdować się tylko na wewnętrznej ściance
ekranu, ponieważ wewnątrz przewodniku nie mogą istnieć ładunki nie skompensowane.
Ponieważ całkowity ładunek ekranu metalicznego nie może zmienić się, z faktu indukowania
215

ładunku Q
−
na wewnętrznej ściance ekranu wynika, że na zewnętrznej ściance ekranu
indukuje się ładunek Q .
Jeżeliby ekran nie był połączony z Ziemią przewodnikiem czyli nie był uziemiony, układ
- (ładunek + ekran), wytwarzałby na zewnątrz układu takie same pole jak ładunek Q .
Uziemienie ekranu elektrycznego powoduję, że potencjał ekranu wyrównuje się z potencjałem
Ziemi, czyli potencjał zewnętrznej powłoki ekranu staje się równym
0
=
ϕ
. Zerowy potencjał
ekranu (
Q
∝
ϕ
) oznacza, że indukowany na zewnętrznej powłoce ekranu ładunek Q
"przepływa" do Ziemi. Wskutek takiego przemieszczenia się ładunku ekran staje się
naładowany, ale właśnie wskutek takiego naładowania ekranu, całkowity ładunek układu -
(ładunek + ekran) staje się równy zeru, a pole elektryczne wytwarzane przez indukowany na
wewnętrznej powłoce ekranu ładunek Q
−
całkowicie kompensuje pole wytwarzane przez
ładunek Q .
11. Między ładunkami elektrycznymi zgromadzonymi na powierzchni przewodnika
działają siły Coulomba, które powodują, że ciśnienie
p
działające na powierzchnię
naładowanego przewodnika jest równe
2
0
0
2
2
2
E
p
⋅
=
=
ε
ε
σ
. (17.8)
Rozważmy na powierzchni naładowanego przewodnika mały element powierzchni
S
∆
,
którego ładunek jest równy
)
(
S
∆
⋅
σ
. Na wybrany element powierzchni działa siła
216

0
)
(
E
S
F
⋅
∆
⋅
=
∆
σ
, (17.9)
gdzie
0
E
jest natężeniem pola elektrycznego, wytwarzanego przez wszystkie ładunki
elektryczne rozmieszczone na pozostałej powierzchni przewodnika w miejscu gdy znajduje się
wybrany element powierzchni
S
∆
.
Oprócz pola o natężeniu
0
E
w pobliżu elementu powierzchni
S
∆
istnieje również pole
elektryczne
1
E
, pochodzące od ładunków elementu powierzchni
S
∆
. Całkowite pole
elektryczne na powierzchni
S
∆
, więc wynosi
1
0
E
E
E
+
=
. (17.10)
Załóżmy, że element powierzchni
S
∆
jest naładowany dodatnie (
0
>
σ
). Wtedy pole
1
E
pochodzące od ładunków tego elementu w pobliżu zewnętrznej powierzchni
S
∆
ma zwrot na
zewnątrz przewodnika, a pole w pobliżu wewnętrznej powierzchni
S
∆
jest skierowane wgłęb
przewodnika. Ponieważ w stanie statycznym pole wewnątrz przewodnika musi być równe zeru
znajdujemy
0
1
0
=
+
=
wew
wew
E
E
E
.
Skąd
wew
E
E
1
0
−
=
. (17.11)
217

Na zewnątrz wybranego elementu
S
∆
przewodnika pole
0
E
zachowuje swój kierunek,
natomiast pole
1
E
zmienia swój zwrot:
wew
zew
E
E
1
1
−
=
Biorąc pod uwagę (17.11), ze wzoru
(17.10) znajdujemy
0
1
0
2E
E
E
E
zew
=
+
=
. (17.12)
Pole elektryczne E
na powierzchni przewodnika określa wzór (17.3). A zatem dla pola
0
E
otrzymujemy
n
E
E
⋅
=
=
0
0
2
2
ε
σ
. (17.13)
Po podstawieniu (17.13) do wzoru (17.9) mamy
n
S
E
S
F
⋅
∆
=
⋅
∆
⋅
=
∆
0
2
0
2
)
(
ε
σ
σ
. (17.14)
Ponieważ
2
σ
∝
∆
F
, w niezależności od znaku ładunku elementu
S
∆
powierzchni, siła
działająca na ten element jest zawsze zwrócona w kierunku normalnej zewnętrznej. Wynik ten
stanowi następstwo odpychania się ładunków powierzchniowych.
Dla ciśnienia, ze wzoru (17.14) otrzymujemy
2
2
2
0
0
2
E
S
F
p
ε
ε
σ =
=
∆
∆
=
. (17.15)
Pojemność elektryczna
Rozważmy przewodnik o dowolnym kształcie. Po udzieleniu temu przewodnikowi
ładunku
q
, ładunek zostaje rozłożony po powierzchni przewodnika z gęstością
)
,
,
(
z
y
x
σ
.
Charakter rozkładu ładunku
q
zależy nie od ładunku całkowitego
q
, lecz jedynie od kształtu
przewodnika. Jeżeli przekażemy temu naładowanemu przewodnikowi jeszcze ładunek
q
, to
charakter rozkładu wypadkowego ładunku q
2 będzie taki sam jak charakter rozkładu ładunku
q
. Zwiększy się tylko o dwa razy gęstość powierzchniowa ładunku w każdym punkcie
powierzchni. Inaczej mówiąc stosunek gęstości powierzchniowej
)
,
,
(
z
y
x
σ
ku ładunkowi
q
218
q
z
y
x
z
y
x
f
)
,
,
(
)
,
,
(
σ
=
(17.16)
określa pewną funkcję współrzędnych dowolnego punktu
)
,
,
(
z
y
x
powierzchni przewodnika.
Funkcja ta zależy wyłącznie od kształtu powierzchni przewodnika.
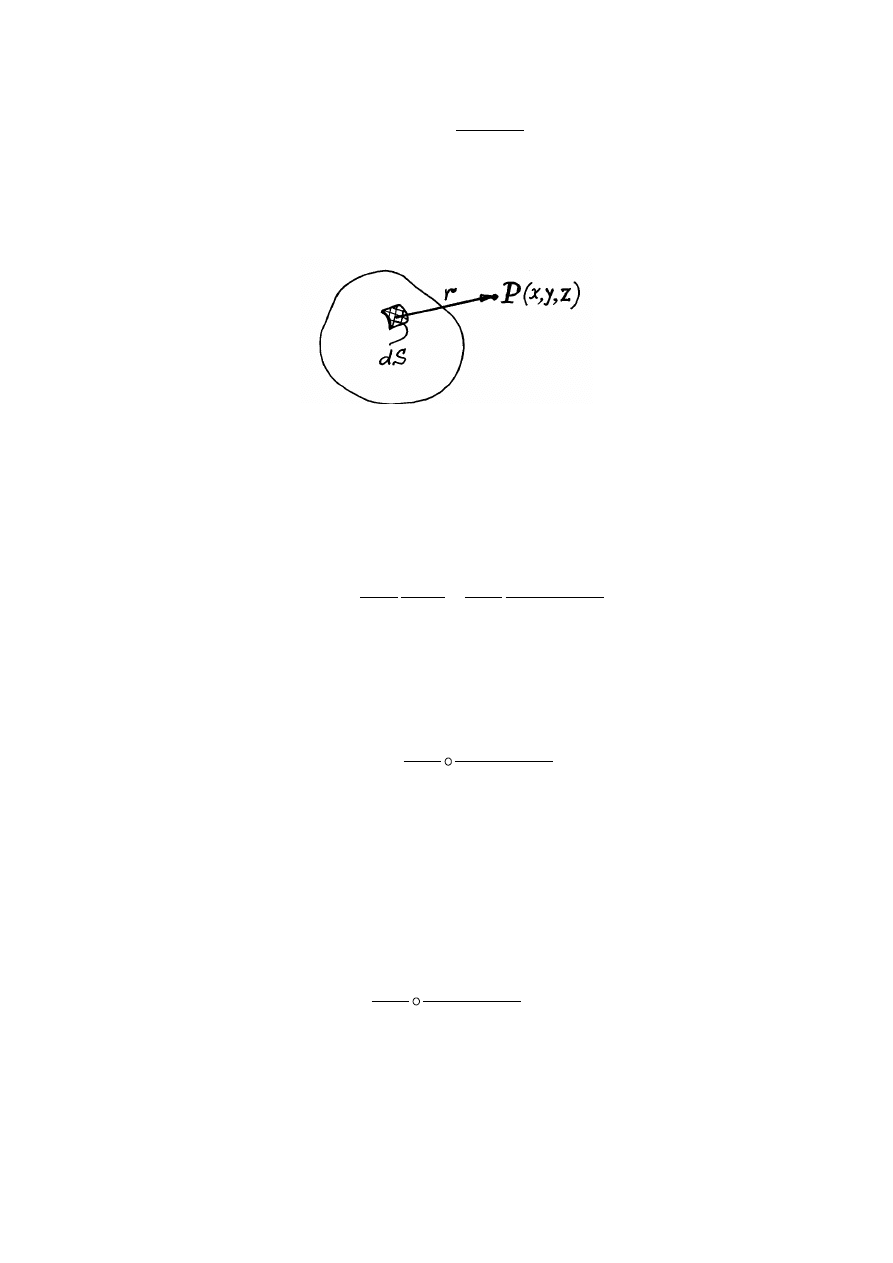
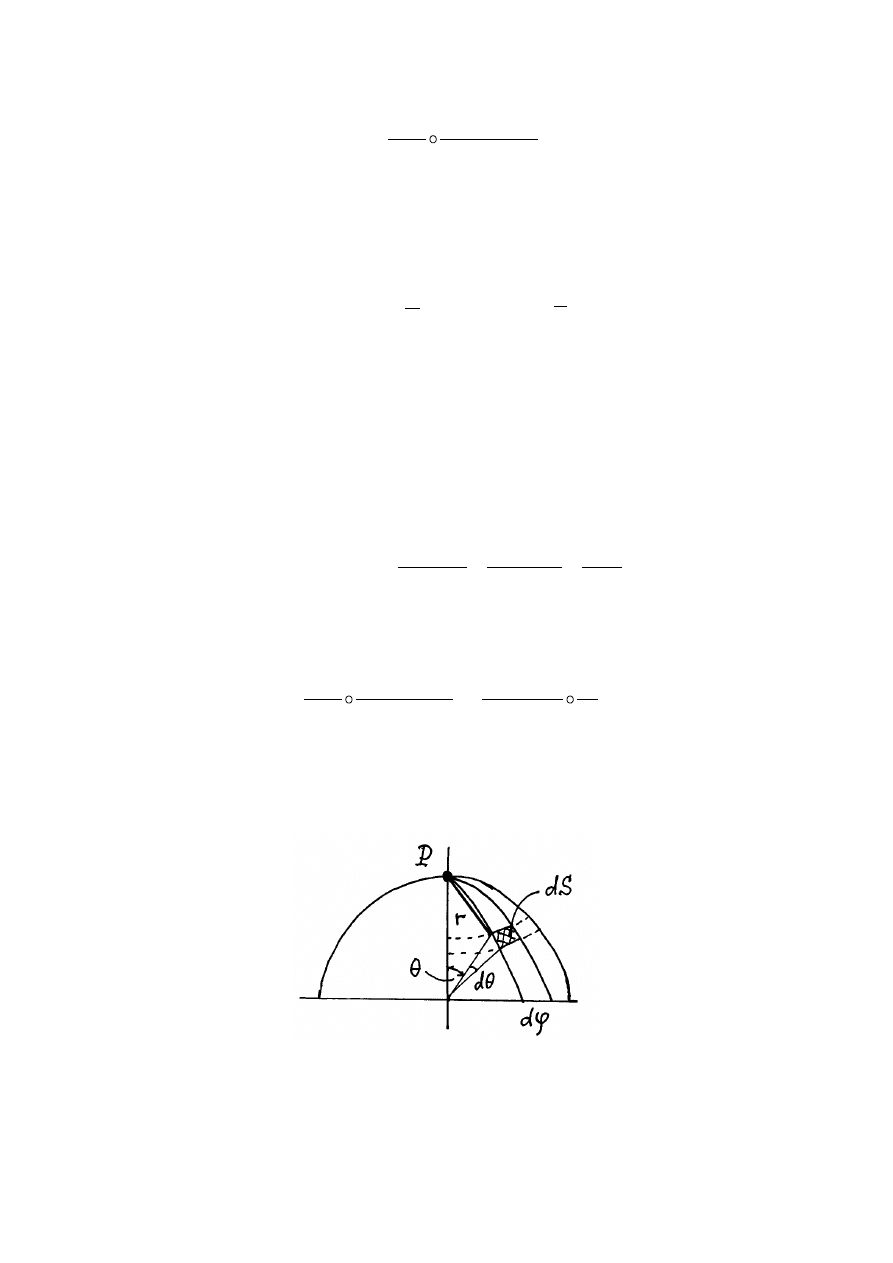
Znajdziemy teraz potencjał pola naładowanego przewodnika w punkcie
P
. Podzielmy
powierzchnię przewodnika na nieskończenie małe elementy
dS
. Potencjał pola ładunku (
dS
⋅
σ
) w punkcie
P
wynosi
r
dS
z
y
x
f
q
r
dS
d
⋅
=
⋅
=
)
,
,
(
4
4
1
0
0
πε
σ
πε
ϕ
. (17.17)
Całkując to wyrażenie względem całej powierzchni przewodnika otrzymujemy dla potencjału
pola naładowanego przewodnika w punkcie
P
:
⋅
⋅
=
∫
S
r
dS
z
y
x
f
q
)
,
,
(
4
1
0
πε
ϕ
. (17.18)
Wzór (17.18) jest słuszny dla dowolnego punktu
P
. Niech ten punkt
P
znajduje się na
powierzchni przewodnika. Ponieważ powierzchnia przewodnika jest powierzchnią
ekwipotencjalną
)
(
const
=
ϕ
, wartość całki we wzorze (17.18) musi nie zależeć od położenia
punktu
P
na powierzchni przewodnika. Więc całka
⋅
∫
S
r
dS
z
y
x
f
)
,
,
(
4
1
0
πε
we wzorze (17.18) wyliczona dla dowolnego punktu na powierzchni przewodnika jest
wielkością zależną jedynie od rozmiarów i kształtu powierzchni przewodnika.
Wielkość
219
1
0
)
,
,
(
4
1
−
⋅
≡
∫
S
r
dS
z
y
x
f
C
πε
(17.19)
nazywa się pojemnością elektryczną przewodnika. Związek (17.18) z uwzględnieniem (17.19)
możemy zapisać w postaci
C
q
=
ϕ
albo
ϕ
q
C
=
. (17.20)
Pojemność elektryczna przewodnika jest równa więc ilości elektryczności (
q
), jakiej należy
udzielić nie naładowanemu przewodnikowi w celu zmiany jego potencjału o jednostkę:
V
1
=
ϕ
.
Korzystając ze wzoru (17.19) obliczmy pojemność elektryczną kuli przewodzącej o
promieniu
R
. Zgodnie ze wzorem (17.16)
2
2
4
1
)
4
(
)
,
,
(
)
,
,
(
R
R
q
z
y
x
z
y
x
f
π
σ
π
σ
σ
=
⋅
=
=
. (17.21)
A zatem
∫
∫
=
⋅
S
S
r
dS
R
r
dS
z
y
x
f
2
0
2
0
)
4
(
1
)
,
,
(
4
1
ε
π
πε
. (17.22)
We wzorze (17.22)
r
jest odległością elementu powierzchni kuli
dS
od dowolnie wybranego
punktu
P
na powierzchni kuli.
220

Wybierzmy punkt
P
na biegunie północnym kuli. Wtedy biorąc pod uwagę, że
ϕ
θ
θ
θ
ϕ
θ
θ
d
d
R
d
d
R
dS
⋅
⋅
=
⋅
⋅
=
2
cos
2
sin
2
sin
2
2
,
2
sin
2
θ
⋅
=
R
r
,
znajdujemy
R
d
d
R
r
dS
R
S
1
4
1
2
cos
)
4
(
1
)
4
(
1
2
0
0
0
0
2
2
0
2
⋅
=
⋅
=
∫ ∫
∫
π
π
πε
θ
θ
ϕ
ε
π
ε
π
. (17.23)
Po podstawieniu tego wyniku do wzoru (17.19) otrzymujemy
R
r
dS
z
y
x
f
C
S
⋅
=
⋅
≡
−
∫
)
4
(
)
,
,
(
4
1
0
1
0
πε
πε
. (17.24)
Oczywiście, że wzór (17.24) również wynika ze wzoru (17.20), jeżeli przypomnimy, że
potencjał kuli o promieniu
R
jest równy
)
4
/(
0
R
q
⋅
=
πε
ϕ
.
W układzie SI jednostką pojemności jest farad (F)
V
C
F
1
1
1
=
.
Ze wzoru (17.24) otrzymujemy, że pojemność elektryczną równą 1 faradowi posiada
kula przewodząca o promieniu (
0
4
1
πε
=
k
=
9
10
9
⋅
Nm
2
/C
2
)
9
0
10
9
4
⋅
=
=
πε
C
R
m =
6
10
9
⋅
km.
Przypomnimy, że promień Ziemi wynosi
6400
=
Z
R
km.
W praktyce stosuje się często pochodne jednostki pojemności elektrycznej: 1 mikrofarad ( F
µ
)
= 10
-6
F; 1 pikofarad ( pF ) = 10
-12
F.
Pojemność układu przewodników. Kondensatory
Pojemność odosobnionego naładowanego przewodnika określa wzór (17.20). Jeżeli jednak
w sąsiedztwie tego przewodnika umieścimy drugi nawet nie naładowany przewodnik, to
221
pojemność naładowanego przewodnika, czyli stosunek ładunku przewodnika
q
do jego
potencjału
ϕ
, zwiększy się. Istota tego zjawiska polega na tym, że w polu elektrycznym
wytwarzanym przez przewodnik naładowany, nie naładowany przewodnik elektryzuje się, przy
czym najbliższymi do naładowanego przewodnika okazują się ładunki przeciwnego znaku. Te
indukowany ładunki wytwarzają swoje pole elektryczne, które ma przeciwny zwrot niż pole
naładowanego przewodnika. Wskutek nałożenia (superpozycji) tych dwóch pól potencjał
naładowanego przewodnika zmniejszy się, a pojemność (
ϕ
q
C
=
) - zwiększy się.
Ta właściwość przewodnika zwiększać pojemność innych przewodników ze swego
otoczenia, znajduje praktyczne zastosowanie w urządzeniach które nazywamy
kondensatorami. Kondensator składa się z dwóch naładowanych przewodników, które
posiadają taki kształt i są tak względem siebie położone, że wytwarzane przez nie pole
elektrostatyczne jest całkowicie lub niemal całkowicie skupione w ograniczonej przestrzeni.
Pojemność kondensatora określamy wzorem
U
q
C
=
, (17.25)
gdzie
0
>
q
- ładunek jednej z okładek i
0
2
1
>
−
=
ϕ
ϕ
U
jest różnicą potencjałów między
okładkami kondensatora.
W zależności od kształtu okładek kondensatory dzielą się na płaskie, kuliste i
cylindryczne.
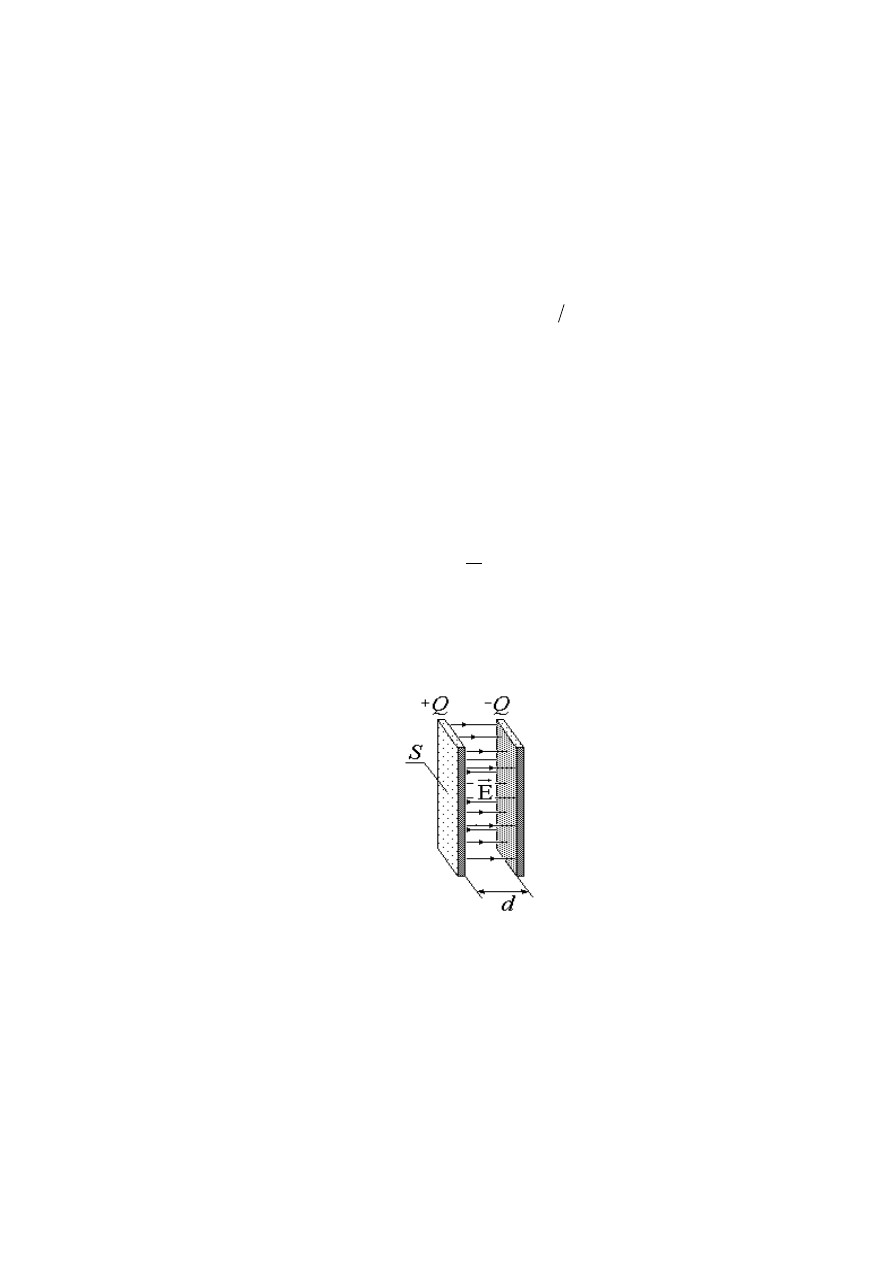
Określimy pojemność płaskiego kondensatora. Różnica potencjałów między okładkami
jest równa
222

S
d
q
d
dx
E
U
d
⋅
=
⋅
=
⋅
=
−
=
∫
0
0
0
2
1
ε
ε
σ
ϕ
ϕ
,
a zatem
d
S
U
q
C
⋅
=
=
0
ε
.
223
Wyszukiwarka
Podobne podstrony:
17. Utworzenie przewodnictwa pierwsi przewodnicytatrzańscy i poza , turystyka i rekreacja, Turystyk
17 Montowanie przewodów instalacji elektrycznej
17 przewodnictwo
Ciecze izolacyjne - referat, dielektryki ciekle, Dielektryki izolatory materiały które bardzo słabo
sekuła, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizyczna,
L.P.T.O. Cwiczenie 17 - Obwody nieliniowe pradu stalego , Element nieliniowy w kierunku przewodzenia
Fizyka- Pomiar przewodności cieplnej izolatorów.4, _________Andrzej G?rczak
Laboratorium Podstaw Fizyki spr 24 Pomiar przewodności cieplnej izolatorów, PWR, MATERIAŁY PWR 1, LA
Pomiar przewodności cieplnej izolatorów, Sprawolki
Fizyka Pomiar Przewodności cieplnej izolatorów
ref fizyka przewodniki i izolatory elektryczne
Instr.zae. i przewozu ZGE 17 41 na pow. StMar, Instrukcje w wersji elektronicznej
Pomiar przewodności cieplnej izolatorów
POMIAR PRZEWODNOSCI CIEPLNEJ IZOLATORÓW 1(1) DOC
Fizyka Pomiar przewodności cieplnej izolatorów 2 DOC
więcej podobnych podstron