1

K

L

UC

Z O

D

P

O

W

IED

ZI

I

ZA

S

A

DY P

U

NKTOWANIA PRÓBNE

GO EGZAMINU

MATURALNEGO Z

MATEMATYKI

PO

Z

IOM PODSTAW

O

WY

Nr

zadania

Odpow

iedz

i Punkty

Badane

umiej

ętno

ści Obsz

ar

sta

ndardu

1.

B 0–1

planuje i wykonuje obliczenia na

liczb

ach rze

czywistych,

w szczególn

oś

ci oblicza pierwiastki,

w tym

pierwiastk

i niep

arzystego

stopnia z liczb ujem

nych

wykorzystanie

i tworzen

ie

reprezentacji

2.

C 0–1

oblicza pot

ęgi o wyk

ładnikach

wym

iernych oraz stosuje prawa

dzia

ła

ń na pot

ęgach o w

yk

ładnikach

wym

iernych i rzeczywistych

wykorzystanie

i interpr

eto

wanie

reprezentacji

3.

B 0–1

rozwi

ązuje równania i nierówno

ści

kwadratowe

wykorzystanie

i tworzen

ie r

eprezen

tac

ji

4.

A

0–1

potrafi na podstawie wykresu funkcji

y = f(x) naszkicowa

ć wykresy funkcji

y = f(x + a), y = f(x) + a, y = – f(x),

y = f(–x)

wykorzystanie

i tworzen

ie

reprezentacji

5.

C 0–1

oblicza warto

ść

liczbow

ą wyra

żenia

wym

iernego dla danej warto

ści

zm

iennej

wykorzystanie

i tworzen

ie

reprezentacji

6.

A 0–1

znajduje zwi

ązki m

iarowe w figurach

pł

askich, tak

że z zas

toso

waniem

trygonom

etrii, równie

ż w zadaniach

um

ieszczon

ych w kontek

ście

praktycznym

uż

ycia i two

rzenia

stra

tegii

2

7.

D

0–1

oblicza warto

ść

liczbow

ą wielom

ianu

dla danej warto

ści zm

iennej

wykorzystanie

i interpr

eto

wanie

reprezentacji

8.

A 0–1

wykorzystuje interpretacj

ę

wspó

łczynników we wzorze funkcji

liniowe

j

wykorzystanie

i interpr

eto

wanie

reprezentacji

9.

B 0–1

znaj

ąc warto

ść

jednej z funkcji

trygonom

etrycznych, wyznacza

warto

ść

innej funkcji tego sam

ego

ką

ta os

trego

wykorzystanie

i tworzen

ie

reprezentacji

10.

B 0–1

pos

ługuje si

ę równaniem okr

ęgu

modelowanie

ma

te

ma

ty

cz

ne

11.

C 0–1

sporz

ądza wykresy funkcji

wyk

ładniczych dla ró

żnych podstaw

wykorzystanie

i interpr

eto

wanie

reprezentacji

12.

C 0–1

stosuje wzór na sum

ę

n pocz

ątkowych

wyrazów ci

ągu arytm

etycznego

wykorzystanie

i tworzen

ie

reprezentacji

13.

A 0–1

zapisu

je zale

żno

ść

mi

ędzy trzem

a

kolejnym

i wyrazam

i ci

ągu

geom

etrycznego

wykorzystanie

i tworzen

ie r

eprezen

tac

ji

14.

C 0–1

oblicza warto

ści logarytmów

wykorzystanie

i interpr

eto

wanie

reprezentacji

3

15.

D 0–1

rozwi

ązuje zadanie um

ieszczone

w kontek

ście prakty

czn

ym

prowadz

ące do równa

ń liniowych

modelowanie

ma

te

ma

ty

cz

ne

16.

A 0–1

stosuje wzór na sum

ę

n pocz

ątkowych

wyrazów ci

ągu arytm

etycznego

w kontek

ście prakty

czn

ym

modelowanie

ma

te

ma

ty

cz

ne

17.

D 0–1

oblicz

a

śred

ni

ą wa

żon

ą wykorzystanie

i tworzen

ie

inf

orm

acji

18.

B 0–1

pos

ługuje si

ę równaniem okr

ęgu wykorzystanie

i tworzen

ie

inf

orm

acji

19.

A 0–1

zlicza obiek

ty w prostych sytuac

jach

kom

binatorycznych,

niewym

agaj

ących

uż

ycia wzorów kom

binatorycznych,

stosuje zasad

ę mn

oż

enia

wykorzystanie

i interpr

eto

wanie

reprezentacji

20.

D 0–1

oblicza przek

ątn

ą prostopad

ło

ścianu

o podanych kraw

ędziach

wykorzystanie

i interpr

eto

wanie

reprezentacji

21.

A 0–1

oblicza powierzchni

ę boczn

ą

wielo

ści

anu

modelowanie

ma

te

ma

ty

cz

ne

22.

C 0–1

oblicza pole powierzchni bocznej

sto

żka

modelowanie

ma

te

ma

ty

cz

ne

4

23.

Odp. x = 3,5

•

Poprawna metoda rozwi

ązania równania – 1 p.

•

Podanie poprawnej odpowiedzi – 1 p.

0–2

rozwi

ązuje równanie wielom

ianowe

me

to

dą

rozk

ładu na czynniki

wykorzystanie

i interpr

eto

wanie

reprezentacji

24.

Odp.

)
,

2

1

7

2

1 1,

(

+∞

<

∪

>

−∞
∈

x

•

Poprawna metoda rozwi

ązania n

ieró

w

no

ści – 1 p.

•

Podanie poprawnej odpowiedzi – 1 p.

0–2

wykorzystuje poj

ęci

e war

to

ści

bezwzgl

ędn

ej i jej inte

rp

reta

cj

ę

geom

etryczn

ą

wykorzystanie

i interpr

eto

wanie

reprezentacji

25.

Odp. P =

π

−

4

16

•

Poprawna metoda rozwi

ązania równania – 1 p.

•

Podanie poprawnej odpowiedzi – 1 p.

0–2

znajduje zwi

ązki m

iarowe w figurach

pł

askich, oblicza pole kwadratu

wykorzystanie

i interpr

eto

wanie

reprezentacji

26.

Odp. 4300

•

Poprawna metoda rozwi

ązania równania – 1 p.

•

Podanie poprawnej odpowiedzi – 1 p.

0–2

stosuje poj

ęcie procentu, oblicza

procent sk

ładany

modelowanie

ma

te

ma

ty

cz

ne

27.

Przyk

ładow

e rozwi

ązanie:

Oznaczm

y przez 2

n + 1 dowoln

ą lic

zb

ę niepa

rzy

st

ą

(n

∈

N). Korzystaj

ąc z warunków zadania, m

am

y:

)

(4

4

4

1
1

4

4

1
)1
2(

2

2

2

2

2

n

n

n

n

n

n

n

+

=

+

=
−
+

+

=

−

+

cnd.

•

Zapisanie warunków zadania w postaci wyra

żenia

algebraicznego – 1 p.

•

Uzasadnienie twierdzenia – 1 p.

0–2

prowadzi proste rozum

owanie

sk

ładaj

ące s

ię

z niewie

lkiej liczby

kroków

rozum

owani

e

i argum

entacja

5

28.

Odp. a) 0,5

Odp. b) 0,25

•

Poprawna metoda rozwi

ązania zadania – 1 p.

•

Podanie poprawnych odpowiedzi – 1 p.

0–2

wykorzystuje sum

ę, iloczyn i ró

żni

cę

zdarze

ń do obliczania

prawdopodobie

ństw zdarze

ń

rozum

owani

e

i argum

entacja

29.

Przyk

ładow

e rozwi

ązanie:

a

n

a

a

n

n

log)1
(

log

1

1

+

=

=

+

+

a
n

a

a

n

n

log

log

=

=

.

log

log

log

log

log

log)1
(

1

const
a

a
n
a

a
n

a
n
a

n

a

a

n

n

=

=

−

+

=

−

+

=

−

+

•

Poprawna metoda rozwi

ązania zadania – 1 p.

•

Poprawne przekszta

łcenia wynikaj

ące ze znajomo

ści

dzia

ła

ń na logarytm

ach – 1 p.

0–2

bada, czy dany ci

ąg jest arytm

etyczny,

stosuje w obliczeniach w

zory na

logarytm

iloczynu, ilorazu lub pot

ęgi

wykorzystanie

i interpr

eto

wanie

reprezentacji

30.

Odp.

1

3

9

2

−

⋅
=

n

n

a

•

Poprawna metoda rozwi

ązania zadania – 1 p.

•

Poprawne zapisanie wzoru ogólnego ci

ągu – 1 p.

0–2

wyznacza wzór ogólny ci

ągu

geom

etrycznego

uż

ycie i two

rzenie

stra

tegii

31.

Odp.

y =

x + 3,

P

= 13,5

•

Poprawna metoda wyznaczenia równania os

i

sym

etrii tró

jk

ąta

ABC

– 2 p.

•

Zapisanie ró

wnania osi s

ym

etrii tró

jk

ąta

ABC

– 1 p.

•

Obliczen

ie p

ola trójk

ąta – 1 p.

0–4

rozwi

ązuje zadanie dotycz

ące

zwi

ązków miarowych w figurach

i wzajem

nego po

ło

żenia prostych na

pł

aszczy

źnie kartezja

ńsk

iej

uż

ycie i two

rzenie

stra

tegii

6

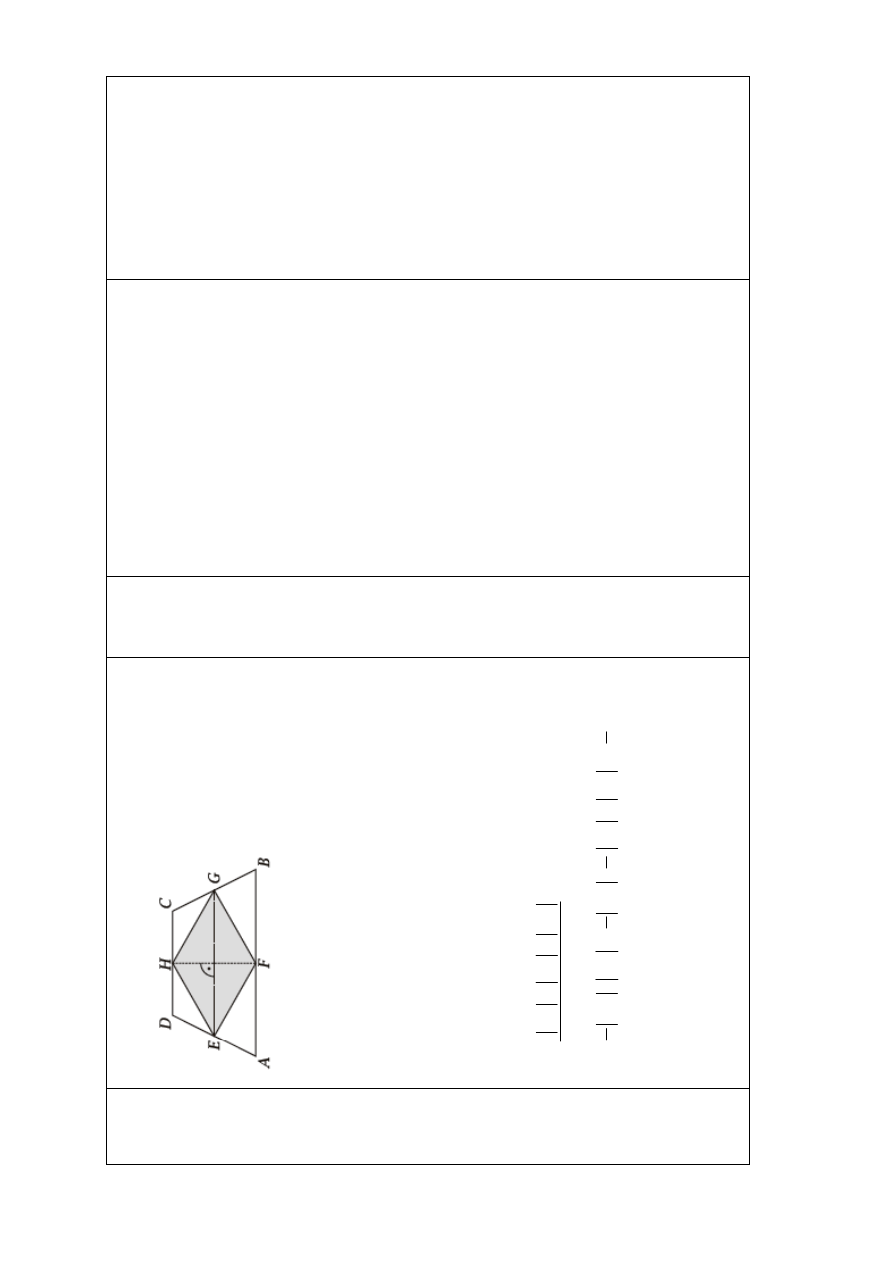
32.

Przyk

ładow

e rozwi

ązanie:

Trapez jest równoram

ienny, wi

ęc odcinek

łą

cz

ący

ś

rodki

podstaw jest do nich prostopad

ły.

Odcinek

łą

cz

ący

środki ram

ion trapezu jest równoleg

ły

do podstaw.

Odcinki

EG

i

HF

podzieli

ły trapez

ABCD

na cztery

czworok

ąty. Z podobie

ństwa tych czworok

ątów wynika,

że odcinki

HF

i

EG

przecinaj

ą si

ę w po

łowie.

Z podobie

ństwa figur wynika:

|EG| = 0,5(|CD| + |AB|)

Zatem

:

2

)

(

H

F

CD

A

B

P

t

⋅

+

=

()

t

r

P

AB

CD

HF

EG

HF

P

⋅
=

+

⋅

=

⋅

=

2

1

2

1

2

1

2

1

•

Uzasadnien

ie,

że powsta

ła figura jest rom

be

m

– 1 p.

•

Wykazanie,

że pole rombu jest po

łow

ą pola trap

ezu

– 1 p.

0–4

znajduje zwi

ązki m

iarowe w figurach

pł

askich

rozum

owani

e

i argum

entacja

7

33.

Odp.

3
36

•

Analiza zadania (rysunek lub opis) – 1 p.

•

Poprawna metoda obliczenia wysoko

ści i p

rzek

ątnej

podstawy – 1 p.

•

Poprawna metoda obliczenia obj

ęto

ści – 1 p.

•

Podanie poprawnej odpowiedzi – 1 p.

0–4

wyznacza zwi

ązki m

iarowe

w wielo

ścianach z zas

to

sowaniem

trygonom

etrii

uż

ycie i two

rzenie

stra

tegii