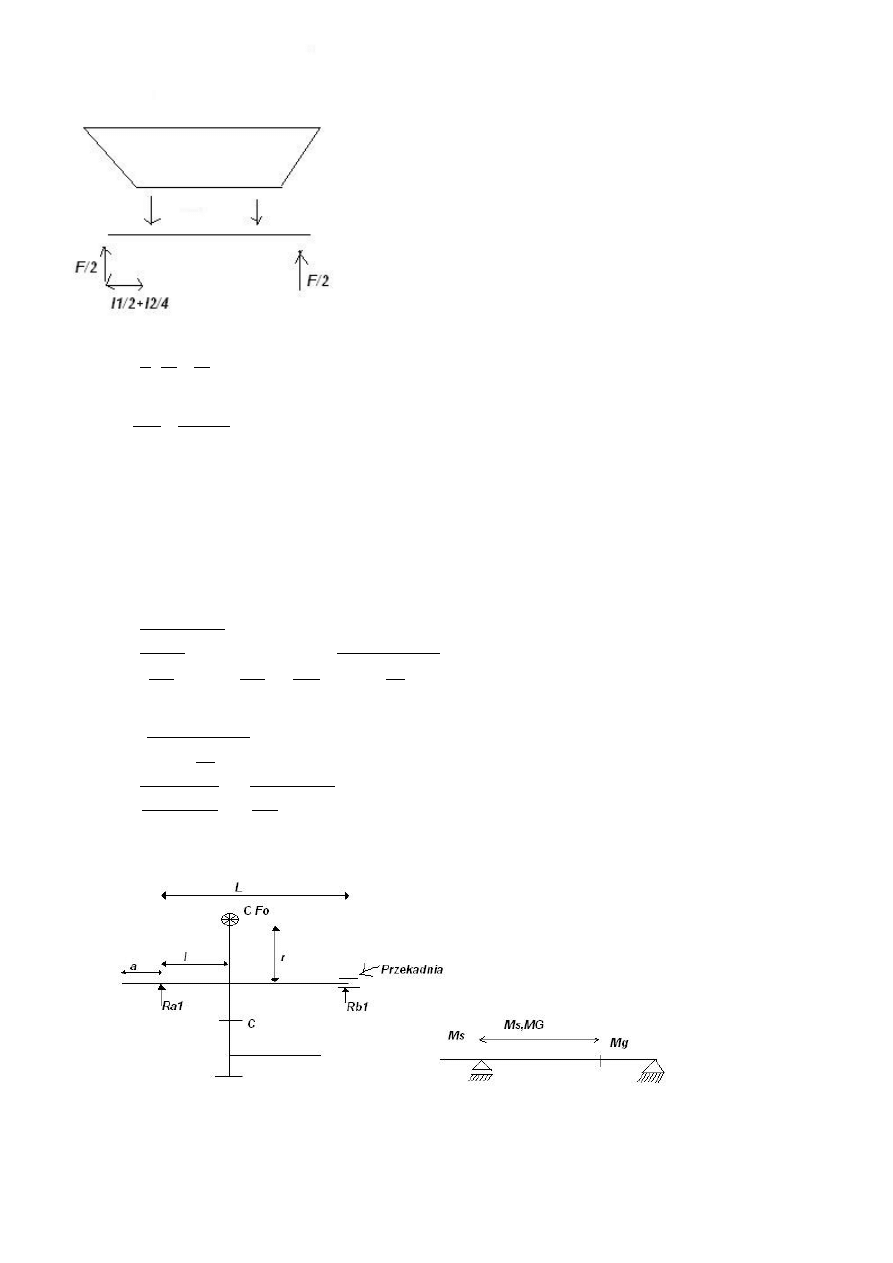
Mg=

t

2



l1

2



l2

4



σg =

Mg
Wg

=

32⋅Mg

⋅

d

3

≤

Kg

W obu przypadkach średnice d wyznaczamy z wzorów 

τ 

t 

 i Gg

Następnie sprawdzamy wytrzymałość połączenia na naciski powierzchni ze wzorów jak wyżej (p1 i p2)

Osie i wały  
tutaj było pusto

Jeżeli obciązony omomentem zginającym i skręcającym

σz =



σy

2



2

⋅

Ts

2

≤

Kg

σz =





Ms
Ws



2



2⋅

Ms
Ws



2

=

1

Wg

⋅



Mg

2





2

4

⋅

Ms

2



kgo j

Ws=2Wg
Moment zastępczy 

Mz=



Mg

2





2

4

⋅

Ms

2

d ≥



32⋅Mz

⋅

Kgo j

3

≈



Mz
0.1

Kgo j

3

Gdyby gdzieś zostało a nie było by poprawione to nie ma Kg dj tylko to jest Kgo(j)

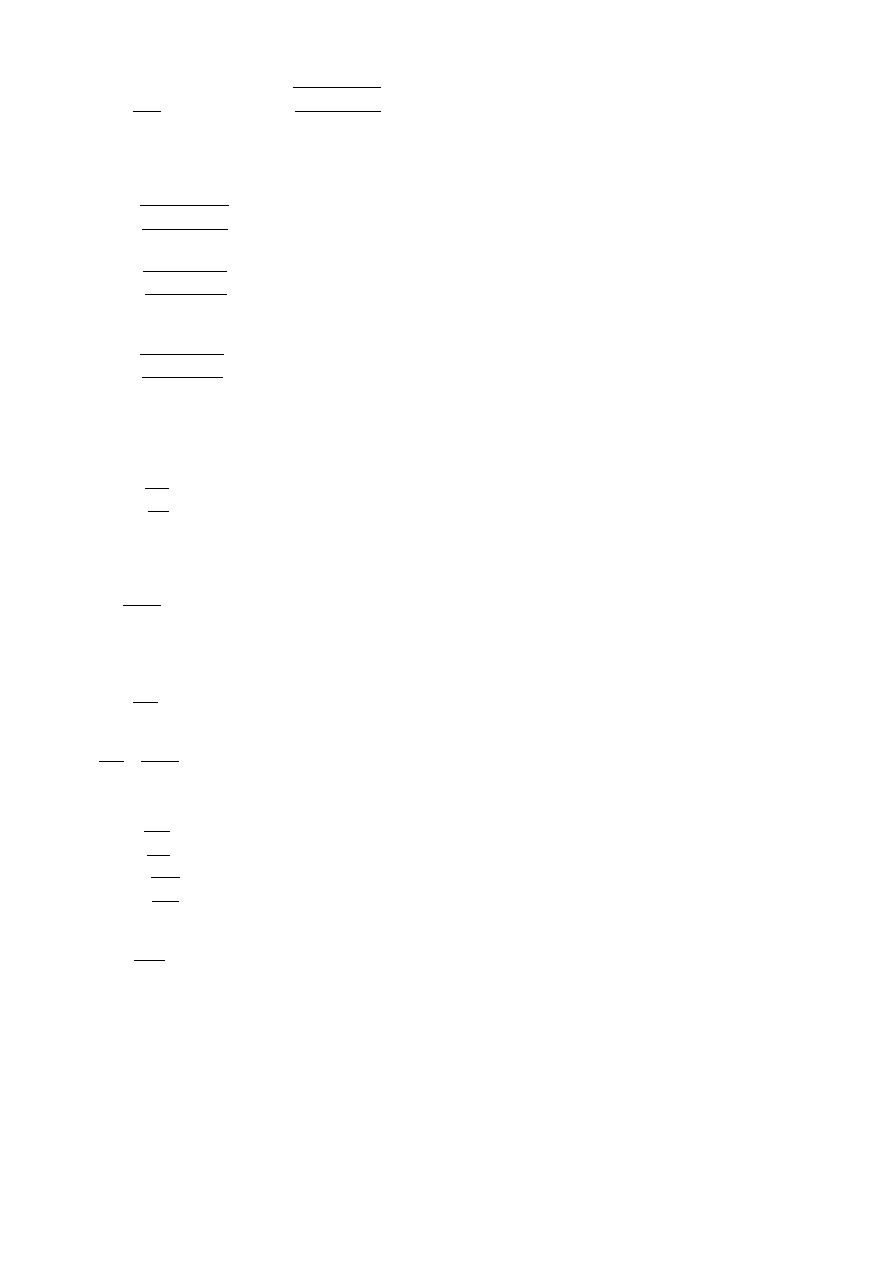
σg =

Mg
Wg

≤

Kgo j⇒ d ≥



Mg

0,1⋅Kgo j

3

P=100Kw
n=100 obr/min
Ms=9550 p/n [Nm]
Na odcinku a srędnia wału wyznaczamy

d ≥



Ms

0,2⋅Kgo j

3

Na odcinku l

D≥



Mz

0,1⋅kgo  j

3

Na odcinku L-l

d ≥



Mg

0,1⋅kgo  j

3

Wały w wyniki oddziaływania periodycznych obicązeń (sił osiowych i sił poprzecznych, momentu skręcajecego , 
zginającego) są pobudzane do drgań

Wały mogą drgać skrętnie, poprzecznie oraz wzdłużnie 

Ws=



Cs

H

Cs-Sztywność skrętna
H-masowy moment bezwładności
Ws-częstość drgań skęcających



e=

Ms⋅l
Io⋅G

Io-biegunowy moment bezwładności
G-moduł kirchoffa



e−Kąt skręcania

Cs=

Ms



e

Ms



e

=

Io⋅G

l

H =m⋅r

2

2

m=T⋅r

2

⋅⋅

l

Wl=



Cp

m

-częstość drgań poprzecznych

Ww=



Cw

m

-częstość drgań wzdłużnych

Wt-wał niewyważony        ws-w przekładni predkość nad i pod rezonansem to wielokrotność (dziwne zdanie)

Fz=

Z⋅n

Go