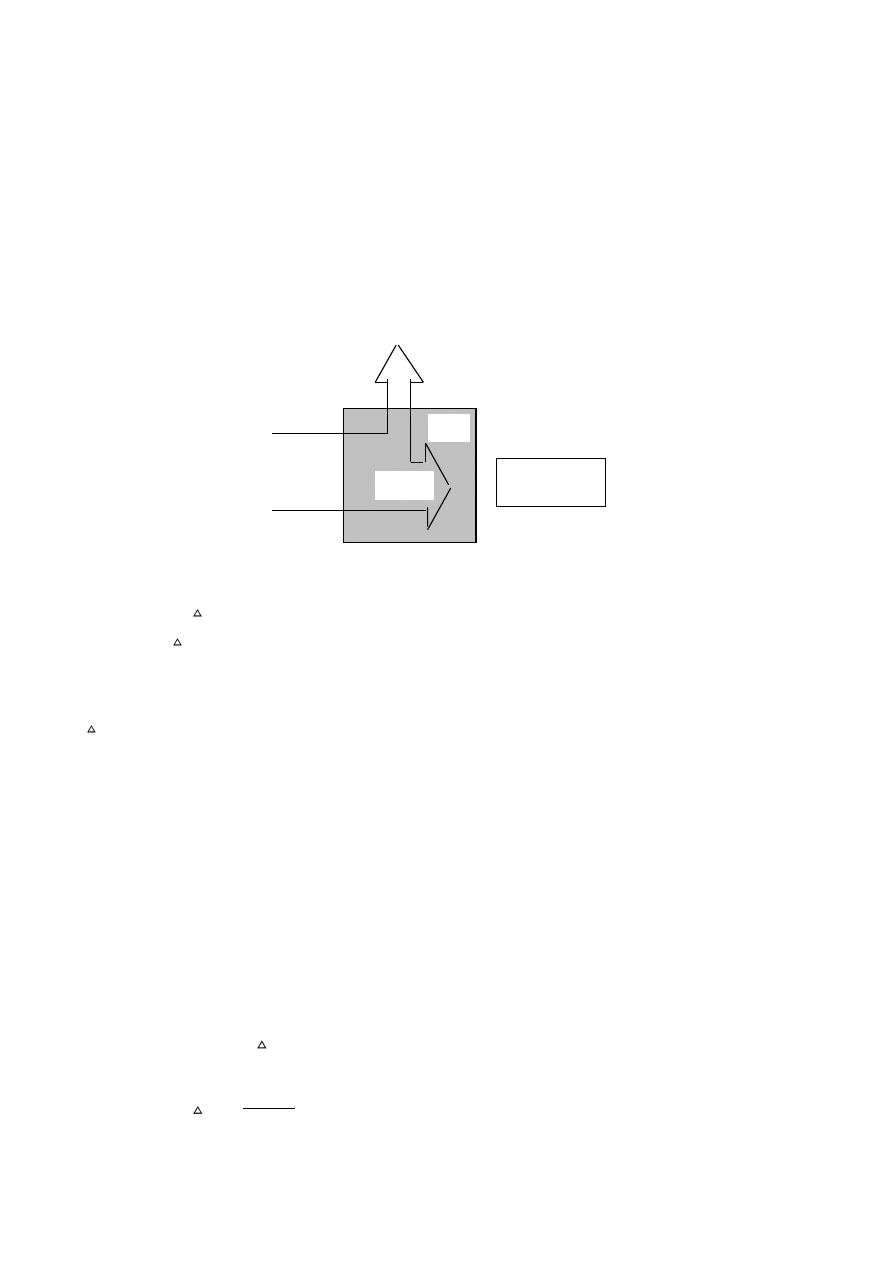
ZJAWISKA CIEPLNE W SILNIKU
Przejdźmy do zjawisk cieplnych zachodzących w silniku. Wiadomo, że zarówno nagrzanie jak i
wystudzenie dowolnego ciała wymaga określonego czasu. Zmienność temperatury silnika w czasie
można wyznaczyć na podstawie modelu, w którym uzwojenia silnika są zastąpione jednorodną bryłą o
masie m i o małym oporze przewodzenia ciepła, do której w czasie dt zostaje doprowadzone ciepło
dt
P
dQ
S
Przypomnijmy, ze symbol
P
S
oznacza moc strat. Zgodnie z zasadą zachowania energii (rys.2.2.3) jest
O
S
dQ
dQ
dQ
+
=
Ciepło dQ
S
pozostaje w bryle nagrzewając ją, zaś ciepło dQ
0
, zostaje odprowadzone do otoczenia, przy
czym
S
p
dQ
m c
d
0
dQ
A
dt
gdzie:
c
p
– ciepło właściwe w
kg
K
/
J
,
- nadwyżka temperatury bryły ponad temperaturę otoczenia w K,
A – powierzchnia bryły przez którą odprowadzane jest ciepło w m
2
,
- współczynnik przejmowania ( oddawania) ciepła w
2
m
K
/
J
dt – przyrost czasu w s.
Przyrost ciepła na skutek strat w silniku
St
s
dQ
P dt
Przy czym
s
P
całkowite straty w silniku
St
0
dQ
dQ
W stanie ustalonym ilość
wytworzonego
ciepła równa się ilości ciepła
akumulowanego czyli
s
u
P
A
, gdzie
u
ustalona temperatura ( brak przyrostu temperatury)
zatem
s
u
P
A
Teraz rozpatrzmy przypadek stanu nieustalonego
dQ
0
dQ
dQ
S
Rys.2.2.3
m
p
m c
d
s
p
P dt
m c
d
A
dt
Wyznaczmy z powyższego równania dt
p
s
m c
d
dt
P
A
To samo równanie można zapisać jeszcze inaczej
p
p
s
u
m c
d
m c
d
dt
P
A
(
)
A
(
)
A
Jeśli warunki przejmowania ciepła ( chłodzenia) są stałe to po scałkowaniu uzyskamy:
u
c
t
ln(
) C
, gdzie
p
c
m c
A
jest termiczną stała czasową.
Trzeba pamiętać, że silnik nie jest ciałem jednorodnym, a w praktyce współczynnik
oddawania ciepła nie jest wielkością stała. Ma to konsekwencje, o których napiszemy
dalej.
Przyjmując warunek początkowy dla czasy t = 0
=
u
i wyznaczając C oraz dokonując
przekształceń uzyskujemy ostatecznie ważny wzór
Wnioski
* Przy powyższych założeniach, osiągnięcie temperatury ustalonej
u
, następuje teoretycznie po ·
nieskończenie długim czasie.
* Ustalony przyrost temperatury
u
zależy od sumy strat w silniku i jest ich liniową funkcją
Stała termiczna zależy do budowy silnik, a nie sposobu jego obciążenia
Uwaga
Stała termiczna silnika zależy od gabarytów silnika (uzwojenia), budowy, sposobu wentylacji
i warunków pracy.
Przy przeciążeniach długotrwałych uzwojenie nie może być traktowane jako odrębny
element maszyny elektrycznej. Należy wówczas przyjąć stałą czasową nagrzewania silnika w
całej swojej masie. Natomiast przy przeciążeniach krótkotrwałych należy brać pod uwagę stałą
czasową nagrzewania uzwojenia, która wynosi zaledwie kilka minut.
c
t
u
1 e
czas
t
m2
u 2
u 2
Przykład
Stała termiczna silnika
t
min 10
20
30 40
50
60 70
80 90
100
120
150
180
200
0
C
17.1 29.2 38 44.2 48.7 52 54.2 56 57.2 57.8 58.5 59.5 59.7 59.8
Tabela 1 Przykładowy przebieg nagrzewania się się silnika dla maksymalnego przyrostu
temperatury.
W MATLABIE
t=[10 20 30 40 50 60 70 80 90 100 120 150 180 200];
teta=[17.1 29.2 38 44.2 48.7 52 54.2 56 57.2 57.8 58.8
59.5 59.7 59.8];
stem(t,teta)
hold
on
plot(t,teta)
xlabel (
't [s]'
)
ylabel(
'delta'
)
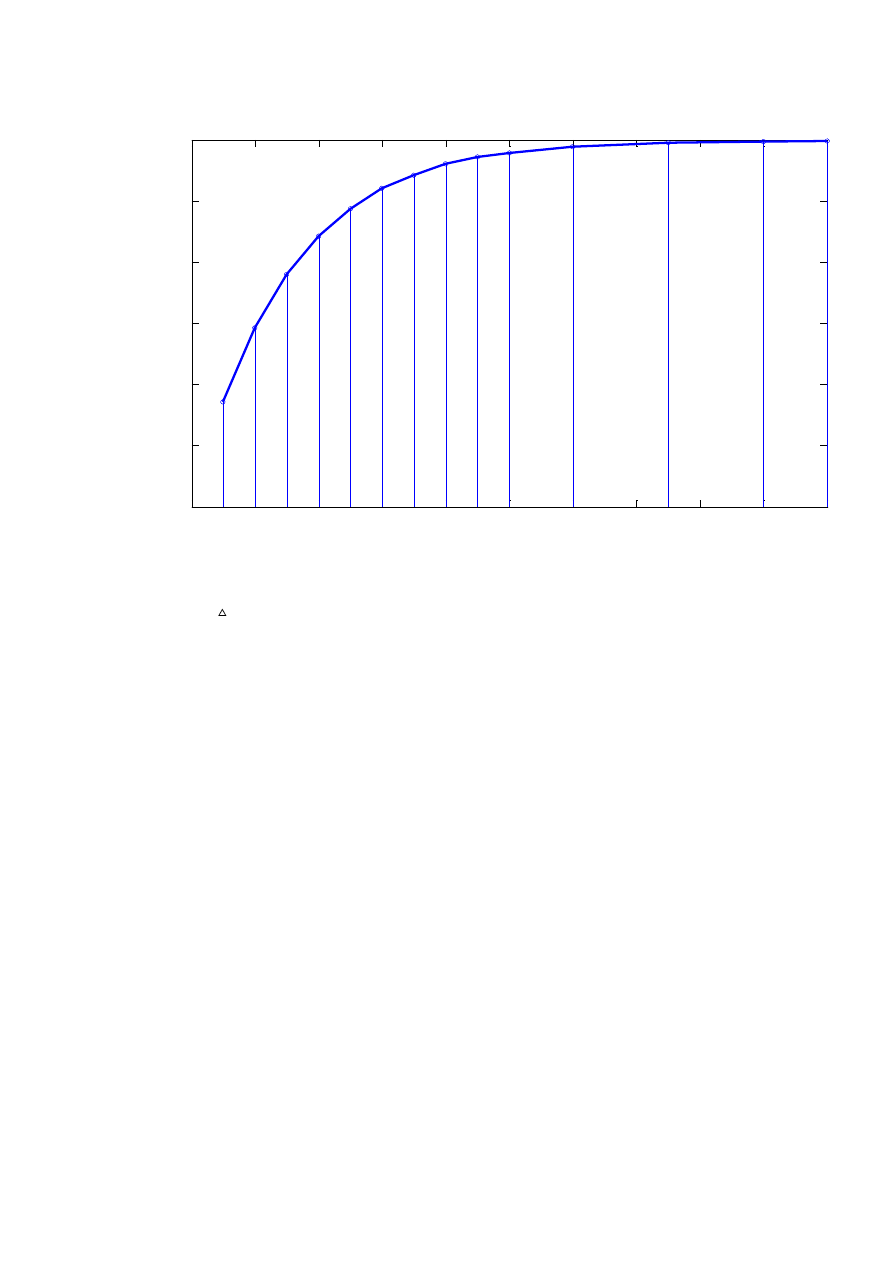
Ile wynosi termiczna stała czasowa?
Jaka jest wartość
u
?
0
20
40
60
80
100
120
140
160
180
200
0
10
20
30
40
50
60
t [s]
d
e
lt
a
Elementy straty w silniku:
W uzwojeniach silnika
2
Cu
P
f (I )
W obwodzie magnetycznym ( na drodze strumienia od pola magnetycznego )
1,3
Fe
P
f (f
)
Mechaniczne:
- tarcia w łożyskach, tarcie szczotek
tar
P
f (n)
;
- wentylatorowe
2
went
P
f (n )
Straty przewodzenia ( na drodze komutator-szczotki)
psz
P
f (I)
Straty dodatkowe ( nieuwzględniane wyżej)
dod
P
Straty dodatkowe
dod
P
zgodnie z polskimi normami wynoszą w maszynach prądu stałego od
0,5%, do 1%, a w maszynach asynchronicznych około 0,5% mocy znamionowej maszyny.
Przy pracy znamionowej straty w uzwojeniach są na ogół większe od pozostałych
strat.
Z przedstawionych tu zależności wynika, że
2
2
2
u
un
un
un
n
n
n
I
M
P
I
M
P
gdzie
un
m
P
P
const
zaś P
m
jest mocą na wale.
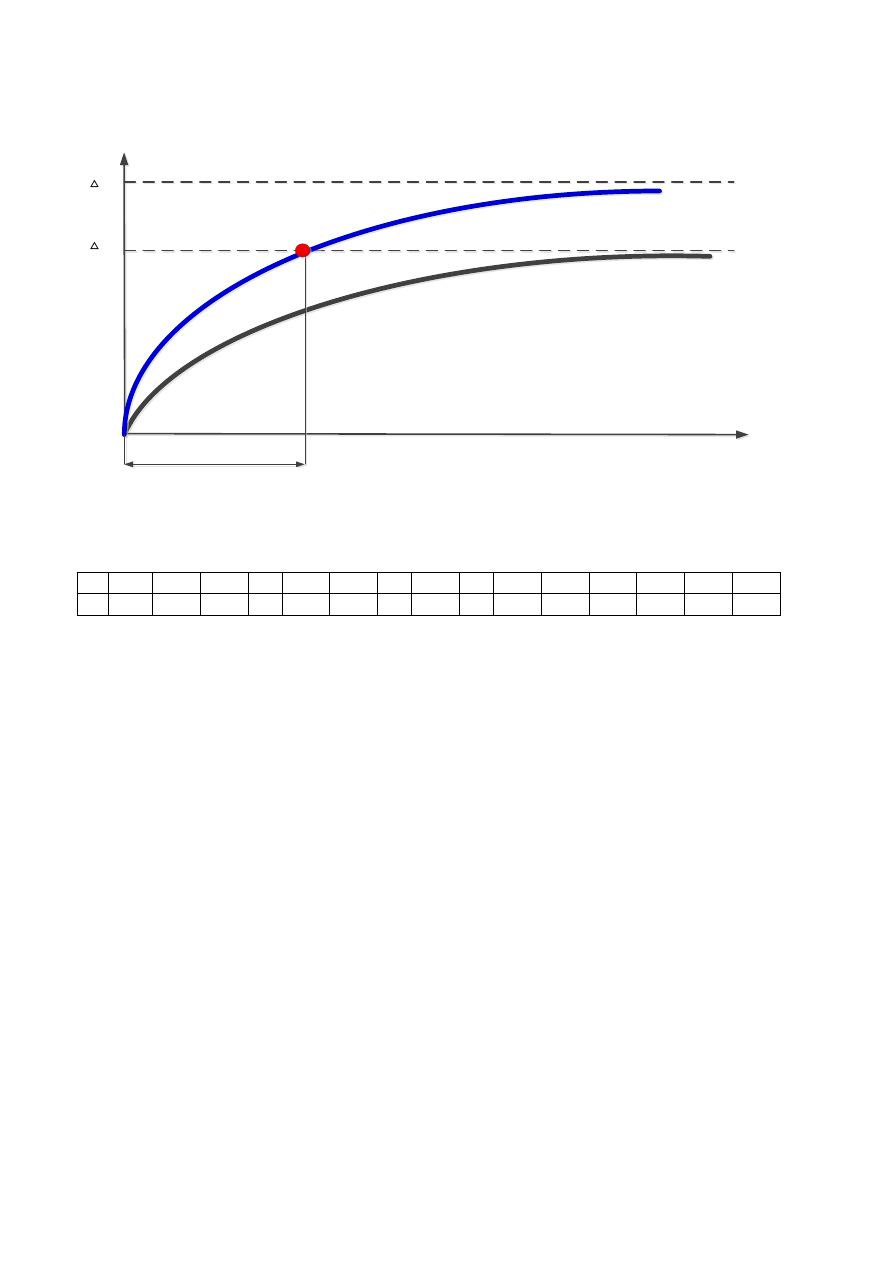
Praca dorywcza silnika
Oznaczmy ustalony przyrost temperatury dla pewnego obciążenia (wyróżnimy go indeksem „1”) na
wale jako
1
u
.
Jeśli silnik poruszać będzie się ze stała prędkością przez nieskończenie długi czas i w chwili t =0 jego
temperatura wynosiła zero to zmiany temperatury opisuje krzywa
c
t
1
u1
1 e
pamiętając, że
2
2
1
1
1
(
)
u
m
m
P
const
M
n
const
(x)
Przypuśćmy teraz, że ten sam silnik obciążamy większym momentem dla tej samej prędkości n
1
Stała
termiczna nie zmieni się, ale zmieni się
u
Mamy więc teraz
c
t
2
u 2
1 e
2
2
2
2
2
1
(
)
u
m
m
P
const
M
n
const
(xx)
Porównując (x) z (xx) mamy
2
2
2
1
1
(
)
m
u
u
m
P
P
Zatem
c
c
t
t
2
m2
2
u 2
u1
m1
P
1 e
(
)
1 e
P
(xxx)
Jeśli P
m1
jest mocą dobraną dla silnika dla pracy ciągłej, zaś P
m2
dla pracy dorywczej wówczas aby silnik
się nie przegrzewał trzeba dodać warunek, że temperatura pod koniec pracy przy obciążeniu dorywczym
jest taka sama jak przy obciążeniu stałym czyli
2
1
Stąd równanie (xxx) będzie miało postać
c
t
2
m2
u1
u1
m1
P
(
)
1 e
P
, a po przekształceniach
(XXXX)
Wnioski
*
Korzystając z wzoru (XXXX) można obliczyć moc danego silnika przy pracy dorywczej
( znanej, jako S2) o ile znamy moc silnika przy pracy ciągłej (S1) i termiczną stała czasową.
*
Im większa jest termiczna stała czasowa tym większa może być wybrana moc przy obciążeniu
dorywcza
,
Przykład 1
Dany jest silnik indukcyjny 3 fazowy budowy zamkniętej Sg 160L-2 o mocy 18,5kW i stałej
nagrzewania 30 min.
Jaką mocą można obciążyć wskazany silnik przy pracy dorywczej przy obciążeniu trwającym 15
minut?
Rozwiązanie
Moc przy pracy dorywczej
m 2
c
m1
m2
t
P
P
1 e
, gdzie P
m1
= 18,5kW, t
m2
= 15 min,
c
= 30 min
m2
15
30
18, 5
P
1 e
= 29,49 kW
MATLAB
Pm2=18.5/(1-exp(-15/30))^0.5
Pm2 =
29.492818613150884
Silnik można obciążyć w trybie S2 mocą 29,49 kW.
m 2
c
m1
m2
t
P
P
1 e
(XXXX
Przykład 2
Silnik asynchroniczny do pracy ciągłej ma moc 22kW, a jego stała czasowa wynosi 60 min.
W jakim czasie można silnik obciążyć mocą 30kW przy pracy dorywczej.
Rozwiązanie
Przekształcając wzór
m 2
c
m1
m2
t
P
P
1 e
otrzymujemy
2
2
m2
m2
c
2
2
2
2
m2
m1
P
30
t
ln
60 ln
P
P
30
22
Przykład 3
Ustalić wartość strat dopuszczalnych przy pracy dorywczej S2 ( 15, 30 i 60 minutowej)
względem strat przy pracy ciągłej dla silnika o stałej cieplnej
c
= 60 min.
Rozwiązanie
Straty dopuszczalne przy pracy dorywczej ( indeks d) wyznaczamy z wzoru
c
c
d
t
P
P
1 e
, gdzie
c
P
są stratami dla pracy ciągłej zaś t=15,30 i 60 min.
Z obliczeń dla pracy 15 minutowej
15
P
=4,53
c
P
Przykład 4
Silnik budowy zamkniętej typu Sg132M-6B o mocy znamionowej 5,5kW, prędkości 950 rad/s i
krotności momentu maksymalnego M
k
/M
N
=3,1 obciążono momentem 2,5 razy większym od
znamionowego. Jak długo może pracować ten silnik bez obawy przegrzania przy takim
obciązeniu? Termiczna stała czasowa jest równa 30 min.
Rozwiazanie
Z treści zadania wynika, że termiczna stała czasowa
c
=30
min
Oznaczmy przyrost temperatury dla silnika pracującego w warunkach znamionowych
dodatkowym indeksem u tj
un
, zaś silnika obciążonego momentem dwu i półkrotnym, jako
u 2,5
. Jak wiadomo ustalony przyrost temperatury
u
jest proporcjonalny do kwadratu
momentu, zatem
u 2,5
2
2
u 2,5
un
un
p
p
Temperatura silnika
c
c
t
t
2
2,5
u 2,5
un
1 e
p
1 e
nie może przekroczyć przyrostu temperatury ustalonej
un
co zapiszemy jako
2,5
un
i dalej
c
t
2
un
un
p
1 e
Stąd po przekształceniu wyznaczamy szukaną wartość t z wzoru
2
2
c
2
2
p
2,5
t
ln
30 ln
p
1
2,5
1
=5,23 minuty
Zwróćmy uwagę, że jest to ilustracja wyprowadzenia oznaczonego (xxxx)