ELEKTRYCZNOSC
Sila elektrostatyczna a grawitacyjna miedzy elektronem i protonem

N

R

m

m

G

F

H

e

p

G

47

2

10

61

,

3

−

⋅

=

=

F

E

= 8,19·10

-8

N,

czyli

2,27·10

39

razy wieksza od F

G

= 3,61·10

-47

N

Kwantyzacja ladunku - Wszystkie ladunki sa wielokrotnoscia e.
Ladunek elementarny e = 1,6·10

-19

C.

w ukl. SI 1 C = 1 As.

Zachowanie ladunku - Wypadkowy ladunek w ukladzie zamknietym (izolowanym) jest staly
(nie zmienia sie w czasie).

Prawo Coulomba

2

2

1

r

q

q

k

F

=

0

4

1

πε

=

k

, ogólnie

ε

πε

0

4

1

=

k

ε

0

= 8,854·10

-12

C

2

/(Nm

2

) - przenikalnosc elektryczna prózni (stala dielektryczna prózni),

ε

- stala dielektryczna substancji lub wzgledna przenikalnoscia elektryczna osrodka

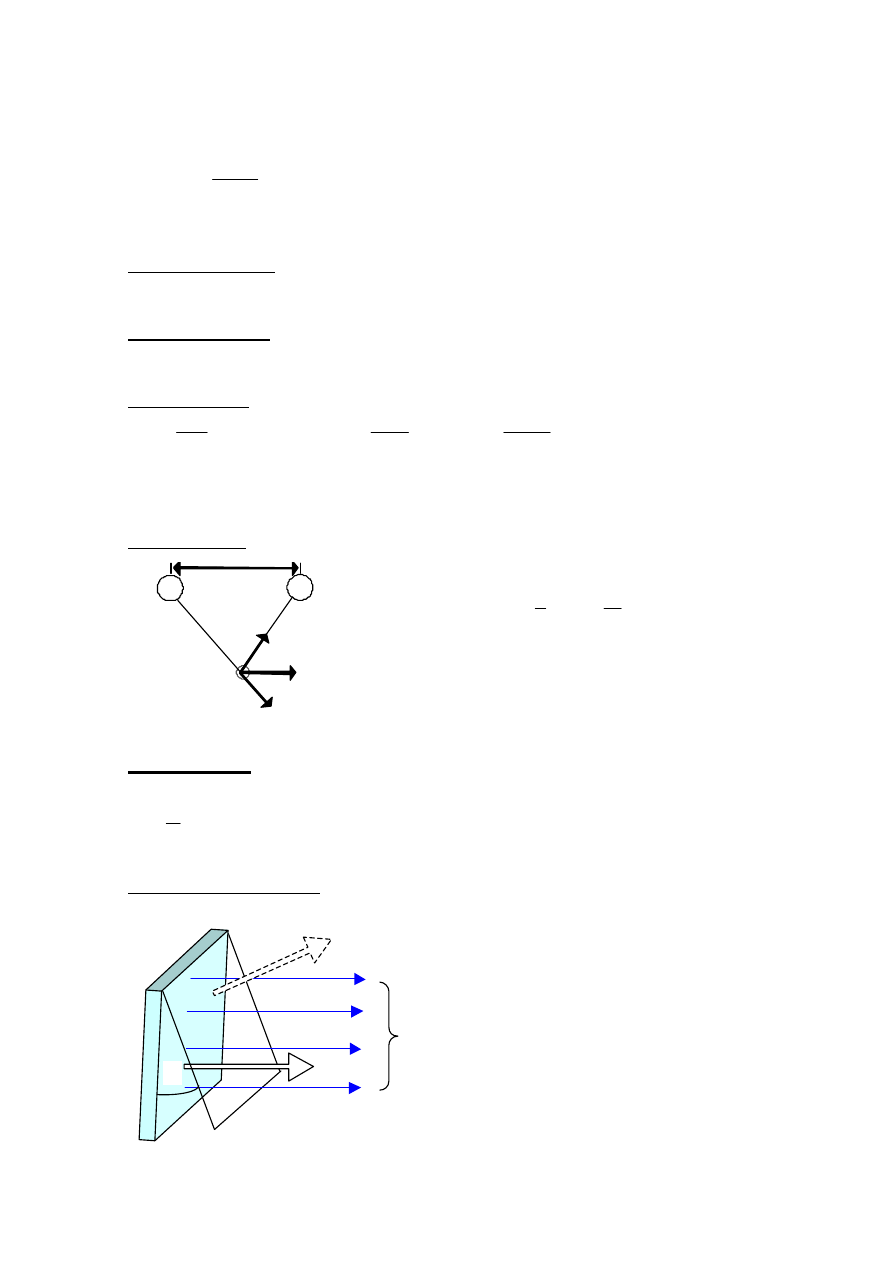
Dipol elektryczny

+Q

-Q

l

q

F

F

2

F

1

r

r

Pole elektryczne - Ladunek próbny jest dodatni (umowa). Kierunek E jest taki sam jak F
(na ladunek dodatni).

q

F

E

r

r

=

Strumien pola elektrycznego

∆

φ = E

∆

S = E

∆

S cos

α α - kat pomiedzy wektorem powierzchni

∆

S i wektorem E

∆S

∆S’

∆

F

E

α

3

1

r

p

qk

F

r

l

F

=

=

gdzie
p = Ql jest momentem di-
polowym.

S

d

d

E

=

φ

∑

∆

=

ia

powierzchn

S

E

r

r

φ

Suma ta przedstawia calke
powierzchniowa

∫

=

S

S

E

r

r

d

φ

Pole elektryczne od n ladunków punktowych jest
równe sumie wektorowej pól elektrycznych (zasada
superpozycji)

Natezenie pola
elektrycznego

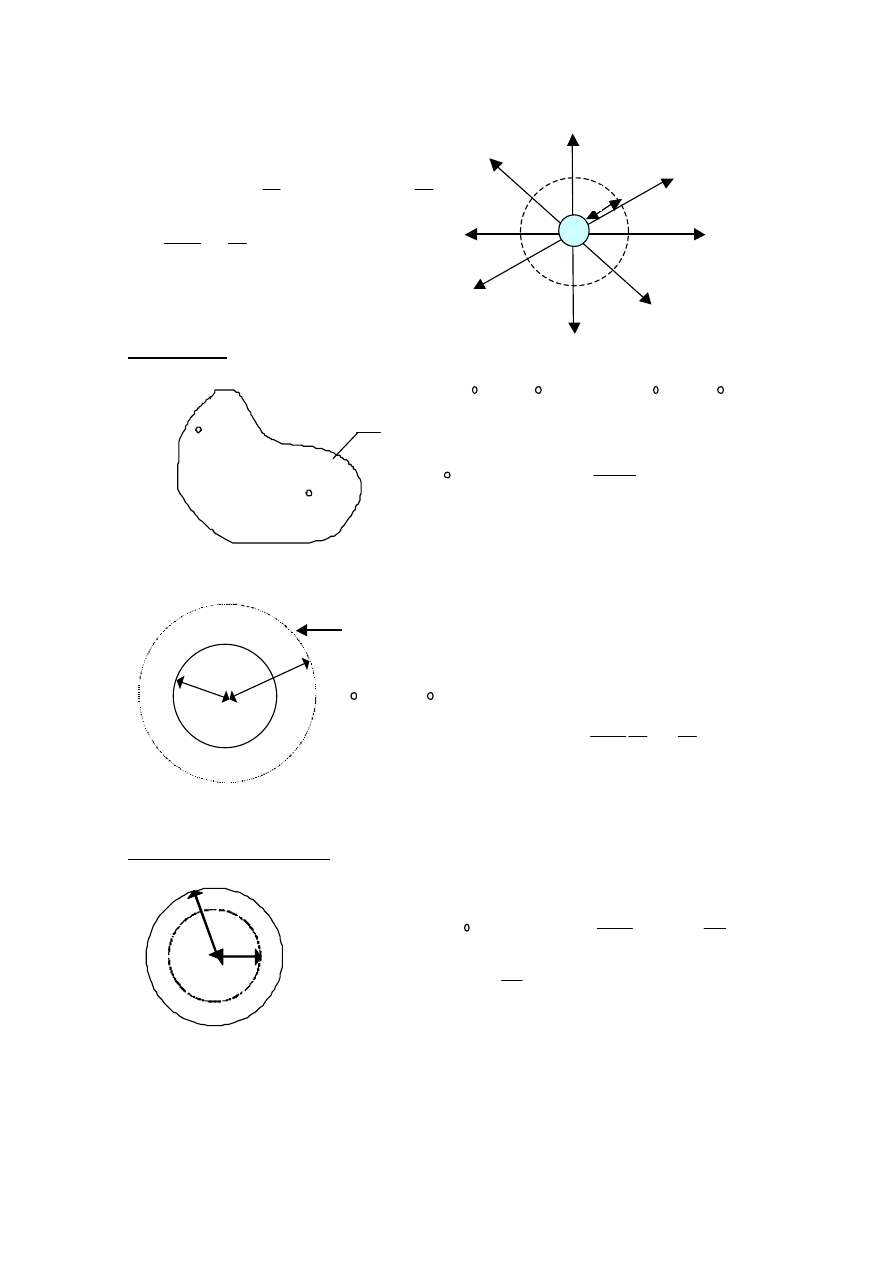
Prawo Gaussa

S

Q

1

Q

2

Jednorodnie naladowana sfera

r

R

+Q

Jednorodnie naladowana kula

R

r

Q

Q

wewn

Wykres E w funkcji odleglosci od srodka jednorodnie naladowanej kuli.

Q

r

E

powierzchnia Gaussa o
promieniu r

k

k

Q

kQ

r

r

Q

k

r

E

π

ε

πε

ε

π

π

π

φ

4

1

4

1

4

)

4

(

)

4

(

0

0

0

2

2

2

=

⇒

=

=

=













=

=

∫

∫

∫

∫

+

=

+

=

=

S

E

S

E

S

E

E

S

E

r

r

r

r

r

r

r

r

r

d

d

d

)

(

d

2

1

2

1

calk

φ

φ

calk

= (Q

1

/

ε

0

) + (Q

2

/

ε

0

) = (Q

1

+ Q

2

)/

ε

0

0

.

.

4

d

ε

π

wewn

wewn

Q

kQ

=

=

∫

S

E

r

r

∫

∫

=

=

)

4

(

d

2

r

E

dS

E

π

S

E

r

r

E(4

π

r

2

) = Q/

ε

0

Dla r > R

2

2

0

4

1

r

Q

k

r

Q

E

=

=

πε

Dla r < R, E = 0









=

=

=

∫

3

3

0

2

4

)

4

(

R

r

Q

k

Q

r

E

S

d

E

wew

π

ε

π

r

r

r

R

Q

k

E

3

=

kQ/R

2

R

E

r

Potencjal elektryczny

Róznica energii potencjalnych

∫

−

=

−

B

A

pA

pB

E

E

r

F d

∫

∫

−

=

−

=

−

=

−

B

A

B

A

pA

pB

B

A

q

E

E

U

U

r

E

r

F

r

r

r

r

d

d

Elektryczna energia potencjalna

F – sila elektrostatyczna dzialajaca na ladunek q.

∫

∞

−

=

=

r

p

q

r

E

r

U

r

E

r

r

d

)

(

)

(

Energia potencjalna jest równa pracy wykonanej przeciw sile elektrycznej

∫

∞

∞

∞







−

−

=

−

=

=

=

r

r

r

p

r

qQk

r

r

Q

k

q

W

r

E

r

U

1

d

)

(

)

(

2

U(r) jest energia potencjalna ladunków q i Q

r

qQ

k

r

E

r

U

p

=

=

)

(

)

(

Potencjal elektryczny

q

r

U

q

W

q

r

E

r

V

r

p

)

(

)

(

)

(

=

=

=

∞

Jedn. [J/C]=[V]

Potencjal dla ladunku punktowego

r

Q

k

V

=

∫

−

=

=

=

−

B

A

AB

A

B

W

U

V

V

r

Ed

Plyty równolegle

∆

V = – Ed

0

4

ε

σ

σ

π

−

=

−

=

k

E

stad

∆

V =

σd/ε

0

S

Qd

V

0

ε

=

∆

Elektronowolt

∆

E

k

= e

∆

V = (1,60·10

-19

C)(1 V) = 1,60·10

-19

J => 1 eV = 1,60·10

-19

J

0

Róznica

potencjalów

d

+s

-s

Powierzchnia kazdego przewodnika jest powierzchnia stalego potencjalu (powierzchnia
ekwipotencjalna).

Pojemnosc

U

Q

V

Q

C

=

∆

=

Jedn. farad. 1F = 1C/1V. Dla kondensatora plaskiego

d

S

U

Q

C

0

ε

=

=

Energia pola elektrycznego

C

Q

q

C

q

q

U

W

Q

Q

2

0

0

2

1

d

d

=













=

=

∫

∫

Energia zgromadzone w kondensatorze

Dla kondensatora plaskiego

ES

Q

czyli

S

Q

E

0

0

,

ε

ε

=

=

oraz

C = e

0

S/d i

(

)

Sd

E

d

S

S

E

C

ES

W

2

2

2

2

0

0

2

2

0

2

0

ε

ε

ε

ε

=

=

=

, Sd - objetosc kondensatora

2

2

0

8

1

2

1

E

k

E

w

π

ε

=

=

Gestosc energii pola elektrycznego

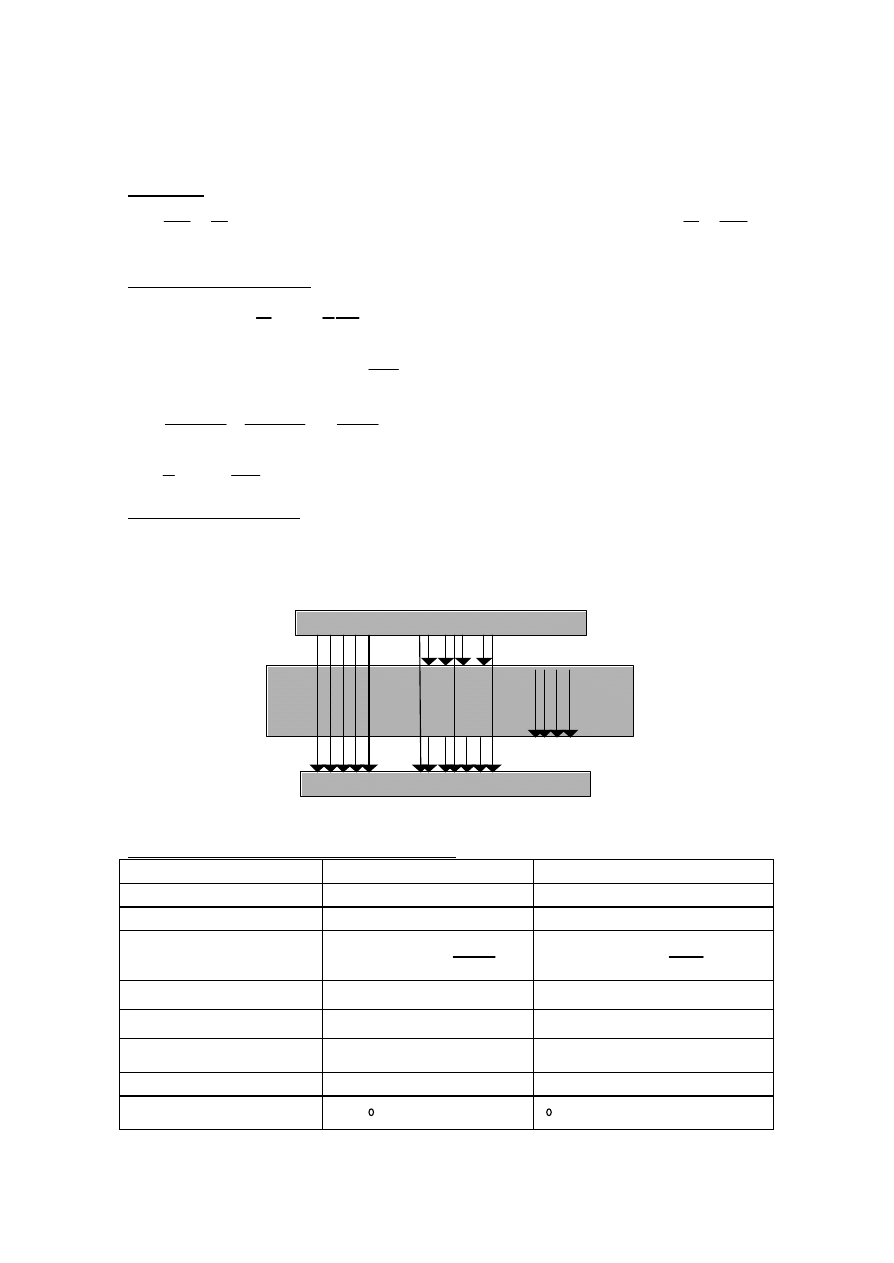
Trzy wektory elektryczne

P

E

D

r

r

r

+

=

0

ε

D, E, P sa wektorami: indukcji elektrycznej, natezenia pola, polaryzacji.
D - ladunek swobodny,

ε

0

E - wszystkie ladunki, P - ladunek polaryzacyjny

+ + + + + + + + + + +

- - - - - - - - - - -

- - - - - - - - - - -

+ + + + + + + + + + +

D

ε

0

E

P

Porównanie pola grawitacyjnego i elektrycznego

Pole grawitacyjne g

Pole elektryczne E

1. zródlo pola

Masa m>0

Ladunek q>0, q<0

2. stosowalnosc

Obowiazuje, gdy v<<c

Obowiazuje zawsze

3. sila

Newtona

r

r

m

m

G

F

r

r

3

2

1

=

Coulomba

r

r

q

q

k

F

r

r

3

2

1

=

4. natezenie pola

r

r

Gm

m

F

g

r

r

r

)

/

(

/

2

=

=

r

r

kq

q

F

E

r

r

r

)

/

(

/

2

=

=

5. energia potencjalna

r

m

Gm

U

g

/

2

1

−

=

r

q

kq

U

E

/

2

1

=

6. potencjal pola

r

Gm

m

U

V

g

g

/

/

=

=

∫

⋅

−

=

=

=

r

d

E

r

kq

q

U

V

E

E

r

r

/

/

7. praca

W

g

= U

g

= mV

g

W

E

= U

E

= qV

E

8. pole zachowawcze

Gdy

∫

=

⋅

0

r

d

F

g

r

r

∫

=

⋅

0

r

d

F

E

r

r