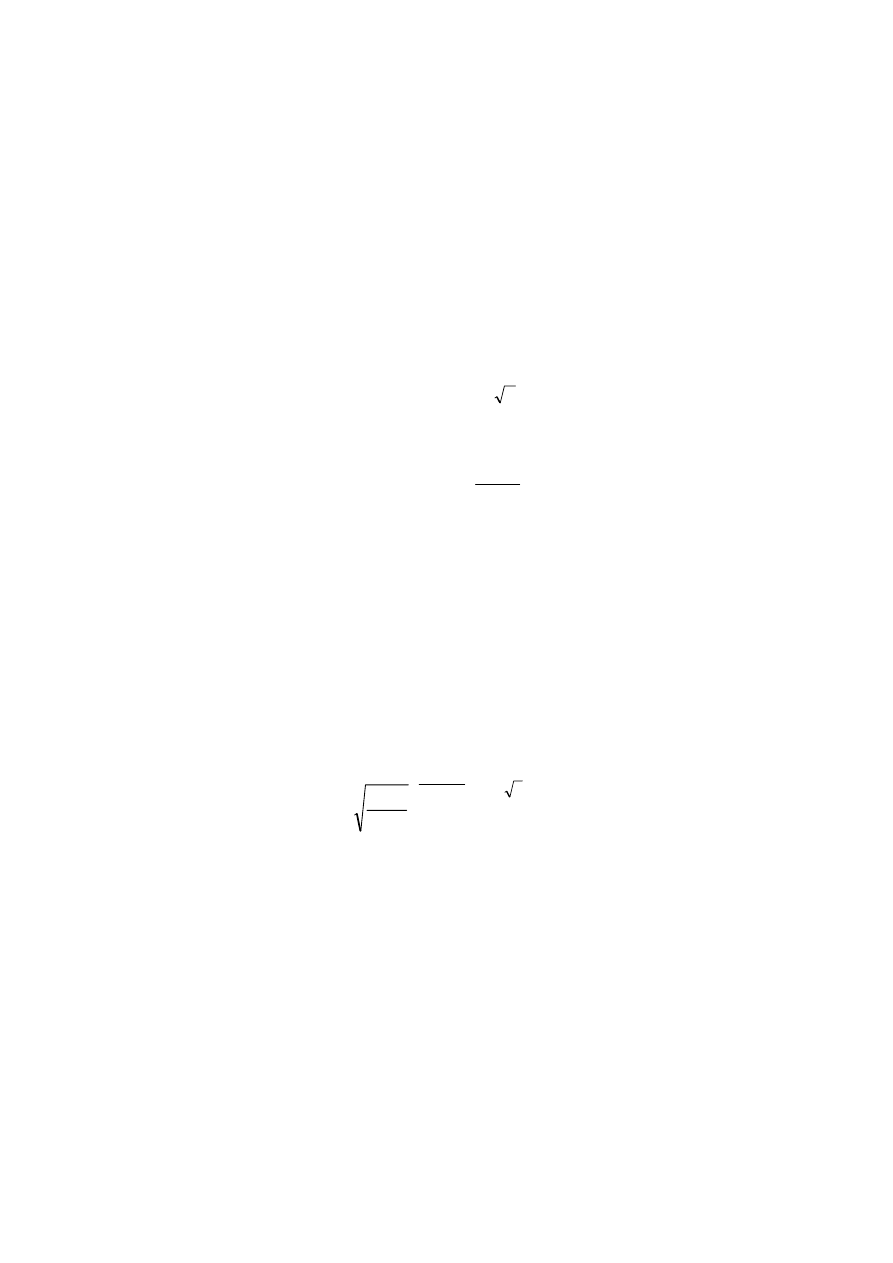
MATEMATYKA

1. W jakim punkcie styczna do krzywej

3

x

y

=

przecina oś

x

or

pod kątem

30

o

?

2. Rozwiązać równanie tg2x = 3tgx.

3. Dla jakiego parametru k nierówność

5

,

1

4

x

kx

2

<

+

jest prawdziwa dla

każdego x?

4. Wyznacz funkcję h(x), której pochodna h’(x) = 2x – 5 i h(2) = 4.

5. Wyznaczyć punkt symetryczny do środka okręgu

(x – 1)

2

+ (y +2)

2

= 4 względem prostej 2x – y +1 = 0.

6. Rozwiązać nierówność

> 0,3

x

2

...

3

2

2

2

1

2

0,3

⋅

+

+

⋅

+

⋅

+

⋅

72

7. Dla jakich parametrów a, b wielomian W(x) = x

3

– ax

2

– (b – 2)x +

+ a + 1 jest podzielny przez (x-1), zaś reszta z dzielenia przez (x + 1) jest
równa 2003.

8. Oblicz wartość

125

3

9

log

3

5

5log

1

7

9

27

1

+















⋅

9. Student zna odpowiedź na dziesięć z piętnastu pytań. Jakie jest

prawdopodobieństwo, że odpowie na co najmniej jedno z czterech
wylosowanych pytań?

10. W kulę o promieniu R wpisano stożek obrotowy o kącie rozwarcia

α.

Oblicz objętość stożka

.

1.

Rozwiązać nierówność 2

-sin3x

+ 4

-sin3x

+ 8

-sin3x

+ ...

≤ 1.

2. A = {(x,y): log

0,5

(x – y)

≥ 1 ∧ x∈R

+

∧ y∈R}

B = {(x,y):

5

,

0

−

x

< 1 – y}.

Wyznaczyć graficznie A

∩ B.

3. Rozwiązać równanie log

sinx

cosx + log

cox

sinx = 2.

4. Punkty A(0,0), B(0,2), C(2,2) są kolejnymi wierzchołkami czworokąta

ABCD. Wyznacz współrzędne punktu D wiedząc, że leży on na prostej
x = 2y oraz, że na czworokącie ABCD można opisać okrąg.

5. Krawędź podstawy graniastosłupa trójkątnego prawidłowego ma długość

a, kąt nachylenia przekątnej ściany bocznej do innej ściany bocznej ma
miarę

α. Oblicz objętość tego graniastosłupa.

6. Pod jakim kątem przecinają się styczne do wykresu funkcji

y =

2

2

3

3x

1

x

+

+

poprowadzone w punktach, dla których y = 1?

7. Z pudełka, w którym są 4 białe i n czarnych kul, losujemy bez zwracania

dwie kule.

Dla jakiej wartości n prawdopodobieństwo wylosowania dwóch kul
białych jest większe od 0,5?

8. Wyznacz funkcję h(x), której pochodna

h’(x) = 3x

2

– 10x oraz h(-2) = -8

9. Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego są kolejnymi

wyrazami ciągu geometrycznego. Podać wzór tego ciągu arytmetycznego
wiedząc, że jego piąty wyraz jest równy 9.

10. Obliczyć długości boków trójkąta prostokątnego, w którym długość

wysokości poprowadzonej z wierzchołka kąta prostego ma 12 cm,
a obwód trójkąta 60 cm.

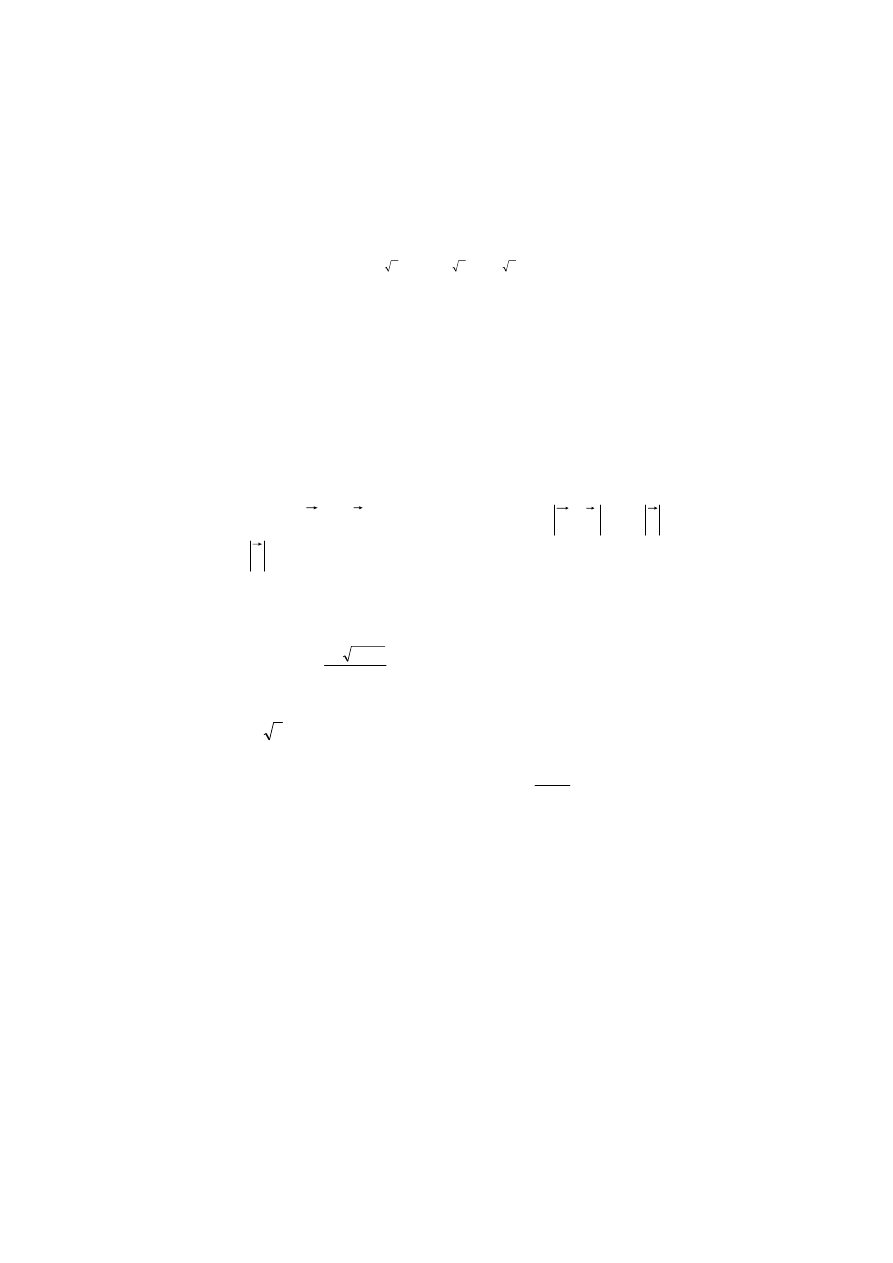
1. Rozwiązać równanie

x

x

x

5

5

5

5

1

2

+

<

+

+

2. Wyznacz funkcję h(x), której pochodna h’(x) = 6x

2

– 2x oraz

h(-1) = 2.

3. Wyznacz największą i najmniejszą wartość funkcji y =

2

dla x

∈<

2

3

3

x

x

−

1,3 >.

4.

Rozwiązać układ równań







−

=

+

+

−

=

+

+

log5

2

y)

log(x

y)

log(x

50

10

y)

log(x

1

5. Wektory

a

i

b

tworzą kąt 60

o

. Obliczyć

b

a

+

jeśli

a

=4

i

b

=10.

6. Oblicz długość promienia kuli wpisanej w czworościan foremny o

krawędzi 1 cm.

7. Obliczyć

x

x

x

sin

1

2

1

lim

0

+

−

→

.

8. Wyznacz pole obszaru ograniczonego liniami x

2

+ y

2

= 4, y = 0,

y =

3

x.

9. Rozwiązać równanie cosx + cos

3

x + cos

5

x + ... =

x

sin

1

.

10. Reszta z dzielenia wielomianu stopnia trzeciego W(x) przez wielomian (x

– 1)(x – 3) jest równa 10x – 14. Liczba –1 jest dwukrotnym
pierwiastkiem wielomianu W(x). Znajdź ten wie

lomian.