EGZAMIN Z MATEMATYKI

dla kandydatów starających się o przyjęcie na I rok studiów 2003/2004
na kierunki techniczne w Politechnice Świętokrzyskiej

Każde zadanie oceniane jest w skali od 0 do 20 punktów.

Czas trwania egzaminu 120 min.

Zadanie 1

Dla jakich wartości parametru m iloczyn dwóch różnych pierwiastków równania (m - 1) x² - 2mx + m - 2 = 0 jest mniejszy od 2?

Zadanie 2

Rozwiązać nierówność

Zadanie 3

W prostokątnym układzie współrzędnych podać interpretację geometryczną zbiorów A, B

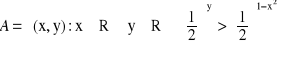
Na osobnych rysunkach zaznaczyć A\B, A
B.

Zadanie 4

W podstawę stożka wpisano kwadrat o boku a. Kąt przy wierzchołku osiowego przekroju stożka jest równy β. Znaleźć objętość stożka i objętość kuli opisanej na tym stożku.

Zadanie 5

Współrzędne wektora
tworzą ciąg geometryczny, którego suma wynosi 26 a iloraz q = 3. Wyznaczyć wektor
i jego długość. Czy wektory
są prostopadłe jeśli A = (2, -3, 4), B + (-1, 1, 2)?

EGZAMIN Z MATEMATYKI

dla kandydatów starających się o przyjęcie na I rok studiów dziennych 2003/2004
na Wydział Elektrotechniki, Automatyki i Informatyki
w Politechnice Świętokrzyskiej

Czas trwania egzaminu 120 min.

Każde zadanie oceniane jest w skali od 0 do 10 punktów.

Zestaw E

Zadanie 1

Dane jest wyrażenie: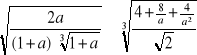
.

1. Znaleźć dla jakich wartości parametru „a” powyższe wyrażenie posiada sens liczbowy.

2. Przekształcić powyższe wyrażenie do prostszej postaci i wyznaczyć jego wartość dla a = 2.

Zadanie 2

Dane są dwa zbiory:

A =
i
.

1. Naszkicować wykresy funkcji
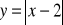
   i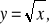
   występujących w definicji zbioru A i osobno wykres funkcji y = 2x - x², występującej w definicji zbioru B.

2. Wyznaczyć zbiór A i zbiór B oraz iloczyn zbiorów A i B.

Zadanie 3

Dany jest ogólny wyraz ciągu

1. Sprawdzić, czy ten ciąg jest rosnący czy malejący.

2. Dla jakich n wyrazy powyższego ciągu spełniają nierówność
   

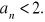
Zadanie 4

Dana jest funkcja

1. Znaleźć dziedzinę tej funkcji i naszkicować jej wykres.

2. Dla jakich x spełniona jest nierówność:
   

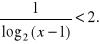
Zadanie 5

Dana jest funkcja

1. Powyższą funkcję f(x) zapisać w postaci: f(x) =
   

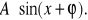
2. Dla jakich x zachodzi:
   

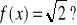
Zadanie 6

Dany jest ciąg:

1. Dla jakich x jest to ciąg geometryczny zbieżny?

2. Dla jakiej wartości x suma wyrazów tego ciągu wynosi 4?

Zadanie 7

Dane są trzy kolejne wierzchołki równoległoboku: A(1,1), B(5,2), C(4,5).

1. Naszkicować położenie wierzchołków w układzie współrzędnych i znaleźć czwarty wierzchołek równoległoboku.

2. Obliczyć długości przekątnych tego równoległoboku i napisać równanie okręgu o środku w punkcie przecięcia się przekątnych i średnicy równej długości większej przekątnej.

Zadanie 8

Dane są równania dwóch prostych:

1. Dla jakiej wartości k oba równania przedstawiają tę samą
   prostą?

2. Znaleźć wartość parametru k, dla którego powyższe równania opisują proste równoległe.

Zadanie 9

W trójkąt równoboczny o boku a wpisano trzy jednakowe okręgi styczne do siebie i boków trójkąta.

1. Wykonać szkic trójkąta i wpisanych do niego okręgów.
   Wyznaczyć promienie tych okręgów.

2. Obliczyć pole trójkąta, którego wierzchołkami są środki
   powyższych okręgów.

Zadanie 10

Dane jest równanie paraboli

1. Narysować tę parabolę i wyznaczyć punkty przecięcia się paraboli z osią OX.

2. Obliczyć długość boku trójkąta równobocznego wpisanego w tę parabolę.

EGZAMIN Z MATEMATYKI

dla kandydatów starających się o przyjęcie na I rok studiów dziennych 2003/2004
na Wydział Elektrotechniki, Automatyki i Informatyki
w Politechnice Świętokrzyskiej

Czas trwania egzaminu 120 min.

Każde zadanie oceniane jest w skali od 0 do 10 punktów.

Zestaw F

Zadanie 1

1. Zapisać wyrażenie
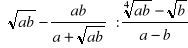
   w prostszej postaci.

2. Znaleźć wartość tego wyrażenia dla a = 16b.

Zadanie 2

1. Daną nierówność doprowadzić do postaci iloczynowej:
   

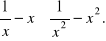
2. Znaleźć rozwiązanie tej nierówności.

Zadanie 3

Dany jest szereg geometryczny: 1 + ctg x + ctg² x + ..., określony
w zbiorze

1. Podać podzbiór zbioru X, w którym ta suma istnieje oraz obliczyć tę sumę.

2. Rozwiązać równanie:
   .

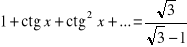
Zadanie 4

1. Dla jakich wartości parametru m proste: l₁: x + y + m = 0,
   l₂: mx + y - 4 = 0 przecinają się. Znaleźć ten punkt przecięcia.

2. Dla jakiej wartości m punkt przecięcia powyższych prostych leży na prostej x - y + 4 = 0?

Zadanie 5

1. W prostokątnym układzie współrzędnych Oxy narysować zbiory A i B:

,
.

2. Na powyższym rysunku zaznaczyć zbiór
   

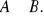
Zadanie 6

1. Zapisać funkcję f(x) = sin x + cos x w postaci:
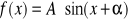
   oraz naszkicować wykres tej funkcji.

2. Na tym samym wykresie naszkicować wykres funkcji g(x) =
   (x - 1)² +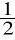
   oraz znaleźć liczbę rozwiązań równania f(x) = g(x).

Zadanie 7

1. Znaleźć postać kanoniczną równania okręgu:

x² - 2x + y² - 4y - 4 = 0

oraz naszkicować ten okrąg w układzie współrzędnych.

2. Wyznaczyć równanie prostej, zawierającej cięciwę tego okręgu wiedząc, że punkt A(2,3) jest środkiem tej cięciwy.

Zadanie 8

Dla jakich wartości parametru a prosta x - y + 2 = 0 jest styczna do wykresu funkcji f(x) = (log₃ a)² - x² + 3x. Podać współrzędne punktu styczności.

Zadanie 9

W trójkąt równoboczny o boku a wpisano kwadrat. Znaleźć
długość boku tego kwadratu.

Zadanie 10

1. Obliczyć granicę g ciągu o wyrazie ogólnym
   

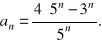
2. Dla jakich
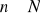
   wyrazy ciągu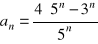
   spełniają nierówność: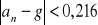
   gdzie g jest granicą tego ciągu.

Egzamin wstępny z matematyki

na kierunek Zarządzanie i Marketing

oraz Zarządzanie i Inżynieria Produkcji

rok akademicki 2003/2004

Zadanie 1

Znaleźć równanie prostej przechodzącej przez punkt A(2,3) i stycznej do paraboli y = x².

Zadanie 2

Trzy liczby, z których pierwsza jest równa 2, tworzą ciąg arytmetyczny. Kwadraty tych liczb (branych w tej samej kolejności) tworzą ciąg geometryczny. Znaleźć te liczby.

Zadanie 3

Kąt ostry równoległoboku ma miarę 60º. Odległości punktu przecięcia przekątnych równoległoboku od jego boków są odpowiednio równe 2 i 3. Oblicz pole równoległoboku i długość jednej z jego przekątnych.

Zadanie 4

Obliczyć objętość ostrosłupa prawidłowego czworokątnego wiedząc, że kąt między przeciwległymi krawędziami bocznymi wynosi 60º, a przekątna podstawy ma długość a.

Zadanie 5

40% żarówek znajdujących się w magazynie pochodzi od producenta A, zaś pozostałe 60% od producenta B. Wśród żarówek pochodzących od producenta A jest 2% wadliwych, a od producenta B jest wadliwych 3%. Jakie prawdopodobieństwo, że wybrana losowo żarówka okaże się wadliwa? Jakie jest prawdopodobieństwo, że wybrana losowo żarówka pochodzi od producenta A, jeśli wiadomo, że jest ona wadliwa?

Czas trwania egzaminu: 120 minut.

Każde zadanie oceniane jest w skali od 0 do 20 punktów.

Egzamin wstępny z matematyki

na kierunek Zarządzanie i Marketing

oraz Zarządzanie i Inżynieria Produkcji

rok akademicki 2003/2004

Zadanie 1

Narysować na płaszczyźnie w układzie współrzędnych zbiór wszystkich punktów P(x,y), których współrzędne spełniają układ nierówności

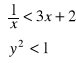
Zadanie 2

Trzy liczby tworzą ciąg geometryczny. Ich suma wynosi 42. Jeżeli do drugiej z nich dodamy 3, a pozostałe pozostawimy bez zmian, to liczby te utworzą ciąg arytmetyczny. Znaleźć te liczby.

Zadanie 3

Dany jest trójkąt równoboczny o boku długości a. Prosta przechodząca przez środek wysokości i nachylona do niej pod kątem 30º odcina od trójkąta trapez. Obliczyć pole i obwód tego trapezu.

Zadanie 4

Długość krawędzi sześcianu wynosi a. Obliczyć długość przekątnej sześcianu. W jakiej odległości od niej znajduje się wierzchołek sześcianu nie leżący na tej przekątnej?

Zadanie 5

Z grupy składającej się z 5 Polaków i 4 Niemców wybrano losowo 3-osobową delegację. Jakie jest prawdopodobieństwo, że wszyscy delegaci pochodzą z tego samego kraju? Jakie jest prawdopodobieństwo, że trzecim delegatem zostanie Niemiec, jeżeli jako pierwszego i drugiego wylosowano Polaka?

Czas trwania egzaminu: 120 minut.

Każde zadanie oceniane jest w skali od 0 do 20 punktów.

9

1

---