1

GGiIŚ

Nazwiska:
1. Monika Siry
2. Kamil Sanicki

ROK

I

GRUPA

XII

ZESPÓŁ

IV

PRACOWNIA
FIZYCZNA

TEMAT:

MOSTEK WHEATSTONE’A

NR ĆWICZENIA

32

Data
wykonania:

15.03.2012

Data
oddania:
22.03.2012

Zwrot do
poprawy:

Data
oddania:

Data
zaliczenia
:

OCENA

Cel doświadczenia:

Wyznaczenie nieznanych oporów pojedynczych oporników, oraz oporów zastępczych

oporników połączonych szeregowo, równolegle i mieszanie, na podstawie zależności

opisujących mostek Wheatstone’a.

Wstęp:

Doświadczenie z Mostkiem Wheatstone’a pozwala na praktyczne sprawdzenie

poprawności trzech praw rządzących obwodami prądu stałego:

Prawo Ohma-

Oporem nazywamy stosunek napięcia do natężenia prądu na końcach przewodnika.

Dla przewodnika jest on wartością stałą. Jednostką oporu jest Ohm [Ω]

� =

�

�

Każdy z materiałów posiada też opór właściwy, który pozwala na obliczenie oporu
dowolnego

przewodnika znając jego długość i pole przekroju.

� = � ∗

Gdzie:

ρ- opór właściwy

l-

długość przewodnika

s- pole przekroju przewodnika

I prawo Kirhoffa-

Dla każdego węzła obwodu (punktu spotkania co najmniej trzech przewodników),
suma

prądów wpływających i wypływających jest równa zeru.

II prawo Kirhoffa-

Suma spadków napięć wzdłuż dowolnego oczka (dowolnej zamkniętej drogi wzdłuż

sieci połączeń obwodu) jest równa sumie sił elektromotorycznych.

Poniższy rysunek przedstawia zastosowany w doświadczeniu Mostek Wheatstone’a,

który pozwala na wyznaczenie wartości oporu dla opornika R

x

, na podstawie znajomości

oporu wzorcowego R

2

i oporów odcinków drutu R

3

i R

4

.

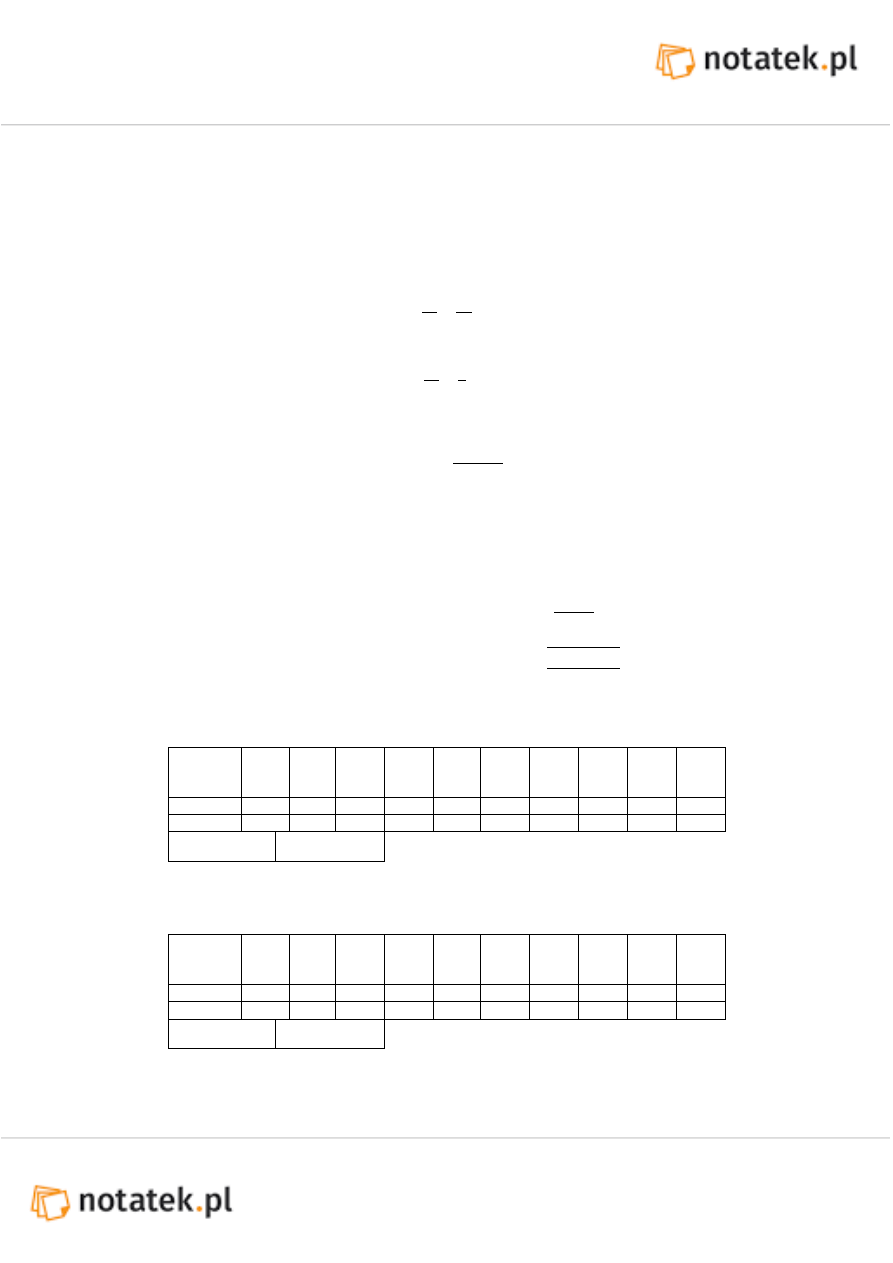
2

Opory oporników R

3

i R

4

, jako że są one fragmentami tego samego drutu, są proporcjonalne

do ich

długości. Metoda pomiaru, polega na tzw. równoważeniu mostka, czyli dobraniu takich

długości (w konsekwencji oporów R

3

i R

4

), aby przy zadanym i znanym oporze wzorcowym

przez galwanometr G nie płynął prąd (aparat wskazywał natężenie równe 0 Amperów).

Wówczas, zależność oporów opisuje równanie:

�
�

2

=

�

3

�

4

Stosunek R

3

do R

4

jest zależny od ich długości, co daje nam równanie:

�

3

�

4

=

Gdzie:

a-

długość opornika R

3

w cm

b- 100cm-a

Pozwala nam to na ostateczne

wyprowadzenie wzoru wykorzystywanego w doświadczeniu:

� = �

2

∗

100

−

Wyniki pomiarów:

Długość drutu l- 1000 mm.

Błąd pomiaru długości- 1 mm

Ilość pomiarów dla każdego opornika i ich kombinacji (n)- 10

Wzór do wyznaczenia kolejnych oporów R

x

-

� = �

2

∗

100

−

Wzór na niepewność pomiarową U(x)-

� =

(

�

− )

2

�=1

∗ −1

Pomiary dla opornika R

x1

Opór

wzorcowy

[Ω]

10

15

20

25

30

35

40

45

50

55

a [mm]

564

458

386

334

296

267

236

215

190

184

R

x1

[Ω]

12,94 12,68 12,57

12,54 12,61 12,75

12,36

12,32

11,73

12,40

R

x1

= 12,49 Ω U(R

x1

)=0,10

Ω

Opór R

x1

jest równy 12,49 Ω z niepewnością 0,10 Ω.

Pomiary dla opornika

R

x2

Opór

wzorcowy

[Ω]

10

15

20

25

30

35

40

45

50

55

a [mm]

679

578

505

449

402

365

336

308

285

266

R

x2

[Ω]

21,15 20,54 20,40

20,37 20,17

20,12 20,24

20,03

19,93

19,93

R

x2

=20,29 Ω U(R

x2

)= 0,12

Ω

3

Opór R

x2

jest równy 20,29 Ω z niepewnością 0,12 Ω.

Pomiary dla opornika R

x3

Opór

wzorcowy

[Ω]

10

15

20

25

30

35

40

45

50

55

a [mm]

759

673

606

550

506

466

432

403

378

356

R

x3

[Ω]

31,49 30,87 30,76

30,56 30,73

30,54 30,42

30,38

30,38

30,40

R

x3

=30,65 Ω U(R

x3

)= 0,11

Ω

Opór R

x3

jest równy 30,65 Ω z niepewnością 0,11 Ω.

Pomiary oporu zastępczego R

sz

dla połączenia szeregowego

oporników R

x1

i R

x2

Teoretyczna wartość oporu zastępczego R

sz obl

, z wzoru na połączenie szeregowe oporników

wynosi:

�

�

=

�

1

+

�

2

= 12.49 + 20.29 = 32,78

Ω

Z niepewnością U(R

sz obl

) wyznaczoną z prawa przenoszenia błędów, z wzoru:

� �

�

= (

� �

1

+

�

2

� �

1

∗ � �

1

)

2

+ (

� �

1

+

�

2

� �

2

∗ � �

2

)

2

Co daje U(R

sz obl

)= 0,16

Ω

Opór

wzorcowy

[Ω]

30

35

40

45

50

55

60

65

70

75

a [mm]

521

482

448

419

393

371

352

334

318

302

R

sz

[Ω]

32,63 32,57 32,46

32,45 32,37 32,44

32,59

32,60

32,64

32,45

R

sz

=32,52 Ω U(R

sz

)= 0,03

Ω R

sz obl

=32,78 Ω U(R

sz obl

)= 0,16

Ω

http://notatek.pl/mostek-wheatstone-a-sprawozdanie?notatka