1
Egzamin maturalny z matematyki
poziom rozszerzony
Czas pracy: 180 minut
Zadanie 1. (4 pkt)
Rozwiąż nierówność
2
3
9
23
x
x
.
Zadanie 2. (6 pkt)
Wyznacz wszystkie wartości parametru
m
, dla których równanie
2
1 0
x
mx
ma dwa
różne pierwiastki rzeczywiste
1
2
,
x
x
takie, że
3
3
2
1
2
4
x
x
m
m
.
Zadanie 3. (4 pkt)
Wyznacz wszystkie wartości parametru
m
, dla których wykres wielomianu
5
4
3
2
2
2
2
2
4
2
W x
x
x
mx
mx
m x
m
ma dokładnie dwa punkty wspólne z osią
Ox
.
Zadanie 4. (4 pkt)
Wykaż, że dla każdych dodatnich liczb rzeczywistych
a
,
b
,
c
,
d
prawdziwa jest
nierówność
a
c b
d
ab
cd
.
Zadanie 5. (5 pkt)
Rozwiąż równanie
2
2
cos 2
3 sin 2
cos
7 sin
x
x
x
x
.
Zadanie 6. (4 pkt)
Trzy liczby, których suma jest równa 26, są jednocześnie trzema kolejnymi wyrazami
ciągu geometrycznego oraz drugim, trzecim i szóstym wyrazem rosnącego ciągu
arytmetycznego. Wyznacz te liczby.
Zadanie 7. (5 pkt)
Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w zapisie których
występuje dokładnie raz cyfra 1, oraz dokładnie dwa razy cyfra 2.
Zadanie 8. (4 pkt)
W trójkącie prostokątnym
ABC
odcinek
CD
jest wysokością opuszczoną
na przeciwprostokątną
AB
. Obwód trójkąta
ADC
jest równy 40, a obwód trójkąta
BDC
jest równy 24. Oblicz obwód trójkąta
ABC
.

2
Zadanie 9. (4 pkt)
Długości przekątnych rombu o kącie ostrym
45
są równe
e
oraz
f
e
f
. Wykaż,
że
2 1
e
f
.
Zadanie 10. (4 pkt)
Punkty
9,12
A
oraz
5,10
B
leżą na okręgu, którego środek leży na prostej
o równaniu
3
0
x
y
. Wyznacz równanie tego okręgu.
Zadanie 11. (6 pkt)
Dany jest zbiór trójkątów równoramiennych o obwodzie 24. Oblicz długości boków
trójkąta należącego do tego zbioru, który przy obrocie dookoła prostej zawierającej jego
podstawę o kąt
360
wyznacza bryłę o największej objętości.

3
Odpowiedzi
Zadanie 1.
Wyróżniamy na osi liczbowej parami rozłączne przedziały, których sumą jest zbiór
wszystkich liczb rzeczywistych:
; 2
,
2;3
,
3;
.
Zapisujemy nierówność w każdym z przedziałów i rozwiązujemy układy nierówności:
1.
2
2 3
9
23
x
x
x
2
4
16
x
x
4
x
lub
2.
2
3
2 3
9
23
x
x
x
2
3
2
12
x
x
; brak rozwiązań
lub
3.
3
2 3
9
23
x
x
x
3
4
30
x
x
7, 5
x
Odpowiedź:
; 4
7, 5 ;
x
.
Zadanie 2.
Zapisujemy warunki zadania
3
3
2
1
2
1.
0
2.
4
x
x
m
m
i kolejno je rozwiązujemy:
1.
2
4
m
,
0
; 2
2;
m
2.
3
3
2
2
2
2
1
2
1
2
1
1 2
2
1
2
1
1 2
2
1 2
2
1
2
1
2
1 2
2
3
3
x
x
x
x
x
x x
x
x
x
x
x x
x
x x
x
x
x
x
x x
Korzystając ze wzorów Viète`a otrzymujemy:
3
3
2
3
1
2
3
3
x
x
m m
m
m
Zatem nierówność jest postaci:
3
2
3
4
m
m
m
m
3
2
4
4
0
m
m
m
2
1
4
1
0
m
m
m
2
1
4
0
m
m
1
2
2
0
m
m
m
Rozwiązaniem tej nierówności jest
2;1
2;
m
.

4
Rozwiązaniem zadania jest część wspólna rozwiązań warunku 1. oraz 2. czyli
2;
m
.
Odpowiedź:
2;
m
.
Zadanie 3.
Zapisujemy wielomian w postaci iloczynowej
5
4
3
2
2
2
4
2
2
2
4
2
2
2
2
2
4
2
2
2
2
2
2
2
2
W x
x
x
mx
mx
m x
m
x
x
mx
x
m
x
x
x
mx
m
x
x
m
Jednym z punktów wspólnych wielomianu
W
z osią
Ox
jest
2, 0
.
Jeżeli
0
m
, to innych punktów wspólnych nie ma.
Jeśli
0
m
, to punkt
0, 0
też jest punktem wspólnym.
Jeśli
0
m
, to punktami wspólnymi są też
, 0
m
i
, 0
m
. Jednym z nich ma być
2, 0
. Stąd wynika, że aby były dwa punkty wspólne, to
2
m
, czyli
4
m
.
Odpowiedź:
1
0
m
,
2
4
m
.
Zadanie 4.
Obie strony nierówności są dodatnie, po podniesieniu obu stron do kwadratu
otrzymujemy nierówności równoważne:
2
a
c b
d
ab cd
abcd
Po redukcji wyrazów podobnych otrzymujemy:
2
ad
bc
abcd
Podnosząc jeszcze raz obie strony do kwadratu otrzymujemy:
2
2
2
4
ad
bc
abcd
abcd
czyli
2
0
ad
bc
Ostatnia nierówność jest prawdziwa dla dowolnych liczb rzeczywistych
a
,
b
,
c
,
d
.

5
Zadanie 5.
Korzystając ze wzorów na
cos 2
oraz
sin 2
zapisujemy równanie w postaci:
2
2
2
2
cos
sin
3 2sin cos
cos
7 sin
x
x
x
x
x
x
czyli
2
6 sin
2 3 sin cos
0
x
x
x
.
cos
0
x
nie jest rozwiązaniem tego równania, możemy więc obie strony tego równania
podzielić przez
2
6 cos x
.
Otrzymujemy:
2
3
tg
tg
0
3
x
x
czyli
3
tg
tg
0
3
x
x
.
Stąd
tg
0
x
lub
3
tg
3
x
.
Odpowiedź:
x
k
lub
5
6
x
k
, gdzie k jest liczbą całkowitą.
Zadanie 6.
Oznaczmy przez
a
pierwszą z trzech liczb (najmniejszą) oraz przez
r
różnicę ciągu
arytmetycznego;
0
r
.
Liczby możemy zapisać w postaci:
,
,
4
a
a
r
a
r
(
a
oznacza drugi wyraz ciągu
arytmetycznego).
Znając sumę tych liczb oraz własność ciągu geometrycznego zapisujemy układ równań:
2
4
26
4
a
a
r
a
r
a
r
a a
r
Po przekształceniach otrzymujemy układ równań:
3
5
26
2
0
a
r
r r
a
Z drugiego równania wynika, że
2
r
a
lub
0
r
. Rozwiązanie
0
r
jest sprzeczne
z założeniem. Stąd
2
r
a
, czyli
2
a
,
4
r
.
Odpowiedź: Liczby opisane w treści zadania to 2, 6, 18.
6
Zadanie 7.
Stwierdzamy, że są trzy parami rozłączne przypadki. Pierwszą cyfrą tej liczby może być:
1. cyfra
1
,
2. cyfra
2
,
3. cyfra należąca do zbioru
3, 4, 5, 6, 7, 8, 9
.
Obliczamy, ile liczb jest w każdym przypadku.
ad. 1.
3
5
1
8
5120
2
ad.2.
3
5
4
1
8
10240
1
1
ad.3.
2
5
4
7
8
13440
1
2
Odpowiedź: Łącznie jest
5120 10240 13440
28800
takich liczb.
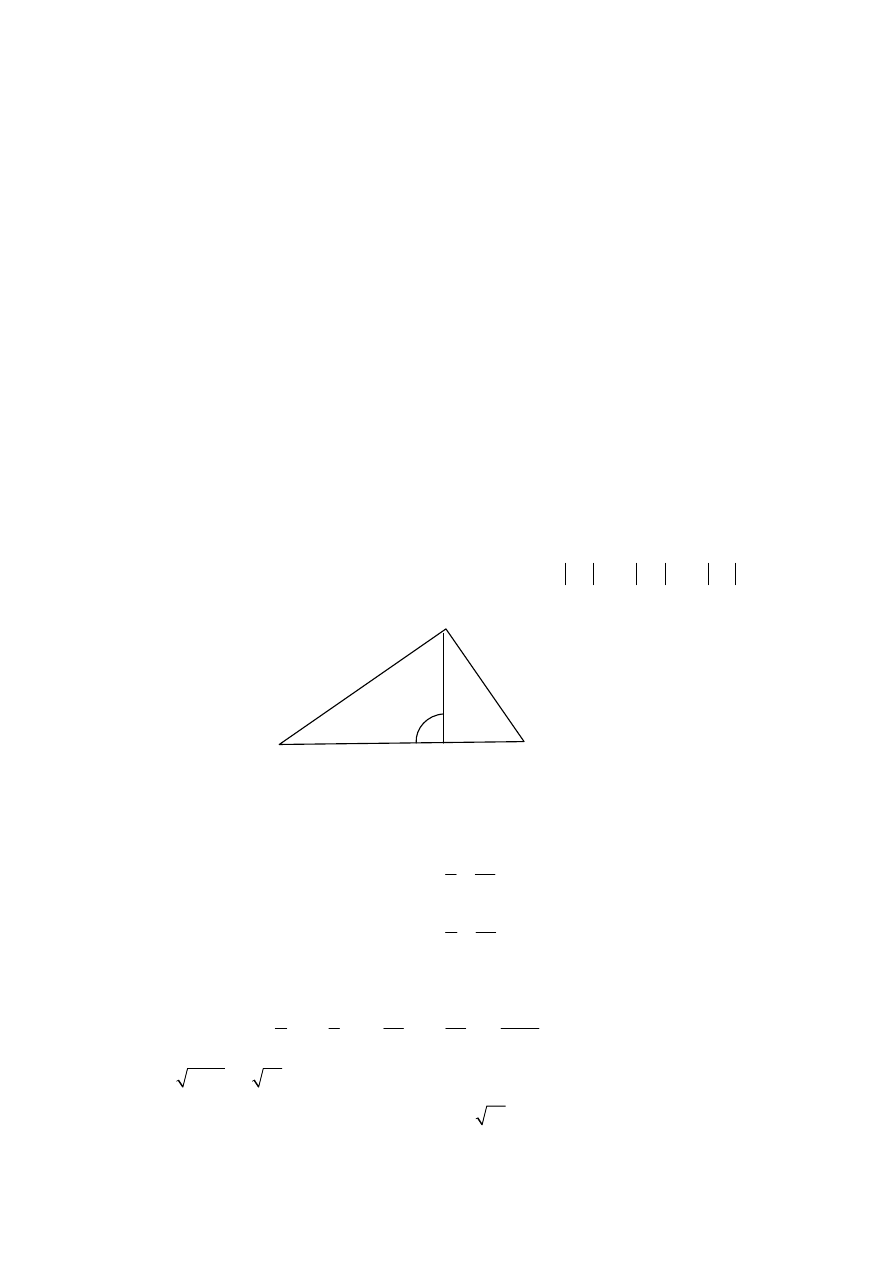
Zadanie 8.
Rysujemy rysunek pomocniczy i wprowadzamy oznaczenia:
,
,
BC
a
AC
b
AB
c
.
Oznaczmy przez
p
obwód trójkąta
ABC
.
Trójkąty
ADC
oraz
ABC
są podobne, stąd
40
b
c
p
.
Trójkąty
BDC
oraz
ABC
są podobne, stąd
24
a
c
p
.
Zapisujemy twierdzenie Pitagorasa dla trójkąta
ABC
i przekształcamy tę równość:
2
2
2
c
a
b
2
2
2
2
2
24
40
2176
1
a
b
c
c
p
p
p
stąd
2176
8 34
p
.
Odpowiedź: Obwód trójkąta
ABC
jest równy
8 34
.
A
B
C
D
a
b
c
.
7
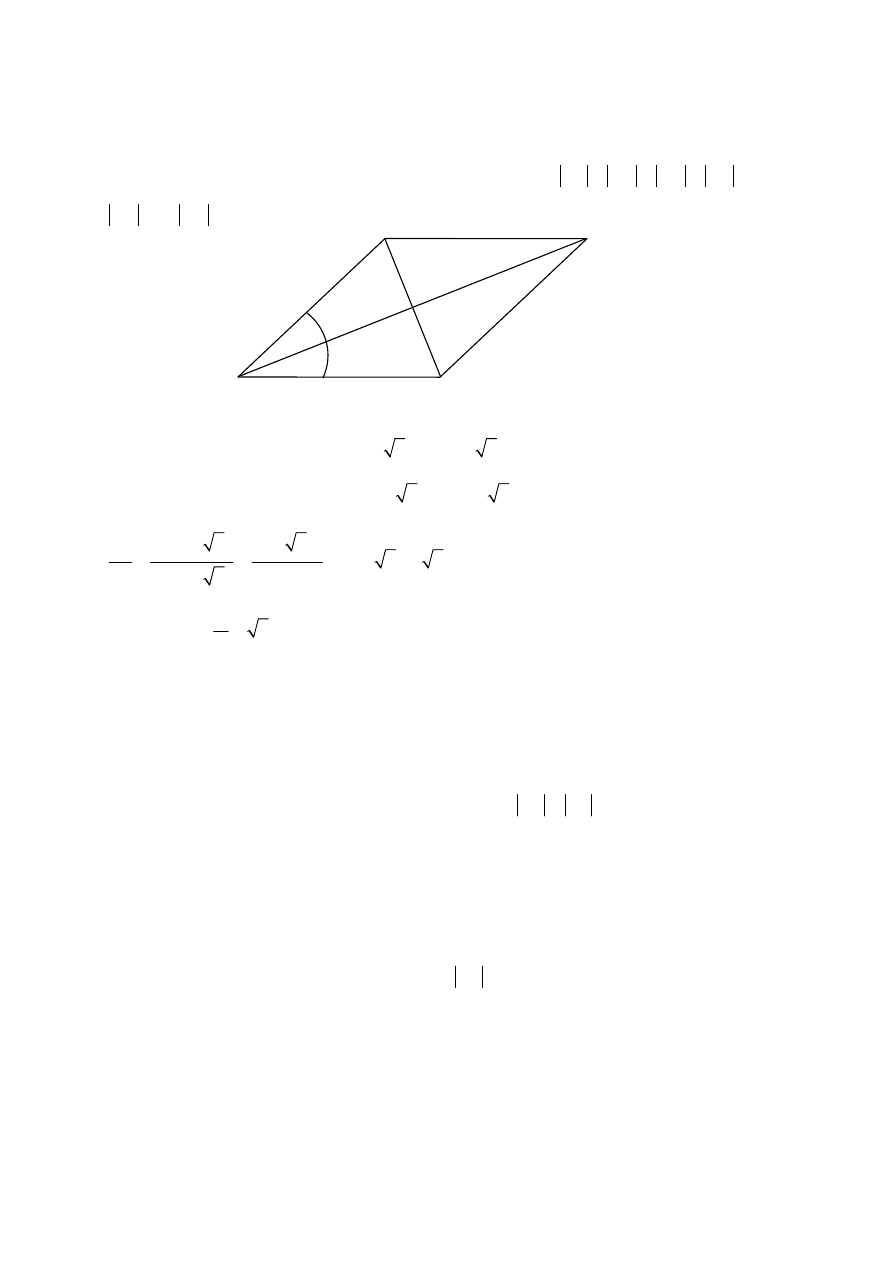
Zadanie 9.
Rysujemy rysunek pomocniczy i wprowadzamy oznaczenia:
AB
BC
CD
DA
a
,
,
BD
e
AC
f
.
Stosując twierdzenie kosinusów do trójkątów
BAD
oraz
ABC
otrzymujemy
2
2
2
2
2
2
2
cos 45
2
2
2
2
e
a
a
a a
a
a
a
2
2
2
2
2
2
2
cos135
2
2
2
2
f
a
a
a a
a
a
a
2
2
2
2
2
2
2
2
2
2
3 2 2
2 1
2
2
2
a
e
f
a
.
Odpowiedź:
2 1
e
f
.
Zadanie 10.
Środek
S
okręgu, to punkt wspólny podanej prostej oraz symetralnej odcinka
AB
.
Symetralna odcinka
AB
ma równanie
2
25
0
x
y
. (Punkt
,
P
x y
leży
na symetralnej odcinka
AB
wtedy i tylko wtedy, gdy
AP
BP
).
Zapisujemy i rozwiązujemy układ równań
3
0
2
25
0
x
y
x
y
Otrzymujemy
28, 31
S
Obliczamy kwadrat promienia
r
okręgu:
2
2
2210
r
AS
.
Odpowiedź: Równanie okręgu jest postaci:
2
2
28
31
2210
x
y
.
A
B
C
D
a
a
a
45

8
Zadanie 11.
Wprowadzamy oznaczenia jak na rysunku.
2
2
24
x
y
, czyli
12
x
y
.
Bryła powstała z obrotu trójkąta dookoła prostej
AB
, to suma dwóch przystających
stożków o promieniu
r
DC
i wysokości
h
x
.
2
1
2
3
V
r
x
2
2
2
12 12 2
r
y
x
y
x
y
x
x
Zapisujemy wzór funkcji
V x
opisującej objętość bryły
V
w zależności od
x
,
0; 6
x
:
1
2
12 12 2
16
6
3
V x
x
x
x
x
Funkcja
V
przyjmuje największą wartość dla
3
x
.
Odpowiedź: Wymiary trójkąta to podstawa o długości 6 i ramiona długości 9.
A
B
C
D
x x
y
y
.
Wyszukiwarka
Podobne podstrony:
matematyka egazmin próbny podstawowy 1
matematyka egazmin CKE rozszerzony
polski egzamin próbny rozszerzony 2
polski egzamin próbny rozszerzony 1
matematyka egazmin CKE podstawowy
polski egzamin próbny rozszerzony 2
polski egzamin próbny rozszerzony 1
więcej podobnych podstron