Egzamin maturalny z matematyki 2011

poziom rozszerzony

Czas pracy: 180 minut

Zadanie 1. (4 pkt)
Uzasadnij, że dla każdej liczby całkowitej

k

liczba

2

4

6

2

k

k

k





jest podzielna przez 36.

Liczbę

2

4

6

2

k

k

k





możemy zapisać w postaci iloczynowej:



 



2

2

2

1

1

k

k

k





Liczbę

2

4

6

2

k

k

k





możemy zapisać w postaci iloczynowej:



 



2

1

1

k

k k













2 p.

Liczba



 



1

1

k

k k





, jako iloczyn trzech kolejnych liczb całkowitych

jest podzielna przez 6, gdyż w tym iloczynie co najmniej jedna liczba
jest parzysta i dokładnie jedna liczba podzielna przez 3. Kwadrat

iloczynu tych liczb jest podzielny przez 36.

Liczba



 



2

2

2

1

1

k

k

k





jako iloczyn trzech kolejnych liczb całkowitych,

gdzie środkowa liczba tego iloczynu jest kwadratem liczby całkowitej,

jest podzielna przez 9 i przez 4, czyli jest podzielna przez 36.

2 p.

Zadanie 2. (4 pkt)

Uzasadnij, że jeżeli

b

a



,



a

c

,



b

c

i

c

b

a

2





, to

2









c

b

b

c

a

a

.

Mnożymy obie strony równości

2









c

b

b

c

a

a

przez







a c b c





i po wykonaniu działań i redukcji wyrazów podobnych otrzymujemy

2

2

0

c

ac bc







Z równania

2

0

c

a b

  

wyznaczamy

2

b

c

a





i wstawiamy

do wyrażenia

a

b

a c

b c







. Po sprowadzeniu do wspólnego mianownika

i przekształceniach otrzymujmy wyrażenie







2

2

2

2

c

a

c

a

a

c







.

2 p.

Uwzględniając założenie, że

2

0

c

a b

  

, równanie

2

2

0

c

ac bc







jest prawdziwe, więc teza też jest prawdziwa.

Korzystając ze wzorów skróconego mnożenia i faktu, że z założenia



a

c

uproszczamy wyrażenie







2

2

2

2

c

a

c

a

a

c







i otrzymujemy 2, co

dowodzi tezę.

2 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

2

Zadanie 3. (6 pkt)

Wyznacz wszystkie wartości parametru

m

, dla których równanie

0

2

6

4

2

3

2













m

m

m

mx

x

ma dwa różne pierwiastki rzeczywiste

1

2

,

x

x

takie, że

).

1

(

8

)

(

2

2

1







m

x

x

Zapisujemy warunki, jakie muszą być spełnione, aby równanie

0

2

6

4

2

3

2













m

m

m

mx

x

posiadało dwa różne pierwiastki rzeczywiste

1

2

,

x

x

takie, że

2

1

2

(

)

8(

1)

x

x

m







:

























1

8

0

2

2

1

m

x

x

Rozwiązujemy nierówność

0

 

, czyli po przekształceniach:

3

2

4

4

0

m

m

m





  

. Jej rozwiązaniem jest



 



1,1

4,

m

 





.

3

2

2

2

0

m

m

m



  

. Jej rozwiązaniem jest



 



1,1

2,

m

 





.

3

2

2

2

0

m

m

m



  

. Jej rozwiązaniem jest



  

, 1

1, 2

m

   

.

3

2

4

4

0

m

m

m



  

. Jej rozwiązaniem jest



  

, 1

1, 4

m

   

.

1 p.

Rozwiązujemy nierówność

2

1

2

(

)

8(

1)

x

x

m







, korzystając ze wzorów Viète’a.

Przekształcamy wyrażenie po lewej stronie nierówności i otrzymujemy, że:





2

1

2

1 2

4

8

8

x

x

x x

m









.





2

1

2

1 2

2

8

8

x

x

x x

m









.

1 p.

Ponieważ

1

2

4

x

x

m





oraz

3

2

1

2

6

2

x x

m

m

m

  



 

, więc po wykonaniu podstawień

i przekształceniach otrzymujemy nierówność postaci:

3

2

4

16

4

16

0

m

m

m









3

2

2

4

6

12

0

m

m

m









3

2

4

40

12

0

m

m

m







3

2

4

8

12

0

m

m

m







2 p.

której rozwiązaniem jest:



  

, 1

0, 3

m

   

4

m





 



2,

3

3,

m

  







 



, 5 2 7

0, 5 2 7

m

   



 

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

3

Wyznaczamy część wspólną zbiorów rozwiązań nierówności:

0

 

i

2

1

2

(

)

8(

1)

x

x

m







, czyli





 

2,

3

1, 4

m

  











5

7,1

2,

m

  





   

0,1

2, 3

m





4

m



1 p.

Zadanie 4. (4 pkt)
Rozwiąż równanie

x

x

x

x

cos

1

cos

sin

2

sin

2

2

2







w przedziale

0, 2



.

Zapisujemy równanie za pomocą jednej funkcji trygonometrycznej
i przekształcamy do postaci

3

2

2 cos

2 cos

cos

1 0

x

x

x





 

a następnie

zapisujemy to równanie w postaci iloczynowej:









2

2 cos

1 cos

1

0

x

x



 

Wyłączamy po lewej stronie równania wspólny czynnik przed nawias
i zapisujemy równanie w postaci iloczynowej. Otrzymujemy:









0

cos

1

1

sin

2

2







x

x

Wyłączamy po lewej stronie równania wspólny czynnik przed nawias

i zapisujemy równanie w postaci iloczynowej. Otrzymujemy:









2

2sin

1 1 cos

0

x

x







1 p.

Zapisujemy otrzymane równanie w postaci alternatywy równań:

2

2

sin





x

lub

2

2

sin



x

lub

1

cos



x

1

sin

2

x

 

lub

1

sin

2

x



lub

1

cos



x

1

cos

2

x

 

lub

1

cos

2

x



lub

cos

1

x

 

1 p.

Zatem rozwiązaniami równania

2

2

2 sin

2sin

cos

1 cos

x

x

x

x



 

w przedziale

0, 2



są:

3

x





,

2

3

x





,

x





,

4

3

x





,

5

3

x





0

x



,



4

1



x

,



4

3



x

,



4

5



x

,



4

7



x

,

2

x





0

x



,

1

6

x





,

5

6

x





,

x





,

7

6

x





,

11

6

x





2 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

4

Zadanie 5. (4 pkt)
O ciągu

 

n

x

dla

1

n



wiadomo, że:

a) ciąg

 

n

a

określony wzorem

3

n

x

n

a



dla

1

n



jest geometryczny o ilorazie

27

q



.

b)

1

2

10

...

145

x

x

x

  



.

Oblicz

1

x

.

Z własności ciągu geometrycznego mamy równość:

1

3

27

n

n

x

x

q







.

1

3

27

n

n

x

x

q









.

10

1

2

145

3

3

... 3

3

x

x

x



 



1 p.

Zatem

1

3

n

n

x

x







dla

1

n



.

1

3

n

n

x

x





dla

1

n



.

1

1

1

1

1

10

10

10

1 2 ... 10

3 55

145

3

3

27... 3

27

3

27

3

3

3

x

x

x

x

x

  





















1 p.

Otrzymujemy równanie:

1

10

155 145

x





Ciąg

 

n

x

jest ciągiem geometrycznym. Z własności ciągu

geometrycznego zapisujemy:





1

2

10

1

1 3

3

... 3

145

x

   



Ciąg

 

n

x

jest ciągiem arytmetycznym. Z własności ciągu

arytmetycznego zapisujemy układ równań:









1

1

1

...

9

145

3

x

x

r

x

r

r



  













1 p.

1

10

290

3

1

x





1

1

x



1

1

x

 

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

5

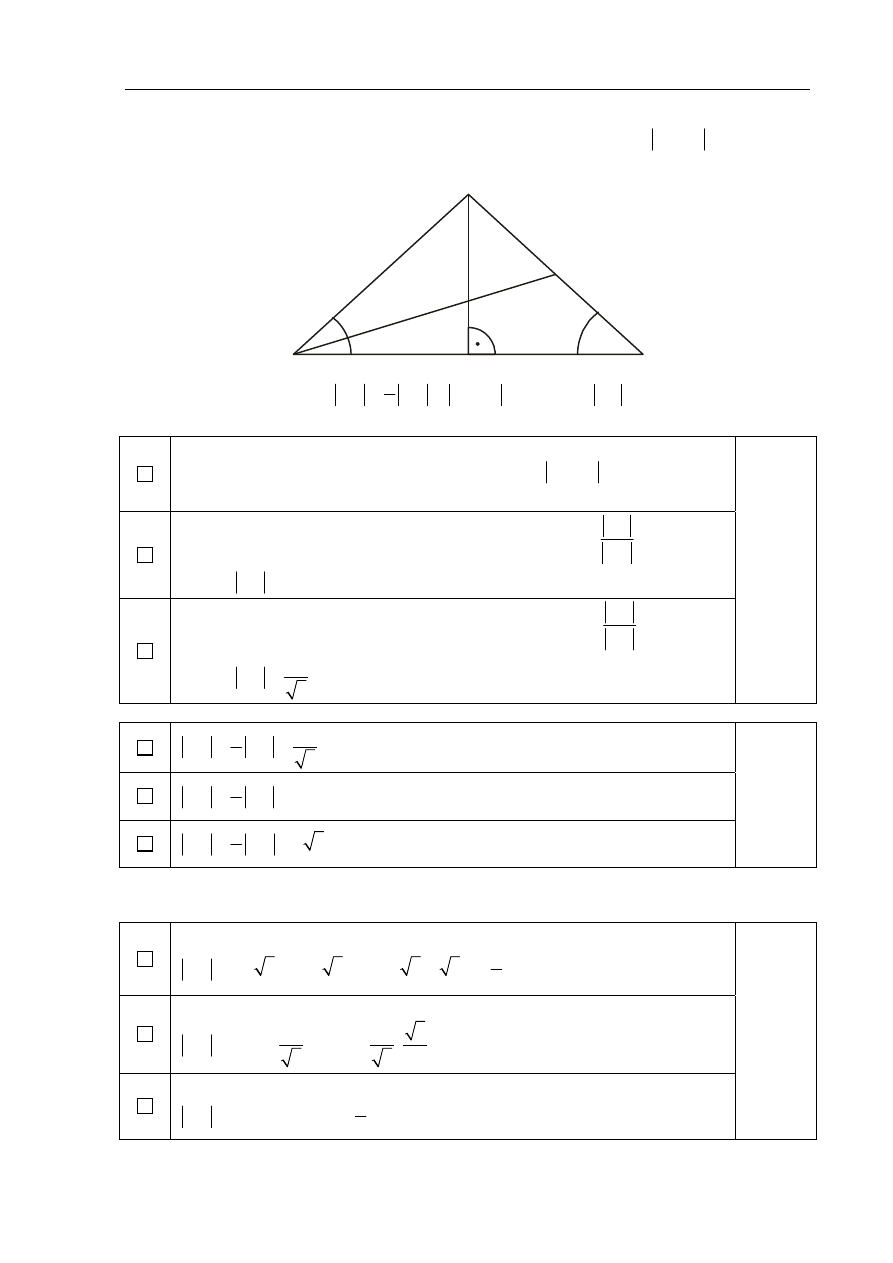
Zadanie 6. (4 pkt)
Podstawa

AB

trójkąta równoramiennego

ABC

ma długość 8 oraz

30

BAC

 



. Oblicz

długość środkowej

AD

tego trójkąta.

30



A

B

E

C

D

Z treści zadania mamy, że

1

2

BD

BC



i

30

ABC

 



oraz

4

BE



.

Oznaczając przez

x

– długość ramienia trójkąta

ABC

, zapisujemy

twierdzenie cosinusów dla trójkąta

ABC

, gdzie

120

ACB







:

2

2

2

2

8

2

cos120

x

x

x









Z trójkąta prostokątnego

BEC

otrzymujemy:

sin 30

BE

BC

 

.

Zatem

8

BC



Z trójkąta prostokątnego

BEC

otrzymujemy:

cos 30

BE

BC

 

.

Zatem

8

3

BC



1 p.

1

4

2

3

BD

BC





1

4

2

BD

BC





1

4 3

2

CD

AC





1 p.

Stosując twierdzenie cosinusów dla trójkąta

ADC

otrzymujemy:

   

2

2

2

1

8 3

4 3

2 8 3 4 3

2

AD









 



 









ABD

otrzymujemy:

2

2

2

4

4

3

8

2 8

2

3

3

AD









  











ABD

otrzymujemy:

2

2

2

1

8

4

2 8 4

2

AD





   

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

6

4 21

3

AD



2 42

AD



4 3

AD



1 p.

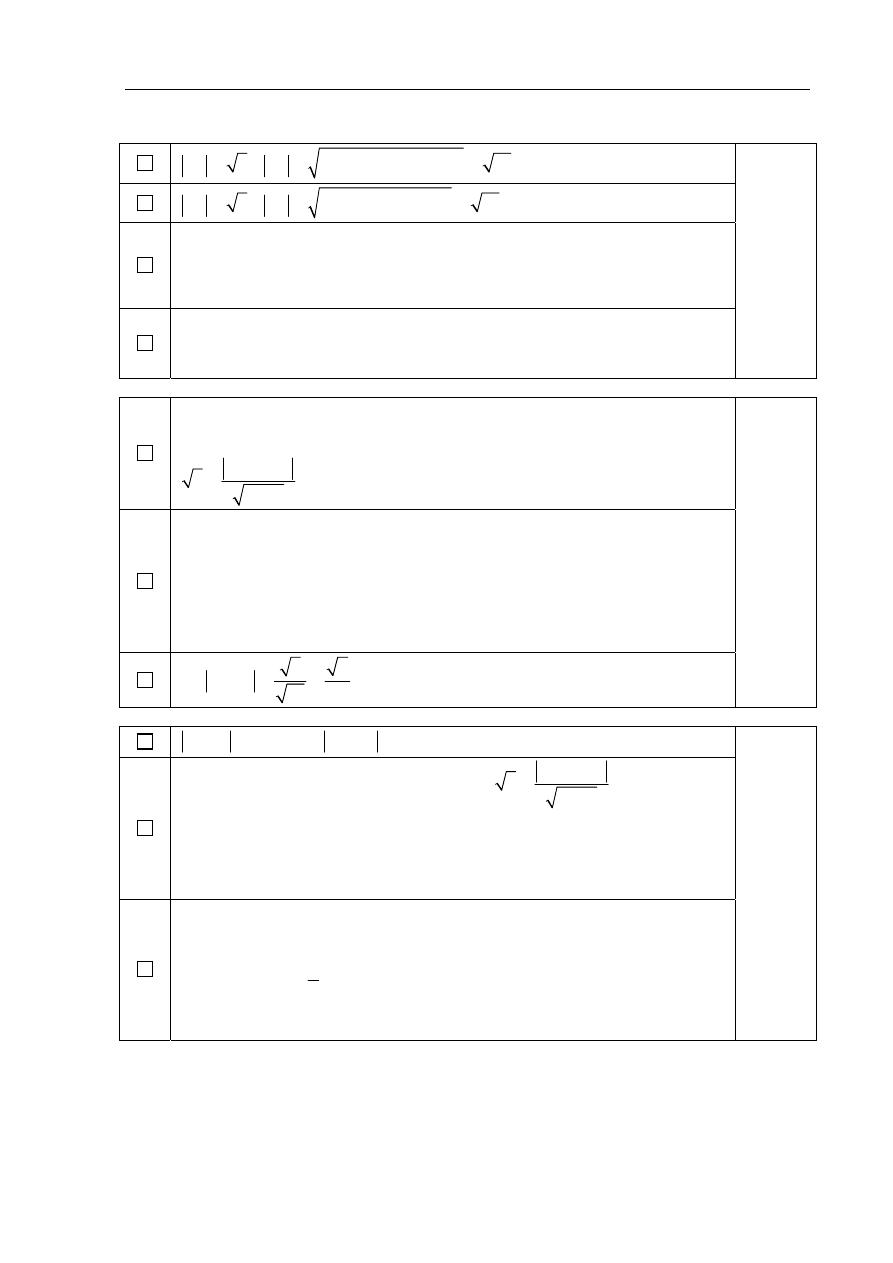
Zadanie 7. (4 pkt)
Oblicz miarę kąta między stycznymi do okręgu

0

3

2

2

2

2











y

x

y

x

poprowadzonymi

przez punkt

)

0

,

2

(



A

.

Sytuację opisaną w zadaniu przedstawia rysunek:

-3

-2

-1

1

2

3

-4

-3

-2

-1

1

2

x

y

A

S

B

C

-3

-2

-1

1

2

3

-2

-1

1

2

3

4

x

y

A

S

B

C

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

7

5

SB



,



 



2

2

1 2

1 0

10

SA



 

  



5

SB



,



 



2

2

1 2

1 0

10

SA



 

 



Zapisujemy równanie prostej przechodzącej przez punkt

)

0

,

2

(



A

i stycznej do okręgu:

2

0

ax

y

a

 



w zależności od parametru

a

, gdzie

a

oznacza

współczynnik kierunkowy prostej stycznej.

Zapisujemy równanie kierunkowe prostej przechodzącej przez punkt

)

0

,

2

(



A

:

2

y

a ax





w zależności od parametru

a

, gdzie

a

oznacza

współczynnik kierunkowy prostej stycznej.

1 p.

Ponieważ promień okręgu jest równy odległości środka okręgu

S

od stycznej, więc korzystając ze wzoru na odległość punktu od prostej
otrzymujemy równanie

2

1 2

5

1

a

a

a

 





Zapisujemy układ równań

2

2

2

2

3

0

2

x

y

x

y

y

ax

a

 





 









i doprowadzamy

do równania kwadratowego z niewiadomą

x

:









2

2

2

2

2

2

3

0

x

ax

a

x

ax

a











 

czyli



 



2

2

2

2

1

4

2

2

4

4

3

0

x

a

x

a

a

a

a







 



 

.

5

2

sin

2

10

SAB







1 p.

45

SAB







czyli

90

BAC

 



Po podniesieniu obu stron równania

2

1 2

5

1

a

a

a

 





do kwadratu

i przekształceniach otrzymujemy równanie kwadratowe

2

2

1

0

a

a

  

,

którego pierwiastkami są:

1

2

2 lub

1

a

a



 

. Ponieważ

1

a

i

2

a

oznaczają współczynniki kierunkowe prostych stycznych, zatem styczne
są do siebie prostopadłe.

Równanie



 



2

2

2

2

1

4

2

2

4

4

3

0

x

a

x

a

a

a

a







 



 

ma dokładnie

jedno rozwiązanie, jeśli

0

 

, czyli

2

2

3

2

0

a

a



 

, co zachodzi dla

1

2

1

2 lub

2

a

a

 



. Ponieważ

1

a

i

2

a

oznaczają współczynniki

kierunkowe prostych stycznych, zatem styczne są do siebie
prostopadłe.

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

8

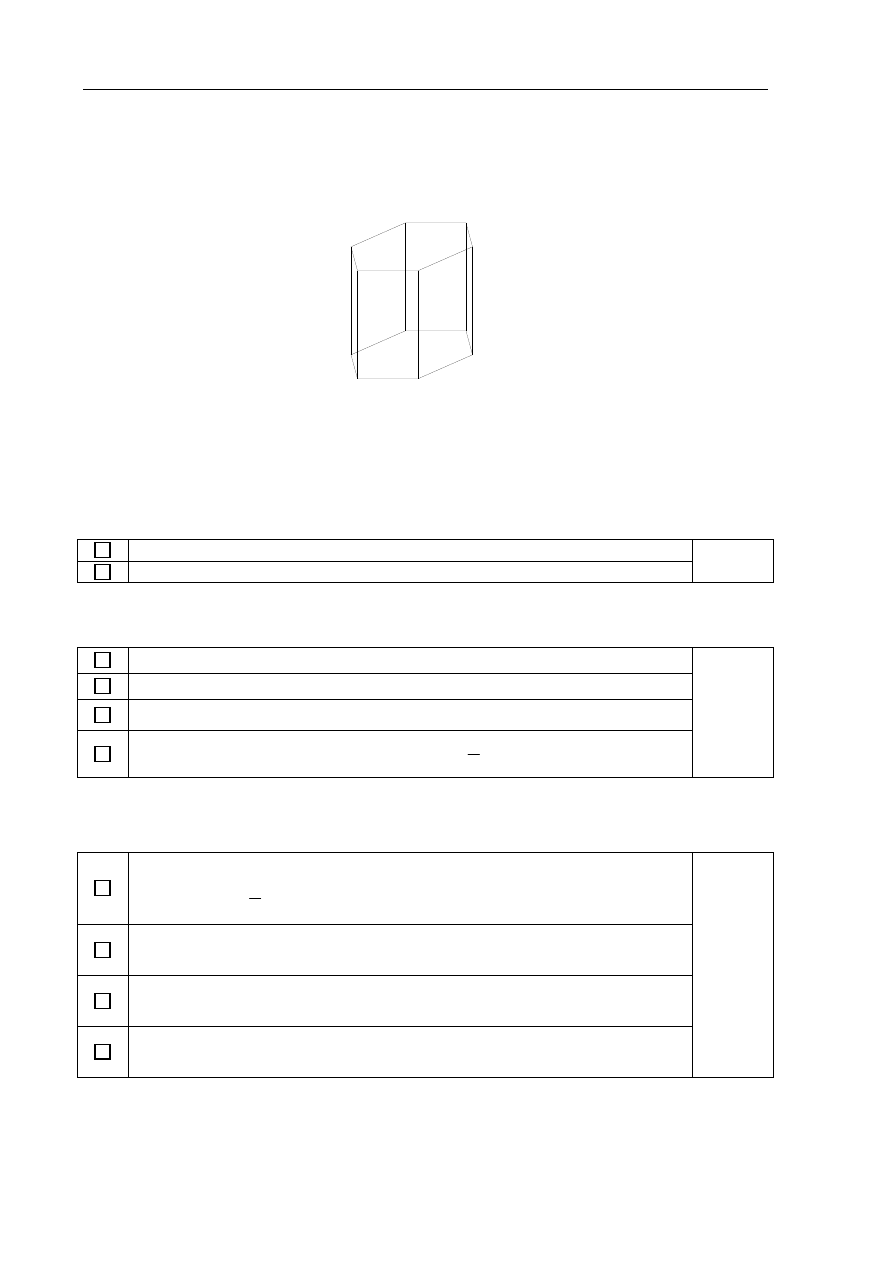
Zadanie 8. (4 pkt)

Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma
długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole

powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.

Wprowadzamy oznaczenia:

a

– długość krawędzi podstawy graniastosłupa,

h

– długość krawędzi bocznej

graniastosłupa.

Z tego, że suma długości wszystkich krawędzi graniastosłupa prawidłowego
sześciokątnego jest równa 24, mamy:

6

12

24

a

h





.

12

6

24

a

h





.

1 p.

Pole

P

powierzchni bocznej jest równe

6

P

ah



dla

 

2

,

0



a

oraz

 

4

,

0



h

, przy czym

4 2

h

a

 

.

 

2

,

0



a

oraz

 

4

,

0



h

, przy czym

2

a

h

 

.

 

0, 4

a



oraz

 

0, 2

h



, przy czym

4 2

a

h

 

.

 

0, 4

a



oraz

 

0, 2

h



, przy czym

2

2

a

h

 

.

1 p.

Aby wyznaczyć długość krawędzi podstawy graniastosłupa, którego pole powierzchni
bocznej jest największe, zapisujemy funkcję

P

w zależności

od zmiennej

a

:

 

6

2

2

a

P a

a

















od zmiennej

h

:

 





6

4 2

P h

h

h





od zmiennej

a

:

 





6

4 2

P a

a

a





od zmiennej

h

:

 





6

2

P h

h

h





1 p.

a

h

Egzamin maturalny z matematyki

Poziom rozszerzony

9

Pole

P

ma największą wartość, gdy

1

a



.

1

h



i

2

a



.

1

h



i

1

a



.

2

a



.

1 p.

Zadanie 9. (4 pkt)
Oblicz, ile jest liczb ośmiocyfrowych, w zapisie których nie występuje zero, natomiast

występują dwie dwójki i występują trzy trójki.

Dwie dwójki mogą wystąpić na

8 7

56

 

miejscach.

Dwie dwójki mogą wystąpić na

8

28

2

 



 

 

miejscach.

1 p.

Trzy trójki mogą wystąpić na

6

20

3

 



 

 

miejscach.

Trzy

trójki

mogą wystąpić na

5 6

30

 

miejscach.

1 p.

Na pozostałych trzech miejscach mogą wystąpić cyfry:

1, 4, 5, 6, 7, 8, 9

. Liczba ciągów

trójelementowych ze zbioru siedmioelementowego jest równa

3

7

7

3

5 6 7

 

1 p.

Jest

7

7

2

28 20 3

3 4 5 7

1224720



     

liczb spełniających warunki

zadania.

Jest

2

2

2

28 20 7 6 5

6 4 5 7

117600



      



liczb spełniających warunki

zadania.

Jest





2

3

56 30 7 6 5

2

5 6 7

352800

    

  



liczb spełniających warunki

zadania.

Jest

3

2

4

28 20 7

4 5 7

192080







 



liczb spełniających warunki zadania.

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

10

Zadanie 10. (3 pkt)
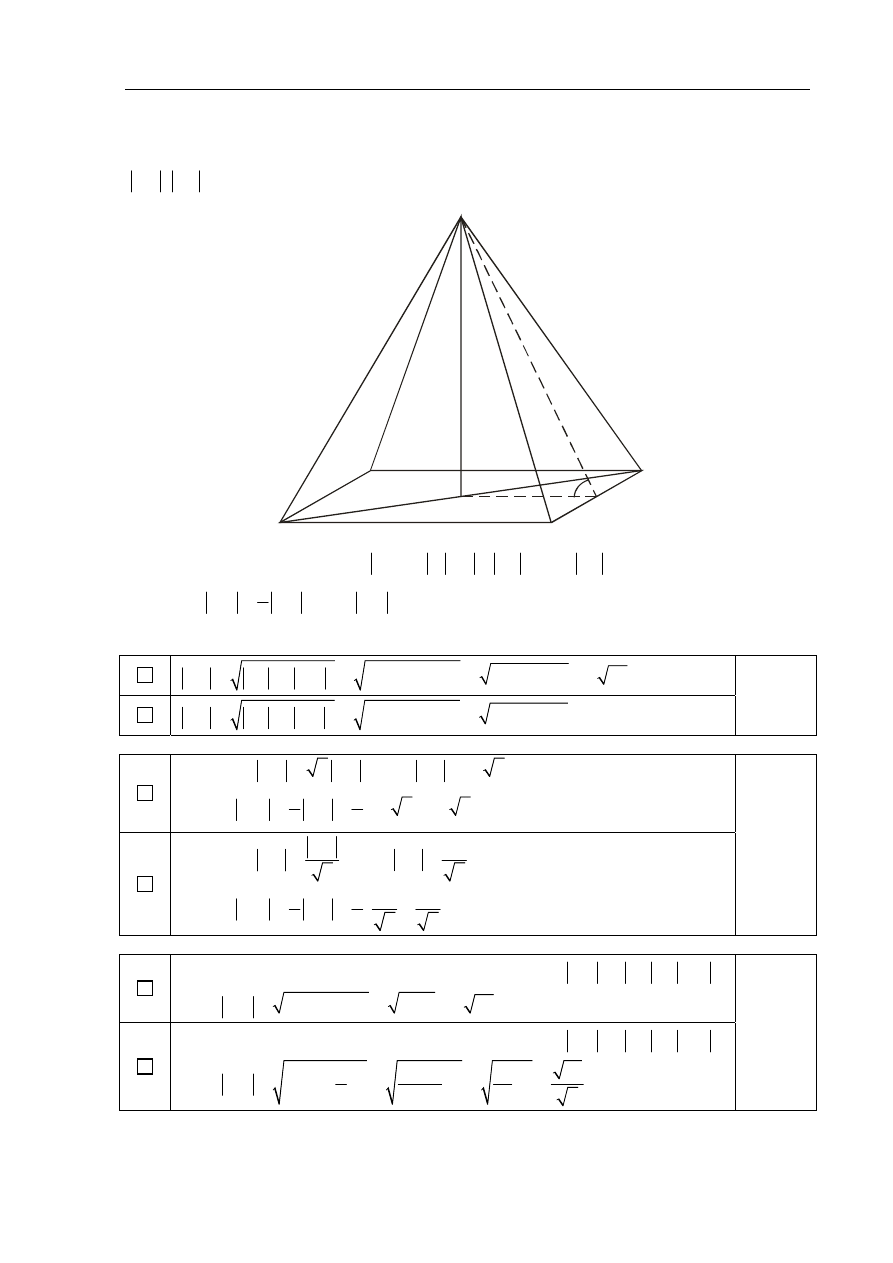
Dany jest czworokąt wypukły

ABCD

niebędący równoległobokiem. Punkty

M

,

N

są

odpowiednio środkami boków

AB

i

CD

. Punkty

P

,

Q

są odpowiednio środkami

przekątnych

AC

i

BD

. Uzasadnij, że

MQ PN



.

Trójkąty

ACD

i

DBC

są podobne, więc odcinki łączące środki

odpowiednich boków tych trójkątów są równe, czyli

NP

NQ



.

Punkty

N

i

P

są środkami boków

DC

i

AC

trójkąta

ADC

, więc

NP AD



.

1 p.

Trójkąty

BAD

i

ABC

są podobne, więc odcinki łączące środki

odpowiednich boków tych trójkątów są równe, czyli

PM

QM



.

Punkty

M

i

Q

są środkami boków

AB

i

DB

trójkąta

ABD

, więc

MQ AD



.

1 p.

Ponieważ

NP

NQ



oraz

PM

QM



, więc czworokąt

PNQM

jest

rombem. Zatem

NP MQ



.

Ponieważ

NP AD



oraz

AD MQ



, więc

NP MQ



.

1 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

11

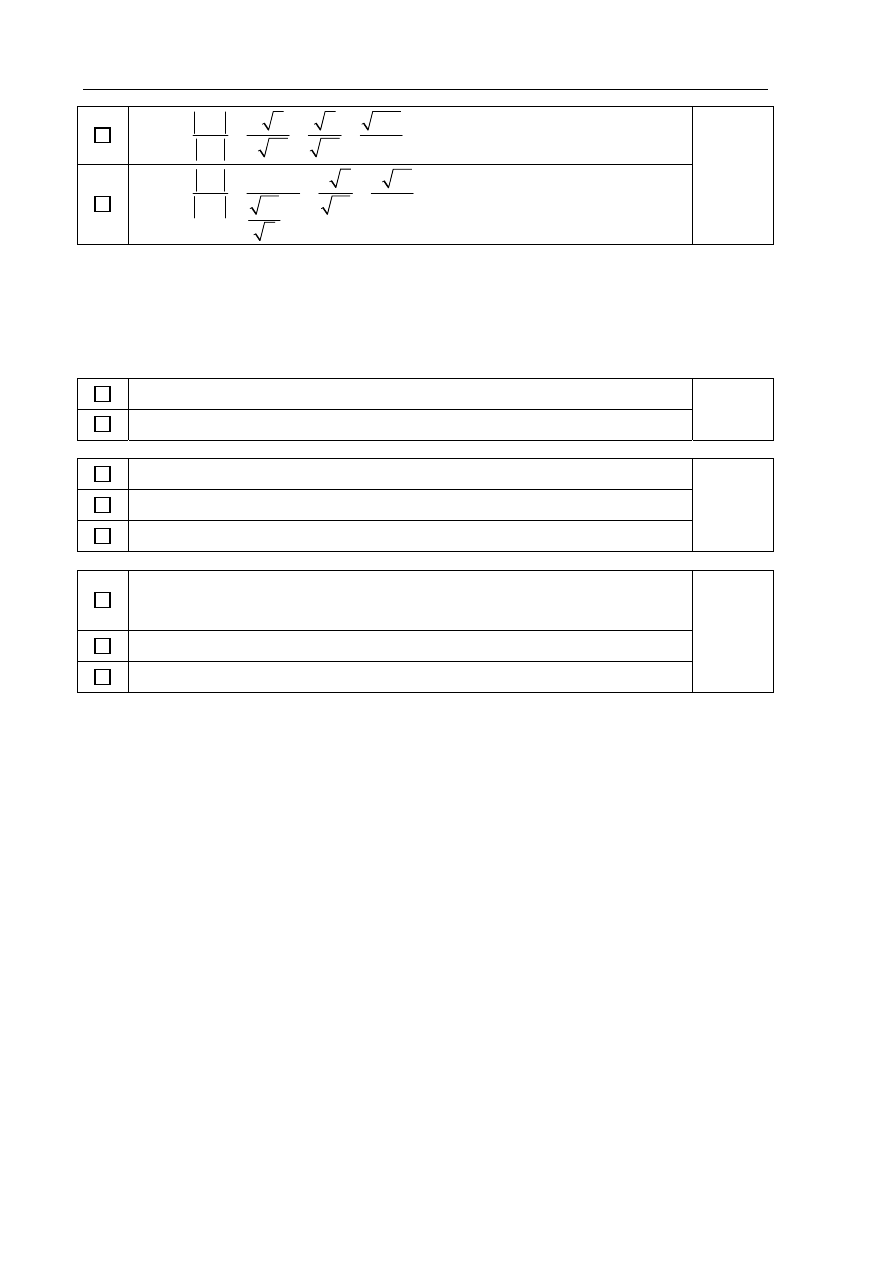
Zadanie 11. (6 pkt)
Dany jest ostrosłup prawidłowy czworokątny

ABCDS

o podstawie

ABCD

. W trójkącie

równoramiennym

ASC

stosunek długości podstawy do długości ramienia jest równy

:

6 : 5

AC

AS



. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

A

B

C

D

S

H

M

Wprowadzamy oznaczenia:

HMS



 

,

6

AC

SC

x





,

5

AS

x



.

Ponieważ

1

2

AH

AC



, stąd

3

AH

x



.

Z twierdzenia Pitagorasa dla trójkąta

CHS

otrzymujemy:

   

2

2

2

2

2

2

5

3

25

9

34

SH

CS

HC

x

x

x

x

x















   

2

2

2

2

2

2

5

3

25

9

4

SH

CS

HC

x

x

x

x

x















1 p.

Ponieważ

2

AC

BC



, stąd

6

2

BC

x



.

Zatem

1

1

6

2

3

2

2

2

CM

BC

x

x



 



.

Ponieważ

2

AC

BC



, stąd

6

2

x

BC



.

Zatem

1

1 6

3

2

2

2

2

x

x

CM

BC



 



.

2 p.

Z twierdzenia Pitagorasa dla trójkąta

MCS

mamy

2

2

2

SM

CS

CM





.

Stąd

2

2

2

25

18

34

34

SM

x

x

x

x









.

Z twierdzenia Pitagorasa dla trójkąta

MCS

mamy

2

2

2

SM

CS

CM





.

Stąd

2

2

2

2

9

50 9

41

41

25

2

2

2

2

SM

x

x

x

x

x















2 p.

Egzamin maturalny z matematyki

Poziom rozszerzony

12

7

7

238

sin

34

34

34

SM

x

SH

x











.

4

4 2

4 82

sin

41

41

41

2

SH

x

SM

x













.

1 p.

Zadanie 12. (3 pkt)

A

,

B

są zdarzeniami losowymi zawartymi w



. Wykaż, że jeżeli

 

0, 9

P A



i

 

0, 7

P B



, to





'

0, 3

P A

B





(

'

B

oznacza zdarzenie przeciwne do zdarzenia

B

).

 

'

0, 3

P B



.





   

P A

B

P A P B







, więc





0, 9 0, 7

0, 63

P A

B









1 p.





   

'

'

P A

B

P A P B







Z faktu, że

'

'

A

B

B





wynika, że





 

'

'

P A

B

P B





.













'

P A

B

P A

B

P A

B











1 p.

Ponieważ





1

P A

B





i





0, 63

P A

B





,

więc





'

1 0, 63

0, 27

0, 3

P A

B



 





   

'

0, 9 0, 3

0, 27

0, 3

P A P B











Ponieważ





 

'

'

P A

B

P B





oraz

 

'

0, 3

P B



, więc





'

0, 3

P A

B





.

1 p.